一线三等角专题
一线三等角例题加答案

一线三等角例题问题描述给定一个等边三角形ABC,已知点D、E、F分别是BC、CA和AB的中点。
连接AD、BE和CF,求证:AD、BE和CF 是等边三角形的边。
证明要证明AD、BE和CF是等边三角形的边,我们需要证明三个长度相等的线段,即AD=BE=CF。
证明AD=BE连接线段AC,并延长线段BE交线段AC于点G,如下图所示:graph TDA((A)) -- AD --> D((D))A((A)) -- AC --> C((C))A((A)) -- AB --> B((B))B((B)) -- BE --> E((E))G((G)) -- BE --> E((E))C((C)) -- CF --> F((F))G((G)) -- CG --> C((C))三角形ACG和BEG,它们共有一条边AC,并且根据各边的定义,两个三角形的另外两条边DG和GE分别平行于AC和BE。
因此,根据平行线间的性质,有:AD/BE = DG/GE而根据题意,DG=AC,GE=BE,因此:AD/BE = AC/BE = 1所以,AD=BE。
证明AD=CF连接线段AB,并延长线段CF交线段AB于点H,如下图所示:graph TDA((A)) -- AD --> D((D))H((H)) -- CF --> F((F))A((A)) -- AC --> C((C))A((A)) -- AB --> B((B))B((B)) -- BE --> E((E))H((H)) -- AH --> A((A))三角形AHC和DFC,它们共有一条边AC,并且根据各边的定义,两个三角形的另外两条边AH和DF分别平行于AB和CF。
因此,根据平行线间的性质,有:AD/CF = AH/DF而根据题意,AH=AB,DF=CF,因此:AD/CF = AB/CF = 1所以,AD=CF。
专题03 一线三等角模型证全等(解析版)
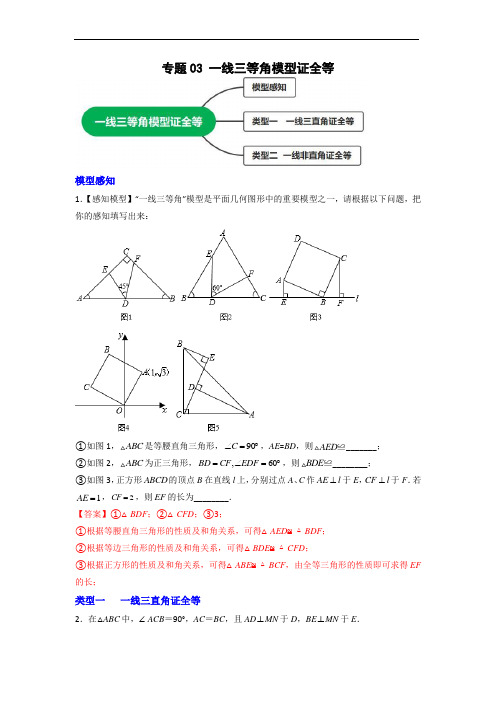
专题03 一线三等角模型证全等模型感知1.【感知模型】“一线三等角”模型是平面几何图形中的重要模型之一,请根据以下问题,把你的感知填写出来:①如图1,ABC 是等腰直角三角形,90C ∠=︒,AE =BD ,则AED ≌_______; ②如图2,ABC 为正三角形,,60BD CF EDF =∠=︒,则BDE ≌________;③如图3,正方形ABCD 的顶点B 在直线l 上,分别过点A 、C 作AE l ⊥于E ,CF l ⊥于F .若1AE =,2CF =,则EF 的长为________.【答案】①△BDF ;②△CFD ;③3;①根据等腰直角三角形的性质及和角关系,可得△AED ≌△BDF ; ②根据等边三角形的性质及和角关系,可得△BDE ≌△CFD ;③根据正方形的性质及和角关系,可得△ABE ≌△BCF ,由全等三角形的性质即可求得EF 的长;类型一 一线三直角证全等2.在△ABC 中,∠ACB =90°,AC =BC ,且AD ⊥MN 于D ,BE ⊥MN 于E .(1)直线MN绕点C旋转到图(1)的位置时,求证:DE=AD+BE;(2)当直线MN绕点C旋转到图(2)的位置时,试问DE、AD、BE具有怎样的等量关系?请直接写出这个等量关系(不写证明过程);(3)当直线MN绕点C旋转到图(3)的位置时,试问DE、AD、BE具有怎样的等量关系?请直接写出这个等量关系(不写证明过程).【答案】(1)证明见详解(2)DE+BE=AD.理由见详解(3)DE=BE-AD(或AD=BE-DE,BE=AD+DE等).理由见详解.【解析】【分析】(1)根据题意由垂直得∠ADC=∠BEC=90°,由同角的余角相等得:∠DAC=∠BCE,因此根据AAS可以证明△ADC≌△CEB,结合全等三角形的对应边相等证得结论;(2)由题意根据全等三角形的判定定理AAS推知△ACD≌△CBE,然后由全等三角形的对应边相等、图形中线段间的和差关系以及等量代换证得DE+BE=AD;(3)由题意可知DE、AD、BE具有的等量关系为:DE=BE-AD(或AD=BE-DE,BE=AD+DE 等).证明的方法与(2)相同.(1)证明:如图1,∵AD⊥MN,BE⊥MN,∴∠ADC=∠BEC=90°,∴∠DAC+∠ACD=90°,∵∠ACB=90°,∴∠ACD+∠BCE=90°,∴∠DAC=∠BCE,在△ADC和△CEB中,∵ADC BECDAC BCE AC BC∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADC≌△CEB;∴DC =BE ,AD =EC , ∵DE =DC +EC , ∴DE =BE +AD . (2)解:DE +BE =AD .理由如下: 如图2,∵∠ACB =90°, ∴∠ACD +∠BCE =90°. 又∵AD ⊥MN 于点D , ∴∠ACD +∠CAD =90°, ∴∠CAD =∠BCE . 在△ACD 和△CBE 中, 90ADC CEB CAD BCEAC BC ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩, ∴△ACD ≌△CBE (AAS ), ∴CD =BE ,AD =CE ,∴DE +BE =DE +CD =EC =AD ,即DE +BE =AD . (3)解:DE =BE -AD (或AD =BE -DE ,BE =AD +DE 等).理由如下: 如图3,易证得△ADC ≌△CEB , ∴AD =CE ,DC =BE ,∴DE =CD -CE =BE -AD ,即DE =BE -AD . 【点睛】本题属于几何变换综合题,考查等腰直角三角形和全等三角形的性质和判定,熟练掌握全等三角形的四种判定方法是关键:SSS 、SAS 、AAS 、ASA ;在证明线段的和与差时,利用全等三角形将线段转化到同一条直线上得出结论. 3.通过对下面数学模型的研究学习,解决下列问题:(1)如图1,点A 在直线l 上,90,BAD AB AD ∠=︒=,过点B 作BC l ⊥于点C ,过点D 作DE l⊥交于点E .由12290D ∠+∠=∠+∠=︒,得1D ∠=∠.又90BCA AED ∠=∠=︒,可以推理得到()ABC DAE AAS ≌.进而得到结论:AC =_____,BC =_____.我们把这个数学模型称为“K 字”模型或“一线三直角”模型;(2)如图2,90,,,BAD MAN AB AD AM AN BM l ∠=∠=︒==⊥于点C ,NG l ⊥于点G ,由(1)易知NG =_______,ND 与直线l 交于点P ,求证:NP DP =. 【答案】(1)DE ,AE ; (2)AC .证明见详解. 【解析】 【分析】(1)根据(AAS)≌ABC DAE ,得出AC =DE ,BC =AE 即可;(2)过D 作DE ⊥直线l 于E ,先证△MCA ≌△AGN (AAS ),得出AC =NG ,由(1)知(AAS)≌ABC DAE ,得出AC =DE ,再证△NGP ≌△DEP (AAS )即可.(1) 解:∵(AAS)≌ABC DAE ,∴AC =DE ,BC =AE , 故答案为DE ,AE ; (2)证明:过D 作DE ⊥直线l 于E , ∵90MAN ∠=︒, ∴∠CAM +∠NAG =90°, ∵BM ⊥l , ∴∠MCA =90°, ∴∠M +∠CAM =90°, ∴∠M =∠NAG , ∵NG l ⊥, ∴∠AGN =90°, 在△MCA 和△AGN 中, MCA AGNM GAN MA AN ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△MCA ≌△AGN (AAS ), ∴AC =NG ,由(1)知(AAS)≌ABC DAE , ∴AC =DE ,在△NGP 和△DEP 中, 90NGP DEP GPN EPDNG DE ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩, ∴△NGP ≌△DEP (AAS ) ∴NP =DP , 故答案为AC .【点睛】本题考查一线三直角全等问题,掌握余角性质,三角形全等判定与性质是解题关键.类型二 一线非直角证全等4.(1)如图1,直线m 经过等边三角形ABC 的顶点A ,在直线m 上取两点D ,E ,使得∠ADB =60°,∠AEC =60°.求证:BD +CE =DE ;(2)将(1)中的直线m 绕着点A 逆时针方向旋转一个角度到如图2的位置,并使∠ADB =120°,∠AEC =120°.若BD =3,CE =7,求DE 的长.【答案】(1)证明见解析;(2)DE =4 【解析】 【分析】(1)利用等边三角形的性质和已知角的度数,证明∠ABD =∠CAE ,利用AAS 证明△ABD ≌△CAE ,推出BD =AE ,AD =CE ,即可证明;(2)同(1)证明△ABD ≌△CAE ,推出BD =AE ,AD =CE ,则DE =AD -AE =CE -BD .(1)证明:∵△ABC 为等边三角形, ∴AB =AC ,∠BAC =60°, ∴∠DAB +∠CAE =120° 又∠ADB =∠AEC =60°, ∴∠ABD +∠DAB =120°, ∴∠ABD =∠CAE , ∴△ABD ≌△CAE (AAS ), ∴BD =AE ,AD =CE , ∴DE =AD +AE =BD +CE . (2)解:∵△ABC 为等边三角形, ∴AB =AC ,∠BAC =60°, ∴∠BAD +∠CAE =60° 又∠ADB =∠AEC =120°, ∴∠ABD +∠BAD =60°, ∴∠ABD =∠CAE , ∴△ABD ≌△CAE (AAS ), ∴BD =AE ,AD =CE , ∴DE =AD -AE =CE -BD =4. 【点睛】本题考查等边三角形的性质,全等三角形的判定和性质,读懂题意,找出图形中的全等三角形是解题的关键.5.已知:CD 是经过BCA ∠的顶点C 的一条直线,CA CB =.E 、F 是直线CD 上两点,BEC CFA α∠=∠=∠.(1)若直线CD 经过BCA ∠的内部,BCD ACD ∠>∠.①如图1,90BCA ∠=︒,90α∠=︒,直接写出BE ,EF ,AF 间的等量关系:__________. ②如图2,α∠与BCA ∠具有怎样的数量关系,能使①中的结论仍然成立?写出α∠与BCA ∠的数量关系,并对结论进行证明;(2)如图3,若直线CD 经过BCA ∠的外部,BCA α∠=∠,①中的结论是否成立?若成立,进行证明;若不成立,写出新结论并进行证明.【答案】(1)①EF BE AF =-;②180BCA α∠+∠=︒,证明见解析;(2)不成立,EF FA BE =+,理由见解析【解析】 【分析】(1)①根据题意,推导得ACF CBE ∠=∠,通过证明ACF CBE ∠≌△,得BE CF =,CE AF =,结合EF CF CE =-,即可得到答案;②结合题意,根据三角形内角和性质,推导得CBE ACF ∠=∠,通过证明BCE CAF ≌△△,即可完成证明;(2)根据题意,结合三角形内角和的性质,推导得CBE ACF ∠=∠,通过证明BCE CAF ≌△△,得EC FA =,BE CF =;根据EF CE CF =+,即可得到答案. 【详解】(1)①∵90BCA ∠=︒,90α∠=︒∴90ACF BCE ∠+∠=︒,90CBE BCE ∠+∠=︒ ∴ACF CBE ∠=∠ ∴BEC CFA ACF CBE CA CB ∠=∠⎧⎪∠=∠⎨⎪=⎩∴ACF CBE ∠≌△ ∴BE CF =,CE AF = ∵EF CF CE =- ∴EF BE AF =-;②满足180BCA α∠+∠=︒,理由如下:∵180CBE BCE BEC ∠+∠+∠=︒,180BCA α∠+∠=︒ ∴CBE BCE BEC BCA α∠+∠+∠=∠+∠ ∴CBE BCE BCE ACF αα∠+∠+∠=∠+∠+∠ ∴CBE ACF ∠=∠∵BEC CFA ∠=∠,CA CB =, ∴BCE CAF ≌△△∴BE CF =,CE AF = ∵EF CF CE =-, ∴EF BE AF =-(2)不成立,EF BE AF =+,理由如下:∵180CBE BCE BEC ∠+∠+∠=︒,180BCE BCA ACF ∠+∠+∠=︒,BEC CFA BCA α∠=∠=∠=∠∴CBE BCE BCE ACF αα∠+∠+∠=∠+∠+∠ ∴CBE ACF ∠=∠∵BEC CFA ∠=∠,CA CB =, ∴BCE CAF ≌△△ ∴BE CF =,CE AF = ∵EF CF CE =+, ∴EF BE AF =+ 【点睛】本题考查了三角形内角和、余角、全等三角形的知识;解题的关键是熟练掌握三角形内角和、全等三角形的性质,从而完成求解.类型三 综合运用6.(1)某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图1,已知:在ABC 中,90BAC ∠=︒,AB AC =,直线l 经过点A ,BD ⊥直线l ,CE ⊥直线l ,垂足分别为点D ,E .求证:DE BD CE =+.(2)组员小明想,如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在ABC 中,AB AC =,D ,A ,E 三点都在直线l 上,并且有BDA AEC BAC α∠=∠=∠=,其中α为任意锐角或钝角.请问结论DE BD CE =+是否成立?若成立,请你给出证明;若不成立,请说明理由.(3)数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,过ABC 的边AB ,AC 向外作正方形ABDE 和正方形ACFG ,AH 是BC 边上的高.延长HA 交EG 于点I .若7AEG S =△,则AEI S =△______.【答案】(1)见解析;(2)结论成立,理由见解析;(3)3.5 【解析】【分析】(1)由条件可证明△ABD ≌△CAE ,可得DA =CE ,AE =BD ,可得DE =BD +CE ;(2)由条件可知∠BAD +∠CAE =180°-α,且∠DBA +∠BAD =180°-α,可得∠DBA =∠CAE ,结合条件可证明△ABD ≌△CAE ,同(1)可得出结论;(3)由条件可知EM =AH =GN ,可得EM =GN ,结合条件可证明△EMI ≌△GNI ,可得出结论I 是EG 的中点. 【详解】解:(1)证明:如图1中,∵BD ⊥直线l ,CE ⊥直线l , ∴∠BDA =∠CEA =90°, ∵∠BAC =90°, ∴∠BAD +∠CAE =90°, ∵∠BAD +∠ABD =90°, ∴∠CAE =∠ABD , 在△ADB 和△CEA 中, ABD CAE BDA CEA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△ADB ≌△CEA (AAS ), ∴AE =BD ,AD =CE , ∴DE =AE +AD =BD +CE . (2)解:成立. 理由:如图2中, ∵∠BDA =∠BAC =α,∴∠DBA +∠BAD =∠BAD +∠CAE =180°-α, ∴∠DBA =∠CAE , 在△ADB 和△CEA 中, BDA AEC DBA CAE AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△ADB ≌△CEA (AAS ), ∴AE =BD ,AD =CE , ∴DE =AE +AD =BD +CE .(3)如图3,过E 作EM ⊥HI 于M ,GN ⊥HI 的延长线于N .∴∠EMI =∠GNI =90°由(1)和(2)的结论可知EM =AH =GN ∴EM =GN在△EMI 和△GNI 中, GIN EIM EM GNGNI EMI ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△EMI ≌△GNI (AAS ), ∴EI =GI , ∴I 是EG 的中点. ∴S △AEI =12S △AEG =3.5. 故答案为:3.5. 【点睛】本题是四边形综合题,考查了全等三角形的判定和性质,正方形的性质,直角三角形的性质,熟练掌握全等三角形的判定与性质是解题的关键.7.(1)如图(1),已知:在△ABC 中,∠BAC =90°,AB =AC ,直线m 经过点A ,BD ⊥直线m , CE ⊥直线m ,垂足分别为点D 、E .证明∶DE =BD +CE .(2)如图(2),将(1)中的条件改为:在△ABC 中,AB =AC ,D 、A 、E 三点都在直线m 上,并且有∠BDA =∠AEC =∠BAC =α,其中α为任意锐角或钝角.请问结论DE =BD +CE 是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)拓展与应用:如图(3),D 、E 是D 、A 、E 三点所在直线m 上的两动点(D 、A 、E 三点互不重合),点F 为∠BAC 平分线上的一点,且△ABF 和△ACF 均为等边三角形,连接BD 、CE ,若∠BDA =∠AEC =∠BAC ,试判断△DEF 的形状.【答案】(1)见解析(2)成立,证明见解析(3)△DEF为等边三角形,证明见解析【解析】【分析】(1)因为DE=DA+AE,故由AAS证△ADB≌△CEA,得出DA=EC,AE=BD,从而证得DE=BD+CE.(2)成立,仍然通过证明△ADB≌△CEA,得出BD=AE,AD=CE,所以DE=DA+AE=EC+BD.(3)由△ADB≌△CEA得BD=AE,∠DBA =∠CAE,由△ABF和△ACF均等边三角形,得∠ABF=∠CAF=60°,FB=F A,所以∠DBA+∠ABF=∠CAE+∠CAF,即∠DBF=∠F AE,所以△DBF≌△EAF,所以FD=FE,∠BFD=∠AFE,再根据∠DFE=∠DF A+∠AFE=∠DF A+∠BFD=600得到△DEF是等边三角形.【详解】解:(1)证明:∵BD⊥直线m,CE⊥直线m,∴∠BDA=∠CEA=90°.∵∠BAC=90°,∴∠BAD+∠CAE=90°.∵∠BAD+∠ABD=90°,∴∠CAE=∠ABD.又AB=AC,∴△ADB≌△CEA(AAS).∴AE=BD,AD=CE.∴DE=AE+AD=BD+CE.(2)成立.证明如下:∵∠BDA =∠BAC=α,∴∠DBA+∠BAD=∠BAD +∠CAE=180°-α.∴∠DBA=∠CAE.∵∠BDA=∠AEC=α,AB=AC,∴△ADB≌△CEA(AAS).∴AE=BD,AD=CE.∴DE=AE+AD=BD+CE.(3)△DEF为等边三角形.理由如下:由(2)知,△ADB≌△CEA,BD=AE,∠DBA =∠CAE,∵△ABF和△ACF均为等边三角形,∴∠ABF=∠CAF=60°.∴∠DBA+∠ABF=∠CAE+∠CAF.∴∠DBF =∠F AE . ∵BF =AF ,∴△DBF ≌△EAF (ASA ). ∴DF =EF ,∠BFD =∠AFE .∴∠DFE =∠DF A +∠AFE =∠DF A +∠BFD =60°. ∴△DEF 为等边三角形. 【点睛】此题考查了全等三角形的性质和判定,等边三角形的性质和判定,解题的关键是熟练掌握全等三角形的性质和判定,等边三角形的性质和判定. 8.通过对下面数学模型的研究学习,解决下列问题: 【模型呈现】(1)如图,90BAD ∠=︒,AB AD =,过点B 作BC AC ⊥于点C ,过点D 作DE AC ⊥于点E .由12290D ∠+∠=∠+∠=︒,得1D ∠=∠.又90ACB AED ∠=∠=︒,可以推理得到ABC DAE ∆∆≌.进而得到AC =__________,BC AE =.我们把这个数学模型称为“K 字”模型或“一线三等角”模型;【模型应用】(2)如图,90BAD CAE ∠=∠=︒,AB AD =,AC AE =,连接BC ,DE ,且BC AF ⊥于点F ,DE 与直线AF 交于点G .求证:点G 是DE 的中点;【深入探究】(3)如图,已知四边形ABCD 和DEGF 为正方形,AFD ∆的面积为1S ,DCE ∆的面积为2S ,则有1S __________2S (填“>、=、<”)(4)如图,点A 、B 、C 、D 、E 都在同一条直线上,四边形ABAH 、KCMG 、DENM 都是正方形,若该图形总面积是16,正方形KCMG 的面积是4,则HKG 的面积是__________.【答案】(1)DE ;(2)见解析;(3)=;(42 【解析】 【分析】(1)根据全等三角形的性质即可得到答案;(2)分别过点D 和点E 作DM FG ⊥于点M ,EN FG ⊥于点N ,由(1)中结论可得到AF =DM ,AF =EN ,然后只需要证明DMG ENG △≌△即可得到答案;(3)过点D 作DO ⊥AF 交AF 于O ,过点E 错EN ⊥OD 交OD 延长线于N ,过点C 作CM ⊥OD 交OD 延长线于M ,然后同(2)中证明AOD DMC △≌△,FOD DNE △≌△,ENP CMP △≌△即可得到答案;(4)同(3)中的方法可以证明GHK KBC CMD GMN S S S S =△△△△==,然后利用勾股定理得到ABKH MDEN KCMG S S S +=正方形正方形正方形即可得到答案.【详解】解:(1)∵ABC DAE △≌△ ∴AC DE =(2)分别过点D 和点E 作DM FG ⊥于点M ,EN FG ⊥于点N ,∴90DAM ADM ∠+∠=︒, ∵90BAD ∠=︒,∴90BAF DAM ∠+∠=︒, ∴BAF ADM ∠=∠ ∵BC AF ⊥,∴90BFA AMD ∠=∠=︒,在ABF ∆和DAM ∆中,BAF ADN ∠=∠,BFA AMD ∠=∠,BA AD =,∴ABF DAM ∆∆≌, ∴AF DM = 同理AF EN = ∴DM EN =,∵DM FG ⊥,EN FG ⊥,∴DMG ENG ∠=∠,在DMG △和ENG △中,DGM EGN ∠=∠,DMG ENG ∠=∠,DM EN =,∴DMG ENG △≌△∴DG EG =,即点G 是DE 的中点;(3)如图所示,过点D 作DO ⊥AF 交AF 于O ,过点E 作EN ⊥OD 交OD 延长线于N ,过点C 作CM ⊥OD 交OD 延长线于M ∵四边形ABCD 与四边形DEGF 都是正方形 ∴∠ADC =∠90°,AD =DC ,DF =DE ∵DO ⊥AF ,CM ⊥OD∴∠AOD =∠CMD =90°,∠OAD +∠ODA =90°,∠CDM +∠DCM =90°, 又∵∠ODA +∠DCM =90° ∴∠A DO =∠DCM ∴AOD DMC △≌△ ∴AOD DMC S S =△△,OD =MC 同理可以证明FOD DNE △≌△ ∴FOD DNE S S =△△,OD =NE ∴MC =NE∵EN ⊥OD ,CM ⊥OD ,∠EPN =∠CMP ∴ENP CMP △≌△ ∴ENP CMP S S △△=∵ADF AOD FOD S S S +△△△=,DCE DCM CMP DEN ENP S S S S S -++△△△△△= ∴=DCE DCM DEN AOD FOD S S S S S ++△△△△△= ∴DCE ADF S S △△=即12S S ;(4)同(3)中的方法可以证明GHK KBC CMD GMN S S S S =△△△△==,且KBC CDM △≌△ 即BC DM =由勾股定理得:222KB BC KC += ∴222KB DM KC +=∴ABKH MDEN KCMG S S S +=正方形正方形正方形∵图形总面积是16,正方形KCMG 的面积是4 ∴=4ABKH MDEN KCMG S S S +=正方形正方形正方形 ∴=8GHK KBC CMD GMN S S S S +△△△△++ ∴2GHK S △=【点睛】本题主要考查了全等三角形的性质与判定,正方形的性质,解题的关键在于能够熟练掌握全等三角形的性质与判定.9.(1)【问题情境】八上《伴你学》第138页有这样一个问题:如图1,把一块三角板(,90AB BC ABC =∠=︒)放入一个“U ”形槽中,使三角形的三个顶点A 、B 、C 分别在槽的两壁及底边上滑动,已知90D E ∠=∠=︒,在滑动过程中,你发现线段AD 与BE 有什么关系?试说明你的结论;(2)【变式探究】小明在解决完这个问题后,将其命名为“一线三等角”模型;如图2,在ABC ∆中,点D 、E 、F 分别在边BC 、AC 、AB 上,若B FDE C ∠=∠=∠,则这三个相等的角之间的联系又会使图形中出现其他的一些等角.请你写出其中的一组,并加以说理; (3)【拓展应用】如图3,在ABC ∆中,BA BC =,45B ∠=︒,点D 、F 分别是边BC 、AB 上的动点,且2AF BD =.以DF 为腰向右作等腰DEF ∆,使得DE DF =,45EDF ∠=︒,连接CE .①试判断线段DC 、BD 、BF 之间的数量关系,并说明理由;②如图4,已知2AC =,点G 是AC 的中点,连接EA 、EG ,直接写出EA EG +的最小值. 【答案】【小问1】AD BE =,说明见解析【小问2】BED FDC ∠=∠,EDB DFC ∠=∠;说理见解析【小问3】①BD BF CD +=,理由见解析;②AE EG +【解析】 【分析】(1)【问题情境】证明()ABD BCE AAS ∆≅∆,即可求解. (2)【变式探究】利用等量代换即可求解.(3)【拓展应用】①等量代换即可求解;②在CD 上截取DM BF =,连接EM ,作点G 关于CE 的对称点N ,连接CN ,AN ,先证明()BDF MED SAS ∆≅∆,得到EM =CM ,在求出22.5ECM MEC ∠=∠=︒,即可确定E 点在射线CE 上运动,当A 、E 、N 三点共线时,EA +EG的值最小,最小值为AN ,在Rt ANC 中求出AN 即可. 【详解】 (1)【问题情境】 AD BE =,理由如下:90ABC ∠=︒, 90ABD CBE ∴∠+∠=︒, 90BAD ABD ∠+∠=︒,BAD CBE ∴∠=∠,AB BC =,()ABD BCE AAS ∴∆≅∆,AD BE ∴=;(2)【变式探究】BED FDC ∠=∠,EDB DFC ∠=∠;理由如下:B FDEC ∠=∠=∠,180EDB BED EDB FDC FDC DFC EDF ∴∠+∠=∠+∠=∠+∠=︒-∠,BED FDC ∴∠=∠,EDB DFC ∠=∠;(3)【拓展应用】 ①AB BC =,AF BF BD CD ∴+=+,2AF BD =,2BD BF BD CD ∴+=+, BD BF CD ∴+=;②在CD 上截取DM BF =,连接EM ,作点G 关于CE 的对称点N ,连接CN ,AN ,45B ∠=︒,45EDF ∠=︒,BFD EDM ∴∠=∠,DF DE =,()BDF MED SAS ∴∆≅∆,BD EM ∴=,EM BD =,45B DME ∠=∠=︒,CD BD BF =+,CM BD ∴=, EM CM ∴=,MCE MEC ∴∠=∠, 45EMD ∠=︒,22.5ECM MEC ∴∠=∠=︒,E ∴点在射线CE 上运动, G 点与N 的关于CE 对称,EG EN ∴=,EA EG EA EN AN ∴+=+,∴当A 、E 、N 三点共线时,EA EG +的值最小,最小值为AN ,45B ∠=︒,AB BC =, 67.5ACB ∴∠=︒,45ACE ∴∠=︒,由对称性可知,ACE ECN ∠=∠,90ACN ∴∠=︒,点G 是AC 的中点,2AC =,1CG ∴=, 1CN ∴=,在Rt ANC 中,AN =AE EG ∴+。
专题3.一线三等角

专题三:一线三等角综合专项练习班级:姓名:例1.(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD ⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE =BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E 三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.练习:1.如图(1),AB⊥AD,ED⊥AD,AB=CD,AC=DE,试说明BC⊥CE的理由;如图(2),若△ABC向右平移,使得点C移到点D,AB⊥AD,ED⊥AD,AB=CD,AD =DE,探索BD⊥CE的结论是否成立,并说明理由.2.如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;(1)若B、C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC;(2)若B、C在DE的两侧(如图所示),且AD=CE,其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.3.如图,在△ABC中,∠ABC=∠ACB,E为BC边上一点,以E为顶点作∠AEF,∠AEF的一边交AC于点F,使∠AEF=∠B.(1)如果∠ABC=40°,则∠BAC=;(2)判断∠BAE与∠CEF的大小关系,并说明理由;(3)当△AEF为直角三角形时,求∠AEF与∠BAE的数量关系.4.如图,AB=12米,CA⊥AB于点A,DB⊥AB于点B,且AC=4米,点P从B向A运动,每分钟走1米,点Q从B点向D运动,每分钟走2米,P、Q两点同时出发,运动几分钟后,△CP A与△PQB全等?。
微专题 一线三等角
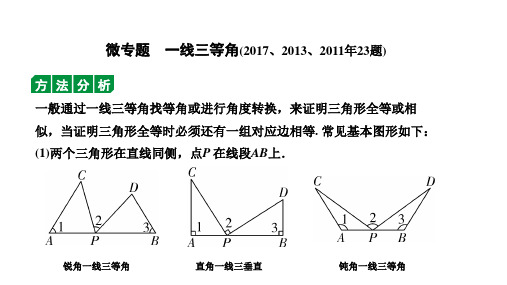
模型应用
1. 如图,在正方形ABCD中,AB=4,点E是DC延长线上的一点,连接BE, 过点E作EF⊥BE,与AD的延长线交于点F,若CE=2,求DF的长.
解:∵四边形ABCD是正方形, ∴∠BCE=∠EDF=90°, ∵EF⊥BE, ∴∠BEF=90°,
∴ AE = AF , DC DE
∵AB=CD=3,AE=4,DE=6F的长为5.
(1)求证:△AEF∽△DCE;
(2)若AB=3,AE=4,DE=6,求线段BF的长. (1)证明:∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∴∠AEF+∠F=90°.
∵EF⊥CE,
∴∠CED+∠AEF=90°, ∴∠CED=∠F,
第2题图
∴△AEF∽△DCE;
(2)解:由(1)知,△AEF∽△DCE,
微专题 一线三等角(2017、2013、2011年23题)
方法分析 一般通过一线三等角找等角或进行角度转换,来证明三角形全等或相 似,当证明三角形全等时必须还有一组对应边相等. 常见基本图形如下: (1)两个三角形在直线同侧,点P 在线段AB上.
锐角一线三等角
直角一线三垂直
钝角一线三等角
已知:∠1=∠2=∠3.利用三角形任意一个外角等于与它不相邻的 两个内角的和得到一组对应角相等从而可得两三角形相似.
【结论】①△CAP∽△PBD; ②当AC=BP或AP=BD或CP=PD时,△CAP≌△PBD.
(2)两个三角形在直线异侧,点P在AB(或BA)的延长线上.
锐角一线三等角
直角一线三垂直
钝角一线三等角
已知:∠1=∠2=∠3.利用三角形任意一个外角等于与它不相邻的两个 内角的和得到一组对应角相等从而可得两三角形相似.
初三相似三角形之一线三等角专题

相似三角形——“一线三等角型”一、知识梳理:一线三等角:两个等角的一边在同一直线上,另一边在该直线的同侧。
若有第三个与之相等的角、其顶点在该直线上,角的两边(或两边所在直线)分别与两等角的非共线边(或该边所在直线)相交,此时通过证明,一般都可以得到一组相似三角形,该组相似三角形习惯上被称为“一线三等角型”相似三角形.(图1)(图2)(1)如图1,已知三角形ABC中,AB=AC,∠ADE=∠B,那么一定存在的相似三角形有;(2)如图2,已知三角形ABC中,AB=AC,∠DEF=∠B,那么一定存在的相似三角形有.二、【例题解析】【例1】如图,等边△ABC中,边长为4,D是BC上动点,∠EDF=60°,(1)求证:△BDE∽△CFD;(2)当BD=1,FC=52时,求BE.【变式1】在边长为4的等边ABC∆中,D是BC的中点,点E、F分别在AB、AC上,且保持ABCEDF∠=∠,连接EF.(1) 已知BE=1,DF=2,求DE的值;(2) 求证:∠BED=∠DEF.【变式2】在边长为4的等边ABC ∆中,若BD =1时,当△DEF 与△AEF 相似,求BE 的值.【变式3】如图,已知边长为3的等边ABC ∆,点F 在边BC 上,CF =1,点E 是射线BA 上一动点,以线段EF 为边向右侧作等边EFG ∆,直线EG ,FG 交直线AC 于点M ,N ,(1)写出图中与BEF ∆相似的三角形;(2)证明其中一对三角形相似;(3)设BE =x ,MN =y ,,求y 与x 之间的函数关系式,并写出自变量x 的取值范围.【例2】在ABC ∆中,O BC AC C ,3,4,90===∠o 是AB 上的一点,且52=AB AO ,点P 是AC 上的一个动点,OP PQ ⊥交线段BC 于点Q (不与点B ,C 重合),已知AP =2,求CQ .【变式1】 如图,在△ABC 中,8==AC AB ,10=BC ,D 是BC 边上的一个动点,点E 在AC 边上,且C ADE ∠=∠.(1) 求证:△ABD ∽△DCE ;(2) 如果x BD =,y AE =,求y 与x 的函数解析式,并写出自变量x 的定义域;(3) 当点D 是BC 的中点时,试说明△ADE 是什么三角形,并说明理由.QC P【变式2】在直角三角形ABC 中,D BC AB C ,,90==∠o是AB 边上的一点,E 是在AC 边上的一个动点(与A ,C 不重合),DF DE DF ,⊥与射线BC 相交于点F .(1) 如图1,当点D 是边AB 的中点时,求证:DF DE =;(2) 如图2,当m DB AD =,求DF DE 的值.图(2)图(1)F CF C A BB A D E D E【例3】已知在梯形ABCD 中,AD ∥BC ,AD <BC ,且AD =5,AB =DC =2,P 为AD 上的一点,满足∠BPC =∠A . ① 求证;△ABP ∽△DPC ; ② 求AP 的长.【变式1】如果点P 在AD 边上移动(点P 与点A 、D 不重合),且满足∠BPE =∠A ,PE 交直线BC 于点E ,同时交直线DC 于点Q ,那么①当点Q 在线段DC 的延长线上时,设AP =x ,CQ =y ,求y 关于x 的函数解析式,并写出函数的定义域;②当CE =1时,写出AP 的长.C B AD C B A D【变式2】在梯形ABCD 中,AD ∥BC ,6AB CD BC ===,3AD =.点M 为边BC 的中点,以M 为顶点作EMF B ∠=∠,射线ME 交腰AB 于点E ,射线MF 交腰CD 于点F ,联结EF .(1)求证:△MEF ∽△BEM ;(2)若△BEM 是以BM 为腰的等腰三角形,求EF 的长;(3)若EF CD ⊥,求BE 的长.【作业】1、如图,在ABC ∆中,90C ∠=︒,6AC =,43=BC AC ,D 是BC 边的中点,E 为AB 边上的一个动点,作90DEF ∠=︒,EF 交射线BC 于点F .设BE x =,BED ∆的面积为y .(1)求y 关于x 的函数关系式,并写出自变量x 的取值范围;(2)如果以B 、E 、F 为顶点的三角形与BED ∆相似,求BED ∆的面积.2、如图,已知在△ABC 中, AB =AC =6,BC =5,D 是AB 上一点,BD =2,E 是BC 上一动点,连结DE ,并作DEF B ∠=∠,射线EF 交线段AC 于F .(1)求证:△DBE ∽△ECF ;(2)当F 是线段AC 中点时,求线段BE 的长;(3)联结DF ,如果△DEF 与△DBE 相似,求FC 的长.3、已知在梯形ABCD 中,AD ∥BC ,AD <BC ,且BC =6,AB =DC =4,点E 是AB 的中点.(1)如图,P 为BC 上的一点,且BP =2.求证:△BEP ∽△CPD ;(2)如果点P 在BC 边上移动(点P 与点B 、C 不重合),且满足∠EPF =∠C ,PF 交直线CD 于点F ,同时交直线AD 于点M ,那么:①当点F 在线段CD 的延长线上时,设BP =x ,DF =y ,求y 关于x 的函数解析式,并写出函数的定义域;②当BEP DMF S S ∆∆=49时,求BP 的长.。
三角形全等几何模型(一线三等角)(精选精练)(专项练习)(教师版) 24-2025学年八年级数学上册

专题12.12三角形全等几何模型(一线三等角)(精选精练)(专项练习)一、单选题(本大题共10小题,每小题3分,共30分)1.(22-23七年级下·辽宁朝阳·期末)王强同学用10块高度都是2cm 的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC BC =,90ACB ∠=︒),点C 在DE 上,点A 和B 分别与木墙的顶端重合.则两堵木墙之间的距离DE 是()A .10cmB .15cmC .20cmD .25cm2.如图所示,,,B C E 三点在同一条直线上,AC CD =,90B E ∠=∠=︒,AC CD ⊥,则下列结论错误的是()A .A ∠与D ∠互余B .2A ∠=∠C .ABC CED △≌△D .12∠=∠3.如下图所示,在△ABC 中,∠ACB=90°,AC=BC ,BE ⊥CE 于点E ,AD ⊥CE 于点D .DE=6cm ,AD=9cm ,则BE 的长是()A .6cmB .1.5cmC .3cmD .4.5cm4.(23-24八年级上·重庆开州·阶段练习)如图,在平面直角坐标系中,ABC 为等腰直角三角形,90,ACB AC BC ∠=︒=.点()0,1B -,点()1,1C .则点A 坐标为()A .()1,3-B .()3,1-C .()2,1-D .()1,2-5.(22-23七年级下·广东深圳·期末)小丽与爸妈在公园里荡秋千.如图,小丽坐在秋千的起始位置A 处,OA 与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1m 高的B 处接住她后用力一推,爸爸在C 处接住她.若妈妈与爸爸到OA 的水平距离BD 、CE 分别为1.4m 和1.8m ,90BOC ∠=︒.爸爸在C 处接住小丽时,小丽距离地面的高度是()A .1mB .1.6mC .1.8mD .1.4m6.(22-23八年级上·山东青岛·单元测试)2002年8月在北京召开的第24届国际数学家大会,会标中的图案如图,其中的四边形ABCD 和EFGH 都是正方形,则ABF DAE ≌的理由是().A .SSSB .AASC .SASD .HL7.(23-24八年级上·河北唐山·期中)如图,在ABC 和CDE 中,点B ,C ,E 在同一条直线上,B E ACD ∠∠∠==,AC CD =,若2AB =,6BE =,则DE 的长为()A .8B .6C .4D .28.(2024·山西吕梁·一模)如图,在平面直角坐标系中,点()0,2A 处有一激光发射器,激光照射到点()1,0B 处倾斜的平面镜上发生反射,使得反射光线照射到点C 处的接收器上,若入射角45α=︒,AB BC =,则点C 处的接收器到y 轴的距离为()A .1B .2C .3D .49.(17-18八年级上·河南郑州·期中)如图中,AE ⊥AB 且AE =AB ,BC ⊥CD 且BC =CD ,若点E 、B 、D 到直线AC 的距离分别为6、3、2,则图中实线所围成的阴影部分面积S 是()A .50B .44C .38D .3210.(22-23八年级下·新疆乌鲁木齐·期末)如图,AB CD ⊥,且AB CD =,E ,F 是AD 上两点,CE AD ⊥,BF AD ⊥.若4CE =,3BF =,2EF =,则AD 的长为()A .3B .5C .6D .7二、填空题(本大题共8小题,每小题4分,共32分)11.(21-22八年级上·山西吕梁·期中)如图,一个等腰直角三角形ABC 物件斜靠在墙角处(∠O =90°),若OA =50cm ,OB =28cm ,则点C 离地面的距离是cm .12.(20-21八年级上·黑龙江·期中)如图,在平面直角坐标系内,OA ⊥OC ,OA=OC ,若点A 的坐标为(4,1),则点C 的坐标为13.(2022·四川成都·二模)如图所示,ABC 中,,90AB AC BAC =∠=︒.直线l 经过点A ,过点B 作BE l ⊥于点E ,过点C 作CF l ⊥于点F .若2,5==BE CF ,则EF =.14.(19-20八年级上·江苏苏州·期中)如图,△ABC 中,∠C =90°,点D 为AC 上一点,∠ABD =2∠BAC =45°,若AD =12,则△ABD 的面积为.15.(23-24八年级上·江苏无锡·期中)如图,两根旗杆间相距12米,某人从点B 沿BA 走向点A ,一段时间后他到达点M ,此时他仰望旗杆的顶点C 和D ,两次视线的夹角为90︒,且CM DM =.已知旗杆BD 的高为9米,该人的运动速度为1米/秒,则这个人运动到点M 所用时间是秒.16.(23-24八年级上·辽宁大连·期末)如图,在ABC 中,90ACB ∠= ,CD 为AB 边上的高,3BC =,6AC =,点E 从点B 出发,在直线BC 上以每秒2cm 的速度移动,过点E 作BC 的垂线交直线CD 于点F ,当点E 运动s 时,AB CF =.17.(19-20八年级上·江苏连云港·阶段练习)如图,线段AB =8cm ,射线AN ⊥AB ,垂足为点A ,点C 是射线上一动点,分别以AC ,BC 为直角边作等腰直角三角形,得△ACD 与△BCE ,连接DE 交射线AN 于点M ,则CM 的长为.18.(22-23七年级下·四川成都·期末)在ABC 中,AB AC =,90BAC ∠<︒,点D 在边BC 上,2CD BD =,点E ,F 在线段AD 上,BED CFD BAC ∠=∠=∠.若ABC 的面积为9,则ABE CDF S S += .三、解答题(本大题共6小题,共58分)19.(8分)如图,在ABC 中,90ACB ∠=︒,AC BC =,BE CE ⊥,于点E AD CE ⊥,于点D .BEC 与CDA 全等吗?请说明理由.20.(8分)如图,90ABC ∠=︒,FA AB ⊥于点A ,D 是线段AB 上的点,AD BC =,AF BD =.(1)判断DF 与DC 的数量关系为,位置关系为.(2)如图2,若点D 在线段AB 的延长线上,点F 在点A 的左侧,其他条件不变,试说明(1)中结论是否成立,并说明理由.21.(10分)如图,在ABC 中,AB BC =.(1)如图1,直线NM 过点B ,AM MN ⊥于点M ,⊥CN MN 于点N ,且90ABC ∠=︒,求证:MN AM CN =+.(2)如图2,直线NM 过点B ,AM 交NM 于点M ,CN 交NM 于点N ,且AMB ABC BNC ∠=∠=∠,则MN AM CN =+是否成立?请说明理由!22.(10分)如图,在ABC 中,2AB AC ==,40B C ∠=∠=︒,点D 在线段BC 上运动(D 不与B 、C 重合),连接AD ,作40ADE ∠=︒,DE 交线段AC 于E .(1)当115BDA ∠=︒时,EDC ∠=°,DEC ∠=°;点D 从B 向C 运动时,BDA ∠逐渐变(填“大”或“小”);(2)当DC 等于多少时,ABD DCE △△≌,请说明理由;(3)在点D 的运动过程中,ADE V 的形状可以是等腰三角形吗?若可以,请直接写出BDA ∠的度数.若不可以,请说明理由.23.(10分)(23-24八年级上·重庆江津·期末)通过对下面数学模型的研究学习,解决下列问题:【模型呈现】(1)如图,90ACE ∠=︒,AC CE =,过点A 作AB BC ⊥于点B ,过点E 作ED BC ⊥交BC 的延长线于点D .由90ACB DCE DCE E ∠+∠=∠+∠=︒,得CAB E ∠=∠.又90ABC CDE ∠=∠=︒,AC CE =,可以推理得到ABC CDE △△≌,进而得到AB =______,BC =______.(请完成填空)我们把这个数学模型称为“K 字”模型或“一线三等角”模型.【模型应用】(2)①如图,90ACE BCD ∠=∠=︒,AC CE =,BC CD =,连接AB 、DE ,且DE CG ⊥于点G ,AB 与直线CG 交于点F ,求证:点F 是AB 的中点;②如图,若点M 为x 轴上一动点,点N 为y 轴上一动点,点P 的坐标为()51,,是否存在以M 、N 、P 为顶点且以PM 为斜边的三角形为等腰直角三角形?若存在,请直接写出点M 的坐标;若不存在,请说明理由.24.(12分)(22-23八年级上·江苏南京·阶段练习)已知,在ABC 中,AB AC =,D A E ,,三点都在直线m 上,且9DE cm BDA AEC BAC =∠=∠=∠,.(1)如图①,若AB AC ⊥,则BD 与AE 的数量关系为___________,CE 与AD 的数量关系为___________;(2)如图②,判断并说明线段BD ,CE 与DE 的数量关系;(3)如图③,若只保持7BDA AEC BD EF cm ∠=∠==,,点A 在线段DE 上以2cm/s 的速度由点D 向点E 运动,同时,点C 在线段EF 上以cm /s x 的速度由点E 向点F 运动,它们运动的时间为s t ().是否存在x ,使得ABD △与EAC 全等?若存在,求出相应的t 的值;若不存在,请说明理由.参考答案:1.C【分析】由题意易得90ADC CEB ∠=∠=︒,则有BCE DAC ∠=∠,进而可证ADC CEB ∆∆≌,然后根据全等三角形的性质求解即可.【详解】解:∵AC BC =,90ACB ∠=︒,AD DE ⊥,BE DE ⊥,∴90ADC CEB ∠=∠=︒,∴90ACD BCE ∠+∠=︒,90ACD DAC ∠+∠=︒,∴BCE DAC ∠=∠,∵在ADC ∆和CEB ∆中,ADC CEB DAC BCE AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴ADC CEB ∆∆≌;∴6cm EC AD ==,14cm DC BE ==,∴20(cm)DE DC CE =+=,故选C .【点拨】本题主要考查全等三角形的性质与判定,熟练掌握三角形全等的判定条件是解题的关键.2.D【分析】利用同角的余角相等求出2A ∠=∠,再利用“角角边”证明ABC 和CED 全等,根据全等三角形对应边相等,对应角相等,即可解答.【详解】∵90B E ∠=∠=︒,∴190A ∠+∠=︒,290D ∠+∠=︒,∵AC CD ⊥,∴1290∠+∠=︒,故D 错误;∴2A ∠=∠,故B 正确;∴90A D ∠+∠=︒,故A 正确;在ABC 和CED 中,2A B E AC CD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()AAS ABC CED ≅ ,故C 正确;故选: D .【点拨】本题考查了全等三角形的判定与性质,等角的余角相等的性质,熟练掌握三角形全等的判定方法并确定出全等的条件2A ∠=∠是解题的关键.3.C【分析】本题可通过全等三角形来求BE 的长.△BEC 和△CDA 中,已知了一组直角,∠CBE 和∠ACD 同为∠BCE 的余角,AC=BC ,可据此判定两三角形全等;那么可得出的条件为CE=AD ,BE=CD ,因此只需求出CD 的长即可.而CD 的长可根据CE 即AD 的长和DE 的长得出,由此可得解.【详解】解:∵∠ACB=90°,BE ⊥CE ,∴∠BCE+∠ACD=90°,∠BCE+∠CBE=90°;∴∠ACD=∠CBE ,又AC=BC ,∴△ACD ≌△CBE ;∴EC=AD ,BE=DC ;∵DE=6cm ,AD=9cm ,则BE 的长是3cm .故选C .【点拨】三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.4.D【分析】本题考查了全等三角形的判定和性质,熟练掌握全等三角形的判定和性质定理是解题的关键.过C 作直线l y ∥轴,过B 作BE l ⊥于E ,过A 作AD l ⊥于D ,于是得到90ADC ACB BEC ∠=∠=∠=︒,得到CAD BCE ∠=∠,根据全等三角形的性质得到,AD CE CD BE ==,根据点()0,1B -,点()1,1C ,得到1,112BE CD AD CE ====+=,于是得到结论.【详解】解:过C 作直线l y ∥轴,过B 作BE l ⊥于E ,过A 作AD l ⊥于D ,∴90ADC ACB BEC ∠=∠=∠=︒,∴90DAC ACD ACD BCE ∠+∠=∠+∠=︒,∴CAD BCE ∠=∠,在ACD 与CBE △中,CAD BCE ADC CEB AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()AAS ACD CBE ≌,∴,AD CE CD BE ==,∵点()0,1B -,点()1,1C ,∴1,112BE CD AD CE ====+=,∴()1,2A -.故选:D .5.D【分析】利用全等三角形判定()AAS ,证得OBD 与COE 全等,根据全等三角形性质可求出OE 和OD 的值,进而求出OA 的值,最后根据OA OE AE -=,即可求出问题答案.【详解】解:90BOC ∠=︒ ,90BOD COE ∴∠+∠=︒,90BDO ∠=︒ ,90CEO ∠=︒,90BOD OBD ∴∠+∠=︒,90COE OCE ∠+∠=︒,COE OBD ∴∠=∠,BOD OCE ∠=∠,又OB CO = ,()OBD COE AAS ∴≅ ,1.4m OE BD ∴==, 1.8m OD CE ==,1.8m 1m 1.4m 1.4m AE OA OE OD DA OE ∴=-=+-=+-=.故选:D .【点拨】本题考查了利用三角形全等测距离的问题,理解题意及熟知三角形的性质与判定是解题关键.6.B【分析】由正方形的性质知,AB DA =,由同角的余角相等知,BAF ADE ∠=∠,又有90AFB DEA ∠=∠=︒,故根据AAS 证得ABF DAE ≌.【详解】证明:∵四边形ABCD是正方形,∴90AB DA BAF DAE =∠+∠=︒,,∵90ADE DAE ∠+∠=︒,∵BAF ADE ∠=∠,在ABF △与DAE 中,BAF ADE AFB AED AB AD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()AAS ABF DAE ≌△△.故选:B .【点拨】本题利用了正方形的性质,同角的余角相等,全等三角形的判定,学生要以常用的几种判定方法掌握并灵活运用.7.C【分析】本题考查了三角形全等的判定与性质,根据三角形内角和定理,证明()AAS ABC CED ≌ ,由DE BC BE AB ==-即可求出结果.【详解】解:180B ACB BAC ∠+∠+∠=︒ ,B E ACD ∠∠∠==,180ACD ACB BAC ∴∠+∠+∠=︒,180ACD ACB DCE ∠+∠+∠=︒,BAC DCE ∴∠=∠,在ABC 和CED △中,BAC DCE B E AC CD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()AAS ABC CED ≌ ,,BC DE AB CE ∴==,2AB =,6BE =,∴624DE BC BE CE BE AB ==-=-=-=,故选:C .8.C【分析】本题主要考查坐标与图形,全等三角形的判定与性质,过点C 作CM x ⊥轴于点M ,证明ABO BCM ≌V V 得出2BM OA ==,进一步得出3OM =即可【详解】解:过点C 作CM x ⊥轴于点M ,如图,则90,CBM BCM ∠+∠=︒根据题意得90,ABC ∠=︒∴90,ABO CBM ∠+∠=︒∴,ABO BCM ∠=∠又,90,AB BC AOB BMC =∠=∠=︒∴,AOB BMC ≌V V ∴2,BVM AB ==∴123,OM OB BM =+=+=即点C 处的接收器到y 轴的距离为3,故选:C9.D【分析】由已知和图形根据“K ”字形全等,用AAS 可证△FEA ≌△MAB ,△DHC ≌△CMB ,推出AM =EF =6,AF =BM =3,CM =DH =2,BM =CH =3,从而得出FH =14,根据阴影部分的面积=S 梯形EFHD -S △EF A -S △ABC -S △DHC 和面积公式代入求出即可.【详解】∵AE ⊥AB ,EF ⊥AF ,BM ⊥AM,∴∠F =∠AMB =∠EAB =90°,∴∠FEA +∠EAF =90°,∠EAF +∠BAM =90°,∴∠FEA =∠BAM ,在△FEA 和△MAB 中F BMA FEA BAM AE AB ∠∠⎧⎪∠∠⎨⎪⎩===,∴△FEA ≌△MAB (AAS ),∴AM =EF =6,AF =BM =3,同理CM =DH =2,BM =CH =3,∴FH =3+6+2+3=14,∴梯形EFHD 的面积=12EF DH FH + ()=126241⨯+⨯()=56,∴阴影部分的面积=S 梯形EFHD -S △EF A -S △ABC -S △DHC =11566322183322-⨯⨯-⨯⨯-⨯⨯=32.故选D .【点拨】本题考查了三角形的面积,梯形的面积,全等三角形的性质和判定等知识点,关键是把不规则图形的面积转化成规则图形的面积.10.B【分析】本题考查全等三角形的判定和性质.正确掌握相关性质内容是解题的关键.由AB CD ⊥可得90A D ∠+∠=︒,由CE AD ⊥,BF AD ⊥可得90CED AFB ∠=∠=︒,A B ∠∠=︒+90,从而B D ∠=∠,进而证得()AAS ABF CDE ≌,可得4AF CE ==,3BF DE ==,推出()AD AF DF AF DE EF =+=+-,代入数据即可解答.【详解】∵AB CD ⊥,∴90A D ∠+∠=︒,∵CE AD ⊥,BF AD ⊥,∴90CED AFB ∠=∠=︒,∴1801809090A B AFB ∠+∠=︒-∠=︒-︒=︒,∴B D ∠=∠,∵AB CD =,∴()AAS ABF CDE ≌,∴4AF CE ==,3BF DE ==,∴()()4325AD AF DF AF DE EF =+=+-=+-=.故选:B11.28【分析】作CD ⊥OB 于点D ,依据AAS 证明D AOB B C ∆≅∆,GMF ,再根据全等三角形的性质即可得到结论.【详解】解:过点C 作CD ⊥OB 于点D,如图,∴90CDB AOB ∠=∠=︒∵ABC ∆是等腰直角三角形∴AB =CB ,90ABC ∠=︒∴90ABO CBD ∠+∠=︒又90CBD BCD ∠+∠=︒∴ABO BCD∠=∠在ABO ∆和BCD ∆中,AOB BDC ABO BCD AB CB ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()ABO BCD AAS ∆≅∆∴28cmCD BO ==故答案为:28.【点拨】本题主要考查了等腰直角三角形的性质、三角形全等的判定与性质,正确作出辅助线构造全等三角形是解答本题的关键.12.(-1,4)【分析】过点A 和点C 作x 轴的垂线,垂足为D ,E ,证明△COE ≌△OAD ,得到OE=AD ,CE=OD ,再根据点A 的坐标可得结果.【详解】解:过点A 和点C 作x 轴的垂线,垂足为D ,E ,∵∠AOC=90°,∴∠COE+∠AOD=90°,又∠CEO=90°,则∠COE+∠OCE=90°,∴∠OCE=∠AOD ,在△COE 与△OAD 中,OCE AOD CEO ODA OC OA ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△COE ≌△OAD (AAS ),∴OE=AD ,CE=OD ,∵点A 的坐标为(4,1),∴OD=4,AD=1,∴CE=OD=4,OE=AD=1,∴点C 的坐标为(-1,4),故答案为:(-1,4).【点拨】本题考查了全等三角形的判定和性质,坐标与图形,解题的关键是利用已知条件,作出辅助线,证明全等.13.7【分析】根据全等三角形来实现相等线段之间的关系,从而进行计算,即可得到答案;【详解】解:∵BE ⊥l ,CF ⊥l ,∴∠AEB =∠CFA =90°.∴∠EAB +∠EBA =90°.又∵∠BAC =90°,∴∠EAB +∠CAF =90°.∴∠EBA =∠CAF .在△AEB 和△CFA 中∵∠AEB =∠CFA ,∠EBA =∠CAF ,AB =AC ,∴△AEB ≌△CFA .∴AE =CF ,BE =AF .∴AE +AF =BE +CF .∴EF =BE +CF .∵2,5==BE CF ,∴257EF =+=;故答案为:7.【点拨】本题考查了全等三角形的判定和性质,余角的性质,解题的关键是熟练掌握所学的知识,正确的证明三角形全等.14.36.【分析】作DE ⊥DB 交AB 于E ,EF 垂直AC 于F ,则∠DEB =90°-∠ABD =45°,证出AE =DE =DB ,通过证明△AEF ≌△BCD ,得出BC ==AF=12AD=6,由三角形面积公式即可得出答案.【详解】作DE ⊥DB 交AB 于E ,EF 垂直AC 于F ,如图所示:则∠DEB =90°-∠ABD =45°,∴△BDE 是等腰直角三角形,∴DB =DE ,∵∠ABD =2∠BAC =45°,∴∠BAC =22.5°,∴∠ADE =∠DEB -∠BAC =22.5°=∠BAC ,∴AE =DE =DB ,∵∠AFE=90°,∴F 是AD 中点,AF=FD ,又∵∠C=90°,∴∠CBD=90°-45°-22.5°=22.5°,在Rt △AEF 和Rt △BCD 中A CBD AFE BCD AE BD =⎧⎪=⎨⎪=⎩∠∠∠∠∴Rt △AEF ≌Rt △BCD (AAS ),∴AF=BC=12AD=6,∴△ABD 的面积S=12AD ×BC =12×12×6=36;故答案为:36.【点拨】本题考查了等腰直角三角形的判定和性质,全等三角形的判定和性质,三角形面积公式的的计算,熟记特殊三角形的判定和性质定理是解题关键.15.3【分析】本题考查了全等三角形的应用;解答本题的关键是利用互余关系找三角形全等的条件,对应角相等,并巧妙地借助两个三角形全等,寻找所求线段与已知线段之间的等量关系.本题的关键是求得ACM BMD ≌.【详解】解:∵90CMD ∠=︒,∴90CMA DMB +=︒∠∠,又∵90CAM ∠=︒,∴90CMA C ︒∠+∠=,∴C DMB ∠=∠,在ACM 和BMD 中,A B C DMB CM MD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()AAS ACM BMD ≌,∴9BD AM ==米,1293BM =-=(米),∵该人的运动速度1米/秒,他到达点M 时,运动时间为313÷=(秒).故答案为:3.16.1.5或4.5【分析】本题考查了全等三角形的判定和性质,直角三角形的性质,分①当点E 在射线BC 上移动时,639BE CE BC ''=+=+=,②当点E 在射线CB 上移动时,()633cm BE AC BC =-=-=,熟练正确全等三角形的判定和性质是解题的关键.【详解】解:∵EF BC ⊥,∴90CEF ACB ∠=︒=∠,在CEF △和ACB △中,ECF A CEF ACB CF AB ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()AAS CEF ACB ≌,∴6CE AC ==,如图,①当点E 在射线BC 上移动时,639BE CE BC ''=+=+=,∵点E 从点B 出发,在直线BC 上以2cm 的速度移动,∴E 移动了:()92 4.5s ÷=;②当点E 在射线CB 上移动时,()633cm BE AC BC =-=-=,∵点E 从点B 出发,在直线BC 上以2cm 的速度移动,∴E 移动了:()32 1.5s ÷=;综上所述,当点E 在射线CB 上移动4.5s 或1.5s 时,CF AB =,故答案为:1.5或4.5.17.4cm.【分析】过点E 作EF ⊥AN 于F ,先利用AAS 证出△ABC ≌△FCE ,从而得出AB=FC=8cm ,AC=FE ,然后利用AAS 证出△DCM ≌△EFM,从而求出CM 的长.【详解】解:过点E 作EF ⊥AN 于F ,如图所示∵AN ⊥AB ,△BCE 和△ACD 为等腰直角三角形,∴∠BAC=∠BCE=∠ACD=∠CFE =90°,BC=CE ,AC=CD∴∠ABC+∠ACB=90°,∠FCE+∠ACB =90°,∴∠ABC =∠FCE ,在△ABC 和△FCE 中BAC CFE ABC FCE BC CE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△FCE∴AB=FC=8cm ,AC=FE∴CD=FE在△DCM 和△EFM 中90DMC EMF DCM EFM CD FE ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩∴△DCM ≌△EFM∴CM=FM=12FC=4cm.故答案为:4cm.【点拨】此题考查的是全等三角形的判定及性质,掌握用AAS 证两个三角形全等是解决此题的关键.18.6【分析】本题属于全等三角形的判定和性质,解题的关键是熟练掌握全等三角形的判定方法.证明ABE ≌CAF V ,推出ABE 与CAF V 面积相等,可得结论.【详解】解:在等腰三角形ABC 中,AB AC =,2CD BD =,ABD ∴ 与ADC △等高,底边比值为1:2,ABD ∴ 与ADC △的面积比为1:2.ABC 的面积为9,ABD ∴ 与ADC △的面积分别为3和6,BED CFD ∠=∠ ,AEB AFC ∴∠=∠.BED ABE BAE ∠=∠+∠ ,BAE CAF BAC ∠+∠=∠,BED BAC ∠=∠,BAC ABE BAE ∴∠=∠+∠,CAF ABE ∴∠=∠.在ABE 和CAF V 中,AEB AFC ABE CAF AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩,()AAS ABE CAF ∴ ≌,ABE ∴ 与CAF V 面积相等,ABE ∴ 与CDF 的面积之和为ADC △的面积,ABE ∴ 与CDF 的面积之和为6.故答案为:6.19.全等,理由见解析【分析】首先证明CAD BCE ∠=∠,即可证明CDA BEC ≌V V ,即可解题.【详解】全等,理由如下:BE CE ⊥,E AD CE ⊥,,90ACB ∠=︒∴90BCE DCA ∠+∠=︒,90DAC DCA ∠+∠=︒.∴CAD BCE ∠=∠;在BEC 和DAC △中,90BCE DAC BEC CDA BC AC ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩∴()AAS BEC DAC ≌V V .【点拨】此题是三角形综合题,主要考查了全等三角形的判定,掌握证明全等三角形的方法是解题的关键.20.(1)CD DF =,CD DF⊥(2)成立,见解析【分析】(1)根据题意可直接证明AFD BDC ≌ ,即可得出结论;(2)仿照(1)的证明过程推出ADF BCD ≌ ,即可得出结论.【详解】(1)解:由题意,90A B ∠=∠=︒,在AFD △与BDC 中,AF BD A B AD BC =⎧⎪∠=∠⎨⎪=⎩∴()SAS AFD BDC ≌ ,∴DF DC =,ADF BCD ∠=∠,在Rt BDC 中,90BDC BCD ∠+∠=︒,∴90BDC ADF ∠+∠=︒,∴90FDC ∠=︒,∴CD DF ⊥,综上可知CD DF =,CD DF ⊥;(2)解:成立,理由如下:AF AB ⊥,∴90DAF ∠=︒,在ADF △和BCD △中,AF DB DAF CBD AD BC =⎧⎪∠=∠⎨⎪=⎩,∴()SAS ADF BCD ≌ ,∴DF DC =,ADF BCD ∠=∠,90BCD CDB ∠+∠=︒,∴90ADF CDB ∠+∠=︒,即90CDF ∠=︒,∴CD DF ⊥;∴(1)中结论仍然成立.【点拨】本题考查全等三角形的判定与性质,以及直角三角形两锐角互余等,熟练掌握全等三角形的判定定理是解题关键.21.(1)见解析(2)成立,理由见解析【分析】(1)本题主要考查全等三角形的判定和性质综合,利用题目中的已知条件导角,可推导CBN BAM ∠=∠,最后证明(AAS)≌AMB BNC ,直接可证.(2)利用AMB ABC ∠=∠及ABN ∠是ABM 的外角,可以推出MAB CBN ∠=∠,再利用AAS 可以判定(AAS)≌AMB BNC ,再利用全等的性质导边即可证明.【详解】(1)证明:∵AM MN ⊥于点M ,⊥CN MN 于点N ;∴90AMB BNC ∠=∠=︒;∴90MAB ABM ∠+∠=︒;∵90ABC ∠=︒,∴90ABM NBC ∠+∠=︒;∴MAB NBC ∠=∠;在ABM 和BCN △中,AMB BNC MAB NBC AB BC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()AAS ABM BCN ≌;∴AM BN =,BM CN =;∴MN BN BM AM CN =+=+.(2)MN AM CN =+成立.理由如下:设AMB ABC BNC α∠=∠=∠=;∴180ABM BAM ABM CBN α∠+∠=∠+∠=︒-;∴BAM CBN ∠=∠;在ABM 和BCN △中;BAM CBN AMB BNC AB BC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()AAS ABM BCN ≌;∴AM BN =,BM CN =;∴MN BN BM AM CN =+=+;故MN AM CN =+成立.22.(1)25;115;小(2)当2DC =时,ABD DCE≌△△(3)可以;BDA ∠的度数为110︒或80︒【分析】(1)由已知平角的性质可得180EDC ADB ADE ∠=︒-∠-∠,再利用三角形内角和定理进而求得DEC ∠,即可判断点D 从B 向C 运动过程中,BDA ∠逐渐变小;(2)当2DC =时,由已知和三角形内角和定理可得140DEC EDC ∠+∠=︒,140ADB EDC ∠+∠=︒,等量代换得ADB DEC ∠=∠,又由2AB AC ==,可得()AAS ABD DCE ≌△△;(3)根据等腰三角形的判定定理,利用三角形内角和定理求解即可.【详解】(1)解:1801801154025EDC ADB ADE ∠=︒-∠-∠=︒-︒-︒=︒,1801802540115DEC EDC C ∠=︒-∠-∠=︒-︒-︒=︒,点D 从B 向C 运动时,BDA ∠逐渐变小,故答案为:25;115;小.(2)解:当2DC =时,ABD DCE ≌△△,理由:40C ∠=︒ ,140DEC EDC ∴∠+∠=︒,又40ADE ∠=︒ ,∴140ADB EDC ∠+∠=︒,ADB DEC ∴∠=∠,又 B C ∠=∠,2AB DC ==,∴()AAS ABD DCE ≌△△;(3)解:当BDA ∠的度数为110︒或80︒时,ADE V 的形状是等腰三角形;理由:110BDA ∠=︒ 时,70704030ADC EDC ∴∠=︒∠=︒-︒=︒,,40C ∠=︒ ,70DAC ∴∠=︒,304070AED C EDC ∠=∠+∠=︒+︒=︒,DAC AED ∴∠=∠,∴ADE V 是等腰三角形;80BDA ∠=︒ 时,100ADC ∴∠=︒,40C ∠=︒ ,40DAC ∴∠=︒,DAC ADE ∴∠=∠,∴ADE V 的形状是等腰三角形.【点拨】本题考查了等腰三角形的判定和性质,全等三角形的判定,熟练掌握知识点是解题的关键.23.(1)CD ,DE ;(2)见解析;(3)存在,()4,0-或()6,0-【分析】本题是三角形综合题目,考查了等腰直角三角形的判定与性质、全等三角形的判定与性质、坐标与图形性质、直角三角形的性质等知识;(1)由全等三角形的性质可得出答案;(2)过点A 作AM FG ⊥交FG 于点M ,过点B 作BN FG ⊥交FG 于点N ,证明(AAS)ACM CEG ≌,得出AM CG =;同理可得:BCN CDG ≌.得出BN CG =,证明(AAS)AMF BNF ≌,由全等三角形的性质可得出AF BF =;(3)分两种情况,由全等三角形的性质可得出答案.【详解】(1)解:由题意可知ABC CDE △≌△,AB CD ∴=,BC DE =,故答案为:CD ,DE ;(2)证明:如图1,过点A 作AM FG ⊥交FG 于点M ,过点B 作BN FG ⊥交FG 于点N,ED CG ⊥ ,90ACE ∠=︒,90ACF ECG ECG E ∴∠+∠=∠+∠=︒,ACF E ∴∠=∠,在ACM △和CEG 中,ACM E AMC CGE AC CE ∠=∠⎧⎪∠=∠⎨⎪=⎩,(AAS)ACM CEG ∴ ≌,AM CG ∴=;同理可得:BCN CDG ≌.BN CG ∴=,AM BN ∴=,在AMF 和BNF 中,AFM BFN AMF BNF AM BN ∠=∠⎧⎪∠=∠⎨⎪=⎩,(AAS)AMF BNF ∴ ≌,AF BF ∴=,∴点F 是AB 的中点.(3)解:如图,当点N 在x 轴正半轴上时,由【模型呈现】可知MEN NDP ≌,5EM DN ∴==,DP EN =,514DP ∴=-=,4EN ∴=,(4,0)M ∴-;当点N 在x 轴负半轴上时,同理可得(6,0)M -.综上所述,点M 的坐标为(4,0)-或(6,0)-.24.(1)BD AE CE AD==,(2)DE BD CE=+(3)12t x ==,或928,49t x ==【分析】(1)利用平角的定义和三角形内角和定理得CAE ABD ∠=∠,再利用AAS 证明ABD CAE ≌, 得BD AE CE AD =,=;(2)由(1)同理可得ABD CAE △△≌,得BD AE CE AD ==,,可得答案;(3)分DAB ECA ≌ 或DAB EAC ≌△△两种情形,分别根据全等三角形的性质可解决问题.【详解】(1)解:∵BDA AEC BAC ∠=∠=∠,∴BAD CAE BAD ABD ∠+∠=∠+∠,∴CAE ABD ∠=∠,∵BDA AEC BA CA ∠=∠=,,∴ABD CAE AAS ≌() ,∴BD AE CE AD ==,,故答案为:BD AE CE AD ==,;(2)DE BD CE =+,由(1)同理可得ABD CAE AAS ≌() ,∴BD AE CE AD ==,,∴DE BD CE =+;(3)存在,当DAB ECA ≌ 时,∴2,7AD CE cm BD AE cm ====,∴1t =,此时2x =;当DAB EAC ≌△△时,∴ 4.5,7,AD AE cm DB EC cm ====∴924AD t ==,928749x =÷=,综上:12t x ==,或928,49t x ==.【点拨】本题是三角形综合题,主要考查了全等三角形的判定与性质,熟练掌握一线三等角基本模型是解题的关键,同时渗透了分类讨论的数学思想.。
专题 相似三角形一线三等角模型(学生版)
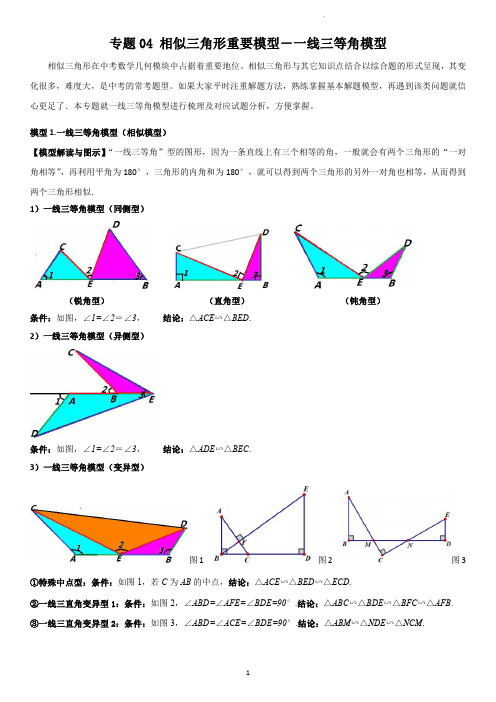
专题04相似三角形重要模型-一线三等角模型相似三角形在中考数学几何模块中占据着重要地位。
相似三角形与其它知识点结合以综合题的形式呈现,其变化很多,难度大,是中考的常考题型。
如果大家平时注重解题方法,熟练掌握基本解题模型,再遇到该类问题就信心更足了.本专题就一线三等角模型进行梳理及对应试题分析,方便掌握。
模型1.一线三等角模型(相似模型)【模型解读与图示】“一线三等角”型的图形,因为一条直线上有三个相等的角,一般就会有两个三角形的“一对角相等”,再利用平角为180°,三角形的内角和为180°,就可以得到两个三角形的另外一对角也相等,从而得到两个三角形相似.1)一线三等角模型(同侧型)(锐角型)(直角型)(钝角型)条件:如图,∠1=∠2=∠3,结论:△ACE∽△BED.2)一线三等角模型(异侧型)条件:如图,∠1=∠2=∠3,结论:△ADE∽△BEC.3)一线三等角模型(变异型)图1图2图3①特殊中点型:条件:如图1,若C为AB的中点,结论:△ACE∽△BED∽△ECD.②一线三直角变异型1:条件:如图2,∠ABD=∠AFE=∠BDE=90°.结论:△ABC∽△BDE∽△BFC∽△AFB.③一线三直角变异型2:条件:如图3,∠ABD=∠ACE=∠BDE=90°.结论:△ABM∽△NDE∽△NCM.是边A.3B.5C.2D.1B (1)如图2,在53⨯个方格的纸上,小正方形的顶点为格点、边长均为1,AB 为端点在格点的已知线段.请用三种不...同连接格点.....的方法,作出以线段AB 为等联线、某格点P 为等联点的等联角,并标出等联角,保留作图痕迹;(2)如图3,在Rt APC △中,90A ∠=,AC AP >,延长AP 至点B ,使AB AC =,作A ∠的等联角CPD ∠和PBD ∠.将APC △沿PC 折叠,使点A 落在点M 处,得到MPC ,再延长PM 交BD 的延长线于E ,连接CE 并延长交PD 的延例5.(2022·浙江·嘉兴一中一模)阅读材料:我们知道:一条直线经过等腰直角三角形的直角顶点,过另外两个顶点分别向该直线作垂线,即可得三垂直模型”如图①:在△ABC 中,∠ACB =90°,AC =BC ,分别过A 、B 向经过点C 直线作垂线,垂足分别为D 、E ,我们很容易发现结论:△ADC ≌△CEB .(1)探究问题:如果AC ≠BC ,其他条件不变,如图②,可得到结论;△ADC ∽△CEB .请你说明理由.(2)学以致用:如图③,在平面直角坐标系中,直线y =12x 与直线CD 交于点M (2,1),且两直线夹角为α,且tanα=32,请你求出直线CD 的解析式.(3)拓展应用:如图④,在矩形ABCD 中,AB =4,BC =5,点E 为BC 边上一个动点,连接AE ,将线段AE 绕点E 顺时针旋转90°,点A 落在点P 处,当点P 在矩形ABCD 外部时,连接PC ,PD .若△DPC 为直角三角形时,请你探究并直接写出BE 的长.例6.(2023·浙江·九年级专题练习)在Rt ABC 中,90BAC ∠=︒,2AB AC ==,点D 在BC 所在的直线上运动,作45ADE ∠=︒(A 、D 、E 按逆时针方向).(1)如图,若点D 在线段BC 上运动,DE 交AC 于E .①求证:ABD DCE △△∽;②当ADE V 是等腰三角形时,求AE 的长;(2)如图,若点D 在BC 的延长线上运动,DE 的反向延长线与AC 的延长线相交于点E ',是否存在点D ,使ADE '△是等腰三角形?若存在,求出线段CD 的长度;若不存在,请简要说明理由;(3)若点D 在BC 的反向延长线上运动,是否存在点D ,使ADE V 是等腰三角形?若存在,写出所有点D 的位置;若不存在,请简要说明理由.上一点,轴9,23A.()9,3B.()3.(2023·湖南长沙·九年级专题练习)如图,在矩形4.(2021·浙江台州·中考真题)如图,点E,F,G分别在正方形ABCD的边AB,BC,AD上,AF⊥EG.若AB=5,AE=DG=1,则BF=_____.分别在边6.(2022秋·安徽淮北·九年级校考阶段练习)如图,在四边形分别在线段AD、DC上(点E与点A、CD=,在BC边上取中点E,连接DE,过点E 8.(2023·山东烟台·九年级统考期末)如图,在正方形ABCD中,4做EF ED⊥与AB交于点G,与DA的延长线交于点F.(1)求证:BEG CDE△∽△;(2)求AFG的面积.⊥交AB于点M,9.(2023·上海·九年级假期作业)在矩形ABCD中,3AB=,4=AD,点E是边AD上一点,EM EC∠=∠.(1)求证:AE是AM和AN的比例中项;(2)当点N在线段AB的延点N在射线MB上(如图),且ANE DCE长线上时,联结AC,且AC与NE互相垂直,求MN的长.的两个等腰直角三角形,(3)【拓展探究】在整个运动过程中,请直接写出N点运动的路径长,及CN的最小值.312.(2023·广东深圳·九年级校考阶段练习)如图,在ABC 中6cm AB AC ==,8cm BC =,点E 是线段BC 边上的一动点(不含B 、C 两端点),连接AE ,作AED B ∠=∠,交线段AB 于点D .(1)求证:BDE CEA△∽△(2)设BE x =,AD y =,请求y 与x 之间的函数关系式.(3)E 点在运动的过程中,ADE V 能否构成等腰三角形?若能,求出BE 的长;若不能,请说明理由.13.(2023春·广东深圳·八年级校考期中)【操作发现】如图1,在边长为1个单位长度的小正方形组成的网格中,ABC 的三个顶点均在格点上.①请按要求画图:将ABC 绕点A 顺时针方向旋转90︒,点B 的对应点为点B ',点C 的对应点为点C ',连接BB ';②在①中所画图形中,AB B '∠=______︒.【问题解决】如图2,在Rt ABC △中,190BC C =∠=︒,,延长CA 到D ,使1CD =,将斜边AB 绕点A 顺时针旋转90︒到AE ,连接DE ,求ADE ∠的度数.【拓展延伸】如图3,在四边形ABCD 中,AE BC ⊥,垂足为E ,BAE ADC ∠=∠,1BE CE ==,3CD =,2=AD AB ,求BD 的长.14.(2023·浙江·九年级专题练习)在平面直角坐标系中,O 为坐标原点,直线AB 与y 轴交于点A ,与x 轴交于点B ,2OA =,AOB 的面积为2.(1)如图1,求直线AB 的解析式.(2)如图2,线段OA 上有一点C ,直线BC 为2(0)y kx k k =-<,AD y ⊥轴,将BC 绕点B 顺时针旋转90︒,交AD 于点D ,求点D 的坐标.(用含k 的式子表示)(3)如图3,在(2)的条件下,连接OD ,交直线BC 于点E ,若345ABC BDO ∠-∠=︒,求点E 的坐标.九年级专题练习)某数学兴趣小组在学习了尺规作图、等腰三角形和相似三角形的有关知识后,在BC=.点E是线段AD上的动点(点E不与18.(2022·湖南郴州·中考真题)如图1,在矩形ABCD中,4AB=,6⊥,交AB于点F.点A,D重合),连接CE,过点E作EF CE∽;(1)求证:AEF DCE⊥,垂足为G,连接AG.点M是线段BC的中点,连接GM.(2)如图2,连接CF,过点B作BG CF①求AG GM+的最小值;②当AG GM+取最小值时,求线段DE的长.。
专题02 全等模型-一线三等角(K字)模型(解析版)

专题02全等模型--一线三等角(K 字)模型全等三角形在中考数学几何模块中占据着重要地位,也是学生必须掌握的一块内容,本专题就全等三角形中的重要模型(一线三等角(K 字)模型)进行梳理及对应试题分析,方便掌握。
模型1.一线三等角(K 型图)模型(同侧型)【模型解读】在某条直线上有三个角相等,利用平角为180°与三角形内角和为180°,证得两个三角形全等。
【常见模型及证法】同侧型一线三等角(常见):锐角一线三等角直角一线三等角(“K 型图”)钝角一线三等角条件:A CED B ∠=∠=∠+CE=DE证明思路:,A B C BED ∠=∠∠=∠+任一边相等BED ACE⇒≅ 例1.(2023·江苏·八年级假期作业)探究:如图①,在ABC 中,90BAC ∠=︒,AB AC =,直线m 经过点A ,BD m ⊥于点D ,CE m ⊥于点E ,求证:ABD CAE ≌ .应用:如图②,在ABC 中,AB AC =,,,D A E 三点都在直线m 上,并且有BDA AEC BAC ∠=∠=∠.求出,DE BD 和CE 的关系.拓展:如图①中,若10DE =,梯形BCED 的面积______.【答案】探究:证明过程见详解;应用:DE BD CE =+,理由见详解;拓展:50【分析】探究:90BAC ∠=︒,AB AC =,可知ABC 是等腰直角三角形,BD m ⊥,CE m ⊥,可知90BDA AEC ∠=∠=︒,可求出BAD ACE ∠=∠,根据角角边即可求证;应用:AB AC =,,,D A E 三点都在(1)如图①,若AB AC ⊥,则BD 与AE 的数量关系为___________,CE 与AD 的数量关系为(2)如图②,判断并说明线段BD ,CE 与DE 的数量关系;(3)如图③,若只保持7BDA AEC BD EF cm ∠=∠==,,点A 在线段DE 上以2cm/s 的速度由点例3.(2022·陕西七年级期末)(1)【问题发现】如图1,△ABC与△CDE中,∠B=∠E=∠ACD=90°,AC=CD,B、C、E三点在同一直线上,AB=3,ED=4,则BE=_____.(2)【问题提出】如图2,在Rt△ABC 中,∠ABC=90°,BC=4,过点C作CD⊥AC,且CD=AC,求△BCD的面积.(3)【问题解决】如图3,四边形ABCD中,∠ABC=∠CAB=∠ADC=45°,△ACD面积为12且CD的长为6,求△BCD的面积.【答案】(1)7;(2)S△BCD=8;(3)S△BCD=6.【分析】(1)∠B=∠E=∠ACD=90°,据同角的余角相等,可得∠ACB=∠D,由已知条件可证△ABC≌△CED,运动(D 不与B 、C 重合),连接AD ,作40ADE ∠=︒,DE 交线段AC 于E .(1)当115BDA ∠=︒时,EDC ∠=_____︒,BAD ∠=_____︒,AED =∠_____︒;点D 从B 向C 运动时,BDA ∠逐渐变_____(填“大”或“小”);(2)当DC 等于多少时,ABD DCE ≌△△,请说明理由;(3)在点D 的运动过程中,ADE V 的形状可以是等腰三角形吗?若可以,请直接写出BDA ∠的度数,若不可以,请说明理由.【答案】(1)25,25,65,小(2)当2DC =时,ABD DCE ≌△△,理由见解析;(3)当BDA ∠的度数为110︒或80︒时,ADE V 的形状是等腰三角形.【分析】(1)先求出ADC ∠的度数,即可求出EDC ∠的度数,再利用三角形的外角性质即可求出AED ∠的度数,根据点D 从B 向C 运动时,BAD ∠逐渐增大,而B ∠不变化,180B BAD BDA ∠+∠+∠=︒,即可得到答案;(2)根据全等三角形的判定条件求解即可;(3)先证明当ADE V 时等腰三角形,只存在AD ED =或AE DE =两种情况,然后分这两种情况讨论求解即可;【详解】(1)解:∵115BDA ∠=︒,∴18011565ADC ∠=︒-︒=︒,∵40ADE ∠=︒,∴25EDC ADC ADE ∠︒=∠-∠=,∵ADC ADE EDC B BAD ∠=∠+∠=∠+∠,∴25BAD EDC ∠=∠=︒,∴65AED EDC C ︒∠=∠+∠=;∵点D 从B 向C 运动时,BAD ∠逐渐增大,而B ∠不变化,180B BAD BDA ∠+∠+∠=︒,∴点D 从B 向C 运动时,BDA ∠逐渐变小,故答案为:25,25,65,小;(2)解:当2DC =时,ABD DCE ≌△△,理由:∵40B C ∠=∠=︒,∴140DEC EDC ∠+∠=︒,又∵40ADE ∠=︒,∴140ADB EDC ∠+∠=︒,∴ADB DEC ∠=∠,又∵2AB AC ==,∴()AAS ABD DCE ≌△△;(3)解:当BDA ∠的度数为110°或80°时,ADE V 的形状是等腰三角形,理由:∵40C ADE ∠=∠=︒,AED C EDC ∠=∠+∠,∴AED ADE ∠>∠,∴当ADE V 时等腰三角形,只存在AD ED =或AE DE =两种情况,模型2.一线三等角(K 型图)模型(异侧型)【模型解读】在某条直线上有三个角相等,利用平角为180°与三角形内角和为180°,证得两个三角形全等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一线三等角专题
1.如图,把矩形纸片OABC 放入平面直角坐标系中,使OA 、OC 分别落在x 、y 轴上,连接AC ,将纸片OABC 沿AC 折叠,使点B 落在点D 的位置.若点B 的坐标为(4,8),则点D 的坐标是____. 2.如图,在平面直角坐标系中,直线y= -2x+2与 x 轴、y 轴分别相交于点A 、B ,四边形ABCD 是正方形,曲线在第一象限经过点D.则________.
3.如图,在四边形ABCD 中,AD ∥BC ,AB=DC=AD=6, ∠ABC=∠C=70°,点E 、F 分别在线段AD 、DC 上,且 ∠BEF=110°, 若AE=3,求DF 的长.
4.点E 为线段BC 上一点,若 ∠B=∠AEF =∠C=90°, 连接AF ,AB=7,CF=4,BC=11,当△ABE 与△EFC 相似时,求BE 的长.
5.如图设M 为线段AB 中点,AE 与BD 交于点C ,∠DME=∠A=∠B=α,且DM 交AC 于F ,EM 交BD 于G .
(1)写出图中三对相似三角形,并对其中一对作出证明; (2)连接FG ,设α=45°,AB=4
,AF=3,求FG 长.
6.如图,已知y 1=k 1x+k 1(k 1≠0)与反比例函数 (k 2≠0)的图象交于点A 、C ,其中A 点坐标(1,1).
(1)求反比例函数的解析式;
(2)根据图象写出在第一象限内,当取何值时,y 1<y 2?
(3)若一次函数y 1=k 1x+k 1与x 轴交于B 点,连接OA ,求△AOB 的面积: (4)在(3)的条件下,在坐标轴上是否存在点P ,使△AOP 是等腰三角形?若存在,请写出P 点的坐标;若不存在,请说明理由.
7.已知:在矩形AOBC 中,OB=3,OA=2.分别以OB 、OA 所在直线为x 轴和y 轴,建立如图所示的平面直角坐标系.若点F 是边BC 上的一个动点(不与B 、C 重合),过F 点的反比例函数(k >0)的图象与边交于点E .
(1)直接写出线段AE 、BF 的长(用含k 的代数式表示); 设△AOE 与△FOB 的面积分别为S 1,S 2,求证:S 1=S 2; (3)记△OEF 的面积为S .
①求出S 与k 的函数关系式并写出自变量k 的取值范围;
②以OF 为直径作⊙N ,若点E 恰好在⊙N 上,请求出此时△OEF 的面积S . (4)当点F 在BC 上移动时,△OEF 与△ECF 的面积差记为S ,求当k 为何值时,S 有最大值,最大值是多少?
(5)请探索:是否存在这样的点E ,使得将△CEF 沿EF 对折后,C 点恰好落在OB 上?若存在,求出点E 的坐标;若不存在,请说明理由.
A
B
C
D
O
y x
图4
F
E C
B
A
8.如图1,△ABC 中,AG ⊥BC 于点G ,以A 为直角顶点,分别以AB 、AC 为直角边,向△ABC 作等腰Rt △ABE 和等腰Rt △ACF ,过点E 、F 作射线GA 的垂线,垂足分别为P 、Q . (1)试探究EP 与FQ 之间的数量关系,并证明你的结论;
(2)如图2,若连接EF 交GA 的延长线于H ,由(1)中的结论你能判断EH 与FH 的大小关系吗?并说明理由.
(3)在(2)的条件下,若BC=AG=24,请直接写出S △AEF=______.
(4)如图3,△ABC 中,AG ⊥BC 于点G ,分别以AB 、AC 为一边向△ABC 外作矩形ABME 和矩形ACNF ,射线GA 交EF 于点H. 若AB= k AE ,AC= k AF ,试探究HE 与HF 之间的数量关系,并说明理由.
9.△ABC 中,AB=AC ,D 为BC 的中点,以D 为顶点作∠MDN=∠B (1)如图(1)当射线DN 经过点A 时,DM 交AC 边于点E ,不添加辅助线,写出图中所有与△ADE 相似的三角形.
(2)如图(2),将∠MDN 绕点D 沿逆时针方向旋转,DM ,DN 分别交线段AC ,AB 于E ,F 点(点E 与点
A 不重合),不添加辅助线,写出图中所有的相似三角形,并证明你的结论.
(3)在图(2)中,若AB=AC=10,BC=12,当△DEF 的面积等于△ABC 的面积的1/4 时,求线段EF 的长.
10.等腰△ABC ,AB=AC=8,∠BAC=120°,P 为BC 的中点,小慧拿着含30°角的透明三角板,使30°角的顶点落在点P ,三角板绕P 点旋转. (1)如图a ,当三角板的两边分别交AB 、AC 于点E 、F 时.求证:△BPE ~△CFP ;
(2)操作:将三角板绕点P 旋转到图b 情形时,
三角板的两边分别交BA 的延长线、边AC 于点E 、
F .
① 探究1:△BPE 与△CFP 还相似吗?
② 探究2:连结EF ,△BPE 与△PFE 是否相似?请说明理由; ③ 设EF=m ,△EPF 的面积为S ,试用m 的代数式表示S .
11.如图,在△ABC 中,AB=AC=5cm ,BC=8,点P 为BC 边上一动点(不与点B 、C 重合),过点P 作射线PM 交AC 于点M ,使∠APM=∠B ;
(1)求证:△ABP ∽△PCM ;
(2)设BP=x ,CM=y .求 y 与x 的函数解析式,并写出函数的定义域. (3)当△APM 为等腰三角形时, 求PB 的长.
图3
M
N
G
F
E
C
B
A
H
A
B
P E F
A
B
C
E
F
A
P
M。
