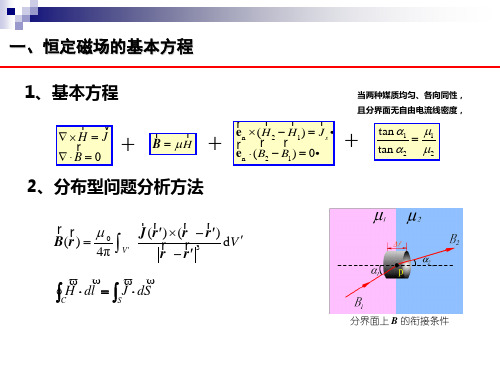
标量磁位和矢量磁位
谢处方《电磁场与电磁波》(第4版)课后习题-第3章 静态电磁场及其边值问题的解【圣才出品】
第3章 静态电磁场及其边值问题的解（一）思考题3.1 电位是如何定义的？中的负号的意义是什么？答：由静电场基本方程▽×E＝0和矢量恒等式可知，电场强度E 可表示为标量函数φ的梯度，即式中的标量函数φ称为静电场的电位函数，简称电位；式中负号表示场强方向与该点电位梯度的方向相反。
3.2“如果空间某一点的电位为零，则该点的电场强度也为零”，这种说法正确吗？为什么？答：不正确。
因为电场强度大小是该点电位的变化率。
3.3“如果空间某一点的电场强度为零，则该点的电位为零”，这种说法正确吗？为什么？答：不正确。
此时该点电位可能是任一个不为零的常数。
3.4 求解电位函数的泊松方程或拉普拉斯方程时，边界条件有何意义？答：边界条件起到给方程定解的作用。
3.5 电容是如何定义的？写出计算电容的基本步骤。
答：两导体系统的电容为任一导体上的总电荷与两导体之间的电位差之比，即其基本计算步骤：①根据导体的几何形状，选取合适坐标系；②假定两导体上分别带电荷＋q和－q；③根据假定电荷求出E；④由求得电位差；⑤求出比值3.6 多导体系统的部分电容是如何定义的？试以考虑地面影响时的平行双导线为例，说明部分电容与等效电容的含义。
答：多导体系统的部分电容是指多导体系统中一个导体在其余导体的影响下，与另一个导体构成的电容。
计及大地影响的平行双线传输线，如图3-1-1所示，它有三个部分电容C11、C12和C22，导线1、2间的等效电容为；导线1和大地间的等效电容为；导线2和大地间的等效电容为图3-1-13.7 计算静电场能量的公式和之间有何联系？在什么条件下二者是一致的？答：表示连续分布电荷系统的静电能量计算公式，虽然只有ρ≠0的区域才对积分有贡献，但不能认为静电场能量只存在于有电荷区域，它只适用静电场。
表示静电场能量存在于整个电场区域，所有E≠0区域对积分都有贡献，既适用于静电场，也用于时变电磁场，当电荷分布在有限区域内，闭合面S无限扩大时，有限区内的电荷可近似为点电荷时，二者是一致的。
电磁场理论课件-5.3矢量磁位
2 ( Ax ex Ay ey Az ez ) 0 (Jx ex J y ey Jz ez )
2A222AAAxzy0J000JJJ可zxy 分解为三AAAzyx个 44标4000量VVV 的JJRJRRzyx泊dddVVV松方CCCzyx程
矢量泊松方程的解为
|2
l
2
e 0I {
( l z) 2
4 2 ( l z)2
2
( l z)
2
}
2 ( l z)2
2
l
l
l
B e 0I {
2
4 2 ( l )2
2
2}
2 ( l )2
2
21:11:50
e 0I 2 e 0I
4
2
15
方法二：先计算矢量磁位 A
再求磁感应强度 B
电流元 Idl在P点产生的矢量磁位为 l
A 0 JdV '
4 V ' R
E
B A
21:21:14
4
5.3 矢量磁位
三、库仑规范 矢量位 A 不是唯一的，它加上任意一个标量 的
梯度后，仍然表示同一个磁场，即
若： B A ，则对于 A A 有 A A A B
而： A A A A 2 0
4 V ' R
0 J (r ')2 ( 1 )dV '
4 V '
R
0 J (r ')[4 (r r ')]dV '
4 V '
0 J (r)
r r'
21:28:59
0
r r'
13
5.3 矢量磁位
《电磁场与电磁波》课程教学大纲
《电磁场与电磁波》课程教学大纲一、课程基本信息课程编码：07S2117B中文名称：电磁场与电磁波英文名称：E1ectromagneticFie1dandE1ectromagneticWave课程类别：专业核心课总学时：48总学分：3适用专业：电子科学与技术专业先修课程：高等数学、大学物理、场论、数学物理方程二、课程性质及目标教学性质：电磁场与电磁波是电子科学与技术专业学生的一门专业核心课程。
通过本课程的学习，要求学生系统地理解电磁场与电磁波的基本概念、基本性质和基本规律，掌握求解电磁场问题的基本方法，为进一步学习其他课程特别是专业课打下基础。
课程目标：1.通过本课程知识的学习，使学生了解电磁场论的发展历程，掌握电磁场论的基本概念、基本性质和基本规律，掌握求解电磁场问题的基本方法，为后续专业课程奠定基础。
引导学生学习科技发展史，树立科技强国意识，感受中国在电子领域的先进成果，激励学生自觉融入到实现中华民族伟大复兴的中国梦进程中。
2.通过本课程知识的学习，使学生掌握电磁场论计算理论的基本方法，并能在具体电子科学与技术专业的具体问题中加以应用。
培养学生解决问题方法的多样性，提高学生数学分析的能力。
3.通过本课程知识的学习，使学生掌握电磁场论分析问题的基本方法，并能在复杂的实际情况中加以应用。
培养学生逻辑思维和创新能力，提高学生设计、开发系统的能力。
不同介质和边界条件对应的场方程形式不同，引导学生用发展的眼光看问题，终身学习，与时俱进，始终拥有先进的理念和较高的职业素养。
I.采用启发式、案例式教学，激发学生主动学习的兴趣，培养学生独立思考、分析问题和解决问题的能力。
2.结合科研生产中的实际例子对课程进行讲解，通过课堂讲解，加强学生对基础知识及基本理论的理解。
3.教学以课堂讲授为主，多媒体辅助教学，提高课堂教学信息量，增强教学的直观性、形象性。
4.通过课内讨论与课外答疑、线下辅导与线上交流相结合的方式，调动学生学习的主观能动性，培养学生的自学能力。
稳恒磁场问题求解
L1 I 12
MI1I 2
1 2
L2
I
2 2
六、磁场能量
【例1】长度为l ,内外导体半径分别为 R1 与 R2 的同轴电缆，通有电流 I ， 试求电缆储存的磁场能量与自感。
【解】由安培环路定律，得
H
I
2
e
I
2 R12
e
I 2
e
0 R1 ••R 1 R2
磁能为 自感
1
a
O
I
b
cIOr来自adrbc e
外磁链
【分析】 该磁通链由三部分磁通形成：外
导体中的磁通，内外导体之间的磁通以及内
导体中的磁通。由于外导体通常很簿，穿过其
内的磁通可以忽略。
I
【解】
由••
H
L
dl
I
Bo
0I
2πr
e •••• a
r
b
Bi
0 Ir
2πa 2
e •••0
r
a
o o
S Bo dS
μ0 I 4π
L L
dz R
ez
ez
μ0 I 4π
L
dz'
L ρ2 (z z')2 1 2
A
ez
μ0 I 4π
ln
ρ2 L z2 L z ρ2 L z2 L z
A
μ0I 2π
ln
2L ρ
ez
(L )
问题：L趋向无限大 该如何处理
B
A
AZ ρ
eφ
μ0 I 2πρ
eφ
A
sin
v B
v A
r er
1
标量位与矢量位
2
A
(
A)
2 A t 2
t
J
2 ( A)
t
已定义了矢量场 A 的旋度， A B ， 必须再规定其散度。
为了简化计算，令
A Φ
t
洛伦兹条件
则前两式可以简化为
2 A 2 A J
t 2
2Φ 2Φ
t 2
仅与电流 J 有 关
仅与电荷 有关
原来两个相互关联的方程变为两个独立方程。
Jr,t r r
A(r,t)
v dV
4π V
r r
式中， V ' 为电流 J 的分布区域。
r2 v2 t2 0
式中 v 1
0 r
上式为函数 ( r) 的齐次波动方程，其通解为
r
f 1t
r v
f
2 t
r v
式中的第二项不符合实际的物理条件，应该舍
去。因此，求得位于原点的时变点电荷产生的标量电
位为
Φ(r,t)
f 1t
r v
r
已知位于原点的静止点电荷 q 产dV生的电位为
4. 标量位与矢量位 设介质是线性均匀且各向同性的，那么由麦
ቤተ መጻሕፍቲ ባይዱ
克斯韦方程可得
E 2 E J
t 2
t
H 2H J
t 2
利用矢量恒等式 A ，同 A时考2虑A 到
及 ，那 么B 上 0述两式 D变为
2 E 2 E J 1
t 2
t
2 H 2 H J
原来电磁场的矢量方程为
2 E 2 E J 1
t 2
t
2 H 2 H J
t 2
在三维空间中需要求解 6 个坐标分量
4.3矢量磁位和标量磁位
'
0 Ia a cos ' x sin ')d ' A ( 1 sin cos ')( y 4r 0 r
x
0 Ia 2 sin A 4r 2
ˆ
A
0 Ia 2 sin ˆ A 2 4r
小电流环也称为磁偶极子
r
大小和方向用磁偶极矩表示
Thinking ！
矢量合成后，得
A
4π
V
JdV R
因此，线电流元引起的磁矢位为
Id l I d l A l 4π R 4π l R
这里事实是给了一种计算磁场的积分方法，先求矢量磁位关于电流的积 分，再对磁位 A 求旋度可得磁场 B 。
矢量磁位 A 、标量磁位 φm 与电位 φ 的比较
例1. 求半径为a电流为I的小电流环在远处(r>>a)的磁场. 0 J (r ' ) 解: 利用矢量磁位计算磁场 A(r ) 4 R dV ' V 对于线电流 JdV ' Idl '
z
取
ˆ' dl ' ad '
A(r ) 0 4
Idl ' R l
取场点
r
r
R
Hale Waihona Puke 源点到场点距离R2
'
I
a
y
ˆ' dl ' ad '
R
2
(r cos ) (r sin ) 2 a 2 2ar sin cos '
r 2 a 2 2ar sin cos '
3.2 矢量磁位
0 1 1 0 a z I a z I ln ln 2 2 r1 r2
0 I r2 a 2 r 2 2ar cos .... ln 2 2 ln A az 2 r a r 2 ar cos 1
B A Aa z A a z 0 A A ar a ? r r
请大家在课后自己完成。
电磁场与电磁波
16
0 I r0 A az ln r 2 A az
0
通常取离开直线电流单位距离 的地方是矢量磁 位的参考0点。 I 1
2
ln
r
13
电磁场与电磁波
例2. 平行(双)传输线周围磁场？
传输线间距：2a 分析：
1. 2. 3. 矢量磁位的方向 磁通密度的方向 如何建立柱座标系？
矢量磁位的方向？
• 与电流同向 • 有时与电流元成简单的线性关系 • 二阶偏微分方程常可分解成标量泊松方程形式
电磁场与电磁波
5
小结
矢量磁位(Vector Mag… Po…)
磁通密度(… Density) B
A
B 0 B 0 J 磁场强度(Magnetic Field Intensity) H B
§3.2 矢量磁位(Vector Magnetic Potential)
在§3.1曾推出——
A 矢量磁位
0 I dl B A 4 C R
由……定理可知：还需要规定 A的散度，才能确定A
电磁场的矢量势与标量势在电磁场计算中的转换
电磁场的矢量势与标量势在电磁场计算中的转换电磁场理论是描述电磁相互作用的基础理论之一，在电磁场的计算和分析中，矢量势和标量势是非常重要的概念。
这两个势函数在电磁场的描述和推导中起着至关重要的作用，通过它们的转换可以简化复杂的计算过程，提供了解释电磁场现象的新视角。
矢量势和标量势的定义矢量势是一种矢量场，用来描述电荷体系产生的电磁场。
矢量势的定义如下：\\[ \mathbf{A} = \frac{\mu_0}{4\pi} \int\frac{\mathbf{J}(\mathbf{r’})}{|\mathbf{r}-\mathbf{r’}|} d\tau’ \\] 其中，$\\mathbf{A}$ 是矢量势，$\\mathbf{J}$ 是电流密度，$\\mu_0$ 是真空中的磁导率，$\\mathbf{r}$ 是观察点的位置，$\\mathbf{r'}$ 是积分变量，$d\\tau'$ 是体积元。
标量势是一种标量场，用来描述电荷体系的电势分布。
标量势的定义如下：\\[ \Phi = \frac{1}{4\pi\epsilon_0} \int \frac{\rho(\mathbf{r’})}{|\mathbf{r}-\mathbf{r’}|} d\tau’ \\] 其中，$\\Phi$ 是标量势，$\\rho$ 是电荷密度，$\\epsilon_0$ 是真空中的介电常数。
矢量势和标量势之间的关系根据麦克斯韦方程组的推导，可以得到矢量势和标量势之间的关系。
电磁场的矢量势和标量势之间的转换关系为： \\[ \mathbf{E} = -abla \Phi - \frac{\partial \mathbf{A}}{\partial t} \\] \\[ \mathbf{B} =abla \times \mathbf{A} \\] 其中，$\\mathbf{E}$ 和 $\\mathbf{B}$ 分别是电场和磁场。
标量位与矢量位
r'
dV'
V' r
ﾢ r' - r (r, t)
(r,t)
1 4π
� � �rﾢ,t
r
rﾢ� v � �dV ﾢ
Vﾢ
r rﾢ
O
y
x
将矢量位方程在直角坐标系中展开，则矢量位
A 各个分量均满足结构相同的非齐次标量波动方程式
即，
2 Ax
2 Ax t 2
J x
2 Ay
2 Ay t 2
J y
O
x
y 空间，位函数 满足的方程式为
2 ( r) r 2
1 v2
2 ( t 2
r)
0
式中 v 1
0r
上式为函数 ( r) 的齐次波动方程，其通解为
r
f1
t
r v
f
2
t
r v
式中的第二项不符合实际的物理条件，应该舍
去。因此，求得位于原点的时变点电荷产生的标量电
位为
Φ(r,t)
f1
t
r v
已知 B 0 ，因此 B 可以表示为矢量场 A 的旋度。
即
B A
式中， A 称为矢量位。
将上式代入式 得
E
E
B t
t
(
中，
A)
上式又可改写为
E
A t
0
可见，矢量场
E
A t
为无旋场。因此可以表示
为一个标量场 的梯度，即
E
A t
式中 称为标量位。求得
E
A t
当 A 与时间无关时
4. 标量位与矢量位
设介质是线性均匀且各向同性的，那么由麦
3.4矢量磁位3.5磁偶极子
Chap.3 恒定电流的电场和磁场—§3.5 磁偶极子
单个电流元在场点产生矢量位dA的 分量（即y分量）
dA
0 Idl cos
4π R
0 Iad cos
4π R
由此得出，载流回路在P点产生的矢量位为
A A e dA e
2π 0
0 Ia cos d 4π R
0 J A dV 4 v R
(体电流)
同理，面电流JsdS、线电流Idl产生的矢量位分别为
Js A dS s 4π R 4π R
0 I
0
(面电流)
I A dl c 4π R 4π R
0 I
0
(线电流)
Chap.3 恒定电流的电场和磁场— §3.4 矢量磁位
可见，两者的磁场相同。与其相对应的电流分布为
J1 J 2 1
0
B1
1
0ቤተ መጻሕፍቲ ባይዱ
(ex cos y ey sin x)
可以验证，矢量位A1满足矢量泊松方程，即
2 A1 0 J1 2 A2 0 J2
可以验证，矢量位A2不满足矢量泊松方程，即
Chap.3 恒定电流的电场和磁场—§3.5 磁偶极子
二、磁偶极子的矢量位
z
P(r , ,0)
半径为a，载流为I的磁偶极子位于xoy平面内， 选取球坐标系如图1所示。
r
R
y
r'
y
Idl2
Idl1
dA1
Idl π 2 (a, , ) 2
π Idl1 (a, , ) 2
x
2dA
dA2
x
第三章 恒定磁场(3)-new
AZ1 =
µJ z
4
(a
2
−ρ
2
),
AZ 2 =
µ0 J z a
2
2
ln
a
ρ
磁感应强度
eφ r r ∂Az v 2 B = ∇× A = − eφ = 2 µ0 J z a v ∂ρ eφ 2ρ
µ Jzρ v
0<ρ ≤a a<ρ <∞
磁位 ϕm与磁矢位 A 磁位 (ϕm ) 适用区域 无电流分布区域
（2）根据 H1t − H2t = K
µ1 µ 2 r r 1 1 ∴ (∇ × A1 ) t − (∇ × A2 ) t = K µ1 µ2 r r v 1 1 v 或 ∴ ( ∇ × A1 − ∇ × A2 ) × en = K µ1 µ2
对于平行平面场， 对于平行平面场，则可写成
, 有
B1t
s s l
wb
在工程数值中经常用此公式计算磁通， 在工程数值中经常用此公式计算磁通，并由此 得到其它等效参数。 得到其它等效参数。 4.边值型问题 边值型问题 当电流分布已知，利用磁矢位A的泊松方程 当电流分布已知，利用磁矢位 的泊松方程 和边界条件求A与 。 和边界条件求 与B。
v v 长直圆柱， 例：长直圆柱，均匀分布体积电流 J = J z ez ，圆 柱半径为 a ，磁导率为 µ ，求圆柱导体内外的磁
0r
a<ρ ≤∞
通解为， 通解为， 边界条件
4 Az 2 ( ρ ) = C3 ln ρ + C4
Az1(ρ) = −
µJ z
ρ + C1 ln ρ + C2
2
(1)
( 2)
(5)
Az1
电磁场与电磁波名词解释复习
安培环路定律1）真空中的安培环路定律在真空的磁场中，沿随意回路取 B 的线积分，其值等于真空的磁导率乘以穿过该回路所限制面积上的电流的代数和。
即2）一般形式的安培环路定律在随意磁场中，磁场强度 H 沿任一闭合路径的线积分等于穿过该回路所包围面积的自由电流（不包含磁化电流）的代数和。
即B( 返回顶端 )边值问题1）静电场的边值问题静电场边值问题就是在给定第一类、第二类或第三类界限条件下，求电位函数的泊松方程() 或拉普拉斯方程() 定解的问题。
2）恒定电场的边值问题在恒定电场中，电位函数也知足拉普拉斯方程。
好多恒定电场的问题，都可归纳为在必定条件下求拉普拉斯方程 () 的解答，称之为恒定电场的边值问题。
3）恒定磁场的边值问题（ 1）磁矢位的边值问题磁矢位在媒质分界面上知足的连接条件和它所知足的微分方程以及场域上给定的界限条件一同构成了描绘恒定磁场的边值问题。
关于平行平面磁场，分界面上的连接条件是磁矢位 A 所知足的微分方程（ 2）磁位的边值问题在平均媒质中，磁位也知足拉普拉斯方程。
磁位拉普拉斯方程和磁位在媒质分界面上知足的连接条件以及场域上界限条件一同构成了用磁位描绘恒定磁场的边值问题。
磁位知足的拉普拉斯方程两种不一样媒质分界面上的连接条件界限条件1．静电场界限条件在场域的界限面S 上给定界限条件的方式有：第一类界限条件( 狄里赫利条件，Dirichlet)已知界限上导体的电位第二类界限条件（聂以曼条件Neumann)已知界限上电位的法导游数( 即电荷面密度或电力线)第三类界限条件已知界限上电位及电位法导游数的线性组合静电场分界面上的连接条件和称为静电场中分界面上的连接条件。
前者表示，分界面双侧的电通量密度的法线重量不连续，其不连续量就等于分界面上的自由电荷面密度；后者表示分界面双侧电场强度的切线重量连续。
电位函数表示的分界面上的连接条件和，前者表示，在电介质分界面上，电位是连续的；后者表示，一般状况下, 电位的导数是不连续的。
电磁场与电磁波(杨儒贵_版)课后思考题答案
电磁场与波课后思考题1-1 什么是标量与矢量?举例说明.仅具有大小特征的量称为标量.如:长度,面积,体积,温度,气压,密度,质量,能量及电位移等.不仅具有大小而且具有方向特征的量称为矢量.如:力,位移,速度,加速度,电场强度及磁场强度.1-2 矢量加减运算及矢量与标量的乘法运算的几何意义是什么?矢量加减运算表示空间位移.矢量与标量的乘法运算表示矢量的伸缩.1-3 矢量的标积与矢积的代数定义及几何意义是什么? 矢量的标积: ,A 矢量的模与矢量B 在矢量A 方向上的投影大小的乘积.矢积: 矢积的方向与矢量A,B 都垂直,且由矢量A 旋转到B,并与矢积构成右 旋关系,大小为1-4 什么是单位矢量?写出单位矢量在直角坐标中的表达式. 模为1的矢量称为单位矢量.1-5 梯度与方向导数的关系是什么?试述梯度的几何意义,写出梯度在直角坐标中的表示式.标量场在某点梯度的大小等于该点的最大方向导数, 方向为该点具有最大方向导数的方向.梯度方向垂直于等值面，指向标量场数值增大的方向在直角坐标中的表示式: 1-6 什么是矢量场的通量?通量值为正,负或零时分别代表什么意义?矢量A 沿某一有向曲面S 的面积分称为矢量A 通过该有向曲面S 的通量,以标量表示，即 通量为零时表示该闭合面中没有矢量穿过. 通量为正时表示闭合面中有源;通量为负时表示闭合面中有洞.1-7 给出散度的定义及其在直角坐标中的表示式. 散度：当闭合面S 向某点无限收缩时，矢量A 通过该闭合面S 的通量 与该闭合面包围的体积之比的极限称为矢量场A 在该点的散度。
直角坐标形式： 1-8 试述散度的物理概念,散度值为正,负或零时分别表示什么意义?物理概念：通过包围单位体积闭合面的通量。
散度为正时表示辐散,为负时表示辐合,为零时表示无能量流过.1-9 试述散度定理及其物理概念.散度定理:建立了区域 V 中的场和包围区域V 的闭合面S 上的场之间的关系θcos B A B A B A B A B A z z y y x x =++=⋅z y x z y x z y x B B B A A A e e e B A =⨯θsin B A e z θsin B A a e zy x e e e γβαcos cos cos ++=z y x e ze y e x ∂∂+∂∂+∂∂=∇⎰⋅=S S A Ψ d VS V Δd lim div 0Δ⎰⋅=→S A A zA y A x A A div z y x ∂∂+∂∂+∂∂= A ⋅∇=物理概念: 散度定理建立了区域 V 中的场和包围区域 V 的闭合面 S 上的场之间的关系。
4.3矢量磁位和标量磁位
l
Id l R
I
4π
l
dl R
这里事实是给了一种计算磁场的积分方法，先求矢量磁位关于电流的积
分，再对磁位 A 求旋度可得磁场 B 。
矢量磁位 A 、标量磁位 φm 与电位 φ 的比较
例1.
解:
取
求d利对半l用'于径矢线为a量d电a电磁流'流位ˆ'为计JdI算的VA磁'小(r场电)Idl流'4环0 A在l(rI远)dRl处'4(0r>V>aJ)的(Rr'磁)dV场' .
ISnˆ
a
I
A
m
ISnˆ
Ia 2 zˆ
0msin 0m
4r 2
4r 2
r
B A
B
m 0
(rˆ2 cos
ˆsin )
4r 3
R
m
r
r'
A(r )
0m
R
4R2
Thinking ！
2
ˆ' ( yˆ cos' xˆ sin' )
A
0 Ia
2
(1
a
sin
cos')( y cos'x sin')d'
4r 0 r
ˆ
A
0Ia2 sin
4r 2
z
I
y
பைடு நூலகம்
' a
dl ' ad'ˆ'
y ˆ'
'
' x
A
A
0Ia2 sin
4r 2
ˆ
小电流环也称为磁偶极子
《电磁场与电磁波》（第四版）习题集：第4章时变电磁场
《电磁场与电磁波》（第四版）习题集：第4章时变电磁场第4章时变电磁场在时变的情况下，电场和磁场相互激励，在空间形成电磁波，时变电磁场的能量以电磁波的形式进行传播。
电磁场的波动方程描述了电磁场的波动性，本章首先对电磁场的波动方程进行讨论。
在时变电磁场的情况下，也可以引入辅助位函数来描述电磁场，使一些复杂问题的分析求解过程得以简化。
本章对时变电磁场的位函数及其微分方程进行了讨论。
电磁能量一如其它能量服从能量守恒原理，本章将讨论电磁场的能流和表征电磁场能量守恒关系的坡印廷定理。
本章在最后讨论了随时间按正弦函数变化的时变电磁场，这种时变电磁场称为时谐电磁场或正弦电磁场。
4. 1 波动方程由麦克斯韦方程可以建立电磁场的波动方程，揭示了时变电磁场的运动规律，即电磁场的波动性。
下面建立无源空间中电磁场的波动方程。
在无源空间中，电流密度和电荷密度处处为零，即0ρ=、0=J 。
在线性、各向同性的均匀媒质中，E 和H 满足的麦克斯韦方程为t ε=?EH （4.1.1） tμ=-?HE （4.1.2） 0?=H （4.1.3） 0?=E （4.1.4）对式（4.1.2）两边取旋度，有()()tμ=-E H 将式（4.1.1）代入上式，得到22()0t με+=?EE利用矢量恒等式2()()=??-?E E E 和式（4.1.4），可得到2220tμε??-=?EE （4.1.5）此式即为无源区域中电场强度矢量E 满足的波动方程。
同理可得到无源区域中磁场强度矢量H 满足的波动方程为2220tμε??-=?H H （4.1.6）无源区域中的E 或H 可以通过求解式（4.1.5）或式（4.1.6）的波动方程得到。
在直角坐标系中，波动方程可以分解为三个标量方程，每个方程中只含有一个场分量。
例如，式（4.1.5）可以分解为222222220x x x xE E E E x y z tμε++-= （4.1.7） 222222220yyyyE E E E x y z t με++-= （4.1.8）222222220z z z zE E E E x y z t με++-= （4.1.9）在其它坐标系中分解得到的三个标量方程都具有复杂的形式。
《电磁场与电磁波》恒定磁场
分界面磁化电流: Km (M1 M2 ) en
Im
M dl
l
安培环路定理
1.真空中的安培环路定理
l B dl 0 I
真空磁场中，磁感应强度沿任意回路的 环路积分等于真空的磁导率乘以穿过该 回路所限定面的电流的代数和；
2.一般形式的安培环路定理
l B dl 0 ( I Im )
H dl H dl I
PaQ
PbQ
c
I
闭合回路PaQcP：
Q
H dl 2I PaQcP
H dl H dl 2I
PaQ
PcQ
规定:积分路径不穿过电流回路所限定的面。
2.标量磁位的边值问题 微分方程
B 0
H 0
H m
m 0
m m 0 均匀媒质：=0
2m 0 标量磁位的微分方程
Sd
（1）常磁链系统：
Wm
1 2
H BdV
V
V
B2 dV
20
B2Sd
2d
20 20S
f
Wm g
k const
2 20 S
吸力：F 2 f
3.虚位移法举例
例：分析电磁铁吸力，气隙截面积S，长d
1. 恒定磁场基本方程 恒定磁场的性质可由下面一组基本方程描述：
磁通连续性定理 SB dS 0 安培环路定理 l H dl I
各向同性线性媒质的构成方程
B 0 H J
B H
恒定磁场的性质：有旋无散。
2.分界面的衔接条件
B 的衔接条件
2
B2n B2
S h
1 B1
B1n
SB dS 0
B1nS B2nS 0 B1n B2n
关于矢量磁位
A
er
(
1 r
Az
A z
)
e
(
Ar z
Az r
)
ez
[
1 r
(rA r
)
1 r
Ar
]
er
1 r
Az
e
Az r
e
Az r
e
r
lim
L
0I 4
ln 4(
L2 r2
z 2)
e
lim
L
0I 4
r2 4(L2
z2)
2 4(L2 r3
z2)
0I 2 r
e
。
可见，虽然空间各点的矢量磁位都等于无穷大，但仍然有 B A 。
下面我们要说明，空间里的矢量磁位处处为无穷大，也不会妨碍我们用它来 计算磁感应强度。
先来看一个问题：求长度为 2L，通以电流 I 的直导线外任一点 P 的矢量磁 位。
4
根据式（11），取 C 0 ，则电流 元 I d l 激发的矢量磁位
dA
0 4
I dl 。
R
根据叠加原理，直电流激发的矢量
的磁场的边值关系，请同学们看课件。当然，这里存在一个问题，就是矢量磁位
的边界条件如何确定？在实际问题中，根据对称性，可以做合理的猜测。当边界
条件不能完全确定，导致 A 中包含了未知的组分 时，并不影响磁感应强度的
确定。磁场的计算与设计是一个技术含量很高的领域，如果某人精于此道，他已
经是国家的高科技人才了，他是不会憋屈在我们这样一所三流大学里的。
2
1
4
f dV C 。 VR
（6）
方程（4）可以写成 2 Ai
fi 1
第5章 恒定磁场2—矢量磁位
（4）矢量磁位媒质交界面条件
12
=A A 因此，分界面上矢量磁位A 是连续的。
120 d 0 n S
n
A A ∇⋅=⇒⋅==⇒⎰A A S 12 d d S
t C
t
A A ∇⨯=⇒⋅==⋅⇒⎰⎰A
B A l B S 但这只是A 本身的要求。
作为位函数，A 必须满足更高的要求，保证B 的连续性条件成立。
由A 的性质，不难得到：
在无限大均匀媒质中，如果电流只有一个方向，则A与之同方向：
const A=
z
在电磁场分析中，A 具有以下一些有用的性质：•在轴对称场中，等 A 线是磁力线。
轴对称场中，如果电流只有周向分量，（媒质分布也满足轴对称条件），则A也只有周向分量。
轴对称线圈（带或者不带铁心）即属此种情况。
可见，不管是平行平面场还是轴对称场，矢量磁位A都只有一个方向的分量（但磁场B具有两个分量），因此只需要求解一个标量方程即可。
因此在工程实践中，二维恒定磁场一般都采用矢量磁位A进行计算。
使用矢量磁位A 分析磁场B
•用A描述的矢量泊松方程与以B 和H 描述的恒定磁场基本方程是等价的。
•矢量磁位A 的引入是为了简化磁场的分析。
分析磁场的常用方法是：先求A，再由A 计算B。
•求解矢量磁位A，可以使用积分公式，也可以求解A 的泊松方程边值问题。
后者是广泛采用的途径。
等位线
电场线
sin )
θθsin )
θθe
（by ANSYS）
电力线等 线等A 线、磁力线
思考：A 线是什么样子的呢？
作业：
5.14, 5. 17。
电磁场名词解释
“电磁场”:名词解释请点击所要查询名词的首字母A B C D E F G H I J K L M N O P Q R S T U V W X Y ZA(返回顶端)安培环路定律1）真空中的安培环路定律在真空的磁场中，沿任意回路取B的线积分，其值等于真空的磁导率乘以穿过该回路所限定面积上的电流的代数和。
即2）一般形式的安培环路定律在任意磁场中，磁场强度H沿任一闭合路径的线积分等于穿过该回路所包围面积的自由电流（不包括磁化电流）的代数和。
即B(返回顶端)边值问题1）静电场的边值问题静电场边值问题就是在给定第一类、第二类或第三类边界条件下，求电位函数的泊松方程()或拉普拉斯方程()定解的问题。
2）恒定电场的边值问题在恒定电场中，电位函数也满足拉普拉斯方程。
很多恒定电场的问题，都可归结为在一定条件下求拉普拉斯方程()的解答，称之为恒定电场的边值问题。
3）恒定磁场的边值问题（1）磁矢位的边值问题磁矢位在媒质分界面上满足的衔接条件和它所满足的微分方程以及场域上给定的边界条件一起构成了描述恒定磁场的边值问题。
对于平行平面磁场，分界面上的衔接条件是磁矢位A所满足的微分方程（2）磁位的边值问题在均匀媒质中，磁位也满足拉普拉斯方程。
磁位拉普拉斯方程和磁位在媒质分界面上满足的衔接条件以及场域上边界条件一起构成了用磁位描述恒定磁场的边值问题。
磁位满足的拉普拉斯方程两种不同媒质分界面上的衔接条件边界条件1．静电场边界条件在场域的边界面S上给定边界条件的方式有：第一类边界条件(狄里赫利条件，Dirichlet)已知边界上导体的电位第二类边界条件（聂以曼条件 Neumann)已知边界上电位的法向导数(即电荷面密度或电力线)第三类边界条件已知边界上电位及电位法向导数的线性组合静电场分界面上的衔接条件和称为静电场中分界面上的衔接条件。
前者表明，分界面两侧的电通量密度的法线分量不连续，其不连续量就等于分界面上的自由电荷面密度；后者表明分界面两侧电场强度的切线分量连续。
5.7 标量磁位
3）可利用静电类比法求解。在静电场中我们得到
1 2 q q k12 q 1 2 2 2 q q (1 k12 )q 1 2
1
将上式中的
I
，得到
I 21 I 2 1
2 1 I 2 1
利用图中所示的位置关系和安培回路定律，容易写出 两个区域的磁感应强度的表达式
a 3 (er cos e sin ) H 0 (e r 2 A1 cos e A1 sin )[( ) H 0 ] r a 3 e z H 0 (e r 2 cos e sin )[( ) A1H 0 ] (r a) 6 r
01:56
上式中第一项为原外磁场 e z H 0，第二顶为磁介质球磁 化后产生的磁场，它等效于磁偶极子产生的磁场强度。 而球内的磁场强度为 30 H 2 (er cos e sin ) A2 H 0 e z H0 2 0 0 ez [H0 H0 ] H 0 H m ra 2 0 0 H0 式中 H m e z ( H m ) e z 2 0
在磁介质分界（ y 0）处，有
A1 | y 0 A2 | y 0
1 A1 1 A2 | y 0 | y 0 1 z 2 z
由此得到
I
1 ( I I ) 2 I
I I I
联立求解可得
2 1 I 2 1
a 3 H e z H 0 (er 2 cos e sin )[( ) A1 H 0 ] r
(r a)
是磁化介质球在球内产生的一个反向磁场。
01:56 7
例2：设磁导率为 和 的两种磁 介质的分界面是一个无限大平面， 1 在 的介质中距离分界面为d处 置有一与分界面平行的无限长线 电流I，求空间各处的磁感应强度。 解：1）用镜象法求解。 设想用镜像电流代替磁化电流的作用，并在界面上保 持原有边界条件不变。