同济版高等数学教案定积分
高等数学教案-定积分及其应用

的面积.
b
b
2. 当 函 数 f (x) 在 [a, b]上 非 正 时 , f (x)dx 的 值 是 一 个 负 值 , f (x)dx 表 示 由 y f (x) , 直 线
a
a
x a, x b 和 x 轴所围成的曲边梯形(在 x 轴的下方)的面积的相反数.
3.当函数
f
b
(x) 在区间[a,b] 上有正有负时,定积分 a
3 dx
例 4.求定积分(1) 1 1 x2 ;
9
(2)
4
x 1
x dx .
1
例 5.求定积分 |1 x | dx . 2
2x 1, x≤2,
例 6.设
f
(x)
1
x2,
2
求 k (2 k x≤4,
2)
的值,使
3 f (x)dx 40 .
k
3
例 7.一辆汽车正以 10 m/s 的速度匀速直线行驶,突然发现一障碍物,于是以-1 m/s2 的加速度减速,求汽
a
a
x
[a,b] 上的函数, 称为积分上限函数, 记作 ( x) f (t)dt , x [a,b] . a
x
2.定理:设函数 f (x) 在区间[a,b] 上连续,则积分上限函数 ( x) f (t)dt 在区间[a,b] 上可导,且 a
(x) ( x f (t)dt) f (x), x [a,b] . a
例 15.求定积分 x arctan x dx . 0
例 16.某工厂排出大量废气,造成了严重污染,于是工厂通过减产来控制废气的排放量,若第 t 年废气的
排放量为
C(t)
20 ln(t 1) (t 1)2
定积分的概念说课稿

定积分的概念说课稿基础教学部高黎明一、教材分析 1、教材的地位和作用本节课选自同济大学《高等数学》第五章第一节定积分的概念与性质,是上承导数、不定积分,下接定积分在几何学及物理学等学科中的应用。
定积分的应用在高职院校理工类各专业课程中十分普遍。
2、教学目标根据教材内容及教学大纲要求,参照学生现有的知识水平和理解能力,确定本节课的教学目标为:(1)知识目标:理解定积分的基本思想和概念的形成过程,掌握解决积分学问题的“四步曲”。
(2)能力目标:培养学生分析和解决问题的能力,培养学生归纳总结能力,为后续的学习打下基础。
(3)情感目标:从实践中创设情境,渗透“化整为零零积整”的辩证唯物观。
3、教学重点和难点教学重点:定积分的概念和思想。
教学难点:理解定积分的概念,领会定积分的思想。
二、教法和学法 1、教法方面以讲授为主:案例教学法(引入概念),问题驱动法(加深理解),练习法(巩固知识),直观性教学法(变抽象为具体)。
2、学法方面板书教学为主,多媒体课件为辅(化解难点、保证重点)。
(1)发现法解决第一个案例;(2)模仿法解决第二个案例;(3)归纳法总结出概念;(4)练习法巩固加深理解。
三、教学程序 1、导入新课:实例1:曲边梯形的面积如何求?首先用多媒体演示一个曲边梯形,然后提出问题:(1)什么是曲边梯形?(2)有关历史:简单介绍割圆术及微积分背景。
(3)探究:提出几个问题(注意启发与探究)。
a、能否直接求出面积的准确值?b、用什么图形的面积来代替曲边梯形的面积呢?三角形、矩形、梯形?采用一个矩形的面积来近似与二个矩形的面积来近似,一般来说哪个值更接近?二个矩形与三个相比呢???探究阶段、概念引入阶段、创设情境、抛砖引玉。
(4)猜想:让学生大胆设想,使用什么方法,可使误差越来越小,直到为零?(5)论证:多媒体图像演示,直观形象模拟,让学生逐步观察到求出面积的方法。
(6)教师讲解分析:“分割成块、近似代替、积累求和、无穷累加”的微积分思想方法。
高等数学同济教案

高等数学同济教案教案标题:高等数学同济教案教案目标:1. 理解高等数学的基本概念和原理。
2. 掌握高等数学的基本运算和方法。
3. 培养学生的数学思维和解决问题的能力。
4. 培养学生的数学推理和证明能力。
教案内容:课时一:导数与微分1. 导数的定义和性质2. 导数的计算方法和应用3. 微分的定义和性质4. 微分的计算方法和应用课时二:不定积分与定积分1. 不定积分的定义和性质2. 不定积分的计算方法和应用3. 定积分的定义和性质4. 定积分的计算方法和应用课时三:微分方程1. 微分方程的基本概念和分类2. 一阶常微分方程的解法3. 二阶常微分方程的解法4. 微分方程的应用课时四:级数与数项级数1. 级数的概念和性质2. 数项级数的概念和性质3. 数项级数的收敛性判定4. 数项级数的求和方法教学方法:1. 讲授结合实例:通过具体的例子引入新的概念和原理,帮助学生理解和记忆。
2. 案例分析:选取一些实际问题,引导学生运用所学知识解决问题,培养学生的应用能力。
3. 互动讨论:鼓励学生在课堂上提问和讨论,促进学生的思维活跃和合作学习。
4. 课堂练习:安排一定数量的练习题,巩固学生的基本运算和方法。
评估方式:1. 课堂表现:学生在课堂上的积极参与和回答问题的能力。
2. 作业完成情况:学生按时完成作业并正确计算和解答问题的能力。
3. 小测验:定期进行小测验,检验学生对所学知识的掌握程度。
4. 期末考试:综合考察学生对整个学期所学内容的理解和应用能力。
教学资源:1. 教材:《高等数学同济版》2. 多媒体教学资源:投影仪、电脑、PPT等3. 额外练习题和习题解析:辅助教材、习题集等教学建议:1. 鼓励学生主动思考和解决问题,培养他们的数学思维和解决问题的能力。
2. 注重理论与实践的结合,通过实际问题的引入,增加学生对数学知识的兴趣和应用意识。
3. 给予学生足够的练习机会,巩固基本运算和方法,提高他们的计算和解题能力。
高等数学同济七版第五章电子教案
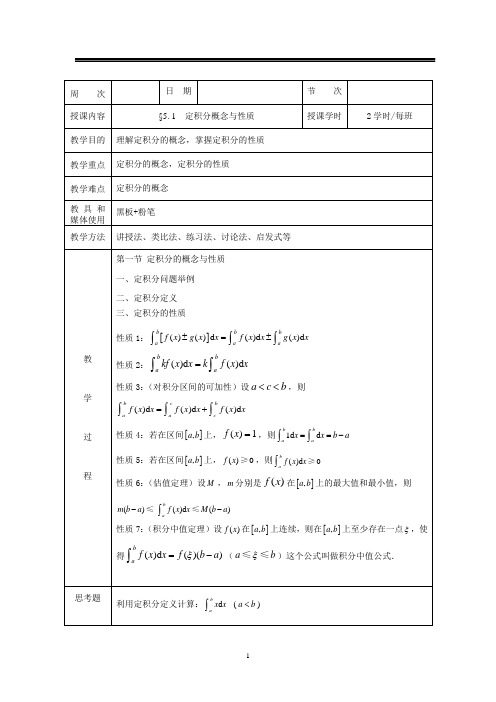
第五章 定积分第一节 定积分的概念与性质一、引例1.曲边梯形的面积定义:将由曲线()y f x =(()0f x ≥且是连续的),直线x a =,x b =和x轴围成的平面图形称为曲边梯形.它在x 轴上的边称为底边,曲线弧()y f x =称为它的曲边.求曲边梯形面积的具体过程如下: 分割:在(,)a b 内任意插入1n -个分点0121n n a x x x x x b -=<<<⋅⋅⋅<<=把[],a b 分成n 个小区间[]1,i i x x -, 它们的长度分别记1ii i x x x -∆=-,1,2,,i n =⋅⋅⋅求近似:任意取一点[]1,i i i x x ξ-∈,1()()()i i i i i i A f x x f x ξξ-∆≈⋅-=∆ 求和:11()n niiii i A A f x ξ===∆≈∆∑∑取极限:01lim ()niii A f xλξ==∆∑→,其中1max{}i i nx λ=∆≤≤ 2.变速直线运动的路程设一物体作直线运动,其速度为()0v v t =≥是时间间隔[]12,T T 上的连续函数,计算在这段时间间隔内物体所经过的位移s . 具体计算步骤如下:分割:在12(,)T T 中任意插入1n -个分点,101212n n T t t t t t T -=<<<⋅⋅⋅<<= 将[]12,T T 分成n 个小时间段[]1,i i t t -,各小时间段的长度分别记为1ii i tt t -∆=-,1,2,,i n =⋅⋅⋅求近似:任意取一点[]1,i i i t t η-∈,()i i i s v t η∆≈⋅∆ 求和:11()n niiii i s s v tη===∆≈∆∑∑取极限:01lim ()ni i i s v t λη==∆∑→,其中1max{}i i nt λ=∆≤≤二、定积分的定义定义:设函数()f x 在[],a b 上有界.在(,)a b 内任意插入1n -个分点,0121n n a x x x x x b -=<<<⋅⋅⋅<<=,把[],a b 分成n个小区间[]1,i i x x -,各个小区间的长度记为1ii i x x x -∆=-,1,2,,i n =⋅⋅⋅.在每个小区间上任取一点i ξ,即1i i i x x ξ-≤≤,作函数值()i f ξ与小区间长度i x ∆的乘积()i i f x ξ∆,并求出和1()ni i i S f x ξ==∆∑.记1max{}ii nx λ=∆≤≤,如果不论对[],a b 怎样划分,也不论在小区间上如何选取点i ξ,只要当0λ→时,和S 总趋于确定的极限I ,那么称这个极限I 为函数()f x 在区间[],a b 上的定积分(简称积分),记作()d b af x x ⎰,即01()d lim ()nbi i a i f x x I f x λξ===∆∑⎰→其中()f x 叫做被积函数,()d f x x 叫做被积表达式,x 叫做积分变量,a 叫做积分下限,b 叫做积分上限,[],a b 叫做积分区间.如果()f x 在区间[],a b 上的定积分存在,则称函数()f x 在区间[],a b 上可积.注:()d ba f x x ⎰与被积函数()f x 和积分区间[],ab 有关,而与积分变量用什么记号无关.如()d ()d ()d b b baaaf x x f t t f u u ==⎰⎰⎰定理:若函数()f x 在区间[],a b 上连续,则()f x 在[],a b 上可积;定理:若函数()f x 在区间[],a b 上有界,且只有有限个间断点,则()f x 在[],a b 上可积. 几何意义:当()0f x ≥,则()d b af x x ⎰表示由曲线()y f x =,直线x a =,x b =,0y =所围成的曲边梯形的面积A ,即 ()d ba f x x A =⎰当()0f x ≤,()d ba f x x ⎰是个负值,它在几何上表示上述曲边梯形面积A 的负值,即()d b af x x A =-⎰当()f x 的值既有正值也有负值,()d b af x x ⎰在几何上表示图形中各部分面积的代数和.图5-2例:利用定积分的几何意义求定积分的值 (1)10(1)d x x -⎰;(2)1201d x x -⎰解:(1)1011(1)d 1122∆-==⨯⨯=⎰OAB x x S (2)122011d 144x x π-=⋅π⋅=⎰例:利用定积分计算120d x x ⎰解:因为函数2()f x x =在区间[]0,1上连续,()f x 在[]0,1上可积,所以积分与[]0,1的分法及i ξ的取法无关.(1)分割:为了计算方便,不妨将区间[]0,1n 等分,分点取,1,2,,1i i x i n n ==⋅⋅⋅-,区间[]1,i i x x -的长度1i x n∆=,1,2,,i n =⋅⋅⋅;(2)近似代替:取i i x ξ=,1,2,,i n =⋅⋅⋅,作积 2i i x ξ∆; (3)求和:222311111()n nn ii i i i i x i nn n ξ===∆=⋅=∑∑∑311=(1)(21)6n n n n ⋅++111=(1)(2)6n n n ++(4)取极限:1,0nλλ=→等价于n →∞,有定积分的定义得 120d x x ⎰2011111lim lim (1)(2)63ni i n i x n n n λξ→→∞==∆=++=∑ 三、定积分的性质 补充规定:①()d ()d b a abf x x f x x =-⎰⎰;②()d 0aaf x x =⎰性质1:[]()()d ()d ()d bbba a a f x g x x f x x g x x ±=±⎰⎰⎰ 证:[][]01()()d lim ()()nbiiiai f x g x x f g x λξξ→=±=±∆∑⎰0011lim ()lim ()n ni i i i i i f x g x λλξξ→→===∆±∆∑∑ ()d ()d b baaf x xg x x =±⎰⎰注:推广到有限个函数仍成立 性质2:()d ()d bbaakf x x k f x x =⎰⎰(k 为常数)性质3:(对积分区间的可加性)设a c b <<,则()d ()d ()d bc baacf x x f x x f x x =+⎰⎰⎰证:因为函数()f x 在[],a b 上可积,所以不论把[],a b 怎样分,积分和的极限总是不变的,因此,在分区间时,可以使c 永远是个分点,那么[],a b 上的积分和等于[],a c 上的积分和加[],c b 上的积分和,记为[][][],,c c,()()()iii ii ia b a b f x f x f x ξξξ∆=∆+∆∑∑∑令0λ→,上式两端同时取极限,即得()d ()d ()d bc baacf x x f x x f x x =+⎰⎰⎰注:推广对于任意的a ,b ,c 都是成立的.性质4:若在区间[],a b 上,()1f x =,则1d d bba a x xb a ==-⎰⎰ 性质5:若在区间[],a b 上,()0f x ≥,则()d 0baf x x ⎰≥推论1:若在区间[],a b 上,()()f x g x ≤,则()d ()d bba a f x x g x x ⎰⎰≤ 推论2:()d ()d bb aaf x x f x x ⎰⎰≤证:因()()()f x f x f x -≤≤,可得()d ()d ()d b b b aaaf x x f x x f x x -≤⎰⎰⎰≤,即()d ()d bb aaf x x f x x ⎰⎰≤例:比较210e d xx ⎰和31e d x x ⎰的大小解:因为当01x ≤≤时,23x x ≥,所以有23e e x x ≥,231100e d e d x xx x >⎰⎰性质6:(估值定理)设M ,m 分别是()f x 在[],a b 上的最大值和最小值,则() ()d ()bam b a f x x M b a --⎰≤≤证:因为 ()m f x M ≤≤,可得d ()d d b b ba a a m x f x x M x ⎰⎰⎰≤≤, 得() ()d ()ba mb a f x x M b a --⎰≤≤例:估计20(1sin )d x x π+⎰的范围解: 因2()1sin f x x =+在[]0,π上最小值为1,最大值为2,所以2(1sin )d 2x x ππ+π⎰≤≤性质7:(积分中值定理)设()f x 在[],a b 上连续,则在[],a b 上至少存在一点ξ,使得()d ()()baf x x f b a ξ=-⎰(a b ξ≤≤)这个公式叫做积分中值公式.证:由() ()d ()bam b a f x x M b a --⎰≤≤,从而1()d b am f x x M b a -⎰≤≤, 再由连续函数的介值定理,[,]a b ξ∃∈使得1() ()d b af f x x b a ξ=-⎰,即()d ()()b a f x x f b a ξ=-⎰(a b ξ≤≤)第二节 微积分基本公式一、积分上限函数及其导数定义:设函数()f x 在区间[],a b 上连续,并x 设为[],a b 上的一点,如上限x 在区间[],a b 上任意变动,则对于每一个取定的x 值,定积分有一个对应值,所以它在[],a b 上定义了一个函数,记作()x Φ:()()d =()d xx aax f x x f t t Φ=⎰⎰,称为积分上限函数(或变上限积分).同理定义:变下限积分()d b xf t t ⎰和变限积分2()d x xf t t ⎰定理:如果函数()f x 在区间[],a b 上连续,则积分上限函数()()d x ax f t t Φ=⎰在[],a b 上可导,并且它的导数()()d ()xa x f t t f x Φ'⎡⎤'==⎢⎥⎣⎦⎰,[],x a b ∈证:①对于(,)x a b ∈,给x 一增量x ∆,使得(,)x x a b +∆∈, 则()()d x x ax x f t t Φ+∆+∆=⎰从而函数的增量为()()()d ()d x x xaax x x f t t f t t ΦΦΦ+∆∆=+∆-=-⎰⎰()d ()d ()d x x x x axaf t t f t t f t t +∆=+-⎰⎰⎰()d x x xf t t +∆=⎰由于()f x 在区间[],a b 上连续,由积分中值定理可得,存在ξ介于x 和x x +∆之间,使得()d ()x x xf t t f x Φξ+∆∆==∆⎰所以00()limlim ()x x x f x ΦΦξ∆∆∆'==∆→→,因为当0x ∆→时x ξ→,且()f x 是连续的,从而()lim ()()xx f f x ξΦξ'==→②当x a =时,取0x ∆>,使得(,)a x a b +∆∈,同上可得()()a f a Φ+'=③当x b =时,取0x ∆<,使得(,)b x a b +∆∈,同上可得()()b f b Φ-'=定理:如果函数()f x 在区间[],a b 上连续,则函数()()d xax f t t Φ=⎰就是()f x 在[],a b 上的一个原函数.注:这个定理肯定了连续函数的原函数的存在性,也初步揭示了定积分与原函数之间的联系.例:求 21cos 2e d limt xx t x -⎰→解:2221cos coscos 200e d e (cos )sin e 1limlim lim 222et x xxx x x t x x x xx ---'-⋅===⎰→→→ 二、牛顿—莱布尼茨公式(New-Leibniz )(微积分基本公式)定理:如果函数()F x 是连续函数()f x 在区间[],a b 上的一个原函数,则()d ()()baf x x F b F a =-⎰证:因为()F x 和()x Φ都是()f x 的原函数,则()()F x x C Φ-=(*), 令=x a ,则()()F a a C Φ-=,而()0a Φ=,则()F a C =, 将()F a C =代入(*),得()=()()x F x F a Φ-,即(t)dt ()()x af F x F a =-⎰令=x b ,则(t)dt ()()b af F b F a =-⎰注:[]()d ()=()()b ba af x x F x F b F a =-⎰这个公式叫做牛顿—莱布尼茨公式,也常叫做微积分基本公式. 例:计算120d x x ⎰解:112300111d (10)333x x x ⎡⎤==-=⎢⎥⎣⎦⎰ 例:计算12d xx--⎰解:[]1122d ln ||ln1ln 2ln 2x x x----==-=-⎰ 例:计算20|sin |d x x π⎰解:220|sin |d sin d sin d x x x x x x ππππ=-⎰⎰⎰[]20cos [cos ]x x πππ=-+[](11)1(1)4=---+--=例:证明积分中值定理:如果函数()f x 在区间[],a b 上连续,则至少存在一点(,)a b ξ∈, 使得()d ()()b af x x f b a ξ=-⎰证:因为函数()f x 在区间[],a b 上连续,设()F x 是()f x 的一个原函数,即()()F x f x '=,根据牛顿—莱布尼茨公式,得()d ()()ba f x x Fb F a =-⎰函数()F x 在[],a b 上满足拉格朗日中值定理的条件,因此,至少存在一点(,)a b ξ∈,使得()()()()F b F a f b a ξ-=-,即()d ()()ba f x x fb a ξ=-⎰注:这一积分性质,将上一节积分中值定理作了进一步的推进,ξ的值可以在开区间(,)a b 内找到.例:设()f x 在[)0+∞,内连续且()0f x >,证明00()d ()=()d xx tf t t F x f t t⎰⎰在()0+∞,内为单调增加函数.证明:()()()022()()d ()()d ()()d ()=()d ()d x xx x x xf x f t t f x tf t tf x x t f t tF x f t tf t t--'=⎰⎰⎰⎰⎰由积分中值定理()()0()d =()0x x t f t t f x x ξξ--⋅>⎰()0F x '∴> ,()F x ∴为单调增加函数第三节 定积分的换元法与分部积分法一、定积分的换元法定理:设()f x 在区间[],a b 上连续,函数()x t ϕ=满足条件: (1)()a ϕα=,()b ϕβ=,(),a t b ϕ≤≤[],t αβ∈; (2)()t ϕ在[],αβ(或[],βα)上具有连续导数,则[]()d ()()d baf x x f t t t βαϕϕ'=⎰⎰证:因为()f x 在区间[],a b 上连续,所以原函数存在,设()F x 是()f x 的一个原函数,则有()d ()()b af x x F b F a =-⎰记[]()()t F t Φϕ=,它是由()F x 和()x t ϕ=复合而成,则由复合函数的求导法则,得[]()()()()()()()t F x t f x t f t t Φϕϕϕϕ'''''===这就是说()t Φ是[]()()f t t ϕϕ'的一个原函数,所以有[][]()'()d ()()()f t t t t ββααϕϕΦΦβΦα==-⎰[][]()()()()F F F b F a ϕβϕα=-=-即[]()d ()()d b af x x f t t t βαϕϕ'=⎰⎰叫做定积分的换元公式注:①换元公式也可以反过来用,即也有如下的换元公式[]()()d ()d b a f x x x f t t βαϕϕ'=⎰⎰ ②积分限相应改变 ③不必还原例:计算0x ⎰(0)a >解:设sin x a t =,0,2t π⎡⎤∈⎢⎥⎣⎦,则d cos d x a t t =,222220cos d (1cos 2)d 2a x at t t t ππ==+⎰⎰⎰2221sin 2224a a t t ππ⎡⎤=+=⎢⎥⎣⎦例:计算40⎰解:令t=,则2x t =,d 2d x t t =,[]42220 000d2d121d2ln(1)2(2ln3)11x t tt t tt t⎛⎫==-=-+=-⎪++⎝⎭⎰⎰⎰例:计算52cos sin dx x xπ⎰解:(写法一)令cost x=,则d sin dt x x=-,1015556201011cos sin d d d66x x x t t t t tπ⎡⎤=-===⎢⎥⎣⎦⎰⎰⎰(写法二)62552200cos11 cos sin d cos d(cos)0666xx x x x xπππ⎡⎤⎛⎫=-=-=--=⎢⎥ ⎪⎝⎭⎣⎦⎰⎰例:计算x⎰解:x⎰32sin cos dx x xπ=⋅⎰332222sin cos d+sin cos dx x x x x xπππ=⋅⋅⎰⎰332222sin cos d sin(cos)dx x x x x xπππ=⋅+⋅-⎰⎰55222222224sin sin()55555x xπππ⎡⎤⎡⎤=-=--=⎢⎥⎢⎥⎣⎦⎣⎦例:证明0,()()2(),()aaaf xf x xf x x f x-⎧⎪=⎨⎪⎩⎰⎰dd为奇函数为偶函数证:由()d()d()da aa af x x f x x f x x--=+⎰⎰⎰而0000()d()(d)()d()da aa af x xx t f t t f t t f x x-=---=-=-⎰⎰⎰⎰所以000()d()d()d=()d()da a a aa af x x f x x f x x f x x f x x--=+-+⎰⎰⎰⎰⎰[]0,()=()+()d2()d,()aaf xf x f x xf x x f x⎧⎪-=⎨⎪⎩⎰⎰为奇函数为偶函数例:若()f x 在[]0,1上连续,证明(1)220(sin )(cos )f x x f x x ππ=⎰⎰d d(2)0(sin )(sin )2xf x x f x x πππ=⎰⎰d d ,由此计算20sin 1cos x x x xπ⎰d + 证:(1)令2x t π=-,则d =d x t -, 02220002(sin )sin (cost)(cos )2f x x f t t f f x x πππππ⎡⎤⎛⎫=-= ⎪⎢⎥⎝⎭⎣⎦⎰⎰⎰⎰d -d dt=d(2)令x t π=-,则d =d x t -,()()()()00(sin )sin sin xf x x t f t t t f t t ππππππ=-=⎡⎤⎣⎦⎰⎰⎰d --d -d ()()()()0sin sin sin sin f t t tf t t f x x xf x x ππππππ=⎰⎰⎰⎰d -d =d -d所以0(sin )(sin )2xf x x f x x πππ=⎰⎰d d 从而()222000sin sin cos tan cos 02221cos 1cos 1cos x x x x x x arc x xx x πππππππ=⎡⎤⎣⎦⎰⎰⎰d d d =-=-+++ 22444ππππ⎛⎫ ⎪⎝⎭=---=例:设函数2-e ,0()1,-01cos x x x f x x xπ⎧≥⎪=⎨<<⎪+⎩,计算41(2)f x x ⎰-d 解:(方法一)令2x t -=,则d =d x t ,242211101(2)()te 1cost f x x f t ++⎰⎰⎰⎰-t ---d =dt=dt dt24021111tan e tan e 1022222t t --⎡⎤⎡⎤-=-+⎢⎥⎢⎥-⎣⎦⎣⎦=注:0002111201sec tan 11cost 2222cos2t t ⎡⎤==⎢⎥-+⎣⎦⎰⎰⎰---dt t t dt=d (方法二)()442111(2)(2)22()f x x f x x x t f t ⎰⎰⎰--d =-d --=dt二、定积分的分部积分法若函数()u u x =,()v v x =在区间[],a b 上有连续导数,由不定积分的分部积分法,可得()()d ()()d ()()()()d b bb a a au x v x x u x v x x u x v x v x u x x ⎡⎤⎡⎤'''==-⎣⎦⎣⎦⎰⎰⎰[]()()()()d bba au x v x v x u x x '=-⎰即d []d bb b aaauv x uv vu x ''=-⎰⎰或d []d b bb a aau v uv v u =-⎰⎰这就是定积分的分部积分法例:计算120arcsin d x x ⎰解:[]1112220arcsin d arcsin x x x x x =-⎰⎰1201126122ππ⎤=⋅+=+-例:计算10x ⎰解:令t=,则2x t =,d 2d x t t =,1111100002e d 2d(e )2[e ]2e d ttt tx t t t t t ===-⎰⎰⎰⎰[]10=2e 2[e ]2e (e 1)2t -=--=例:证明定积分公式2200sin d cos d n n n I x x x x ππ⎛⎫== ⎪⎝⎭⎰⎰1331,24221342,253n n n n n n n n n n π--⎧⋅⋅⋅⎪⎪-=⎨--⎪⋅⋅⎪-⎩为正偶数为大于1正奇数 证:()11222200sindcos =cos sin1sin cos 20n n n n I x x x x n x xdx πππ---⎡⎤=--+-⎣⎦⎰⎰ ()()()()22220=1sin1sin 11n n n n n xdx n xdx n I n Iππ-----=---⎰⎰由此21=n n n I I n --,递推公式243=,2n n n I I n ----220002123531=,1d =2226422m m m I I I x m m ππ--⋅⋅⋅⋅=-⎰()22+1110222642=1,2,,sin d =12+121753m m m I I m I x x m m π-⋅⋅⋅⋅==-⎰所以22123531=2226422m m m I m m π--⋅⋅⋅⋅- ()2+1222642=1,2,2+121753m m m I m m m -⋅⋅⋅=-例:计算1020sin d x x π⎰解:102097531sin d =1086422x x ππ⋅⋅⋅⋅⋅⎰第四节 反常积分一、无穷限的反常积分定义:设函数()f x 在区间[,)∞+a 上连续,取t a >,如果极限lim ()d →∞+⎰tat f x x 存在,则称此极限为函数()f x 在无穷区间[,)∞+a 上的反常积分,记作()d ∞+⎰af x x ,即()d lim()d ∞→∞++=⎰⎰taat f x x f x x这时也称反常积分()d ∞+⎰af x x 收敛;如果上述极限不存在,则称此反常积分发散.定义:设函数()f x 在区间(,]∞-b 上连续,取t b <,如果极限lim ()d →∞-⎰btt f x x 存在,则称此极限为函数()f x 在无穷区间(,]∞-b 上的反常积分,记作()d b f x x -⎰∞,即()d lim()d b b tt f x x f x x --=⎰⎰∞→∞这时也称反常积分()d ∞-⎰b f x x 收敛;如果上述极限不存在,则称此反常积分发散.定义:设函数()f x 在区间(,)∞∞-+上连续,若对任意常数c ,反常积分()d ∞-⎰c f x x 和()d ∞+⎰cf x x 都收敛,则称上述两反常积分之和为函数()f x 在无穷区间(,)∞∞-+上的反常积分,记作()d ∞∞+-⎰f x x ,即()d ()d ()d c cf x x f x x f x x ++--=+⎰⎰⎰∞∞∞∞这时也称反常积分()d ∞∞+-⎰f x x 收敛;否则称反常积分()d ∞∞+-⎰f x x 发散.以上反常积分统称为无穷限的反常积分(简称为无穷积分) 计算无穷积分可用牛顿—莱布尼茨公式的记法,()d ∞+⎰af x x []=()()()=lim ()()a x F x F F a F x F a ++=+--∞→∞∞[]()d ()()()()lim ()b bx f x x F x F b F F b F x ---==--=-⎰∞∞→∞∞[]()d ()()(=)lim ()lim ()x x f x x F x F F F x F x ++--+-==+---⎰∞∞∞∞→∞→∞∞∞例:计算反常积分2d 1∞∞+-+⎰x x解:[]2d arctan lim arctan lim arctan 1∞∞∞∞→∞→∞++--+-==-+⎰t t x x t t x 22ππ⎛⎫=--=π ⎪⎝⎭例:计算反常积分0pt te dt +-⎰∞,其中 p 是常数且0p >解:(1)01==00pt pt pt te dt te dt tde p +---++⎡⎤⎡⎤-⎢⎥⎢⎥⎣⎦⎣⎦⎰⎰⎰∞∞∞211=000pt pt pt pt t t e e dt e e p p p p ----+++⎡⎤⎡⎤⎡⎤-+=--⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎰∞∞∞()22111=-lim 001pt t te p p p-→+∞---= 注:11lim =lim =lim =lim 0pt ptpt pt t t t t t te e pe pe --→+∞→+∞→+∞→+∞= 例:证明反常积分d ∞+⎰Paxx (0a >)当1p >时收敛,当1p ≤时发散 证明:(1)当1p =时,[]d d ln ∞∞∞∞+++===+⎰⎰P a aa x x x x x(2) 当1p ≠时,有11,1d ,111p p P aap x x a p p x p +-+-+<⎧⎡⎤⎪==⎨⎢⎥>-⎣⎦⎪-⎩⎰∞∞∞ 因此,当1p >时收敛,其值为11pa p --;当1p ≤时发散二、无界函数的反常积分定义:如果函数()f x 在点a 的任一邻域内都无界,则称点a 为函数()f x 的瑕点(或称无界间断点). 无界函数的反常积分也称为函数的瑕积分.定义:设函数()f x 在(,]a b 上连续,点a 为()f x 的瑕点.取t a >,如果极限lim ()d btt af x x +⎰→存在,则称此极限为函数()f x 在(,]a b 上的反常积分,仍记作()d baf x x ⎰,即()d lim ()d bbatt af x x f x x +=⎰⎰→这时也称反常积分()d b af x x ⎰收敛. 如果上述极限不存在,则称此反常积分发散. 定义:设函数()f x 在[,)a b 上连续,点b 为()f x 的瑕点.取t b <,如果极限lim ()d ta t bf x x -⎰→存在,则称此极限为函数()f x 在[,)a b 上的反常积分,仍记作()d b af x x ⎰,即()d lim ()d bta at bf x x f x x -=⎰⎰→这时也称反常积分()d b af x x ⎰收敛.如果上述极限不存在,则称此反常积分发散.定义:设函数()f x 在[,]a b 上除点c (a c b <<)外连续,点c 为()f x 的瑕点. 如果两个反常积分()d caf x x ⎰和()d bcf x x ⎰都收敛,则定义()d ()d ()d b c baacf x x f x x f x x =+⎰⎰⎰;否则,就称反常积分()d baf x x ⎰发散.计算无界函数的反常积分也可以利用牛顿—莱布尼茨公式, 若a 是瑕点,则反常积分[]()d =()()lim ()b ba ax af x x F x F b F x +→=-⎰例:计算反常积分a ⎰(0a >)解:0arcsin lim arcsin 02→aa x a x x a a -π⎡⎤==-=⎢⎥⎣⎦⎰例:讨论反常积分121d xx -⎰的收敛性解:02101d 11lim 1→∞x x x x x ---⎡⎤⎛⎫=-=--=+ ⎪⎢⎥⎣⎦⎝⎭⎰ 所以反常积分021d xx-⎰发散,从而反常积分121d x x -⎰发散注:此题若忽略了瑕点0x =,而直接用牛顿—莱布尼茨公式计算11211d 1(11)2x x x --⎡⎤=-=-+=-⎢⎥⎣⎦⎰是错误的 例:证明反常积分d a qxx ⎰(0a >,0q >),(1)当1q <时收敛;(2)当1q ≥时发散 解:(1)当1q =时[]000d ln ln lim ln ∞+→==-=+⎰a ax x x a x x即反常积分是发散的(2)当1q ≠时1111000,1d lim 1111,1∞qaqqqa qx a q x x a x q q q q x q +----→⎧<⎡⎤⎪==-=-⎨⎢⎥---⎣⎦⎪+>⎩⎰所以反常积分d a qxx ⎰当01q <<时收敛,当1q ≥时发散复习题 1.填空题:(1)42|3|d x x -=⎰(2)211e ,22()11,2≤<≥x x x f x x ⎧-⎪⎪=⎨⎪-⎪⎩,则212(1)d f x x -⎰=(3)110I =⎰与12I =⎰的大小关系是(4)由曲线sin y x =、直线2x π=-、2x π=及x 轴所围成的平面图形面积为 (5)2121tan sin d 1x xx x -+⎰= (6)22222lim 12n nn n n n n n →∞⎛⎫++⋅⋅⋅+= ⎪+++⎝⎭2.选择题:(1)函数()f x 在区间[,]a b 上连续,是()f x 在区间[,]a b 上可积的( ) A .充要条件; B .充分条件; C .必要条件; D .无关条件 (2)下列积分中可直接用牛顿—莱布尼茨公式计算的是( ) A .221d 1xx -+⎰; B .11d x x -⎰; C .11ed ln xx x⎰; D .120d x x ⎰(3)π20d sin d d x t t x ⎰=( ) A . 0; B .sin x x ; C . 1;D . x(4)设220()sin d x f x t t =⎰,6()g x x =,则当0x →时,()f x 是()g x 的( )A .等价无穷小;B .同阶但非等价无穷小;C .高阶无穷小;D .低阶无穷小 3.求下列极限:(1)101lim (1sin 2)d xt x t t x →+⎰; (2)00ln(1)d x t t→-⎰4.计算下列积分: (1)x ⎰; (2)14211sin d x x x π-⎰;(3)21d e e ∞+-+⎰x xx ; (4)20|sin |d x x x π⎰ 5.已知0sin d 2∞x x x π+=⎰,求220sin d ∞x x x +⎰。
同济版高等数学教案定积分

同济版高等数学教案定积分
一、定积分
定积分(Definite Integrals)是在研究一些实际问题时非常有用的技术。
它以一种形式求解不同函数的积分,当我们需要求解其中一个函数的积分,我们可以使用定积分来进行求解。
1、定积分的定义
定积分是指在给定积分范围内,用定积分公式计算函数的积分值。
它是一种特殊的分积分,即:求在其中一范围内函数值的积分。
定积分的表示形式为∫a bf(x)dx,其中f(x)是定积分中的函数,a 是定积分的下限,b是定积分的上限,dx为微元。
2、定积分的应用
定积分在很多实际问题中都有重要的应用,如:求两个函数之间的差值,求函数的积分变化,求曲线的面积,计算不同函数的积分,求曲线在其中一区间上曲线的斜率等。
3、定积分的求解方法
(1)逐步法:将定积分分解为无穷多个小积分,并求出每个小积分的结果,然后把所有小积分的结果相加,即可求出定积分的结果。
(2)积分变换法:利用换元的思想,将定积分转化为更易于计算的积分形式,通过以上两种方法,可以比较方便地求出定积分的结果。
4、梯形积分法
梯形积分法是一种求定积分的简便方法,它是将定积分区间分割为若干个小区间,把每一小区间内的函数值用梯形近似。
06定积分应用(同济教材)39页20180926

a 2 2
a
0
(a x )dx
2 2
x y 例: 计算由椭圆 2 2 1 围成的图形 a b
2
2
绕 y 轴旋转一周所成的旋转体(称为旋
转椭球体)的体积。
2 a Vy 2 x dy 2 0 b 4 2 a b 3
dV y dx f ( x)dx
2 2
y=f(x)
x dx
a
x
b 2 b 2
b
Vx y dx f ( x)dx
a a
求由曲线 x=(y) ,(假设曲线 (y) 与 y 轴不相交)与直线 y=c,y=d (c<d) 及 y 轴所围成的平面图形绕 y 轴旋转一 周而成的旋转体的体积。
U dU (x ) 注意:这样表示的前提条件是: 否则可能造成失误,这里,称 dU 为量U的元 素。
3、对元素关系式 dU f ( x )dx 在 [a,b] 上作定积分,即得所求量 U 的积分 表达式 b
U ∫ f ( x ) dx . a
上述这种解决问题的方法称为元素 法,也称微元法。
y
y=f(x)
dA
o
a
b a
x x+dx b
x
A f ( x)dx
y
a
x x+dx b
o
y=f(x)
x
dA
A f ( x)dx
a
b
求由曲线 x=(y), x=(y) ((y)≤(y))及 直线 y=c,y=d (c<d) 围成的平面图形的 dA 面积 A。 y
同济大学高等数学§3.1定积分的概念与性质
。
y f (x)
3.若
f
( x)C[a,b],且 f ( x)
有正有负时,则
b a
f ( x)dx
等于由连续曲线 y f ( x) ,直线 x a , xb 及 x 轴 所
围成的几个曲边梯形面积的代数和,在 x 轴 上方的面积
取正号,在 x 轴 下方的面积取负号。
y
A1
ao
y f (x)
A2
A3
b
∴ f ( x) 在[0,1]上单增, f ( x) f (0)0 ,
即 xln (1 x)0 ,故 xln(1 x) 。
∴由性质 5 知
1 xdx
0
1
ln(1
0
x
)dx
。
例
4.证明不等式
2 4e
2
e
x
2
x
dx
2e
2
。
0
证:设 f (x) ex2x ,则 f (x)C[0, 2] 。
f ( x)(2x 1)e x 2 x ,令 f ( x)0 ,得驻点x 1 ,
b
f
() a
f ( x)g( x)dx
b
a g( x)dx
,即
b a
f
( x)g( x)dx
f
()
b a
g(
x)dx
。
推论:若 f ( x)C[a,b],则 [a,b] ,使得
b a
f
(
x)dx
f
()(ba)
。
在[a, b] 上以连续曲线
y
y f ( x) 为曲边的曲边梯 形面积等于以区间[a, b] f ()
x
b
同济版高等数学教案第五章 定积分
第五章定积分教学目的:1、理解定积分的概念。
2、掌握定积分的性质及定积分中值定理,掌握定积分的换元积分法与分部积分法.3、理解变上限定积分定义的函数,及其求导数定理,掌握牛顿-莱布尼茨公式.4、了解广义积分的概念并会计算广义积分.教学重点:1、定积分的性质及定积分中值定理2、定积分的换元积分法与分部积分法。
3、牛顿—莱布尼茨公式。
教学难点:1、定积分的概念2、积分中值定理3、定积分的换元积分法分部积分法。
4、变上限函数的导数。
§5. 1 定积分概念与性质一、定积分问题举例1.曲边梯形的面积曲边梯形:设函数y=f(x)在区间[a,b]上非负、连续.由直线x=a、x=b、y=0及曲线y=f(x)所围天津工业大学理学院基础数学系高等数学、经济数学教研室1成的图形称为曲边梯形,其中曲线弧称为曲边.求曲边梯形的面积的近似值:将曲边梯形分割成一些小的曲边梯形,每个小曲边梯形都用一个等宽的小矩形代替,每个小曲边梯形的面积都近似地等于小矩形的面积,则所有小矩形面积的和就是曲边梯形面积的近似值.具体方法是:在区间[a,b]中任意插入若干个分点a=x0<x1<x2<⋅⋅⋅<x n-1<x n=b,把[a,b]分成n个小区间[x0,x1], [x1,x2],[x2,x3],⋅⋅⋅,[x n-1,x n],它们的长度依次为∆x1= x1-x0, ∆x2= x2-x1,⋅⋅⋅,∆x n= x n-x n-1.经过每一个分点作平行于y轴的直线段,把曲边梯形分成n个窄曲边梯形.在每个小区间[x i-1,x i]上任取一点ξ i,以[x i-1,x i]为底、f (ξ i)为高的窄矩形近似替代第i个窄曲边梯形(i=1, 2,⋅⋅⋅,n),把这样得到的n个窄矩阵形面积之和作为所求曲边梯形面积A的近似值,即A≈f (ξ 1)∆x1+ f(ξ 2)∆x2+⋅⋅⋅+ f (ξ n)∆x n.求曲边梯形的面积的精确值:显然,分点越多、每个小曲边梯形越窄,所求得的曲边梯形面积A的近似值就越接近曲边梯形面积A的精确值,因此,要求曲边梯形面积A的精确值,只需无限地增加分点,使每个小曲边梯形的宽度趋于零.记λ=max{∆x1,∆x2,⋅⋅⋅,∆x n},于是,上述增加分点,使每个小曲边梯形的宽度趋于零,相当于令λ→0.所以曲边梯形的面积为.2.变速直线运动的路程设物体作直线运动,已知速度v=v(t)是时间间隔[T 1,T 2]上t的连续函数,且v(t)≥0,计算在这段时间内物体所经过的路程S.天津工业大学理学院基础数学系高等数学、经济数学教研室2求近似路程:我们把时间间隔[T1,T2]分成n个小的时间间隔∆t i,在每个小的时间间隔∆t i内,物体运动看成是均速的,其速度近似为物体在时间间隔∆t i内某点ξ i的速度v(τ i),物体在时间间隔∆t i内运动的距离近似为∆S i= v(τ i) ∆t i.把物体在每一小的时间间隔∆t i内运动的距离加起来作为物体在时间间隔[T 1,T 2]内所经过的路程S的近似值.具体做法是:在时间间隔[T 1,T 2]内任意插入若干个分点T 1=t0<t 1<t2<⋅⋅⋅<t n-1<t n=T 2,把[T 1,T 2]分成n个小段[t 0,t 1],[t 1,t 2],⋅⋅⋅,[t n-1,t n] ,各小段时间的长依次为∆t 1=t 1-t 0,∆t 2=t 2-t 1,⋅⋅⋅,∆t n=t n-t n-1.相应地,在各段时间内物体经过的路程依次为∆S 1,∆S 2,⋅⋅⋅,∆S n.在时间间隔[t i-1,t i]上任取一个时刻τi(t i-1<τi<t i),以τi时刻的速度v(τi)来代替[t i-1,t i]上各个时刻的速度,得到部分路程∆S i的近似值,即∆S i= v(τi) ∆t i(i=1, 2,⋅⋅⋅,n).于是这n段部分路程的近似值之和就是所求变速直线运动路程S的近似值,即;求精确值:记λ= max{∆t 1,∆t 2,⋅⋅⋅,∆t n},当λ→0时,取上述和式的极限,即得变速直线运动的路程.设函数y=f(x)在区间[a,b]上非负、连续.求直线x=a、x=b、y=0天津工业大学理学院基础数学系高等数学、经济数学教研室3及曲线y=f (x)所围成的曲边梯形的面积.(1)用分点a=x0<x1<x2<⋅⋅⋅<x n-1<x n=b把区间[a,b]分成n个小区间:[x0,x1],[x1,x2],[x2,x3],⋅⋅⋅, [x n-1,x n],记∆x i=x i-x i-1 (i=1, 2,⋅⋅⋅,n).(2)任取ξ i∈[x i-1,x i],以[x i-1,x i]为底的小曲边梯形的面积可近似为(i=1, 2,⋅⋅⋅,n);所求曲边梯形面积A的近似值为.(3)记λ=max{∆x1,∆x2,⋅⋅⋅,∆x n},所以曲边梯形面积的精确值为.设物体作直线运动,已知速度v=v(t)是时间间隔[T 1,T 2]上t的连续函数,且v(t)≥0,计算在这段时间内物体所经过的路程S.(1)用分点T1=t0<t1<t2<⋅⋅⋅<t n-1<t n=T2把时间间隔[T 1,T 2]分成n个小时间段:[t0,t1],[t1,t2],⋅⋅⋅,[t n-1,t n],记∆t i=t i-t i-1(i=1, 2,⋅⋅⋅,n).(2)任取τi∈[t i-1,t i],在时间段[t i-1,t i]内物体所经过的路程可近似为v(τi)∆t i(i=1, 2,⋅⋅⋅,n);所求路程S的近似值为.(3)记λ=max{∆t1,∆t2,⋅⋅⋅,∆t n},所求路程的精确值为.二、定积分定义抛开上述问题的具体意义,抓住它们在数量关系上共同的本质与特性加以概括,就抽象出下述定积分的定义.天津工业大学理学院基础数学系高等数学、经济数学教研室4定义设函数f(x)在[a,b]上有界,在[a,b]中任意插入若干个分点a=x0<x1<x2<⋅⋅⋅<x n-1<x n=b,把区间[a,b]分成n个小区间[x0,x1],[x1,x2],⋅⋅⋅,[x n-1,x n],各小段区间的长依次为∆x1=x1-x0,∆x2=x2-x1,⋅⋅⋅,∆x n=x n-x n-1.在每个小区间[x i-1,x i]上任取一个点ξi(x i-1<ξi<x i),作函数值f (ξi)与小区间长度∆x i的乘积f(ξi) ∆x i (i=1, 2,⋅⋅⋅,n),并作出和.记λ=max{∆x1,∆x2,⋅⋅⋅,∆x n},如果不论对[a,b]怎样分法,也不论在小区间[x i-1,x i]上点ξi怎样取法,只要当λ→0时,和S总趋于确定的极限I,这时我们称这个极限I为函数f(x)在区间[a,b]上的定积分,记作,即.其中f(x)叫做被积函数,f(x)dx叫做被积表达式,x叫做积分变量,a叫做积分下限,b叫做积分上限,[a,b]叫做积分区间.定义设函数f(x)在[a,b]上有界,用分点a=x0<x1<x2<⋅⋅⋅<x n-1<x n=b把[a,b]分成n个小区间:[x0,x1],[x1,x2],⋅⋅⋅,[x n-1,x n],记∆x i=x i-x i-1(i=1, 2,⋅⋅⋅,n).任ξi∈[x i-1,x i](i=1, 2,⋅⋅⋅,n),作和.记λ=max{∆x1,∆x2,⋅⋅⋅,∆x n},如果当λ→0时,上述和式的极限存在,且极限值与区间[a,b]的分法和ξi的取法无关,则称这个极限为函数f(x)在区间[a,b]上的定积分,记作,即.天津工业大学理学院基础数学系高等数学、经济数学教研室5根据定积分的定义,曲边梯形的面积为.变速直线运动的路程为.说明:(1)定积分的值只与被积函数及积分区间有关,而与积分变量的记法无关,即.(2)和通常称为f (x)的积分和.(3)如果函数f(x)在[a,b]上的定积分存在,我们就说f(x)在区间[a,b]上可积.函数f(x)在[a,b]上满足什么条件时,f (x)在[a,b]上可积呢?定理1设f(x)在区间[a,b]上连续,则f(x)在[a,b]上可积.定理2设f (x)在区间[a,b]上有界,且只有有限个间断点,则f(x)在[a,b]上可积.定积分的几何意义:在区间[a,b]上,当f(x)≥0时,积分在几何上表示由曲线y=f(x)、两条直线x=a、x=b与x轴所围成的曲边梯形的面积;当f(x)≤0时,由曲线y=f (x)、两条直线x=a、x=b与x轴所围成的曲边梯形位于x轴的下方,定义分在几何上表示上述曲边梯形面积的负值;.当f (x)既取得正值又取得负值时,函数f(x)的图形某些部分在x轴的上方,而其它部分在x轴的下方.如果我们对面积赋以正负号,在x轴上方的图形面积赋以正号,在x轴下方的图形面积赋以负号,则在一般情形下,定积分的几何意义为:它是介于x轴、函数f(x)的图形及两条直线x=a、x=b之间的各部分面积的代数和.用定积分的定义计算定积分:例1。
同济大学(高等数学)_第五章_定积分及其应用
(x)dx
7
推论
2
|
b
a
f
(x)dx| ab|
f
(x) | dx
(ab)
这是因为|f (x)| f (x) |f (x)|所以
ab|
f
(x) | dx
b
a
f
(x)dx
ab|
f
(x) | dx
b
b
即 | a
f (x)dx | a
f (x)dx.
ab[
f
(x)
g(x)]dx
b
a
f
(x)dx
abg(x)dx
证明:
ab[ f
(x) g(x)]dx
n
lim [ f 0 i1
(i) g(i)]xi
6
n
n
lim
0
i1
fபைடு நூலகம்
(i)xi
lim
0
i1
g(i)xi
b
a
f
( x)dx
第 1 节 定积分的概念与性质
1.1 定积分问题举例 1.1.1 曲边梯形的面积
曲边梯形 设函数 y f (x) 在区间 a,b上非负、连续 由直线 x a, x b, y 0 及
曲线 y f (x) 所围成的图形称为曲边梯形 其中曲线弧 y f (x) 称为曲边
把 a,b分成 n 个小区间
x0 , x1 , x1, x2 , x2 , x3 , L ,xn1, xn ,
它们的长度依次为 x1 x1 x0 , x2 x2 x1,L , xn xn xn1. 经过每一个分点作平行于 y 轴的直线段 把曲边梯形分成 n 个窄曲边梯形在每个小区
高等数学教案-定积分及其应用
第 5 章 定积分及其应用
授课序号 01
教学基本指标
教学课题 教学方法 教学重点
第 5 章 第 1 节 定积分的概念与性质 讲授、课堂提问、讨论、启发、自学 定积分的定义与性质
课的类型 教学手段 教学难点
新知识课 黑板多媒体结合 用定积分的定义求定积分
参考教材 同济七版《高等数学》
作业布置 课后习题
a
a
x
[a,b] 上的函数, 称为积分上限函数, 记作 ( x) f (t)dt , x [a,b] . a
x
2.定理:设函数 f (x) 在区间[a,b] 上连续,则积分上限函数 ( x) f (t)dt 在区间[a,b] 上可导,且 a
(x) ( x f (t)dt) f (x), x [a,b] . a
性质 6(定积分中值定理)设函数 f (x) 在区间[a,b] 上连续,则在区间[a,b] 上至少存在一点 ,使得
五.例题讲解
例 1.计算定积分 1 1 x2 dx . 0
b f (x)dx f ( )(b a) . a
2
例 2.用定义求定积分 1 x2dx . 0
例 3.不计算定积分的值,比较下列定积分的大小.
大纲要求 1、理解定积分的概念。
2、掌握定积分的性质及定积分中值定理.
教 学 基本内容
一.定积分的概念 1.两个实际问题 引例 1 曲边梯形的面积问题
设函数 y f (x) 在区间[a,b] 上非负连续,由曲线 y f (x) ,直线 x a , x b 以及 x 轴所围成图形称为曲 边梯形,求曲边梯形的面积 A .
b
f (x)dx ,
c
a a
b c
其中 c 是任意的常数, a 是小于 c 的任意数, b 是大于 c 的任意数.此广义积分 f (x)dx 只有当上述等式中
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章定积分教学目的:1、理解定积分的概念。
2、掌握定积分的性质及定积分中值定理,掌握定积分的换元积分法与分部积分法。
3、理解变上限定积分定义的函数,及其求导数定理,掌握牛顿—莱布尼茨公式。
4、了解广义积分的概念并会计算广义积分。
教学重点:1、定积分的性质及定积分中值定理2、定积分的换元积分法与分部积分法。
3、牛顿—莱布尼茨公式。
教学难点:1、定积分的概念2、积分中值定理3、定积分的换元积分法分部积分法。
4、变上限函数的导数。
§5. 1 定积分概念与性质一、定积分问题举例1.曲边梯形的面积曲边梯形:设函数y=f(x)在区间[a,b]上非负、连续.由直线x=a、x=b、y=0及曲线y=f(x)所围成天津工业大学理学院基础数学系高等数学、经济数学教研室1天津工业大学理学院基础数学系高等数学、经济数学教研室2的图形称为曲边梯形, 其中曲线弧称为曲边.求曲边梯形的面积的近似值:将曲边梯形分割成一些小的曲边梯形, 每个小曲边梯形都用一个等宽的小矩形代替, 每个小曲边梯形的面积都近似地等于小矩形的面积, 则所有小矩形面积的和就是曲边梯形面积的近似值. 具体方法是: 在区间[a , b ]中任意插入若干个分点a =x 0< x 1< x 2< ⋅ ⋅ ⋅< x n -1< x n =b ,把[a , b ]分成n 个小区间[x 0, x 1], [x 1, x 2], [x 2, x 3], ⋅ ⋅ ⋅ , [x n -1, x n ],它们的长度依次为∆x 1= x 1-x 0 , ∆x 2= x 2-x 1 , ⋅ ⋅ ⋅ , ∆x n = x n -x n -1 .经过每一个分点作平行于y 轴的直线段, 把曲边梯形分成n 个窄曲边梯形. 在每个小区间[x i -1, x i ]上任取一点ξ i , 以[x i -1, x i ]为底、f (ξ i )为高的窄矩形近似替代第i 个窄曲边梯形(i =1, 2, ⋅ ⋅ ⋅ , n ) , 把这样得到的n 个窄矩阵形面积之和作为所求曲边梯形面积A 的近似值, 即A ≈f (ξ 1)∆x 1+ f (ξ 2)∆x 2+⋅ ⋅ ⋅+ f (ξ n )∆x n ∑=∆=ni i i x f 1)(ξ.求曲边梯形的面积的精确值:显然, 分点越多、每个小曲边梯形越窄, 所求得的曲边梯形面积A 的近似值就越接近曲边梯形面积A 的精确值, 因此, 要求曲边梯形面积A 的精确值, 只需无限地增加分点, 使每个小曲边梯形的宽度趋于零. 记λ=max{∆x 1, ∆x 2,⋅ ⋅ ⋅, ∆x n }, 于是, 上述增加分点, 使每个小曲边梯形的宽度趋于零, 相当于令λ→0. 所以曲边梯形的面积为∑=→∆=ni i i x f A 10)(lim ξλ. 2. 变速直线运动的路程天津工业大学理学院基础数学系高等数学、经济数学教研室3设物体作直线运动, 已知速度v =v (t )是时间间隔[T 1, T 2]上t 的连续函数, 且v (t )≥0, 计算在这段时间内物体所经过的路程S .求近似路程:我们把时间间隔[T 1, T 2]分成n 个小的时间间隔∆t i , 在每个小的时间间隔∆t i 内, 物体运动看成是均速的, 其速度近似为物体在时间间隔∆t i 内某点ξ i 的速度v (τ i ), 物体在时间间隔∆t i 内 运动的距离近似为∆S i = v (τ i ) ∆t i . 把物体在每一小的时间间隔∆t i 内 运动的距离加起来作为物体在时间间隔[T 1 , T 2]内所经过的路程S 的近似值. 具体做法是:在时间间隔[T 1 , T 2]内任意插入若干个分点T 1=t 0< t 1< t 2<⋅ ⋅ ⋅< t n -1< t n =T 2,把[T 1 , T 2]分成n 个小段[t 0, t 1], [t 1, t 2], ⋅ ⋅ ⋅, [t n -1, t n ] ,各小段时间的长依次为∆t 1=t 1-t 0, ∆t 2=t 2-t 1,⋅ ⋅ ⋅, ∆t n =t n -t n -1.相应地, 在各段时间内物体经过的路程依次为∆S 1, ∆S 2, ⋅ ⋅ ⋅, ∆S n .在时间间隔[t i -1, t i ]上任取一个时刻τ i (t i -1<τ i < t i ), 以τ i 时刻的速度v (τ i )来代替[t i -1, t i ]上各个时刻的速度, 得到部分路程∆S i 的近似值, 即∆S i = v (τ i ) ∆t i (i =1, 2, ⋅ ⋅ ⋅ , n ).于是这n 段部分路程的近似值之和就是所求变速直线运动路程S 的近似值, 即∑=∆≈ni i i t v S 1)(τ;求精确值:记λ = max{∆t 1, ∆t 2,⋅ ⋅ ⋅, ∆t n }, 当λ→0时, 取上述和式的极限, 即得变速直线运动的路程天津工业大学理学院基础数学系高等数学、经济数学教研室4∑=→∆=n i i i t v S 10)(lim τλ. 设函数y =f (x )在区间[a , b ]上非负、连续. 求直线x =a 、x =b 、y =0及曲线y =f (x )所围成的曲边梯形的面积.(1)用分点a =x 0<x 1<x 2< ⋅ ⋅ ⋅<x n -1<x n =b 把区间[a , b ]分成n 个小区间:[x 0, x 1], [x 1, x 2], [x 2, x 3], ⋅ ⋅ ⋅ , [x n -1, x n ], 记∆x i =x i -x i -1 (i =1, 2, ⋅ ⋅ ⋅ , n ).(2)任取ξ i ∈[x i -1, x i ], 以[x i -1, x i ]为底的小曲边梯形的面积可近似为i i x f ∆)(ξ (i =1, 2, ⋅ ⋅ ⋅ , n ); 所求曲边梯形面积A 的近似值为∑=∆≈ni ii x f A 1)(ξ. (3)记λ=max{∆x 1, ∆x 2,⋅ ⋅ ⋅, ∆x n }, 所以曲边梯形面积的精确值为∑=→∆=ni ii x f A 10)(lim ξλ.设物体作直线运动, 已知速度v =v (t )是时间间隔[T 1, T 2]上t 的连续函数,且v (t )≥0, 计算在这段时间内物体所经过的路程S .(1)用分点T 1=t 0<t 1<t 2<⋅ ⋅ ⋅<t n -1<t n =T 2把时间间隔[T 1 , T 2]分成n 个小时间段: [t 0, t 1], [t 1, t 2], ⋅ ⋅ ⋅, [t n -1, t n ] , 记∆t i =t i -t i -1 (i =1, 2, ⋅ ⋅ ⋅ , n ).(2)任取τi ∈[t i -1, t i ], 在时间段[t i -1, t i ]内物体所经过的路程可近似为v (τi )∆t i(i =1, 2, ⋅ ⋅ ⋅ , n ); 所求路程S 的近似值为天津工业大学理学院基础数学系高等数学、经济数学教研室5∑=∆≈ni ii t v S 1)(τ. (3)记λ=max{∆t 1, ∆t 2,⋅ ⋅ ⋅, ∆t n }, 所求路程的精确值为∑=→∆=ni ii t v S 10)(lim τλ.二、定积分定义抛开上述问题的具体意义, 抓住它们在数量关系上共同的本质与特性加以概括, 就抽象出下述定积分的定义.定义 设函数f (x )在[a , b ]上有界, 在[a , b ]中任意插入若干个分点a =x 0< x 1< x 2< ⋅ ⋅ ⋅< x n -1< x n =b ,把区间[a , b ]分成n 个小区间[x 0, x 1], [x 1, x 2], ⋅ ⋅ ⋅, [x n -1, x n ] ,各小段区间的长依次为∆x 1=x 1-x 0, ∆x 2=x 2-x 1,⋅ ⋅ ⋅, ∆x n =x n -x n -1.在每个小区间[x i -1, x i ]上任取一个点ξ i (x i -1< ξ i < x i ), 作函数值f (ξ i )与小区间长度∆x i 的乘积 f (ξ i ) ∆x i (i =1, 2,⋅ ⋅ ⋅, n ) , 并作出和∑=∆=ni i i x f S 1)(ξ.天津工业大学理学院基础数学系高等数学、经济数学教研室6记λ = max{∆x 1, ∆x 2,⋅ ⋅ ⋅, ∆x n }, 如果不论对[a , b ]怎样分法, 也不论在小区间[x i -1, x i ]上点ξ i 怎样取法, 只要当λ→0时, 和S 总趋于确定的极限I , 这时我们称这个极限I 为函数f (x )在区间[a , b ]上的定积分, 记作⎰b a dx x f )(,即 ∑⎰=→∆=n i i i b a x f dx x f 10)(lim )(ξλ.其中f (x )叫做被积函数, f (x )dx 叫做被积表达式, x 叫做积分变量, a 叫做积分下限, b 叫做积分上限, [a , b ]叫做积分区间.定义 设函数f (x )在[a , b ]上有界, 用分点a =x 0<x 1<x 2< ⋅ ⋅ ⋅<x n -1<x n =b 把[a , b ]分成n 个小区间: [x 0, x 1], [x 1, x 2], ⋅ ⋅ ⋅, [x n -1, x n ] , 记∆x i =x i -x i -1(i =1, 2,⋅ ⋅ ⋅, n ).任ξ i ∈[x i -1, x i ] (i =1, 2,⋅ ⋅ ⋅, n ), 作和∑=∆=ni i ix f S 1)(ξ.记λ=max{∆x 1, ∆x 2,⋅ ⋅ ⋅, ∆x n }, 如果当λ→0时, 上述和式的极限存在, 且极限值与区间[a , b ]的分法和ξ i 的取法无关, 则称这个极限为函数f (x )在区间[a , b ]上的定积分, 记作⎰ba dx x f )(,即 ∑⎰=→∆=ni i i ba x f dx x f 10)(lim )(ξλ.根据定积分的定义, 曲边梯形的面积为⎰=b a dx x f A )(.变速直线运动的路程为dt t v S TT )(21⎰=. 说明:天津工业大学理学院基础数学系高等数学、经济数学教研室7(1)定积分的值只与被积函数及积分区间有关, 而与积分变量的记法无关, 即⎰⎰⎰==ba b a b a du u f dt t f dx x f )()()(.(2)和∑=∆n i i i x f 1)(ξ通常称为f (x )的积分和.(3)如果函数f (x )在[a , b ]上的定积分存在, 我们就说f (x )在区间[a , b ]上可积.函数f (x )在[a , b ]上满足什么条件时, f (x )在[a , b ]上可积呢?定理1 设f (x )在区间[a , b ]上连续, 则f (x ) 在[a , b ]上可积.定理2 设f (x )在区间[a , b ]上有界, 且只有有限个间断点, 则f (x ) 在[a , b ]上可积. 定积分的几何意义:在区间[a , b ]上, 当f (x )≥0时, 积分⎰b a dx x f )(在几何上表示由曲线y =f (x )、两条直线x =a 、x =b 与x 轴所围成的曲边梯形的面积; 当f (x )≤0时, 由曲线y =f (x )、两条直线x =a 、x =b 与x 轴所围成的曲边梯形位于x 轴的下方, 定义分在几何上表示上述曲边梯形面积的负值;⎰∑∑⎰--=∆--=∆==→=→b a n i i i n i i i b a dx x f x f x f dx x f )]([)]([lim )(lim )(1010ξξλλ.当f (x )既取得正值又取得负值时, 函数f (x )的图形某些部分在x 轴的上方, 而其它部分在x 轴的下方. 如果我们对面积赋以正负号, 在x 轴上方的图形面积赋以正号, 在x 轴下方的图形面积赋以负号, 则在一般情形下, 定积分⎰ba dx x f )(的几何意义为: 它是介于x 轴、函数f (x )的图形及两条直线x =a 、x =b 之间的各部分面积的代数和.用定积分的定义计算定积分:天津工业大学理学院基础数学系高等数学、经济数学教研室8例1. 利用定义计算定积分dx x 210⎰.解 把区间[0, 1]分成n 等份, 分点为和小区间长度为n i x i =(i =1, 2,⋅ ⋅ ⋅, n -1), nx i 1=∆(i =1, 2,⋅ ⋅ ⋅, n ) . 取n i i =ξ(i =1, 2,⋅ ⋅ ⋅, n ), 作积分和 ∑∑∑===⋅=∆=∆ni i n i i i n i i n n i x x f 121211)()(ξξ )12)(1(61113123++⋅==∑=n n n n i n n i )12)(11(61n n ++=. 因为n1=λ, 当λ→0时, n →∞, 所以 31)12)(11(61lim )(lim 10210=++=∆=∞→=→∑⎰n n x f dx x n n i i i ξλ. 利定积分的几何意义求积分:例2. 用定积分的几何意义求⎰-10)1(dx x .解: 函数y =1-x 在区间[0, 1]上的定积分是以y =1-x 为曲边, 以区间[0, 1]为底的曲边梯形的面积. 因为以y =1-x 为曲边, 以区间[0, 1]为底的曲边梯形是一直角三角形, 其底边长及高均为1, 所以211121)1(10=⨯⨯=-⎰dx x .三、定积分的性质天津工业大学理学院基础数学系高等数学、经济数学教研室9两点规定:(1)当a =b 时, 0)(=⎰b a dx x f .(2)当a >b 时,⎰⎰-=a b b a dx x f dx x f )()(. 性质1 函数的和(差)的定积分等于它们的定积分的和(差) 即⎰⎰⎰±=±b a b a b a dx x g dx x f dx x g x f )()()]()([.证明:⎰±b a dx x g x f )]()([∑=→∆±=ni i i i x g f 10)]()([lim ξξλ ∑∑=→=→∆±∆=ni i i n i i i x g x f 1010)(lim )(lim ξξλλ ⎰⎰±=b a b a dx x g dx x f )()(.性质2 被积函数的常数因子可以提到积分号外面 即⎰⎰=b a b a dx x f k dx x kf )()(.这是因为∑⎰=→∆=n i i i b a x kf dx x kf 10)(lim )(ξλ⎰∑=∆==→b a n i i i dx x f k x f k )()(lim 10ξλ. 性质3 如果将积分区间分成两部分 则在整个区间上的定积分等于这两部分区间上定积分之和 即⎰⎰⎰+=bc c a b a dx x f dx x f dx x f )()()(. 这个性质表明定积分对于积分区间具有可加性.天津工业大学理学院基础数学系高等数学、经济数学教研室10 值得注意的是不论a ,b ,c 的相对位置如何总有等式⎰⎰⎰+=bc c a b a dx x f dx x f dx x f )()()( 成立. 例如, 当a <b <c 时, 由于⎰⎰⎰+=c b b a c a dx x f dx x f dx x f )()()(, 于是有⎰⎰⎰-=c b c a b a dx x f dx x f dx x f )()()(⎰⎰+=bc c a dx x f dx x f )()(. 性质4 如果在区间[a b ]上f (x )≡1 则a b dx dx ba b a -==⎰⎰1. 性质5 如果在区间[a , b ]上 f (x )≥0, 则⎰≥ba dx x f 0)((a <b ). 推论1 如果在区间[a , b ]上 f (x )≤ g (x ) 则⎰⎰≤b a ba dx x g dx x f )()((a <b ). 这是因为g (x )-f (x )≥0, 从而⎰⎰⎰≥-=-b a b a b a dx x f x g dx x f dx x g 0)]()([)()(, 所以⎰⎰≤b a b a dx x g dx x f )()(.天津工业大学理学院基础数学系高等数学、经济数学教研室11 推论2 ⎰⎰≤b a b a dx x f dx x f |)(||)(|(a <b ).这是因为-|f (x )| ≤ f (x ) ≤ |f (x )|, 所以⎰⎰⎰≤≤-b a b a b a dx x f dx x f dx x f |)(|)(|)(|,即 ⎰⎰≤b a b a dx x f dx x f |)(||)(|| .性质6 设M 及m 分别是函数f (x )在区间[a , b ]上的最大值及最小值, 则⎰-≤≤-b a a b M dx x f a b m )()()((a <b ).证明 因为 m ≤ f (x )≤ M , 所以⎰⎰⎰≤≤b a b a b a Mdx dx x f mdx )(, 从而⎰-≤≤-b a a b M dx x f a b m )()()(.性质7 (定积分中值定理) 如果函数f (x )在闭区间[a , b ]上连续, 则在积分区间[a , b ]上至少存在一个点ξ , 使下式成立:⎰-=ba ab f dx x f ))(()(ξ. 这个公式叫做积分中值公式.证明 由性质6⎰-≤≤-ba ab M dx x f a b m )()()(,各项除以b -a 得天津工业大学理学院基础数学系高等数学、经济数学教研室12⎰≤-≤b aM dx x f a b m )(1, 再由连续函数的介值定理, 在[a , b ]上至少存在一点ξ , 使⎰-=b adx x f a b f )(1)(ξ, 于是两端乘以b -a 得中值公式⎰-=ba ab f dx x f ))(()(ξ. 积分中值公式的几何解释:应注意: 不论a <b 还是a >b , 积分中值公式都成立.§5. 2 微积分基本公式一、变速直线运动中位置函数与速度函数之间的联系设物体从某定点开始作直线运动,在t时刻所经过的路程为S(t),速度为v=v(t)=S'(t)(v(t)≥0),则在时间间隔[T1,T2]内物体所经过的路程S可表示为天津工业大学理学院基础数学系高等数学、经济数学教研室13天津工业大学理学院基础数学系高等数学、经济数学教研室14)()(12T S T S -及dt t v T T )(21⎰, 即 )()()(1221T S T S dt t v TT -=⎰.上式表明, 速度函数v (t )在区间[T 1, T 2]上的定积分等于v (t )的原函数S (t )在区间[T 1, T 2]上的增量.这个特殊问题中得出的关系是否具有普遍意义呢?二、积分上限函数及其导数设函数f (x )在区间[a , b ]上连续, 并且设x 为[a , b ]上的一点. 我们把函数f (x )在部分区间[a , x ]上的定积分dx x f xa )(⎰ 称为积分上限的函数. 它是区间[a ,b ]上的函数, 记为Φ(x )dx x f x a )(⎰=, 或Φ(x )=dt t f xa )(⎰.定理1 如果函数f (x )在区间[a , b ]上连续, 则函数Φ(x )dx x f x a )(⎰=在[a , b ]上具有导数, 并且它的导数为Φ'(x ))()(x f dt t f dx d x a ==⎰(a ≤x <b ). 简要证明 若x ∈(a , b ), 取∆x 使x +∆x ∈(a , b ).∆Φ=Φ(x +∆x )-Φ(x )dt t f dt t f xa x x a )()(⎰⎰-=∆+天津工业大学理学院基础数学系高等数学、经济数学教研室15 dt t f dt t f dt t f x a x x xx a )()()(⎰⎰⎰-+=∆+ x f dt t f x x x ∆==⎰∆+)()(ξ,应用积分中值定理, 有∆Φ=f (ξ)∆x ,其中ξ在x 与x +∆x 之间, ∆x →0时, ξ→x . 于是Φ'(x ))()(lim )(lim lim 00x f f f x xx x ===∆∆Φ=→→∆→∆ξξξ. 若x =a , 取∆x >0, 则同理可证Φ+'(x )= f (a ); 若x =b , 取∆x <0, 则同理可证Φ-'(x )= f (b ). 定理2 如果函数f (x )在区间[a , b ]上连续, 则函数Φ(x )dx x f x a )(⎰=就是f (x )在[a , b ]上的一个原函数.定理的重要意义: 一方面肯定了连续函数的原函数是存在的, 另一方面初步地揭示了积分学中的定积分与原函数之间的联系.三、牛顿--莱布尼茨公式定理3 如果函数F (x )是连续函数f (x )在区间[a , b ]上的一个原函数, 则)()()(a F b F dx x f ba -=⎰. 此公式称为牛顿--莱布尼茨公式, 也称为微积分基本公式.这是因为F (x )和Φ(x )=dt t f xa )(⎰都是f (x )的原函数,所以存在常数C , 使F (x )-Φ(x )=C (C 为某一常数).天津工业大学理学院基础数学系高等数学、经济数学教研室16由F (a )-Φ(a )=C 及Φ(a )=0, 得C =F (a ), F (x )-Φ(x )=F (a ).由F (b )-Φ(b )=F (a ), 得Φ(b )=F (b )-F (a ), 即)()()(a F b F dx x f ba -=⎰. 证明: 已知函数F (x ) 是连续函数f (x ) 的一个原函数, 又根据定理2, 积分上限函数 Φ(x )=dt t f x a )(⎰也是f (x )的一个原函数. 于是有一常数C , 使F (x )-Φ(x )=C (a ≤x ≤b ).当x =a 时, 有F (a )-Φ(a )=C , 而Φ(a )=0, 所以C =F (a ); 当x =b 时, F (b )-Φ(b )=F (a ),所以Φ(b )=F (b )-F (a ), 即)()()(a F b F dx x f ba -=⎰. 为了方便起见, 可把F (b )-F (a )记成b a x F )]([, 于是)()()]([)(a F b F x F dx x f b a ba -==⎰. 进一步揭示了定积分与被积函数的原函数或不定积分之间的联系.例1. 计算⎰102dx x .解: 由于331x 是2x 的一个原函数, 所以 31031131]31[33103102=⋅-⋅==⎰x dx x .天津工业大学理学院基础数学系高等数学、经济数学教研室17例2 计算2311x dx +⎰-. 解 由于arctan x 是211x +的一个原函数, 所以 31231][arctan 1--=+⎰x x dx)1arctan(3arctan --=πππ127)4 (3 =--=. 例3. 计算⎰--121dx x. 解: 1212|]|[ln 1----=⎰x dx x =ln 1-ln 2=-ln 2. 例4. 计算正弦曲线y =sin x 在[0, π]上与x 轴所围成的平面图形的面积.解: 这图形是曲边梯形的一个特例. 它的面积ππ00]cos [sin x xdx A -==⎰=-(-1)-(-1)=2.例5. 汽车以每小时36km 速度行驶, 到某处需要减速停车.设汽车以等加速度a =-5m/s 2刹车. 问从开始刹车到停车, 汽车走了多少距离?解 从开始刹车到停车所需的时间:当t =0时, 汽车速度v 0=36km/h 3600100036⨯=m/s =10m/s . 刹车后t 时刻汽车的速度为v (t )=v 0+at =10-5t .当汽车停止时, 速度v (t )=0, 从天津工业大学理学院基础数学系高等数学、经济数学教研室18v (t )=10-5t =0得, t =2(s ).于是从开始刹车到停车汽车所走过的距离为dt t dt t v s )510()(2020-==⎰⎰10]21510[202=⋅-=t t (m ), 即在刹车后, 汽车需走过10m 才能停住.例6. 设f (x )在[0, +∞)内连续且f (x )>0. 证明函数⎰⎰=x xdt t f dt t tf x F 00)()()( 在(0, +∞)内为单调增加函数.证明: )()( 0x xf dt t tf dx d x =⎰, )()(0x f dt t f dx d x =⎰. 故 2000))(()()()()()(⎰⎰⎰-='x x xdt t f dtt tf x f dt t f x xf x F 200))(()()()(⎰⎰-=x x dt t f dt t f t x x f .按假设, 当0<t <x 时f (t )>0, (x -t )f (t )> 0 , 所以0)(0>⎰dt t f x , 0)()(0>-⎰dt t f t x x, 从而F '(x )>0 (x >0), 这就证明了F (x ) 在(0, +∞)内为单调增加函数.例7. 求21cos 02lim x dt e x t x ⎰-→.解: 这是一个零比零型未定式, 由罗必达法则,e x xe x dt e x dte x x x t x x t x 212sin lim lim lim 222cos 02cos 1021cos 0==--→-→-→⎰⎰.天津工业大学理学院基础数学系高等数学、经济数学教研室19提示: 设⎰-=Φx t dt e x 12)(, 则⎰-=Φx t dt e x cos 12)(cos .x u x t e x x e dxdu u du d x dx d dt e dx d 222cos cos 1sin )sin ()()(cos ---⋅-=-⋅=⋅Φ=Φ=⎰.天津工业大学理学院基础数学系高等数学、经济数学教研室20§5. 3 定积分的换元法和分部积分法一、换元积分法定理 假设函数f (x )在区间[a , b ]上连续, 函数x =ϕ(t )满足条件:(1)ϕ(α )=a , ϕ(β)=b ;(2)ϕ(t )在[α, β](或[β, α])上具有连续导数, 且其值域不越出[a , b ],则有dt t t f dx x f b a )()]([)(ϕϕβα'=⎰⎰.这个公式叫做定积分的换元公式.证明 由假设知, f (x )在区间[a , b ]上是连续, 因而是可积的; f [ϕ(t )]ϕ'(t )在区间[α, β](或[β, α])上也是连续的, 因而是可积的.假设F (x )是f (x )的一个原函数, 则 dx x f b a )(⎰=F (b )-F (a ).天津工业大学理学院基础数学系高等数学、经济数学教研室21另一方面, 因为{F [ϕ(t )]}'=F '[ϕ(t )]ϕ'(t )= f [ϕ(t )]ϕ'(t ), 所以F [ϕ(t )]是f [ϕ(t )]ϕ'(t )的一个原函数, 从而dt t t f )()]([ϕϕβα'⎰=F [ϕ(β )]-F [ϕ(α )]=F (b )-F (a ).因此 dt t t f dx x f b a )()]([)(ϕϕβα'=⎰⎰. 例1 计算⎰-adx x a 022(a >0).解⎰⎰⋅-=20sin 022cos cosπtdt a t a dx x a ta x a令⎰⎰+==2022022)2cos 1(2cos ππdt t atdt a220241]2sin 21[2a t t a ππ=+=. 提示:t a t a a x a cos sin 22222=-=-, dx =a cos t . 当x =0时t =0, 当x =a 时2π=t .例2 计算xdx x sin cos 520⎰π. 解 令t =cos x , 则x xd xdx x cos cos sin cos 520520⎰⎰-=ππ61]61[ 106105015cos ===-⎰⎰=t dt t dt t tx 令.提示: 当x =0时t =1, 当2π=x 时t =0. 或x xd xdx x cos cos sin cos 520520⎰⎰-=ππ天津工业大学理学院基础数学系高等数学、经济数学教研室22610cos 612cos 61]cos 61[66206=+-=-=ππx . 例3 计算⎰-π053sin sin dx x x . 解dx x x dx x x |cos |sin sin sin 230053⎰⎰=-ππ⎰⎰-=πππ2232023cos sin cos sin xdx x xdx x⎰⎰-=πππ2232023sin sin sin sin x xd x xd54)52(52]sin 52[]sin 52[2252025=--=-=πππx x . 提示: |cos |sin )sin1(sin sin sin 232353x x x x x x =-=-.在]2 ,0[π上|cos x |=cos x , 在] ,2[ππ上|cos x |=-cos x . 例4 计算dx x x ⎰++4122.解⎰⎰⎰+=⋅+-++=+312312124)3(21221 122dt t tdt t t dx x x t x 令322)]331()9327[(21]331[21313=+-+=+=t t .提示: 212-=t x , dx =tdt ; 当x =0时t =1, 当x =4时t =3.例5 证明: 若f (x )在[-a , a ]上连续且为偶函数, 则⎰⎰=-aa a dx x f dx x f 0)(2)(.天津工业大学理学院基础数学系高等数学、经济数学教研室23证明 因为dx x f dx x f dx x f aa aa )()()(00⎰⎰⎰+=--, 而⎰⎰⎰⎰-=-=---=-aa a tx a dx x f dt t f dt t f dx x f 0000)()()()(令,所以⎰⎰⎰+-=-aaaa dx x f dx x f dx x f 00)()()(⎰⎰⎰==+-=-aaa adx x f dx x f dx x f x f 00)(2)(2)]()([. 讨论:若f (x )在[-a , a ]上连续且为奇函数, 问=⎰-aa dx x f )(? 提示: 若f (x )为奇函数, 则f (-x )+f (x ) =0, 从而0)]()([)(0=+-=⎰⎰-aa a dx x f x f dx x f .例6 若f (x )在[0, 1]上连续, 证明 (1)⎰⎰=2020)(cos )(sin ππdx x f dx x f ;(2)⎰⎰=πππ0)(sin 2)(sin dx x f dx x xf .证明 (1)令t x -=2π, 则dt t f dx x f )]2[sin()(sin 0220--=⎰⎰πππ⎰⎰=-=202)(cos )]2[sin(πππdx x f dt t f .天津工业大学理学院基础数学系高等数学、经济数学教研室24(2)令x =π-t , 则⎰⎰---=0)][sin()()(sin ππππdt t f t dx x xf⎰⎰-=--=πππππ00)(sin )()][sin()(dt t f t dt t f t ⎰⎰-=πππ00)(sin )(sin dt t tf dt t f ⎰⎰-=πππ00)(sin )(sin dx x xf dx x f , 所以⎰⎰=πππ0)(sin 2 )(sin dx x f dx x xf .例7 设函数⎪⎩⎪⎨⎧<<-+≥=-01 cos 110)(2x xx xe x f x , 计算⎰-41)2(dx x f .解 设x -2=t , 则⎰⎰⎰⎰---++==-20121412cos 11)()2(dtte dt tdt t f dx x f t 212121tan ]21[]2[tan 420012+-=-=---e e t t .提示: 设x -2=t , 则dx =dt ; 当x =1时t =-1, 当x =4时t =2. 二、分部积分法设函数u (x )、v (x )在区间[a , b ]上具有连续导数u '(x )、v '(x ), 由 (uv )'=u 'v +u v '得u v '=u v -u 'v , 式两端在区间[a , b ]上积分得vdx u uv dx v u ba b a ba '-='⎰⎰][, 或vdu uv udv ba ba ba ⎰⎰-=][.天津工业大学理学院基础数学系高等数学、经济数学教研室25这就是定积分的分部积分公式. 分部积分过程:][][⋅⋅⋅='-=-=='⎰⎰⎰⎰vdx u uv vdu uv udv dx v u ba ba ba b a ba ba . 例1 计算xdx arcsin 21⎰.解xdx arcsin 21⎰x xd x x arcsin ]arcsin [21210⎰-= dx x x 22101621--⋅=⎰π )1(11211222210x d x --+=⎰π2102]1[12x -+=π12312-+=π. 例2 计算⎰10dx e x . 解 令t x =, 则⎰⎰=10102tdt e dx e t x⎰=102t tde ⎰-=1010 2 ][2dt e te t t 2 ][221 0 =-=t e e .天津工业大学理学院基础数学系高等数学、经济数学教研室26例3 设⎰=20sin πxdx I n n , 证明(1)当n 为正偶数时, 22143231π⋅⋅⋅⋅⋅--⋅-=n n n n I n ; (2)当n 为大于1的正奇数时, 3254231⋅⋅⋅⋅--⋅-=n n n n I n .证明 ⎰=20sin πxdx I n n ⎰--=201cos sin πx xd n⎰--+-=2012 01sin cos ]sin[cos ππx xd x x n n⎰--=2022sin cos )1(πxdx x n n ⎰--=-202)sin (sin )1(πdx x x n n n ⎰⎰---=-20202sin )1(sin )1(ππxdxn xdx n n n=(n -1)I n - 2-(n -1)I n , 由此得21--=n n In n I .2214342522232212Im m m m m m I m ⋅⋅⋅⋅--⋅--⋅-=,112325432421222122Im m m m m m I m ⋅⋅⋅⋅--⋅--⋅+=+,而2200ππ==⎰dx I , 1sin 201==⎰πxdx I ,因此22143425222322122π⋅⋅⋅⋅⋅--⋅--⋅-=m m m m m m I m ,天津工业大学理学院基础数学系高等数学、经济数学教研室2732543242122212212⋅⋅⋅⋅--⋅--⋅+=+m m m m m m I m .例3 设⎰=20sin πxdx I n n (n 为正整数), 证明 22143425222322122π⋅⋅⋅⋅⋅--⋅--⋅-=m m m m m m I m ,32543242122212212⋅⋅⋅⋅--⋅--⋅+=+m m m m m m I m .证明 ⎰=20sin πxdx I n n ⎰--=201cos sin πx xd n⎰---+-=20222 01sin cos )1(]sin[cos ππxdx x n x x n n⎰--=-202)sin (sin )1(πdx x x n n n ⎰⎰---=-20202sin )1(sin )1(ππxdxn xdx n n n=(n -1)I n - 2-(n -1)I n , 由此得 21--=n n I nn I . 02214342522232212I m m m m m m I m ⋅⋅⋅⋅⋅--⋅--⋅-=,112325432421222122I m m m m m m I m ⋅⋅⋅⋅⋅--⋅--⋅+=+.特别地 2200ππ==⎰dx I , 1sin 201==⎰πxdx I .天津工业大学理学院基础数学系高等数学、经济数学教研室28因此 22143425222322122π⋅⋅⋅⋅⋅--⋅--⋅-=m m m m m m I m ,32543242122212212⋅⋅⋅⋅--⋅--⋅+=+m m m m m m I m .天津工业大学理学院基础数学系高等数学、经济数学教研室29§5. 4 反常积分 一、无穷限的反常积分定义1 设函数f (x )在区间[a , +∞)上连续, 取b >a . 如果极限dx x f bab )(lim⎰+∞→存在, 则称此极限为函数f (x )在无穷区间[a , +∞)上的反常积分, 记作dx x f a )(⎰+∞, 即dx x f dx x f bab a)(lim)(⎰⎰+∞→+∞=.天津工业大学理学院基础数学系高等数学、经济数学教研室30这时也称反常积分dx x f a )(⎰+∞收敛.如果上述极限不存在, 函数f (x )在无穷区间[a , +∞)上的反常积分dx x f a )(⎰+∞就没有意义, 此时称反常积分dx x f a )(⎰+∞发散.类似地, 设函数f (x )在区间(-∞, b ]上连续, 如果极限dx x f baa )(lim⎰-∞→(a <b ) 存在, 则称此极限为函数f (x )在无穷区间(-∞, b ]上的反常积分, 记作dx x f b)(⎰∞-, 即dx x f dx x f baa b )(lim )(⎰⎰-∞→∞-=. 这时也称反常积分dx x f b)(⎰∞-收敛. 如果上述极限不存在, 则称反常积分dx x f b)(⎰∞-发散. 设函数f (x )在区间(-∞, +∞)上连续, 如果反常积分dx x f )(0⎰∞-和dx x f )(0⎰+∞都收敛, 则称上述两个反常积分的和为函数f (x )在无穷区间(-∞, +∞)上的反常积分, 记作dx x f )(⎰+∞∞-, 即dx x f dx x f dx x f )()()(00⎰⎰⎰+∞∞-+∞∞-+=dx x f dx x f bb a a )(lim)(lim⎰⎰+∞→-∞→+=.天津工业大学理学院基础数学系高等数学、经济数学教研室31这时也称反常积分dx x f )(⎰+∞∞-收敛.如果上式右端有一个反常积分发散, 则称反常积分dx x f )(⎰+∞∞-发散. 定义1' 连续函数f (x )在区间[a , +∞)上的反常积分定义为dx x f dx x f bab a)(lim)(⎰⎰+∞→+∞=. 在反常积分的定义式中, 如果极限存在, 则称此反常积分收敛; 否则称此反常积分发散. 类似地, 连续函数f (x )在区间(-∞, b ]上和在区间(-∞, +∞)上的反常积分定义为dx x f dx x f baa b)(lim)(⎰⎰-∞→∞-=.dx x f dx x f dx x f bb a a )(lim)(lim)(0⎰⎰⎰+∞→-∞→+∞∞-+=.反常积分的计算: 如果F (x )是f (x )的原函数, 则ba b ba b ax F dx x f dx x f )]([lim )(lim)(+∞→+∞→+∞==⎰⎰ )()(lim )()(lim a F x F a F b F x b -=-=+∞→+∞→.可采用如下简记形式:)()(lim )]([)(a F x F x F dx x f x a a-==+∞→∞++∞⎰.类似地)(lim )()]([)(x F b F x F dx x f x bb-∞→∞-∞--==⎰,)(lim )(lim )]([)(x F x F x F dx x f x x -∞→+∞→∞+∞-+∞∞--==⎰.天津工业大学理学院基础数学系高等数学、经济数学教研室32例1 计算反常积分dx x211+⎰+∞∞-.解∞+∞-+∞∞-=+⎰][arctan 112x dx x x x x x arctan lim arctan lim -∞→+∞→-=πππ=--=)2(2 .例2 计算反常积分⎰+∞-0dt te pt (p 是常数, 且p >0). 解∞+-∞+-+∞-⎰⎰⎰-==000]1[][pt pt pt tde pdt te dt te∞+--⎰+-=0]11[dt e p te p pt pt ∞+----=02]11[pt pt e pte p 22211]11[lim p p e p te p pt pt t =+--=--+∞→. 提示: 01lim lim lim ===+∞→+∞→-+∞→pt t pt t pt t pe e t te . 例3 讨论反常积分dx x pa 1⎰+∞(a >0)的敛散性.解 当p =1时,dx x pa1⎰+∞dx x a 1⎰+∞=+∞==∞+ ][ln a x .当p <1时,dx x pa1⎰+∞+∞=-=∞+- 1]11[ap x p .当p >1时,1]11[11 1-=-=-∞+-+∞⎰p a x p dx x p ap pa.天津工业大学理学院基础数学系高等数学、经济数学教研室33因此, 当p >1时, 此反常积分收敛, 其值为11--p a p; 当p ≤1时, 此反常积分发散.二、无界函数的反常积分定义2 设函数f (x )在区间(a , b ]上连续, 而在点a 的右邻域内无界. 取ε>0, 如果极限dx x f bt at )(lim ⎰+→存在, 则称此极限为函数f (x )在(a , b ]上的反常积分, 仍然记作dx x f ba )(⎰, 即dx x f dx x f bta tb a )(lim )(⎰⎰+→=.这时也称反常积分dx x f ba )(⎰收敛.如果上述极限不存在, 就称反常积分dx x f ba )(⎰发散.类似地, 设函数f (x )在区间[a , b )上连续, 而在点b 的左邻域内无界. 取ε>0, 如果极限dx x f ta bt )(lim ⎰-→存在, 则称此极限为函数f (x )在[a , b )上的反常积分, 仍然记作dx x f ba )(⎰, 即dx x f dx x f ta bt b a )(lim )(⎰⎰-→=.这时也称反常积分dx x f b a )(⎰收敛. 如果上述极限不存在, 就称反常积分dx x f ba )(⎰发散.设函数f (x )在区间[a , b ]上除点c (a <c <b )外连续, 而在点c 的邻域内无界. 如果两个反常积分dx x f c a )(⎰与dx x f bc )(⎰天津工业大学理学院基础数学系高等数学、经济数学教研室34都收敛, 则定义dx x f dx x f dx x f bc c a b a )()()(⎰⎰⎰+=.否则, 就称反常积分dx x f ba )(⎰发散.瑕点: 如果函数f (x )在点a 的任一邻域内都无界, 那么点a 称为函数f (x )的瑕点, 也称为无界 定义2' 设函数f (x )在区间(a , b ]上连续, 点a 为f (x )的瑕点. 函数f (x )在(a , b ]上的反常积分定义为dx x f dx x f bta tb a )(lim )(⎰⎰+→=.在反常积分的定义式中, 如果极限存在, 则称此反常积分收敛; 否则称此反常积分发散. 类似地,函数f (x )在[a , b )(b 为瑕点)上的反常积分定义为dx x f dx x f ta bt b a )(lim )(⎰⎰-→=.函数f (x )在[a , c )⋃(c , b ] (c 为瑕点)上的反常积分定义为dx x f dx x f dx x f bt ct t a ct b a )(lim )(lim )(⎰⎰⎰+-→→+=.反常积分的计算:如果F (x )为f (x )的原函数, 则有bt at bt at ba x F dx x f dx x f )]([lim )(lim )(++→→==⎰⎰ )(lim )()(lim )(x Fb F t F b F ax at ++→→-=-=.天津工业大学理学院基础数学系高等数学、经济数学教研室35可采用如下简记形式:)(lim )()]([)(x F b F x F dx x f ax ba ba +→-==⎰. 类似地, 有)()(lim )]([)(a F x F x F dx x f bx ba ba -==-→⎰, 当a 为瑕点时,)(lim )()]([)(x F b F x F dx x f ax b a ba +→-==⎰;当b 为瑕点时,)()(lim )]([)(a F x F x F dx x f bx b a ba -==-→⎰.当c (a <c <b )为瑕点时,)](lim )([)]()(lim [)()()(x F b F a F x F dx x f dx x f dx x f cx cx bc c a b a +-→→-+-=+=⎰⎰⎰.例4 计算反常积分⎰-adx xa 0221.解 因为+∞=--→221lim xa ax , 所以点a 为被积函数的瑕点.a aa x dx x a 022][arcsin 1=-⎰20arcsin lim π=-=-→a x a x .例5 讨论反常积分⎰-1121dx x的收敛性.解 函数21x在区间[-1, 1]上除x =0外连续, 且∞=→201lim x x .由于+∞=--=-=-→--⎰1)1(lim ]1[1001012x x dx xx ,天津工业大学理学院基础数学系高等数学、经济数学教研室36即反常积分⎰-0121dx x 发散, 所以反常积分⎰-1121dx x发散.例6 讨论反常积分⎰-ba qa x dx )(的敛散性.解 当q =1时,+∞=-=-=-⎰⎰b a ba ba q a x ax dx a x dx )][ln()(.当q >1时,+∞=--=--⎰b a q ba q a x q a x dx 1])(11[)(. 当q <1时,q b a q ba q ab q a x qa x dx ----=--=-⎰1 1)(11])(11[)(. 因此, 当q <1时, 此反常积分收敛, 其值为q ab q ---1)(11; 当q ≥1时, 此反常积分发散.天津工业大学理学院基础数学系高等数学、经济数学教研室37天津工业大学理学院基础数学系高等数学、经济数学教研室38天津工业大学理学院基础数学系高等数学、经济数学教研室39天津工业大学理学院基础数学系高等数学、经济数学教研室40高等数学教案第五章定积分天津工业大学理学院基础数学系高等数学、经济数学教研室41。
