道路勘测设计交点要素计算
《道路勘测设计》25-7-2定线

计算方位角:
i1
(0
2)
i1
90(Ls
R
2l)
i
(0
2)
i
90(Ls
R
2l)
习题:
已知某二级公路有一弯道,偏角α左=23°56′36″, 半径R=700m,缓和曲线Ls=150。JD=K3+763.39。 交点坐标x=65230.56,y=21238.72,起始边方位角 为263 °15′28″。
l = Lcz – HY 或 l = Lcz – ZY
切线方位角:
q
i1
(0
)
i1
90(Ls l)
R
弦切角:
l 180
2R
2)以圆曲线起、终点为基点计算圆曲线点(Lcz)坐标
(1)以起点(ZY、HY)为基点(计算HY~YH)
设圆曲线起点坐标(xHY,yHY),起点计算方位角为φi-1。 则曲线起点与计算点Lcz间的距离为 :
第三节 定线的解析计算方法
▪ 定线方法:直线型定线方法
▪
曲线型定线方法
▪ 一、直线型定线方法
▪ 1.交点坐标确定:
▪ (1)直接采集法
▪ 在绘有网格的地形图上直接读取各交点坐标。
▪ 适用于交点前后直线方向和位置限制不严的情况。
▪ (2)定前后直线间接推算交点坐标
▪ 在相邻两条边各取2个点坐标,再用相邻直线相交的解析 法计算交点坐标。
y yZH x`/ cos sin
计算方位角:
i1
i1
90l 2
A2
3)以缓和曲线起点为基点计算缓和曲线段坐标 ▪ (2)以第二缓和曲线起点(HZ)坐标计算
l HZ Lcz
l2
交点法、线元法坐标计算

3、交点法、线元法坐标计算坐标计算是根据图纸中“直线及曲线转角一览表”提供的数据计算道路中桩坐标,然后和图纸提供的“逐桩坐标表”比对,如果一样则说明输入平曲线参数输入正确,可以计算边桩坐标和其他结构物坐标了;如果中桩坐标不一样,一般是平曲线参数输入有误,需要重新检查输入,另一种结果是图纸有错,这种情况少见,但不代表没有。
“直线及曲线转角一览表”和“逐桩坐标表”见附件1、附件2。
线元法是以路线的起点坐标、方位角、起终点桩号等节点元素来计算出要求的坐标;交点法是以路线的交点要素和路线的主要要素来求得坐标。
①交点法交点:路线的转折点,路线改变方向是相邻两直线的延长线相交的点。
用JD表示,有些图纸上用IP 表示。
看下图:交点是针对曲线的(包含圆曲线和缓和曲线),一段曲线就有一个交点。
交点参数有:坐标(X,Y)、交点桩号、转角值、圆曲线半径R、缓和曲线长度。
教学提供软件(轻松测量、双心软件、测量工具)交点法曲线要素输入说明:1、QD起点坐标:起点坐标必须在直线段上,或填写前一交点的坐标。
2、JD交点曲线要素:(1)交点桩号(2)交点坐标(X,Y)(3)曲线半径R(4)第一缓和曲线长度LS1,若为0,输入0,不能为空。
(5)第二缓和曲线长度LS2,若为0,输入0,不能为空。
3、ZD终点坐标:终点坐标也必须在直线段上,或填写后一交点的坐标。
检核数据是否输入正确的方法:软件生成的圆曲线要素中切线长、外距、交点里程:注意校正起点里程、等与设计图纸是否一致。
如果上述数据和图纸不一样,请认真检查有错误的交点处的数据输入是否正确,如果输入没有错误,请考虑是否包含不完整缓和曲线,使用公式A2=R*Ls检查是否包含不完整缓和曲线。
如果包含不完整缓和曲线,那就需要用线元法也叫积木法计算了。
有的设计院给出的直曲表是整条设计线路的直曲表的一部分,以其中某个交点作为起始点的话,起始里程有时候需要校正,当然,并不是每个图纸给出的起点里程都需要校正,大多数图纸的起点里程已经被设计院校正过,我们输入平曲线的时候需要验证一下。
测绘技术中的相交测量与相交计算技巧

测绘技术中的相交测量与相交计算技巧在测绘技术中,相交测量与相交计算是非常重要的一部分。
它们可应用于土地测量、建筑设计、道路规划等多个领域。
相交测量主要用于测定两个对象之间的交点位置,而相交计算则用于计算交点之间的距离、角度等相关参数。
本文将探讨相交测量与相交计算的一些技巧和应用。
1. 相交测量技巧相交测量是指通过观测两条或多条直线的交点来确定各直线之间的相对位置。
在实际应用中,我们常常会遇到需要精确测量两个交叉道路的交点位置的情况。
这时,我们可以选取两个已知固定点,通过测量它们与待测交点的距离和方位角,进而计算出待测点的坐标。
在进行相交测量时,有几点需要注意:a. 测量仪器的选择:选择具有高精度和稳定性的测量仪器,如全站仪或高精度电子经纬仪,可以提高测量结果的准确性。
b. 观测数据的处理:在进行相交测量时,要确保取得足够的测量角度和距离数据,以提高测量精度。
同时,应仔细处理观测数据,排除异常值和误差,以获得可靠的结果。
c. 地形和环境的考虑:在进行相交测量时,应考虑地形和环境因素对观测误差的影响。
如有大坡度地形或遮挡物时,应采用适当的测量方法和措施。
2. 相交计算技巧相交计算是指根据已知的相交点和其它相关参数,通过数学计算来确定交点之间的距离、角度、倾斜等相关参数。
相交计算常用于土木工程、建筑设计等领域,如确定道路上两条直线的交叉角度,计算建筑物的相交面积等。
在进行相交计算时,需要掌握一些技巧:a. 坐标转换:通常情况下,相交计算需要将测量点的坐标从某个坐标系转换到另一个坐标系。
因此,熟练掌握坐标转换公式和方法是十分重要的。
b. 角度计算:对于需要计算交角的情况,我们可以运用向量的知识来进行计算。
通过计算向量之间的夹角,可以准确求得交角的数值。
c. 倾斜计算:在计算两个相交面的倾斜角度时,可以利用三角函数公式进行计算。
根据已知的高度和底边长度,可以求得两个面的倾斜角。
3. 相交测量与相交计算的应用相交测量与相交计算在土地测量、建筑设计、道路规划等领域有广泛应用。
公路路线的交点曲线计算方法_secret

公路路线的交点曲线计算方法1.前言传统的公路平面敷设计算方法是以交点(JD)转角(α)为基础,以外距(E)为控制,通过求算切线长(T)来计算平曲线要素及各主点桩号的,与此相应的平面设计表达便是路线“直线、曲线及转角表”。
这种表达方式除了具有直观、方便的特点以外,更为重要的是它体现出公路路线设计的两个面,一是与之相适应直线加弯道的设计思路、定线方式、中线敷设和施工放样方法,另一个则是与汽车动力学相关的各项道路几何指标,因而应该说是十分经典并为大家所习惯采用的。
现在随着光电测距仪、全站仪、GPS等先进的测量仪器的出现,公路中线敷设及施工放线广泛采用极坐标法,从而摆脱了对特定计算方法的依赖,但对于较长距离的公路主线,传统的交点转角设计定线方法和“直线、曲线及转角表”的表达方式,却仍是其他方法和方式所不能取代的。
然而,当路线因为受到限制而不得不采用,诸如不对称曲线、卵形曲线、复曲线、凸曲线、双卵形曲线等复杂曲线,特别是需要曲线反算的情况下,采用传统的交点转角计算方法是很困难的。
对于复杂曲线的计算,一般采用了在传统方法的基础上,按曲线类型分别推导计算公式,并编写功能单一的计算程序进行计算的方法。
显然这种方法局限性大、程序功能单一,即使编写了针对不同类型曲线的许多模块,也不能涵盖任意的线形组合和曲线类型等情况。
笔者通过设计实践和纬地道路辅助设计系统的研究开发,在许多技术人员熟知的传统交点转角法布设平曲线的基础上,提出一种利用计算机进行平曲线计算的新交点转角法,该方法适用于任意复杂线形的设计计算。
2.交点曲线计算法该方法以适用于任意线元组合的复杂线形设计计算为目标,是以三种基本线元的统一参数模型为基础约定,以三线元捆绑式结构为通用的单交点曲线模型的交点可组合的计算方法,有别于传统的交点转角计算方法,暂称之为交点曲线计算法。
2.a 基本线元统一参数模型的建立我们知道,公路线形的曲线分为直线、圆曲线和缓和曲线(回旋曲线)三种线元,缓和曲线线元则又分为完全缓和曲线(R->∞)、(∞-> R)和部分缓和曲线(R1->R2)。
道路工程测量中平曲线要素相关公式计算

道路工程测量中平曲线要素计算一、路线转角、交点间距的计算(一)在地形图上量出路线起终点及各路线交点的坐标:()()()21Q 23810,27180JD 2399626977JD 2468426591D 、,、,、()3JD 24848025885,、()4JD 2535025204,、()ZD 2606225783,(二)计算公式及方法设起点坐标为()00,QD X Y ,第i 个交点坐标为(),,1,2,3,4,i i i JD X Y i =则坐标增量11,i i i i DX X X DY Y Y --=-=-交点间距D =象限角 arctanDYDXθ= 方位角A 是由象限角推算的:转角1i i i A A α-=- 1.1JD QD 与之间:坐标增量10=2396623810=1860DX X X =-->1026977271802030DY Y Y =-=-=-<交点间距275.33D m === 象限角 203arctanarctan 47.502186DY DX θ-=== 方位角036036047.502312.498A θ=-=-= 2.12JD JD 与之间:坐标增量21X =2468423966=6880DX X =-->21Y 26591269773860DY Y =-=-=-<交点间距788.89D m === 象限角 386arctanarctan 29.294688DY DX θ-=== 方位角136036029.294330.706A θ=-=-= 转角110=330.706312.49818.208A A α-=-= 3. 23JD JD 与之间:坐标增量32X =2484024684=1560DX X =-->32Y 25885265917060DY Y =-=-=-<交点间距723.03D m === 象限角 706arctanarctan 77.54156DY DX θ-=== 方位角236036077.54282.46A θ=-=-= 转角221=282.46330.70648.246A A α-=-=- 4. 34JD JD 与之间:坐标增量43X =2535024840=5100DX X =-->43Y 25204258856810DY Y =-=-=-<交点间距850.8D m === 象限角 510arctanarctan 53.171681DY DX θ===- 方位角336036053.171306.829A θ=-=-= 转角332=306.829282.4624.369A A α-=-= 5. 4ZD JD 与之间:坐标增量4X =2606225350=7120DX X =-->4Y 25783252045790DY Y =-=-=>交点间距917.706D m === 象限角 579arctanarctan 39.118712DY DX θ=== 方位角039.118A θ==转角443=39.118312.49892.289A A α-=-= 二、各平曲线要素的计算 (一)JD 1曲线要素计算取800m R =,设计速度为h km /60,JD 1桩号为K 0+275.33,转角18.208α= 1.缓和曲线长度S L ,则:33600.0360.0369.72(m)800S V L R ==⨯=)m (5036.36036.3=⨯=⨯≥V L S 800~~80088.89~800(m)99S R L R ===取整数,采用缓和曲线长120m (《公路工程技术标准》规定:=V h km 60时,最小缓和曲线长度为m 50).2.圆曲线内移值R ∆2424331201200.75(m)242688()248002688(800)S SL L R R R ∆=-=-=⨯⨯⨯3.总切线长h T先求332212012059.989(m)22402240800S S L L q R =-=-=⨯ 所以18.208()tan (8000.75)tan59.989188.31(m)22h T R R q α=+∆+=++= 4.曲线总长度h L=0.0752SL Rβ=(2)2+374.22(m)180180h S S L R L R L ππαβα=-+=∙=5.五个基本桩号1JD K 0+274.33 )- h T 188.311ZH K 0+087.02 )+ S L 120.00 1HY K 0+207.02 )+ )2(S h L L - 134.22 1YH K 0+341.24 )+ S L 120.001HZ K 0+461.24)- h 21L187.111QZ K 0+274.1318.208()sec(8000.75sec80010.97(m)22h E R R R α=+∆-=+-= 超距h 22188.31374.22 2.4(m)D T L =-=⨯-=。
公路路线的交点曲线计算法

公路路线的交点曲线计算法
随着时代的发展,科技的进步,交通运输的革新对加快国
家各项经济建设有着重大的意义。
路网规划是道路设计的基础,计算交点曲线有助于评估路网建设质量和探究不同道路特性。
首先,计算交点曲线时,需要确定公路路线上所有路口和
路段。
将所有节点定位信息、路段连接信息连接起来,形成路
段网络,实现路线图形化及数据化模拟,定位出路网的交叉点,形成的图中的顶点就是路段的交点。
其次,使用经过空间坐标定位的位置学方法可以很容易地
确定交点曲线的方位。
即,首先需要对路网的每一个节点进行
测量,对空间坐标进行变换,并根据相应的变形规律,根据实
际路网图和图形叠加,得到每个节点相应位置坐标,根据坐标
计算曲线上点到曲线外点的最短距离,确定曲线方位,可以在
规划道路时将交点曲线考虑进去。
最后,要改善公路的运行情况,计算交点曲线可以帮助信
息化管理系统比较有效地调节路口交通信号,以提高路口通行
效率。
另外,计算交点曲线还可以评价路口容量,实现进口规
划和车辆识别,还可以帮助规划路面布局,计算车辆行驶安全
距离,以提高路网安全性。
总之,计算交点曲线虽然是一个复杂的技术难点,但能够
帮助管理人员更加有效地规划公路路线,提升公路的安全性和
运行效率,也是未来发展的趋势。
112道路勘测设计公式
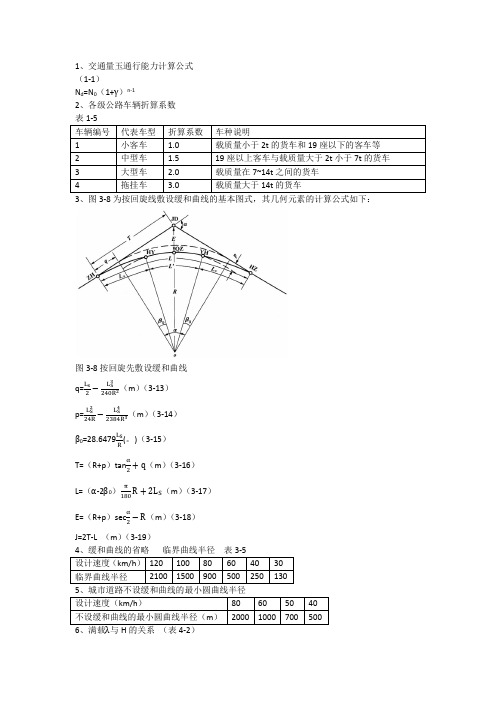
1、交通量玉通行能力计算公式 (1-1)N d =N 0(1+γ)n-12、各级公路车辆折算系数3、图3-8为按回旋线敷设缓和曲线的基本图式,其几何元素的计算公式如下:图3-8按回旋先敷设缓和曲线 q=L s2−L S3240R 2(m )(3-13)p=L S 224R −L S 42384R 3(m )(3-14) β0=28.6479LS R (。
)(3-15)T=(R+p )tan α2+q (m )(3-16) L=(α-2β0)π180R +2L S (m )(3-17)E=(R+p )sec α2−R (m )(3-18)J=2T-L (m )(3-19)6、满载λ与H 的关系 (表4-2)8、平均纵坡公式(4-3)I p =HL 式中:H —相对高差(m ) L —路线长度(m )取xoy 坐标系如图4-3所示,设坡点相邻两直坡段坡度分别为i 1和i 2它们的代数差用ω表示,即ω=i 1-i 2。
当ω为“+”时,表示凹形竖曲线;ω为“—”时,表示凸形竖曲线。
竖曲线要素示意图在图坐标系下,二次抛物线一般方程为:y=12KX 2+iX在竖曲线上任一点P ,其斜率为:i p =dydx =xk +i 抛物线上任一点的曲率半径为:R=[1+(dy dx )2]3/2/d 2y dx 2式中dydx =i,d 2y dx 2=1k ,代入上式,得:R=k (1+i 2)3/2因为i 介于i 1和i 2之间,且i 1i 2均很小,故i 2可略去不计,则:R ≈k 当x=0时,i=i 1则:y=x 22R +i 1x 当x=L 时,i=Lk +i 1=i 2,则:k=L i 2−i 1=L ω即R=L ωL=R ω 因为T=T 1≈T 2 则 T=L 2=Rω2竖曲线上任一点竖距h :因为h=PQ=y P -y Q =x 22R +i 1x −i 1x , 则h=x 22R 竖曲线外距 E=T 22R 或E =Rω28=Lω8=Tω411、※计算题某山领区二级公路,变坡点桩号为K5+030.00,高程为427.68,i 1=+5%,i 2=-5%,竖曲线半径R=2000m 。
公路工程常用公式

ZY 里程=JD 里程-T ; YZ 里程=ZY 里程+L ;公路工程常用公式一、三角函数公式:1)、在直角三角形 ABC 中,如果/ C=90°,Z A ,Z B ,Z C 所对的边分别为a , b , c ,那么®锐角之间的关系为/ A+Z B=90°O 边角之间的关系为(4)其他有关公式公路测量常用公式:|'1 LU◎S = R0EC —— 1] 外距: 2(1 )主点里程的计算①三边之间的关系为肚'+沪三F(勾股定理)sin A =—csmB =— ccosB =—Ctail A =-□tanB =— a c ot A = 一a acotB =—h= —ab 面积公式:2-Ckc 2 (hc 为c 边上的高)2)、正弦公式,即为正弦定理在一个三角形中,各边和它所对角的 等。
正弦的比相(2R 在同一个三角形中是恒量,是此三角形外接圆的半径的两倍)这一定理对于任意三角形ABC,都有貝卩 a/sinA=b/sinB=c/sinC=2R(1)a/sinA=b/sinB=c/sinC=2RR 为三角形外接圆半径正弦定理的变形公式⑴ a=2RsinA, b=2RsinB, c=2RsinC;3)任意三角形余弦公式: a 2=b 2+c 2-2bc (cosA ) 二、弧长公式:n n r/180;扇形面积公式:n n r 2/360(2) sinA : sinB ; sinC = a : b : c;2 2 2;cosA=(b +c -a )/2bc一、圆曲线:曲线要素的计算 若已知:转角a 及半径R ,则:切线长: ;曲线长:QZ里程=YZ里程-L/2 ;JD里程=QZ里程+D/2 (用于校核)(1)切线角公式P上丄比Q——缓和曲线长所对应的中心角。
(2 )缓和曲线角公式(3)缓和曲线的参数方程(4)圆曲线终点的坐标k ISO"枣血――缓和曲线全长J所对应的中心角亦称缓和曲线角。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
道路勘测设计交点要素计算
篇一:
道路勘测设计交点要素计算是道路勘测设计过程中非常重要的一步,它涉及到道路的几何形状、尺寸、交点位置等要素的确定。
下面将详细介绍交点要素计算的方法和应用。
一、交点要素计算的方法
交点要素计算的方法主要包括以下几种:
1. 几何要素计算法:根据道路的几何形状和尺寸,通过数学计算方式确定交点的位置和形状。
该方法需要使用专业的数学软件,如Excel、CAD等。
2. 测量要素计算法:通过测量道路的几何形状和尺寸,计算出交点的位置和形状。
该方法需要使用专业的测量工具,如GPS、激光扫描仪等。
3. 模拟要素计算法:通过计算机模拟道路的运行过程,计算出交点的位置和形状。
该方法需要使用专业的软件,如有限元分析软件、三维建模软件等。
二、交点要素计算的应用
交点要素计算的应用非常广泛,主要包括以下几个方面:
1. 道路勘测设计:交点要素计算是道路勘测设计的基础,它决定了道路的几何形状和尺寸,以及交点的位置和数量。
通过交点要素计算,可以确定道路的设计方案,为道路的建设提供重要的依据。
2. 道路养护管理:交点要素计算也是道路养护管理的基础,它决定了道路的磨损程度和维修方案。
通过交点要素计算,可以及时发现道路的异常情况,并及时采取措施。
3. 交通工程:交点要素计算也是交通工程的基础,它决定了道路的交通流量
和拥堵程度。
通过交点要素计算,可以计算出道路的交点数量、交点位置和拥堵程度等信息,为交通工程的设计和管理提供重要的依据。
交点要素计算是道路勘测设计、道路养护管理和交通工程中非常重要的一环。
只有正确地计算交点要素,才能确保道路的正常使用和安全性。
篇二:
道路勘测设计交点要素计算是道路勘测设计过程中非常重要的一步,它是为了保证道路的可行性和安全性所必需的。
交点要素计算包括计算道路各个相交部位的几何形状、尺寸、位置、交通流量等参数,以确保相交道路的通行能力和安全性。
以下是交点要素计算的一般步骤和注意事项:
1. 几何形状计算:根据道路设计规范和地形图等资料,计算道路各个相交部位的几何形状和尺寸。
这通常需要使用专业的数学软件和算法,如AutoCAD、Revit、SAP2000等,进行三维建模和计算。
2. 交通流量计算:交点要素计算的另一个关键步骤是计算相交道路的交通
流量。
交通流量计算包括计算每个相交道路的车流量、车速、车辆密度等参数,以确保道路的通行能力和安全性。
3. 安全参数计算:除了交通流量之外,交点要素计算还需要计算道路的各个部位的安全性参数,如路面宽度、路面厚度、桥梁高度、涵洞深度等。
这些参数对于道路的安全性和可行性至关重要。
4. 交点要素审核:交点要素计算完成后,需要对计算结果进行审核,以确保
计算结果的准确性和合理性。
审核过程中需要注意各种细节和参数的准确性,以确保道路的安全性和可行性。
注意事项:
1. 交点要素计算需要使用专业的数学软件和算法,并需要遵守相关的道路设计和勘测规范。
2. 交点要素计算的结果需要经过审核和验证,以确保计算结果的准确性和合理性。
3. 在道路设计中,交点要素计算的结果对于道路的可行性和安全性有着至关重要的作用,因此需要认真对待交点要素计算的结果。
4. 在道路设计中,需要根据不同的地形和交通需求,采用不同的设计方案,以确保道路的可行性和安全性。
道路勘测设计交点要素计算是道路设计过程中非常重要的一步,它关系到道路的可行性和安全性,因此需要认真对待。
