保守力名词解释
动力学5-势能-机械能

(3)弹性势能:
弹性势能以弹簧原长为零 势能点。
注意:零势能点可以任意取,前述是一般取法。
小结:
1、只有在保守力场中,才可引入相应的势能;只要
§4-3 保守力的功 势能 1、保守力:有些力作功只与 作功路径的始 末位置有关,而与路径的具体形状无关。这 种力称为保守力。 保守力场:在施力物体周围存在的一种作用。 当其他物体进入其作用范围内时,会受到力 的作用。
典型的保守力和保守力场:重力与重力场、 万有引力与引力场、弹性力与弹力场。
与保守力相对应的是耗散力——作功与路径形状有关
一般情况下,保守力沿某方向的分量就等于势能 沿该方向的方向导数的负值。
保守力与势能的关系:W保 E p dW dE p F dr dE P
F dr Fx dx F y dy Fz dz
Fx E p x , Fy E p y , Fz
m
0
M
h
解:从子弹以初速击中沙箱到获得共同速度可看作
在平衡位置完成的完全非弹性碰撞。水平方向
受外力为0,由动量守恒有
m 0 (m M )
子弹射入沙箱后,只有重力作功,子弹,沙箱 地球组成的系统机械能守恒。
mv0 v mM
1 2 ( m M ) ( m M ) gh 2 ( m M ) 2 gh 0 m
由动量守恒
两边平方
mv mv1 mv2 v v1 v 2 2 2 2 v v1 2v1 v2 v2
浅谈保守力

一、力的分类1.保守力。
所做功只与物体的相对起始和终点所在之处相关联,而与其物体的过程轨迹无关的力,即为保守力[1]。
假若一力学体系里,所有的作用力都是保守力,则称此系统为保守系统。
若场力的积分,则W ABC=W ADC,由此W ABCDA= W ABC+W CDA=W ABC-W ADC=0。
从其定义已经了解到对象的相对起始和终点所在之处决定了保守力做功的多少,假若在此力的作用下,物体的运动在一个封闭的路径绕行一个周期后回到起始位置,则作功是零。
假若空间中存在某一质点,质点不论在其周围任何位置,其所受到的力f与向量同向或反向,即受到吸引力或排斥力,力的大小是标量的单值函数,我们称这样的力为有心力。
所有的有心力都是保守力,如万有引力(重力)。
如果在一个孤立的系统中,所有的作用力都是保守力,则为机械能守恒的系统。
2.非保守力。
力所做的功与其运动轨迹有关的作用力即为非保守力。
通常由于能量守恒原理,非保守力做功的能量损耗被转移到其他地方。
例如,物体间摩擦力做功会使机械能转变为热能,有时候也伴随着声能等。
游船在水中移动时,水对船身的阻力将船所具有的机械能转变,如热能、声能和波能等。
从热力学第二定律可推断出,非保守力的能量损耗不可逆。
3.耗散力。
作用力对质点体系做功为负,从此导致整个系统的机械能总体减少的力即为耗散力。
耗散力做功与力使物体运动所经过的轨迹有关[2-4]。
力的划分根据力做功与运动轨迹是否相关而区分为保守力与非保守力;耗散力、非耗散力是非保守力的两个组成部分。
我们在力学体系内了解的非保守力基本上都为耗散型力,因而长久以来耗散力就几乎等同于非保守力的代替词。
然而非保守力并不都是耗散力,这二者是有区别的,例如,一根绳子跨过一个上端固定的轻质滑轮,此绳两端分别连接有两个重量不相等的重物,在放开物体令其自由运动后,绳子的拉力对下降的物体做功为负,对上升的物体做功为正。
但是根据能量守恒定律,在整个过程中机械能并无损失,而是转变为相应内能等,所以此拉力既不是属于保守力之列,也不是属于耗散力之列,即为非耗散力。
非保守力判定条件

非保守力判定条件力是物理学中的基本概念之一,是描述物体运动和相互作用的重要因素。
在物理学中,保守力和非保守力是两种不同类型的力。
保守力是指在力所做的功与路径无关,而非保守力则是指在力所做的功与路径有关。
非保守力判定条件是指判断一个力是否为非保守力的一些规则和方法。
下面将介绍一些常见的非保守力判定条件。
当力的大小与物体的速度有关时,该力可以被认为是非保守力。
例如,摩擦力就是一种非保守力。
当物体在运动时,摩擦力的大小与物体的速度成正比,因此摩擦力是一个非保守力。
当力所做的功与路径有关时,该力也可以被认为是非保守力。
例如,阻力就是一种非保守力。
当物体在空气中运动时,阻力的大小与物体的运动路径有关,因此阻力是一个非保守力。
当力的大小与物体的形状和位置有关时,该力也可以被认为是非保守力。
例如,重力就是一种非保守力。
当物体的形状和位置发生变化时,重力的大小也会发生变化,因此重力是一个非保守力。
当力所做的功与时间有关时,该力也可以被认为是非保守力。
例如,阻尼力就是一种非保守力。
当物体在受到阻尼力的作用下运动时,阻尼力所做的功与时间有关,因此阻尼力是一个非保守力。
总的来说,非保守力判定条件主要包括力的大小与物体的速度、力所做的功与路径、力的大小与物体的形状和位置、力所做的功与时间等因素有关。
通过对这些因素的观察和分析,我们可以判断一个力是否为非保守力。
非保守力在物理学中起着重要的作用,它们可以改变物体的运动状态,使物体发生加速度或减速度。
在日常生活中,我们经常会遇到非保守力的存在,如摩擦力、阻力、重力等。
了解非保守力的判定条件可以帮助我们更好地理解物体的运动规律,进而应用于实际问题的解决中。
非保守力判定条件是一些用于判断一个力是否为非保守力的方法和规则。
通过对力的大小与物体的速度、力所做的功与路径、力的大小与物体的形状和位置、力所做的功与时间等因素的观察和分析,我们可以确定一个力是否为非保守力。
非保守力在物理学中具有重要的意义,它们可以改变物体的运动状态,影响物体的加速度和减速度。
大学物理单元知识点归纳3)

因为物体对地球的引力不足以使地球产生 位移,所以对地球用动能定理有:
1 mgh m v 2 2
0 00
1 mgh m v 2 2 1 1 2 mg (z 1 z 2 ) m v mgz 1 m v 2 mgz 2 2 2
此即机械能守恒定律.所以地球上进行的力学实验中一般 不考虑地球能量的变化 系统的动能定理为:
M2
M1
M1 F dr F dr E p
M2
保守力的功 A 等于质点在始末两位置势能增量的负值 微分形式
dA dE p
A E p
(1)势能 为状态量,是状态(位置)的单值 函数。其数值还与零势能点的选取有关。
(2)势能属于物体与系统所共有。
讨论
1. 能量守恒定律可以适用于任何变化过程
2. 功是能量交换或转换的一种度量 3. 机械能守恒定律是普遍的能量守恒定律在 机械运动范围内的体现
六.三个宇宙速度
第一宇宙速度
在地面上发射航天器,使之能绕地球圆轨道运行所需的最
小发射速度,即发射人造卫星所需的最小速度
Mm v2 GM G 2 m v r r r
取: EP ( M 0 ) 0 (势
M0(选参考点)
M0
M
F dr
势能是位置的函数,在数值上等 于从 M 到 势能零点 保守力所做的 功,该函数通常称作势能函数。 势能是系统具有的做功本领
讨论
(1) 因势能零点可以任选,所以某一点的势能值是相对的。
第三宇宙速度
在地面上发射航天器,使之不但能脱离地球引力场,还要脱 离太阳的引力场所需的最小发射速度。 计算在地球公转轨道上需以多大速度发射,才能脱离太阳的 引力场。代入太阳质量 Ms,地球到太阳的距离 Rs
3-5 保守力和非保守力
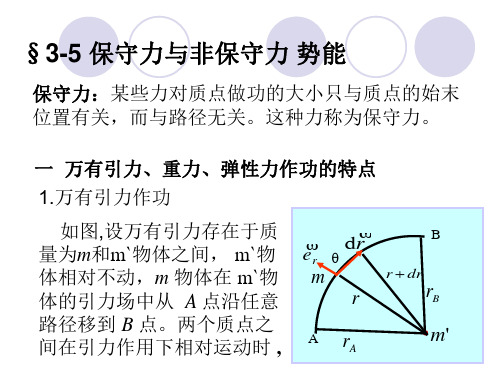
保守力 重 力 弹 力
势能(E p ) mgh
1 2
势能零点 h=0
Ep
0
势能曲线 h
Ep
kx
2
x=0
Ep
0 0
x r
引 力
mM G r
r=∞
3.势能和保守力的关系: 势能是保守力对路径的线积分,EP=
dEP F dl F cos dl Fdl l
dE P Fl dl
Mm 1 EP= r -G r 2 dr GMm r
F m r
M
o
③弹性势能
Wab
xb
xa
1 2 1 2 kxdx ( kxb kxa ) EP 2 2
弹性势能以弹簧原长为零势能点。
1 1 2 E P kxdx (0 kx ) kx 2 x 2 2 势能曲线对照表(势能随位置变化的曲线~势能曲线)
m
C
L1
F
B
A
L2
D
WACB WADB F dr
ACB
ADB
F dr
(路径L1)
(路径L2)
对沿闭合路径ACBDA运动一周的物体做功为
W F dr
L ACB
F dr
BDA
F dr
BDA
保守力在 l 方向投影 E p 在 l 方向空间变化率
b
a
F dl
F
m
a
θ
dl
b
l
Fl
保守力沿某一给定的l方向的分量等于与此保守力 相应的势能函数沿l方向的空间变化率。 若势能为EP(x,y,z)
3-3保守力与非保守力 势能
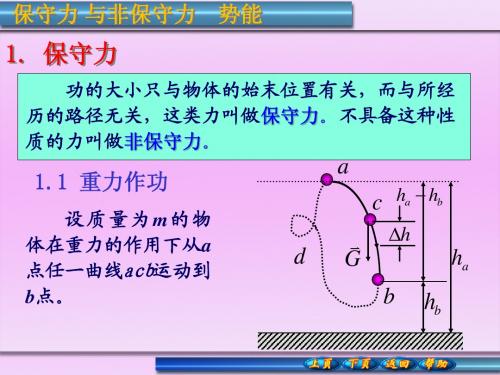
解 放手后,物体运动到 x 1 处和弹簧分离。在整个过程中, 1 2 kx1 弹簧弹性力作功 2
摩擦力作功
mgx2 1 2 根据动能定理有 kx1 mgx2 0 0 2 2 2
x1
x2
kx1 100 0.02 0.20 2mgx2 2 0.1 9.8 0.1
保守力做功在数值上等于系统势能的减少。 保守力功与势能的积分关系: W Ep
保守力功与势能的微分关系: dW dEp
例
一轻弹簧的劲度系数为k =100N/m,用手推一质量 m
=0.1 kg 的物体把弹簧压缩到离平衡位置为x1=0.02m处, 如图 所示。放手后,物体沿水平面移动到x2=0.1m而停止。 求物体与水平面间的滑动摩擦系数。
保守力 与非保守力 势能
1. 保守力
功的大小只与物体的始末位置有关,而与所经 历的路径无关,这类力叫做保守力。不具备这种性 质的力叫做非保守力。
1.1 重力作功
设质量为m的物 体在重力的作用下从a 点任一曲线acb运动到 b点。
a
c ha hb
d
G
h
ha
b
hb
重力作功
力 G 所做的元功是
在元位移 s 中,重
a
c ha hb
A G coss h d G mg cos s b hb mgh A A mgh mg h mgha mghb
ha
重力作功
A mgha mghb
由此可见,重力作 功仅仅与物体的始末位 置有关,而与运动物体 所经历的路径无关。
A F d s 0
3. 势能
势能(E P) :由物体的相对位置所确定的系
高二物理竞赛课件:保守力 成对力的功 势能
保守力 成对力的功 势能 一、 保守力
根据各种力做功的特点,可将力分为保守力和 非保守力。 保守力(conservative force):
做功与路径无关,只与始末位置有关的力。 如:重力、万有引力、弹性力以及静电力等。 非保守力(non-conservative force): 做功不仅与始末位置有关,还与路径有关的力。 如:摩擦力、回旋力等。
摩擦力所做的功:
A4 Ff l cos180 1453 435(J)
(2)合力所做的功:
A A1 A2 A3 A4 165 J
返回 退出
(3)如改用起重机把木箱吊上汽车。 所用拉力 F' 至少要等于重力。这时拉力所做的功为
A Fl sin30 980 30 0.5 1.47 103(J)
重力所做的功
A2 Gl co(s 180 60) 980 3( 0.5) 1.47 103(J)
正压力所做的功
A3 FNl cos90 0
返回 退出
根据牛顿第二定律:
FN F sin10 G cos30 0
FN G cos30 F sin10 727(N) Ff μFN 0.20 727 145(N)
例 柔软均质物体以初速v0 送上平台,物体前端在平台 上滑行 s 距离后停止。设滑道上无摩擦,物体与台面间
的摩擦因数为 ,且 s >L,求初速度v0 。
解:
返回 退出
由动能定理:
返回 退出
重力的功 设物体m从a点沿任一曲线移动到b点。
在元位移 dr中,重力所做的元功为
dA mg cosds mgdh
返回 退出
弹性力的功 设光滑水平桌面一端固定 的轻弹簧(k),另一端连接 质点 m,当质点由a点运 动到b点的过程中 :
4保守力势能功能原理
④.势能的绝对值没有意义,只关心势能 的相对值。 如果一块石头放在地面你对它并不关心。
§4.保守力、势能、功能原理 / 二、势能
如果把石头放在楼顶,并摇摇欲坠,你 就不会不关心它,你可能要离它远些, 因为它对你的生命安全造成威胁。
§4.保守力、势能、功能原理 / 二、势能
dv f mg cos m dt 摩擦力的功 W阻 fdr
A
R
f N
n
d
o
B
解2:动能定理 由质点动能定理: W Ek Ek 0 Ek 受力分析:只有重力和摩擦力作功,
W重 W阻 Ek Ek 0 A A点物体动能 Ek 0 0 mg cos dr W阻 Ek 1 90 2 W阻 mv 0 mg cos Rd 2 1 2 mv mgR 2
初态机械能: 1 2 E A mvA mgh 2 h AC sin 36.9
36.9º
f
vA
h
末态机械能:
n
1 2 EC k( BC ) 2
n i 1 i 1
由功能原理: Wi外 Wi内非 E
§4.保守力、势能、功能原理 / 五、方法应用举例
i 1
Wi外 0,
§4.保守力、势能、功能原理 / 二、势能
三、功能原理 利用质点系的动能定理:
i 1
Wi外 Wi内 Ek Ek 0 Ek
i 1 n i 1
n
n
其中内力作功的代数和项 Wi内 可分为 系统内部保守力的功和内部非保守力的功,
i 1 n n n
Wi内 Wi内保 Wi内非
保守力的功
摩擦力所做的功与物体实际经过的路 径有关,与物体的始末位置无关。
上面四种力:
只有重力、弹力、万有引力作功有共同特征:
共同特征: 作功与所经过的路径无关, 只与始末(相对)位置有关 具有这种特征的力称为保守力,否则称 为非保守力。
重力、弹簧弹性力、万有引力是保守力;摩擦 力是非保守力。
保守力定义有两种表述 表述一(文字叙述):
作功与路径无关,只与始末位置有关的力
称为保守力 表述二(数学表示) :
F保 dr 0
L
保守力的环流为零。
10
第二种表述:
L
F保 dr
F保 dr -
b
b2a
a1b
F保 dr
F保 dr
1
b2a
a 2b
F保 dr
b b)
0
x
特点:重力的功只与物体始末两点的位置有关而 与物体所经过的路径无关。
弹簧弹性力的功
弹簧 自然长度 0
F
X
特点:弹簧弹性力所作的功只与物体的始末两点 的位置有关而与物体所经过的路径无关。
特点:万有引力所作的功只与物体的始末两点的 位置有关而与物体所经过的路径无关。
摩擦力的功
b
1
a
2
2
a
a 2b
L
F保 dr a1b来自 F保 dr
F保 dr 0
L
F保 dr 0
11
大学物理学
保守力
保守力的定义
力所做功的大小只与物体的始末位置有关与物 体运动所经过的路径无关,这类力叫保守力。
保守力、保守力场、保守量
根据 Vg = Wy 及
所选定的基准面,决定质点位置以量测 V。
若质点在空间中任一位置 (x, y, z),则其位能函数 V = V(x, y, z)。质点自(x1, y1, z1)
移动至(x2, y2, z2),保守力所做之功,可以其函数差量测,即
U1-2 = V1 - V2
例如,重 W 之质点,悬挂于弹簧上,其位能函数可用位置 s 表达,此位置是从弹簧未受力之
(5.4-27) 当一质点在势力场中沿路径 l 运动,考虑到上式,由式(5.4-7),力场对其所作的功可表为
(5.4-28) 其中 U0与 U 和 V0与 V 分别为路径 l 的起点与终点的势函数和势能值。由此式表明,质点在势 力场中运动势力的功仅与路径的起始与终点的位置有关而与路径无关。考虑到势力场的功为 两位置势函数(或势能)值的差,因此势力场的绝对大小已不太重要。如果在力场中的某点 r0 定义其势函数(或势能)值为零,即令
保守力
名词简介
在物理系统里,假若一个粒子,从起始点移动到终结点,由于受到作用力,所做的功, 不因为路径的不同而改变。则称此力为保守力(Conservative Force)。假若一个物理系统里, 所有的作用力都是保守力,则称此系统为保守系统。 做功
保守力的功与物体运动所经过的路径无关,只与运动物体的起点和终点的位置有关,当 然也与保守力场的性质有关。
图5-14 等势面 则由式(5.4-28),有
(5.4-29) 此式表明,质点在势力场某位置的势能为质点由零势能位置移动到该位置势力所作的功的负 值。 在势力场中,势函数(或势能)为常值 c 的点构成了一曲面(见图5-14),即
这些曲面称为等势面。c 为零的曲面称为零势面。根据势力与势函数的关系式(5.4-25)可见, 势力的方向沿等势面的法向。质点在等势面上移动,势力不作功。
