初中最基本的尺规作图总结
最新人教版 初中数学 七年级上册尺规作图_知识点讲解1
如图24.4.2，我们可以先画射线AB，然后用圆 规量出线段MN的长，再在射线AB上截取AC＝ MN，线段AC就是所要画的线段．
图 24.4.2
2、作一个角等于已知角 已知： AOB(图1) 求作： A`O`B`,使 A`O`B`= AOB
B D
B` D`
O
A C
O`
C`
A`
1、作射线O`A`。 2、以点O为圆心，以任意长为半径作弧，交OA于
C，交OB于D。 3、以点O`为圆心，以OC长为半径作弧，交O`A`于
C`。 4、以点C`为圆心，以CD长为半径作弧，交前弧于D`。 5、经过点D`作射线O`B`，∠A`O`B`就是所求的角。
B D
B` D`
O
A
C
O`
C`
A`
• 证明：
,由作法可知
• △C`O`D`≌△COD(SSS),
• ∴∠C`O`D`=∠COD(全等三角形的对应角相等)，
的垂直平分线．
5.过定点作已知直线的垂线 ①.如图，点C在直线l上，试过点C画出直线l的垂 线．
能否利用画线段垂直平分线的方法解决呢？试试看，ห้องสมุดไป่ตู้成
整个作图．
图 24.4.8
以C为圆心，任一线段的长为半径画弧，交l于A、B两点，
则C是线段AB的中点．因此，过C画直线l的垂线转化为
画线段AB的垂直平分线．
• 即∠A`O`B`=∠AOB。
3、平分已知角
已知： AOB（图2） 求作：射线OC，使 AOC= BOC
B
E
C
•
O
D
A
1、在OA和OB上，分别截取OD、OE，使OD=OE。
• 2、分别以D、E为圆心，大于DE的长为半径作弧，
初中数学考点尺规作图
过直线外一点作已知直线的垂线
步骤：1.在直线另一侧取点M；2.以P为圆心，以PM为半径画弧,交直线于A、B两点；3.分别以A、B为圆心，以大于12AB长为半径画弧，交M同侧于点N；4.连接PN,则直线PN即为所求垂线
过直线上一点作已知直线的垂线
步骤：1.以点O为圆心，任意长为半径向点O两侧作弧，交直线于A、B两点；2.分别以点A、B为圆心，以大于 AB长为半径向直线两侧作弧，交点分别为M、N；3.连接MN，MN即为所求垂线
作线段的垂直平分线
步骤：1.分别以点A、B为圆心，以大于 AB的长为半径，在AB两侧作弧；2.连接两弧交点所成直线即为所求线段的垂直平分线
作一个角等于已知角
步骤：1.在∠α上以点O为圆心、以适当的长为半径作弧，交∠α的两边于点P、Q；2.作射线O′A；3.以O′为圆心、OP长为半径作弧，交O′A于点M；4.以点M为圆心，PQ长为半径作弧，交前弧于点N；5.过点N作射线O′B，∠BO′A即为所求角
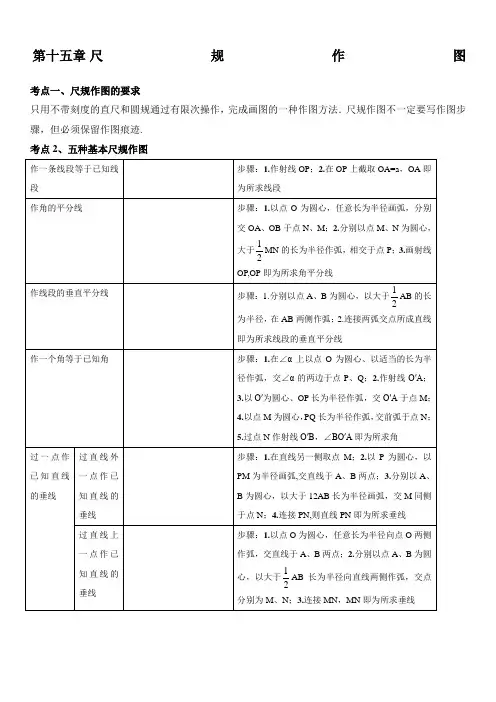
第15章尺规作图
考点一、尺规作图的要求
只用不带刻度的直尺和圆规通过有限次操作，完成画图的一种作图方法．尺规作图不一定要写作图步骤，但必须保留作图痕迹.
考点2、五种Βιβλιοθήκη 本尺规作图作一条线段等于已知线段
步骤：1.作射线OP；2.在OP上截取OA=a，OA即为所求线段
作角的平分线
步骤：1.以点O为圆心，任意长为半径画弧，分别交OA、OB于点N、M；2.分别以点M、N为圆心，大于 MN的长为半径作弧，相交于点P；3.画射线OP,OP即为所求角平分线
中考专题复习——初中最基本的尺规作图总结与典型例题
初中基本尺规作图总结与典型例题一、理解“尺规作图”的含义1.在几何中，我们把只限定用直尺（无刻度）和圆规来画图的方法，称为尺规作图．其中直尺只能用来作直线、线段、射线或延长线段；圆规用来作圆和圆弧．由此可知，尺规作图与一般的画图不同，一般画图可以动用一切画图工具，包括三角尺、量角器等，在操作过程中可以度量，但尺规作图在操作过程中是不允许度量成分的．2.基本作图：（1）用尺规作一条线段等于已知线段；（2）用尺规作一个角等于已知角. 利用这两个基本作图，可以作两条线段或两个角的和或差.二、熟练掌握尺规作图题的规范语言1.用直尺作图的几何语言：①过点×、点×作直线××；或作直线××；或作射线××；②连结两点××；或连结××；③延长××到点×；或延长（反向延长）××到点×，使××＝××；或延长××交××于点×；2.用圆规作图的几何语言：①在××上截取××＝××；②以点×为圆心，××的长为半径作圆（或弧）；③以点×为圆心，××的长为半径作弧，交××于点×；④分别以点×、点×为圆心，以××、××的长为半径作弧，两弧相交于点×、×. 三、了解尺规作图题的一般步骤尺规作图题的步骤：1.已知：当作图是文字语言叙述时，要学会根据文字语言用数学语言写出题目中的条件；2.求作：能根据题目写出要求作出的图形及此图形应满足的条件；3.作法：能根据作图的过程写出每一步的操作过程.当不要求写作法时，一般要保留作图痕迹.对于较复杂的作图，可先画出草图，使它同所要作的图大致相同，然后借助草图寻找作法.在目前，我们只要能够写出已知，求作，作法三步（另外还有第四步证明）就可以了，而且在许多中考作图题中，又往往只要求保留作图痕迹，不需要写出作法，可见在解作图题时，保留作图痕迹很重要.尺规作图的定义：尺规作图是指用没有刻度的直尺和圆规作图。
(完整版)初中最基本的尺规作图总结
尺规作图一、理解“尺规作图”的含义1.在几何中，我们把只限定用直尺（无刻度）和圆规来画图的方法，称为尺规作图．其中直尺只能用来作直线、线段、射线或延长线段；圆规用来作圆和圆弧．由此可知，尺规作图与一般的画图不同，一般画图可以动用一切画图工具，包括三角尺、量角器等，在操作过程中可以度量，但尺规作图在操作过程中是不允许度量成分的．2.基本作图：（1）用尺规作一条线段等于已知线段；（2）用尺规作一个角等于已知角. 利用这两个基本作图，可以作两条线段或两个角的和或差.二、熟练掌握尺规作图题的规范语言1.用直尺作图的几何语言：①过点×、点×作直线××；或作直线××；或作射线××；②连结两点××；或连结××；③延长××到点×；或延长（反向延长）××到点×，使××＝××；或延长××交××于点×；2.用圆规作图的几何语言：①在××上截取××＝××；②以点×为圆心，××的长为半径作圆（或弧）；③以点×为圆心，××的长为半径作弧，交××于点×；④分别以点×、点×为圆心，以××、××的长为半径作弧，两弧相交于点×、×. 三、了解尺规作图题的一般步骤尺规作图题的步骤：1.已知：当作图是文字语言叙述时，要学会根据文字语言用数学语言写出题目中的条件；2.求作：能根据题目写出要求作出的图形及此图形应满足的条件；3.作法：能根据作图的过程写出每一步的操作过程.当不要求写作法时，一般要保留作图痕迹.对于较复杂的作图，可先画出草图，使它同所要作的图大致相同，然后借助草图寻找作法.在目前，我们只要能够写出已知，求作，作法三步（另外还有第四步证明）就可以了，而且在许多中考作图题中，又往往只要求保留作图痕迹，不需要写出作法，可见在解作图题时，保留作图痕迹很重要.尺规作图的定义：尺规作图是指用没有刻度的直尺和圆规作图。
初中数学知识点总结：掌握五种基本作图
初中数学知识点总结：掌握五种基本作图知识点总结
一、基本作图的有关概念：
1.尺规作图：用没有刻度的直尺和圆规来作图的方法，叫做尺规作图。
2.五种基本作图：五种基本作图是尺规作图的基础，数学中的五种基本作图是指作一条线段等于已知线段、作一个角等于已知角、作一个角的角平分线、过定点作已知直线的垂线、作线段的垂直平分线。
二、基本作图的原理和步骤：
1.原理：边边边公理
2.步骤：作图题的方法与证明题解法不相同，对于作图题首先将文字叙述转化为数学语言，即要写出题目的已知、求作、作法、证明。
三、尺规作图的优点：尺规作图只能使用圆规和无刻度的直尺这两种工具。
工具虽少但能正确地画出的图形，比度量法画出的图形更精确。
常见考法
(1)考查五种基本作图中的一种，要求写出已知、求证、作法、证明过程。
有时考题不要求写作法，但要求保留作图痕迹;(2)利用尺规作图和勾股定理画出数轴上的无理
数点;(3)利用尺规作图作一些正多边形(如正三角形、正六
边形等)。
误区提醒。
中考复习----五种基本尺规作图
D
A
C
B
l
②.如图，如果点C不在直线l上，应采取怎样的步骤，过 点C画出直线l的垂线？
图 24.4.10
A D
B
五种基本作图：
►做一条线段等于已知线段
►做一个角等于已知角
►做一条线段的垂直平分线
►做一个角的角平分线
►过一点做已知线段的垂线
构扒初中
魏利
做一条线段等于已知线段
做一个角等于已知角
五种 基本 作图
做一条线段的垂直平分线
做一个角的角平分线
过一点做已知线段的垂线
1.作一条线段等于已知线段
已知：线段AB． 求作：线段A′B′， 使A′B′＝AB． 作法与示范：
A B
A′
B′
C′
2、作一个角等于已知角
已知： ∠AOB。
求作： ∠A`O`B`,使∠A`O`B`= ∠AOB。
B
D D`
B`
O
C
A
O`
C`
A`
3、画已知线段的垂直平分线
已知：线段AB。
求作：O.
C A B
D
4、平分已知角
►已知： ∠AOB。
►求作：射线OC，使
∠
AOC= ∠ BOC。
B
E
C
O
D
A
5.过定点作已知直线的垂线
尺规作图资料(完整)
1：尺规作出正三角形2尺规作出正方形3：尺规作出正六边形4：尺规作出正十边形5：尺规作出正十六边形6:尺规作出正十七边形7：尺规作出正十五边形8：尺规作出正五边形9:单尺作出正八边形10：单尺作出正方形11：单尺作出正六边形12：单尺作出正五边形13：单规找出两点间的三等分点14：单规找出两点间的中点15:单规作出等边三角形16：单规作出正八边形17：单规作出正方形18：单规作出正六边形19：单规作出正十边形20:单规作出正十二边形21：单规作出正十六边形22：单规作出正十五边形23单规作出正五边形24：只有两个刻度的直尺作出正三角形25:只有两个刻度的直尺作出正方形初中数学尺规作图专题讲解张远波尺规作图是起源于古希腊的数学课题.只使用圆规和直尺，并且只准许使用有限次，来解决不同的平面几何作图题。
平面几何作图，限制只能用直尺、圆规.在历史上最先明确提出尺规限制的是伊诺皮迪斯.他发现以下作图法：在已知直线的已知点上作一角与已知角相等。
这件事的重要性并不在于这个角的实际作出,而是在尺规的限制下从理论上去解决这个问题.在这以前，许多作图题是不限工具的.伊诺皮迪斯以后，尺规的限制逐渐成为一种公约，最后总结在《几何原本》之中。
初等平面几何研究的对象,仅限于直线、圆以及由它们（或一部分）所组成的图形，因此作图的工具,习惯上使用没有刻度的直尺和圆规两种。
限用直尺和圆规来完成的作图方法，叫做尺规作图法。
最简单的尺规作图有如下三条:⑴经过两已知点可以画一条直线;⑵已知圆心和半径可以作一圆;⑶两已知直线；一已知直线和一已知圆；或两已知圆,如果相交，可以求出交点;以上三条，叫做作图公法.用直尺可以画出第一条公法所说的直线；用圆规可以作出第二条公法所说的圆;用直尺和圆规可以求得第三条公法所说的交点.一个作图题，不管多么复杂，如果能反复应用上述三条作图公法，经过有限的次数,作出适合条件的图形,这样的作图题就叫做尺规作图可能问题；否则,就称为尺规作图不能问题.历史上，最著名的尺规作图不能问题是：⑴三等分角问题：三等分一个任意角；⑵倍立方问题：作一个立方体，使它的体积是已知立方体的体积的两倍;⑶化圆为方问题：作一个正方形，使它的面积等于已知圆的面积。
尺规作图题型总结-2024年中考数学答题技巧与模板构建(学生版)
尺规作图题型总结题型解读|模型构建|通关试练本专题主要对初中阶段的一般考查学生对基本作图的掌握情况和实践操作能力,并且在作图的基础上进一步推理计算(或证明)。
尺规作图是指用没有刻度的直尺和圆规作图。
尺规作图是中考必考知识点之一，复习该版块时要动手多画图，熟能生巧！本专题主要总结了五个常考的基本作图题型，(1)作相等角；(2)作角平分线；(3)作线段垂直平分线；(4)作垂直(过一点作垂线或圆切线)；(5)用无刻度的直尺作图。
模型01作相等角①以∠α的顶点O为圆心，以任意长为半径作弧，交∠α的两边于点P，Q；②作射线O'A'；③以O'为圆心，OP长为半径作弧，交O'A'于点M；④以点M为圆心，PQ长为半径作弧，交③中所作的弧于点N；⑤过点N作射线O'B'，∠A'O'B'即为所求作的角.原理：三边分别相等的两个三角形全等；全等三角形对应角相等延伸：作平行线模型02作角平分线①以O为圆心，任意长为半径作弧，分别交OA，OB于点M，N；②分别以点M，N为圆心，以大于MN的长为半径作弧，两弧相交于点P；③过点O作射线OP，OP即为∠AOB的平分线.原理：三边分别相等的两个三角形全等；全等三角形对应角相等延伸：②到两边的距离相等的点②作三角形的内切圆模型03作线段垂直平分线①分别以点A，B为圆心，大于AB长为半径，在AB两侧作弧，分别交于点M和点N；②过点M，N作直线MN，直线MN即为线段AB的垂直平分线.原理：到线段两端距离相等的点在这条线段的垂直平分线上延伸：①到两点的距离相等的点②作三角形的外接圆③找对称轴(旋转中心)④找圆的圆心模型04作垂直(过一点作垂线或圆切线)(点P在直线上)①以点P为圆心，任意长为半径向点P两侧作弧，分别交直线l于A，B两点；②分别以点A，B为圆心，以大于AB的长为半径作弧，两弧交于点M；③过点M，P作直线MP，则直线MP即为所求垂线.原理：等腰三角形的“三线合一”，两点确定一条直线延伸：确定点到直线的距离(内切圆半径)(点P 在直线外)①以点P 为圆心，大于P 到直线l 的距离为半径作弧，分别交直线l 于A ，B 两点；②分别以A ，B 为圆心，以大于AB 的长为半径作弧交于点N ；③过点P ，N 作直线PN ，则直线PN 即为所求垂线.原理：到线段两端距离相等的点在这条线段的垂直平分线上模型05仅用无刻度直尺作图无刻度直尺作图通常会与等腰三角形的判定，三角形中位线定理，矩形的性质和勾股定理等几何知识点结合，熟练掌握相关性质是解题关键.模型01作相等角考|向|预|测做相等角该题型近年主要以解答题形式出现，一般为解答题型的其中一问，难度系数较小，在各类考试中基本为送分题型。
初中最基本的尺规作图总结讲解学习
初中最基本的尺规作图总结尺规作图一、熟练掌握尺规作图题的规范语言1. 用直尺作图的几何语言：①过点X、点X作直线XX;或作直线XX;或作射线XX；②连结两点XX；或连结XX；③延长XX到点X;或延长（反向延长）XX到点X,使XX = XX ;或延长XX 交XX于点X;2. 用圆规作图的几何语言：①在XX上截取XX=XX;②以点X为圆心，XX的长为半径作圆（或弧）；③以点X为圆心，XX的长为半径作弧，交XX于点X;④分别以点X、点X为圆心，以XX、XX的长为半径作弧，两弧相交于点x、x.三、了解尺规作图题的一般步骤尺规作图题的步骤：1. 已知：当作图是文字语言叙述时，要学会根据文字语言用数学语言写出题目中的条件；2. 求作：能根据题目写出要求作出的图形及此图形应满足的条件；3. 作法：能根据作图的过程写出每一步的操作过程.当不要求写作法时，一般要保留作图痕迹.对于较复杂的作图，可先画出草图，使它同所要作的图大致相同，然后借助草图寻找作法.在目前，我们只要能够写出已知，求作，作法三步（另外还有第四步证明）就可以了，而且在许多中考作图题中，又往往只要求保留作图痕迹，不需要写出作法，可见在解作图题时，保留作图痕迹很重要.五种基本作图：1、作一条线段等于已知线段；2、作一个角等于已知角；3、作已知线段的垂直平分线；4、作已知角的角平分线；5、过一点作已知直线的垂线；题目一：作一条线段等于已知线段。
已知：如图，线段a .求作：线段AB使AB = a .作法：（1）作射线AP;（2）在射线AP上截取AB=a .则线段AB就是所求作的图形。
（作线段写于已知线段）题目二：作已知线段的中点已知：如图，线段MN. 求作：作法：点0,使M0=NQ即0是MN的中点）（1）分别以M N为圆心，大于的相同线段为半径画弧，两弧相交于P, Q;（2）连接PQ交MNT O则点0就是所求作的MN的中点。
（作线段的中点）(试问：PQ 与MN 有何关系？)题目三：作已知角的角平分线。
初中尺规作图总结
2. 基本作图：（1）用尺规作一条线段等于已知线段； （2）用尺规作一个角等于已知角 .
利用这两个基本作图，可以作两条线段或两个角的和或差 . 二、熟练掌握尺规作图题的规范语言 1. 用直尺作图的几何语言： ①过点×、点×作直线××；或作直线××；或作射线××；
②连结两点××；或连结××；
③延长××到点×；或延长（反向延长）××到点×，使××＝××；或延长××交
则线段 AB就是所求作的图形。 题目二：作已知线段的中点。 已知：如图，线段 MN. 求作：点 O，使 MO=N（O即 O是 MN的中点） . 作法： （１）分别以 M、N为圆心，大于
的相同线段为半径画弧， 两弧相交于 P，Q； （２）连接 PQ交 MN于 O． 则点 O就是所求作的ＭＮ的中点。 （试问： PQ与ＭＮ有何关系？） 题目三：作已知角的角平分线。 已知：如图，∠ AOB， 求作：射线 OP, 使∠ AOP＝∠ BOP（即 OP平分∠ AOB）。 作法： （1）以 O为圆心，任意长度为半径画弧，
题时，保留作图痕迹很重要 . 尺规作图的定义： 尺规作图是指用没有刻度的直尺和圆规作图。最基本
规作图 , 通常称 基本作图 。一些复杂的尺规作图都是由基本作图组成的。 五种基本作图： 1、 作一条线段等于已知线段；
2 、作一个角等于已知角； 3 、作已知线段的垂直平分线； 4 、作已知角的角平分线； 5 、过一点作已知直线的垂线； 题目一：作一条线段等于已知线段。 已知：如图，线段 a . 求作：线段 AB，使 AB = a . 作法： （ 1）作射线 AP； （ 2）在射线 AP上截取 AB=a .
图（ 2）
图（ 3）
正解 如图（ 3）． （1）作直线 PQ，在直线 PQ上任取一点 D，作 DM⊥ PQ； （2）在 DM上截取线段 DA=h；
初中尺规作图技巧+数学尺规典型案例复习+历年中考尺规例题
初中尺规作图+数学尺规典型案例复习+历年中考尺规例题基本作图示范：1、作一条线段,等于已知线段;已知线段MN。
求作：一条线段等于已知线段.作法：图先画射线AB,然后用圆规在射线AB上截取AC= MN.线段AC就是所要作的线段.2、作一个角等于已知角。
(其理论依据为“SSS”理);作法：①作射线0'A‘;②以点0为圆心，以任意长为半径作弧，交OA于C,交OB于D;③以点0'为圆心，以OC长为半径作弧，交0'A'于C‘;④以点C'为圆心，以CD为半径作弧，交前弧于D‘;⑤经过点D'作射线0'B'，∠A' 0'B'就是所求的角. 连结CD、C'D'，由作法可知△C'O'D≌△COD(SSS)∴∠C'O'D'=∠COD(全等三角形对应角相等)．即∠A'O'B'=∠AOB．3、作已知角的平分线(其理论依据为“SSS”公理);已知∠AOB,求作：射线OC,使∠AOC= ∠BOC.作法：①在OA和OB上，分别截取OD. OE.②分别以D.E为圆心，大于DE 的长为半径作弧，在∠AOB内，两弧交于点C；③作射线OC.OC就是所求的射线.连结CD、CE，由作法可知△ODC≌△OEC(SSS)∴∠COD=∠COE(全等三角形的对应角相等)．即∠AOC=∠BOC．4、经过一点(点在直线上或点在直线外)作已知直线的垂线;a.经过已知直线上的一点作这条直线的垂线.已知：直线AB和AB上一点C,求作：AB的垂线，使它经过点C.第一步:作平角ACB的平分线CD;第二步:反向延长射线CD.作法：作平角ACB的平分线CF,直线CF就是所求的垂线.b.经过已知直线外一点作这条直线的垂线.作法：①任意取一点K,使K和C在AB的两旁;②以C为圆心,CK长为半径作弧，交AB于点D和E;③分别以D和E为圆心，大于DE的长为半径作弧，两弧交于点F.④作直线CF.直线CF就是所求的垂线，注意：经过已知直线上的一点，作这条直线的垂线转化成画线段垂直平分线的方法解决.典型例题分析历年中考好题精选题目练习。
初中尺规基本作图
【学习目标】1．了解什么是尺规作图．2．学会用尺规作图法完成下列五种基本作图：(1)画一条线段等于已知线段；(2)画一个角等于已知角；(3)画线段的垂直平分线；(4)过已知点画已知直线的垂线；(5)画角平分线．3．了解五种基本作图的理由．4．学会使用精练、准确的作图语言叙述画图过程．5．学会利用基本作图画三角形等较简单的图形．6．通过画图认识图形的本质，体会图形的内在美．【基础知识精讲】1．尺规作图：限定只用直尺和圆规来完成的画图，称为尺规作图．注意：这里所指的直尺是没有刻度的直尺，由于免去了度量，因此，用尺规作图法画出的图形的精确度更高，它在工程绘图等领域应用比较广泛．2．尺规作图中的最基本、最常用的作图称为基本作图．3．基本作图共有五种：(1)画一条线段等于已知线段．如图24-4-1，已知线段DE．求作：一条线段等于已知线段．作法：①先画射线AB．②然后用圆规在射线AB上截取AC＝MN．线段AC就是所要作的线段．(2)作一个角等于已知角．如图24-4-2，已知∠AOB．求作：∠A′O′B′，使∠A′O′B′＝∠AOB．作法：①作射线O′A′；②以点O为圆心，以任意长为半径作弧，交OA于C，交OB于D．③以点O′为圆心，以OC长为半径作弧，交O′A′于C′．④以点C′为圆心，以CD为半径作弧，交前弧于D′．⑤经过点D′作射线O′B′，∠A′O′B′就是所求的角．(3)作线段的垂直平分线．如图24-4-3，已知线段AB．求作：线段AB的垂直平分线．作法：①分别以点A和点B为圆心，大于AB21的长为半径作弧，两弧相交于点C和D．②作直线CD．直线CD就是线段AB的垂直平分线．注意：直线CD与线段AB的交点，就是AB的中点．(4)经过一点作已知直线的垂线．a．经过已知直线上的一点作这条直线的垂线，如图24-4-4．已知：直线AB和AB上一点C，求作：AB的垂线，使它经过点C．作法：作平角ACB的平分线CF．直线CF就是所求的垂线，如图24-4-4．b．经过已知直线外一点作这条直线的垂线．如图24-4-5，已知：直线AB和AB外一点C．求作：AB的垂线，使它经过点C．作法：①任意取一点K，使K和C在AB的两旁．②以C为圆心，CK长为半径作弧，交AB于点D和E．③分别以D和E为圆心，大于DE21的长为半径作弧，两弧交于点F．④作直线CF．直线CF就是所求的垂线．注意：经过已知直线上的一点，作这条直线的垂线转化成画线段垂直平分线的方法解决．(5)平分已知角．如图24-4-6，已知∠AOB．求作：射线OC，使∠AOC＝∠BOC．作法：①在OA和OB上，分别截取OD、OE．②分别以D、E为圆心，大于DE21的长为半径作弧，在∠AOB内，两弧交于点C．③作射线OC．OC就是所求的射线．注意：以上五种基本作图是尺规作图的基础，一些复杂的尺规作图，都是由基本作图组成的，同学扪要高度重视，努力把这部分内容学习好．通过这一节的学习，同学们要掌握下列作图语言：(1)过点×和点×画射线××，或画射线××．(2)在射线××上截取××＝××．(3)以点×为圆心，××为半径画弧．(4)以点×为圆心，××为半径画弧，交××于点×．(5)分别以点×，点×为圆心，以××，××为半径作弧，两弧相交于点×．(6)在射线××上依次截取××＝××＝××．(7)在∠×××的外部或内部画∠×××＝∠×××．注意：学过基本作图后，在作较复杂图时，属于基本作图的地方，不必重复作图的详细过程，只用一句话概括叙述就可以了．如：(1)画线段××＝××．(2)画∠×××＝∠×××．(3)画××平分∠×××，或画∠×××的角平分线．(4)过点×画××⊥××，垂足为点×．(5)作线段××的垂直平分线××，等等．但要注意保留全部的作图痕迹，包括基本作图的操作程序，不能因为作法的叙述省略而作图就不按程序操作，只有保留作图痕迹，才能反映出作图的操作是否合理．【经典例题精讲】例1已知两边及其夹角，求作三角形．如图24-4-7，已知：∠α，线段a、b，求作：△ABC，使∠A＝∠α，AB＝a，AC＝b．作法：①作∠MAN＝∠α．②在射线AM、AN上分别作线段AB＝a，AC＝b．③连结BC．如图24-4-8，△ABC即为所求作的三角形．注意：一般几何作图题，应有下面几个步骤：已知、求作、作法，比较复杂的作图题，在作图之前可根据需要作一些分析．例2如图24-4-9，已知底边a，底边上的高h，求作等腰三角形．已知线段a、h．求作：△ABC，使AB＝AC，且BC＝a，高AD＝h．分析：可先作出底边BC，根据等腰三角形的三线合一的性质，可再作出BC的垂直平分线，从而作出BC边上的高AD，分别连结AB和AC，即可作出等腰△ABC来．作法：(1)作线段BC＝a．(2)作线段BC的垂直平分线MN，MN与BC交于点D．(3)在MN上截取DA，使DA＝h．(4)连结AB、AC．如图24-4-10，△ABC即为所求的等腰三角形．例3已知三角形的一边及这边上的中线和高，作三角形．如图24-4-11，已知线段a，m，h(m>h)．求作：△ABC使它的一边等于a，这边上的中线和高分别等于m和h(m>h)．分析：如图24-4-12，假定△ABC已作出，其中BC＝a，中线AD＝m，高AE＝h，在△AED 中AD＝m，AE＝h，∠AED＝90°，因此这个Rt△AED可以作出来(△AED为奠基三角形)．当Rt△AED作出后，由a21DCBD==的关系可作出点B和点C，于是△ABC即可得到．作法：(1)作△AED ，使∠AED ＝90°，AE ＝h ，AD ＝m ． (2)延长ED 到B ，使a 21DB =． (3)在DE 或BE 的延长线上取a 21DC =．(4)连结AB 、AC ．则△ABC 即为所求作的三角形．注意：因为三角形中，一边上的高不能大于这边上的中线，所以如果h>m ，作图题无解；若m ＝h ，则作出的图形为等腰三角形．例4 如图24-4-13，已知线段a ．求作：菱形ABCD ，使其半周长为a ，两邻角之比为1∶2．分析：因为菱形四边相等，“半周长为a ”就是菱形边长为2a，为此首先要将线段a 等分，又因为菱形对边平行，则同旁内角互补，由“邻角之比为1∶2”可知，菱形较小内角为60°，则菱形较短对角线将菱形分成两个全等的等边三角形．所以作图时只要作出两个有公共边的等边三角形，则得到的四边形即为所求的菱形ABCD ．作法：(1)作线段a 的垂直平分线，等分线段a ．(2)作线段AC ，使2a AC =． (3)分别以A 、C 为圆心，2a为半径，在AC 的两侧画弧，两弧分别交于B ，D ．(4)分别连结AB 、BC 、CD 、DA 得到四边形ABCD ，则四边形ABCD 为所求作的菱形(如图24-4-14)．注意：这种通过先画三角形，然后再画出全部图形的方法即为“三角形奠基法”．例5 如图24-4-15，已知∠AOB 和C 、D 两点．求作一点P ，使PC ＝PD ，且使点P 到∠AOB 的两边OA 、OB 的距离相等．分析：要使PC ＝PD ，则点P 在CD 的垂直平分线上，要使点P 到∠AOB 的两边距离相等，则P 应在∠AOB 的角平分线上，那么满足题设的P 点就是垂直平分线与角平分线的交点了．作法：(1)连结CD ．(2)作线段CD 的中垂线l ．(3)作∠AOB 的角平分线OM ，交l 于点P ，P 点为所求．注意：这类定点问题应需确定两线，两直线的交点即为定点，当然这两直线应分别满足题目的不同要求．【中考考点】 例6 (2000·安徽省)如图24-4-16，直线321ll l ，，表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有( )A ．一处B ．二处C ．三处D ．四处分析：到直线21l l ，距离相等的点在21l l ，相交所构成的角的平分线上，可利用作角平分线的方法找到这些点．解：分别作321ll l ，，相交所构成的角平分线，共可作出六条，三条角平分线相交的交点共有四个．答案：D ．注意：本题应用了角平分线的性质，在具体作图时，不可只作出位于中心位置的一处，而要全面考虑其他满足条件的点．例7 (2002·陕西省)如图24-4-17，△ABC 是一块直角三角形余料，∠C ＝90°，工人师傅要把它加工成—个正方形零件，使C 为正方形的—个顶点，其他三个顶点分别在AB 、BC 、AC 边上．(1)试协助工人师傅用尺规画出裁割线(不写作法，保留作图痕迹)；(2)工人师傅测得AC ＝80 cm ，BC ＝120cm ，请帮助工人师傅算出按(1)题所画裁割线加工成的正方形零件的边长．解：(1)作∠ACB 的平分线与AB 的交点E 即为正方形—顶点，作CE 线段的中垂线HK 与AC 、BC 的交点F 、D 即为所作正方形另两个顶点，如图24-4-17．(2)设这个正方形零件的边长为x cm ， ∵DE ∥AC ，∴BC BDAC DE =， ∴120x 12080x -=． ∴x ＝48．答：这个正方形零件的边长为48cm ．注意：本题是几何作图和几何计算相结合题目，要求读者对基本作图务必掌握，同时对作出图形的性质要清楚．例8 (2002·山西省)如图24-4-18①，有一破残的轮片(不小于半个轮)，现要制作一个与原轮片同样大小的圆形零件，请你根据所学的有关知识，设计两种方案，确定这个圆形零件的半径．分析：欲确定这个圆形零件的半径，可以借助三角板，T 形尺或尺规作图均可，图②中MN 21是这个零件的半径，图③中OB 是这个零件半径．解：如图24-4-18②③所示．【常见错误分析】例9 如图24-4-19，已知线段a 、b 、h ．求作△ABC，使BC＝a，AC＝b，BC边上的高AD＝h．并回答问题，你作出的三角形唯一吗？从中你可以得到什么结论呢？错解：(1)作法：①作Rt△ADC，使AD＝h，AC＝b．②在直线CD上截取CB＝a．如图24-4-20，则△ABC就是所求作的三角形．(2)作出的三角形唯一．(3)得出结论：有两边及一边上的高对应相等的两三角形全等．误区分析：本题错解在于忽略了三角形的高可能在三角形内部也可能在三角形的外部．正解：如图24-4-21，作法：①作Rt△ADC，使AD＝h，AC＝b．②在直线CD上截取CB＝a(在点C的两侧)．则△ABC，△AB′C都是所求作三角形．(2)作出的三角形不唯一．(3)得出结论有两边及—边上的高对应相等的两三角形不一定全等．注意：与三角形的高有关的题目应慎之又慎．【学习方法指导】学习本单元基本作图，主要是运用观察法，通过具体的操作，了解各种基本作图的步骤，掌握作图语言．【规律总结】画复杂的图形时，如一时找不到作法，—般是先画出一个符合所设条件的草图，再根据这个草图进行分析，逐步寻找画图步骤．有时，也可以根据已知条件和基本作图，先作局部三角形，再以此为基础，根据有关条件画出其余部分，从而完成全图，这种方法称为三角形奠基法．【同步达纲练习】1．下列画图语言表述正确的是( )A．延长线段AB至点C，使AC＝BCB．以点O为圆心作弧C．以点O为圆心，以AC长为半径画弧D．在射线OA上截取OB＝a，BC＝b，则有OC＝a＋b2．过点C画直线l的垂线的思想方法是：把这个问题转化为画_________的方法来解决．3．作线段的垂直平分线的理论根据是_________和两点确定一条直线．4．把一个角四等分的步骤是：第一步：先把这个角__________等分，第二步：把得到的两个角分别再___________等分．5．已知∠α和∠β，求作一个角，使它等于) (21β∠+α∠．6．求作三角形三条角平分线的交点．7．已知一腰和底边上的高，作等腰三角形．8．已知，三个自然村A、B、C的位置如图24-4-22所示．现计划建一所小学，使其到A、B、C三个自然村的距离相等．请你设计出学校所在的位置O(不写作法，保留作图痕迹)．9．如图24-4-23，在直线l上求作—点P，使PA＝PB(不写作法，保留作图痕迹)．10．已知．求作：的中点P．。
初中尺规作图典型例题归纳总结
初中尺规作图典型例题归纳典型例题一例 线段a 、b ，画一条线段，使其等于b a 2+．分析 所要画的线段等于b a 2+，实质上就是b b a ++．画法：1．画线段a AB =．2．在AB 的延长线上截取b BC 2=．线段AC 就是所画的线段．说明1．尺规作图要保存画图痕迹，画图时画出的所有点和线不可随意擦去．2．其它作图都可以通过画根本作图来完成，写画法时，只需用一句话来概括表达根本作图． 典型例题二例 如下列图，线段a 和b ，求作一条线段AD 使它的长度等于2a －b ．错解 如图〔1〕，〔1〕作射线AM ；〔2〕在射线AM 上截取AB =BC =a ，CD =b ，那么线段AD 即为所求． 错解分析 主要是作图语言不严密，当在射线上两次截取时，要写清是否顺次，而在求线段差时，要交待截取的方向．图〔1〕 图〔2〕正解 如图〔2〕，〔1〕作射线AM ；〔2〕在射线AM 上，顺次截取AB =BC =a ；〔3〕在线段CA 上截取CD =b ，那么线段AD 就是所求作的线段．典型例题三例 求作一个角等于角∠MON 〔如图1〕．图〔1〕 图〔2〕错解 如图〔2〕，〔1〕作射线11M O ；〔2〕在图〔1〕，以O 为圆心作弧，交OM 于点A ，交ON 于点B ； 〔3〕以1O 为圆心作弧，交11M O 于C ；〔4〕以C 为圆心作弧，交于点D ；〔5〕作射线D O 1．那么∠D CO 1即为所求的角．错解分析 作图过程中出现了不准确的作图语言，在作出一条弧时，应表达为：以某点为圆心，以其长为半径作弧．正解 如图〔2〕，〔1〕作射线11M O ；〔2〕在图〔1〕上，以O 为圆心，任意长为半径作弧，交OM 于点A ，交ON 于点B ；〔3〕以1O 为圆心，OA 的长为半径作弧，交11M O 于点C ；〔4〕以C 为圆心，以AB 的长为半径作弧，交前弧于点D ；〔5〕过点D 作射线D O 1． 那么∠D CO 1就是所要求作的角．典型例题四例 如下列图，∠α及线段a ，求作等腰三角形，使它的底角为α，底边为a ．分析 先假设等腰三角形已经作好，根据等腰三角形的性质，知两底角∠B =∠C =∠α，底边BC =a ，故可以先作∠B =∠α，或先作底边BC =a ．作法 如下列图〔1〕∠MBN =∠α；〔2〕在射线BM 上截取BC =a ；〔3〕以C 为顶点作∠PCB =∠α，射线CP 交BN 于点A ．△ABC 就是所要求作的等腰三角形．说明 画复杂的图形时，如一时找不到作法，一般是先画出一个符合条件的草图，再根据这个草图进展分析，逐步寻找画图步骤．典型例题五例 如图〔1〕，直线AB 及直线AB 外一点C ，过点C 作CD ∥AB 〔写出作法，画出图形〕．分析 根据两直线平行的性质，同位角相等或内错角相等，故作一个角∠ECD =∠EFB 即可．作法 如图〔2〕．图〔1〕 图〔2〕〔1〕过点C 作直线EF ，交AB 于点F ；〔2〕以点F 为圆心，以任意长为半径作弧，交FB 于点P ，交EF 于点Q ；〔3〕以点C 为圆心，以FP 为半径作弧，交CE 于M 点；〔4〕以点M 为圆心，以PQ 为半径作弧，交前弧于点D ；〔5〕过点D 作直线CD ，CD 就是所求的直线．说明 作图题都应给出证明，但按照教科书的要求，一般不用写出，但要知道作图的原由．典型例题六例 如下列图，△ABC 中，a =5cm ，b =3cm ，ccm ，∠B =︒36，∠C =︒44，请你从中选择适当的数据，画出与△ABC 全等的三角形〔把你能画的三角形全部画出来，不写画法但要在所画的三角形中标出用到的数据〕．分析 此题实质上是利用原题中的5个数据，列出所有与△ABC 全等的各种情况，依据是SSS 、SAS 、AAS 、ASA ．解 与△ABC 全等的三角形如下列图所示．典型例题七例 正在修建的中山北路有一形状如下列图所示的三角形空地需要绿化．拟从点A 出发，将△ABC 分成面积相等的三个三角形，以便种上三种不同的花草，请你帮助规划出图案〔保存作图痕迹，不写作法〕．〔2003年，桂林〕分析 这是尺规作图在生活中的具体应用．要把△ABC 分成面积相等的三个三角形，且都是从A 点出发，说明这三个三角形的高是相等的，因而只需这三个三角形的底边也相等，所以只要作出BC 边的三等分点即可．作法 如下列图，找三等分点的依据是平行线等分线段定理．典型例题八例 ∠AOB ，求作∠AOB 的平分线OC ．错解 如图〔1〕作法 〔1〕以O 为圆心，任意长为半径作弧，分别交OA 、OB 于D 、E 两点； 〔2〕分别以D 、E 为圆心，以大于21DE 的长为半径作弧，两弧相交于C 点； 〔3〕连结OC ，那么OC 就是∠AOB 的平分线．错解分析 对角平分线的概念理解不够准确而致误．作法〔3〕中连结OC ，那么OC 是一条线段，而角平分线应是一条射线．图〔1〕 图〔2〕正解 如图〔2〕〔1〕以点O 为圆心，任意长为半径作弧，分别交OA 、OB 于D 、E 两点；〔2〕分别以D 、E 为圆心，以大于21DE 的长为半径作弧，两弧交于C 点； 〔3〕作射线OC ，那么OC 为∠AOB 的平分线．典型例题九例 如图〔1〕所示，线段a 、b 、h 〔h ＜b 〕．求作△ABC ，使BC =a ，AB =b ， BC 边上的高AD =h ．图〔1〕错解 如图〔2〕，〔1〕作线段BC =a ；〔2〕作线段BA =b ，使AD ⊥BC 且AD =h ．那么△ABC 就是所求作的三角形．错解分析 ①不能先作BC ；②第2步不能同时满足几个条件，完全凭感觉毫无根据；③未考虑到此题有两种情况．对于这种作图题往往都是按照由里到外的顺序依次作图，如此题先作高AD ，再作AB ，最后确定BC ．图〔2〕 图〔3〕正解 如图〔3〕．〔1〕作直线PQ ，在直线PQ 上任取一点D ，作DM ⊥PQ ；〔2〕在DM 上截取线段DA =h ；〔3〕以A 为圆心，以b 为半径画弧交射线DP 于B ；〔4〕以B 为圆心，以a 为半径画弧，分别交射线BP 和射线BQ 于1C 和2C ；〔5〕连结1AC 、2AC ，那么△1ABC 〔或△2ABC 〕都是所求作的三角形．典型例题十例 如下列图，线段a ，b ，求作Rt △ABC ，使∠ACB =90°，BC =a ，AC =b 〔用直尺和圆规作图，保存作图痕迹〕．分析 此题解答的关键在于作出∠ACB =90°，然后确定A 、B 两点的位置，作出△ABC ．作法 如下列图〔1〕作直线MN ：〔2〕在MN 上任取一点C ，过点C 作CE ⊥MN ；〔3〕在CE 上截取CA =b ，在CM 上截取CB =a ；〔4〕连结AB ，△ABC 就是所求作的直角三角形．说明 利用根本作图画出所求作的几何图形的关键是要先分析清楚作图的顺序．假设把握不好作图顺序，要先画出假设图形．典型例题十一例 如下列图，钝角△ABC ，∠B 是钝角．求作：〔1〕BC 边上的高；〔2〕BC 边上的中线〔写出作法，画出图形〕．分析 〔1〕作BC 边上的高，就是过点A 作BC 边所在直线的垂线；〔2〕作BC 边上的中线，要先确定出BC 边的中点，即作出BC 边的垂直平分线． 作法 如下列图〔1〕①在直线CB 外取一点P ，使A 、P 在直线CB 的两旁；②以点A 为圆心，AP 为半径画弧，交直线CB 于G 、H 两点；③分别以G 、H 为圆心，以大于21GH 的长为半径画弧，两弧交于E 点； ④作射线AE ，交直线CB 于D 点，那么线段AD 就是所要求作的△ABC 中BC 边上的高．〔2〕①分别以B 、C 为圆心，以大于21BC 的长为半径画弧，两弧分别交于M 、N 两点； ②作直线MN ，交BC 于点F ；③连结AF ，那么线段AF 就是所要求作的△ABC 中边BC 上的中线．说明 在三角形中求作一边上的高线、中线、角平分线时，首先要把握好高线、中线、角平分钱是三条线段；其次，高线、中线的一个端点必须是三角形中这边所对的顶点，而关键是找出另一个端点．典型例题十二例 如图〔1〕所示，在图中作出点C ，使得C 是∠MON 平分线上的点，且AC =OC ．图〔1〕 图〔2〕分析 由题意知，点C 不仅要在∠MON 的平分线上，且点C 到O 、A 两点的距离要相等，所以点C 应是∠MON 的平分线与线段OA 的垂直平分线的交点．作法 如图〔2〕所示 〔1〕作∠MON 的平分线OP ；〔2〕作线段OA 的垂直平分线EF ，交OP 于点C ，那么点C 就是所要求作的点．说明〔1〕根据题意弄清要求作的点的特征是到各直线距离相等，还是到各端点距离相等．〔2〕两条直线交于一点．典型例题十三例 如下列图，线段a 、b 、∠α、∠β．求作梯形ABCD ，使AD =a ，BC =b ，AD ∥BC ，∠B =∠α；∠C =∠β．分析 假定梯形已经作出，作AE ∥DC 交BC 于E ，那么AE 将梯形分割为两局部，一局部是△ABE ，另一局部是AECD ．在△ABE 中，∠B =∠α，∠AEB =∠β，BE =b -a ，所以，可以首先把它作出来，而后作出AECD ．作法 如下列图．〔1〕作线段BC=b；〔2〕在BC上截取BE=b-a；〔3〕分别以B、E为顶点，在BE同侧作∠EBA=∠α，∠AEB=∠β，BA、EA交于A；〔4〕以EA、EC为邻边作AECD．四边形ABCD就是所求作的梯形．说明根本作图是作出较简单图形的根底，三角形是最简单的多边形，它是许多复杂图形的根底．因此，要作一个复杂的图形，常常先作一个比拟容易作出的三角形，然后以此为根底，再作出所求作的图形．典型例题十四例如下列图，在一次军事演习中，红方侦察员发现蓝方指挥部在A区内，到铁路与公路的距离相等，且离铁路与公路穿插处B点700米，如果你是红方的指挥员，请你在图示的作战图上标出蓝方指挥部的位置．〔2002年，青岛〕分析依据角平分线的性质可以知道，蓝方指挥部必在A区内两条路所夹角的平分线上，然后由蓝方指挥部距Bcm，就可以确定出蓝方指挥部的位置．解如下列图，图中C点就是蓝方指挥部的位置．典型例题十五例如图〔1〕，有公共端点的线段AB、BC．求作⊙O，使它经过点A、B、C〔要求：尺规作图，不写作法，保存作图痕迹〕．〔2002年，大连〕图〔1〕 图〔2〕分析 因为A 、B 、C 三点在⊙O 上，所以OA =OB =OC =R ．根据到线段AB 、BC 各端点距离相等的点在线段的垂直平分线上，故分别作线段AB 、BC 垂直平分线即可．解 如图〔2〕说明 角平分线的性质、线段垂直平分线的性质在作图题中的应用是近几年中考中的又一道风景，它往往与实际问题严密联系在一起．典型例题十六例 如图，是一块直角三角形余料，︒=∠90C ．工人师傅要把它加工成一个正方形零件，使C 为正方形的一个顶点，其余三个顶点分别在AB 、BC 、AC 边上．试协助工人师傅用尺规画出裁割线．分析 要作出符合条件的正方形，可先作出有三个角为90°的四边形，并设法让相邻的一组边相等即可．作法 如图．① 作ACB ∠的角平分线CD ，交AB 于点G ；②过G 点分别作AC 、BC 的垂线，垂足为E 、F ．那么四边形ECFG 就是所要求作的正方形．。
专题12尺规作图题型总结-2024年中考数学答题技巧与模板构建(解析版)
专题12尺规作图题型总结题型解读｜模型构建｜通关试练本专题主要对初中阶段的一般考查学生对基本作图的掌握情况和实践操作能力,并且在作图的基础上进一步推理计算(或证明)。
尺规作图是指用没有刻度的直尺和圆规作图。
尺规作图是中考必考知识点之一，复习该版块时要动手多画图，熟能生巧！本专题主要总结了五个常考的基本作图题型，（1）作相等角；（2）作角平分线；（3）作线段垂直平分线；（4）作垂直（过一点作垂线或圆切线）；（5）用无刻度的直尺作图。
模型01作相等角①以∠α的顶点O为圆心，以任意长为半径作弧，交∠α的两边于点P，Q；②作射线O'A'；③以O'为圆心，OP长为半径作弧，交O'A'于点M；④以点M为圆心，PQ长为半径作弧，交③中所作的弧于点N；⑤过点N作射线O'B'，∠A'O'B'即为所求作的角.原理：三边分别相等的两个三角形全等；全等三角形对应角相等延伸：作平行线模型02作角平分线①以O为圆心，任意长为半径作弧，分别交OA，OB于点M，N；②分别以点M，N为圆心，以大于MN的长为半径作弧，两弧相交于点P；③过点O作射线OP，OP即为∠AOB的平分线.原理：三边分别相等的两个三角形全等；全等三角形对应角相等延伸：2到两边的距离相等的点②作三角形的内切圆模型03作线段垂直平分线①分别以点A，B为圆心，大于AB长为半径，在AB两侧作弧，分别交于点M和点N；②过点M，N作直线MN，直线MN即为线段AB的垂直平分线.原理：到线段两端距离相等的点在这条线段的垂直平分线上延伸：①到两点的距离相等的点②作三角形的外接圆3找对称轴（旋转中心）4找圆的圆心模型04作垂直（过一点作垂线或圆切线）（点P在直线上）①以点P为圆心，任意长为半径向点P两侧作弧，分别交直线l于A，B两点；②分别以点A，B为圆心，以大于AB的长为半径作弧，两弧交于点M；③过点M，P作直线MP，则直线MP即为所求垂线.原理：等腰三角形的“三线合一”，两点确定一条直线延伸：确定点到直线的距离（内切圆半径）（点P在直线外）①以点P为圆心，大于P到直线l的距离为半径作弧，分别交直线l于A，B两点；②分别以A，B为圆心，以大于AB的长为半径作弧交于点N；③过点P，N作直线PN，则直线PN即为所求垂线.原理：到线段两端距离相等的点在这条线段的垂直平分线上模型05仅用无刻度直尺作图无刻度直尺作图通常会与等腰三角形的判定，三角形中位线定理，矩形的性质和勾股定理等几何知识点结合，熟练掌握相关性质是解题关键.模型01作相等角考｜向｜预｜测做相等角该题型近年主要以解答题形式出现，一般为解答题型的其中一问，难度系数较小，在各类考试中基本为送分题型。
初中最基本的尺规作图总结
尺规作图一、熟练掌握尺规作图题的规范(guīfàn)语言1.用直尺作图的几何(jǐ hé)语言：①过点×、点×作直线(zhíxiàn)××；或作直线(zhíxiàn)××；或作射线(shèxiàn)××；②连结两点××；或连结××；③延长××到点×；或延长（反向延长）××到点×，使××＝××；或延长××交××于点×；2.用圆规作图的几何语言：①在××上截取××＝××；②以点×为圆心，××的长为半径作圆（或弧）；③以点×为圆心，××的长为半径作弧，交××于点×；④分别以点×、点×为圆心，以××、××的长为半径作弧，两弧相交于点×、× .三、了解尺规作图题的一般步骤尺规作图题的步骤：1.已知：当作图是文字语言叙述时，要学会根据文字语言用数学语言写出题目中的条件；2.求作：能根据题目写出要求作出的图形及此图形应满足的条件；3.作法：能根据作图的过程写出每一步的操作过程.当不要求写作法时，一般要保留作图痕迹.对于较复杂的作图，可先画出草图，使它同所要作的图大致相同，然后借助草图寻找作法.在目前，我们只要能够写出已知，求作，作法三步（另外还有第四步证明）就可以了，而且在许多中考作图题中，又往往只要求保留作图痕迹，不需要写出作法，可见在解作图题时，保留作图痕迹很重要.五种基本作图：1、作一条线段等于已知线段；2、作一个角等于已知角；3、作已知线段的垂直平分线；4、作已知角的角平分线；5、过一点作已知直线的垂线；题目一：作一条(yī tiáo)线段等于已知线段。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
尺规作图一、熟练掌握尺规作图题的规范语言
用直尺作图的几何语言：1. ①过点×、点×作直线××；或作直线××；或作射线××；②连结两点××；或连结××；③延长××到点×；或延长（反向延长）××到点×，使××＝××；或延长××交××于点×；
用圆规作图的几何语言：2. ①在××上截取××＝××；；②以点×为圆心，××的长为半径作圆（或弧）③以点×为圆心，××的长为半径作弧，交××于点×；.
④分别以点×、点×为圆心，以××、××的长为半径作弧，两弧相交于点×、×
三、了解尺规作图题的一般步骤
尺规作图题的步骤：
当作图是文字语言叙述时，要学会根据文字语言用数学语言写出题目中的条件；1.已知：
2.求作：能根据题目写出要求作出的图形及此图形应满足的条件；
一般要保留作图当不要求写作法时，作法：能根据作图的过程写出每一步的操作过程.3.对于较复杂的作图，可先画出草图，使它同所要作的图大致相同，然后借助草图寻找.痕迹.
作法
在目前，我们只要能够写出已知，求作，作法三步（另外还有第四步证明）就可以了，可见在解作图题不需要写出作法，而且在许多中考作图题中，又往往只要求保留作图痕迹，. 时，保留作图痕迹很重要五种基本作图：1、作一条线段等于已知线段；
2、作一个角等于已知角；
3、作已知线段的垂直平分线；
4、作已知角的角平分线；
5、过一点作已知直线的垂线；
题目一：作一条线段等于已知线段。
已知：如图，线段a .
AB = a . AB，使求作：线段作法： AP；）作射线（1AB=a . AP上截取）在射线（2 AB就是所求作的图形。
则线段
题目二：作已知线段的中点。
MN.
已知：如图，线段
. MNO是的中点）求作：点O，使MO=NO（即作法：（１）分别以M、N为圆心，大于
的相同线段为半径画弧， Q；两弧相交于P， O．（２）连接PQ交MN于就是所求作的ＭＮ的中点。
O则点与ＭＮ有何关系？）（试问：PQ
题目三：作已知角的角平分线。
，已知：如图，∠AOB ）。
（即OP平分∠AOB
使∠求作：射线OP, AOP＝∠BOP
作法： 1）以O为圆心，任意长度为半径画弧，（；，N分别交OA，OB于M、Ｎ为圆心，大于（2）分别以M
内于Ｐ；的相同线段为半径画弧，两弧交∠AOB 。
（3）作射线OP 则射线OP 就是∠AOB的角平分线。
题目四：作一个角等于已知角。
MON（如图1）．求作一
个角等于已知角∠
MO，1）上，以O为圆心，任意长为半径作弧，交OM于点A（1）作射线（；2）在图（11OMO （于点B；3）以为圆心，OA的长为半径作弧，交于点C；ON交111DO的长为半径作弧，交前弧于点为圆心，以）以（4CABDD5（；）过点作射线．1．
COD就是所要求作的角．则∠1
题目五：已知三边作三角形。
c.
，a，b已知：如图，线段BC = a. ，AB = c，AC = b求作：△ABC，使作法：；作线段AB = c（1）为半径作弧，为圆心b2）以A（为半径作弧与为圆心a 以B ；前弧相交于C 。
，BC）连接AC（3 就是所求作的三角形。
则△ABC
题目六：已知两边及夹角作三角形。
?.
m，n, ∠已知：如图，线段?AC=n. ，，AB=m，使∠求作：△ABCA=∠作法：?A=∠；（1）作∠上截取AB=m ,AC=n；（2）在AB BC。
）（3 连接 ABC就是所求作的三角形。
则△
题目七：已知两角及夹边作三角形。
，??m . ，∠线段已知：如图，∠??,AB=m. B=，使∠求作：△ABCA=∠∠，∠作法：；AB=m（1）作线段 AB）在的同旁2（??，A=作∠∠B=，作∠∠ B与∠的另一边相交于C。
A∠。
ABC则△就是所求作的图形（三角形）。