图的M着色算法演示
chap12 图的着色

点着色的应用
课程安排问题 某大学数学系要为这个夏季安排课程表。所要开设 的课程为:图论(GT), 统计学(S),线性代数(LA), 高等 微积分(AC), 几何学(G)和近世代数(MA)。现有10名 学生(如下所示)需要选修这些课程。根据这些信息, 确定开设这些课程所需要的最少时间段数,使得学 生选课不会发生冲突。(学生用Ai表示)
5
K可着色的图例
v1
1
v2
G
v3 v4
v5
2 3
S
:V(G) →S,满射 是正常3着色,G是3可着色的。
6
K色图
定义12.1.2 图G的正常k着色中最小的k称为G的色
数,记为(G),即(G)=min{k|G存在正常k着色}。
若(G) =k,则称G是k色图。 显然,含环的图不存在正常着色,而多重边与一条 边对正常着色是等价的。以后总设G为简单图。 问题:已知一个图G(p,q),如何求色数(G)?
又因k>0, 所以与(G)定义矛盾。结论成立。 注意此定理与定理12.1.2的区别。 定理12.1.2 若G是一个临界图,则(G) ≤(G)+1
21
Brooks 定理
定理12.1.5 若连通图G既不是奇回路,也不是完全 图,则(G) (G) . 例如,对Petersen图应用Brooks定理,可得: (G) (G) =3 . 此定理说明只有奇回路 或完全图这两类图的色 数才是(G) +1。
第一步:建图。 把每门课程做为图G的顶点,两顶点连线当且仅当 有某个学生同时选了这两门课程。
色给同一时 段的课程顶点染色,那么,问 题转化为在状态图中求点色数 问题。
MA
S
G
AC 选课状态图
LA
回溯法实验(图的m着色问题)
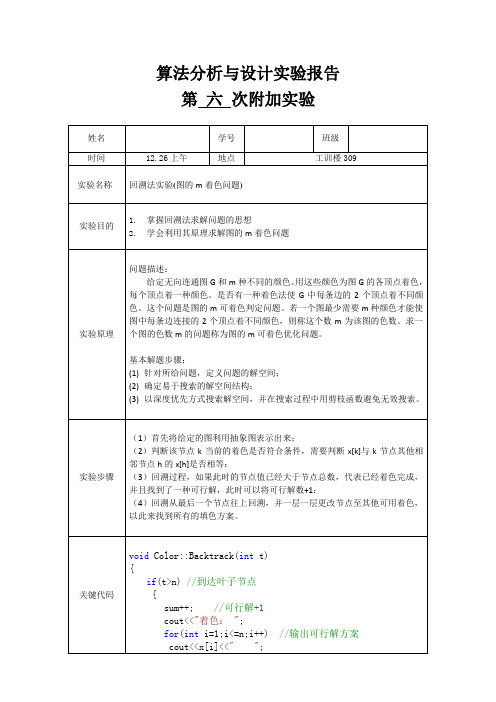
算法分析与设计实验报告第六次附加实验cout<<endl;}elsefor(int i=1;i<=m;i++){x[t]=i;if(ok(t)) Backtrack(t+1);//回溯,继续寻找下一层x[t]=0;//回到最初状态,使x[1]继续尝试其他填色的可能解}}测试结果当输入图如下时:结果如下:12435只要输入边即可当输入的图如下时:结果如下:附录:完整代码(回溯法)//图的m着色问题回溯法求解#include<iostream>using namespace std;class Color{friend void mColoring(int,int,int **);private:bool ok(int k);void Backtrack(int t);int n, //图的顶点个数m, //可用颜色数**a, //图的邻接矩阵*x; //当前解long sum; //当前已找到的可m着色的方案数};bool Color::ok(int k) //检查颜色可用性{for(int j=1;j<=n;j++)if((a[k][j]==1)&&(x[j]==x[k])) //两个点之间有约束且颜色相同return false;return true;}void Color::Backtrack(int t){if(t>n) //到达叶子节点{sum++; //可行解+1cout<<"着色: ";for(int i=1;i<=n;i++) //输出可行解方案cout<<x[i]<<" ";cout<<endl;}elsefor(int i=1;i<=m;i++){x[t]=i;if(ok(t)) Backtrack(t+1);//回溯,继续寻找下一层x[t]=0;//回到最初状态,使x[1]继续尝试其他填色的可能解 }}void mColoring(int n,int m,int **a){Color X;//初始化XX.n=n;X.m=m;X.a=a;X.sum=0;int *p=new int[n+1];for(int i=0;i<=n;i++)p[i]=0;X.x=p;cout<<"顶点: ";for(int i=1;i<=n;i++) //用于输出结果cout<<i<<" " ;cout<<endl;X.Backtrack(1); //从顶点1开始回溯delete []p;cout<<"解法个数:"<<X.sum<<endl;}int main(){int n;int m;cout<<"please input number of node:";cin>>n;cout<<"please input number of color:";cin>>m;int **a=new int*[n+1];for(int i=0;i<=n;i++)a[i]=new int[n+1];for(int i=0;i<=n;i++) //利用抽象图实现图的邻接矩阵for(int j=0;j<=n;j++)a[i][j]=0;int edge;cout<<"please input adjacent edge number:";cin>>edge;int v,w;cout<<"please inout adjacent edge:"<<endl; //只要输入边即可for(int i=0;i<edge;i++){cin>>v>>w; //由于是无向图,所以对应的邻接矩阵对应的边都有,即v->m,m->v都有边a[v][w]=1;a[w][v]=1;}mColoring(n,m,a);system("pause");return 0;}。
图的着色问题--C++实现(含详细注释)

图的着色问题一、题目简述(1) 图的m-着色判定问题给定一个无向连通图 G 和 m 种不同的颜色。
用这些颜色为图 G 的各顶点着色,每个顶点着一种颜色,是否有一种着色法使 G 中任意相邻的两个顶点着不同颜色?(2) 图的m-着色优化问题若一个图最少需要 m 种颜色才能使图中任意相邻的两个顶点着不同颜色,则称这个数 m 为该图的色数。
求一个图的最小色数 m 的问题称为m-着色优化问题。
二、算法思想1. m-着色判定问题总体思想:通过回溯的方法,不断为每一个节点着色,每个点的颜色由一个数字代表,初始值为1。
在对前面 step - 1 个节点都合法的着色之后,开始对第 step 个节点进行着色。
如果 n 个点均合法,且颜色数没有达到 m 种,则代表存在一种着色法使 G中任意相邻的两个顶点着不同颜色。
具体步骤:1. 对每个点 step ,有 m 种着色可能性,初始颜色值为1。
2. 检查第 step 个节点颜色的可行性,若与某个已着色的点相连且颜色相同,则不选择这种着色方案,并让颜色值加1,继续检查该点下一种颜色的可行性。
3. 如果第 step 点颜色值小于等于 m ,且未到达最后一个点,则进行对第 step + 1 点的判断。
4. 如果第 step 点颜色值大于 m ,代表该点找不到合适的分配方法。
此时算法进行回溯,首先令第 step 节点的颜色值为0,并对第 step - 1 个点的颜色值+1后重新判断。
5. 如果找到一种颜色使得第 step 个节点能够着色,说明 m 种颜色的方案是可行的。
6. 重复步骤2至5,如果最终 step 为0则代表无解。
2. m-着色优化问题基于问题1,对于一个无向图 G ,从1开始枚举染色数,上限为顶点数,第一个满足条件的颜色数即为所求解。
三、实现过程(附代码)1. m-着色判定问题#include<iostream>using namespace std;int color[100]; // 每个点的颜色int mp[100][100]; // 图的邻接矩阵int n, m, x; // n顶点,m种颜色方案,x条边bool check(int step) {// 判断与step点相邻的点,颜色是否与step点相同,若相同则返回falsefor (int i=1; i<=n; i++) {if (mp[step][i] ==1&&color[i] ==color[step]) {return false;}}return true;}bool Solve(int m) {// 求解是否可以找到一种可行的染色方案int step=1; // step指示当前节点while (step>=1) {color[step] +=1; // 假定颜色值从1开始,若为回溯,选择下一种方案while (color[step] <=m) { // 按照问题条件选择第step点颜色if (check(step)) {break;} else {color[step]++; // 搜索下一个颜色}}if (color[step] <=m&&step==n) { // 如果找完n个点,且染色方法小于等于m种 return true;} else if (color[step] <=m&&step<n) {step++; // 求解下一个顶点} else { // 如果染色数大于m个,回溯color[step] =0; // 回溯,该点找不到合适的分配方法,对上一点进行分析step--;}}// 如果step退到0,则代表无解return false;}int main() {int i, j;bool ans=false;cout<<"输入顶点数n和着色数m"<<endl;cin>>n>>m;cout<<"输入边数"<<endl;cin>>x;cout<<"具体输入每条边"<<endl;for (int p=0; p<x; p++) { // 以无向邻接矩阵存储边cin>>i>>j;mp[i][j] =1;mp[j][i] =1;}if (Solve(m)) {cout<<"有解";} else {cout<<"无解";}return0;}2. m-着色优化问题#include<iostream>using namespace std;int color[100]; // 每个点的颜色int mp[100][100]; // 图的邻接矩阵int n, m, x; // n顶点,m种颜色方案,x条边bool check(int step) {// 判断与step点相邻的点,颜色是否与step点相同,若相同则返回falsefor (int i=1; i<=n; i++) {if (mp[step][i] ==1&&color[i] ==color[step]) {return false;}}return true;}bool Solve(int m) {// 求解是否可以找到一种可行的染色方案int step=1; // step指示当前节点while (step>=1) {color[step] +=1; // 假定颜色值从1开始,若为回溯,选择下一种方案while (color[step] <=m) { // 按照问题条件选择第step点颜色if (check(step)) {break;} else {color[step]++; // 搜索下一个颜色}}if (color[step] <=m&&step==n) { // 如果找完n个点,且染色方法小于等于m种 return true;} else if (color[step] <=m&&step<n) {step++; // 求解下一个顶点} else { // 如果染色数大于m个,回溯color[step] =0; // 回溯,该点找不到合适的分配方法,对上一点进行分析step--;}}// 如果step退到0,则代表无解return false;}int main() {int i, j;bool ans=false;cout<<"输入顶点数n"<<endl;cin>>n;cout<<"输入边数"<<endl;cin>>x;cout<<"具体输入每条边"<<endl;for (int p=0; p<x; p++) { // 以无向图邻接矩阵存储边 cin>>i>>j;mp[i][j] =1;mp[j][i] =1;}for (m=1; m<=n; m++) { // 从小到大枚举着色数mif (Solve(m)) { // 如果有解,输出答案并跳出循环cout<<"最小色数m为 "<<m;break;}}return0;}四、结果及分析问题1测试用例:问题2测试用例:经检验,最少着色数的范围为2-4,意味着使 G 中任意相邻的两个顶点着不同颜色最多需要4种颜色。
图的着色问题

问题来源
图的着色
通常所说的着色问题是指下述两类问题: 通常所说的着色问题是指下述两类问题: 1.给定无环图G=(V,E),用m种颜色为图中 的每条边着色,要求每条边着一种颜色, 的每条边着色,要求每条边着一种颜色,并 使相邻两条边有着不同的颜色, 使相邻两条边有着不同的颜色,这个问题称 为图的边着色问题。 为图的边着色问题。 2.给定无向图G=(V,E),用m种颜色为图中 的每个顶点着色,要求每个顶点着一种颜色, 的每个顶点着色,要求每个顶点着一种颜色, 并使相邻两顶点之间有着不同的颜色, 并使相邻两顶点之间有着不同的颜色,这个 问题称为图的顶着色问题。 问题称为图的顶着色问题。
化简得
( a + bd )(b + aceg )(c + bdef )( d + aceg )(e + bcdf )( f + ceg )( g + bdf )
求极小覆盖法- 求极小覆盖法-布尔代数法
Step3:从中挑选所用极大独立集个数最小者, Step3:从中挑选所用极大独立集个数最小者, 即为X 即为X(G) 但上述子集的颜色数都不是X ),正确的应 但上述子集的颜色数都不是X(G),正确的应 该是X =3,该子集为: {b,d,f}中的 该是X(G)=3,该子集为:给{b,d,f}中的 b,d,f涂颜色 涂颜色1 {a,e,g}中a,e,g涂颜色 涂颜色2 b,d,f涂颜色1,为{a,e,g}中a,e,g涂颜色2为 {a,c,g}中的 涂颜色3 中的c {a,c,g}中的c涂颜色3。 由此可见, 由此可见,求色数其需要求极大独立集以 及一切若干极大独立集的和含所有顶点的子 对于大图, 集,对于大图,因为图计算量过大而成为实 际上难以凑效的算法,所以不是一个好算法, 际上难以凑效的算法,所以不是一个好算法, 一般我们采用贪心法等近似算法来求解 。
0030算法笔记——最大团问题和图的m着色问题

3if (OK)// 进入左子树 3{ 33x[i] = 1; 33cn++; 33Backtrack(i+1); 33x[i] = 0; 33cn--; 3}
if (cn + n - i >= bestn)// 进入右子树 3{ 33x[i] = 0; 33Backtrack(i+1); 3} }
3333 如果U∈V且对任意u,v∈U有(u, v)不属于E,则称U是G的空子图。G的空子图U是G的独立集当且仅当U不包 含在G的更大的空子图中。G的最大独立集是G中所含顶点数最多的独立集。
3333 对于任一无向图G=(V, E),其补图G'=(V', E')定义为:V'=V,且(u, v)∈E'当且仅当(u, v)∈E。 3333 如果U是G的完全子图,则它也是G'的空子图,反之亦然。因此,G的团与G'的独立集之间存在一一对应的 关系。特殊地,U是G的最大团当且仅当U是G'的最大独立集。
图的着色问题 ppt课件

PPT课件
3
顶点着色-基本概念
• 独立集:对图G=(V,E),设S是V的一个子集,若 中任意两个顶点在G中均不相邻,则称S为G的一 个独立集。
• 最大独立集:如果G不包含适合|S'|>|S|的独立 集S',则称S为G的最大独立集。
• 极大覆盖:设K是G的一个独立集,并且对于V-K 的任一顶点v,K+v都不是G的独立集,则称K是 G的一个极大覆盖。
先求图G的极小覆盖,
பைடு நூலகம்
化简得
(a bd)(b aceg)(c bdef )(d aceg)(e bcdf )( f ceg)(g bdf )
aceg bc deg bdef bdef bcdf
故G的极小覆盖为 {a,c,e, g},{b,c, d,e, g},{b, d,e, f },{b,c, d, f } 取其补集,得到G的所有 极大独立集: • Step2:求出一切若干极大独立集和所有{b,顶d,点f }的,{a子, f集},{a,c, g},{a,e, g}
但上述子集的颜色数都不是X(G),正确的应 该是X(G)=3,该子集为:给{b,d,f}中的 b,d,f涂颜色1,为{a,e,g}中a,e,g涂颜色2为 {a,c,g}中的c涂颜色3。
由此可见,求色数其需要求极大独立集以
及一切若干极大独立集的和含所有顶点的子
集,对于大图,因为图计算量过大而成为实
际上难以凑效的算法,所以不是一个好算法,
(ii)若G为偶图,则X(G)=2 (iii)对任意图G,有X(G)≤Δ+1(这里Δ表示为顶点 数最大值)
PPT课件
5
顶点着色-求顶色数的算法设计
我们由“每个同色顶点集合中的两两顶点不相邻”可以看出,同色顶 点集实际上是一个独立集,当我们用第1种颜色上色时,为了尽可 能扩大颜色1的顶点个数,逼近所用颜色数最少的目的,事实上就 是找出图G的一个极大独立集并给它涂上颜色1。用第2种颜色上色 时,同样选择另一个极大独立集涂色,...,当所有顶点涂色完毕, 所用的颜色数即为所选的极大独立集的个数。
《算法设计与分析》课程实验报告 (回溯法(二))
《算法设计与分析》课程实验报告实验序号:10实验项目名称:实验十一回溯法(二)一、实验题目1.图的着色问题问题描述:给定无向连通图G和m种不同的颜色。
用这些颜色为图G的各顶点着色,每个顶点着一种颜色。
如果有一种着色法使G中每条边的2个顶点着不同颜色,则称这个图是m可着色的。
图的m着色问题是对于给定图G和m种颜色,找出所有不同的着色法。
2.旅行商问题问题描述:给出一个n个顶点的带权无向图,请寻找一条从顶点1出发,遍历其余顶点一次且仅一次、最后回到顶点1的最小成本的回路——即最短Hamilton回路。
3.拔河比赛问题描述:某公司的野餐会上将举行一次拔河比赛。
他们想把参与者们尽可能分为实力相当的两支队伍。
每个人都必须在其中一只队伍里,两队的人数差距不能超过一人,且两队的队员总体重应该尽量接近。
4.批处理作业调度问题描述:给定n个作业的集合J=(J1,J2, .. Jn)。
每个作业J都有两项任务分别在两台机器上完成。
每个作业必须先由机器1处理,再由机器2处理。
作业i需要机器j的处理时间为tji(i=1,2, ..n; j=1,2)。
对于一个确定的作业调度,设Fji是作业i在机器j上完成处理的时间,则所有作业在机器2上完成处理的时间和,称为该作业调度的完成时间和。
批处理作业调度问题要求,对于给定的n个作业,制定最佳作业调度方案,使其完成时间和达到最小。
二、实验目的(1)通过练习,理解回溯法求解问题的解状态空间树与程序表达的对应关系,熟练掌握排列树、子集树的代码实现。
(2)通过练习,体会减少搜索解空间中节点的方法,体会解的状态空间树的组织及上界函数的选取对搜索的影响。
(3)通过练习,深入理解具体问题中提高回溯算法效率的方法。
(4)(选做题):在掌握回溯法的基本框架后,重点体会具体问题中解的状态空间搜索时的剪枝问题。
三、实验要求(1)每题都必须实现算法、设计测试数据、记录实验结果,并给出时间复杂度分析。
四、实验过程(算法设计思想、源码)1.图的着色问题(1)算法设计思想用邻接矩阵a[i][j]存储无向图,对于每一个顶点有m种颜色可以涂。
图论课件第七章图的着色
平面图的着色问题是一个经典的图论问题,其目标是在满足相邻顶点颜色不同 的条件下,使用最少的颜色对平面图的顶点进行着色。
详细描述
平面图的着色问题可以使用欧拉公式和Kuratowski定理进行判断和求解。此外 ,也可以使用贪心算法、分治策略等算法进行求解。
树图的着色问题
总结词
树图的着色问题是一个经典的图论问 题,其目标是使用最少的颜色对树图 的顶点进行着色,使得任意两个相邻 的顶点颜色不同。
分支限界算法
总结词
分支限界算法是一种在搜索树中通过剪枝和 优先搜索来找到最优解的算法。
详细描述
在图的着色问题中,分支限界算法会构建一 个搜索树,每个节点代表一种可能的着色方 案。算法通过优先搜索那些更有可能产生最 优解的节点来加速搜索过程,同时通过剪枝 来排除那些不可能产生最优解的节点。分支 限界算法可以在较短的时间内找到最优解,
尤其适用于大规模图的着色问题。
03
图的着色问题的复 杂度
计算复杂度
确定图着色问题的计算复杂度为NP-完全,意味着该问题在多项式时间 内无法得到确定解,只能通过近似算法或启发式算法来寻找近似最优解 。
图着色问题具有指数时间复杂度,因为对于n个顶点的图,其可能的颜色 组合数量为n^k,其中k为每个顶点可用的颜色数。
02
图的着色算法
贪心算法
总结词
贪心算法是一种在每一步选择中都采取当前状态下最好或最优(即最有利)的选 择,从而希望导致结果是最好或最优的算法。
详细描述
贪心算法在图的着色问题中的应用是通过逐个对顶点进行着色,每次选择当前未 被着色的顶点中颜色数最少的颜色进行着色,直到所有顶点都被着色为止。这种 算法可以保证最小化使用的颜色数量,但并不保证得到最优解。
图着色问题——精选推荐
图着⾊问题⼀、图着⾊问题(1)图的m可着⾊判定问题给定⽆向连通图G和m种不同的颜⾊。
⽤这些颜⾊为图G的各顶点着⾊,每个顶点着⼀种颜⾊。
是否有⼀种着⾊法使G中每条边的2个顶点着不同颜⾊。
(2)图的m可着⾊优化问题若⼀个图最少需要m种颜⾊才能使图中每条边连接的2个顶点着不同颜⾊,则称这个数m为该图的⾊数。
⼆、m可着⾊判定问题的解法【算法】(1)通过回溯的⽅法,不断的为每⼀个节点着⾊,在前⾯cur-1个节点都合法的着⾊之后,开始对第cur-1个节点进⾏着⾊,(2)这时候枚举可⽤的m个颜⾊,通过和第cur-1个节点相邻的节点的颜⾊,来判断这个颜⾊是否合法(3)如果找到那么⼀种颜⾊使得第cur-1个节点能够着⾊,那么说明m种颜⾊的⽅案在当前是可⾏的。
(4)cur每次迭代加1,如果cur增加到N并通过了检测,说明m种颜⾊是可满⾜的。
(5)注意,这⾥只是要求判断m种颜⾊是否可满⾜,所以找到任何⼀种⽅案就可以了。
【代码实现】#include<iostream>#include<cstring>using namespace std;const int maxn = 105;int G[maxn][maxn];int color[maxn];bool ans;int n,m,k;void init(){ans = 0;memset(G, 0 , sizeof G);memset(color, 0 , sizeof color);}void dfs(int cur){if(cur > n) {ans = 1;return;}for(int i=1; i<=m; i++){ //对cur结点尝试使⽤每⼀种颜⾊进⾏涂⾊bool flag = 1;//cur之前的结点必被涂⾊for(int j=1; j<cur; j++){if(G[j][cur] == 1 && color[j] == i){flag = 0;//只要有⼀个冲突都不⾏break;}}//如果可以涂上i颜⾊,则考虑下⼀个结点的情况if(flag){color[cur] = i;dfs(cur + 1);}//如果到这⼀步第cur个结点⽆法着⾊,则返回探寻其他⽅案else color[cur] = 0;//回溯 ;}}int main(){while(cin>>n>>k>>m){init();for(int i=1; i<=k; i++){int x,y;cin>>x>>y;G[x][y] = G[y][x] = 1;}dfs(1);cout<<ans<<endl;}return0;}三、m可着⾊拓展【问题】在上述基础上,求出m种颜⾊能够给图G涂⾊的总总⽅案数量【算法】由于这个时候要求总⽅案数量,所以在找到⼀种可⾏⽅案后,总是进⾏回溯再搜索其他的解决⽅案,与上⾯不同,上⾯是只需要找出⼀种⽅案即可,所以如果找到了就不需要再回溯了,所以在这⾥只需要把回溯语句的位置写到dfs语句的后⾯即可。
图着色
我们可以把问题简化为3个点来分析,现给定
如下图,怎样求解呢?
1
该图的色数是多少? 怎样用解空间树来表示呢?
3
2
由图可知,对于每一个顶点可选的颜色可以有3种不 同的选择,所以每一个节点有3个儿子节点,有4层。
判断条件
新加入节点t取某一种颜色i时,依次和上层的每一个节点 j(j<t)比较。如果a[t][j]=1并且x[t]=x[j],那么它是不可着色的。
在网络中,每个小区的信道需求用一个有n个元素的矢量来描 述,称作需求矢量D。
信道分配的问题就转换为:
对于一个带权图(G,w),其中G=(V,E,c0,c1,…,ck),建 立一个分配函数f,其值域为一个非负整数集,定义域 为图的顶点集合V,满足下列条件:
CoMP
(Coordinated e Points)
int OK(int t,int i) { int j; for( j=1;j<t;j++) {
if(a[t][j]&&x[j]==i)
return 0; } return 1; }
1
模拟演示
3 t=1
2
t=2
t=3
t=4
当前节 点
颜色的种 类
void Backtrace(int t,int m)
int main() { int m; int i; printf("请输入颜色种类:\n"); scanf("%d",&m); for(i=1;i<=m;i++)//初始化 x[i]=0; Backtrace(1,m); if(sum==0) { printf("不是%d可着色的!\n",m); } return 0;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
for( j=1;j<t;j++) {
if(a[t][j]&&x[j]==i)
return 0; }
return 1; }
t=2
t=3 t=4
模拟演示
t=1
当前节 点
颜色的 种类
void Backtrace(int t,int m)
当搜索的当前节点t<=N时,m种颜色 依次试用,调用函数OK进行判断。 如果当前颜色可以,则进入下一层搜索。
当搜索到最叶子节 点时(t>N),即 可输出一种方案
for( i=1;i<=m;i++) {
if(OK(t,i)) { x[t]=i;
Backtrace(t+1,m); }
}
if(t>N) {
sum++; printf("第%d种方案:\n",sum);
for( i=1;i<=N;i++) printf("%d ",x[i]); }
我们可以把问题简化为3个点来分析,现给定如下图 ,怎样求解呢?
1
该图的色数是多少?怎样 用解空间树来表示呢?
3 2
由图可知,对于每一个顶点可选的颜色可以有3种不同的选择,所以每一个 节点有3个儿子节点,有4层。
判断条件是什么?
新加入来得节点t取某一种颜色i时,依次和上层的每一个节点j(j<t)比较。 如果a[t][j]=1并且x[t]=x[j],那么它是不可着色的。
四、程序代码
#include<stdio.h> #include<string.h> #define N 3//图中节点的个数 int a[N+1][N+1]={
0,0,0,0, 0,1,1,1, 0,1,1,1, 0,1,1,1, };//邻接矩阵 int x[N+1];//记录颜色 int sum=0;//保存可以着色的方案数 int OK(int t,int i)//判断函数 { int j; for( j=1;j<t;j++) { if(a[t][j]&&x[j]==i) return 0; } return 1; }
运行结果
当N=5时,色数又是多少呢?
N =5时的子集树
X[1]=1 X[1]=2 X[1]=3 X[1]=4 X[2]=1 2 3 4
X[3]=1 2 3 4
X[4]=1 X[5]=1
谢谢大家的观看!
谢谢观赏!
图的m着色问题
讲课 : 吴双燕 PPT制作 : 谭晓雅
目录
一
问题产生的背景
二
问题描述
三
算法设计与分析
四
程序运行及结果
一、产生背景
图的着色问题是由地图的着色问题引申而来的,用 m种颜色为地图着色,使得地图上的每一个区域着 一种颜色,且相邻区域颜色不同。
二、问题描述
给定无向连通图G和m种不同的颜色。用这些颜色为图G 的各顶点着色,每个顶点着一种颜色。是否有一种着色法 使G中每条边的2个顶点着不同颜色。如果有则称这个图 是m可着色,否则称这个图不是m可着色。若一个图最少 需要k种颜色才能使图中每条边连接的2个顶点着不同颜 色,则称这个数k为该图的色数。
Hale Waihona Puke void Backtrace(int t,int m) {
int i; if(t>N)//算法搜索至叶子节点 {
sum++; printf("第%d种方案:\n",sum); for( i=1;i<=N;i++)
printf("%d ",x[i]); printf("\n"); } else { for( i=1;i<=m;i++) {
三、算法设计
输入:颜色种类m 输出:如果这个图不是m可着 色,给出否定回答;如果这个图是m可着色的,找出所有 不同的着色法。
思考?
如何将给定的 无向图存储在 计算机中?
1
2 3
5 4
可以用一下邻接矩阵来表示
11110 11111 11110 11111 01011
邻接矩阵中通常用二维数组来存放边之间的关系,用一 维数组来存放顶点的信息。所以在接下来的求解问题中 我们将用到二维数组a来存放两边是否相邻,用一维数组 x来存放每个顶点的颜色;x[i]=j表示第i个节点图第j中颜色。
if(OK(t,i)) { x[t]=i;
Backtrace(t+1,m); } } } }
int main() {
int m; int i; printf("请输入颜色种类:\n"); scanf("%d",&m); for(i=1;i<=m;i++)//初始化 x[i]=0; Backtrace(1,m); if(sum==0) { printf("不是%d可着色的!\n",m); } return 0; }
