复合材料层合板结构振动声辐射优化
复合材料层合板的力学行为与优化设计

复合材料层合板的力学行为与优化设计复合材料层合板是由两个或多个不同材料的层按照一定方式堆叠而成的结构材料。
它具有优异的力学性能和设计灵活性,在航空航天、汽车制造、建筑工程等领域得到广泛应用。
本文将从力学行为和优化设计两个方面对复合材料层合板进行探讨。
首先,复合材料层合板的力学行为是理解和研究该材料的基础。
复合材料层合板的力学性能受到多种因素的影响,包括材料的性质、层间粘结强度、层间厚度比、层间角度等。
其中,材料的性质是决定层合板力学性能的关键因素。
复合材料层合板通常由纤维增强复合材料和基体材料组成。
纤维增强复合材料具有高强度、高刚度和低密度的特点,而基体材料则具有良好的韧性和耐磨性。
通过选择不同的纤维和基体材料,可以实现对层合板力学性能的调控。
其次,复合材料层合板的优化设计是提高材料性能和降低成本的重要手段。
优化设计的目标是找到最佳的材料组合、层间厚度比和层间角度,以满足特定的工程要求。
优化设计可以通过数值模拟和实验测试相结合的方式进行。
数值模拟可以通过有限元分析等方法,预测不同设计参数对层合板力学性能的影响。
实验测试可以通过拉伸、弯曲、剪切等试验,验证数值模拟结果的准确性。
在优化设计过程中,需要考虑的因素包括强度、刚度、韧性、疲劳寿命和成本等。
强度是指材料抵抗外力破坏的能力,刚度是指材料对应力的响应程度,韧性是指材料在受到外力作用下的变形能力,疲劳寿命是指材料在循环加载下的使用寿命。
通过优化设计,可以在满足这些要求的前提下,尽量降低材料的成本。
在实际应用中,复合材料层合板的优化设计需要综合考虑多个因素。
例如,层间厚度比的选择既要考虑强度和刚度的要求,又要考虑材料的成本和制造工艺的可行性。
层间角度的选择既要考虑层间剪切强度的要求,又要考虑层间粘结强度和制造工艺的限制。
因此,在优化设计中需要综合考虑材料的性能、制造工艺和经济性等多个方面的因素。
总之,复合材料层合板的力学行为与优化设计是研究和应用该材料的重要内容。
薄板结构振动声辐射特性分析及优化

第18卷第4期2020年8月福建工程学院学报JournalofFujianUniversityofTechnologyVol.18No.4Aug.2020doi:10.3969/j.issn.1672-4348.2020.04.013薄板结构振动声辐射特性分析及优化刘成武ꎬ郭小斌(福建工程学院机械与汽车工程学院ꎬ福建福州350118)摘要:利用有限元法与边界元法结合对薄板进行振动声辐射特性分析ꎬ研究了薄板结构在简谐力作用下表面声压分布状况ꎬ分析了不同边界条件㊁材料以及加筋形式等因素对薄板结构振动声辐射特性的影响ꎬ并对简支矩形薄板厚度进行了优化ꎮ研究表明ꎬ边界约束的增加会导致薄板刚度变大ꎬ进而导致薄板辐射声功率与辐射效率随之改变ꎻ不同材料对结构的辐射声功率均有影响ꎬ而对辐射效率影响很小ꎻ加筋对薄板声辐射特性影响显著ꎬ十字型加筋形式减震降噪效果最好ꎻ对薄板厚度进行优化ꎬ优化后薄板辐射声功率级下降了4.29dBꎮ关键词:薄板ꎻ振动声辐射ꎻ辐射声功率ꎻ辐射效率中图分类号:TB532文献标志码:A㊀㊀㊀㊀㊀文章编号:1672-4348(2020)04-0375-06AnalysisandoptimizationofvibrationacousticradiationcharacteristicsofthinplatestructureLIUChengwuꎬGUOXiaobin(SchoolofMechanicalandAutomotiveEngineeringꎬFujianUniversityofTechnologyꎬFuzhou350118ꎬChina)Abstract:Finiteelementmethodcombinedwiththeboundaryelementmethodwasemployedtoanalyzethevi ̄brationandacousticradiationcharacteristicsofthethinplate.Thedistributionofacousticpressureonthesur ̄faceofathinplatestructuresubjectedtoharmonicforcewasstudied.Theinfluenceofsuchfactorsasdifferentboundaryconditionsꎬmaterialsandstiffenedtypesonthevibrationacousticradiationcharacteristicsofthinplatestructurewasanalyzedꎬandthethicknessofthesimply ̄supportedrectangularplatewasoptimized.Re ̄sultsshowthatthestiffnessofthethinplateincreaseswithanincreasingboundaryconstraintꎬwhichfurtheraf ̄fectstheradiationpowerandradiationefficiencyaccordingly.Differentmaterialscanaffecttheradiationsoundpowerofthestructureꎻhoweverꎬtheyhavelittleinfluenceontheradiationefficiency.Thestiffeninghasasig ̄nificanteffectontheacousticradiationcharacteristicsofthethinplateꎬandthecross ̄stiffenedplateshavebeenproventobethebestshockandnoiseabsorbers.Aftertheoptimizationofthethicknessoftheplateꎬtheleveloftheradiatedsoundpowerisdecreasedby4.29dB.Keywords:thinplatesꎻvibrationacousticradiationꎻacousticradiationpowerꎻradiationefficiency㊀㊀在实际工程应用中ꎬ板类件由于其结构简单㊁适用性强被广泛使用ꎮ因此ꎬ研究板类件的振动声辐射特性对于结构的减振降噪有着重要意义ꎮ文献[1-3]对薄板声辐射理论进行了研究ꎬ为进一步对声辐射特性分析奠定了理论基础ꎮ张媛媛等[4-6]根据理论公式利用MATLAB编程研究了作用力位置㊁尺寸参数等因素对薄板声辐射特性的影响ꎮ刘宝等[7]以混合势计算结构表面振速与声压ꎬ并以简支矩形板为例分析了板厚对声辐射参数的影响ꎬ但对其他边界条件情况没有分析ꎮ收稿日期:2020-03-04基金项目:福建省自然科学基金项目(2018J01628)第一作者简介:刘成武(1975 )ꎬ男ꎬ安徽枞阳人ꎬ教授ꎬ博士ꎬ研究方向:车辆NVH技术㊁结构多学科设计优化ꎮ福建工程学院学报第18卷范鑫等[8]利用声学软件Virtural.LabAcoustical对蜂窝层板进行声辐射特性仿真分析ꎬ并对面板厚度㊁壁长等设计变量对传声性能的影响进行了研究ꎮ上述文献完善了薄板振动声辐射的理论ꎬ并对声辐射特性进行了研究ꎬ但还不够全面充分ꎬ如:不同材料㊁边界条件㊁使用加强筋等情况未考虑ꎮ本文在上述文献的基础上ꎬ利用有限元法计算薄板的振动响应ꎬ结合边界元方法计算薄板声辐射特性ꎬ主要研究了不同边界条件㊁材料属性和薄板加筋㊁不同加筋形式情况下结构声辐射特性的变化规律并对矩形简支薄板在某一厚度进行了优化ꎬ为实际工程应用提供方法与理论指导ꎮ1㊀薄板振动有限元理论设薄板长为a㊁宽为bꎬ厚度为lꎬ横向振动位移为ωꎮ薄板横向振动平衡方程为:∂4ω∂x4+2∂4ω∂x2∂y2+∂4ω∂y4=p(xꎬy)D(1)式中D=Eh312(1-μ2)为弯曲刚度矩阵ꎬE为材料的弹性模量ꎬμ为材料的泊松比ꎬp(xꎬy)为薄板自由振动时的惯性载荷ꎮp(xꎬy)可表示为:p(xꎬy)=-ρt∂2ω∂2t(2)把式(2)带入式(1)使用分离变量法ꎬ可得薄板自由振动方程为DÑ4ω+ρh∂2ω∂2t=0(3)式中ρ为材料的密度ꎬÑ4为微分算子ꎮÑ4=∂2∂2x+∂2∂2yæèçöø÷2(4)对于四边简支矩形薄板由于其结构简单固有频率精确解析解为ω=π2Dρhm2a2+n2b2æèçöø÷(5)2㊀薄板声辐射理论假设薄板位于刚性障板上ꎬ薄板障板尺寸远大于薄板ꎬ设薄板的表面积为Sꎬ传播介质为空气ꎬ当薄板在圆频率ω下振动ꎬ该板薄板表面声压为:P(Lꎬω)=jkρ0c2π∬V(Qꎬω)e-ikrrdS(Q)(6)式中ꎬj为虚数单位ꎬρ0为空气密度ꎬc为空气声速ꎬk=ω/c为波数ꎬV(Qꎬω)为薄板表面法向振速ꎬL为场点ꎬQ为源点ꎬr为两点距离ꎮ假设薄板表面是由无限多个面单元组成ꎬ经单元离散后ꎬ结构表面辐射阻抗R可以表示为Rmn=k2(ΔS)2ρc4π(7)已知薄板表面辐射阻抗ꎬ薄板总的辐射声功率为[9]:W=NHRN(8)式中R为辐射阻抗矩阵ꎬN为薄板各小面积单元上法向振速组成的M阶列向量ꎮ根据辐射效率公式ꎬ可知薄板声辐射效率为σmn=Wmnρcab‹v2›(9)式中<v2>为均方根振速ꎮ3㊀数值仿真设一矩形薄板长㊁宽分别为1.0m和0.8mꎬ材料为钢材ꎬ弹性模量为E=211GPaꎬ泊松比为0.3ꎬ密度为7830kg/m3ꎮ3.1㊀薄板的自由振动计算薄板边界条件设为四边简支ꎬ薄板厚度设为0.003mꎬ运用MATLAB对其精确解析式进行编程求其结果ꎬ与ABAQUS数值仿真结果进行对比ꎬ验证有限元仿真计算的准确性ꎮ计算结果如表1所示ꎮ表1㊀四边简支矩形薄板前8阶固有频率Tab.1㊀Thefirsteightnaturalfrequenciesofsimply ̄supportedrectangularthinplateswithfouredges阶数频率/HzMATLABABAQUS118.9318.98241.1541.24353.7453.86475.9276.06578.4278.596112.32112.567113.14113.208131.10131.35从表1可以看出ꎬ用MATLAB编程与ABAQUS仿真计算所得固有频率结果基本一致ꎮ通过结果对比ꎬ证明使用ABAQUS进行薄板结构振动分析673第4期刘成武ꎬ等:薄板结构振动声辐射特性分析及优化完全可靠㊁准确ꎮ3.2㊀薄板的声辐射特性分析假设薄板的传播介质为空气ꎬ密度为1.225kg/m3ꎬ声音传播速度为340m/sꎬ板厚为6mmꎬ约束条件为四边简支ꎮ采用基于模态的稳态动态分析计算薄板在简谐作用力下的薄板表面振动速度ꎬ再联合Virtural.Lab计算薄板辐射声功率㊁辐射声效率以及表面声压分布等薄板声学特性指标ꎬ前4阶薄板结构表面声压如图1所示ꎮ图1㊀矩形薄板前4阶表面声压分布Fig.1㊀Surfacedistributionofthesoundpressureofthefirstfourordersoftherectangularthinplate从图1可以看出ꎬ四边简支矩形薄板表面声压分布与结构振型图形状相似ꎬ这也说明了薄板在振动幅值峰值处声辐射最大ꎬ两者具有一致性ꎬ在考虑薄板减振降噪时也应考虑薄板的声辐射特点ꎬ在振动峰值处应特别注意ꎮ3.3㊀边界条件对薄板声辐射特性影响在实际工程中ꎬ不同边界条件会被应用在各种结构ꎮ四边简支㊁四边固支两种边界条件薄板前四阶固有频率如表2ꎮ结构辐射的声功率级和声辐射效率分别如图2㊁图3所示ꎮ表2㊀不同边界条件前4阶固有频率对比Tab.2㊀Comparisonofthefirstfournaturalfrequenciesofdifferentboundaryconditions阶数频率/Hz四边固支四边简支1703821238231611084210152图2㊀不同边界条件下薄板辐射声功率级Fig.2㊀Radiationsoundpowerlevelofthinplatesunderdifferentboundaryconditions㊀㊀根据图2可以看出ꎬ在外部条件一定情况下ꎬ四边简支薄板辐射的声功率级低于四边固支边界条件下声辐射功率级ꎮ主要原因是四边固支薄板约束的增加对薄板刚度的增大效果明显ꎬ即改变边界条件ꎬ相当于改变了结构的刚度ꎬ结构的辐射声功率随之受到影响ꎮ从图3可以看出ꎬ边界条件的不同ꎬ薄板辐射效率也明显不一样:在相同激励力条件下ꎬ由于四边固支薄板刚度增加ꎬ固有频率相应增加ꎬ四边固773福建工程学院学报第18卷支辐射效率相比四边简支向右偏移ꎬ但整体趋势是四边固支薄板辐射效率高于四边简支辐射效率ꎮ图3㊀不同边界条件薄板声辐射效率Fig.3㊀Acousticradiationefficiencyofthinplatesunderdifferentboundaryconditions3.4㊀不同材料对薄板振动声辐射的影响在实际工程应用中ꎬ钢与铝是应用最广泛的两种材料ꎬ对这两种材料探究在相同尺寸㊁外部激励相同条件下振动与声辐射特性具有重要实际意义ꎮ两种材料的基本参数如表3所示ꎮ表3㊀铝板与钢板基本参数Tab.3㊀Basicparametersofaluminumplatesandsteelplates材料长/m宽/m高/mm弹性模量/GPa密度/(kg m-3)泊松比钢板1.00.86.021178300.30铝板1.00.86.07027000.33为了保证结果的可参考性ꎬ两种材料薄板均采用四边简支边界条件ꎬ外部激励力幅值均为500Nꎬ频率范围设为20~600Hzꎬ力作用点坐标为(0.22mꎬ0.28m)ꎮ利用LMSVirtural.Lab对两种材料薄板进行声学分析ꎬ获得的两种不同材料的辐射声功率级和辐射效率如图4㊁图5所示ꎮ由图4可以看出ꎬ针对铝和钢两种材料ꎬ在结构尺寸参数㊁边界条件㊁激励位置和大小相同情况下ꎬ在20~600Hz频率范围内铝板辐射声功率大于钢板辐射声功率ꎮ同时ꎬ在薄板固有频率处会出现一个辐射声功率的峰值ꎮ由此得出ꎬ不同材料所辐射的声功率差别很大ꎬ在实际工程应用中要考虑材料对设备声学性能的影响ꎮ图4㊀钢板和铝板的辐射声功率级Fig.4㊀Radiationsoundpowerlevelsofsteelplatesandaluminumplates图5㊀铝板和钢板辐射效率Fig.5㊀Radiationefficiencyofaluminumplatesandsteelplates图5表明ꎬ在一定条件下ꎬ钢板㊁铝板两种材料效率在20~600Hz频率段声辐射效率曲线几乎完全重合ꎮ说明矩形薄板结构的声辐射效率与结构材料没有关系ꎬ即结构噪声的辐射效率与材料本身属性无关ꎬ而对结构辐射的声功率有明显影响ꎮ4㊀加筋对薄板声辐射特性的影响以基板为参考对象ꎬ探讨加筋对薄板声学特性的影响ꎮ边界条件相同均为四边简支ꎬ激励力为100Nꎬ作用在部件中心位置ꎮ利用ABAQUS对基板与单道加筋板进行谐响应分析ꎬ分别提取两者表面振动速度ꎬ导入LMSVirtural.Lab中进行声学分析ꎬ声学求解范围为10~600Hzꎬ步长为窄频5Hzꎮ得到两者辐射声功率级与辐射效率的对比结果如图6所示ꎮ由图6可以看出ꎬ加筋对减低薄板声功率有873第4期刘成武ꎬ等:薄板结构振动声辐射特性分析及优化图6㊀基板与加筋板辐射声功率级与声辐射效率Fig.6㊀Radiantsoundpowerlevelsandradiantefficiencyofbaseplateandstiffenedplate显著效果ꎬ从200Hz以后加筋板辐射声功率就低于基板ꎬ且在同一频率处最大相差10dBꎮ随着频率的升高ꎬ加筋板的峰值随之向右移动ꎮ在声辐射效率方面ꎬ加筋板辐射效率高于基板ꎬ且相应峰值相差很大ꎮ5㊀不同加筋形式对薄板声辐射特性的影响㊀㊀为了探讨筋条布置形式对板结构声辐射的影响ꎬ拟通过对板结构分别添加沿长度方向的 二字型 加筋板ꎬ 十字型 加筋板ꎬ X字型 加筋板来对板结构的声辐射特性进行研究ꎮ不同加筋形式对薄板结构表面辐射声功率和辐射效率的影响如图7所示ꎮ由图可知ꎬ不同加筋形式筋板的声功率级的变化趋势基本一致ꎮ但从整个频率范围来看十字型加筋板辐射声功率级较低ꎬ相比其他两种加筋形式声功率级比较稳定ꎮ从辐射声效率图中可以发现在第一个峰值处十字型加筋板最高ꎬX字型次之ꎬ二字型最低ꎮ且X字型加筋形式有两个显著波峰ꎬ随着频率增加三种加筋形式声辐射效率均有上升趋势ꎮ图7㊀不同加筋形式辐射声功率级与辐射声效率Fig.7㊀Radiatingsoundpowerlevelsandradiatingsoundefficiencyofdifferentstiffenedforms6㊀薄板声辐射特性优化矩形薄板为例ꎬ薄板长㊁宽分别为1.0m和0.8mꎬ厚度为0.006mꎬ约束条件为四边简支ꎬ材料的弹性模量E=211GPaꎬ泊松比为0.3ꎬ密度为7830kg/m3ꎮ以薄板厚度为设计参数ꎬ薄板第一阶固有频率为约束条件ꎬ声功率级最小为优化目标ꎮ薄板厚度在5~7mm内以间隔0.2mm分别对其进行声辐射分析ꎬ各种板厚声功率级如图8所示ꎮ由3.3节可知ꎬ四边简支薄板第一阶固有频率为38Hzꎮ在38Hz处薄板辐射声功率级如表4所示ꎮ973福建工程学院学报第18卷图8㊀不同板厚声功率级Fig.8㊀Soundpowerlevelsofdifferentplatethicknesses表4㊀一阶固有频率处薄板辐射声功率级Tab.4㊀Radiatingsoundpowerlevelsofthethinplateatthefirstnaturalfrequency板厚/mm声功率级/dB5.2138.625.4138.655.6132.785.8142.686.0132.106.2136.746.4127.816.6133.236.8136.57㊀㊀由图8可以看出ꎬ随着薄板厚度的增加ꎬ薄板辐射声功率级曲线逐渐向右移动ꎬ但曲线趋势基本相同ꎮ由表4可以看出ꎬ当板的厚度选取为6.4mm时ꎬ在一阶固有频率处薄板辐射声功率级最小ꎬ相比初始薄板厚度6.0mmꎬ辐射声功率级下降了4.29dBꎮ7㊀结论1)四边固支薄板与四边简支薄板相比ꎬ增加边界条件约束ꎬ相当于增大了结构刚度ꎬ造成结构辐射声功率级变大ꎬ辐射能量升高ꎮ材料属性的改变对结构辐射声功率级有很大影响ꎬ对辐射效率影响可以忽略不计ꎮ2)加筋对薄板声辐射功率及声辐射效率有显著影响ꎬ加筋能降低薄板辐射声功率ꎬ而声辐射效率高于未加筋薄板ꎮ通过对比3种不同加筋形式薄板ꎬ十字加筋板的减震降噪效果优于X字型和二字型加筋板ꎮ3)通过对薄板厚度进行优化ꎬ薄板辐射声功率级从132.1dB下降到127.81dBꎬ下降了4.29dBꎬ优化效果显著ꎮ参考文献:[1]任惠娟ꎬ盛美萍.矩形薄板的模态声辐射效率[J].机械科学与技术ꎬ2010ꎬ29(10):1397-1400.[2]刘宝ꎬ王德石ꎬ朱拥勇.障板对于平板声辐射特性的影响分析[J].噪声与振动控制ꎬ2018ꎬ38(3):26-30ꎬ41. [3]高宏林ꎬ黎胜ꎬ孟春霞.改进的半空间频率均方声压法计算结构频带振动声辐射[J].声学学报ꎬ2019ꎬ44(1):106-115. [4]张媛媛ꎬ沈火明.基于Matlab板的振动响应与声辐射研究[J].重庆理工大学学报(自然科学版)ꎬ2014ꎬ28(8):34-38. [5]王宇星ꎬ沈火明.薄板声辐射特性的数值模拟与分析[J].应用数学和力学ꎬ2014ꎬ35(S1):236-240. [6]赵峰.矩形板声振特性研究[D].大连:大连理工大学ꎬ2018.[7]刘宝ꎬ王德石ꎬ周奇郑.板厚对无障薄板声辐射特性影响的分析[J].声学学报ꎬ2017ꎬ42(5):593-600. [8]范鑫ꎬ崔洪宇ꎬ洪明.基于Virtual.LabAcoustics的蜂窝夹层板结构传声特性分析[J].噪声与振动控制ꎬ2017ꎬ37(4):34-39ꎬ68.[9]李双ꎬ陈克安.基于振动模态和声辐射模态的结构声辐射分析[C]ʊ中国声学学会2006年全国声学学术会议论文集.厦门ꎬ2006:305-306.(责任编辑:方素华)083。
高刚度复合结构覆盖层声振耦合机理与调控方法研究

高刚度复合结构覆盖层声振耦合机理与调控方法研究1. 引言1.1 研究背景高刚度复合结构覆盖层是一种常见的工程结构,具有较高的强度和刚度,被广泛应用于航空航天、汽车工业以及建筑领域。
随着现代工程技术的发展,对复合结构覆盖层的性能要求也越来越高,其中一个重要的问题就是其在声振环境下的耦合效应。
声振耦合是指复合结构在受到声波激励时产生的振动响应,这种耦合效应不仅会影响结构的稳定性和性能,还会对整个系统的工作状态产生重要影响。
在实际工程中,如何有效地控制复合结构覆盖层的声振耦合效应,是一个具有挑战性的问题。
通过深入研究复合结构覆盖层的结构特点和声振耦合机理,可以为制定合理的调控方法提供理论基础。
本文旨在探讨高刚度复合结构覆盖层的声振耦合机理及调控方法,通过实验验证和数值模拟结果,为工程实践提供参考。
1.2 研究目的本研究旨在探究高刚度复合结构覆盖层在声振耦合作用下的机理,并提出有效的调控方法,以应对振动噪声问题。
具体目的包括:1. 深入分析高刚度复合结构覆盖层的结构特点,探讨其在声振耦合作用下的振动特性;2. 研究高刚度复合结构覆盖层与基底结构之间的声振耦合机理,揭示其振动传递方式和能量耦合机制;3. 探讨通过结构参数设计、材料优化、声学隔离等手段实现对声振耦合效应的调控方法;4. 进行实验验证,验证调控方法的有效性,并探讨实际工程应用中的可行性;5. 进行数值模拟分析,揭示声振耦合机理的数学模型,为后续工程设计提供依据和参考;通过以上研究,旨在深入理解高刚度复合结构覆盖层的声振耦合机理,为工程实践提供科学的指导和技术支持。
1.3 研究意义在现代复合材料应用领域中,高刚度复合结构覆盖层广泛应用于航空航天、汽车制造等领域。
本研究旨在探究高刚度复合结构覆盖层在声振耦合方面的机理及调控方法,为相关领域的工程应用提供理论支持和技术指导。
研究意义主要体现在以下几个方面:通过分析高刚度复合结构覆盖层的声振耦合机理,可以更好地理解声波与结构振动之间的相互作用规律,为提高结构的抗振性能和降低噪声传播提供科学依据。
基于有限元方法的复合材料层合板自由振动分析
ga aah S Ltew r等 人 主 要 利 用 一 阶… 、 ar ga 、 . a sa A h 二 阶 J三 阶 以及高 阶 H 剪切 变形 理 论 和经 典 、 函数 来求 解 。但 是 实 际 问题 中 , 值 问题 的求 解 边 十分困难 。除 少数 简单 边值 问题可用 解 析法求 出 精确 解外 , 般 都 只能 用 数 值 法求 解 。 国 内有 北 一
文 章 编 号 :0 7—1 8 ( 0 8 0 0 5 0 10 3 5 2 0 ) 4— 0 2— 4
基 于有 限元 方法 的复合 材 料 层 合 板 自由振 动 分 析
晁爱 芳 沙云东 傅 文君
10 3 1 16) ( 阳航 空工 业 学 院飞 行 器 动 力 与 能 源 工 程学 院 , 沈 辽宁 沈 阳
警 O 。 ,y y d x 。 。 。 o o
第 4期
晁爱芳等 : 基于有 限元方 法的复合材料层合 板 自由振动分析
5 3
+
O y
+D:
Oy
一
(y O +
o y
)一M ( ”
(
+ O :一, x 2
( 4 1)
O w
)+M ( + ] : ,业2 0O t
() 3
= 0; = 0; 0
( )固支 , :0; :0 =0; b W ; ( )自由 , =0; =0 c Q ; =0 其中 ns 别 表示法线和切线 方 向; 、分
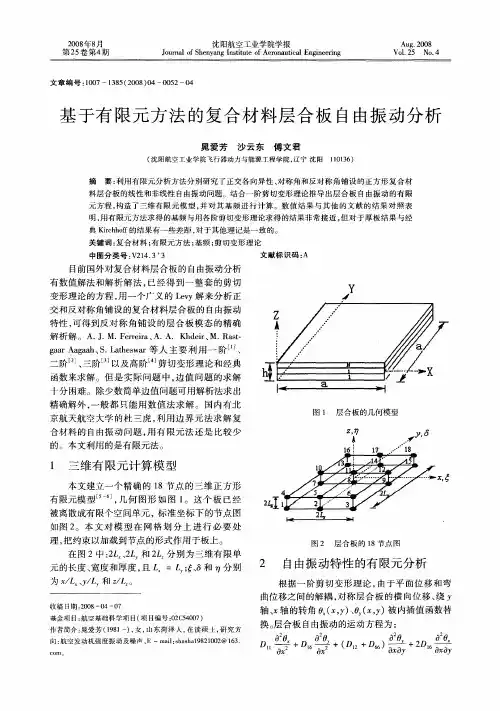
图 2 层合板 的 1 节点 图 8
2 自由振 动 特性 的有 限元 分 析
根 据一 阶剪 切 变形 理论 , 由于平 面 位 移 和弯
曲位移 之 间的解耦 , 对称 层 合 板 的横 向位移 、 Y 绕
复合材料结构中声波传播规律的研究

复合材料结构中声波传播规律的研究声波传播是一种重要的力学现象,在复合材料结构中的研究尤为关键。
本文旨在探寻复合材料结构中声波传播的规律,并揭示其在材料工程中的应用前景。
1. 引言随着科学技术的不断发展,复合材料作为一种结构新颖、性能优越的材料类型,被广泛应用于航空航天、汽车制造、船舶工程等领域。
而声波传播作为材料性能的一个重要指标,对于材料的可靠性和稳定性有着不可忽视的影响。
因此,深入研究复合材料结构中声波传播的规律具有重要的科学意义和工程应用前景。
2. 轻质复合材料中声波传播的特点轻质复合材料通常由纤维增强材料和基体材料组成,其独特的结构为声波传播带来了一些特殊条件。
首先,纤维增强材料可以有效降低材料的密度,使其具备轻质化的特点。
这样一来,在声波传播过程中,材料对声波的传播速度具有较高的响应能力。
其次,纤维增强材料的结构具有一定的吸能和消声效果,能够有效吸收声波中的能量,减弱声波的传播强度。
因此,轻质复合材料在声学性能方面具有明显的优势。
3. 复合材料结构中声波传播的数学模型为了更好地研究复合材料结构中声波的传播规律,必须建立相应的数学模型。
常用的数学模型有弹性波方程、层合板理论等。
其中,弹性波方程是描述声波在材料中传播的基本方程,可以通过求解该方程得到声波的传播速度、传播路径等信息。
而层合板理论则是一种将复合材料结构简化为具有等效各向同性的层合板结构的理论模型,通过这种模型可以得到材料中不同方向上声波的传播速度和传播模式。
4. 声波传播规律与复合材料结构设计声波传播规律的研究对于复合材料结构的设计和优化是至关重要的。
在实际工程应用中,希望能够通过合理的结构设计来改变声波的传播特性,以满足不同的工程需求。
例如,在汽车制造领域,为了降低车内的噪音污染,可以利用复合材料的特殊声学性能,设计出适宜的车身结构,从而减少外界声音的传播。
此外,在航空航天领域,人们也希望能够通过合理的结构设计,改变飞机机翼等部件的声学性能,降低噪音污染对环境和机组人员的影响。
复合材料粘接结构超声声谐振检测技术_陈颖

收稿日期:2010-12-15作者简介:陈颖,1972年出生,博士,高级工程师,主要从事无损检测技术研究。
E -m ai:l nd t_cen ter_casc @126.co m复合材料粘接结构超声声谐振检测技术陈 颖 何双起(航天材料及工艺研究所,北京 100076)文 摘 分析了超声声谐振检测技术原理,采用该技术对编织石英/酚醛树脂复合材料粘接结构进行了检测技术研究。
结果表明:采用所建立的超声声谐振检测装置,对于厚度为7和9mm 编织石英/酚醛树脂复合材料粘接结构可分别实现 10和 15mm 以上的脱粘缺陷检测。
关键词 超声,谐振,检测,粘接,复合材料U ltrasonic Resonant Inspecti on of Co mposite Bond StructuresChen Y ing H e Shuangq i(A erospace R esearch Instit ute o fM ater ials&P rocessi ng T echno l ogy ,Be iji ng 100076)Abst ract The u ltrason ic resonant NDT technique w as analytically discussed and the i n spection techno l o gy ofco m posite bond str uctures w as st u died w it h the deve l o ped ultrason ic resonant equ i p m en,t the result suggests t h at the de bond defects m ore than 10mm i n the bond str uctures for the co mposite layer of 7mm thick,and the de bond de fectsm o re than 15mm in t h e bond structures for t h e co mposite layer of 9mm thick can be found ou.tK ey w ords U ltrason ic ,Resonan,t Inspection ,Bond ,Co m posite 0 引言目前复合材料粘接结构的检测主要采用声学(包括脉冲超声反射、脉冲超声穿透、声阻、声谐振、超声导波以及敲击等)、光学(包括激光全息照相和错位散斑成像)以及红外热波成像等方法。
(多层复合)圆柱壳体的振动和声辐射研究的开题报告
(多层复合)圆柱壳体的振动和声辐射研究的开题报告1. 研究背景多层复合材料圆柱壳体(Multi-Layered Composite Cylindrical Shell, MLCCS)在工业和军事领域有着广泛的应用,如飞机机身、舰船壳体、天线罩等结构。
然而,在长期使用过程中,MLCCS常常会遭受外力的作用而发生振动,同时也会对周围环境产生噪声污染,影响人类生活和健康。
因此,研究MLCCS的振动与声辐射问题具有重要意义。
2. 研究内容本课题的研究内容包括以下几个方面:(1)MLCCS振动模态分析:通过有限元方法(Finite Element Method, FEM)建立MLCCS的有限元模型,分析其在自由振动状态下的振动模态特性,并基于该特性对其振动稳定性进行评估。
(2)MLCCS受激振动分析:将MLCCS作为被动结构,通过有限元方法建立其与外界相互作用的系统,对其在受激情况下的动力响应特性进行研究。
(3)MLCCS声辐射分析:基于声学理论及有限元模型,分析MLCCS噪声产生机理、传播途径、辐射场,对其声辐射特性进行分析和预测。
(4)MLCCS振动与声辐射控制:通过材料特性研究、结构参数优化等方法,探究降低MLCCS振动和声辐射的有效途径,并制定控制策略。
3. 研究方法本课题采用有限元数值模拟、声学测量技术等方法进行研究。
(1)有限元数值模拟:通过商业有限元软件对MLCCS的结构进行建模和分析,得到MLCCS的振动模态、受激振动和声辐射场等信息。
(2)声学测量技术:采用声场测量系统对MLCCS进行室内或室外噪声测试,并通过傅里叶变换等处理手段对其声谱特性进行分析。
4. 预期成果本课题的预期成果包括:(1)建立MLCCS的有限元模型,分析其振动特性、受激振动响应以及声辐射特性;(2)量化MLCCS振动和声辐射的程度,并制订控制策略;(3)为提高MLCCS的振动稳定性和降低噪声水平提供理论依据和技术支持。
复合材料层合板低频声辐射优化
Abstract: In order ta optimiae the low frequenco acoustic radiation perfomianco of the composite mateeal laminate, according ta the characteestics of the infinite acoustic fiell, the theora and method of the finite element and infinite element coupling are introduced ta analyze the acoustic radiation perfomianco, and the 6X6001X1 is veefied by two exampks. The finite element soVwco Abaqus and the numeecal optimization softwca Isight are combined ta optimize the composite material layeeng angle, and then the iOex of layer-ziso optimization is proposed. Taking the composite mateeal laminate with eight single-layer plates and one core damping layer as the research object, taking the layeeng angle as the design yvedble, the lyw-wiso optimization method ( LOM) is used ta optimize the acoustic perfomiance of the eaminate, and theefectofthecoaedampingeayeaon theacousticaadiation oftheeaminateisanaeyaed. Theaesuetsshowthatthefiastoadeanatuaaefaequencyofthecompositemateaiaeeaminatecan beincaeased bytheaeasonabeeeayeaingangee, and then theacousticaadiation peak numbeaand theaadiation acoustic poweaaaeaeduced.Theacousticaadiation peakscan besuppaesed byaddingthecoaedampingeayea,
振动层合板结构的多尺度建模与优化设计
振动层合板结构的多尺度建模与优化设计引言振动层合板是一种由多层材料构成的结构,其具有较高的强度和刚度,因此在工程领域得到了广泛的应用。
在振动层合板结构的设计中,多尺度建模和优化设计是两个关键的方面。
本文将讨论振动层合板结构的多尺度建模和优化设计的方法和技术。
1. 多尺度建模1.1 宏观层级建模宏观层级建模是将振动层合板整体看作一个连续体进行建模。
在宏观层级建模中,可以采用有限元方法进行结构的数值分析,确定结构的强度和刚度等力学性能。
此外,还可以考虑振动层合板的非线性特性,如几何非线性、材料非线性等。
1.2 微观层级建模微观层级建模是将振动层合板的每一层材料单元进行建模。
在微观层级建模中,可以考虑每一层材料的弹性模量、泊松比等参数,并将其作为输入条件,通过有限元分析得到振动层合板的力学性能。
微观层级建模可以更精确地描述振动层合板的材料行为,但计算成本较高。
2. 优化设计2.1 结构拓扑优化设计在振动层合板的结构拓扑优化设计中,可以通过改变结构的形状和布局,以达到最优的性能。
最常用的方法是基于有限元的拓扑优化,通过将材料的分数设定为设计变量,并设置约束条件来优化结构的拓扑。
通过结构拓扑优化设计,可以大大提高振动层合板的强度和刚度。
2.2 材料优化设计在振动层合板的材料优化设计中,可以通过调整每一层材料的厚度和性能,来达到最优的性能。
最常用的方法是基于有限元的材料优化设计,通过改变材料的属性和分数设定为设计变量,并设置约束条件来优化结构的材料。
通过材料优化设计,可以提高振动层合板的耐磨性和耐腐蚀性。
3. 多尺度优化设计在振动层合板的多尺度优化设计中,可以将宏观层级建模和微观层级建模相结合,以实现最佳的性能。
首先,在宏观层级进行结构优化,确定结构的形状和布局。
然后,在微观层级进行材料优化,确定每一层材料的厚度和性能。
最终,将两个层级的优化结果进行整合,得到最优的振动层合板结构。
4. 应用案例振动层合板结构的多尺度建模与优化设计在许多领域都得到了广泛应用。
复合材料结构振动噪声耦合机理与控制
复合材料结构振动噪声耦合机理与控制复合材料,这个词一听就让人觉得高大上,其实它就像生活中那些看似复杂却又充满魅力的事情。
想象一下,你身边的某个运动器材,或者一架飞得高高的飞机,它们身上的材料都是经过精心设计的,既要轻又要结实,真是个难得的组合。
可别小看这些材料,它们的振动和噪声可不是小事儿。
你知道吗,振动就像是你在聚会时那种隐约的背景音乐,乍一听没什么,但时间一久就会让你觉得有点烦人,甚至分心。
我们今天聊聊这些振动噪声的“背后故事”。
当复合材料被用在某些结构上,比如飞机的机翼或者赛车的车身,它们在运动时就会产生振动,进而引发噪声。
想象一下,驾驶着一辆高科技跑车,车速飞快,但这引擎的咆哮声和风声混在一起,简直让人心潮澎湃。
然而,长时间的噪声可不是件好事,久而久之,耳朵可受不了,甚至可能影响驾驶的专注力。
这些振动和噪声并不是无缘无故的。
就像你在家里做饭时,锅碗瓢盆碰撞的声音,复合材料在运转时也会因为材料特性、结构设计等各种因素而发出声响。
这里面还有个“耦合”问题,简单来说就是不同部分之间的相互影响。
材料的弹性、密度、厚度,以及设计的形状,都能让振动的传递和噪声的产生变得更加复杂。
想想你打篮球时,球弹到地上,每一次反弹都有不同的声音,这就是耦合的体现。
如何控制这些烦人的噪声呢?这可不是简单的事情。
控制噪声就像是在熬汤,你得把火候掌握好,调料也得合适。
可以通过改进材料的组成,或者调整结构的设计来减少振动。
比如,有的材料可以添加一些吸声的成分,就像给音响加个消音器,声音就不会那么刺耳。
此外,合理的结构设计也能有效降低噪声,像是在音响中增加一些缓冲材料,效果显著。
说到这里,你可能会想,为什么不早早就想到这些呢?很多时候,人们在追求性能和轻量化的同时,往往忽略了振动和噪声的问题。
就像你买了一双漂亮的鞋子,但走起来却发现磨脚。
这时候,设计师们就得像厨师一样,不断试验和调整,才能找到那个“恰到好处”的平衡点。
而在实际应用中,噪声控制的技术也在不断进步。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6.3铺层角度优化 四边简支矩形复合材料层合板优化。结构与例1
相同,具体优化模型及其优化结果如表5所示。从表 中可以看出,在保证满足约束条件的情况下,层合板声 辐射功率从91.2ldB下降到85.69 dB。其目标函数优 化迭代历史如图3所示,由于铺层角度与目标函数之 间的关系要比铺层厚度与目标函数的关系复杂,因此 优化过程也复杂一点,经过11次迭代,目标函数才收 敛。铺层角度的优化结果如表6所示,从表格中可以 看出,与铺层厚度优化结果一样,优化后的铺层角度中 心对称分布。不同的是其优化迭代历史(如图4所 示),各铺层角度的迭代趋势不是一致的。
3优化模型及求解方法
肘瓦Ou+c瓦Ou+K瓦Ou= f,sin(tot)+fC08(tot)
,=蓑∥ 8K ——S Oct^
f c:掣co
clotk
aK ——C
dd^
(14)
其中,没计变量Ot。代表层合板第k层的铺层厚度或者
铺层角度,这里假定阻尼矩阵与设计变量无关。由上
பைடு நூலகம்式可以看出,需要计算其质量矩阵和弹性刚度阵对设 计变量的灵敏度,其中,质量矩阵对铺层厚度的灵敏度
‘戈让≤戈i s戈iu i=(1,2,…,n) 其中抓z)为目标函数,凡为设计变量Xi个数,m为约束
函数gj(石)个数,石倒和石让分别为设计变量石i的上界和下 界。在本文中,复合材料层合板的声辐射功率作为优 化目标,铺层厚度和角度作为设计变量,约束函数中既 考虑了结构的指标:质量和基频,又考虑了声场性质参 数:场点声压。
可得到简单的解析形式,而对铺层角度的灵敏度为零。
弹性刚度阵的灵敏度分析见文[13]和[14]。
求解方程(14),即可得到动态响应的灵敏度。由 于灵敏度的求解方程左端就是结构的振动方程(1)左
端,同样利用振型分解法求解,得到如下形式的解:
结构优化设计问题¨2 3可表示为如下的一般数学 形式:
fmi叭石) {s.t. gf(菇)≤0 J=(1,2,…,7礼) (12)
O
O
O8 O6 O4
O O2 O ∞ ∞ ∞ ∞ ∞ ∞ O2●,l● O
6数值算例
6.1 灵敏度分析和校核 四边简支矩形复合材料层合板,其长宽分别为
0.8 m x0.6 m板厚为0.001 4 m,各向异性材料参数:
Ell=135.6 GPa,E22=9.9 GPa,G12=G13=G23=4.5
GPa,弘=0.3,P=1 415 kg/m3。空气密度Po=1.21 kg/m3,空气中声速%=343 m/s。有限元模型网格16 ×12,由221个节点和192个四边形单元构成,激励位 于层合板的中心处,振幅为1N,频率为50 Hz,场点位 于层合板正上方1 m处,不考虑阻尼影响。层合板初 始铺层厚度为:0.000 2 m初始铺层角度为:一600/一
状结构表面上一点或者板的一侧流体区域中的一点。
对方程(4)中瑞利积分板表面离散,当单元尺寸比 较小时,可以认为单元表面振速和声压是均匀的,则单
元表面声压:
P=ZV
(6)
其中,Z代表声阻抗行向量;’,代表板表面离散单元的
法向速度列向量。
板表面上所有单元声压的离散表示为:
P=Zv
(7)
32
振动与冲击
2008年第27卷
万方数据
尼阵,p(£)是由外加动荷载引入的简谐激励,不妨设为
p(t)=p。COS(mt)的形式,∞是激励的圆频率。该方程 利用振型叠加法求解,得到下列形式的解:
“=ssin(∞t)+CCOS(∞£)
(2)
其中,s和c是结构模态的线性组合。本文采用文[8]
中提出的四边形复合材料层合板单元,该单元能解决
?
(1 1)
上式中R=R』Jsz],詹是实对称;声辐射功率不可能为
负数,|大l此,足正定矩阵。其表达式如下:
SlS2sin(krl2)
S1S。sin(krl。)
后r12
矗rlm
R=掣 是一 &一 生
S;
…
;
Z丌C
i
’.
i
&一墨一 簧州百;州瓦 叠
…
…
5j:l
其中,ri是单元i和单元.,之间的距离;.s;是单元i的面 积。这种方法表达简洁适合数值计算…1,并且适合于 求解不规则的结构振动声辐射功率。
础上,给出考虑振动声辐射特性的复合材料层合板的优化设计模型,研究简谐激励力下的结构灵敏度计算,重点推导了声
学灵敏度分析公式,并采用序列线性规划方法进行了优化求解。数值算例表明通过层合板铺层厚度和角度的优化可以有
效降低结构的振动声辐射,同时验证了灵敏度算法的精度和优化方法的有效性。
关键词:有限元;层合板;声辐射;优化;灵敏度
表5层合板的优化约束条件和目标函数值
表4声功率对铺层厚度优化的数据和结果
表6声功率对铺层角度优化的数据和结果
妮
叭 粥
眇 一≥军。一.2∞口Yo参oA
髂
盯
3I苗;ou《 % 1
2
3
4
5
Iteration
图1声功率迭代历史
0 O3 O O 0 28
O O2 6
O O24
O O22 O 0O
O —矗、∞o口)『u—o_r
声辐射功率对设计变量的灵敏度分析通过对式
(11)求导得:
瓦0w=秽“R老+争H拳 d仅‘
∥a●
Z
d仅‘
(·8)
由于铺层厚度和铺层角度对足没有影响,故可简化为:
_0W=…秽“●冠罢
(、11/ 9),
O‘O/k
口aI
其分贝表示形式为:
鬻da_I10上InlU竺dotk
(20)
5.2场点声压灵敏度
场点声压灵敏度对于设计变最的灵敏度分析,对
200/200/600/200/一20。/一60。。
声功率和场点声压对于铺层厚度(t.一t,)和铺层 角度(0,一0,)的灵敏度分析与本文差分法计算结果分 别见表1和表2。从表中可以看出,灵敏度分析计算结 果与本文差分法吻合的很好,表明本文灵敏度分析具 有很高的精度。需要指出的是:本文算例中,声辐射功 率和场点声压及其相应的灵敏度均采用分贝形式。
l结构振动有限元计算
结构在简谐激励下的振动方程如下式所示:
Mu+Cu+Ku=P(t)
(1)
式中M、K分别为结构的质量阵和刚度阵,C是结构阻
基金项目:国家自然科学基金(10772038,10421202,10302006)资助 收稿日期:2008—03—24修改稿收到日期:2008—04—24 第一作者刘宝山男,博士生,1979年1月生
式中矩阵z是由g组合而成。
数做一阶近似,把原问题近似为线形规划问题,求解后
而板的一侧流体区域中场点声压离散形式可表 得到新的设计变量,重复这一过程直至迭代收敛。如
示为:
果目标函数和约束函数用Taylor展开来近似,则原问
P。=乞秽
(8)
其中,乙是从式(4)右端积分求得系数行向量,与场点
和结构位置关系,分析频率以及流体介质密度有关。
本文采用序列线形规划算法求解优化问题式 (12)。在当前设计点将约束函数做一阶近似,目标函
万方数据
其中,
一Ou:塑+丝
a“I
a口^
aa^
(15)
警:驴in(∞£)¨c。s(tot)
tYOtk
警:即in(∞£)+印。s(tot)
(16)
(70[k
同理,s。、c。、s。和c。是结构模态的线性组合。采用这个
(4)
毒
其中,i2=一1,P是流体介质的密度,S为板状结构上
表面,秽。(X’)为SP上一点x’的法向速度,G。(x’,X)为
半无限自由空间的格林函数,其表达式为:
G^(X’,x)=。三一渐
(5)
二7『r,
式中k=∥c,c为流体中声传播速度;r=Ix’一XI是
两点的距离,x’是板状结构表面上的任意一点。x是板
“剪切自锁”问题并具有厚薄板通用的性能。
求得结构位移响应,对其进行转换可得结构表面
法向速度:
移=imTu
(3)
其中,r为转换矩阵,仅与结构表面形状有关。
2结构振动声辐射计算
对于嵌在无限大障碍板上的板状结构而言,其简 谐激励下板的一侧以及板表面上的声压可以由瑞利积 分求得,即:
P(x)=i(叩IG^(X’,x)秽。(x’)赵’
而基于结构表面振速的声功率计算公式一·10 3为:
1
/-
埘=÷JR。{P(F)’口(∥)}dX"
(9)
二:
式巾s是表示振动结构的积分表面,P(r)是表面上一
点F=(石,Y)的复声压,秽(F)是结构表面上这一点上
题式(12)可转化为下列线形规划问题:
fminf(石o)+V 1以戈o)Ax
{s.t.gj(xo)+V 79j(xo)Ax≤0
算法,显著减少了动态响应灵敏度的计算工作量,并易
于考虑瑞利阻尼、结构阻尼等多种阻尼形式。
求得结构表面位移响应灵敏度,对其进行转化可
得结构表面法向速度灵敏度,如下式:
i—O— v==t‘O』)r—罢—
(I 1l1/)J
第12期
刘宝山等:复合材料层合板结构振动声辐射优化
33
5声学响应灵敏度分析
5.1声功率灵敏度
(13)
【石正s戈。5 zⅢ
其中,vf(‰)、和Vgj(石。)是目标函数和约束函数的 梯度向量。从式(13)可以看到,优化求解的关键汁算
目标函数和约束函数对没计变量的灵敏度。
的复法向速度,尺,{}表示取两者乘积的实数部分。
·4结构响应灵敏度分析
同理,式(9)的离散化表达式为:
W=÷尺e[z7“印]
(10)
