13_梁的应力
梁的应力

m
中性层
O y
d) m
m b a m
n b a n
O
(e)
层
m
纯弯曲直梁的受力变形的两个假设 :
(1) 平面假设:认为梁的横截面在弯曲后仍保 持为平面,且仍与变形后的梁轴线保持垂直。 (2)单向受力假设:认为梁的各纵向纤维之间没 有因纯弯曲而引起相互挤压作用,则横截面上 各点处的纵向线段均处于单向应力状态。
t max
* QS z max dI z
腹板上的最小剪应力t min应出现在腹板和翼缘交界 处 ( y h ) 处:
2
t min
QS dI z
* z min
2.3 圆形截面梁的剪应力
假定:
(1)在圆截面上离中性轴等距离处,即与中性轴z 平行的任一直线mn上的各点剪应力,其方向都 相交于剪力Q平行的主惯性轴y轴上的一点C(如 图)。 (2)在圆截面上离中性轴等距离处(如mn直线上) 各点的剪应力,其沿剪力Q方向的分量t y的大小 都相等。
2. 物理关系
(f) M z x y y
纯弯曲直梁上有正应力sz ,而sy=0 。若梁内的应 力不超过材料的比例极限sp ,且材料的拉伸与压缩弹性模 量相同时,胡克定律,即得
x
E
y kEy
(2)
该式表明,梁横截面上任一点的正应力与该点距中性轴的 距离y成正比,而且距中性轴等远处的各点正应力相等。
1 b 1 2 h Q z d c x a 1 dx b y 2
(2)横截面上距中性轴距离 相等的各点(y相同)的剪 应力相等,即剪应力沿横 截面宽度保持不变(如图 ),该假设适用于高度h大 于其宽度b的矩形截面。
梁的应力计算公式全部解释

梁的应力计算公式全部解释应力是材料受力时产生的内部力,它是描述材料内部抵抗外部力的能力的物理量。
在工程领域中,计算材料的应力是非常重要的,可以帮助工程师设计和选择合适的材料,以确保结构的安全性和稳定性。
梁的应力计算公式是计算梁在受力时产生的应力的公式,它可以帮助工程师了解梁在不同条件下的应力情况,从而进行合理的设计和分析。
梁的应力计算公式是由弹性力学理论推导而来的,它可以根据梁的几何形状、受力情况和材料性质来计算梁的应力。
在工程实践中,梁的应力计算公式通常包括弯曲应力、剪切应力和轴向应力三种类型的应力。
下面将分别对这三种类型的应力计算公式进行详细解释。
1. 弯曲应力计算公式。
梁在受到外部力的作用时,会产生弯曲应力。
弯曲应力是由于梁在受力时产生的弯曲变形所引起的,它可以通过以下公式进行计算:σ = M c / I。
其中,σ表示梁的弯曲应力,单位为N/m^2;M表示梁的弯矩,单位为N·m;c表示梁截面内的距离,单位为m;I表示梁的惯性矩,单位为m^4。
弯曲应力计算公式可以帮助工程师了解梁在受力时产生的弯曲应力大小,从而进行合理的设计和分析。
在工程实践中,通常会根据梁的几何形状和受力情况选择合适的弯曲应力计算公式进行计算。
2. 剪切应力计算公式。
梁在受到外部力的作用时,会产生剪切应力。
剪切应力是由于梁在受力时产生的剪切变形所引起的,它可以通过以下公式进行计算:τ = V Q / (I b)。
其中,τ表示梁的剪切应力,单位为N/m^2;V表示梁的剪力,单位为N;Q 表示梁的截面偏心距,单位为m;I表示梁的惯性矩,单位为m^4;b表示梁的截面宽度,单位为m。
剪切应力计算公式可以帮助工程师了解梁在受力时产生的剪切应力大小,从而进行合理的设计和分析。
在工程实践中,通常会根据梁的几何形状和受力情况选择合适的剪切应力计算公式进行计算。
3. 轴向应力计算公式。
梁在受到外部力的作用时,会产生轴向应力。
轴向应力是由于梁在受力时产生的轴向变形所引起的,它可以通过以下公式进行计算:σ = N / A。
梁横截面上的应力

2)计算C截面上的最大拉应力和最大压应力。
C截面上的最大拉应力和最大压应力为
tC
M C y2 I
2.5103 N m 8.810-2 m 7.6410-6 m4
Z
28.8106 P a 28.8MP a
cC
M
B
y 1
Iz
2.5 103 N m 5.2 10-2 m 7.6410-6 m 4
17.0 106 P a 17.0MP a
3)计算B截面上的最大拉应力和最大压应力。
B截面上的最大拉应力和最大压应力为
tB
M
B
y 1
Iz
4 103 N m 5.2 10-2 m 7.6410-6 m 4
27.2 106 P a 27.2MP a
cB
M B y2 Iz
4 103 N m 8.810-2 m 7.6410-6 m4
【例4.17】 求图(a,b)所示T形截面梁的最大拉 应力和最大压应力。已知T形截面对中性轴的惯性矩 Iz=7.64106 mm4,且y1=52 mm。
【解】 1)绘制梁的弯矩图。
梁的弯矩图如图(c)所示。 由图可知,梁的最大正弯矩发 生在截面C上,MC=2.5kNm; 最 大负弯矩发生在截面B上,MB= -4kNm。
入,求得的大小,再根据弯曲变形判断应力的正(拉)
或负(压)。即以中性层为界,梁的凸出边的应力为拉 应力,凹入边的应力为压应力。
(2)横截面上正应力的分布规律和最大正应力 在同一横截面上,弯矩M 和惯性矩Iz 为定值,因此
由公式可以看出,梁横截面上某点处的正应力σ与该点到 中性轴的距离y成正比,当y=0时,σ=0,中性轴上各点处 的正应力为零。中性轴两侧,一侧受拉,另一侧受压。离 中性轴最远的上、下边缘y=ymax处正应力最大,一边为最 大拉应力σtmax,另一边为最大压应力σcmax。
梁的应力计算

( // Fs )
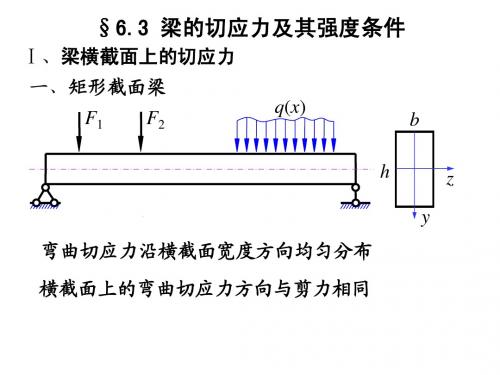
§6-4 矩形截面梁的切应力
一、矩形截面梁
切应力计算公式: FSSZ IZb
(6-11)
式中,FS-横截面上的剪力;IZ-截面对中性轴的惯性矩; b-截面的宽度;SZ-为面积A*对中性轴的静矩。
A*是过欲求应力点的水平线到截面边缘间的面积。
FS、SZ均代绝对 值,切应力方向
依剪力方向确定。
b´
b´
m´ n´
平面假设:
横截面变形后保持为平面,且仍 然垂直于变形后的梁轴线,只是绕截 面内某一轴线偏转了一个角度。
§6-1 (纯弯曲)梁的正应力
设想梁是由无数 层纵向纤维组成
凹入一侧纤维缩短 突出一侧纤维伸长
中间一层纤维长度不变- -中性层
中性层与横截面的交线- -中性轴
目录
§6-1 (纯弯曲)梁的正应力
MCy2 2.7 103 N m 0.038 m 103 N m2
MBy1 1.8103 N m 0.072 m 129 N m2
因MCy2<MBy1,所以最大拉应力发生在B截面上,即
t,max
MB IZ
y1
129N m2 0.573105 m4
22.5106 Pa
2.5MPa
My m a x IZ
WZ
IZ ymax
max
M WZ
min
M WZ
§6-1 (纯弯曲)梁的正应力
常见截面的 IZ 和 WZ
IZ y2dA
A
Wz
IZ y max
圆截面
d 4
IZ 64
Wz
d3
32
矩形截面
空心圆截面
空心矩形截面
bh3 IZ 12
梁的内力与应力(图片版)

σ=FbA,其中F为作用在梁上的力,b 为梁的宽度,A为梁的横截面积。
描述
正应力表示梁在承受拉伸或压缩时, 截面上产生的应力。
剪应力
剪应力
与截面相切的应力,主要由于剪 切而产生。
描述
剪应力表示梁在承受剪切时,截面 上产生的应力。
公式
τ=FsA,其中Fs为作用在梁上的剪 力,A为梁的横截面积。
弯曲应力
致梁发生断裂或严重变形。
强度失效的原因可能包括材料缺 陷、设计不当或制造工艺问题等。
弯曲失稳
弯曲失稳是指梁在受到垂直于 轴线的横向力作用时,发生弯 曲变形并最终失去稳定性。
弯曲失稳通常发生在梁的长度、 跨度较大或支撑不足时,导致 梁发生过大弯曲和扭曲。
弯曲失稳的原因可能包括梁的 刚度不足、支撑条件不当或外 力过大等。
。
混凝土
适用于桥梁、房屋和基础设施 等需要承受较大荷载且稳定性
要求较高的场合。
木料
适用于临时建筑、小型建筑和 家庭装修等需要较低承载能力
的场合。
其他材料
如铝合金、玻璃钢等,适用于 特殊场合和特定需求。
优化设计
截面优化
根据梁的跨度、承载能力和稳定性要求,选择合适的截面尺寸和 形状,以减小材料用量和提高承载能力。
梁的内力与应力(图片 版)
目录 CONTENT
• 梁的简介 • 梁的内力 • 梁的应力 • 梁的强度与稳定性 • 梁的设计与优化 • 梁的案例分析
01
梁的简介
梁的种类
01
02
03
简支梁
简支梁是两端支撑在支座 上的单跨梁,其载荷作用 在跨中位置。
连续梁
连续梁是多跨梁,载荷可 以作用在任意位置。
悬臂梁
梁的切应力及其强度条件
100
240
q 6.1kN/m
100
3)抗剪强度
20 S z ,max 180 20 (100 ) 2 100 45 100 2 2 846103 mm3
y
45 45
t max
FS, maxS z ,max bIz
2q 103 846103 [t ] 1.1MPa 4 901473610
D D
0.4m 0.6m
140
B
FB
C
10
FA
y
10
解 1)求内力 FA 66kN D截面的剪力
FB 44kN FS 66kN
t max
FS S z ,max dIz
103 47
A
F=110 kN
10
220
10
220 a
10
C y 10
2)求最大切应力 103 * 2 S z ,max 10310 2 1061 102 mm3
t1max tmax O
tmax
2 h FS 2 t max b h d y 2I z d 2
FS t1 h 2I z
tmin
切应力流
y
最大剪应力一般发生在中性轴上
10 320 10 50kN 50kN 50kN
100
9.5
F1
F2
C B A 1.5 m 1.5 m 1.5 m 1.5 m FA FB
y
解 1)求内力
FA 75kN
FB 75kN
10 320 10
50kN 50kN 50kN
梁的应力
384 MPa
t max 178 MPa , c max 384 MPa
5. C 截面曲率半径ρ
30
A
1m
FAY
B C
l = 3m
x
K
C 截面弯矩
M C 60kN m
z y
FBY
I Z 5.832 10 m
1 M EI
9
5
4
FS 90kN
x 90kN
C
EI Z MC
200 10 5.832 10 60 10
3
5
q=60kN/m
180
3. C 截面最大正应力
120
A
1m
FAY
B C
l = 3m
30
C 截面弯矩
M C 60kN m
x
K
z y
Cmax
FBY
I Z 5.832 10 m
M C ymax IZ
3
5
4
FS 90kN
x 90kN x
60 10
180
二 、纯弯曲梁横截面上的正应力公式
(一)变形几何关系: 由纯弯曲的变形规律→纵向线应变的变化规律。 1、观察实验:
2、变形规律: ⑴、横向线:仍为直线, 只是相对转动了一个角度 且仍与纵向线正交。
⑵、纵向线:由直线变为 曲线,且靠近上部的纤维 缩短,靠近下部的纤维伸 长。 3、假设: M
a
c
b
a
§ 梁横截面的正应力和正应力强度条件
一、 纯弯曲和横力弯曲的概念
剪力“Fs”——切应力“τ”; 弯矩“M”——正应力“σ”
梁的应力
ac
M
⑵、纵向线:由直线变为曲
线,且靠近上部的纤维缩短,
靠近下部的纤维伸长。
b
d
3、假设:
(1)弯曲平面假设:梁变形前原为平面的横截面变形后仍为平 面,且仍垂直于变形后的轴线。
第九章 梁的应力
梁是由许多纵向纤维组成的
凹入一侧纤维缩短
突出一侧纤维伸长
根据变形的连续性可知, 梁弯曲时从其凹入一侧的 纵向线缩短区到其凸出一 侧的纵向线伸长区,中间 必有一层纵向无长度改变
z
A2 20120mm2 y2 80mm
yc
80 2010 120 2080 80 20 120 20
52mm
(2)求截面对中性轴z的惯性矩
Iz
Hale Waihona Puke 80 203 1280 20 422
y
201203 20120 282
12
7.64106 m4
第九章 梁的应力
横截面上应力分布
b
d2
c,m ax
h yt,max yc,max d1
oz y
Oz
y b
t,m ax
中性轴 z 不是横截面的对称轴时,其横截面上最大拉
应力值和最大压应力值为
t,m ax
My t ,m a x Iz
c,m ax
Myc ,m a x Iz
第九章 梁的应力
例 对于图示 T形截面梁,求横截面上的最大拉应力和最大压 应力.已知: I z 290 .6 10 8 m4
d
在弹性范围内, E E Ey ...... (2)
O
O1
A1
B1 x
y
第九章 梁的应力
应力的分布图:
梁的应力和强度计算
梁的应力和强度计算1.梁的基本假设梁的基本假设包括:梁材料是均匀各向同性的,梁截面是平面截面,梁的纵向伸缩变形可以忽略,梁的横向收缩变形可以忽略,梁截面平面保持平直。
2.梁的受力分析在进行梁的应力和强度计算之前,需要对梁的受力进行分析。
常见的梁的受力包括弯曲、剪切和轴向拉压等。
2.1弯曲弯曲是梁的一种主要受力状态,发生在梁受到弯矩作用时。
对于弯曲受力的梁,可以运用梁弯曲理论进行应力和强度计算。
常见的梁弯曲理论包括欧拉-伯努利梁理论和延性梁理论。
2.2剪切剪切是梁的另一种重要受力状态,发生在梁上部分截面受到剪力作用时。
剪切力引起梁截面上的剪应力,可以通过剪切变形理论进行计算。
2.3轴向拉压轴向拉压发生在梁上部分截面受到轴向拉力或压力作用时。
轴向拉力或压力引起梁截面上的轴向应力,可以通过轴向变形理论进行计算。
3.梁的应力分析根据梁的基本假设和受力分析,可以进行梁的应力分析。
梁的应力分析包括黄金区和非黄金区的判断、应力分布的计算和强度设计的确定。
3.1黄金区和非黄金区判断黄金区是指梁截面上应力最大的区域,通常位于材料的纤维处。
在黄金区内,应力达到梁材料的屈服强度。
非黄金区则是指其他区域,应力小于屈服强度。
3.2应力分布计算根据梁的受力和应力分析,可以计算出梁截面上的应力分布。
应力分布的计算可以通过梁的几何形状、外力和边界条件以及材料的性质来确定。
常见的应力分布包括弯曲应力、剪切应力和轴向应力等。
4.梁的强度设计梁的强度设计是根据计算得到的应力分布进行的。
根据材料的强度,可以确定梁的尺寸和形状,以满足梁的极限状态和使用状态的要求。
总结起来,梁的应力和强度计算是梁力学中的基本问题,包括梁的受力分析、应力分布计算和强度设计等内容。
通过合理的计算和设计,可以确保梁的安全和可靠性,提高结构的性能。
梁的应力及强度计算
梁的应力及强度计算梁是一种常见的结构元件,用于承受或分配荷载。
在设计和分析梁的过程中,计算梁的应力及强度是非常重要的。
本文将详细介绍梁的应力及强度计算方法。
首先,梁的应力定义为单位面积上的力,用公式表示为:σ=M*y/I其中,σ表示梁的应力,M表示梁的弯矩,y表示距离中性轴的垂直距离,I表示梁的截面惯性矩。
梁的应力通常包括弯曲应力、剪切应力和轴向应力。
弯曲应力是由于弯曲力引起的应力,计算公式为:σ_b=M*y/I其中,σ_b表示弯曲应力。
剪切应力是由于纵向剪力引起的应力,计算公式为:τ=V*Q/(b*t)其中,τ表示剪切应力,V表示纵向剪力,Q为形状系数,b为梁的宽度,t为梁的厚度。
轴向应力是由于轴向力引起的应力,计算公式为:σ_a=N/A其中,σ_a表示轴向应力,N表示轴向力,A表示梁的截面积。
梁的强度是指在给定的荷载下梁能够承受的最大应力。
在计算梁的强度时,通常需要将不同种类的应力进行合并。
弯曲强度是指梁在弯曲荷载下的抗弯矩能力。
根据材料的弯曲性能和形状,可以采用破坏理论或变形理论计算梁的弯曲强度。
剪切强度是指梁在剪切荷载下的抗剪切能力。
根据材料的剪切性能和梁的几何形状,可以计算出梁的剪切强度。
轴向强度是指梁在轴向荷载下的抗轴向力能力。
轴向强度的计算通常基于材料的抗拉性能。
在进行梁的应力及强度计算时,还需要考虑其他因素,如材料的弹性模量、断裂韧性和安全系数等。
总之,梁的应力及强度计算是结构设计和分析中必不可少的一部分。
通过合理的计算方法,可以确保梁在荷载下的正常工作和安全使用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8
处达到最大值。
为了确定水平切应力随垂直位置 y 而变化的规律,可从梁中高于中性轴为 y 处切出一
宽为 d x 的自由体,如图 9 所示。设自由体左端横截面上的弯矩为 M (x) ,右端横截面上的
矩形横截面,其 I 值为:
∫ I = h/2 y2b d y = bh3
−h/ 2
12
(5)
从式(4)解出梁的曲率 v,xx 为:
v, xx
=
M EI
(6)
3
5、将式(6)代入式(3),即可得到应力的直接计算式:
σx
=
−yE
M EI
=
−M I
y
(7)
最后得到的正应力表达式(7),与圆轴扭转时的切应力表达式τθ z = Tr/ J 相似:横截
y = ∫A y d A ∫A d A
因此 y = 0 ,也就是中性轴通过梁横截面的形心。经过思考,这一结果是显而易见的:因为
在中性轴上方受压侧和下方受拉侧的应力都以相同的变化率线性地增加,仅当中性轴正好 通过形心时,这些应力才能自相平衡,使水平方向的合力为零,保持梁在水平方向的平衡。
压应力和拉应力虽可互相平衡使得水平方向无合力,但是这些应力还会产生一个逆时
梁的应力
MA 02139,剑桥 麻省理工学院
材料科学与工程系 David Roylance
引言
2000 年 11 月 21 日
为了弄清楚梁由弯曲载荷而引起的应力,人们经历了漫长的岁月。伽利略曾经研究过 这个问题,但通常认为,我们今天应用的理论主要由伟大的数学家欧拉,L.(Leonard Euler 1707-1783)所创建。我们下面将讲到梁在横截面上正应力的变化规律:在下(或上)边 缘处拉应力达到最大值,靠近中性层时拉应力渐减,在中性层上应力为零,到上(或下) 边缘处达到最大压应力。梁在横截面上也有切应力,但是当梁的跨度与梁高之比很大时, 切应力与正应力相比往往可以忽略不计。当梁受到不同载荷的作用或是梁的横截面形状不 同时,其横截面上应力的计算方法,恐怕是简明的材料力学教程中最重要的内容了,我们 将在下面详加论述。学习这一理论前,要求读者已具备画梁的剪力图和弯矩图的能力,相 关知识可参见前面的模块(如模块 12)。
最大正应力:
( ) σ
x
=
c2d
4
+
3d2c +6abd+3ab2 wL2 4abcd3 +6ab2cd2 + 4ab3cd
+
a2b4
在实际运算中,每一步求解都得到一个具体数值,而不是代数表达式。
在纯弯曲情况下,梁的横截面上只有弯矩、没有横向或轴向的内力,仅有正应力σ x ,
其值由式(7)给出。所有其他的应力都为零,即σ y = σ z = τ xy = τ xz = τ yz = 0 。但是由
弯矩出现在与墙相连的固定端,容易求得其值为 Mmax = (wL)(L/ 2) 。随后可用式(7)求
应力,但要先知道中性轴的位置,因为 y 和 I 值都由中性轴位置而定。 用“组合图形定理”(见习题 1)可求出梁的底部到过形心的中性轴的距离 y 。该定理
指出:若总图形由若干个简单图形组合而成,则总图形的形心到任一轴的距离,等于各个 简单图形的面积与其形心到该轴的距离的乘积的代数和除以这些图形面积之和(即总图形 的面积):
注意到与 Pcr 与 L2 有关,所以屈曲载荷与杆长的平方成反比。
既然杆长对屈曲载荷有如此明显的影响,就不难理解横向支承对预防屈曲的重要性了。 如果在梁的中点处加支承(见图 7)以消除中点处的挠度,将迫使屈曲形态下挠曲线的波
长变为 L ,不再是原来的 2L 。这相当于梁的长度减半,从而使临界屈曲载荷增至原来的四
正应力
梁在正弯矩的作用下,其轴线将会变成一条向上凹的曲线。直觉告诉我们,这意味着
靠近梁顶部的材料在 x 方向(即轴线方向)受压;而梁的底部区域则受拉。在压缩区和拉
伸区之间的过渡线上,应力为零,这条线就是梁的中性轴。像粉笔和玻璃这一类抗拉能力 差的材料,将先在梁底部受拉表面产生裂纹,然后裂缝扩展,直至最后断裂。如果材料抗 拉能力强而抗压能力弱,梁会先在顶部受压表面发生破坏,这一现象可以从木条压弯时的 外表纤维的屈曲中观察到。
4、平衡关系:由于梁在轴向( x 方向)不受外载荷的作用,于是,由正应力σ x (图
2 所示)引起的总的轴向力必须为零,可用下式表示
图 2 梁的力矩平衡和力平衡
2
要上式成立,必须
∑ ∫ ∫ Fx = 0 =
σ
A
x
d
A
=
A− yEv,xx ຫໍສະໝຸດ A∫A y d A = 0
而中性轴到横截面形心的距离 y 为:
v,xx ≡ d2v/dx2 是梁的挠曲线的斜率的变化率,是“斜率的斜率”,称为梁的曲率。
3、本构方程:由于应力是直接从胡克定律
σ x = Eε x = −yEv,xx
(3)
求得的,这就限定由此得出的结果只适用于线弹性材料。上式表明,梁横截面上的轴向正 应力也像线应变一样,从中性轴上的零值线性地增加,在梁横截面的上、下边缘处达到最 大值。
于泊松效应,除了线应变 ε x 外,还有其他方向的线应变。泊松效应并不会引起切应变,
γ xy = γ xz = γ yz = 0 。各个方向的线应变为:
[ ( )] εx
=
1 E
σx
−ν
σ
y
+σz
= σx E
[ ] εy
=
1 E
σy
−ν (σ x
+σz )
= −ν
σx E
[ ( )] εz
=
1 E
σz
x 的导数来近似1,于是 x 方向的位移为:
u = − yv,x
(1)
( ) 式中的逗号表示对其后的变量求导数 v,x ≡ d v /d x 。中性轴上方的 y 值为正,但中性轴在
1曲率的精确表达式是
当分母中导数项的平方与 1 相比很小时,就得出θ ≈ dv / dx 。
1
梁内的位置尚未确定。
图 1 梁弯曲时的几何关系
切应力
如前所述,横向载荷引起的梁沿 x 轴方向的拉、压应变使梁弯曲。另外,横向载荷引
起的剪切效应有使横截面沿截面的切线方向相对滑动的趋势,如图 8 所示,与扑克牌相对
图 8 粱弯曲时的剪切位移
滑动的情形十分相似。与剪切作用相关的切应力τ xy 合成铅垂方向的剪力V 。现研究梁横 截面上切应力的分布规律。由于τ xy =τ yx ,横截面上某点处的切应力必定与过该点的水平
−ν
σx
+σy
= −ν σx E
这些应变也可以用曲率来表示。从式(2)可得,梁沿着轴向的曲率为:
v, xx
=
−εx y
梁同时还有横向(垂直于轴线方向)的曲率,其值由下式给出:
v,zz
=−
εz y
=νεx y
=−νv,xx
这种横向弯曲如图 5 所示,称为鞍形弯曲。如果你用手指弯曲一块“红珍珠”牌橡皮,就 可看到这种弯曲。
针方向的力矩,此力矩必须等于该横截面上的弯矩值 M(x) ,这一结论从对 O 点的力矩平
衡方程就能看出:
∑ ∫ Mo
=
0=M+
σ
A
x
⋅
y
dA
∫ ( ) ∫ M =
A
yEv,xx
⋅ y d A = Ev,xx
y2 d A
A
(4)
图 3 矩形横截面的惯性矩
∫ 式中, y2 d A是矩形对水平形心轴的惯性矩,记作 I 。对于图 3 所示的高为 h 、宽为 b 的
面上的正应力在中性轴上为零,随 y绝对值的增加而线性地变化,到上、下边缘处达到最
大值。正应力与横截面的惯性矩成反比,与材料的性质无关。正如设计师喜欢用空心的驱
动轴以得到最大的极惯性矩 J 一样,梁的上、下表面处常带有宽的翼缘,以增加惯性矩 I 。
图 4 T 形截面悬臂梁
例 1 T 形截面悬臂梁的尺寸如图 4 所示,梁上均布载荷的集度为 w N m。梁的最大
∑ y = i Ai yi ∑i Ai
对本例,上式即
y = (d /2)(cd)+(d +b/2)(ab)
cd +ab
组合图形中的各组成部分对其自身形心轴的惯性矩分别为 ab3 /12 和 cd3 /12 。应用“平
行轴定理”(见习题 3),可从这些惯性矩进一步求得各组成部分对通过组合图形形心的水
平轴的惯性矩。该定理指出:若任意轴 z′平行于过图形形心的轴 z ,两轴间的距离为 d , 则图形对 z′轴的惯性矩 Iz′ 等于图形对 z 轴的惯性矩 Iz 加上图形面积 A 和距离 d 平方的乘
v = c1 sin
P EI
x
+
c2
cos
Px EI
因为在 x = 0 和 x = L 处挠度为零,显然 c2 必须等于零。此外,在上述两处正弦项必须为 零,这就要求长度 L 恰是正弦函数半波长的正整数倍:
n = 1时,得到能使梁变弯的 P 的最小值,即临界屈曲载荷 Pcr
Pcr
=
π 2EI L2
(11)
引起的一种弯曲现象。现研究图 6 所示两端铰支、受到轴向压力 P 作用的梁,一个偶然的 侧向载荷或横截面的缺陷,使梁产生横向偏移 v , 于是 P 力在梁的各横截面上引起的弯矩
为
M (x) = P v(x)
(9)
梁自身的刚度有消除这种偏移、并重新恢复原来直线形状的趋势,但是弯矩的影响使梁产 生更大的偏移。这好比是一场“对抗”,看哪种影响胜出。如果弯矩使偏移增加的趋势超过
