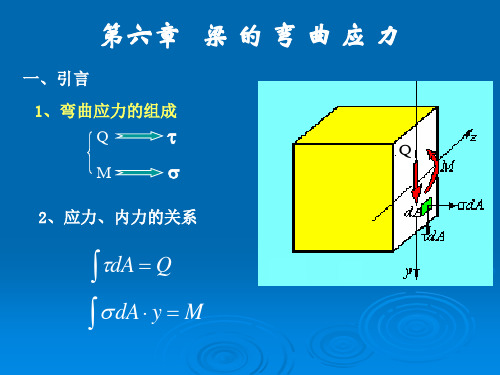
梁的应力计算

M max 38103 N m 3 3 3 WZ 0 . 223 10 m 223 cm 170106 Pa
§6-2 梁的正应力强度条件及其应用
例题6-4 根据算得的WZ值，在 附录型钢表上查出与 该值相近的型号，就 是我们所需的型号。 附录A，附表4，P232页。 查出20a钢相近WZ值237cm3，故选择20a号工字钢。 注意：选择的工字钢型号WZ值一般要求≥计算值，才能满 足强度要求。 如选取的工字钢WZ值略小于计算值，则应再校核下强度， 当σmax不超过[σ]的5%时，还是满足工程需要的。
FSSZ IZb
§6-4 矩形截面梁的切应力
二、矩形截面梁切应力分布
b h2 2 SZ y 2 4
ቤተ መጻሕፍቲ ባይዱ
§6-2 梁的正应力强度条件及其应用
例题6-5一⊥形截面的外伸梁如图所示，已知l=600mm， a=40mm，b=30mm，c=80mm，F1=24kN,F2=9kN,材料 的许用应力[σt]=30MPa，许用压应力[σc]=90MPa。试校 核梁的强度。
解：先画出弯矩图。需算出形心C的位置及截面对中性轴 的惯性矩，算得结果为：
第六章 梁的应力
§6-1 梁的正应力（纯弯曲） §6-2 梁的正应力强度条件及其应用 §6-3 梁的合理截面形状及变截面梁 （工程上提高弯曲强度的一些措施） §6-4 矩形截面梁的切应力
§6-6 梁的切应力强度条件
§6-1 （纯弯曲）梁的正应力
回顾与比较 内力 应力
FN A
T IP
截面对中性轴（水平对称轴）的惯性矩为：
bh 3 0.12m 0.183 m3 IZ 0.583104 m 4 12 12
§6-1 梁的正应力
例6-1 长为l的矩形截面梁，在自由端作用一集中力F， 已知，h=0.18m，b=0.12m，y=0.06m,a=2m， F=1.5kN。试求C截面上K点的正应力。
§6-3 变截面梁形状及变截面梁
设计梁原则： 满足强度条件 经济性，尽量节省材料 需要选择合理的截面形状和尺寸 一、截面的合理形状 M max max 强度条件： WZ 单从强度来看，WZ越大越合理。 WZ和截面形状和尺寸有关。
在截面面积相同的情况下分析矩形、方形、圆形截面形状 的合理性。
§6-3 变截面梁形状及变截面梁
换个角度思考： WZ值与截面高度和面积分布有关，截面高度越大、面 积分布离中性轴越远的话，WZ值就越大，这也是工字 型形梁更合理的主要原因之一。 从应力角度分析：
M
§6-3 变截面梁形状及变截面梁
二、变截面梁
A
q=2kN/m
B C
变截面梁——横截面沿梁轴 线变化的梁 Mx max WZ x
根据公式：
MC 3 103 N m K y 0.06m 3.09MPa 4 4 IZ 0.58310 m
代入公式时，不考虑正负号。 C截面弯矩为负，K点位于中性轴上面，所以K点应力 为拉应力。
§6-2 梁的正应力强度条件及其应用
弯曲正应力强度条件
σmax
M
max
y max
Mx WZ x
x l = 4m
xm
M
ql 2 / 8 4kN m

x
等强度梁——梁强度沿轴线 均匀分布
Mx WZ x
§6-3 变截面梁形状及变截面梁
当荷载比较复杂时，等强度梁难以加工，增加了加工 制造成本，一般很少采用等强度梁。
§6-3 变截面梁形状及变截面梁
K
§6-4 矩形截面梁的切应力
二、矩形截面梁切应力分布 公式中，对某一截面来说， FS、IZ、b均为常数，只有 静矩是变量。
SZ A y0 h h b y y y / 2 2 2
b h2 2 y 2 4
max MC y2 IZ
MB y1 1.8 103 N m 0.072m 129N m2 因MCy2<MBy1，所以最大拉应力发生在B截面上，即 MB 129N m2 6 t ,max y1 22 . 5 10 Pa 2.5MPa t 5 4 IZ 0.57310 m 满足强度要求。
满足强度要求。
§6-2 梁的正应力强度条件及其应用
例题6-4 简支梁上作用两个集 中力，已知l=6m， F1=15kN，F2=21kN。 如果梁采用热轧普通 工字钢，钢的许用应 力[σ]=170MPa，试选 择工字钢的型号。 解：先画出弯矩图，最大弯矩发生在F2作用截面上，其值 为38kN﹒m。根据强度条件，梁所需的弯曲截面系数为：
M
FS
? ?
§6-1 （纯弯曲）梁的正应力
纯弯曲
梁段CD上，只有弯矩，没有剪力－－纯弯曲
梁段AC和BD上，既有弯矩，又有剪力－－横力弯曲
目录
§6-1 （纯弯曲）梁的正应力
一、几何方面
m a b n
d
m´ n´
a
b
a´
b´ m´ 平面假设：
m dx n
a´ b´
n´
横截面变形后保持为平面，且仍 然垂直于变形后的梁轴线，只是绕截 面内某一轴线偏转了一个角度。

§6-1 （纯弯曲）梁的正应力
三、静力学方面
FN、My、Mz
M EI Z
EIZ ——弯曲刚度
1
§6-1 （纯弯曲）梁的正应力
变形几何关系 物理关系
E
1

y
E
1
y
M 静力学关系 EI Z

My 正应力公式 IZ
为曲率半径， 为梁弯曲变形后的曲
max
M max ymax M max IZ WZ
§6-1 梁的正应力
例6-1 长为l的矩形截面梁，在自由端作用一集中力F， 已知，h=0.18m，b=0.12m，y=0.06m,a=2m， F=1.5kN。试求C截面上K点的正应力。
解：先算出C截面上的弯矩
MC F a 1.5 103 N 2m 3103 N m
M max max WZ
2.选择截面
M max WZ
3.计算梁所能承载的最大荷载
Mmax W Z
§6-2 梁的正应力强度条件及其应用
q=2kN/m x l = 4m
FBY
例题6-2
140
210 B
A C
[σ]=10MPa，试校核该梁 的强度。
xm
FAY
M
ql 2 / 8 4kN m
a
F
b
A
FAY
x1
C x2
l
B
FBY
M

x
§6-4 矩形截面梁的切应力
分几种截面形状讨论弯曲切应力
一、矩形截面梁切应力
b y A n x n1 dx P m m1
q(x)
m h
m
m1 O
Fs z q1
B x
p n dx p1 n1 y
y x
关于切应力的分布作两点假设： 1、横截面上各点的切应力方向平行于剪力 2、切应力沿截面宽度均匀分布
§6-2 梁的正应力强度条件及其应用
（2）校核最大压应力 与分析最大拉应力一样，要比较C、B两个截面。C截面上 最大压应力发生在上边缘。因MC、y1分别大于MB、y2，所 以最大压应力一定发生在C截面上。即 MC 2.7 103 N m 0.072m c,max y1 33.9MPa c 5 4 IZ 0.57310 m 满足强度要求。
常见截面的 IZ 和 WZ
I Z y 2 dA
A
IZ Wz y max
圆截面
矩形截面
4
空心圆截面
空心矩形截面
IZ Wz
d
64
bh IZ 12
3
3
IZ
D
3
4
64
(1 4 )
b0 h0 bh3 IZ 12 12
3
d
32
Wz
bh 6
2
3 3 b h bh D 0 0 ) /(h0 / 2) Wz (1 4 ) Wz ( 12 12 32
Iz

M
max
WZ
σ
1.等截面梁弯矩最大的截面上 2.离中性轴最远处 3.变截面梁要综合考虑 M 与 I z 4.脆性材料抗拉和抗压性能不同，两方面都要考虑
t ,max t
c,max c
§6-2 梁的正应力强度条件及其应用
根据弯曲正应力强度条件 1.强度校核

x
FAy 4kN FBy 4kN ql 2 4kN m 2. 求最大弯矩 M max 8 2 2 bh 0.14m 0.21 m 2 WZ 0.103102 m3 6 6
解：1. 求支反力
最大正应力为：
Mmax 4 103 N m max 3.88MPa 10MPa 2 3 WZ 0.10310 m
y1 0.072m, y2 0.038m, I Z 0.57310 m
5
4
§6-2 梁的正应力强度条件及其应用
因材料的抗拉与抗压性能不同，截面对中性轴又不对称， 所以需对最大拉应力与最大压应力分别进行校核。 （1）校核最大拉应力
由于截面对中性轴不对称。而正负弯矩都存在，因此，最 大拉应力不一定发生在弯矩绝对值最大的截面上。应该对 最大正弯矩和最大负弯矩两个截面上的拉应力进行分析比 较。
§6-3 变截面梁形状及变截面梁
矩形截面
方形截面b=h=a
圆截面