流体力学第五章习题
李玉柱流体力学课后题答案 第五章

第五章 层流、紊流及其能量损失5—1 (1)某水管的直径d =100 mm ,通过流量Q =4 L/s ,水温T =20℃;(2)条件与以上相同,但管道中流过的是重燃油,其运动粘度6215010m /s ν-=⨯。
试判别以上两种情况下的流态。
解:(1) 200C 时,水的运动粘性系数ν=1.007×10-6m 2/s ,24Q u d π=水的雷诺数Re 为:-3-6244 4 L/s 10Re 5060020001.00710m /s 3.140.1mud Q v v d π⨯⨯====>⨯⨯⨯,紊流 (2) 石油:-3-6244 4 L/s 10Re 339.7200015010m /s 3.140.1m ud Q v v d π⨯⨯====<⨯⨯⨯,层流 5—2 温度为0℃的空气,以4 m/s 的速度在直径为l00 mm 的圆管中流动,试确定其流态(空气的运动粘度为521.3710m /s ν-=⨯)。
若管中的流体换成运动粘度为621.79210m /s ν-=⨯的水,问水在管中呈何流态?解:空气的雷诺数Re 为:-524 m/s 0.1m Re 2919720001.3710m /sud v ⨯===>⨯,紊流 水的雷诺数Re 为:-624 m/s 0.1m Re 223 21420001.79210m /sud v ⨯===>⨯,紊流 5—3 (1)一梯形断面排水沟,底宽0.5m ,边坡系数cot θ=1.5(θ为坡角),水温为20℃,水深0.4m ,流速为0.1m /s ,试判别其流态;(2)如果水温保持不变,流速减小到多大时变为层流?解:200C 时,水的运动粘性系数ν=1.007×10-6m 2/s 水力直径为(0.520.60.5)0.4/20.23m 0.50.722AR χ+⨯+⨯===+⨯ 4-620.1m/s 0.23m Re 2.24101.00710m /sR uR ν⨯===⨯⨯,42.24102000⨯>,湍流 水流为层流时Re 500uR ν≤=(明渠流),故 63Re 500 1.00710 2.210m/s 0.23u R ν--⨯⨯≤==⨯ 5—4 由若干水管组装成的冷凝器,利用水流经过水管不断散热而起到冷凝作用。
流体力学龙天渝课后答案第五章孔口管嘴管路流动
解�由题得� � � �
1 � 0.707
l
� d � �� �1
6.如上题�当管嘴外空气压强为当地大气压强时�要求管嘴出流流速为 30m/s。此时静压箱 内应保持多少压强�空气密度为 ρ=1.2kg/m3。
解� v � � 2 �p �得 �p � 1.08kN / m 2 �
7.某恒温室采用多孔板送风�风道中的静压为 200Pa�孔口直径为 20mm�空气温度为 20℃� μ=0.8。要求通过风量为 1m3/s。问需要布置多少孔口�
∴负压值为-2.93m 16.如图水泵抽水系统�管长、管径单位为 m�ζ 给于图中�流量 Q=40×10-3m3/s�λ=0.03。 求�
�1�吸水管及压水管的 S 数。 �2�求水泵所需水头。 �3�绘制总水头线。
5
解��1� S H1
=
� 8�� �
�
L1 d1
�
��1 �
2
d
4 1
g
�
2
� �� �
� 8� l1
解�(1)
S P1 �
d1
�
2
d
4 1
�8� l2
SP2 �
d2
�
2
d
4 2
� 8(� l3 � 1)
SP3 �
d3
�
2
d
4 3
S P � S P1 � S P 2 � S P3
p � SPQ2
解得� p � 2500 Pa
�2�铅直安装不会改变总压�因为同种气体位压等于零 �3� p � S P Q 2 � 2830 Pa 18. 并联管路中各支管的流量分配�遵循什么原理�如果要得到各支管中流量相等�该如何 设计管路�
流体力学第五章题库

名词解释1.黏性流体单位中立形式的伯努利方程:w a a h gv g pz g v g p +++=++22z 22222111αραρ2.方程适用条件1.流动为定常流动2流体为黏性不可压缩的重力流体3列方程的两过流断面必须是缓变流截面,而不必顾忌两截面间是否有急变流。
3.动能修正系数α的大小取决于过流断面上流速分布的均匀程度,以及断面的形状和大小,流速分布越均匀,其数值越接近于一,流速分布越不均匀,其数值就越大,。
4.流体在其流动过程中要克服黏性摩擦力,总流的机械能沿流程不断减小,总水头线不断降低。
5.相似准则:在几何相似的条件下,两种物理现象保证相似的条件或准则。
6.牛顿数:作用力与惯性力的比值。
Ne=F/ρl ²v ²7.弗劳德数:物理意义为惯性力与重力的比值。
Fr=v/(gl )½ 8.雷诺数:物理意义为惯性力与黏性力的比值。
Re=vl/υ 9.欧拉数:物理意义为总压力与惯性力的比值。
Eu=Δp/ρv ² 10.柯西数:物理意义为惯性力与弹性力的比值。
Ca=ρv ²/K 11.马赫数:(流场中流体为气体)物理意义为惯性力与弹性力的比值。
Ma=v/c 12.韦伯数:物理意义为惯性力与表面张力的比值。
We=ρv ²l/σ13.斯特劳哈尔数:物理意义为当地惯性力与迁移惯性力的比值。
Sr=l/vt14.层流:着色流体和周围的流体互不掺混,流线为直线,流体质点只有沿圆管轴向的运动,而没有径向运动,这种流动状态称为层流或片流。
15.紊流:流体质点不仅有轴向运动,也具有径向运动,处于一种无序的紊乱状态,这种流动状态称为紊流或湍流。
16.边界层:黏性流体流经固体壁面时,在固体壁面法线方向上存在一速度急剧变化的薄层,称为边界层。
17.管道进口段:边界层相交以前的管段称为管道进口段(或称起始段),其长度以L*表示。
18.准定常流动/时均定常流:流场中的时均参数不随时间改变的紊流流动称为准定常流动或时均定常流。
工程流体力学第五章自测题答案

第5章 压力管路的水力计算
5-1.某水罐1液面高度位于地平面以上z 1=60m ,通过分支管把水引向高于地
平面z 2=30m 和z 3=15m 的水罐2和水罐3,假设l 1=l 2=l 3=2500m, d 1=d 2=d 3=0.5m, 各管的沿程阻力系数均为λ=0.04。
试求引入每一水罐的流量。
解:取1-1、2-2两液面列伯努利方程:
2121f f h h z z ++=
g
V d L h g
V
d L h f f 222
22222
2
1
1111
λλ==
所以,41.42221=+V V (1) 取1-1、3-3两液面列伯努利方程:
3131f f h h z z ++=
所以,94.22321=+V V (2)
又 ⎩⎨⎧==+=321
321d d d Q Q Q Ö 321V V V += (3)
得 ⎪⎩⎪
⎨⎧===s m V s m V s m V /39.0/28.1/67.13
21 Ö
⎩⎨⎧==s
m Q s
m Q /0765.0/251.03
332
5-2.
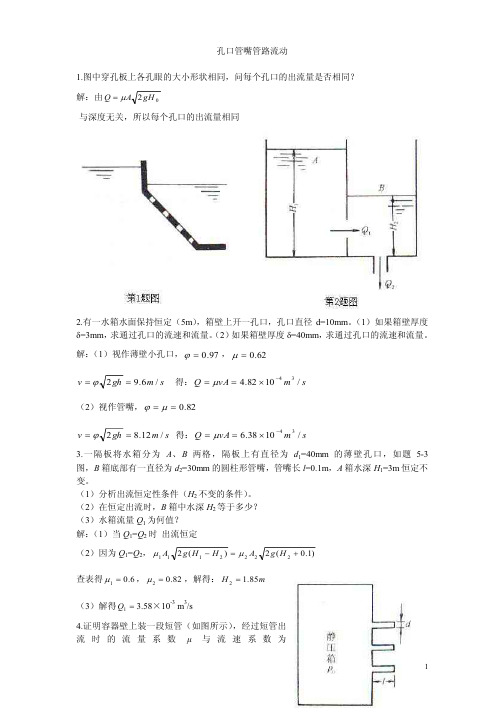
水从封闭水箱上部直径d 1=30mm 的孔口流至下部,然后经d 2=20mm 的圆柱行管嘴排向大气中,流动恒定后,水深h 1=2m ,h 2=3m ,水箱上的压力计读数为4.9MPa ,
求流量Q 和下水箱水面上的压强p 2,设为稳定流。
6.01=μ,82.02=μ。
解:经过孔口的流量Q 1
经过管嘴的流量Q 2
因为稳定流,所以Q 1=Q 2 整理得:Pa p 421034.4×=。
李玉柱流体力学课后题答案第五章

第五章 层流、紊流及其能量损失5—1 (1)某水管的直径d =100 mm ,通过流量Q =4 L/s ,水温T =20℃;(2)条件与以上相同,但管道中流过的是重燃油,其运动粘度6215010m /s ν-=⨯。
试判别以上两种情况下的流态。
解:(1) 200C 时,水的运动粘性系数ν=×10-6m 2/s ,24Qu d π= 水的雷诺数Re 为:-3-6244 4 L/s 10Re 5060020001.00710m /s 3.140.1mud Q v v d π⨯⨯====>⨯⨯⨯,紊流(2) 石油:-3-6244 4 L/s 10Re 339.7200015010m /s 3.140.1mud Q v v d π⨯⨯====<⨯⨯⨯,层流 5—2 温度为0℃的空气,以4 m/s 的速度在直径为l00 mm 的圆管中流动,试确定其流态(空气的运动粘度为521.3710m /s ν-=⨯)。
若管中的流体换成运动粘度为621.79210m /s ν-=⨯的水,问水在管中呈何流态解:空气的雷诺数Re 为:-524 m/s 0.1mRe 2919720001.3710m /sud v ⨯===>⨯,紊流 水的雷诺数Re 为:-624 m/s 0.1mRe 223 21420001.79210m /sud v ⨯===>⨯,紊流 5—3 (1)一梯形断面排水沟,底宽0.5m ,边坡系数cot θ=(θ为坡角),水温为20℃,水深0.4m ,流速为0.1m /s ,试判别其流态;(2)如果水温保持不变,流速减小到多大时变为层流解:200C 时,水的运动粘性系数ν=×10-6m 2/s水力直径为(0.520.60.5)0.4/20.23m 0.50.722AR χ+⨯+⨯===+⨯4-620.1m/s 0.23m Re 2.24101.00710m /sR uRν⨯===⨯⨯,42.24102000⨯>,湍流 水流为层流时Re 500uRν≤=(明渠流),故63Re 500 1.00710 2.210m/s 0.23u R ν--⨯⨯≤==⨯5—4 由若干水管组装成的冷凝器,利用水流经过水管不断散热而起到冷凝作用。
(完整word版)流体力学习题及答案-第五章

第五章 势流理论5-1流速为u 0=10m/s 沿正向的均匀流与位于原点的点涡叠加。
已知驻点位于(0,-5),试求: (1)点涡的强度;(2) (0,5)点的流速以及通过驻点的流线方程。
答:(1)求点涡的强度Γ:设点涡的强度为Γ,则均匀流的速度势和流函数分别为:x u 01=ϕ,y u 01=ψ;点涡的速度势和流函数为:xy arctg πϕ22Γ-=,r y x ln 2)ln(221222ππψΓ=+Γ=; 因此,流动的速度势和流函数为:θπθπϕϕϕ2cos 20021Γ-=Γ-=+=r u x y arctg x u , r y u y x y u ln 2sin )ln(202122021πθπψψψΓ+=+Γ+=+=;则速度分布为:2202y x yu y x u +⋅Γ+=∂∂=∂∂=πψϕ, 222yx x x y v +⋅Γ=∂∂-=∂∂=πψϕ; 由于)5,0(-为驻点,代入上式第一式中则得到:0)5(052220=-+-⋅Γ+πu , 整理得到:ππ100100==Γu 。
(2)求)5,0(点的速度:将π100=Γ代入到速度分布中,得到:222222050102100102y x y y x y y x y u u ++=+⋅+=+⋅Γ+=πππ,2222225021002y x x y x x y x x v +=+⋅=+⋅Γ=πππ; 将0=x 、5=y 代入上述速度分布函数,得到:201010505501022=+=+⨯+=u (m/s ),05005022=+⨯=v (m/s );(3)求通过)5,0(点的流线方程:由流函数的性质可知,流函数为常数时表示流线方程C =ψ,则流线方程为:C y x y u =+Γ+21220)ln(2π;将0=x 、5=y 代入,得到:5ln 5050)50ln(21005102122+=+⨯+⨯=ππC ;则过该点的流线方程为:5ln 5050)ln(2100102122+=++y x y ππ,整理得到:5ln 55)ln(52122+=++y x y5-2 平面势流由点源和点汇叠加而成,点源位于(-1,0),其流量为θ1=20m 3/s ,点汇位于(2,0)点,其流量为θ2=40m 3/s ,已知流体密度为ρ=1.8kg/m 3,流场中(0,0)点的压力为0,试求点(0,1)和(1,1)的流速和压力。
流体力学第五章习题答案
第五章习题答案选择题(单选题)5.1 速度v ,长度l ,重力加速度g 的无量纲集合是:(b )(a )lv g ;(b )v gl ;(c )l gv ;(d )2v gl。
5.2 速度v ,密度ρ,压强p 的无量纲集合是:(d )(a )p v ρ;(b )v p ρ;(c )2pv ρ;(d )2p v ρ。
5.3 速度v ,长度l ,时间t 的无量纲集合是:(d )(a )v lt ;(b )t vl ;(c )2l vt ;(d )lvt。
5.4 压强差p ,密度ρ,长度l ,流量Q 的无量纲集合是:(d )(a )2Qpl ρ;(b )2lpQ ρ;(c )plQρ;(d 。
5.5 进行水力模型实验,要实现明渠水流的动力相似,应选的相似准则是:(b )(a )雷诺准则;(b )弗劳德准则;(c )欧拉准则;(d )其他。
5.6 进行水力模型实验,要实现有压管流的动力相似,应选的相似准则是:(a )(a )雷诺准则;(b )弗劳德准则;(c )欧拉准则;(d )其他。
5.7 雷诺数的物理意义表示:(c )(a )粘滞力与重力之比;(b )重力与惯性力之比;(c )惯性力与粘滞力之比;(d )压力与粘滞力之比。
5.8 明渠水流模型实验,长度比尺为4,模型流量应为原型流量的:(c )(a )1/2;(b )1/4;(c )1/8;(d )1/32。
5.9 压力输水管模型实验,长度比尺为8,模型水管的流量应为原型输水管流量的:(c )(a )1/2;(b )1/4;(c )1/8;(d )1/16。
5.10 假设自由落体的下落距离s 与落体的质量m 、重力加速度g 及下落时间t 有关,试用瑞利法导出自由落体下落距离的关系式。
解: ∵s Km g t αβγ=[]s L =;[]m M =;[]2g T L -=;[]t T =∴有量纲关系:2L M TL T αββγ-=可得:0α=;1β=;2γ= ∴2s Kgt =答:自由落体下落距离的关系式为2s Kgt =。
《流体力学》徐正坦主编课后答案第五章
第五章习题简答5-1有一薄壁圆形孔口,直径d= 10mm ,水头H 为2m 。
现测得射流收缩断面的直径d c为8mm ,在32.8s 时间内,经孔口流出的水量为0.01m 3,试求该孔口的收缩系数ε,流量系数μ,流速系数φ及孔口局部损失系数ζ。
解: 64.010822=⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛==d d A A c c εs m d Q v /06.6008.08.32/01.04422=⨯⨯==ππ 62.097.064.006.0197.011197.028.9206.62222=⨯===-=-==⨯⨯==⇒=εϕμϕζϕϕgHvgH v5-2薄壁孔口出流,直径d=2cm ,水箱水位恒定H=2m ,试求:(1)孔口流量Q ;(2)此孔口外接圆柱形管嘴的流量Q n ;(3)管嘴收缩断面的真空高度。
题5-2图解:(1)孔口出流流量为s L s m gH A Q /219.1/10219.128.9202.0462.02332=⨯=⨯⨯⨯⨯⨯==πϕ(2)s L gH A Q n /612.128.9202.0482.022=⨯⨯⨯⨯⨯==πμ(3)真空高度:m H gpg p C Cv 48.1274.074.0=⨯==-=ρρ 5-3 水箱用隔板分为A 、B 两室,隔板上开一孔口,其直径d 1=4cm ,在B 室底部装有圆柱形外管嘴,其直径d 2=3cm 。
已知H=3m ,h 3=0.5m 试求:(1)h 1,h 2;(2)流出水箱的流量Q 。
题5-3图解:隔板孔口的流量 112gh A Q μ=圆柱形外管嘴的流量 ()()132222h H g A h h g A Q -=+=μμ由题意可得Q 1=Q 2,则()()1212122212111211303.082.004.062.022h h h H d h d h H g A gh A -⨯⨯=⨯⨯-=-=μμμμ解得m h 07.11=sL s m gh A Q mh h H h /56.3/1056.307.18.9204.0462.0243.15.007.1333211312=⨯=⨯⨯⨯⨯⨯==∴=--=--=∴-πμ5-4 有一平底空船,其船底面积Ω为8m 2,船舷高h 为0.5m ,船自重G 为9.8kN 。
工程流体力学第五章 思考题、练习题 - 副本
第五章 不可压缩流体一维层流流动思考题建立流体流动微分方程依据的是什么基本原理?有哪几个基本步骤导致流体流动的常见因素有哪些?流体流动有哪几种常见的边界条件?如何确定这些边界条件? 对缝隙流动、管内流动或降膜流动,关于切应力和速度的微分方程对牛顿流体和非牛顿流体均适用吗?为什么一、选择题1、圆管层流过流断面的流速分布为A 均匀分布;B 对数曲线分布;C 二次抛物线分布;D 三次抛物线分布。
2、两根相同直径的圆管,以同样的速度输送水和空气,不会出现____情况。
A 水管内为层流状态,气管内为湍流状态;B 水管、气管内都为层流状态;C 水管内为湍流状态,气管内为层流状态;D 水管、气管内都为湍流状态。
3、变直径管流,细断面直径为d 1,粗断面直径为d 2,122d d 粗断面雷诺数Re 2与细断面雷诺数Re 1的关系是:A Re 1=0.5Re 2B Re 1=Re 2C Re 1=1.5Re 2D Re 1=2Re 24、圆管层流,实测管轴线上的流速为4m/s,则断面平均流速为:A 4m/sB 3.2m/sC 2m/sD 2.5m/s5 圆管流动中过流断面上的切应力分布如图 中的哪一种?A 在过流断面上是常数B 管轴处是零,且与半径成正比C 管壁处为零 ,向管轴线性增大D 抛物线分布9.下列压强分布图中哪个是错误的?B10.粘性流体总水头线沿程的变化是( A ) 。
A. 沿程下降B. 沿程上升C. 保持水平D. 前三种情况都有可能。
1.液体粘度随温度的升高而___,气体粘度随温度的升高而___( A )。
A.减小,增大;B.增大,减小;C.减小,不变;D.减小,减小四、计算题(50分)30.(6分)飞机在10000m 高空(T=223.15K,p=0.264bar)以速度800km/h 飞行,燃烧室的进口扩压通道朝向前方,设空气在扩压通道中可逆压缩,试确定相对于扩压通道的来流马赫数和出口压力。
(空气的比热容为C p =1006J/(kg ·K),等熵指数为k=1.4,空气的气体常数R 为287J/(kg ·K))T 0=T ∞+v C p ∞=+⨯⨯23222231580010360021006/.()/() =247.69K M ∞=v a ∞∞=⨯⨯⨯=(/)...80010360014287223150743 P 0=p ∞11221+-⎡⎣⎢⎤⎦⎥∞-k M kk =0.26411412074038214141+-⨯⎡⎣⎢⎤⎦⎥=-.....bar31.(6分)一截面为圆形风道,风量为10000m 3/h ,最大允许平均流速为20m/s ,求:(1)此时风道内径为多少?(2)若设计内径应取50mm 的整倍数,这时设计内径为多少?(3)核算在设计内径时平均风速为多少?依连续方程(ρ=C )v 1A 1=v 2A 2=q v(1)v 1π412d q v = d 1=100004360020⨯⨯π=0.42m=420mm (2)设计内径应取450mm 为50mm 的9倍,且风速低于允许的20m/s(3) 在设计内径450mm 时,风速为 v q d m s v 2222441000036000451746==⨯⨯=ππ../ 32.(7分)离心式风机可采用如图所示的集流器来测量流量,已知风机入口侧管道直径d=400mm,U 形管读数h=100mmH 2O ,水与空气的密度分别为ρ水=1000kg/m 3,ρ空=1.2kg/m 3,忽略流动的能量损失,求空气的体积流量q v 。
李玉柱流体力学课后题答案 第五章
第五章 层流、紊流及其能量损失5—1 (1)某水管的直径d =100 mm ,通过流量Q =4 L/s ,水温T =20℃;(2)条件与以上相同,但管道中流过的是重燃油,其运动粘度6215010m /s ν-=⨯。
试判别以上两种情况下的流态。
解:(1) 200C 时,水的运动粘性系数ν=×10-6m 2/s ,24Qu d π= 水的雷诺数Re 为:-3-6244 4 L/s 10Re 5060020001.00710m /s 3.140.1m ud Q v v d π⨯⨯====>⨯⨯⨯,紊流(2) 石油:-3-6244 4 L/s 10Re 339.7200015010m /s 3.140.1mud Q v v d π⨯⨯====<⨯⨯⨯,层流 5—2 温度为0℃的空气,以4 m/s 的速度在直径为l00 mm 的圆管中流动,试确定其流态(空气的运动粘度为521.3710m /s ν-=⨯)。
若管中的流体换成运动粘度为621.79210m /s ν-=⨯的水,问水在管中呈何流态解:空气的雷诺数Re 为:-524 m/s 0.1m Re 2919720001.3710m /sud v ⨯===>⨯,紊流 水的雷诺数Re 为:-624 m/s 0.1mRe 223 21420001.79210m /sud v ⨯===>⨯,紊流 5—3 (1)一梯形断面排水沟,底宽0.5m ,边坡系数cot θ=(θ为坡角),水温为20℃,水深0.4m ,流速为0.1m /s ,试判别其流态;(2)如果水温保持不变,流速减小到多大时变为层流 ,解:200C 时,水的运动粘性系数ν=×10-6m 2/s 水力直径为(0.520.60.5)0.4/20.23m 0.50.722AR χ+⨯+⨯===+⨯4-620.1m/s 0.23mRe 2.24101.00710m /sR uRν⨯===⨯⨯,42.24102000⨯>,湍流 水流为层流时Re 500uRν≤=(明渠流),故63Re 500 1.00710 2.210m/s 0.23u R ν--⨯⨯≤==⨯5—4 由若干水管组装成的冷凝器,利用水流经过水管不断散热而起到冷凝作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P125 第五章习题5-1 流速为o u =10m/s 沿正向的均匀流与位于原点的点涡叠加。
已知驻点位于(0,5),试求(1)点涡的强度;(2)点(0,5)的流速;(3)通过驻点(0,-5)的流线方程。
均匀流与位于原点的点涡叠加后的速度势为ϕ。
ϕ=0v θcos r ⋅θπ20Γ- 其中0Γ为沿顺时针方向点涡涡在极坐标下:θθϕcos 0cos 00v v rv r =-=∂∂= r v r v πθθϕθ2sin 100Γ--=∂∂⋅=驻点为(0,5),则5,23==r πθ(1)0)23cos(0==πv v r052)23sin(00=⨯Γ--=ππθv v π100=Γ⇒ π1000=v 即点涡强强度π1000=Γ(2)点(0,5)的流速 5,2==r πθ代入θv v r ,)/(20101002100sin 0cos 000s m v r v v v v r -=--=--==⋅=ππππθθθ s m u v /20,0==⇒即 负号表示θ以逆时针方向为正(3)通过驻点(0,5)的流线方程均匀流与位于原点点涡叠加后的流函数ψ r r v ln 2sin 00πθψΓ+⋅⋅= 将(0,5)对应5,23==r πθ代入上ψ式得:5ln 50505ln 501-510+-=⋅+⨯⨯=)(驻点ψ即55ln 5055ln 5ln 505ln 5050ln 500=++=+-++-=+⋅ry r y r y ψ5-2平面势流由点源和点汇叠加而成,点源位于(-1,0),其流量为s m /2031=θ,点汇位于(2,0)点,其流量为s m /4032=θ,已知流体密度为3/8.1m kg =ρ,流场中(0,0)点的压力为0,试求点(0,1)和(1,1)的流速和压力。
解:平面势流点源和点汇构成的速度势为:222221222221222221)(2)(2)(2)(2)(ln 2)(ln 2y x x y m y x x y m v y x x x x m y x x x x m u y x x my x x m B A B B A A B A +-⋅-+-⋅=+--⋅-+--⋅=+--+-=ππππππϕ 因:2,1,/40,/20322311=-=====B A x x s m m s m m θθ则 22222222)2(220)1(10)2(220)1(110y x x y x y v y x x y x x u +--⋅-++⋅=+--⋅-+++⋅=ππππ(1)则点(0,1)的速度为:(2) )/(1522021101)20(1201)10(110)/(13522021101)20(20201)10(101022222222s m v s m u ππππππππππ=⋅-⋅=+-⋅-++⋅==⋅+⋅=+--⋅-+++⋅=因为全流场中任意一点满足伯努力方程的拉格朗日形式(p72,)即c z Pv =++ρ22 则(0,0),(0,1),(1,1)都满足上式,因0)0,0(=P )/(200)20(20200)10(101022)0,0()0,0(s m u v πππ=+--⋅-+++⋅==A (源) B(汇)则12)1()13(22)1,0(22)1,0()1,0(2)1,0()0,0()0,0(2)0,0(+++⇒++=++ρππρρP z P vz P v)/(17.192)1,0(m N P =⇒(2) (1,1)点 流速与压力)/(8212051101)21(1201)11(110)/(14212052101)21(21201)11(11102222)1,1(2222)1,1(s m v s m u ππππππππππ-=⋅-⋅=+-⋅-++⋅==-⋅-⋅=+--⋅-+++⋅=因:)/(97.101701226040012)8()14(2)20(222)1,1()1,1(2)1,1(22)1,1(222)1,1()1,1(2)1,1()0,0()0,0(2)0,0(m N P P P P z P v z P v =⇒=-=--+++=++=++ρπρππρπππρρ5-3直径为2m 的圆柱体在水下深度为H=10m 以平移速度0u 运动,试求(1)A 、B 、C 、D 四点的绝对压力 (2)若圆柱体运动的同时还受到本身轴线以角速度60r/min 转动,试决定驻点的位置以及B 、D 两点的速度和压力。
此时若水深增至100m ,求产生空泡时的速度(注:温度为c15时,水的饱和蒸汽压力为310332.2⨯N/2m 。
)等效于: 均匀流+偶极偶极强度:202a v M ⋅=πππ202,/10,12000=⋅⋅=⇒===a v M s m u v m au x均匀流与偶极叠加的速度势:)1(sin 1)1(cos cos 2cos cos 2cos 220220200ra v r v r a v r M v r v rM r v r +⋅-=∂∂⋅=-=⋅-⋅=∂∂=⋅+=θθϕθθπθϕθπθϕθ 代入r=a 的圆柱表面的速度分布为:{θθsin 2,00v v v r -==0=θ 0==C A v v πθ= :2πθ= 02v v B -=:πθ23=02v v D = 从无穷远流体流向:A Q →,列出伯努力方程:)(10994.11081.91010013.15350帕⨯=⨯⨯+⨯=+=hg P P Q ρ注:0P 取1标准大气压)/(104.24910494.210105.010994.121212123523520220m N v P P v P v P Q A A A Q ⨯=⨯=⨯⨯+⨯=+=+=+ρρρ若取0P 为一个工程大气压: Pa P 5010981.0⨯=则 )/(102.24623m N P A ⨯= (与课后答案一致,暂取0P 为一个工程大气压) gh P P B A ρ+='gR P P A B ρ-=⇒'(静止状态,液体静力学方程) A 、B 两点列伯努力方程B B B A A A gz v P v P gz ρρρρ++=++22212102,0,,0v v v R z z B A B A -====gRV P P B A ρρ+-+=20)2(21)/(104.361081.910200102.246181.9101041021102.24642123333323320m N gRv P P A B ⨯=⨯-⨯-⨯=⨯⨯-⨯⨯⨯-⨯=-⋅-=⇒ρρA 、D 列伯努力方程)/(101.561041021181.910102.246)2(21)2(212323332020m N v P gR P v P P gR A D D A ⨯=⨯⨯⨯-⨯⨯-⨯=-+=+=+ρρρρ)/(102.24623m N P P C A ⨯==(2)等效于绕圆柱有环量流动2020020)2(,1)/(260/260min /6022)(cos πππωπωθπθϕ=Γ⇒==⨯==⋅=ΓΓ-+=m a s rad r a r a r v速度分布:rr av r v ra v r v r πθθϕθϕθ2)1(sin 1)1(cos 0220220Γ-+-=∂∂⋅=-=∂∂= 圆柱表面r=a 上速度分布为:rv v v r πθθ2sin 2000Γ--==假设无穷远处0'0,v v P P ==由定常运动的伯努力方程的圆柱表面压力分布为: (质量力忽略不计)220'02121θρρv P v P +=+20020'02sin 22121⎥⎦⎤⎢⎣⎡Γ---+=a v v P P πθρρ其中)/(10962.11081.91010981.025350'0m N gH P P ⨯=⨯⨯+⨯=+=ρs m av v A /28.612)2(2sin 2200-=⋅-=Γ--=⇒=πππθπθsm v a v v D sm a v v C sm v a v v B C C B /72.1312)2()1(22sin 223:/28.62sin 20:/28.2612)2(122sin 22:2000002000=⨯--⋅⨯-=Γ--=⇒=-=Γ--=⇒==⨯-⋅⨯-=Γ--=⇒=πππθπθπθθπππθπθ 列A 、B 两点伯努力方程233232352220'028.61021181.91028.26102110102110962.1212121⨯⨯+⨯⨯-⨯⨯-⨯⨯+⨯=+--+=A B B v gR v v P P ρρρρ驻点位置:)314.0arcsin(314.0202sin 12)2(sin 1022sin 202sin 220000±=-=-=⨯-=⨯Γ-==Γ--=πθπθππθπθπθθa v av v当H 增加到100米,B v 速度>D v ,应B v 先产生气泡,其速为[][]sm a ac b b v v v v v v v v v v v gR v v v gH m N P v gR v P P B A A B B A A B /68.29)(3949657.1257.1224094957.125.10)281.9981332.2(57.125.12281.95.098145.081.95.0981332.22121212110332.2)/(10332.221212200202020202020202022********取正=⨯+±=-±-==--=++-+-++--⋅+=+⨯--⋅+=--+-+=⨯⨯=--+=ππππρρρρρρρρρ5-4写出下列流动的复势(1);sin ,cos 00ααU v U u ==(2)强度为m ,位于(a ,0)点的平面点源;(3)强度为Γ位于原点的点涡;(3)强度为M ,方向为α,合于原点的平面偶极(1)αααααααααααααψϕααψααϕi e z U i z U z U i z U iy x U i z U ix y U iy x U x U y U i y U x U i z w xv y u x U y U y U x U y v x u -⋅⋅=-⋅⋅=⋅⋅⋅-⋅⋅=+⋅⋅⋅-+⋅⋅=-⋅⋅++⋅⋅=⋅⋅-⋅⋅+⋅⋅+⋅⋅=+=⋅-⋅=⋅⋅-⋅⋅=⋅⋅+⋅⋅=⋅+⋅=000000000000000000)sin (cos sin cos )(sin )(cos )(sin )(cos )sin cos (sin cos )(sin cos sin cos(2)强度为m ,位于(a,0)点源的复势,只需求强度为m ,位于(0,0)点的复势源强 []zme r m e r m m i r m i z w md m rd v dr v r m dr r m rd v dr v v rmv v r m i i r r r r ln 2)ln(2ln ln 22ln 2)(22ln 220,22πππθππψϕθπθπθψππθϕππθθθθθ=⋅=+=+=+==⎰=⋅+-⎰==⎰=⋅+⎰===⋅=则合于(a ,0)的点源复势为)ln(2)(a z m z w az -==π(3)位于原点点涡复势---⋅Γ=⋅⋅Γ=+⋅Γ=⋅+-Γ=Γ+Γ-=+=Γ=Γ-=z i e r i i r i r i r i i z w r i ln 2)(ln 2)(ln 2)ln (2)ln 2(2)(ln 2,2ππθπθππθπψϕπψθπϕθ 位于(a,0)点涡的复势为:)ln(2)(a z iz w a z -⋅Γ==π(4)强度为M ,方向为α,位于原点的平面偶极0220tan x yy x δδαδδδε=+=)点汇位于()点源现在位于(汇位于原点汇的速度势:源位于原点源的速度势:000000,x ,,x )(ln 2)(ln 2y y x y r mr mδδπψπϕ++-------=--------=求解推导如下:点源位于(00,y x ) 点汇位于),(0000y y x x δδ++ 则源和汇叠加流场的速度势为:[][][][][]2020002020200200002002002020)()(ln ,,,f )()(ln )(()((ln 4lim )(()((ln 4)()(ln 400y y x x y y x x y y x x y y y x x x m y y y x x x my y x x m y x -+-=-+--+-++--=+-++---+-=→→)(令偶极的速度势为,δεδδπϕδδππϕδδ汇),000y y x δ+可知上式就是),,,(00y y x x f 在δε方向上的方向导数 它等于:ααεsin cos 00⋅∂∂+⋅∂∂=∂∂y f x f f 则:)()(tan arc 22tanarc 22sin sin 2cos cos 2sin sin 12cos cos 12sin )()()1()(22cos )()()1()(24)sin cos (40000002020020200x x x y y y MM x x y y MM rM r M r M r M y y x x y y My y x x x x M yfx f M δδπθπψπθπψαθπαθπαθπαθπαπαπααπϕ+-+--=-=--==⋅+⋅=⋅⋅-⋅-⋅⋅-⋅-=⋅-+--⋅-⋅-⋅-+--⋅-⋅-=∂∂+∂∂-=汇的流函数为:同样:源的流函数为:则源和汇叠加的流场的速度势为:求导),对方向上的方向导数(注在令0000000000000000000000000),,,()arctan()()(arctan 2lim )arctan()()(arctan 2lim )()(arctan )arctan(2limy x y y x x g x x y y x x x y y y M x x y y x x x y y y m x x x y y y x x y y mδεδεδδπδεδδπεδδπψδεδεδε⎥⎦⎤⎢⎣⎡---+-+--=⎥⎦⎤⎢⎣⎡---+-+-⋅-=⎥⎦⎤⎢⎣⎡+-+----=→→→θπαθπαθαθπααπϕθθααπϕco sin 2sin cos 2sin cos cos sin 2sin cos 2cos 1)()()(111arctansin )()()()()(11arctan sin cos 200020202002000000200202020200200000000⋅-⋅=⎥⎦⎤⎢⎣⎡⋅-⋅-=⎥⎦⎤⎢⎣⎡⋅∂∂+⋅∂∂-=-=--⋅-+--=--⋅⎪⎪⎭⎫ ⎝⎛--+=∂⎥⎦⎤⎢⎣⎡--∂=∂∂=--⋅-+--=--⋅⎪⎪⎭⎫ ⎝⎛--+=∂⎥⎦⎤⎢⎣⎡--∂=∂∂⎥⎦⎤⎢⎣⎡⋅∂∂+⋅∂∂-=r M r M r r M y g x g M r x x y y x x x x x x x x y y y x x y y y g r x x y y y y x x x x x x y y x x y y x x x y y x g y gx g M 则方向为α的平面偶极的复势为:[][][]z e M e r e M i r e M i r e M e i r M e r M i rM i r M r M r M i r M r M i z w i i i i i i i ⋅⋅=⋅⋅=⋅+⋅=⋅-⋅=-⋅⋅+⋅⋅=⋅-⋅+⋅+⋅=⎥⎦⎤⎢⎣⎡⋅⋅-⋅⋅+⋅⋅+⋅⋅=+=ππθθπθθπθπθπααθπααθπαθπαθπαθπαθπψϕαθααααα22sin cos 12sin cos 2)(sin 2cos 2cos sin sin 2sin cos cos 2cos sin 2sin cos 2sin sin 2cos cos 2)(5-5设在A (a,0)点放置一强度为2π的平面点源,x=0是一固壁面,试求(1)固壁上流体的速度分布及速度达到最大值的位置,(2)固壁上的压力分布,设无穷远处压力为∞P ;(3)若点源源强m=m(t),其中t 为时间变量,求壁面上的压力分布对应的复势为:x222222''121111)()ln()ln()ln(2)ln(2)()()()ln()ln(2)(y a iy y a iy a y a iy a a iy a iy V iyz a z a z dz z dw V a z a z a z ma z m z f z f z w a z a z mz w +-=+-++--=++-==++-==++-=++-=-+=-=-=壁面处:映像据奇点映像法:平壁面πππ(1)aa a V V a y a a y y a ya y a y y y a y V yVV y a yV u 122max ,0a 00)(22)(22)(202,02222222222222±=±=±=-±=⇒=+-=+⋅-+=∂∂=∂∂⇒----------⎩⎨⎧+==,则代入当)),(,点为(即速度达到最大值对立达最大值当固壁上流体速度分布(2)固壁上压力分布`)y (y 2)y (y 421y y 221v 21210,,211)ln()ln()(222222222222222+-=+-=++=+=+=⇒∞→∞→=+=++-==⇒-+-=∞∞∞∞∞a P P a P P a P P P v P v y z o u y a yv az a z dz dw V a z a z z w ρρρρ壁壁壁)(时壁面所受的合力为下:据普拉休斯合力公式:[][][]πρπρπρπϕπρρεπρρρ-==-=-=⋅==-===+-⋅-==-=--==+∞→∞-==∑⎰∑∑⎰⎰⎰⎰⎰⎰⎰→→∞+∞∞+∞∞+∞P P P i i z z R s i dz a z z i P a a a z a z z a z z z R s z z z R s dx x R P dxx R dz a z z dz a z z dz az z i dz dz dw i P z x c dz dz dw i P k c a z a z k k k c c c c 则为实部,无虚部因则为奇),(复变函数的留级中无穷积分公式的积分,参考复变函数属于其中变化从的壁面,为22),(Re i 22)2(2144lim )()(4)(lim ),(Re ,),(Re i 2)(164)()2()2()2(2)(20,)(2222222222---22222222222(3)222222222222222222)()(2121)(44)(22)(,022)(112)()ln(2)()ln(2)()(y a y t m P V P P y a y t m V y a yt m v u y a iy t m a z a z t m dz dw V a z t m a z t m z w +-=-=+=+==+-⋅=⎥⎦⎤⎢⎣⎡++-==++-=∞∞πρρππππππ5-6已知复势为z i zz z w ln 382)(++=,求(1)流场的速度分布及绕圆周1022=+y x 的环量;(2)验证有一条流线与422=+y x 的圆柱表面重合,并用卜拉休斯公式求圆柱体的作用力(1)[]zi zz z w y x xy x xy v y x y y x y x u y x xiy x i xy y x y y x y x y x iy x i y x xyi y x y x iy x i y x y x xyi y x iy x i xyi y x z iy x i iy x z V iyx z z i z z dz z dw V zi zz z w ln 382)(3)(16,3)()(823)(163)()(82)(3)(16)(82)(34)(2)(823283)(838)(ln 382)(22222222222222222222222222222222222222222222++=+-+-=+⎩⎨⎧++--=+++⋅++++--=+-++---=+-++----=+++--=+++-=+=+-==++=则令为均匀流,偶极,点涡叠加后的复势πππππππ610632ln 3ln 2)(w 168282)(w /22)(2232001=Γ=+=Γ⇒=Γ⇒=Γ==⇒=⇒===⇒==的环量为则绕圆周点涡复势:偶极复势:均匀流复势:y x z i z i z M Mz z M z sm v z z v z w(2)422216,2,0)1(cos 02)(cos 2220220r 020=+⇒±=⇒±=⇒=⋅==⇒=-=∂∂=∂∂Γ-+==y x r a M a v M a r ra v r rr a r v a 的圆周物面为半径为又因为则将速度势代入物面条件ππθϕϕθπθϕ (3)πρπρπρπρπππρρ12,01212)24(2241222)4812329644()382()382(2)(21322422222==⇒+=⇒⋅=⋅-=-=-=⋅=⋅=-+--+=+-+-==-⎰⎰⎰⎰Y X iY X P i P ii P i i c i dz z iz i z z z dz z i z dz zi z i dz dz dw i P C C C 因:5-7如题5-3图所示,设直径为2m 的圆柱体在水下深度为H=10m 的水平面上以速度s m u /100=做匀速直线运动,(1)试写出流动的绝对速度势,牵连速度势,相对速度势及对立的单位速度势;(2)求出圆柱体表面上A 、B 、C 、D 及θ=45、135六点的绝对速度解:圆柱直航相当于均匀流与偶极叠加{2202202202202020020200200200sin )sin (1,cos cos cos )2(cos ,cos cos cos cos cos cos cos ,2cos 2cos r a v r a v r v r a v r a v r v r a v ra r ra r r a v r u ra v r u a v M r M r u r e e e θθθθϕθϕθϕθϕθθϕθϕϕϕθϕθθϕπθπθϕθ⋅-=⋅-=⋅-=-⋅=∂∂=⇒⋅=⋅=-=⋅+=⋅=+=-=⋅+==⋅+=****单位速度势:绝对速度势:牵连速度势:相对速度势: 0000000022,2213522,2245,01,23:0,1,0:,01,2:0,1,:v v v v v v v v v v v r D v v v r C v v v r B v v v r A r r r r r r -==⇒=-=-=⇒===⇒===-=⇒==-==⇒====⇒==θθθθθθθθπθθπθπθ5-8若一半径为0r 的圆球在静水中从速度为零加速到0u ,试求需对其做多少功B203020303030211030112)2(31)3234(2134)(2132,21u r u r r w r m u m w T T r mv T u πρρρπρπρπλρπλ球水水球球+=+==+==-==5-9无限深液体中有一长为L ,半径为R 的垂直圆柱体,设其轴心被长度为l 的绳子系住,它一方面以角速度Ω在水平面内绕绳子固定端公转,另一方面又以另一角速度w 绕自身轴线自转,已知圆柱体重量为G ,假定R l >>,试求绳子的拉力同向时为负,反向为正与)(流动此时圆柱相当于有环量自转圆柱可以认为均匀流作用于则公转切向加速度自转:由于方向相反与力绳子受到反向力,离心)()(公转向心力:长圆柱体的附加质量:加质量:公转:单位圆柱体的附水水物环公总水环环水物水物w L l R w L l R F F F R w L l R w F L l L v F l v R l F F Ll R l L R L R l F LR R Ω⋅⋅⋅⋅Ω±⋅Ω⋅+=+=⋅=Γ⋅⋅⋅⋅Ω=⇒⋅Γ⋅Ω=⋅Γ⋅⋅=Ω=>>⋅Ω⋅+=Ω⋅+⋅=Ω+=⋅==222202000'22222211211211222)(m L πρπρρππρρρπρρπρπρλρπλρπλ5-10设有一半径为R 的二元圆柱体在液体中以水平分速度)/(0s m t U u =运动,设t=0时,它静止于坐标原点,液体密度为ρ,圆柱体密度为λ,试求出流体作用于圆柱体上的推力及t=2s 时圆柱体的位置w0200220002112022)2(2121212221)()()(U dl U dl U U dl v dl dt dv v T U U t v s t U a dtdv x dl x v T U R t i m F =⇒⋅=⋅=⇒⋅===⋅==⋅==⋅==⋅⋅+=+=λλρπλλπσρλ时,tU u ⋅=0。
