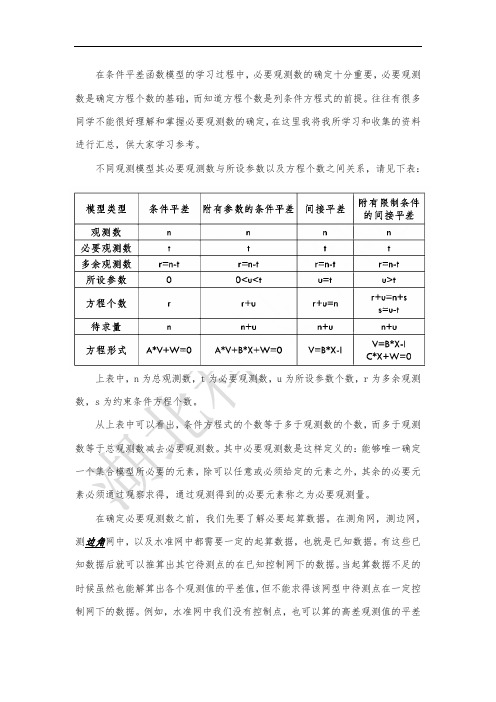
相关观测值条件平差

N[i] = 0.0;
double *M = new double[r*n];//临时数组M,存放系数阵与权逆阵的乘积B*Q for (int i = 0; i < r*n; i++)
M[i] = 0.0;
//计算M for (int i = 0; i < r; i++)
for (int j = 0; j < n; j++) for (int k = 0; k < n; k++) M[i*n + j] += B[i*n + k] * Q[ij(k, j)];
double *a0 = new double[n]; for (int k = 0; k < n; k++)
1
Jack 专属
{ double a00 = a[0]; if (a00 + 1.0 == 1.0) { delete[]a0; return false; } for (int i = 1; i < n; i++) { double ai0 = a[i*(i + 1) / 2];
double ki = 0.0; for (int j = 0; j < r; j++)
ki -= N[ij(i, j)] * W[j]; K[i] = ki; pvv -= ki*W[i];
}
//计算V for (int i = 0; i < n; i++) {
double vi = 0.0; for (int j = 0; j < r; j++)
2
Jack 专属
{ fprintf(fp, fmt, A[i*t + j]);
} fprintf(fp, fmt, b[i]); } }
///////////////////////////////////////////////////// //向文件输出数组 void PrintM(FILE *fp, double A[], int size, int t, char*fmt, char*title, bool IsLabel) {
//计算联系数法方程系数阵N=M*B' int index = 0; for (int i = 0; i < r; i++)
for (int j = 0; j <= i; j++) { for (int k = 0; k < n; k++)
N[index] += M[i*n + k] * B[j*n + k]; index++; }
//法矩阵求逆 if (inverse(N, r) == false) {
delete[]N; delete[]M; return -1.0;
}
double *K = new double[r];
4
Jack 专属
double pvv = 0.0; for (int i = 0; i < r; i++) {
Jack 专属
/////////////////////////////////////////////////////////
//
基于 Visual Studio2013 编写
// 3.4 相关观测值条件平差.cpp : 定义控制台应用程序的入口点。
//
#include "stdafx.h" #include <stdarg.h> #include <stdio.h> #include <iostream> using namespace std; /////////////////////////////////////////// //对称矩阵的下标计算 int ij(int i, int j) {
fclose(fp);
}
int _tmain(int argc, _TCHAR* argv[]) {
Co_Condition_Example(); cout << "程序输出成功！！！" << endl; cin.get(); cin.get(); return 0; }
Data 数据： 63
0.53 0.58 0.23 0.08 0.03 0.01 -6.00 0.01 0.02 0.04 0.11 0.29 -0.24 9.00 0.41 0.24 0.31 -0.31 -0.24 -0.41
PrintM(fp, V, n, 1, "%6.3lf", "观测值的改正数（V)", true);
fprintf(fp, "单位权中误差：μ=%.3lf", m); double F[] = { 1.9, -0.27, 0.27, 0.11, 0.04, 0.01 }; double q = Calculate_q(Q, F, n); fprintf(fp, "\n函数的中误差：m=%.3lf", m*sqrt(q));
fprintf(fp, fmt, A[i]); } fprintf(fp, "\n"); }
////////////////////////////////////////////////////////// // 权倒数计算函数 double Calculate_q(double *Q, double *F, int t) {
fscanf_s(fp, "%lf", Q + i); } fclose(fp);
fopen_s(&fp, "result.txt", "w");
6
Jack 专属
PrintEquation(fp, B, W, r, n, "%6.2lf", "条件方程"); double m = Co_Condition(n, r, B, W, Q, V);
int n, r;
FILE *fp; fopen_s(&fp, "data.txt", "r"); if (fp == NULL) {
MyBreak("数据文件打不开"); return; } fscanf_s(fp, "%d%d", &n, &r);
double *B = new double[r*n]; double *W = new double[r]; double *Q = new double[n*(n + 1) / 2]; double *V = new double[n];
double q = 0.0; for (int i = 0; i < t; i++)
for (int j = 0; j < t; j++) q += Q[ij(i, j)] * F[i] * F[j];
return q;
} /////////////////////////////////////////////////////////
if (title) fprintf(fp, "\n %s: ", title);
int j = 0; for (int i = 0; i < size; i++) {
if (i%t == 0) {
j++; if (IsLabel)
fprintf(fp, "\n%3d", j); else
fprintf(fp, "\n"); }
vi += M[j*n + i] * K[j]; V[i] = vi; }
//计算QX index = 0; for (int i = 0; i < n; i++)
for (int j = 0; j <= i; j++) { for (int k = 0; k < r; k++)
for (int s = 0; s < r; s++) Q[index] -= M[k*n + i] * N[ij(k, s)] * M[s*n + j];
#endif//VC_EXTRALEN
} //////////////////////////////////////////////////////// /////////////////////////////////////////////// // 对称正定矩阵求逆（仅存下三角元素） bool inverse(double a[], int n) {
6.00
10.0
//By Jack 7
-6.0 10.5 1.0 -4.5 6.5 0.0 0.5 -4.5 10.0 0.0 0.0 1.0 -4.5 6.0 0.0 0.0 0.0 0.5 -3.0 5.0
Jack 专属
8
char buffer[256]; va_list argptr; va_start(argptr, fmt); vsprintf_s(buffer, fmt, argptr); va_end(argptr);
#ifdef VC_EXTRALEN AfxMessageBox(buffer);
#else printf(buffer); getchar();
} } for (int i = 1; i < n; i++) {