北京大学1991年有机考研题
北京大学物理化学1991(含结构化学)真题

北京大学1991年研究生入学考试试题考试科目:物理化学(含结构化学) 考试时间:2月3日上午招生专业: 研究方向:指导教师:试 题:单独考试者不答带“*”号的题答案一律写在答案纸上,在试题纸上答题无效物理化学部分(60分)(一)化学热力学(26分)1.设氢气遵守下列物态方程PV m =RT +αP 其中α=1.481×10-5m 3mol -1(a )请证明氢气的内能只是温度的函数;(b )请导出两个状态(T ,P 1)与(T ,P 2)的逸度比公式;(c )假设氢气在P θ为理想气体,求氢气在300K ,20P θ的逸度。
2.HgO 的两种晶型在298K 的热力学数据如下:1m f mol kJ /H -θ⋅∆1m mol K J /S -θ⋅⋅1mf mol kJ /G -θ⋅∆HgO (c ,红)-90.7172.0-58.53HgO (c ,黄)-90.2173.0-58.40(a )通过计算结果,判断298K ,101.325kPa 下哪种HgO 晶型稳定?(b )在101.325kPa 下,请估算稳定晶型在何温度下开始变为不稳定?3.Mg 和Ni 的正常熔点分别是924K 和1725K ,它们可生成两种化合物MgNi 2和Mg 2Ni 。
前者的正常熔点为1418K ,后者于1043K 分解为含38%(质量%,下同)Ni 的液相与MgNi 2固体。
体系有两个低共熔点,其温度和组成分别为783K ,23%Ni 及1353K ,89%Ni 。
各个固体之间都完全不互溶。
请据上述事实绘出该体系的等压相图。
Mg 与Ni 的摩尔质量分别为24.312gmol -1与58.71gmol -1(二)统计热力学(8分)1.设双原子分子的振动是简谐振动,请论证任何双原子分子的理想气体,在T =θv 时分子占据振动量子数v 的能级上的几率都相等,并求出占据第一振动激发能级的几率。
(θv 为振动特征温度)2.F 2分子的平衡核间距离r =1.418×10-10m ,F 原子的摩尔质量M =0.0189984kgmol -1。
北京大学1995年研究生入学考试试题
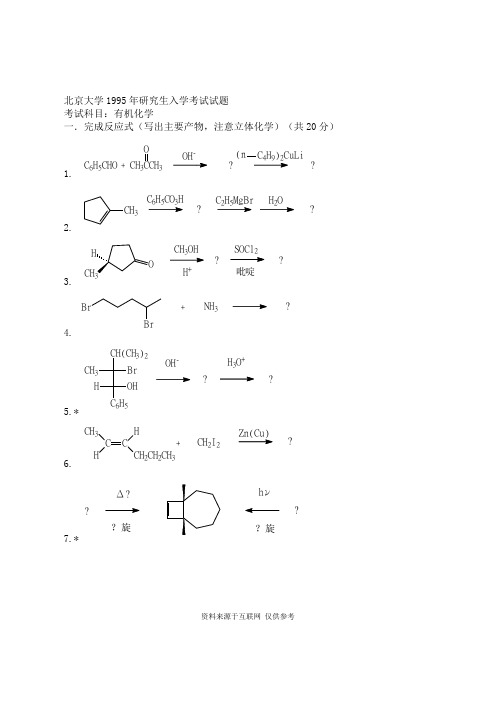
北京大学1995年研究生入学考试试题考试科目:有机化学一.完成反应式(写出主要产物,注意立体化学)(共20分)1. C6H5CHO CH33O+-(n C H)CuLi??2.C H CO H??C H MgBr H OCH33.?? CH3OHH+SOCl2吡啶4.Br NH3+?5.*CH(CH3)2BrCH3OHHC6H5OH-H3O+??6.C CHCH2CH2CH3HCH3+CH2I2?7.*?旋???旋Δ?νh资料来源于互联网仅供参考资料来源于互联网 仅供参考8.COOH NH 2??RONOCH 2Cl 2,Δ9.OO CO 2EtOEtONa?10. CH 322CH 3NBSKOH EtOH???二.用苯、甲苯、丙二酸酯、乙酰乙酸酯及不超过四个碳的有机原料合成下列化合物(共30分)1. 2.* 3.C CHCH 2CH 2CH 2CHO HCH 3CH 2PhPhCO 2EtOO4. 5.COOHCOOH三.写出下列反应机理(12分)1.CNH 2O +Br 2CH 3ONa CH 3OHNHCOCH 3O2. *资料来源于互联网 仅供参考OHEtOH 3O +O四.推测结构(共12分)。
1. 化合物(A )C 7H 12,在KMnO 4-H 2O 中回流。
反应液中只有O;(A )与HCl 反应得(B ),(B )在EtONa-EtOH 中反应得(C ),(C )使Br 2褪色生成(D ),(D )用EtONa-EtOH 处理得(E ), (E )用KMnO 4-H 2O 回流得HO 2CCH 2CH 2CO 2H和CH 32HO;(C )用O 3氧化后还原水解得CH 32CH 2CH 2CH 2CHOO。
请写出(A )-(E )的构造式。
2. 一分子式为C 6H 10O 2的化合物,其IR 的特征吸收峰(cm -1)为:1720(强),1650(中强),1190(强);1HNMR 谱(δ值,ppm):1.30(3H ,多重峰,J=6.9Hz),2.11(3H ,二重峰,J=6.0Hz),4.12(2H ,四重峰,J=6.9Hz),5.80(1H ,二重峰,J=18Hz),6.65(1H ,八重峰,J 1=18Hz ,J 2=6.0Hz)。
北师大1991-2014年硕士研究生入学考试细胞生物学真题

一、名词解释(每题4分,共40分)1、着丝点与着丝粒2、核层3、多线染色体4、cdc2(cell division cycle gene 2)5、受体介导的内吞作用6、蛋白印迹法(western blotting)7、G蛋白8、同源盒9、原位杂交10、 原癌基因二、问答题(共40分)1简述细胞连接的几种类型及其功能。
(10分)2简述微管、微丝组装的动力学不稳定模型。
(8分)3试述染色体包装的拌环结构模型(8分)4从细胞增殖的角度,试举例说明在高等动物机体内有几种细胞类群?举例说明鉴别细胞群体中各个不同周期时相细胞的方法 。
(14分)三、人体及动物生理试题(20分)现在已经不考了,没有参考价值,故没有打上。
一、名词解释(每题3分,共30分)1、胞内体2、信号肽与导肽3、跨细胞转运4、微管组织中心5、踏车行为6、核纤层7、驱动蛋白8、成虫盘9、桥粒与半桥粒10、周期素二、问答题(每题10分,共50分)1膜离子通道的类型及其调节机制2糖蛋白的加工部位及其转运3细胞有丝分裂过程中染色体的运动及其机理4以果蝇举例说明动物体节分化的基因调节5核仁组成结构与功能的分子学基础三、人体及动物生理试题(20分)现在已经不考了,没有参考价值,故没有打上。
一、名词解释(每题3分,共30分)1、信号识别蛋白和停泊蛋白2、微体(microbody)和微粒体(microsome)3、自我剪接4、杂交瘤技术5、基因调节蛋白6、 管家基因和奢侈基因7、间隙联结8、DNA复制子9、免疫印迹10、 G蛋白二、问答题(每题10分,共50分)1细胞质膜的主要功能2试述鉴别动物细胞各周期时相群体的方法3 试述非肌肉细胞中肌球蛋白和肌动蛋白相互作用的调节机制4 如何用实验证明细胞被决定5甾类激素调节基因表达的机制三、人体及动物生理试题(20分)现在已经不考了,没有参考价值,故没有打上。
一、名词解释(每题4分)1、荧光原位杂交2、 内含子、外显子、原初转录体的关系3、southwestern (blotting )4、编程性细胞死亡5、中心体6、受体介导的胞饮7、小核糖核蛋白颗粒(snRNPs)8、同源异型突变9、联会复合体10、转基因动物二、问答题(每题10分)1试述高尔基体对蛋白质的加工及分选功能2粘着斑的结构与功能3 细胞周期中G1至S期、G2至M期调控事件 4亲脂类和肽类外信号分子细胞信号传导的异同 三、人体及动物生理试题(20分)现在已经不考了,没有参考价值,故没有打上一、名词解释(每题4分)1、细胞粘附分子2、 钙调素3、离子通道4、 Rb和p53蛋白5、限制点6、分子伴娘7、细胞因子8、细胞被9、胚胎诱导10、 PKC和PKA二、问答题(每题10分)1蛋白质磷酸化和去磷酸化在分子水平上对细胞周期运行的调节作用(举例说明)。
北大有机题库c.doc

完成下列转变: HC ≡CHCH 3C ≡C ─D0091 比较CH 3─CH 2CH 3(I), CH 3─CH =CH 2(II), CH 3─C ≡CH(III)三种化合物的C ─C 单键键长次序为: (A) I>II>III (B) III>II>I(C) II>I>III (D) III>I>II 0093比较CH 4(I),NH 3(II),CH 3C ≡CH(III),H 2O(IV)四种化合物中氢原子的酸性大小: (A) I>II>III>IV (B) III>IV>II>I(C) I>III>IV>II (D) IV>III>II>I0094丙炔与H 2O 在硫酸汞催化作用下生成的主要产物是:0098下列哪一种化合物能与氯化亚铜氨溶液作用产生红色沉淀?0099 2-戊炔 顺-2-戊烯应采用下列哪一种反应条件?(A) H 2,Pd/BaSO 4,喹啉 (B) Na,液氨(C) B 2H 6 (D) H 2,Ni0101 产物为:0102 产物为:(A) CH 3CH 2CHO (B) CH 3COCH 3(C) CH 3CHCH 2OH (C) CH 3CHCHO (A) CH 3CH (C)CHCH 3(B) CH 3CH 2C (D) CH 3CH CH CH CH CH 2CH CH 2 CH 3CH CHCH (OH)C CH +H 2Lindlar(A) CH 3CH 2CH 2CH(OH)C (C) CH 3CH 2CH 2CH(OH)CH 2CH 3CH (B) CH 3CH (D) CH 3CH 2CH 2CH(OH)CH CH 2CHCH(OH)CHCH 2 CH 3C CCH 2CH 2CH 2C CCH 3Na (A) CH 3CH 2CH 2CH 2CH 2CH 2CH 2CH 2CH 3(B)C C H CH 3(CH 2)3H C H C CH 3H(C)C C H CH 3H (CH 2)3C H C H CH 3(D)C C H CH 3H (CH 2)3C H C HCH 3已知RC ≡CH + NaNH 2 ──> RC ≡CNa + NH 3,炔钠加水又能恢复成炔烃,RC ≡CNa + H 2O ──> RC ≡CH + NaOH,据此可推测酸性大小为:(A) NH 3>RC ≡CH>H 2O (B) H 2O>RC ≡CH>NH 3(C) H 2O>NH 3>RC ≡CH (D) HN 3>H 2O>RC ≡CH0105制造维尼纶的原料醋酸乙烯酯由下式合成, 这种加成反应属于:(A) 亲电加成反应 (B) 亲核加成反应(B) (C) 自由基加成 (D) 协同加成0106炔烃经臭氧化可得到什么产物?(A) 过氧化物 (B) 醛或酮 (C) 环氧化物 (D) 羧酸0108区别丙烯、丙炔、环丙烷时鉴别丙炔最好的办法是采用:(A) Br 2,CCl 4 (B) KMnO 4,H +(C) 臭氧化 (D) Cu 2Cl 2,NH 3溶液0109从庚烷、1-庚炔、1,3-己二烯中区别出1-庚炔最简明的办法是采用:(A) Br 2 + CCl 4 (B) Pd + H 2(C) KMnO 4,H + (D) AgNO 3,NH 3溶液1307写出下列反应的主要有机产物或所需之原料和试剂(如有立体化学问题请注明)。
1991年硕士学位研究生入学考试试题

1991年硕士学位研究生入学考试试题(生物化学)一.填空(20分)1.1.萜类化合物结构上的特点是,都具有。
2.2.一碳单位次甲基的结构式为,亚甲基的结构式为。
3.3.构成蛋白质的酸性氨基酸有;碱性氨基酸有(氨基酸以英文缩写符号表示)。
4.4.构成生物膜的主要成分是。
5.5.辅酶Ⅰ的中文全名是,辅酶Ⅱ的中文全名是。
6.6.蛋白质的生物合成过程大致可以分成四个阶段,即。
7.7.α—酮酸可以经过两种途径生成氨基酸,即。
8.8.脂肪酸的β—氧化作用,包括五个循环的反应,即9.9.TCA循环的中间产物中属于羧基酸的有等;属于不饱和酸的有等;属于酮酸的有等。
10.10.食品防腐剂安息香酸钠的结构式为。
11.11.稳定蛋白质α—螺旋的次级键是和之间的氢键。
12.12.写出下列生化名词缩写的中文名称:Cyt c,cAMP,ψ,Tyr,FADH2,Gua。
二.改错(60分):请对下列叙述中的错处作简要的修正和说明,但是不能仅答以“不”或“错”。
1.1.葡萄糖,麦芽糖,蔗糖,乳糖都分别可以用费林试剂法直接测定其含量。
2.2.淀粉分子中连接葡萄糖单位的是β—1,4-糖苷键,而纤维素分子中连接葡萄糖单位的是α—1,4-糖苷键。
3.3.一克脂肪被完全皂化所需要的氢氧化钠的克数,称为皂化价。
4.4.迄今为止,所有已发现的生物催化剂——酶,都是以蛋白质为主要成分构成的。
5.5.凯氏定氮法中,样品在“消化”时,加入硫酸铜和硫酸钾的作用是为了提高反应的沸点。
6.6.蛋白质的含氮量在6.25%左右;对于核酸样品来讲,每含一克磷约相当于9克核酸。
7.7.蛋白质的最大吸收波长在260nm左右;而核酸溶液的最大吸收波长在280唉左右。
8.8.自然界的DNA都具有双螺旋结构,而RNA都具有单链结构,所以,DNA有增色效应,而RNA没有增色效应。
9.9.DNA用酶法水解可以得到四种脱氧核苷酸,即5’-dAMP,5’-dGMP,5’-dCMP,5’-dUMP,而RNA被碱解成5’-AMP,5’-GMP,5’-CMP,5’-TMP。
北大古代文学考研真题整理

北京大学古代文学历年考研试题北京大学1997年古代文学考研试题一,名词解释两都赋与二京赋明清文学短篇小说狭邪小说雷锋塔传奇二,论述1,屈原与老子作品艺术特色比较2,南唐五代词对北宋词的影响北京大学1997年古代文学专业基础考研试题(1)评价钟嵘《诗品》(2)五四文学革命的实绩(3)评价朦胧诗(4)试论汉初的“文景之治”与“休养生息”政策北京大学1998年古代文学专业考研试题一,名词解释郊寒岛瘦、温李班马常州词派元曲选二,论述a,黄庭坚诗论及其创作艺术成就b,大小谢山水诗成就及地位c,《三》《水》人物形象塑造的艺术成就d,《诗经》《离骚》比兴手法异同北京大学1998年古代文学专业基础考研试题一,名词解释神韵说甘露之变词源新旧党争二,论述a,评论汉武帝b,从“诗言志”到“诗缘情”c,评述曹禺,闻一多的创作成就北京大学1999年古代文学考研试题一,名词解释(5/30)1,二南2,吴声西曲3,《诗式》4,神魔小说5,花部与雅部6,《雷锋塔传奇》二,论述1,简论《论语》《孟子》《庄子》《韩非子》散文的不同风格2,陈子昂说:“汉魏风骨,晋宋莫传”试结合诗歌发展史加以评论。
3,论辛弃疾词的成就及其对南宋词坛的影响3,对比分析《儒林外史》中杜少卿与〈红楼梦〉中贾宝玉的形象。
北京大学1999年古代文学专业基础考研试题一,论述1,简评白居易的诗歌理论。
2,简述从汉代到唐代选举制度的变迁。
3,为什么鲁迅把自己“五四”时期的创作称为“遵命文学”?试结合具体作品加以分析。
4,试分析汪曾琪小说创作的主要特点。
二,名词解释1,淝水之战2,陈桥兵变3,〈艺概〉4,〈文学改良刍议〉北京大学2000年古代文学考研试题一、名词解释(10/40)1、《诗经》六义(六文)。
2、六朝志怪小说的特点,举出三部代表作。
3、谈谈宋词中的“易安体”。
4、“临川派”与“吴江派”戏曲理论之对立(汤显祖与沈颢在戏剧创作上有何不同主张)。
二、标点,并解释下加横线的词语(10分)三、论述题(选做两题,25/50)1、《楚辞》与《汉赋》的联系。
(完整word版)(整理)北京大学有机化学研究生入学考试试题.
精品文档精品文档北京大学研究生入学考试试题试题:(一)写出下列各反应的最主要的一个产物(注意:只写一个,多写扣分)(20分)(1)CCH3CH2+.H O2.NaOH??B2H6(2)CH3CH2CH2C CHKOH,C H OH?Δ(3)CH2NH2OHHNO?(4)CH2CH2CH2COOCH3CHCH2CH2OHCH3CH3C5H11ONa+?回流,分馏异-(5)NH2NaHSO3H2OΔ?(6)?顺,顺,顺-CH3CH CHCH CHCH CHCH3(7)CH3COCH2COOC2H5+NHNH2Δ?(8)CH3CHCH2CH2CH3N+(CH3)3 OH-Δ?(9)NH2NH2+CH3Δ?精品文档精品文档(10)(浓)CF 3++?H 2SO 4HNO 3(浓)(三)用分子含不多于五个碳原子的开链化合物或不含取代基的芳环化合物作为起始物,和必要的无机试剂,合成以下的化合物。
(25分)(1)HOOCCH 2CHCH 2CH 2COOH COOH(2)CH 3OOCH 3(3)ClBr(5)NNO 2(4)(CH 3)2NNN北京大学研究生入学考试试题(一)完成下列反应(30分,注意:只写一个最主要的产物,多写扣分) (1)HCCCHCH 2+HCl?(2)MeCO 3H??LiAlH 4(3)Me+CH 2CHCCH 3O?Δ(4)HONMe 2+N +N Cl -HOAc NaOAc?精品文档精品文档(5)CCH 3N CH 3PCl 5?(6)CH C OOHOO??Cu(OAc)2HOAc Δ.KOH Δ2.HCl(7)NH O HOAc???HNO 3H 2SO 4PCl(8)HCH 3HOCO 2Me ?Δ(9)C CH COCH 3CH 3CH 3Al(OCHMe 2)3Me 2CHOH?Δ+(10)CH 2CHCH 2N +Me 3 Br -+Br 2?(二)自指定原料合成指定的化合物:(30分,注意:用反应式表示,并注明反应条件) a) 自甲苯和必要的试剂合成4-硝基-2-甲基苯甲腈。
1991年考研数学一试题及完全解析(Word版)
1991年考研数学⼀试题及完全解析(Word版)1991年全国硕⼠研究⽣⼊学统⼀考试数学⼀试题⼀、填空题(本题满分15分,每⼩题3分.)(1) 设21,cos ,x t y t ?=+?=? 则22d y dx =__________.(2)由⽅程xyz +=(,)z z x y =在点(1,0,1)-处的全微分dz =__________.(3) 已知两条直线的⽅程是1123:101x y z L ---==-;221:211x y zL +-==,则过1L 且平⾏于2L 的平⾯⽅程是__________.(4) 已知当0x →时,123(1)1ax +-与cos 1x -是等价⽆穷⼩,则常数a =__________.(5) 设4阶⽅阵 5 2 0 02 1 0 00 0 1 20 0 1 1A ?? ?= -,则A 的逆阵1A -=__________.⼆、选择题(本题满分15分,每⼩题3分.) (1) 曲线2211x x e y e--+=- ( )(A) 没有渐近线 (B) 仅有⽔平渐近线(C) 仅有铅直渐近线 (D) 既有⽔平渐近线⼜有铅直渐近线 (2) 若连续函数()f x 满⾜关系式20()ln 22xt f x f dt ??=+,则()f x 等于 ( ) (A) ln 2xe (B) 2ln 2xe(C) ln 2xe + (D) 2ln 2xe +(3) 已知级数11(1)2n n n a ∞-=-=∑,2115n n a ∞-==∑,则级数1n n a ∞=∑等于 ( )(A) 3 (B) 7 (C) 8 (D) 9(4) 设D 是xOy 平⾯上以(1,1)、(-1,1)和(-1,-1)为顶点的三⾓形区域,1D 是D 在第⼀象限的部分,则(cos sin )Dxy x y dxdy +??等于 ( )(A) 12cos sin D x ydxdy ?? (B) 12D xydxdy ??(C) 14(cos sin )D xy x y dxdy +?? (D) 0(5) 设n 阶⽅阵A 、B 、C 满⾜关系式ABC E =,其中E 是n 阶单位阵,则必有 ( ) (A) ACB E = (B) CBA E =(C) BAC E = (D) BCA E =三、(本题满分15分,每⼩题5分.)(1)求0lim x x π+→. (2) 设n 是曲⾯222236x y z ++=在点(1,1,1)P 处的指向外侧的法向量,求函数u =P 处沿⽅向n 的⽅向导数. (3) 22()x y z dV Ω++,其中Ω是由曲线22,0y z x ?=?=?绕z 轴旋转⼀周⽽成的曲⾯与平⾯4z =所围成的⽴体.四、(本题满分6分)在过点(0,0)O 和(,0)A π的曲线族sin (0)y a x a =>中,求⼀条曲线L ,使沿该曲线从O 到A 的积分3(1)(2)Ly dx x y dy +++?的值最⼩.五、(本题满分8分.)将函数()2||(11)f x x x =+-≤≤展开成以2为周期的傅⽴叶级数,并由此求级数211n n∞=∑的和.六、(本题满分7分.)设函数()f x 在[0,1]上连续,(0,1)内可导,且1233()(0)f x dx f =?,证明在(0,1)内存在⼀点c ,使()0f c '=.七、(本题满分8分.)已知1(1,0,2,3)α=,2(1,1,3,5)α=,3(1,1,2,1)a α=-+,4(1,2,4,8)a α=+,及(1,1,3,5)b β=+.(1) a 、b 为何值时,β不能表⽰成1234αααα、、、的线性组合?(2) a 、b 为何值时,β有1234αααα、、、的唯⼀的线性表⽰式?并写出该表⽰式.⼋、(本题满分6分)设A 为n 阶正定阵,E 是n 阶单位阵,证明A E +的⾏列式⼤于1.九、(本题满分8分)在上半平⾯求⼀条向上凹的曲线,其上任⼀点(,)P x y 处的曲率等于此曲线在该点的法线段PQ 长度的倒数(Q 是法线与x 轴的交点),且曲线在点(1,1)处的切线与x 轴平⾏.⼗、填空题(本题满分6分,每⼩题3分.)(1) 若随机变量X 服从均值为2,⽅差为2σ的正态分布,且{}240.3P X <<=,则{}0P X <=_______.(2) 随机地向半圆0y <<(a 为正常数)内掷⼀点,点落在半圆内任何区域的概率与区域的⾯积成正⽐,则原点和该点的连线与x 轴的夹⾓⼩于4π的概率为_______.⼗⼀、(本题满分6分)设⼆维随机变量(,)X Y 的概率密度为(2)2, 0,0(,)0, x y e x y f x y -+?>>=??其他,求随机变量2Z X Y =+的分布函数.1991年全国硕⼠研究⽣⼊学统⼀考试数学⼀试题解析⼀、填空题(本题满分15分,每⼩题3分.) (1)【答案】3sin cos 4t t tt- 【解析】这是个函数的参数⽅程,满⾜参数⽅程所确定函数的微分法,即如果 ()()x t y t φ?=?? =?, 则 ()()dy t dx t ?φ'='. 所以 sin 2dydy tdt dx dx t dt-==, 再对x 求导,由复合函数求导法则得22sin 1()()22d y d dy dt d t dx dt dx dx dt t t-=?=? 232cos 2sin 1sin cos 424t t t t t t=. (2)【答案】dx【解析】这是求隐函数在某点的全微分,这⾥点(1,0,1)-的含义是(1,0)1z z ==-. 将⽅程两边求全微分,由⼀阶全微分形式不变性得222()0d xyz +=,再由全微分四则运算法则得()()xy dz ydx xdy z ++=,令1,0,1x y z ===-,得dy =即dz dx =. (3)【答案】320x y z -++=【解析】所求平⾯∏过直线1L ,因⽽过1L 上的点(1,2,3);因为∏过1L 平⾏于2L ,于是∏平⾏于1L 和2L 的⽅向向量,即∏平⾏于向量1(1,0,1)l =-和向量2(2,1,1)l =,且两向量不共线,于是平⾯∏的⽅程1231010211x y z ----=, 即320x y z -++=. (4)【答案】32-【解析】因为当0x →时,11sin ,(1)1nx x x x n+-, 当0x →时20ax →,所以有122223111(1)1,cos 1sin ,322ax ax x x x +--=--所以 12233lim lim 1cos 132x x axax a x x →→+-==---.因为当0x →时,123(1)1ax +-与cos 1x -是等价⽆穷⼩,所以213a -=,故32a =-. (5)【答案】12002500120033110033-??--. 【解析】为求矩阵的逆可有多种办法,可⽤伴随,可⽤初等⾏变换,也可⽤分块求逆.根据本题的特点,若知道分块求逆法,则可以简单解答.注意: 1110000A AB B ---=,111000A B B A---??= ? ?. 对于2阶矩阵的伴随矩阵有规律:a b A c d ??=,则求A 的伴随矩阵*a b d b A c d c a *-== ? ?-.如果0A ≠,这样a b d b d b c d c a c a A ad bc---== ? ?---. 再利⽤分块矩阵求逆的法则:1110000A AB B ---??=,易见 112002500120033110033A --??- =-.⼆、选择题(本题共5个⼩题,每⼩题3分,满分15分.) (1)【答案】(D)【解析】由于函数的定义域为0x ≠,所以函数的间断点为0x =,222211lim limlim11x x x x x x x e e y ee --→→→++===∞--,所以0x =为铅直渐近线,2211lim limlim111x x x x x x x e e y ee --→∞→∞→∞++====--,所以1y =为⽔平渐近线.所以选(D).【相关知识点】铅直渐近线:如函数()y f x =在其间断点0x x =处有0 lim ()x x f x →=∞,则0x x =是函数的⼀条铅直渐近线;⽔平渐近线:当lim (),(x f x a a →∞=为常数),则y a =为函数的⽔平渐近线.(2)【答案】(B) 【解析】令2tu =,则2,2t u dt du ==,所以 20()ln 22()ln 22xx t f x f dt f u du ??=+=+,两边对x 求导,得()2()f x f x '=,这是⼀个变量可分离的微分⽅程,即[()]2()d f x dx f x =.解之得2()xf x Ce =,其中C 是常数.⼜因为0(0)2()ln 2ln 2f f u du =+=?,代⼊2()x f x Ce =,得0(0)ln 2f Ce ==,得ln 2C =,即2()ln 2x f x e =?.(3)【答案】(C) 【解析】因为112342121(1)n n n n n a a a a a a a ∞--=-=-+-++-+∑1234212()()()n n a a a a a a -=-+-++-+ 21 2212111()n n n n n n n aa a a ∞∞∞--====-=-∑∑∑(收敛级数的结合律与线性性质),所以1221111(1)523n nn n n n n aa a ∞∞∞--====--=-=∑∑∑.⽽12342121()()()nn n n aa a a a a a ∞-==+++++++∑212212111()n n n n n n n aa a a ∞∞∞--====+=+∑∑∑538=+=,故应选(C).(4)【答案】(A)【解析】如图,将区域D 分为1234,,,D D D D 四个⼦区域. 显然,12,D D 关于y 轴对称,34,D D 关于x 轴对称.令 12cos sin DDI xydxdy I x ydxdy ?==,由于xy 对x 及对y 都是奇函数,所以12340,0D D D D xydxdy xydxdy ++==??.⽽cos sin x y 对x 是偶函数,对y 是奇函数,故有34121cos sin 0,cos sin 2cos sin D D D D D x ydxdy x ydxdy x ydxdy ++==??,所以 112(cos sin )2cos sin DD xy x y dxdy II x ydxdy +=+=,故选(A).(5)【答案】(D)【解析】矩阵的乘法公式没有交换律,只有⼀些特殊情况可以交换.由于A 、B 、C 均为n 阶矩阵,且ABC E =,对等式两边取⾏列式,据⾏列式乘法公式||||||1A B C =,得到0A ≠、0B ≠、0C ≠,知A 、B 、C 均可逆,那么,对于ABC E =,先左乘1A -再右乘A 有 1ABC E BC A BCA E -=→=→=,故应选(D).其实,对于ABC E =先右乘1C -再左乘C ,有1ABC E AB C CAB E -=→=→=.三、(本题满分15分,每⼩题5分.) (1)【解析】这是1∞型未定式求极限.0lim(1x x x π++→→=+令1t =,则0x +→时0t -→,所以1lim(1lim(1)tx t t e +-→→+=+=, 所以0limlim(1lim x x x e→++→→+==.因为当0x →时,sin x x ,所以220002sin 2limlim lim 2x x x x x πππ+++→→→--===-,故02x x x e eππ→+-→==.(2)【解析】先求⽅向n 的⽅向余弦,再求,,u u ux y z,最后按⽅向导数的计算公式 cos cos cos u u u u n x y z αβγ=++求出⽅向导数. 曲⾯222236x y z ++=在点(1,1,1)P 处的法向量为{}{}{}(1,1,1)4,6,24,6,222,3,1Px y z x y z ±==±,在点(1,1,1)P 处指向外侧,取正号,并单位化得}}{}2,3,12,3,1cos ,cos ,cos .n αβγ=== ⼜P P P u x u y u z ?=========????, 所以⽅向导数cos cos cos u u u un x y z αβγ=++ 117==. (3)【解析】由曲线22,0y z x ?=?=?绕z 轴旋转⼀周⽽围成的旋转⾯⽅程是222x y z +=.于是,Ω是由旋转抛物⾯221()2z x y =+与平⾯4z =所围成.曲⾯与平⾯的交线是 228,4x y z +==.选⽤柱坐标变换,令cos ,sin ,x r y r z z θθ===,于是:02,04,0z r θπΩ≤≤≤≤≤≤,因此 22()I x y z dV Ω=++4220)dz d r z rdr πθ=+?4240242r r r r z dz π==+ ?42025643z dz ππ==四、(本题满分6分)【解析】曲线sin ,([0,])y a x x π= ∈,则cos dy a xdx =,所以 3(1)(2)L I y dx x y dy =+++?30[1(sin )(2sin )cos ]a x x a x a x dx π=+++??23301sin 2cos sin 22a a x ax x x dx π=+++233sin 2cos sin 22a axdx a x xdx xdx ππππ=+++232(cos 1)cos 2sin sin 224a ax d x a xd x xd x ππππ=+-++[][]2330001cos cos 2sin cos cos 234a a x x a x x x x ππππ??=+-+++-3443a a π=+-. 对关于a 的函数3443I a a π=+-两边对a 求导数,其中0a >,并令0,I '=得2440I a '=-=.所以1a =, 且 0,010,1I a I a '<<'><<+∞.故1a =为函数344,(0)3I a a a π=+->的极⼩值点,也是最⼩值点.故所求的曲线为 sin ,([0,])y x x π= ∈.五、(本题满分8分.)【解析】按傅式级数公式,先求()f x 的傅式系数n a 与n b .因()f x 为偶函数,所以1()sin0(1,2,3,)l n l n b f x xdx n l l π-== =? , 012()cos()cos l l n l n n a f x xdx f x xdx l l l l ππ-==?? 11100022(2)cos 4cos sin x n xdx n xdx xd n x n ππππ=+=+ 122022(cos 1)sin (1,2,3,)n n xdx n n n ππππ-=-= =? ,1002(2)5a x dx =+=?.因为()2||f x x =+在区间(11)x -≤≤上满⾜狄利克雷收敛定理的条件,所以01()2||cos sin2n n n a n n f x x a x b x l lππ∞=??=+=++∑ 22152(cos 1)cos 2n n n x n πππ∞=-=+∑221541cos(21)(11)2(21)n n x x n ππ∞==-- -≤≤-∑. 令0x =,有221541(0)20cos02(21)n f n π∞==+=--∑,所以,2211(21)8n n π∞==-∑. ⼜ 222221111111111(21)(2)(21)4n n n n n n n n n ∞∞∞∞====??=+=+??--??∑∑∑∑, 所以, 2213148n n π∞==∑,即 22116n nπ∞==∑.六、(本题满分7分.)【解析】由定积分中值定理可知,对于123()f x dx ?,在区间2(,1)3上存在⼀点ξ使得12321()()(1)()33f x dx f f ξξ=-=?,即1233()()(0)f x dx f f ξ==?.由罗尔定理可知,在区间(0,1)内存在⼀点(01)c c ξ<<<,使得()0f c '=.七、(本题满分8分)【解析】设11223344x x x x ααααβ+++=,按分量写出,则有123423341234123412123(2)4335(8)5x x x x x x x x x a x x b x x x a x α+++=??-+=??++++=+??++++=?.对⽅程组的增⼴矩阵作初等⾏变换:第⼀⾏分别乘以有()2-、()3-加到第三⾏和第四⾏上,再第⼆⾏乘以()1-、()2-加到第三⾏和第四⾏上,有111111111101121011212324301213518502252A a b a b a a--=→ ? ?+++ ?+-+ 1111101121001000010a b a ??- → ?+ ?+??, 所以,当1,0a b =-≠时,()1()r A r A +=,⽅程组⽆解.即是不存在1234x ,x ,x ,x 使得11223344x x x x ααααβ+++=成⽴,β不能表⽰成1234αααα、、、的线性组合;当1a ≠-时,()() 4.r A r A ==⽅程组有唯⼀解21,,,0111Tb a b b a a a ++??- ?+++??,故β有唯⼀表达式,且1234210111b a b ba a a βαααα++=-+++?+++. 【相关知识点】⾮齐次线性⽅程组有解的判定定理:设A 是m n ?矩阵,线性⽅程组Ax b =有解的充分必要条件是系数矩阵的秩等于增⼴矩阵()A A b = 的秩,即是()()r A r A =(或者说,b 可由A 的列向量12,,,n ααα线表出,亦等同于12,,,n ααα与12,,,,n b ααα是等价向量组).设A 是m n ?矩阵,线性⽅程组Ax b =,则 (1) 有唯⼀解 ? ()().r A r A n == (2) 有⽆穷多解 ? ()().r A r A n =< (3) ⽆解 ? ()1().r A r A +=b 不能由A 的列向量12,,,n ααα线表出.⼋、(本题满分6分)【解析】⽅法1:因为A 为n 阶正定阵,故存在正交矩阵Q ,使121T N Q AQ Q AQ λλλ-?? ?==Λ= ? ?, 其中0(1,2,)i i n λ>= ,i λ是A 的特征值. 因此 ()T T T Q A E Q Q AQ Q Q E +=+=Λ+两端取⾏列式得 |||||||||()|||(1)T T iA E Q A E Q Q A E Q E λ+=+=+=Λ+=+∏,从⽽ ||1A E +>.⽅法2:设A 的n 个特征值是12n ,,,.λλλ由于A 为n 阶正定阵,故特征值全⼤于0.由λ为A 的特征值可知,存在⾮零向量α使A αλα=,两端同时加上α,得()()1A E αλα+=+.按特征值定义知1λ+是A E +的特征值.因为A E +的特征值是12111n ,,,.λλλ+++ 它们全⼤于1,根据i A λ=∏,知||(1)1i A E λ+=+>∏.【相关知识点】阵特征值与特征向量的定义:设A 是n 阶矩阵,若存在数λ及⾮零的n 维列向量X 使得AX X λ=成⽴,则称λ是矩阵A 的特征值,称⾮零向量X 是矩阵A 的特征向量.九、(本题满分8分)【解析】曲线()y y x =在点(,)P x y 处的法线⽅程为1()Y y X x y -=--'(当0y '≠时), 它与x 轴的交点是(,0)Q x yy '+,从⽽122||(1)PQ y y '==+.当0y '=时,有(,0),||Q x PQ y =,上式仍然成⽴. 因此,根据题意得微分⽅程3122221(1)(1)y y y y ''=''++,即21yy y '''=+.这是可降阶的⾼阶微分⽅程,且当1x =时,1,0y y '==.令()y P y '=,则dP y Pdy ''=,⼆阶⽅程降为⼀阶⽅程21dP yP P dy =+,即21PdP dy P y=+.即y =C 为常数.因为当1x =时,1,0y P y '===,所以1C =,即y ==所以y '=分离变量得dx =±.令sec y t =,并积分,则上式左端变为sec tan ln sec tan tan t tdtt t C t==++?ln sec ln t C y C =+=+.因曲线在上半平⾯,所以0y >,即(ln y C x =±.故 x y Ce ±+=.当1x =时,1,y =当x 前取+时,1C e -=,1x y e -=,111x x y e e --====;当x 前取-时,C e =,1x y e -++ =,111x xy e e --====;所以 (1)(1)1()2x x y e e ---=+.⼗、填空题(本题满分6分,每⼩题3分.)(1)【解析】⼀般说来,若计算正态分布随机变量在某⼀范围内取值的概率,应该已知分布的两个参数µ和2σ,否则应先根据题设条件求出µ,2σ,再计算有关事件的概率,本题可从2()0.8σΦ=,通过查()x Φ表求出σ,但是注意到所求概率(0)P x <即是2()σ-Φ与2()σΦ之间的关系,可以直接由2()σΦ的值计算出2()σ-Φ.因为2(2,)X N σ ,所以可标准化得 2(0,1)X N σ- ,由标准正态分布函数概率的计算公式,有4222(24)()()P x σσ--<<=Φ-Φ,2()(24)(0)0.8P x σΦ=<<+Φ=.由正态分布函数的对称性可得到 0222(0)()()1()0.2P x σσσ-<=Φ=Φ-=-Φ=.(2)【解析】设事件A =“掷的点和原点的连线与x 轴的夹⾓⼩于4π”, 这是⼀个⼏何型概率的计算问题.由⼏何概率公式()DS P A S =半圆,⽽ 212S a π=半圆,22141124D OAC S S S a a π=+=+ 圆, 故 222111124()122a aP A a πππ+==+.⼗⼀、(本题满分6分)【解析】⼆维连续型随机变量的概率等于对应区域的⼆重积分,所以有{}{}2()2(,)x y zF z P Z z P X Y z f x y dxdy +≤=≤=+≤=.当0z ≤时,()0F z =.因为2x y z +=在直线20x y +=的下⽅与0,0x y >>(即第⼀象限)没有公共区域所以()0F z =.当0z >时,2xy z +=在直线20x y +=的上⽅与第⼀象限相交成⼀个三⾓形区域D ,此即为积分区间.(2)20()2()1z x zzx y x z z z F z dx edy e e dx e ze --+----==-=--?? .0=所以2Z X Y =+的分布函数 0, 0, ()1, 0. z zz F z e ze z --。
(NEW)北京大学药学院《970有机化学》历年考研真题汇编
目 录2014年北京大学970有机化学考研真题(回忆版)2013年北京大学药学院970有机化学考研真题2012年北京大学970有机化学考研真题(回忆版)2011年北京大学药学院970有机化学考研真题2009年北京大学960有机化学考研真题(回忆版)2003年北京大学药学院有机化学考研真题2002年北京大学药学院有机化学考研真题2001年北京大学药学院有机化学考研真题2000年北京大学药学院有机化学考研真题1999年北京大学药学院有机化学考研真题1998年北京大学药学院有机化学考研真题1997年北京大学药学院有机化学考研真题1996年北京大学药学院有机化学考研真题1995年北京大学药学院有机化学考研真题1994年北京大学药学院有机化学考研真题1993年北京大学药学院有机化学考研真题1991年北京大学药学院有机化学考研真题1990年北京大学药学院有机化学考研真题1989年北京大学药学院有机化学考研真题1988年北京大学药学院有机化学考研真题1987年北京大学药学院有机化学考研真题1986年北京大学药学院有机化学考研真题1985年北京大学药学院有机化学考研真题2014年北京大学970有机化学考研真题(回忆版)一、选择题(15分)考察了各种物质的酸性比较,碱性比较,酯的水解速率排序,醇解速率排序,4n+2规则等等。
总体比较简单。
二、填空考察了烯烃亲电加成,hoffman消除,reformansky反应,高锰酸钾氧化双键,硼氢化钠还原硝基,羰基的亲核加成等等,也比较简单。
三、机理(36分)考察了mannich反应的机理,碳负离子对羰基的加成,hoffman消除,醇的各种卤代。
四、合成(36分)考察了联苯胺重排,多取代苯的制备,claisen缩合与michael加成的使用,wittig试剂的使用,逆合成分析法的使用。
五、(9分)hoffman重排,darzen反应,reformansky反应,claisen缩合,favorsky重排各举一个例子。
(整理)北京大学有机化学研究生入学考试试题.
精品文档精品文档北京大学研究生入学考试试题试题:(一)写出下列各反应的最主要的一个产物(注意:只写一个,多写扣分)(20分)(1)CCH3CH2+.H O2.NaOH??B2H6(2)CH3CH2CH2C CHKOH,C H OH?Δ(3)CH2NH2OHHNO?(4)CH2CH2CH2COOCH3CHCH2CH2OHCH3CH3C5H11ONa+?回流,分馏异-(5)NH2NaHSO3H2OΔ?(6)?顺,顺,顺-CH3CH CHCH CHCH CHCH3(7)CH3COCH2COOC2H5+NHNH2Δ?(8)CH3CHCH2CH2CH3N+(CH3)3 OH-Δ?(9)NH2NH2+CH3Δ?精品文档精品文档(10)(浓)CF 3++?H 2SO 4HNO 3(浓)(三)用分子含不多于五个碳原子的开链化合物或不含取代基的芳环化合物作为起始物,和必要的无机试剂,合成以下的化合物。
(25分)(1)HOOCCH 2CHCH 2CH 2COOH COOH(2)CH 3OO3(3)ClBr(5)NNO 2(4)(CH 3)2NNN北京大学研究生入学考试试题(一)完成下列反应(30分,注意:只写一个最主要的产物,多写扣分) (1)HCCCHCH 2+HCl?(2)MeCO 3H??LiAlH 4(3)Me+CH 2CHCCH 3O?Δ(4)HONMe 2+N +N Cl -HOAc NaOAc?精品文档精品文档(5)CCH 3N CH 3PCl 5?(6)CH C OOHOO??Cu(OAc)2HOAc Δ.KOH Δ2.HCl(7)NH O HOAc???HNO 3H 2SO 4PCl(8)HCH 3HOCO 2Me ?Δ(9)C CH COCH 3CH 3CH 3Al(OCHMe 2)3Me 2CHOH?Δ+(10)CH 2CHCH 2N +Me 3 Br -+Br 2?(二)自指定原料合成指定的化合物:(30分,注意:用反应式表示,并注明反应条件) a) 自甲苯和必要的试剂合成4-硝基-2-甲基苯甲腈。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京大学1991年研究生入学考试试题
考试科目:有机化学考试时间:二月三日下午
招生专业:化学系各专业研究方向:
指导教师:
试题:注:①单独考试的考生,第二大题(合成题)选作四题,第三大题(机理题)选作一题,考卷成绩×100/87为实得成绩。
②答案写在答题纸上。
一.完成反应式,写出主要产物(30%)
1. CH3
2.
C6H5C
CH3
C
OH
CH3
C6H5
NH2HCl
NaNO2
3.
C
Br
2
H5
3CH COO-
[ ]
500℃
4.
CH3ONa C
CH3
CH3
Br
CH3CH2
+
5.
C CH
CH3
CH3
C CH3
O(CH
3
)2CuLi H3O+
[ ]
Br2NaOH
6. (C6H5)3P BrCH2COOC2H5
C2H5ONa C H CHO
[ ]
+
7. CH32CHCH2COOC2H5
O
3
C H ONa
8.
OCH2CH CHC6H5
CH3Δ
9. N CH3
NaNHC H H O
10.
CH2N2+H5C2OOC C C COOC2H5
二.从指定的化合物出发,用不超过四个碳原子的有机原料及必要的无机试剂合成下列化合物(35%)
1.从甲苯合成
CH3
NO2 Cl
2.从丙二酸二乙脂合成O
O
COOH
3.从乙酰乙酸乙脂合成O CH3
C CH
4.从CH3
合成
3
5.从苯合成
N
H
Cl CH3
C6H5
三.(12%)
i.为下列反应提供一个可能的机理:
O
O
COOH
COOH
(过量)
Δ
H3O+
+CHCl3 Cl2KOH
ii.写出下述立体选向反应的主要产物(用Fischer投影式表示),并解释其原因:
H CH3
CHO
C6H5
+HCN[ ]
四.有一个化合物C5H8,它的1HNMR只在高场区域出现一个单峰。
试写出它的结构式,并提出一条简便易行的合成它的路线(7%)
提示:用甲醛和乙醛为原料
五.实验(16%)
1.把100ml苯、10g苯酚和10g醋酸放在分水器中一起加热,收集到两层液体。
试问上层是什么?下层是什么?并解释所发生的现象。
2.用减压蒸馏提纯苯甲醛(主要含苯甲酸),U形压力计的压差为730毫米汞柱。
下表是苯甲醛在不同温度下的蒸气压数据,请据此确定在此压力下苯
甲醛的沸点和应当收集的沸程,并指出加热的快慢对结果的影响和原因。
(设大气压力为760毫米汞柱)
温度(℃)蒸气压(毫米汞柱)179 (760)
95 (50)
84 (30)
79 (25)
75 (20)
69 (15)
62 (10)
50 (5)。
