初中数学各章节考点练习试题汇编13.2 垂直平分线
人教版_部编版八年级数学上册第十三章第一节线段的垂直平分线的性质考试复习题一(含答案) (134)

人教版_部编版八年级数学上册第十三章第一节线段的垂直平分线的性质考试复习题一(含答案) 某校A与直线公路BD距离AB为300米,与该公路上某车站D的距离为500米.(1) 现要在公路边建一个小商店C,使之与学校A及车站D的距离相等,请用尺规作图法找出点C的位置.(2) 求点C与车站D的距离是多少米?【答案】(1)见解析米.(2)点C与车站D的距离是25008【解析】【分析】(1)依题意做AD的垂直平分线,交BD与C点,即为所求;(2)连接AC,先利用勾股定理求出BD,设CD=x,则AC=CD=x,BC =400-x,在直角三角形ABC中使用勾股定理,即可求出x,即点C与车站D的距离.【详解】(2)解:连结AC.∵CE垂直平分AD,∵AC=CD.∵AB=300,AD=500,∵BD400.设CD=x,则AC=CD=x,BC=400-x,∵x2=(400-x)2+3002..解得:x=25008答:点C与车站D的距离是2500米.832.如图所示,四边形EFGH是一个矩形的球桌面,有黑白两球分别位于A、B两点,试说明怎样撞击B,才使白球先撞击台球边EF,反弹后又能击中黑球A?【答案】详见解析【解析】【分析】可作出点A关于台球边EF的对称点A1,连接BA1交EF于点O,即为所求的点.【详解】解:先作出点A关于台球边EF的对称点A1,连接BA1交EF于点O.将球杆沿BOA1的方向撞击B球,可使白球先撞击台球边EF,然后反弹后又能击中黑球A.【点睛】熟练掌握对称的性质,能够解决一些简单的作图问题.33.如图所示,∠BAC=105°,若MP和NQ分别垂直平分AB和AC.求∠PAQ的度数.【答案】30°【解析】【分析】先根据三角形内角和等于180°求出∠ABP+∠ACQ=75°,再根据线段垂直平分线的性质∠PAB=∠ABP,∠QAC=∠ACQ,所以∠PAB+∠QAC=75°,便不难求出∠PAQ的度数为30°.【详解】解:∵∠BAC=105°,∴∠ABP+∠ACQ=180°-105°=75°,∵MP、NQ分别垂直平分AB和AC,∴PB=PA,QC=QA.∴∠PAB=∠ABP,∠QAC=∠ACQ,∴∠PAB+∠QAC=∠ABP+∠ACQ=75°,∴∠PAQ=105°-75°=30°.【点睛】利用三角形内角和定理和线段垂直平分线的性质求解.34.如图所示,∠ABC内有一点P,在BA、BC边上各取一点P1、P2,使∠PP1P2的周长最小.【答案】见解析【解析】【分析】根据对称性即可求解.【详解】如图,以BC为对称轴作P的对称点M,以BA为对称轴作出P的对称点N,连MN交BA、BC于点P1、P2.∵∵PP1P2为所求作三角形.35.为了推进农村新型合作医疗制度改革,准备在某镇新建一个医疗点P,使P到该镇所属A村、B村、C村的村委会所在地的距离都相等(A、B、C不在同一直线上,地理位置如下图),请你用尺规作图的方法确定点P的位置.要求:写出已知、求作;不写作法,保留作图痕迹.【答案】:见解析【解析】【分析】根据垂直平分线的性质得出,两垂直平分线的交点即是所求答案.【详解】解:已知A村、B村、C村,求作新建一个医疗点P,使P到该镇所属A村、B村、C村的村委会所在地的距离都相等;36.如图,在∠ABC和∠ACD中,CB=CD,设点E是CB的中点,点F 是CD的中点.(1)请你在图中作出点E和点F(尺规作图,保留作图痕迹,不写作法与证明);(2)连接AE、AF,若∠ACB=∠ACD,请问∠ACE∠∠ACF吗?请说明理由.【答案】(1)答案见解析;(2)全等,理由见解析.【解析】【分析】(1)根据尺规作图的要求,分别作出线段BC,CD的垂直平分线交点即为所求;(2)由已知条件可以用SAS判定△ACE≌△ACF.【详解】解:(1)如图所示:(2)∵CB=CD,设点E是CB的中点,点F是CD的中点.∵CE=CF,∵∵ACB=∵ACD,AC=AC,∵∵ACE∵∵ACF.【点睛】本题考查了全等三角形的判定,常见的判断方法有5种,选用哪一种方法,取决于题目中的已知条件,若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.37.为进一步打造“宜居重庆”,某区拟在新竣工的矩形广场的内部修建一个音乐喷泉,要求音乐喷泉M到广场的两个入口A、B的距离相等,且到广场管理处C的距离等于A和B之间距离的一半,A、B、C的位置如图所示.请在答题卷的原图上利用尺规作图作出音乐喷泉M的位置.(要求:不写已知、求作、作法和结论,保留作图痕迹,必须用铅笔作图)【答案】解:作AB的垂直平分线,以点C为圆心,以AB的一半为半径画弧交AB 的垂直平分线于点M 即可.【解析】【分析】【详解】易得M 在AB 的垂直平分线上,且到C 的距离等于AB 的一半.38.如图,已知ABC ∆中.(1)用直尺和圆规作AC 的垂直平分线交BC 于点D ;(保留作图痕迹,不写作法)(2)连接AD ,若28C ∠=︒,AB BD =,求B 的度数.【答案】(1)见解析;(2)68B ∠=︒【解析】【分析】(1)根据垂直平分线的作法即可求解;(2)根据垂直平分线的性质得DA DC =,再利用外角定理及等腰三角形的性质即可求解.【详解】解:(1)作图如解图:分别以点A 、C 为圆心,大于12AC 长为半径画弧,两弧相交于点M 、N ,连接MN ,交BC 于点D ,MN 即为所求.(2)由垂直平分线的性质得DA DC =,∵28C DAC ∠=∠=︒,∵56ADB C DAC ∠=∠+∠=︒,又∵AB BD =,∵56BAD BDA ∠=∠=︒,则18068B BAD BDA ∠=︒-∠-∠=︒.【点睛】此题主要考查垂直平分线的性质,解题的关键是熟知等腰三角形的性质及垂直平分线的特点.39.如图,已知∠AOB 及边OB 上一点P 求作⊙M ,使⊙M 与边OA 、OB 相切,且其中一个切点为点P【答案】详见解析【解析】【分析】根据切线的判定和性质先作∠AOB平分线,再过点P作OB的垂线,确定点M,据此作图可得.【详解】作法:如图,1、作∠AOB的平分线OE,2、过点P作射线OB的垂线PD,3、PD与OE的交点即为点M,4、以点M为圆心、MP为半径作圆,则⊙M即为所求.【点睛】本题主要考查作图-复杂作图,解题的关键是掌握圆的切线的判定与性质及角平分线的性质.40.如图,已知四边形ABCD是平行四边形.(1)用直尺和圆规作出对角线AC的垂直平分线,分别交AD,BC于E,F;(保留作图痕迹,不写作法)(2)在(1)作出的图形中,连接CE,AF,若AB=4,BC=8,且AB⊥AC,求四边形AECF的周长.【答案】(1)见详解;(2)四边形AECF的周长为16.【解析】【分析】(1)分别以A,C为圆心,比AC的一半长为半径画弧,交于两点,确定出垂直平分线即可;(2)根据平行四边形的判定和菱形的判定与性质解答即可.【详解】解:(1)如图所示:直线EF即为所求.(2)由(1)作图可知F是BC的中点,BC=4,则FC=12∴AE=CF=4,∵AE∥FC,∴四边形AECF是平行四边形,∵AC⊥EF,∴四边形AECF是菱形,∴四边形AECF的周长为16.【点睛】此题主要考查了垂直平分线的做法及其性质,菱形的判定与性质,熟练地掌握作图技巧是解决问题的关键.。
北师版数学下册1.3.2 线段垂直平分线的应用(练习题课件)

8.如图,在已知的△ABC 中,按以下步骤作图: ①分别以 B,C 为圆心,以大于12BC 的长为半径作弧,两弧 相交于两点 M,N; ②作直线 MN 交 AB 于点 D, 连接 CD. 若 CD=AC,∠A=50°,则∠ACB 的度数为( D ) A.90° B.95° C.100° D.105°
7.如图,已知线段 a,h,作等腰三角形 ABC,使 AB=AC,且 BC=a,BC 边上的高 AD=h.张红的作法如下:
①作线段 BC=a; ②作线段 BC 的垂直平分线 MN,MN 与 BC 相交于点 D; ③在直线 MN 上截取线段 h; ④连接 AB,AC,△ABC 为所求作的等腰三角形. 上述作法的四个步骤中,有错误的一步是( C ) A.① B.② C.③ D.④
证明:如图,延长 ED 至点 M,使 DM=ED,连接 MC,MF,
则 EF=FM. BD=CD,
在△BDE 和△CDM 中,∠EDB=∠MDC, ED=MD,
∴△BDE≌△CDM(SAS).∴BE=CM.
∵CF+CM>MF,∴BE+CF>EF.
使用 说明
此课件下载后
背
景 图 片 可 单击输入您的封面副标题
【答案】B
6.(中考·北京)阅读下面材料: 在数学课上,老师提出如下问题:
小芸的作法如下:
老师说:“小芸的作法正确.” 请回答:小芸的作图依据是_到__一__条__线__段___两__个__端__点__距__离__相__等__ _的__点__,__在__这__条__线__段__的__垂__直__平__分__线__上__及__两__点__确__定__一__条__直__线____.
2.平面内到不在同一条直线上的三个点 A,B,C 的距离相等的 点有( B ) A.0 个 B.1 个 C.2 个 D.3 个
人教版数学八年级上册 第十三章 13.1.2 线段的垂直平分线的性质 同步练习 (含答案)

人教版数学八年级上册第十三章13.1.2 线段的垂直平分线的性质同步练习一、选择题1.如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是()A.AB=AD B.AC平分∠BCDC.AB=BD D.△BEC≌△DEC2. 如图所示,线段AB,AC的垂直平分线相交于点P,则PB与PC的关系是()A.PB>PC B.PB=PCC.PB<PC D.PB=2PC3. 如图,在△ABC中,△ACB=90°,△B=22.5°,AB边的垂直平分线交BC于点D,则下列结论中错误的是()A.△ADC=45° B.△DAC=45°C.BD=AD D.BD=DC4. 在数学课上,老师提出如下问题:如图,已知△ABC中,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PB=BC.下面是四名同学的作法,其中正确的是()5. 如图,在△ABC 中,DE 是AC 的垂直平分线,且分别交BC ,AC 于点D 和E ,△B =60°,△C =25°,则△BAD 为( )A .50°B .70°C .75°D .80°6. 如图,在△ABC 中,DE 垂直平分AB ,交AB 于点E ,交BC 于点D ,若AD=4,BC=3DC ,则BC 等于 ( )A.4B.4.5C.5D.67. 如图,C ,E 是直线l 两侧的点,以点C 为圆心,CE 的长为半径画弧交直线l于A ,B 两点.又分别以点A ,B 为圆心,大于12AB 的长为半径画弧,两弧交于点D ,连接CA ,CB ,CD ,则下列结论不一定正确的是 ( )A .CD△直线lB .点A ,B 关于直线CD 对称C .点C ,D 关于直线l 对称D .CD 平分△ACB 8. 如图,在Rt ABC 中,90ACB ∠=︒,分别以点B 和点C 为圆心,大于12BC 的长为半径作弧,两弧相交于D E ,两点,作直线DE 交AB 于点F ,交BC 于点G ,连接CF .若3AC =,2CG =,则CF 的长为( )A .52 B .3 C .2 D .72 9. 如图,在△ABC 中,AB 的垂直平分线交AB 于点D ,交BC 于点E ,若BC=6,AC=5,则△ACE 的周长为( )A .8B .11C .16D .1710. 如图,在△ABC 中,直线MN 为BC 的垂直平分线,交BC 于点E ,点D 在直线MN 上,且在△ABC 的外面,连接BD ,CD ,若CA 平分△BCD ,△A=65°,△ABC=85°,则△BCD 是( )A.等边三角形B.等腰三角形C.直角三角形D.等腰直角三角形二、填空题11. 如下图,△ABC 中,AB=AC=14cm ,D 是AB 的中点,DE△AB 于D 交AC 于E ,△EBC 的周长是24cm ,则BC= .12. 如图,在Rt△ABC中,△C=90°,边AB的垂直平分线交BC点D,AD平分△BAC,则△B度数为.13. 如图,△ABC中,AC=8,BC=5,AB的垂直平分线DE交AB于点D,交边AC于点E,则△BCE的周长为________.14. 如图,DE是△ABC的边AC的垂直平分线,若BC=9,AD=4,则BD=________.15. 如图,在△ABC中,△C=90°,DE是AB的垂直平分线,AD恰好平分△BAC.若DE=1,则BC的长是________.三、解答题16.现要在三角地带ABC内(如图)建一座中心医院,使医院到A,B两个居民小区的距离相等,并且到公路AB和AC的距离也相等,请你确定这座中心医院的位置.17. 如图,已知△ABC.(1)用直尺和圆规分别作出AB,AC边的垂直平分线l1,l2;(2)若直线l1,l2的交点为O,连接OB,OC.求证:OB=OC.18. 如图,在△ABE中,AD△BE于点D,C是BE上一点,DC=BD,且点C在AE的垂直平分线上.若△ABC的周长为22 cm,求DE的长.19. 如图,在△ABC中,AB边的垂直平分线DE分别与AB边和AC边交于点D 和点E,BC边的垂直平分线FG分别与BC边和AC边交于点F和点G,若△BEG 的周长为16,GE=3,求AC的长.20. 如图,点P是△AOB外的一点,点Q与P关于OA对称,点R与P关于OB 对称,直线QR分别交OA、OB于点M、N,若PM=PN=4,MN=5.(1)求线段QM、QN的长;(2)求线段QR的长.21. 如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M. (1)若∠B=70°,则∠MNA的度数是.(2)连接NB,若AB=8cm,△NBC的周长是14cm.①求BC的长;②在直线MN上是否存在P,使由P、B、C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,说明理由.22. 如图,△ABC中,△ABC=30°,△ACB=50°,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.(1)直接写出△BAC的度数;(2)求△DAF的度数,并注明推导依据;(3)若△DAF的周长为20,求BC的长.人教版数学八年级上册第十三章13.1.2 线段的垂直平分线的性质同步练习--参考答案一、选择题1.如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是()A.AB=AD B.AC平分∠BCDC.AB=BD D.△BEC≌△DEC【答案】C2. 如图所示,线段AB,AC的垂直平分线相交于点P,则PB与PC的关系是()A.PB>PC B.PB=PCC.PB<PC D.PB=2PC【答案】B[解析] 如图,连接AP.△线段AB,AC的垂直平分线相交于点P,△AP=PB,AP=PC.△PB=PC.3. 如图,在△ABC中,△ACB=90°,△B=22.5°,AB边的垂直平分线交BC于点D,则下列结论中错误的是()A.△ADC=45° B.△DAC=45°C.BD=AD D.BD=DC【答案】D[解析] △AB的垂直平分线交BC于点D,△AD=BD,故C正确;△AD=BD,△△B=△BAD=22.5°.△△ADC=45°,故A正确;△DAC=90°-△ADC=90°-45°=45°,故B正确.故选D.4. 在数学课上,老师提出如下问题:如图,已知△ABC中,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PB=BC.下面是四名同学的作法,其中正确的是()【答案】C[解析] △PA+PB=BC,而PC+PB=BC,△PA=PC.△点P为线段AC的垂直平分线与BC的交点.显然只有选项C符合题意.5. 如图,在△ABC中,DE是AC的垂直平分线,且分别交BC,AC于点D和E,△B=60°,△C=25°,则△BAD为()A.50°B.70°C.75°D.80°【答案】B6. 如图,在△ABC中,DE垂直平分AB,交AB于点E,交BC于点D,若AD=4,BC=3DC,则BC等于()A.4B.4.5C.5D.6【答案】D[解析] △DE垂直平分AB,AD=4,△BD=AD=4.△BC=3DC,△BD=2CD.△CD=2.△BC=BD+CD=6.故选D.7. 如图,C,E是直线l两侧的点,以点C为圆心,CE的长为半径画弧交直线l于A,B两点.又分别以点A,B为圆心,大于12AB的长为半径画弧,两弧交于点D,连接CA,CB,CD,则下列结论不一定正确的是()A .CD△直线lB .点A ,B 关于直线CD 对称C .点C ,D 关于直线l 对称D .CD 平分△ACB 【答案】C [解析] 由作法可知CD 垂直平分AB ,故选项A ,B 正确; △CD 垂直平分AB ,△CA =CB.设CD 与AB 交于点G ,易证Rt△ACG△Rt△BCG ,△△ACG =△BCG , 即CD 平分△ACB ,故选项D 正确;△AB 不一定平分CD ,故选项C 错误.故选C.由线段垂直平分线的性质可得PA =PB ,但不能得到OP =OF.8. 如图,在Rt ABC 中,90ACB ∠=︒,分别以点B 和点C 为圆心,大于12BC 的长为半径作弧,两弧相交于D E ,两点,作直线DE 交AB 于点F ,交BC 于点G ,连接CF .若3AC =,2CG =,则CF 的长为( )A .52B .3C .2D .72【答案】A【解析】由作法得GF 垂直平分BC ,∴FB FC =,2CG BG ==,FG BC ⊥, ∵90ACB ∠=︒,∴FG AC ∥,∴BF CF =,∴CF 为斜边AB 上的中线,∵5AB ==,∴1522CF AB ==.故选A . 9. 如图,在△ABC 中,AB 的垂直平分线交AB 于点D ,交BC 于点E ,若BC=6,AC=5,则△ACE 的周长为( )A.8B.11C.16D.17【答案】答案为:B.10. 如图,在△ABC中,直线MN为BC的垂直平分线,交BC于点E,点D在直线MN上,且在△ABC的外面,连接BD,CD,若CA平分△BCD,△A=65°,△ABC=85°,则△BCD是()A.等边三角形B.等腰三角形C.直角三角形D.等腰直角三角形【答案】A二、填空题11. 如下图,△ABC中,AB=AC=14cm,D是AB的中点,DE△AB于D交AC 于E,△EBC的周长是24cm,则BC=.【答案】10cm12. 如图,在Rt△ABC中,△C=90°,边AB的垂直平分线交BC点D,AD平分△BAC,则△B度数为.【答案】答案为:30°13. 如图,△ABC中,AC=8,BC=5,AB的垂直平分线DE交AB于点D,交边AC于点E,则△BCE的周长为________.【答案】13【解析】△DE垂直平分AB,△AE=BE,△AE+EC=8,△EC+BE=8,△△BCE的周长为BE+EC+BC=13.14. 如图,DE是△ABC的边AC的垂直平分线,若BC=9,AD=4,则BD=________.【答案】515. 如图,在△ABC中,△C=90°,DE是AB的垂直平分线,AD恰好平分△BAC.若DE=1,则BC的长是________.【答案】3[解析] △AD平分△BAC,且DE△AB,△C=90°,△CD=DE=1.△DE是AB的垂直平分线,△AD=BD.△△B=△DAB.△△DAB=△CAD,△△CAD=△DAB=△B.△△C=90°,△△CAD+△DAB+△B=90°.△△B=30°.△BD=2DE=2.△BC=BD+CD=2+1=3.三、解答题16.现要在三角地带ABC内(如图)建一座中心医院,使医院到A,B两个居民小区的距离相等,并且到公路AB和AC的距离也相等,请你确定这座中心医院的位置.【答案】解:作线段AB的垂直平分线EF,作△BAC的平分线AM,EF与AM相交于点P,则点P处即为这座中心医院的位置.17. 如图,已知△ABC.(1)用直尺和圆规分别作出AB,AC边的垂直平分线l1,l2;(2)若直线l1,l2的交点为O,连接OB,OC.求证:OB=OC.【答案】解:(1)如图所示.(2)证明:如图,连接OA.△l1是AB的垂直平分线,△OA=OB.同理,OA=OC.△OB=OC.18. 如图,在△ABE中,AD△BE于点D,C是BE上一点,DC=BD,且点C在AE的垂直平分线上.若△ABC的周长为22 cm,求DE的长.【答案】解:△BD=DC,AD△BE,△AB=AC.△点C在AE的垂直平分线上,△AC=CE.△△ABC的周长是22 cm,△AC+AB+BD+CD=22 cm.△AC+CD=11 cm.△DE=CD+CE=CD+AC=11 cm.19. 如图,在△ABC中,AB边的垂直平分线DE分别与AB边和AC边交于点D 和点E,BC边的垂直平分线FG分别与BC边和AC边交于点F和点G,若△BEG 的周长为16,GE=3,求AC的长.【答案】解:△DE垂直平分线段AB,GF垂直平分线段BC,△EB=EA,GB=GC.△△BEG的周长为16,△EB+GB+GE=16.△EA+GC+GE=16.△GA+GE+GE+GE+EC=16.△AC+2GE=16.△GE=3,△AC=10.20. 如图,点P是△AOB外的一点,点Q与P关于OA对称,点R与P关于OB对称,直线QR分别交OA、OB于点M、N,若PM=PN=4,MN=5.(1)求线段QM、QN的长;(2)求线段QR的长.【答案】【解答】解:(1)△P,Q关于OA对称,△OA垂直平分线段PQ,△MQ=MP=4,△MN=5,△QN=MN﹣MQ=5﹣4=1.(2)△P,R关于OB对称,△OB垂直平分线段PR,△NR=NP=4,△QR=QN+NR=1+4=5.21. 如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M. (1)若∠B=70°,则∠MNA的度数是.(2)连接NB,若AB=8cm,△NBC的周长是14cm.①求BC的长;②在直线MN上是否存在P,使由P、B、C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,说明理由.【答案】解:(1) 50(2) ①∵MN垂直平分AB.∴NB=NA,又∵△NBC的周长是14cm,∴AC+BC=14cm,∴BC=6cm.②当点P与点N重合时,由点P、B、C构成的△PBC的周长值最小,最小值是14cm.22. 如图,△ABC中,△ABC=30°,△ACB=50°,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.(1)直接写出△BAC的度数;(2)求△DAF的度数,并注明推导依据;(3)若△DAF的周长为20,求BC的长.【答案】【解答】解:(1)△△ABC+△ACB+△BAC=180°,△△BAC=180°﹣30°﹣50°=100°;(2)△DE是线段AB的垂直平分线,△DA=DB,△△DAB=△ABC=30°,同理可得,△FAC=△ACB=50°,△△DAF=△BAC﹣△DAB﹣△FAC=100°﹣30°﹣50°=20°;(3)△△DAF的周长为20,△DA+DF+FA=20,由(2)可知,DA=DB,FA=FC,△BC=DB+DF+FC=DA+DF+FA=20.。
线段的垂直平分线练习题

线段的垂直平分线练习题线段的垂直平分线是指将一条线段垂直平分的直线。
其性质是,垂直平分线将线段分成两个相等的部分。
也就是说,如果一条线段的垂直平分线为AD,那么AB=AC。
这个性质可以用来解决一些几何问题。
判定线段的垂直平分线的方法是,如果一条直线通过线段的中点,并且垂直于这条线段,那么这条直线就是这条线段的垂直平分线。
举例来说,如果在△ABC中,AD垂直平分BC,且AB=5,那么AC=5,因为AD是BC的垂直平分线。
在△ABC中,如果AB的中垂线交BC于点E,且BE=2,则AE的长度为3.这个问题可以通过应用垂直平分线的性质来解决。
如果AB垂直平分CD,且AC=1.6cm,BC=2.3cm,则四边形ABCD的周长为4.6cm。
这个问题可以通过计算各边长度来解决。
如果NM是线段AB的中垂线,则①AB⊥MN,③MN⊥AB,⑤AB是MN的垂直平分线。
这个问题可以通过应用垂直平分线的性质来解决。
正确的说法有三个:①若直线PE是线段AB的垂直平分线,则EA=EB,PA=PB;②若PA=PB,EA=EB,则直线PE垂直平分线段AB;③若PA=PB,则点P必是线段AB的垂直平分线上的点。
解答问题时,可以利用垂直平分线的性质和判定方法来解决问题。
例如,在△ABC中,如果DE是AB边的垂直平分线,AE平分∠BAC,且∠B=30,则∠C的度数为60度。
另一个例子是,在直线AB上找一点P,使PC=PD。
可以通过画出垂直平分线来解决这个问题。
最后一个例子是,在△ABC中,AB=AC=16cm,AB的垂直平分线ED交AC于D点。
根据给定条件,可以求出BE的长度,BC的长度以及△BEC的周长。
1.角平分线上的性质角平分线是指将一个角平分成两个相等的角的线段。
对于一个角ABC,它的平分线可以记作BD,其中D是BC上的一点。
那么,BD到AB和BD到AC的距离是相等的,因为BD 将角ABC平分成了两个相等的角。
同样地,如果一个点在角ABC的平分线上,那么它到AB和AC的距离也是相等的。
《垂直平分线》练习题(含答案)
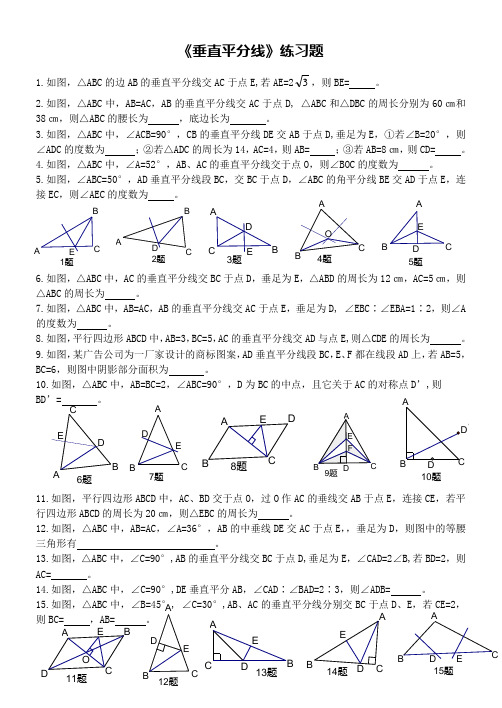
1题A B E C 2题D A B C 3题D AB EC 4题A B C O 5题D A BE C 11题D A B E C O 12题D A B E C 13题D A B E C 14题D A B E C 15题D A B E C6题D A BE C 8题D A B E C 7题D A B E C 10题'9题《垂直平分线》练习题1.如图,△ABC 的边AB 的垂直平分线交AC 于点E,若AE=23,则BE= 。
2.如图,△ABC 中,AB=AC ,AB 的垂直平分线交AC 于点D, △ABC 和△DBC 的周长分别为60㎝和38㎝,则△ABC 的腰长为 ,底边长为 。
3.如图,△ABC 中,∠ACB=90°,CB 的垂直平分线DE 交AB 于点D,垂足为E ,①若∠B=20°,则∠ADC 的度数为 ;②若△ADC 的周长为14,AC=4,则AB= ;③若AB=8㎝,则CD= 。
4.如图,△ABC 中,∠A=52°,AB 、AC 的垂直平分线交于点O ,则∠BOC 的度数为 。
5.如图,∠ABC=50°,AD 垂直平分线段BC ,交BC 于点D ,∠ABC 的角平分线BE 交AD 于点E ,连接EC ,则∠AEC 的度数为 。
6.如图,△ABC 中,AC 的垂直平分线交BC 于点D ,垂足为E ,△ABD 的周长为12㎝,AC=5㎝,则△ABC 的周长为 。
7.如图,△ABC 中,AB=AC ,AB 的垂直平分线交AC 于点E ,垂足为D, ∠EBC ∶∠EBA=1∶2,则∠A 的度数为 。
8.如图,平行四边形ABCD 中,AB=3,BC=5,AC 的垂直平分线交AD 与点E,则△CDE 的周长为 。
9.如图,某广告公司为一厂家设计的商标图案,AD 垂直平分线段BC ,E 、F 都在线段AD 上,若AB=5,BC=6,则图中阴影部分面积为 。
10.如图,△ABC 中,AB=BC=2,∠ABC=90°,D 为BC 的中点,且它关于AC 的对称点D ’,则 BD ’= 。
人教版_部编版八年级数学上册第十三章第一节线段的垂直平分线的性质考试复习题三(含答案) (52)

人教版_部编版八年级数学上册第十三章第一节线段的垂直平分线的性质考试复习题三(含答案)如图,在ABC ∆中,AB BC >,分别以顶点A ,B 为圆心,大于12AB 长为半径作弧,两弧交于点M ,N ,作直线MN 交CB 于点D .若5AD =,3CD =,则BC 长是( )A .7B .8C .12D .13【答案】B【解析】【分析】 根据垂直平分线的判定和性质,得到AD=BD ,即可得到BC 的长度.【详解】解:根据题意可知,直线MN 是AB 的垂直平分线,∴BD=AD=5,∴BC=BD+CD=5+3=8;故选:B.【点睛】本题考查了线段垂直平分线的判定和性质,解题的关键是熟练掌握垂直平分线的性质定理进行解题.12.如图,在△ABC 中,DE 是边AC 的垂直平分线,AE =5cm ,△ABD的周长为26cm ,则△ABC 的周长为A .29B .32C .36D .38【答案】C【解析】【分析】 根据线段的垂直平分线的性质得到DA =DC ,AC =2AE =10,根据三角形的周长公式计算,得到答案.【详解】∵DE 是边AC 的垂直平分线,∴DA =DC ,AC =2AE =10,∵△ABD 的周长为26,∴AB +BD +AD =AB +BD +CD =AB +BC =26,∴△ABC 的周长=AB +BC +AC =26+10=36(cm ),故选:C .【点睛】本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.13.在ABC ∆中,顶点A 在底边BC 的垂直平分线上,且3AB =,则AC 的值为( )A .1B .2C .3D .4【答案】C【解析】【分析】根据垂直平分线的性质定理,即可得到AC=AB=3.【详解】解:∵在ABC ∆中,顶点A 在底边BC 的垂直平分线上,∴3AC AB ==;故选:C.【点睛】本题考查了垂直平分线的性质定理,解题的关键是掌握定理.14.如图,Rt ABC ∆中,90C ∠=︒,DE 是AB 的垂直平分线,AD 分CAB ∠为两个角,且:2:1CAD DAB ∠∠=,则B 的度数为( )A .20︒B .22.5︒C .25︒D .30【答案】B【解析】【分析】 由DE 是AB 的垂直平分线,利用线段的垂直平分线的性质得∠B =∠BAD ,结合∠CAD :∠DAB =2:1与直角三角形两锐角互余,可以得到答案.【详解】在Rt ∠ABC 中∠DE是AB的垂直平分线∴AD=BD∠∠B=∠BAD∠∠CAD:∠DAB=2:1∴∠CAD=2∠B=2∠DAB∵∠CAB+∠B=90°∠4∠B=90°∠∠B=22.5°故选:B.【点睛】此题主要考查线段的垂直平分线的性质等几何知识.线段的垂直平分线上的点到线段的两个端点的距离相等.由已知条件得出4∠B=90°是正确解答本题的关键.15.对于ABC嘉淇用尺规进行了如下操作如图:(1)分别以点B和点C为圆心,BA,CA为半径作弧,两弧相交于点D;(2)作直线AD交BC边于点E,根据嘉淇的操作方法,可知线段AE是()A.边BC的垂直平分线B.ABC的中线C.ABC的高线D.ABC的角平分线【解析】【分析】利用基本作图可判断BC垂直平分AD,然后利用三角形高的定义进行判断.【详解】由作法得BC垂直平分AD,所以AE⊥BC,AE=DE,即AE为BC边上的高.故选:C.【点睛】此题考查作图-基本作图,解题关键在于熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).16.如图,在四边形ABCD中,AB=AD,CB=CD,BD和AC交于点O,下列结论错误的是()A.AC垂直平分BD B.图中共有三对全等三角形AC•BD C.∠OCD=∠ODC D.四边形ABCD的面积等于12【答案】C【解析】根据线段垂直平分线的判定和全等三角形的判定定理判断即可.【详解】∵AB=AD,CB=CD,∴AC垂直平分BD,故A正确;∴OB=OD,∵AO=AO,CO=CO,∴△ABO≌△ADO(SSS),△CBO≌△CDO(SSS),△ABC≌△ADC(SSS);故图中共有三对全等三角形,故B正确;∵OD不一定等于OC,∴∠OCD不一定等于∠ODC,故C错误;∵AC垂直平分BD,∴BO=DO,∵四边形ABCD的面积S=S△ABC+S△ADC=12AC×BO+12AC×DO=12AC×BD,故D正确,故选:C.【点睛】本题考查了全等三角形的判定和性质,线段垂直平分线的性质,三角形面积公式,熟练运用这些性质进行推理是本题的关键.17.下列命题中,正确的说法有()(1)两个图形关于某直线成轴对称,这两个图形一定全等;(2)直线l经过线段AB的中点,则l是线段AB的垂直平分线;(3)等腰三角形是轴对称图形,对称轴是顶角的角平分线;(4)等腰三角形两腰上的中线相等.A.1 个B.2 个C.3个D.4 个【答案】B【解析】【分析】根据轴对称的概念、线段垂直平分线的概念、等腰三角形的性质判断即可.【详解】(1)两个图形关于某直线成轴对称,这两个图形一定全等,本说法正确;(2)直线l经过线段AB的中点,并且垂直于线段AB,则l是线段AB 的垂直平分线,本说法错误;(3)等腰三角形是轴对称图形,对称轴是顶角的角平分线所在的直线,本说法错误;(4)等腰三角形两腰上的中线相等,本说法正确;故选:B.【点睛】本题考查轴对称的概念、线段垂直平分线的概念、等腰三角形的性质,解题的关键是掌握轴对称的概念、线段垂直平分线的概念、等腰三角形的性质.18.如图,在△ABC中,BD平分∠ABC,BC的垂直平分线交BC于点E,交BD于点F,连结CF和DE,若∠A=70°,∠DCF=50°,BC=8.则AB长为( )A.4 B.C.8 D.【答案】C【解析】【分析】根据角平分线的定义得到∠ABD=∠CBD,根据线段垂直平分线的性质得到FB=FC,得到∠FCB=∠CBD,根据三角形内角和定理得到∠BCA=∠A,根据等腰三角形的判定定理解答.【详解】解:∵BD平分∠ABC,∴∠ABD=∠CBD,∵EF是BC的垂直平分线,∴FB=FC,∴∠FCB=∠CBD,∴∠ABD=∠CBD=∠FCB,∠ABD+∠CBD+∠FCB+∠A+∠DCF=180°,解得,∠FCB=20°,∴∠BCA=70°,∴∠BCA=∠A,∴AB=BC=8,故选:C.【点睛】本题考查的是线段垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.19.如图,锐角三角形ABC中,O为三条边的垂直平分线的交点,I为三个角的平分线的交点,若∠BOC的度为x,∠BIC的度数为y,则x、y之间的数量关系是()A.x+y=90° B.x﹣2y=90°C.x+180°=2y D.4y﹣x=360°【答案】D【解析】【分析】根据线段垂直平分线的性质可得x=2∠A,根据角平分线的定义可得y=90°+1A,整理即可得到结论.2【详解】解:作OD⊥BC与点D,作OE⊥AB与点E,作OF⊥AC与点F,连接OA,∵O为三条边的垂直平分线的交点,∴OA=OB=OC,∴∠OBC=∠OCB, ∠OAB=∠OBA, ∠OAC=∠OCA,∵∠OBC+∠OCB+ ∠OAB+∠OBA+∠OAC+∠OCA=180°, ∠OBC+∠OCB=180°-x,∴180°-x+2∠A=180°,∠x=2∠A,∠I为三个角的平分线的交点,∠∠ABI=∠CBI, ∠ACI=∠BCI,y=180°-(12∠ABC+12∠ACB), ∠ABC+∠ACB=180°-∠A,∠y=90°+12∠A,∠y=90°+14 x,∠4y﹣x=360°,故选:D.【点睛】本题考查了线段垂直平分线的性质,角平分线的定义,三角形的内角和,正确的理解题意是解题的关键.20.在数学课上,老师提出如下问题;如图,已知ABC中,AB BC<,用尺规作图的方法在BC上取一点P,使得PA PB BC+=.下面是四个同学的作法,其中正确的是()A.B.C.D.【答案】C【解析】【分析】分别利用线段垂直平分线的性质结合圆的性质分析得出答案.【详解】A的作法:如图1,以点B为圆心,小于AB的长为半径画弧,交BC于点P,则点P就是所求的点.无法得出AP=BP,故无法得出PA+PB=BC,故此选项错误;B的作法:如图2,作线段AB的垂直平分线交BC于点P,则点P就是所求的点.PA=PB,不能得出PA=PC,故无法得出PA+PB=BC,故此选项错误;C的作法:如图3,作线段AC的垂直平分线交BC于点P,则点P就是所求的点.PA=PC,故得出PA+PB=PC+PB=BC,故此选项正确;...的平分线交BC于点P,则点P就是所求的点.不D的作法:如图4,作BAC能得出PA=PC,故无法得出PA+PB=BC,故此选项错误.故选:C【点睛】本题主要考查了复杂作图,正确把握线段垂直平分线的性质是解题关键.。
人教版_部编版八年级数学上册第十三章第一节线段的垂直平分线的性质考试复习题一(含答案) (133)
人教版_部编版八年级数学上册第十三章第一节线段的垂直平分线的性质考试复习题一(含答案) 如图(1),凸四边形ABCD,如果点P满足∠APD=∠APB=α.且∠BPC=∠CPD=β,则称点P为四边形ABCD的一个半等角点.(1)在图(3)正方形ABCD内画一个半等角点P,且满足α≠β;(2)在图(4)四边形ABCD中画出一个半等角点P,保留画图痕迹(不需写出画法);(3)若四边形ABCD有两个半等角点P1、P2(如图(2)),证明线段P1P2上任一点也是它的半等角点.【答案】(1)所画的点P在AC上且不是AC的中点和AC的端点.(2)画点B关于AC的对称点B’,延长DB’交AC于点P,点P为所求(不写文字说明不扣分).(3)证明见解析【解析】【分析】(1)根据题意可知,所画的点P在AC上且不是AC的中点和AC的端点.因为在图形内部,所以不能是AC的端点,又由于α≠β,所以不是AC的中点.(2)画点B关于AC的对称点B’,延长DB’交AC于点P,点P为所求.(因为对称的两个图形完全重合)(3)先连P1A、P1D、P1B、P1C和P2D、P2B,根据题意∠AP1D=∠AP1B,∠DP1C=∠BP1C∠∠AP1B+∠BP1C=180度.∠P1在AC上,同理,P2也在AC 上,再利用ASA证明∠DP1P2∠∠BP1P2而,那么∠P1DP2和∠P1BP2关于P1P2对称,P是对称轴上的点,所以∠DPA=∠BPA,∠DPC=∠BPC.即点P是四边形的半等角点【详解】(1)所画的点P在AC上且不是AC的中点和AC的端点.(2)画点B关于AC的对称点B’,延长DB’交AC于点P,点P为所求(不写文字说明不扣分).(3)连P1A、P1D、P1B、P1C和P2D、P2B,根据题意,∠AP1D=∠AP1B,∠DP1C=∠BP1C,∠∠AP1B+∠BP1C=180度.∠P1在AC上,同理,P2也在AC上.在∠DP1P2和∠BP1P2中,∠DP2P1=∠BP2P1,∠DP1P2=∠BP1P2,P1P2公共,∠∠DP1P2∠∠BP1P2.所以DP1=BP1,DP2=BP2,于是B、D关于AC对称.设P是P1P2上任一点,连接PD、PB,由对称性,得∠DPA=∠BPA,∠DPC=∠BPC,所以点P是四边形的半等角点.22.按要求作图(不写作法,但要保留作图痕迹)已知点P、Q分别在∠AOB的边OA,OB上(如图所示)①作直线PQ;②过点P作OB的垂线;③过点Q作OA的平行线.【答案】详见解析【解析】【分析】①用直尺过Q,P画直线即可;②让三角尺的直角的一边与OB重合,另一直角边经过点P画出垂线,即为0B边上的垂线;③过点Q作∠EQB=∠O,即可得出OA的平行线.【详解】解:如图所示:【点睛】此题考查学生的基本作图能力.23.如图,AB=AC,∠A=50°,AB的垂直平分线MN交AC于点D,求∠BCD各角的度数.【答案】15o【解析】【分析】根据线段垂直平分线性质可得AD=BD,证∠DAB=∠DBA,∠ABC=∠ACB=65o可得结论.【详解】解:∵MN垂直平分AB∴AD=BD∴∠DAB=∠DBA=50o∴∠BDC=100o∵AC=BC∴∠ABC=∠ACB=65o又∵∠DBA=50o∴∠DBC=15o【点睛】线段垂直平分线性质.24.已知:如图,AB=AE,BC=ED,AF是CD的垂直平分线,求证:∠B=∠E.【答案】略【解析】【详解】证明:连接AC,AD∵AF⊥CD且F是CD的中点∴可知AF 是CD 的垂直平分线,线段垂直平分线上的点到线段两端的距离相等∴AC=AD ,在ABC ∆和AED ∆中{AB AEBC ED AC AD===()ABC AED SSS ∴∆≅∆B E ∴∠=∠25.已知: ∠AOB,点M 、N.求作:点P ,使点P 在∠AOB 的平分线上,且PM=PN.(要求:用尺规作图,保留作图痕迹,不写作法)【答案】点P 就是所求的点【解析】作出∠AOB 的平分线;连接MN ,作出MN 的垂直平分线,角平分线与垂直平分线的交点即为所求的点.26.环城一周的民心河是石家庄一道靓丽的风景线,民心河的水源来自滹沱河上游的水库,年耗水量达3000多万立方米,占石家庄用水量的八分之一.为了缓解这种用水负担,现规划一座污水处理厂,向民心河东线和西线供水,为了节约资金,计划把处理厂建在到东线和西线距离相等的位置,但还要求处理厂到两个污水储存池M、N的距离也相等,如果你作为设计师你认为应把污水处理厂建在何处?并简要说明你设计的理由.【答案】见解析【解析】【分析】根据角平分线上的点到角的两边距离相等,作出东线与西线夹角的平分线,根据垂直平分线上的点到线段两端的距离相等,作出MN的垂直平分线,角平分线与垂直平分线的交点就是污水处理厂的位置.【详解】如图所示,污水处理厂建在P点,理由如下:根据角平分线上的点到角的两边距离相等,可得P点到东线与西线的距离相等,根据垂直平分线上的点到线段两端的距离相等,可得P点到M,N的距离相等,所以P点就是污水处理厂的位置.27.如图(1),一群小孩以同样的速度同时从A村出发到B村,要过一条公路a,其中只有一个小孩用最快的时间到达B村.你知道这个聪明的小孩的行程路线吗?在图上标出示意图.如图(2),在公路的同侧有两村庄,要在公路上建立一个站点,使到A、B 两村的距离相等,请标出站点位置.【答案】0,4【解析】(1)根据两点之间,线段最短可知,连接AB,线段AB就是小孩的行程路线;(2)到两村距离相等,即作出线段AB的中垂线与a相交,交点即为站点位置.28.如图,AD是∠ABC的角平分线,DE,DF分别是∠ABD和∠ACD的高.AD和EF有什么关系?请说明理由.【答案】AD垂直平分EF,理由见解析【解析】【分析】先利用角平分线的性质证明∠AED∠∠AFD,及DE=DF,再利用全等三角形的性质得到AE=AF,即可得到AD垂直平分EF【详解】解:AD垂直平分EF,理由如下∠AD是∠ABC的角平分线,且DE,DF分别是∠ABD和∠ACD的高∠DE=DF,∠DEA=∠DFA=90°,在Rt∠AED和Rt∠AFD中AD=AD∴Rt∠AED∠Rt∠AFD∴AE=AF又DE=DF∠AD垂直平分EF29.如图,在∠ABC中,∠A=50°,∠C=65°,AB=12,BC=10,DE垂直平分AB交AC、AB于E、D两点.求:(1)∠EBC的度数;(2)∠BCE的周长.【答案】(1) 15°;(2)22【解析】【分析】(1)根据三角形的内角和定理求出∠ABC,再根据线段垂直平分线上的点到线段两端点的距离相等可得EB=EA,根据等边对等角的性质求出∠ABE=∠A,然后求解即可;(2)根据角的度数求出∠ABC=∠C,再根据等角对等边可得AB=AC,然后求出△BCE的周长=AC+BC,然后代入数据进行计算即可得解.【详解】解:(1)在△ABC中,∠A=50°,∠C=65°,∴∠ABC=180°-(∠A+∠C)=180°-(50°+65°)=65°,∵DE是线段AB的垂直平分线,∴EB=EA,∴∠ABE=∠A=50°,∴∠EBC=∠ABC-∠ABE=65°-50°=15°;(2)∵∠ABC=∠C=65°,∴AC=AB=12,∵EA=EB,∴EB+EC=EA+EC=AC=12,∴△BCE的周长=AC+BC=12+10=22.【点睛】考查了线段垂直平分线上的点到线段两端点的距离相等的性质,三角形的内角和定理,等边对等角的性质,熟记性质是解题的关键.30.如图,∠ABC中,AC的垂直平分线DE交AC于点E,交BC于点D, 若AB=DC,∠C=35°,求∠B的度数.【答案】70∘【解析】【分析】连接AD,根据垂直平分线的性质得AD=CD,则∠DAC=∠C=35∘,再利用三角形的外角定理得∠ADB=∠DAC+∠C=35∘+35∘=70∘,再根据等腰三角形的性质得∠B=∠ADB=70∘.【详解】解:连接AD,∵DE垂直平分AC ,∴DA=DC,∵∠C=35∘,∴∠DAC=∠C=35∘∴∠ADB=∠DAC+∠C=35∘+35∘=70∘∵AB=DC,∴AB=AD,∴∠B=∠ADB=70∘.。
专题13.2线段的垂直平分线专题(限时满分培优训练)-【拔尖特训】2024-2025学年八年级数学上
【拔尖特训】2024-2025学年八年级数学上册尖子生培优必刷题(人教版)专题13.2线段的垂直平分线专题(限时满分培优训练)班级:___________________ 姓名:_________________ 得分:_______________注意事项:本试卷满分100分,试题共23题,其中选择10道、填空6道、解答7道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.(2022秋•防城港期末)如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,连接AE,若AE=4,EC=2,则BC的长是()A.8B.6C.4D.22.(2022秋•东宝区期末)和三角形三个顶点的距离相等的点是()A.三条角平分线的交点B.三边中线的交点C.三边上高所在直线的交点D.三边的垂直平分线的交点3.(2022秋•黄石港区期末)如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AB,AC于点M,N,△BCN的周长是7cm,则BC的长为()A.4cm B.3 cm C.2cm D.1cm4.(2022秋•长安区校级期末)某地兴建的幸福小区的三个出口A、B、C的位置如图所示,物业公司计划在不妨碍小区规划的建设下,想在小区内修建一个电动车充电桩,以方便业主,要求到三个出口的距离都相等,则充电桩应该在△ABC()A.三条高线的交点处B.三条中线的交点处C.三个角的平分线的交点处D.三条边的垂直平分线的交点处5.(易错题)(2023秋•青秀区校级月考)已知:△ABC是三边都不相等的三角形,点P是三个内角平分线的交点,点O是三边垂直平分线的交点,当P、O同时在不等边△ABC的内部时,那么∠BOC和∠BPC 的数量关系是()A.2∠BOC+∠BPC=360°B.∠BOC+2∠BPC=360°C.3∠BOC﹣∠BPC=360°D.4∠BPC﹣∠BOC=360°6.(易错题)(2022秋•汉南区校级期末)如图,锐角三角形ABC中,O为三条边的垂直平分线的交点,I 为三个角的平分线的交点,若∠BOC的度数为x,∠BIC的度数为y,则x、y之间的数量关系是()A.x+y=90°B.x﹣2y=90°C.x+180°=2y D.4y﹣x=360°7.(易错题)(2022秋•东阿县校级期末)如图,线段AB,BC的垂直平分线l1、l2相交于点O.若∠OEB =46°,则∠AOC=()A.92°B.88°C.46°D.86°8.(易错题)(2022春•雅安期末)如图所示,在△ABC中,DM,EN分别垂直平分AB和AC,交BC于点D,E,若∠DAE=40°,则∠BAC=()A.105°B.100°C.110°D.140°9.(培优题)(2022春•舞钢市期末)如图,四边形ABCD中,DE和DF恰好分别垂直平分AB和BC,则以下结论不正确的是()A.AD=CD B.∠B=∠A+∠CC.∠EDF=∠ADE+∠CDF D.BE=BF10.(培优题)(2022春•周村区期末)如图,在△ABC中,∠BAC=80°,边AB的垂直平分线交AB于点D,交BC于点E,边AC的垂直平分线交AC于点F,交BC于点G,连接AE,AG.则∠EAG的度数为()A.35°B.30°C.25°D.20°二.填空题(共6小题)11.(2022秋•句容市期末)如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,连接AE,若AE=4,EC=2,则BC的长.12.(2022秋•德城区校级期末)如图,在△ABC中,AF平分∠BAC,AC的垂直平分线DE交BC于点E,交AC于点D,∠B=70°,∠F AE=19°,则∠C=°.13.(易错题)(2023春•甘州区校级期末)如图,在△ABC中,AC的垂直平分线与AC,BC分别交于点E,D,CE=4,△ABC的周长是25,则△ABD的周长为.14.(易错题)(2023春•荔湾区期末)在平面直角坐标系中,已知A(8,0),B(0,4),作AB的垂直平分线交x轴于点C,则点C坐标为.15.(2023春•振兴区校级期中)如图,AE是∠CAM的角平分线,点B在射线AM上,DE是线段BC的中垂线交AE于E,过点E作AM的垂线交AM于点F.若∠ACB=26°,∠EBD=25°,则∠AED=.16.(2023春•振兴区校级期中)如图,在△ABC中,边AB的垂直平分线OM与边AC的垂直平分线ON交于点O,这两条垂直平分线分别交BC于点D、E.已知△ADE的周长为11cm,分别连接OA、OB、OC,若△OBC的周长为23cm,则OA的长为.三.解答题(共7小题)17.(2023•渭南一模)如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高,求证:AD 垂直平分EF.18.(2022春•合浦县期中)如图,已知点D是BC上一点,DE⊥AB,DF⊥AC,垂足分别为E、F,连接AD,若AD垂直平分EF,求证:AD是△ABC的角平分线.19.(易错题)(2023春•新民市期中)如图,在△ABC中,∠C=90°,点P在AC上运动,点D在AB上,PD始终保持与P A相等,BD的垂直平分线交BC于点E,交BD于点F,连接DE.(1)判断DE与DP的位置关系,并说明理由;(2)若AC=6,BC=8,P A=2,求线段DE的长.20.(易错题)(2023春•丰城市期末)如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G.(1)若BC=9,求△AEG的周长.(2)若∠BAC=130°,求∠EAG的度数.21.(培优题)(2023春•榆林期末)如图,在△ABC中,AC边的垂直平分线分别交BC、AC于点E、F,连接AE,作AD⊥BC于点D,且D为BE的中点.(1)试说明:AB=CE;(2)若∠C=32°,求∠BAC的度数.22.(培优题)(2023春•定边县校级期末)已知,如图,AD是△ABC的高线,AD的垂直平分线分别交AB,AC于点E,F.(1)若∠B=40°,求∠AEF的度数;(2)求证:∠B=12∠AED.23.(培优题)(2023春•兴庆区校级期末)如图,△ABC中,D、E在AB上,且D、E分别是AC、BC的垂直平分线上一点.(1)若△CDE的周长为4,求AB的长;(2)若∠ACB=100°,求∠DCE的度数;(3)若∠ACB=a(90°<a<180°),则∠DCE=.。
专题 垂直平分线的性质(含答案)
专题垂直平分线的性质一.解答题(共12小题)1.如图,AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D,求∠DBC的度数.2.如图,在△ABC中,∠B=30°,边AB的垂直平分线分别交AB、BC于D、E两点,连接AE,若AE平分∠BAC,求∠C的度数.3.如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAE=10°,求∠C的度数.4.如图所示,在△ABC中,MP和NQ分别垂直平分AB和AC,MP分别交AB、BC于M、P两点,NQ分别交AC、BC于N、Q两点,连接AP、AQ.(1)若△APQ的周长为18,求BC的长;(2)若∠BAC=110°,求∠PAQ的度数.5.如图,△ABC中,边AB、AC的垂直平分线ED、GF分别交AB、AC于点E、G,交BC于点D、F,连接AD,AF,若∠DAF=40°,求∠BAC的度数.6.如图,在△ABC中,∠C=90°,边AB的垂直平分线DE交AC于D.CA=16cm,BC=8cm,求DC的长度;7.如图,在△ABC中,BC边的垂直平分线交AC边于点D,连接BD.(1)如图CE=4,△BDC的周长为18,求BD的长.(2)求∠ADM=60°,∠ABD=20°,求∠A的度数.8.如图,在△ABC中,∠C=90°,DE为AB的垂直平分线,DE交AC于点D,连接BD.若∠ABD=2∠CBD,求∠A的度数.9.如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.(1)若∠BAE=40°,求∠C的度数;(2)若△ABC周长13cm,AC=6cm,求DC长.10.如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.(1)若BC=10,则△ADE周长是多少?为什么?(2)若∠BAC=128°,则∠DAE的度数是多少?为什么?11.在△ABC中,DE垂直平分AB,分别交AB、BC于点D、E,MN垂直平分AC,分别交AC、BC于点M、N,连接AE,AN.(1)如图1,若∠BAC=100°,求∠EAN的度数;(2)如图2,若∠BAC=70°,求∠EAN的度数;专题垂直平分线的性质参考答案与试题解析一.解答题(共12小题)1.【解答】解:∵AB=AC,∴∠ABC=∠ACB ==70°,∵MN的垂直平分AB,∴DA=DB,∴∠A=∠ABD=40°,∴∠DBC=∠ABC﹣∠ABD=70°﹣40°=30°.故答案为:30°.2.【解答】解:∵DE是线段AB的垂直平分线,∠B=30°,∴∠BAE=∠B=30°,∵AE平分∠BAC,∴∠EAC=∠BAE=30°,即∠BAC=60°,∴∠C=180°﹣∠BAC﹣∠B=180°﹣60°﹣30°=90°.3.【解答】解:∵∠B=90°,∠BAE=10°,∴∠BEA=80°.∵ED是AC的垂直平分线,∴AE=EC,∴∠C=∠EAC.∵∠BEA=∠C+∠EAC,∴∠C=40°.4.(【解答】解:(1)∵MP和NQ分别垂直平分AB和AC,∴PA=PB,QA=QC,∵△APQ的周长为18,∴AP+PQ+AQ=BP+PQ+QC=18,∴BC=18;(2)∵∠BAC=110°,∴∠B+∠C=70°,∵PA=PB,QA=QC,∴∠PAB=∠B,∠QAC=∠C,∴∠PAB+∠QAC=∠B+∠C=70°,∴∠PAQ=40°.5.【解答】解:在△ADF中,∵∠DAF=40°,∴∠ADF+∠AFD=180°﹣40°=140°,∵边AB、AC的垂直平分线ED、GF分别交AB、AC于点E、G,∴AD=BD,AF=CF,∴∠BAD=∠B,∠CAF=∠C,∴∠ADF=∠BAD+∠B=2∠B,∠AFD=∠CAF+∠C=2∠C,∴2∠B+2∠C=∠ADF+∠AFD=140°,∴∠B+∠C=70°,∴∠BAC=180°﹣(∠B+∠C)=110°.6.【解答】解:(1)∵DE垂直平分线段AB,∴DA=DB,设CD=x,则AD=BD=(16﹣x)cm,在Rt△BDC中,∵BD2=CD2+BC2,∴(16﹣x)2=x2+82,∴x=6,∴CD=6cm.7.【解答】解:(1)∵MN垂直平分BC,∴DC=BD,CE=EB,又∵EC=4,∴BE=4,又∵△BDC的周长=18,∴BD+DC=10,∴BD=5;(2)∵∠ADM=60°,∴∠CDN=60°,又∵MN垂直平分BC,∴∠DNC=90°,∴∠C=30°,又∵∠C=∠DBC=30°,∠ABD=20°,∴∠ABC=50°,∴∠A=180°﹣∠C﹣∠ABC=100°.8.【解答】解:∵DE为AB的垂直平分线,∴∠A=∠ABD,又∵∠ABD=2∠CBD,∴∠A=∠ABD=2∠CBD,设∠A=α,则∠ABD=α,∠CBD =α,又∵∠C=90°,∴∠A+∠ABC=90°,即α+α+α=90°,解得α=36°,∴∠A=36°.9.【解答】解:(1)∵AD垂直平分BE,EF垂直平分AC,∴AB=AE=EC,∴∠C=∠CAE,∵∠BAE=40°,∴∠AED=70°,∴∠C =∠AED=35°;(2)∵△ABC周长13cm,AC=6cm,∴AB+BE+EC=7cm,即2DE+2EC=7cm,∴DE+EC=DC=3.5cm.10.【解答】解:(1)C△ADE=10.(1分)∵AB、AC的垂直平分线分别交BC于D、E,∴AD=BD,AE=CE.(3分)C△ADE=AD+DE+AE=BD+DE+CE=BC=10.(4分)(2)∠DAE=76°.(5分)∵AB、AC的垂直平分线分别交BC于D、E,∴AD=BD,AE=CE.∴∠B=∠BAD,∠C=∠CAE.∵∠BAC=128°,∴∠B+∠C=52°.(7分)∴∠DAE=∠BAC﹣(∠BAD+∠CAE)=∠BAC﹣(∠B+∠C)=76°.(8分)11.【解答】解:(1)∵DE垂直平分AB,∴AE=BE,∴∠BAE=∠B,同理可得:∠CAN=∠C,∴∠EAN=∠BAC﹣∠BAE﹣∠CAN,=∠BAC﹣(∠B+∠C),在△ABC中,∠B+∠C=180°﹣∠BAC=80°,∴∠EAN=∠BAC﹣(∠BAE+∠CAN)=100°﹣80°=20°;(2)∵DE垂直平分AB,∴AE=BE,∴∠BAE=∠B,同理可得:∠CAN=∠C,∴∠EAN=∠BAE+∠CAN﹣∠BAC,=(∠B+∠C)﹣∠BAC,在△ABC中,∠B+∠C=180°﹣∠BAC=110°,∴∠EAN=∠BAE+∠CAN﹣∠BAC=110°﹣70°=40°;温馨提示:最好仔细阅读后才下载使用,万分感谢!。
线段的垂直平分线、角平分线经典习题及答案
线段的垂直平分线、角平分线经典习题及答案由于A、B都在CD的垂直平分线上,所以直线AB是CD的垂直平分线。
证毕。
例4:解:连接EF,由于AB=AC,所以∠BAC=60°,∴∠DEG=30°,∠GFC=60°,又因为DE⊥AB,FG⊥AC,所以DEGF是一个菱形,且DG=GF=7.5cm,所以EG=2DGsin30°=7.5cm。
例5:证明:因为BD=BC,所以∠XXX∠CBD,又因为BE⊥CD,CF⊥BD,所以∠BEC=∠BCF,所以BE平分∠XXX,CF平分∠CBD,又因为∠XXX∠CBD,所以BE和CF都平分∠BCD,即BE垂直平分CD。
证毕。
例6:证明:连接OF,OE,MN,∵MN∥BC,∴∠EOF=∠ACB,又∠XXX∠EOM+∠MOF,∠XXX∠EOM+∠EOF,∴∠MOF=∠ACB-∠EOF,又因为EF是AC的角平分线,∴∠XXX∠EAF,又因为EF是AC的外角平分线,∴∠XXX∠XXX,∴∠MOF=∠ACB-∠XXX,又因为OE⊥AC,OF⊥AC,所以OE=OF,证毕。
例7:证明:连接AD,因为AD是∠A的平分线,所以∠EAD=∠FAD,又因为BD=BC,所以∠XXX∠DCB,又因为AD⊥DE,所以∠EDB=90°-∠XXX,又因为DF⊥CF,所以∠XXX°-∠DCB,所以∠EDB=∠XXX,又因为∠EAD=∠FAD,所以三角形ADE与三角形ADF全等,所以DE=DF,又因为BE⊥DE,CF⊥DF,所以BE=DEsin∠EDB=DFsin∠FDC=CF,证毕。
例4:根据题意,作AH垂直BC于点H,可以得到HC 的长度为15/2.由于△ABC是等腰三角形,所以∠ACB=∠ABC=30°。
根据正弦定理,可以求得AC的长度为5√3.由于F是AC的中点,所以FC的长度为5/2√3.根据勾股定理,可以得到CG和BE的长度都为5.因此,EG的长度也为5.例5:由于DE垂直于AB,而∠ACB=90°,所以∠BDE=∠ACB=90°。
