噪声估计算法范文
噪声系数的计算及测量方法

噪声系数的计算及测量方法(一)时间:2012-10-25 14:32:49 来源:作者:噪声系数(NF)是RF系统设计师常用的一个参数,它用于表征RF放大器、混频器等器件的噪声,并且被广泛用作无线电接收机设计的一个工具。
许多优秀的通信和接收机设计教材都对噪声系数进行了详细的说明.现在,RF应用中会用到许多宽带运算放大器和ADC,这些器件的噪声系数因而变得重要起来。
讨论了确定运算放大器噪声系数的适用方法。
我们不仅必须知道运算放大器的电压和电流噪声,而且应当知道确切的电路条件:闭环增益、增益设置电阻值、源电阻、带宽等。
计算ADC的噪声系数则更具挑战性,大家很快就会明白此言不虚。
公式表示为:噪声系数NF=输入端信噪比/输出端信噪比,单位常用“dB”。
该系数并不是越大越好,它的值越大,说明在传输过程中掺入的噪声也就越大,反应了器件或者信道特性的不理想。
在放大器的噪声系数比较低的情况下,通常放大器的噪声系数用噪声温度(T)来表示。
噪声系数与噪声温度的关系为:T=(NF-1)T0 或NF=T/T0+1 其中:T0-绝对温度(290K)噪声系数计算方法研究噪声的目的在于如何减少它对信号的影响。
因此,离开信号谈噪声是无意义的。
从噪声对信号影响的效果看,不在于噪声电平绝对值的大小,而在于信号功率与噪声功率的相对值,即信噪比,记为S/N(信号功率与噪声功率比)。
即便噪声电平绝对值很高,但只要信噪比达到一定要求,噪声影响就可以忽略。
否则即便噪声绝对电平低,由于信号电平更低,即信噪比低于1,则信号仍然会淹没在噪声中而无法辨别。
因此信噪比是描述信号抗噪声质量的一个物理量。
1 噪声系数的定义要描述放大系统的固有噪声的大小,就要用噪声系数,其定义为设Pi为信号源的输入信号功率,Pni为信号源内阻RS产生的噪声功率,Po和Pno 分别为信号和信号源内阻在负载上所产生的输出功率和输出噪声功率,Pna表示线性电路内部附加噪声功率在输出端的输出。
噪声预测思路
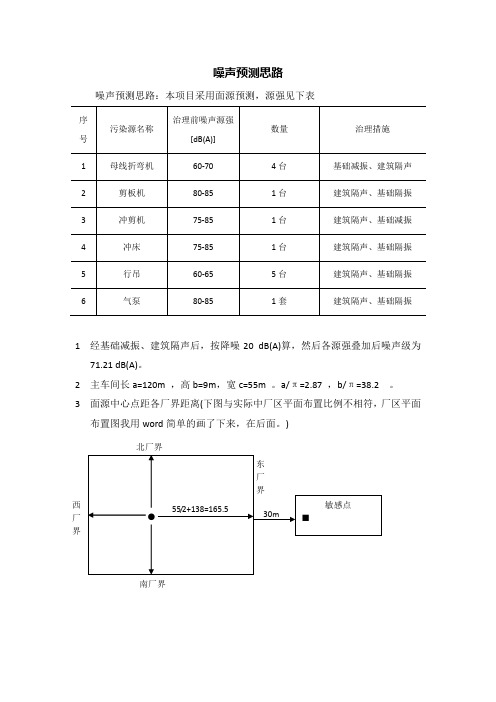
噪声预测思路噪声预测思路:本项目采用面源预测,源强见下表1 经基础减振、建筑隔声后,按降噪20 dB(A)算,然后各源强叠加后噪声级为71.21 dB(A)。
2 主车间长a=120m ,高b=9m ,宽c=55m 。
a/π=2.87 ,b/π=38.2 。
3 面源中心点距各厂界距离(下图与实际中厂区平面布置比例不相符,厂区平面布置图我用word 简单的画了下来,在后面。
)西厂界 北厂界南厂界声环境影响面源预测模式采用公式如下:当r≤a/π时,噪声传播途中的声压级值与距离无关,基本无明显衰减;当a/π≤r≤b/π时,声源面可近似为线源,预测公式为:L(r)=L(r0)-10log(r/r0)-ΔL;当r≥b/π时,可近似认为声源为点源,预测公式为:L(r)=L(r0)-20log(r/r0)-ΔL;r0 =1m,ΔL=0 面源中心源强叠加后噪声级为71.21dB(A) (1)西厂界:a/π≤r1≤b/π ,则L(r1)=L(r0)-10log(r/r0)-ΔL =71.21-14.98-0=56.23 dB(A) (2)北厂界:r2≥b/π ,则L(r2)=L(r0)-20log(r/r0)-ΔL=71.21-36.26-0=34.95 dB(A) (3)南厂界:r3≥b/π ,则L(r3)=L(r0)-20log(r/r0)-ΔL=71.21-38.4-0=32.81 dB(A) (4)东厂界:r4≥b/π ,则L(r4)=L(r0)-20log(r/r0)-ΔL=71.21-44.4-0=26.81 dB(A) (5)敏感点:r5≥b/π ,则L(r5)=L(r0)-20log(r/r0)-ΔL=71.21-45.82-0=25.39 dB(A)。
空间噪声计算公式(一)

空间噪声计算公式(一)空间噪声计算公式引言空间噪声是城市环境中一个重要的环境问题,它直接影响到人们的生活质量和健康状况。
为了评估、监测和控制空间噪声,需要使用合适的计算公式来对其进行量化分析。
以下列举了一些常见的空间噪声计算公式,并提供了相应的解释和示例。
等效声级(Leq)等效声级是指在一定时间内,各级声级加权值和声级平方和的总和,经一系列计算得到的一个对于平均声级的指示值。
计算公式:Leq = 10 * log10(1/T * ∫(10^(L/10))dt)其中,Leq表示等效声级,T表示时间段,L表示每个时间段内的声级。
示例:假设在一个小时内,噪声水平分别为60、70、80分贝,时间均匀分布。
则等效声级的计算可以按照以下步骤进行: 1. 将分贝转换为声级:L1 = 10^(60/10), L2 = 10^(70/10), L3 =10^(80/10) 2. 计算声级平方和:(L1^2 + L2^2 + L3^2) 3. 除以时间段:(L1^2 + L2^2 + L3^2) / 3600 4. 取对数并乘以10:10 * log10((L1^2 + L2^2 + L3^2) / 3600)等效声源级(Lw)等效声源级是指与某个特定声源产生的噪声等效的单一理想点源的声级。
计算公式:Lw = Leq + 10 * log10(Ac/A)其中,Lw表示等效声源级,Leq表示等效声级,Ac表示等效源面积,A表示实际距离远离噪声源的点的面积。
示例:假设在距离噪声源10米处,等效声级为70分贝,测点面积10平方米,远离噪声源的点面积100平方米。
根据上述计算公式,可以计算出等效声源级: Lw = 70 + 10 * log10(100/10)噪声减幅(NR)噪声减幅是指噪声信号在传播过程中,由于各种因素(如距离衰减、障碍物阻挡等)引起的声级衰减。
计算公式:NR = L1 - L2其中,NR表示噪声减幅,L1表示噪声源级,L2表示接收点处的声级。
相关噪声中的TOA估计算法研究

相关噪声中的TOA估计算法研究戴红霞;丁一坤;赵力【摘要】In the actual environment,there are often cases where the signalis related to noise. Therefore,an efficient and accurate channel parameter estimation algorithm in a correlated noise environment is very important for the construction of a wireless communication system. This paper first studies the TOA parameter estimation algorithm based on the MUSIC algorithm. The simulation shows that this algorithm performs well in the white Gaussian noise environment,but it is not suitable for the relevant noise environment. For the relevant noise environment,we studied the improved MUSIC algorithm in TOA parameter estimation and verified it by simulation. Simulation results show that the improved algorithm can be applied to high-resolution TOA estimate in correlated noise environment.%实际环境中,常存在信号与噪声相关的情况,因此相关噪声环境中高效准确的信道参数估计算法的研究对于无线通信系统的构建至关重要.首先研究了基本MUSIC算法的TOA参数估计算法,仿真表明此种算法在高斯白噪声环境表现良好,但是并不适合相关噪声环境.针对相关噪声环境,研究了TOA参数估计中的MUSIC改进算法,并进行了仿真验证.仿真结果表明,改进算法完全可以适合于相关噪声环境中进行高分辨率TOA估计.【期刊名称】《电子器件》【年(卷),期】2018(041)003【总页数】5页(P725-729)【关键词】相关噪声;TOA估计;MUSIC算法【作者】戴红霞;丁一坤;赵力【作者单位】江苏信息职业技术学院电子信息工程系,江苏无锡214153;东南大学信息科学与工程学院南京210096;东南大学信息科学与工程学院南京210096【正文语种】中文【中图分类】TN911.7近几年来,无线通信技术飞速发展,并且在通信领域中开辟了一块崭新的世界。
噪声估计算法

太原理工大学毕业设计(论文)任务书噪声估计算法的研究及MATLAB仿真摘要日常的通信过程中,语音会常常受到环境噪声的干扰而使通话质量下降,严重时使得语音处理系统不能正常工作。
因此,必须采用信号处理方法通过语音增强来抑制背景噪声从而提高语音通信质量,而噪声估计的准确性又直接影响语音的增强效果。
可见,噪声估计是语音增强的一个非常重要的部分,所以研究噪声估计算法有很好的实用价值。
本文主要研究两种噪声估计算法:基于最小统计和最优平滑的噪声估计算法和最小值控制递归平均法的噪声估计算法,通过实验仿真比较最终研究了一种改进的最小值统计量控制递归平均噪声估计算法。
本文的主要工作总结归纳为以下几方面:首先,本文对几种经典的噪声估计算法进行研究,了解它们的各自优缺点,在此基础上选定两种较好的算法进行具体分析。
其次,了解最小统计和最优平滑和噪声功率谱统计跟踪的噪声估计算法的原理,它的基本思路是先用最优平滑滤波器对带噪语音的功率谱滤波,得到一个噪声的粗略估计,然后找出粗略估计噪声中的在一定时间窗内的最小值,对这个最小值进行一些偏差修正,即得到所要估计的噪声的方差。
通过MATLAB仿真看其特征。
再次,研究了基于非平稳噪声的估计算法,最后通过比较研究了一种改进的最小值控制递归平均算法。
算法采用递归平均进行噪声估计,其递归平均的平滑量控制递归平均噪声估计算因子受语音存在概率控制,而语音存在概率的计算采用了两次平滑和最小统计量跟踪。
与I.Cohen提出的IMCRA算法相比,本文研究采用了一种快速有效的最小统计量跟踪算法。
仿真结果表明:在非平稳噪声条件下,该算法具有较好的噪声跟踪能力和较小的噪声估计误差,可以有效地提高语音增强系统的性能。
最后,对整体论文总结,通过研究发现改进的最小统计量控制递归平均噪声算法在IMCRA算法的基础上,采用了一种简单有效地最小统计量估计算法,在保证噪声估计准确性的同时,减小了算法的复杂度。
同时,基于这种噪声估计的语音增强系统能有效地提高增强语音的信噪比,并且能有效地消除增强语音中的音乐噪声。
噪音计算方法rms

噪音计算方法rms嘿,朋友们!今天咱来聊聊这个噪音计算方法 RMS。
啥是 RMS 呀?简单来说,它就像是一把尺子,专门用来衡量噪音有多大的尺子呢!你想想看,我们生活中到处都有声音,有好听的音乐声,有鸟儿的叫声,可也有那些让我们心烦意乱的噪音呀!那怎么知道这些噪音到底有多厉害呢?这时候 RMS 就派上用场啦。
它可不是随随便便就得出结果的哦。
就好像我们要知道一个人的身高,不能只看一眼就说个大概吧,得用尺子好好量一量才行。
RMS 计算也是一样,要通过一系列复杂的步骤和运算呢。
比如说,我们得先把噪音的信号收集起来,就像把那些声音都装进一个小盒子里。
然后呢,再对这些信号进行各种处理和分析,找出它们的特点和规律。
这可不是一件容易的事儿呀,就跟解开一道很难的数学题似的。
那有人可能会问啦,这 RMS 计算出来有啥用呢?用处可大啦!比如在一些工厂里,要是噪音太大,不仅会影响工人的工作效率,还可能对他们的身体健康造成伤害呢。
这时候通过 RMS 计算,就能知道噪音到底有多严重,然后采取相应的措施来降低噪音呀。
再比如在我们居住的小区里,如果有个地方总是很吵,那大家肯定都不高兴呀。
通过 RMS 计算,就能找到噪音的源头,然后想办法解决问题,让大家的生活环境变得安静舒适。
而且哦,这 RMS 计算还挺神奇的呢。
它就像一个聪明的小侦探,能从那些乱七八糟的声音里找出关键信息,然后告诉我们噪音的真相。
你说这是不是很有意思呀?我们平时可能觉得噪音就是吵吵嚷嚷的,没想到背后还有这么一套计算方法来衡量它呢。
就好像我们看一个人,不能只看表面,还要深入了解他的内心一样。
所以啊,下次当你再听到噪音的时候,不妨想想这个神奇的 RMS计算方法,想想它是怎么工作的,怎么帮我们解决噪音问题的。
说不定你会对噪音有一个全新的认识呢!总之呢,RMS 虽然听起来有点复杂,但它可是在我们的生活中有着重要作用的哦。
它能让我们更好地了解噪音,更好地应对噪音带来的挑战。
噪声计算公式范文

噪声计算公式范文1.均方根噪声公式:均方根噪声是一种表示噪声强度的常见指标,可用以下公式计算:RMS=√(∑(x_i)^2/n)其中,x_i表示每个测量值,n表示测量值数量。
2.分贝噪声公式:分贝是用于度量噪声强度的常见单位,可用以下公式计算:L = 10 * log10(P / P0)其中,L表示噪声级别(单位:分贝),P表示实际声压级,P0表示参考声压级(一般取20微帕)。
3.白噪声计算公式:白噪声是一种在所有频率上具有相等功率的噪声信号,可以用以下公式计算:S=k*√(B)其中,S表示白噪声的功率密度(单位:瓦特/赫兹),k是常数(常取1),B表示频率带宽。
4.声压级公式:声压级是用于描述声音强度的指标,可用以下公式计算:L_p = 20 * log10(p / p0)其中,L_p表示声压级(单位:分贝),p表示实际声压,p0表示参考声压(一般取20微帕)。
5.频率加权噪声计算公式:频率加权噪声用于考虑不同频率下噪声对人耳的影响,常用的加权曲线有A、B、C、D等L_w=L*W其中,L_w表示频率加权噪声级别,L表示未加权的噪声级别,W表示频率加权因子。
6.噪声指数计算公式:噪声指数是对噪声特性进行描述的指标,可用以下公式计算:NI=∑(L_i*W_i)/∑W_i其中,NI表示噪声指数,L_i表示每个频率段的加权噪声级别,W_i 表示每个频率段的权重。
以上是一些常见的噪声计算公式,它们可以根据具体情况进行选择和应用,用于对不同噪声情况进行分析和评估。
需要注意的是,不同的应用领域可能会有不同的噪声描述和计算要求,因此在具体使用时需要根据实际情况进行相应的调整和修正。
噪声计算公式范文

噪声计算公式范文1.声压级(SPL)计算公式:声压级是噪声强度的常用指标,通常以分贝(dB)为单位。
声压级的计算公式如下:SPL = 20 * log10(p/p0)其中,SPL为声压级,p为声压,p0为参考声压(通常为20微帕)。
2. 声功率级(Sound Power Level)计算公式:声功率级用于描述噪声源的总发声能力,通常以分贝(dB)为单位。
声功率级的计算公式如下:SWL = 10 * log10(P/P0)其中,SWL为声功率级,P为声功率,P0为参考声功率(通常为10^-12瓦)。
3.噪声指数计算公式:噪声指数用于综合考虑不同频率范围内的声压级。
常用的噪声指数计算公式有以下几种:- 均方根声压级(Root Mean Square Sound Pressure Level,RMS SPL):RMSSPL=√[1/(n*∑(10^0.1*L_i))]其中,L_i为频率为i的频谱级,n为频谱的总数量。
- 均方根声能级(Root Mean Square Sound Energy Level,RMS SEL):RMS SEL = 10 * log10[1/(n*∏(10^(-0.1*L_i/10)))]其中,L_i为频率为i的频谱级,n为频谱的总数量。
- 均方根声压级增益(Root Mean Square Sound Pressure Level Gain,RMS SPL Gain):RMS SPL Gain = RMS SPL - L0其中,RMSSPL为均方根声压级,L0为参考声压级。
4.声频谱计算公式:声频谱是指不同频率范围内噪声的分布情况。
常用的声频谱计算公式有以下几种:- A频谱权重调整(A-weighted Spectrum Adjustment):LA=L+KA其中,L为原始频谱级,KA为A频谱的校正系数。
- C频谱权重调整(C-weighted Spectrum Adjustment):LC=L+KC其中,L为原始频谱级,KC为C频谱的校正系数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
噪声估计算法范文
噪声估计算法是指通过对信号进行分析和处理,估计出信号中的噪声
成分的方法。
在实际应用中,噪声是不可避免的,它会干扰信号的传输和
处理,影响信号质量和系统性能。
因此,准确地估计噪声的特性对于信号
处理和系统设计具有重要意义。
本文将介绍几种常用的噪声估计算法。
1.统计估计法:统计估计法是一种基于统计分析方法的噪声估计算法。
该方法通过对信号进行统计分析,计算出信号的一些统计特性,如均值、
方差等,然后根据这些特性来估计噪声的性质。
例如,对于高斯白噪声,
可以使用样本均值和样本方差来估计其均值和方差。
该方法简单易用,但
对信号的统计特性有一定的要求。
2.自回归模型法:自回归模型法是一种基于自回归模型的噪声估计算法。
该方法通过对信号进行自回归建模,利用自回归模型的参数来估计噪
声的自相关性。
常用的自回归模型包括AR模型和ARMA模型。
该方法在信
号存在较强自相关性时效果比较好,但对信号的自相关性有一定的要求。
3.小波变换法:小波变换法是一种基于小波变换的噪声估计算法。
该
方法通过对信号进行小波分解,得到信号的小波系数,然后根据小波系数
的特性来估计噪声的性质。
常用的小波变换包括离散小波变换(DWT)和连
续小波变换(CWT)。
该方法在时频域分析中常用,可以对不同频率的噪声
进行估计。
4. 光谱估计法:光谱估计法是一种基于频域分析的噪声估计算法。
该方法通过对信号进行频谱分析,得到信号的频谱特性,然后根据频谱特
性来估计噪声的频谱密度。
常用的光谱估计方法包括传统的周期图法和现
代的最小二乘法、Yule-Walker方法、扩展最小二乘法等。
该方法在频域分析和信号处理中广泛应用,可以对不同频率的噪声进行估计。
以上是几种常用的噪声估计算法,每种算法都有其适用的场景和优缺点。
在具体应用中,可以根据实际需求选择合适的算法,并结合实际情况进行参数调整和优化,以获得准确的噪声估计结果。
噪声估计在通信、音频处理、图像处理等领域都有广泛的应用,对于提高系统性能和信号质量具有重要意义。
同时,噪声估计也是研究噪声特性和噪声去除的基础,对于进一步研究和应用噪声相关的问题具有重要价值。
