九年级数学上册-相似练习题
湘教版九年级数学上册《3.4 相似三角形的判定与性质》练习题-带参考答案

湘教版九年级数学上册《3.4 相似三角形的判定与性质》练习题-带参考答案学校:___________班级:___________姓名:___________考号:___________一、选择题1.已知△ABC∽△A′B′C′且ABA′B′=12,则S△ABC∶S△A′B′C′为( )A.1∶2B.2∶1C.1∶4D.4∶12.如图,△ABC与△DE F相似,相似比为1∶2,BC的对应边是EF,若BC=1,则EF的长是( )A.1B.2C.3D.43.已知△ABC∽△DEF,且AB∶DE=1∶2,则△ABC的面积与△DEF的面积之比为( )A.1∶2B.1∶4C.2∶1D.4∶14.如图,在平行四边形ABCD中,E为CD上一点,连接AE、BE、BD,且AE、BD交于点F,S△DEF :S△ABF=4:25,则DE:EC=()A.2:3 B.2:5 C.3:5 D.3:25.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,则图中相似三角形共有( )A.1对B.2对C.3对D.4对6.如图,P是Rt△ABC的斜边BC上异于B、C的一点,过P点作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有( )A.1条B.2条C.3条D.4条7.如图,点P是△ABC的边AB上的一点,过点P作直线(不与直线AB重合)截△ABC,使截得的三角形与原三角形相似.满足这样条件的直线最多有( )A.2条B.3条C.4条D.5条8.如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在格点为( )A.P1 B.P2C.P3D.P49.要做甲、乙两个形状相同(相似)的三角形框架,已知三角形框架甲的三边分别为50cm,60cm,80cm,三角形框架乙的一边长为20cm,那么符合条件的三角形框架乙共有( )A.1种B.2种C.3种D.4种10.如图,在△ABC中,CD⊥AB,且CD2=AD•DB,AE平分∠CAB交CD于F,∠EAB=∠B,CN=BE.①CF=BN;②∠ACB=90°;③FN∥AB;④AD2=DF•DC.则下列结论正确的是( )A.①②④B.②③④C.①②③④D.①③二、填空题11.若△ABC∽△DEF,且△ABC与△DEF的相似比为1:2,则△ABC与△DEF的面积比值为.12.若两个相似三角形的周长比为2:3,则它们的面积比是.13.若△ABC∽△A′B′C′,且AB:A′B′=3:4,△ABC的周长为12 cm,则△A′B′C′的周长为____________.14.下图中的每个点(包括△ABC的各个顶点)都在边长为1的小正方形的顶点上,在P、Q、G、H中找一个点,使它与点D、E构成的三角形与△ABC相似,这个点可以是.(写出满足条件的所有的点)15.如图,平行四边形ABCD中,E是BC边延长线上一点,AE交CD于F,则图中相似三角形有对.16.如图,在平面直角坐标中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线l于点B,过点B1作直线l的垂线交y轴于点A1,以A1B.BA为邻边作▱ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1.B1A1为邻边作▱A1B1A2C2;…;按此作法继续下去,则Cn的坐标是.三、解答题17.如图,在等边三角形ABC中,点D,E分别在BC,AB上,且∠ADE=60°. 求证:△ADC∽△DEB.18.如图,A、B、C、P四点均在边长为1的小正方形网格格点上.(1)判断△PBA与△ABC是否相似,并说明理由;(2)求∠BAC的度数.19.如图所示,已知AB∥CD,AD,BC相交于点E,F为BC上一点,且∠EAF=∠C.求证:(1) ∠EAF=∠B;(2) AF2=FE·FB.20.如图,在△ABC中,AD和BG是△ABC的高,连接GD.(1)求证△ADC∽△BGC;(2)求证CG·AB=CB·DG.21.如图,已知P是正方形ABCD边BC上一点,BP=3PC,Q是CD的中点(1)求证:△ADQ∽△QCP;(2)若AB=10,连接BD交AP于点M,交AQ于点N,求BM,QN的长.22.在等腰三角形ABC中,AB=AC,D是AB延长线上一点,E是AC上一点,DE交BC于点F.(1)如图①,若BD=CE,求证:DF=EF.(2)如图②,若BD=1nCE,试写出DF和EF之间的数量关系,并证明.(3)如图③,在(2)的条件下,若点E在CA的延长线上,那么(2)中结论还成立吗?试证明.答案1.C2.B3.B4.A5.C.6.C7.C.8.B9.C.10.C.11.答案为:1:4.12.答案为:4:9.13.答案为:16cm.14.答案为:Q.15.答案为:4.16.答案为(﹣3×4n﹣1,4n).17.证明:∵△ABC是等边三角形∴∠B=∠C=60°∴∠ADB=∠CAD+∠C=∠CAD+60°∵∠ADE=60°∴∠ADB=∠BDE+60°∴∠CAD=∠BDE∴△ADC∽△DEB.18.解:(1)△PBA与△ABC相似,理由如下:∵AB=5,BC=5,BP=1∴∵∠PBA=∠ABC∴△PBA∽△ABC;(2)∵△PBA∽△ABC∴∠BAC=∠BPA∵∠BPA=90°+45°=135°∴∠BAC=135°.19.证明:(1)∵AB∥CD∴∠B=∠C又∠C=∠EAF∴∠EAF=∠B(2)∵∠EAF=∠B,∠AFE=∠BFA ∴△AFE∽△BFA则AFBF=FEFA∴AF2=FE·FB20.解:(1) ∵在△ABC中,AD和BG是△ABC的高∴∠BGC=∠ADC=90°.又∠C=∠C∴△ADC∽△BGC.(2)∵△ADC∽△BGC∴CGDC=BCAC.∴CGBC=DCAC.又∠C=∠C∴△GDC∽△BAC.∴CGBC=DGAB.∴CG·AB=CB·DG.21.证明:(1)∵正方形ABCD中,BP=3PC,Q是CD的中点∴PC=14﹣BC,CQ=DQ=12CD,且BC=CD=AD∴PC :DQ =CQ :AD =1:2 ∵∠PCQ =∠ADQ =90° ∴△PCQ ∽△ADQ (2)∵△BMP ∽△AMD ∴BM :DM =BP :AD =3:4 ∵AB =10 ∴BD =10 2 ∴BM =同理QN =53 5.22.证明:(1)在题图①中作EG ∥AB 交BC 于点G 则∠ABC =∠EGC ,∠D =∠FEG. ∵AB =AC ,∴∠ABC =∠C. ∴∠EGC =∠C.∴EG =EC. ∵BD =CE ,∴BD =EG. ∵∠D =∠FEG ,∠BFD =∠GFE ∴△BFD ≌△GFE. ∴DF =EF. (2)解:DF =1nEF.证明:在题图②中作EG ∥AB 交BC 于点G ,则∠D =∠FEG.由(1)得EG =EC. ∵∠D =∠FEG ,∠BFD =∠EFG ∴△BFD ∽△GFE.∴BD EG =DF EF. ∵BD =1n CE =1n EG∴DF =1n EF.(3)解:成立.证明:在题图③中作EG ∥AB 交CB 的延长线于点G则仍有EG=EC,△BFD∽△GFE.∴BDEG=DFEF.∵BD=1nCE=1nEG,∴DF=1nEF.。
浙教版数学九年级上册 第四章 相似三角形 单元练习(含答案)

浙教版数学九年级上册第四章相似三角形一、选择题1.如果2a =5b ,那么下列比例式中正确的是( )A .a b =25B .a 5=2b C .a 2=b 5D .a 5=b 22.如图,直线l 1∥l 2∥l 3,AC =6,DE =3,EF =2,则AB 的长为( )A .3B .125C .165D .1853.如图,点P 是线段AB 的黄金分割点,且PA >PB ,若AB =2,则PA 的长度是( )A .5−1B .3−5C .25−4D .14.如图, 在▱ABCD 中, E 是边AB 上一点, 连结AC ,DE 相交于点F . 若AE EB =23,则 AF CF 等于( )A .13B .23C .25D .355.如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC 相似的是( )A .B .C.D.6.△ABC和△DEF是两个等边三角形,AB=2,DE=4,则△ABC与△DEF的面积比是( ) A.1:2B.1:4C.1:8D.1:27.如图,在△ABC中,BC=6,AC=8,∠C=90°,以B为圆心,BC长为半径画弧,与AB交于点D,再分别以点A,D为圆心,大于12AD的长为半径画弧,两弧交于点M,N,作直线MN,分别交AC,AB于点E,F,则AE的长度为( )A.52B.103C.3D.228.如图,△ABC和△A1B1C1是以点O为位似中心的位似图形,点A在线段O A1上,若OA:A A1=1:2,则△ABC和△A1B1C1的周长之比为( )A.1:2B.2:1C.1:3D.3:19.如图,在△ABC中,D为线段AC上一点,点E在AC的延长线上,过点D作DF∥AB交BC于点F,连结BE,EF,若A C2+D E2=A E2,则△BEF与△DCF的面积比为( )A.1:2B.1:3C.2:3D.2:510.如图,矩形ABCD中,AB=4,AD=2,E为边AD上一个动点,连接BE,取BE的中点G,点G绕点E逆时针旋转90°得到点F,连接CF,则△CEF面积的最小值是( )A .4B .154C .3D .114二、填空题11.如图,AC 、BD 交于点O ,连接AB 、CD ,若要使△AOB ∽△COD ,可以添加条件 .(只需写出一个条件即可)12.已知△ABC ∽△DEF ,且AB:DE =1:3,△ABC 与△DEF 的周长比是 .13.如图,在这架小提琴中,点C 是线段AB 的黄金分割点(BC >AC ).若AB =60cm ,则BC = cm .14.如图,在Rt △ABC 中,∠ABC =90°,AB =4,AC =5,AE 平分∠BAC ,点D 是AC 的中点,AE 与BD交于点O ,则的值AOOE .15.如图,矩形ABCD 中,AB =3 6 ,BC =12,E 为AD 中点,F 为AB 上一点,将△AEF 沿EF 折叠后,点A 恰好落到CF 上的点G 处,则折痕EF 的长是 .16.如图,正方形ABCD 中,BF =FG =CG ,BE =2AE ,CE 交DF 、DG 于M 、N 两点,有下列结论:①DF ⊥EC ;②S △MFC =59S 四边形MFBE ;③DM :MF =2:1;④MN NC =913.其中,正确的有 .三、解答题17.(1)已知线段a =2,b =6,求线段a ,b 的比例中项线段c 的长.(2)已知x :y =3:2,求2x−yx的值.18.如图,已知D 、E 分别是△ABC 的边AB 、AC 上的点,DE ∥BC ,AD BD =32,求DE BC 的值.19.如图,AD 、BC 相交于点P ,连接AC 、BD ,且∠1=∠2,AC =6,CP =4,DP =2,求BD 的长.20. 如图,在平行四边形ABCD 中,E 为DC 边上一点,∠EAB =∠EBC .(1)求证:△ABE∽△BEC ;(2)若AB=4,DE=3,求BE的长.21.如图,在四边形ABCD中,OA=OC,OB=OD,AB=BC,AC=12,BD=16.(1)求证:四边形ABCD时菱形;(2)延长BC至点M,连接OM交CD于点N,若∠M=12∠BAC,求MNOM.22.如图,AB∥CD,且AB=2CD,E是AB的中点,F是边BC上的动点(F不与B,C重合),EF与BD相交于点M.(1)求证:△FDM∽△FBM;(2)若F是BC的中点,BD=18,求BM的长;(3)若AD=BC,BD平分∠ABC,点P是线段BD上的动点,是否存在点P使DP⋅BP=BF⋅CD,若存在,求出∠CPF的度数;若不存在,请说明理由.23.如图,在平面直角坐标系中,已知抛物线y=12x2+bx+c与x轴交于A、B两点,与y轴交于C点,且OB=OC=4.(1)求抛物线的解析式;(2)在抛物线上是否存在点M,使∠ABC=∠BCM,如果存在,求M点的坐标,如果不存在,说明理由;(3)若D是抛物线第二象限上一动点,过点D作DF⊥x轴于点F,过点A、B、D的圆与DF交于E点,求△ABE的面积.答案解析部分1.【答案】D2.【答案】D3.【答案】A4.【答案】C5.【答案】B6.【答案】B7.【答案】A8.【答案】C9.【答案】A10.【答案】B11.【答案】∠A=∠C(答案不唯一)12.【答案】1:313.【答案】(305−30)14.【答案】9415.【答案】21516.【答案】①④17.【答案】(1)解:∵线段a=2,b=6,线段c是线段a、b的比例中项,∴c2=ab=12,∴c=23(负值舍去);(2)解:∵x:y=3:2,∴可设x=3k,y=2k(k≠0),∴2x−yx=6k−2k3k=43.18.【答案】3519.【答案】BD=320.【答案】(1)证明:∵平行四边形ABCD,∴AB//CD,∴∠EBA=∠BEC,又∵∠EAB=∠EBC,∴△ABE∽△BEC.(2)解:∵四边形ABCD 平行四边形,∴AB =DC =4,∵DE =3,∴CE =1,∵△ABE∽△BEC ,∴AB EB =EBEC,∴AB ⋅CE =B E 2=4×1=4,∴BE =2.21.【答案】(1)证明:∵ 在四边形ABCD 中,OA=OC ,OB=OD∴ 四边形ABCD 是平行四边形 ∵ AB=BC∴ 平行四边形ABCD 是菱形。
数学九年级上册相似试卷【含答案】

数学九年级上册相似试卷【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 若两个三角形的对应角相等,则它们是相似的,这句话是否正确?A. 正确B. 错误2. 在ΔABC和ΔDEF中,若AB/DE = BC/EF = AC/DF,则这两个三角形是否相似?A. 相似B. 不相似3. 两个相似三角形的面积比是9:1,它们的边长比是:A. 3:1B. 1:3C. 9:1D. 1:94. 若ΔABC ∽ ΔA'B'C',则以下哪个比例是错误的?A. AB/A'B' = BC/B'C'B. AB/A'B' = AC/A'C'C. AB/A'B' = (BCAC)/(B'C'A'C')D. AB/A'B' = (BC+AC)/(B'C'+A'C')5. 在ΔABC中,AB = 6cm, BC = 8cm, ∠B = 90°,若ΔDEF ∽ ΔABC,且EF = 4cm,则DE的长度是:A. 3cmB. 4cmC. 5cmD. 6cm二、判断题(每题1分,共5分)6. 相似三角形的对应边长之比相等。
()7. 相似三角形的面积比等于对应边长比的平方。
()8. 若两个三角形的对应边成比例,则这两个三角形一定相似。
()9. 在ΔABC中,若AB = AC,则ΔABC是等腰三角形。
()10. 两个全等三角形的面积比一定是1:1。
()三、填空题(每题1分,共5分)11. 在ΔABC和ΔDEF中,若AB/DE = BC/EF = AC/DF = 2/3,则ΔABC与ΔDEF______。
12. 若ΔABC ∽ ΔA'B'C',且AB = 6cm, A'B' = 9cm,则BC与B'C'的长度之比是______。
图形的相似(压轴专练)(十大题型)(原卷版)—2024-2025学年九年级数学上册(北师大版)

图形的相似(压轴专练)(十大题型)题型1:相似三角形解答证明题1.在ABC V 中,AB AC =,点D 在线段CB 的延长线上,连接AD ,过点B 作BE BC ^交线段AD 于点,2120E BED BAC Ð+Ð=°.(1)如图1,求CAD Ð的度数.(2)如图2,若32DE AE =,求BD BC的值.(3)如图3,在(2)的条件下,连接,EC EC 交线段AB 于点F ,若BD =AF 的长.2.如图1,在ABC V 中,90BAC AB AC BD CD Ð=°=^,,于点D ,连接AD ,在CD 上截取CE ,使CE BD =,连接AE .(1)直接判断AE 与AD 的位置关系(2)如图2,延长AD ,CB 交于点F ,过点E 作EG AF ∥交BC 于点G ,试判断FG 与AB 之间的数量关系,并证明;(3)在(2)的条件下,若2AE =,CE =EG 的长.题型2:相似三角形在特殊平行四边形中的应用3.如图1,四边形ABCD 是正方形,点E 在边BC 的延长线上,点F 在边AB 上,且AF CE =,连接EF 交DC 于点P ,连接AC 交EF 于Q ,连接DE DF 、.(1)求证:EQ FQ =;(2)连接BQ ,如图2,①若AQ DP ×=BQ 的长;②若FP FD =,则PE PQ = .4.综合与实践已知:矩形ABCD ,M 是AD 边上一点.【基本图形】(1)如图1,AM MD =,BM 交AC 于F 点,BM 的延长线与CD 的延长线交于点E ,连AE ,求证:MF EM BF EB=;【类比探究】(2)如图2,AM MD =,过点D 任意作直线与BM ,BC 的延长线分别交于点E ,点P ,连AE ,求证:EAD PAD ÐÐ=;【扩展延伸】(3)如图3,E 是CD 延长线上一点,P 是BC 延长线上一点,AP 交CD 于Q 点,BE 交AD 于M 点,延长AD 交EP 于N 点,若M 是AN 的中点,且3AB =,4BC =,求AEP △的面积.题型3:翻折问题5.菱形ABCD 中,5AB =,点F 是AD 边上的点,点Q 是AB 边上的点.(1)如图1,若点F 是AD 的中点,CQ AB ^,连接CF 并延长交BA 的延长线于点P ,连接QF ,①求证:PAF CDF △≌△;②判定FCQ V 的形状,并说明理由;(2)若菱形面积为20,将菱形ABCD 沿CQ 翻折,点B 的对应点为点E .①如图2,当点E 落在BA 边的延长线上时,连接BD ,交CQ 于R ,交EC 于点M ,求DR BM 的值;②如图3,当CE AD ^,垂足为点F ,交AD 于点N ,求四边形CFNQ 的面积.6.如图1,在矩形ABCD 中,3AB =,4=AD ,点E 在BC 上,连接AE ,把ABE V 沿直线AE 翻折得到AFE △,直线EF 与直线CD 交于点G ,连接DF .(1)当DFG GEC Ð=Ð时,求BE 的长.小星看到把ABE V 沿直线AE 翻折得到AFE △,就想到翻折图形的特征特点,对应边相等,对应角相等,对应点连线被对称轴垂直平分,那么他就知道BE FE =,AB AF =,90ABE AFE Ð=Ð=°,根据DFG GEC Ð=Ð,他延长EG 与AD 的延长线相交于点H ,可证AD DF DH ==,AH EH =,再通过勾股定理即可求出BE 的长.请用小星的方法或自己的方法求BE 的长;(2)当G 是CD 的中点时,求BE 的长;(3)如图2,已知等边ABC V 的边长为6,点D 在边BC 上,连接AD ,把ABD △沿直线AD 翻折得到AED △,直线DE 与直线AC 交于点F ,若12CF =,求BD 的长.7.(1)发现:如图1,正方形ABCD 中,点E 在CD 边上,将ADE V 沿AE 对折得到AFE △,延长EF 交BC 边于点G ,连接AG .证明:BG DE EG +=.(2)探究:如图2,矩形ABCD 中AD AB >,O 是对角线的交点,过O 任作一直线分别交BC AD 、于点M 、N ,四边形AMNE 是四边形CMND 沿MN 翻折得到的,连接CN ,若CDN △的面积与CMN V 的面积比为1:3,求MN DN的值.(3)拓展:如图3,在菱形ABCD 中,6AB =,E 为CD 边上的三等分点,60D Ð=°,将ADE V 沿AE 翻折得到AFE △,直线EF 交BC 于点P ,求PC 的长.题型4:旋转问题8.如图,ABC V 和ADE V 是有公共顶点的等腰直角三角形,90BAC DAE Ð=Ð=°.(1)如图1,连接BE 、CD ,BE 的延长线交AC 于F ,交CD 于点P ,求证:①ABE ACD V V ≌;②BP CD ^;(2)如图2,把ADE V 绕点A 顺时针旋转,当点D 落在AB 上时,连接BE 、CD ,CD 的延长线交BE 于点P ,若BC =3AD =.①求证:BDP CDA △∽△,②PDE △的面积是 .9.问题背景:如图(1),在ABC V 和ADE V 中,AB AC AD AE ==,,BAC DAE Ð=Ð,求证:ABD ACE △△≌;尝试应用:如图(2),在ABC V 和ADE V 中,90ABC ADE Ð=Ð=°,30ACB AED Ð=Ð=°,连接CE ,点F 是CE 的中点.判定以B ,D ,F 为顶点的三角形的形状,并证明你的结论;拓展创新:如图(3),在ABC V 中,AC BC =AB 绕点A 逆时针旋转90°得到AD ,连接BD CD ,.若点E 是CD 的中点,连接BE ,直接写出BE 的最大值.10.如图,在V 锐角ABC 中,AB =3BC =,45ACB Ð=°,将ABC V 绕点B 按逆时针方向旋转得到11A BC V .(1)如图①,当点1C 在线段CA 的延长线上时,求11CC A Ð的度数;(2)如图②,连接1AA ,1CC ,若1ABA △的面积为2,求1CBC △的面积;(3)如图③,点E 为线段AB 中点,点P 是线段AC 上的动点,在ABC V 绕点B 按逆时针方向旋转过程中,点P 的对应点是点1P ,求线段1EP 长度的最大值与最小值.题型5:最值问题11.如图,在ABC V 中,90,BAC AB AC Ð=°=,点D 为AC 一点,连接BD .(1)如图1,若CD =,15ABD Ð=°,求AD 的长;(2)如图2,过点A 作AE BD ^于点E ,交BC 于点M ,AG BC ^于点G ,交BD 于点N ,求证:BM CM =;(3)如图3,将ABD △沿BD 翻折至BDE V 处,在AC 上取点F ,连接BF ,过点E 作EH BF ^交AC 于点G ,GE 交BF 于点H ,连接AH ,若:2GE BF =,AB =AH 的最小值.12.如图1和图2,平面上,四边形ABCD 中1582AB BC ==,,252CD =,6DA =,90A Ð=°,点M 在AD边上,且2DM =.点P 从点A 沿折线AB BC -上运动到点C ,将APM △沿MP 翻折,点A 的对应点为点A ¢,设点P 的运动路径长为x (0)x >.(1)如图1,连接BD ,①求CBD Ð的度数;②求证:AB CD ∥.(2)如图2,当点A ¢落到四边形ABCD 内部时,求x 的取值范围.(3)①当点A ¢落在AD 的延长线上时,请直接写出x 的值.②设点A ¢到边BC 所在直线的距离为h ,请直接写出h 的最小值.13.如图,在Rt ABC △中,90ACB Ð=°,AC BC =,点D 在直线AB 上,点E 在直线AC 上,连接BE ,DE ,且BE DE =,直线DE 交BC 于点F .(1)如图①,当点D 在线段AB 上时,AD 4AC =,求BE 的长;(2)如图②,当D 是AB 的中点时,求证:CE CF BF +=;(3)如图③,连接CD ,将ADC △沿着CD 翻折,得到A CD ¢△,M 是AB 上一点,且37BM AB =,当A M ¢最短时,请直接写出DF BE 的值.题型6:比值问题14.如图1,在ABC D 中,AB AC =,点D 、E 分别在边AB 、AC 上,AD AE =,连接DC ,点F 、P 、G分别为DE 、DC 、BC 的中点,连接FP ,PG .(1)图1中,求证:PF PG =;(2)当ADE V 绕点A 旋转到如图2所示的位置时,①PF PG =是否仍然成立?若成立请证明;若不成立,说明理由;②若:1:(1)AD AB n n =>,PDF △和PGC V 的面积分别是1S ,2S ,ABC V 的面积为3S ,求123S S S +的值.15.【特例感知】(1)如图1,在正方形ABCD 中,点P 在边AB 的延长线上,连接PD ,过点D 作DM PD ^,交BC 的延长线于点M .求证:DP DM =.【变式求异】(2)如图2,在Rt ABC △中,90ABC Ð=°,点D 在边AB 上,过点D 作DQ AB ^,交AC 于点Q ,点P 在边AB 的延长线上,连接PQ ,过点Q 作QM PQ ^,交射线BC 于点M .已知8BC =,10AC =,AD =2DB ,求PQ QM的值.【拓展应用】(3)如图3,在Rt ABC △中,90BAC Ð=°,点P 在边AB 的延长线上,点Q 在边AC 上(不与点A ,C 重合),连接PQ ,以Q 为顶点作PQM PBC Ð=Ð,PQM Ð的边QM 交射线BC 于点M .若AC mAB =,CQ nAC =(m ,n 是常数),直接写出PQ QM的值(用含m ,n 的代数式表示).题型7:“手拉手”模型16.在ABC V 中,90ACB Ð=°,AC BC =,点D 是BC 边上一动点,过点C 作CE AD ^交AB 于点E .(1)如图1,若AC AE =,求ADB Ð的度数;(2)如图2,点F 是BD 上一点,连接EF 并延长交AD 的延长线于点G .若点P 为AD 的中点,CP DG =,2G CAD Ð=Ð,求证:2CE EF FG +=;(3)点F 是BC 边上一点,射线EF 与射线AD 交于点G ,BFE ADC Ð=Ð,点H 是AC 上一点,且14CH AC =,连接HF ,H G ,点M 是射线AD 上一动点,连接MH ,MF .在点D 的运动过程中,当GH 取得最小值m 时,在平面内将HFM △沿直线HM 翻折得到HNM V ,连接EN .在点M 的运动过程中,若EN 的最大值为n ,直接写出n m的值.17.如图所示,在ABC V 中,D 、E 分别是AB 、AC 上的点,DE BC ∥,如图1,然后将ADE V 绕A 点顺时针旋转一定角度,得到图2,然后将BD 、CE 分别延长至M 、N ,使DM =12BD ,EN =12CE ,得到图3,请解答下列问题:(1)若AB AC =,请探究下列数量关系:①在图2中,BD 与CE 的数量关系是 ;②在图3中,猜想AM 与AN 的数量关系、MAN Ð与BAC Ð的数量关系,并证明你的猜想;(2)若·1AB k AC k =(>),按上述操作方法,得到图4,请继续探究:AM 与AN 的数量关系、MAN Ð与BAC Ð的数量关系,直接写出你的猜想,不必证明.题型8:定值问题18.如图1,在ABCD Y 中,60A Ð=°,4=AD ,8AB =.Y的面积;(1)请计算ABCD△沿着AC翻折,D点的对应点为D¢,线段CD¢交AB于点M,请计算AM的长度;(2)如图2,将ADC^交AD¢的延(3)如图3,在(2)的条件下,点P为线段CM上一动点,过点P作PN AC^于点N,PG AD¢长线于点G.在点P PG+的长度是否为定值?如果是,请计算出这个定值;如果不是,请说明理由.题型9:情景探究题19.[问题情境](1)王老师给爱好学习的小明和小颖提出这样一个问题:如图①,在ABC V 中,AB AC =,P 为边BC 上的任一点,过点P 作,PD AB PE AC ^^,垂足分别为D ,E ,过点C 作CF AB ^,垂足为F .求证:PD PE CF +=.小明的证明思路是:如图①,连接AP ,由ABP V 与APC △面积之和等于ABC V 的面积可以证得:PD PE CF +=.小颖的证明思路是:如图②,过点P 作PG CF ^,垂足为G ,可以证得:,PD GF PE CG ==,则PD PE CF +=.请你选择小明、小颖两种证明思路中的任意一种,写出详细的证明过程.[变式探究](2)如图③,当点Р在BC 延长线上时,问题情境中,其余条件不变,则PD PE CF 、、之间的数量关系是______.[结论运用](3)如图④,将矩形ABCD 沿EF 折叠,使点D 落在点B 上,点C 落在点C ¢处,点P 为折痕EF 上的任一点,过点Р作,PG BE PH BF ^^,垂足分别为G ,H ,若18,5AD CF ==,求PG PH +的值.[迁移拓展](4)图⑤是一个机器模型的截面示意图,在四边形ABCD 中,E 为AB 边上的一点,,ED AD EC CB ^^,垂足分别为D ,C ,且,3cm,AD CE DE BC AB AD BD ====××,M 、N 分别为AE BE ,的中点,连接DM CN ,,请直接写出DEM △与CEN V 的周长之和___________.题型10:相似三角形在平面直角坐标系的应用20.如图,在平面直角坐标系中;一次函数y kx b =+的图象与x 轴交于点A ,与y 轴交于点B (0,3),与直线OC 交于点8,13C æöç÷èø.(1)求直线AB 的函数表达式;(2)过点C 作CD x ^轴于点D ,将ACD V 沿射线CB 平移得到的三角形记为A C D ¢¢¢△,点A ,C ,D 的对应点分别为A ¢,C ¢,D ¢,若A C D ¢¢¢△与BOC V 重叠部分的面积为S ,平移的距离CC m ¢=,当点A ¢与点B 重合时停止运动,当925S =时,求m 的值.21.综合运用如图1,在平面直角坐标系中,AOB V 是等腰直角三角形,AO BO =,点A 的坐标为()0,6.点C 是边OB 上一点,连接AC ,将线段AC 绕点C 顺时针旋转90°,得到线段CD ,连接AD ,BD .(1)当AB 平分CAD Ð时,OAC Ð=________°;(2)若13CO BO =,求BD 的长;(3)如图2,作点C 关于AD 的对称点E ,连接BE ,CE ,DE .设BDE V 的面积S =,CO m =,求S 关于m 的函数表达式.。
九年级数学上册第四章《图形的相似》测试卷-北师大版(含答案)

九年级数学上册第四章《图形的相似》测试卷-北师大版(含答案)(满分120分)一、选择题(每题3分,共30分)1.若两个相似三角形的面积之比为4 :9,则它们对应角的平分线之比为()A. 49B.32C.23D.622.下列各组线段中,能成比例的是()A. 1c m,3c m,4c m,6c m,B. 1c m,3c m,4c m,12c m,C. 1c m,2c m,3c m,4c m,D. 2c m,3c m,4c m,5c m,3.下列说法中,正确的是()A.相似三角形都是全等三角形B.所有的矩形都相似C.所有的等腰三角形都相似D.所有的等腰直角三角形都相似4.如图,DE// BC ,A D = 2BD,下列结论错误的是()A. A E=2CEB. BC=2DEC. DE:BC=2:3D. C△A D E:C△ABC=2 :35.在比例尺1:10000的地图上,相距2C m的两地的实际距离是()A.200c mB.200 d mC.200 mD.200 km6.如图,l//l2//l3,两条直线与这三条平行线分别交于点A,B,C和D,E,F,已知32ABBC=,则DEDF的值为()A. 32B.23.C.25D.357.下列四个三角形,与左图中的三角形相似的是()8.△ABC与△DEF相似,且相似比是23.,反之,△DEF与△ABC的相似比是()A. 23. B.32C.25D.499.如图,由下列条件不能判定△ABC与△A D E相似的是()A. AE ACAD AB= B.∠B=∠A D EC. AE DEAC BC= D.∠C=∠A E D10.小明在测量楼高时,先测出楼房落在地面上的影长BA为15米(如图),然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为()A.10米B.12米C.15米D.22.5米二、填空题(每题4分,共28分)。
11.若1a+b,2ab b==则_____________。
浙教版九年级数学上册第四章:相似三角形基本模型练习题(含答案)
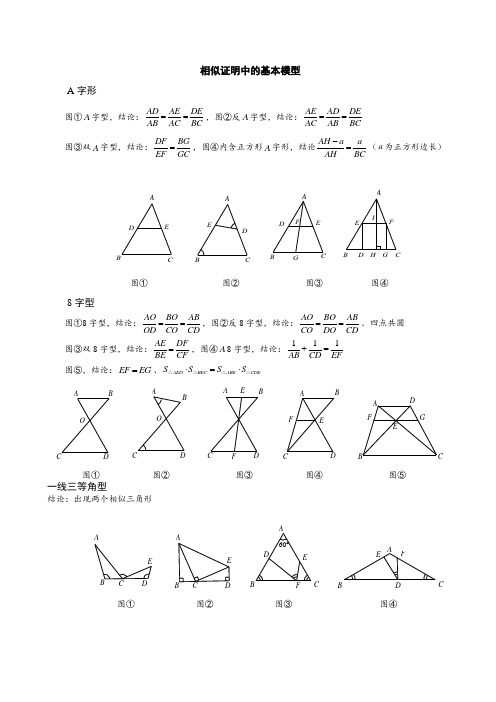
相似证明中的基本模型A 字形图①A 字型,结论:AD AE DE AB AC BC ==,图②反A 字型,结论:AE AD DEAC AB BC== 图③双A 字型,结论:DF BG EF GC =,图④内含正方形A 字形,结论AH a aAH BC-=(a 为正方形边长)IH G FED CB AGFEDC BAEDCB A ED C BA图① 图② 图③ 图④8字型图①8字型,结论:AO BO AB OD CO CD ==,图②反8字型,结论:AO BO AB CO DO CD==、四点共圆 图③双8字型,结论:AE DF BE CF=,图④A 8字型,结论:111AB CD EF += 图⑤,结论:EF EG =、AED BEC ABE CDE S S S S ⋅=⋅△△△△EFD C BA F ED C BAOD C BAODC BAGFED CB A图① 图② 图③ 图④ 图⑤一线三等角型结论:出现两个相似三角形HE DC B AE DC BAEDCBAC60°F E DCB AFED CB A图① 图② 图③ 图④角分线定理与射影定理图①内角分线型,结论:AB BD AC DC =,图②外角分线型,结论:AB BDAC CD= 图③斜射影定理型,结论:2AB BD BC =⋅,图④射影定理型,结论:1、2AC AD AB =⋅,2、2CD AD BD =⋅,3、2BC BD BA =⋅D C BD BCAEDB AD B A梅涅劳斯型常用辅助线G FEDCBAGFEDCBA G E DC B ADEFCBA四、相似证明中的面积法面积法主要是将面积的比,和线段的比进行相互转化来解决问题. 常用的面积法基本模型如下:如图:1212ABC ACDBC AHS BCS CD CD AH ⋅⋅==⋅⋅△△. 图1:“山字”型H DC B A如图:1212ABC BCDBC AHS AH AO S DG OD BC DG ⋅⋅===⋅⋅△△. 图2:“田字”型G HODCBA如图:ABD ABD AED ACE AED ACE S S S AB AD AB ADS S S AE AC AE AC⋅=⋅=⋅=⋅△△△△△△.图3:“燕尾”型CDEB A考点一:相似三角形【例1】 如图,D 、E 是ABC ∆的边AC 、AB 上的点,且AD AC ⋅=AE AB ⋅,求证:ADE B ∠=∠.EDCBA【答案】∵AD AC AE AB ⋅=⋅ ∴AD ABAE AC=∵DAE BAC ∠=∠∴DAE ∆∽BAC ∆∴ADE B ∠=∠ 【例2】 如图,在ABC ∆中,AD BC ⊥于D ,CE AB ⊥于E ,ABC ∆的面积是BDE ∆面积的4倍,6AC =,求DE 的长.ED CB A【答案】∵AD BC ⊥,CE AB ⊥,ABD CBE ∠=∠ ∴ABD ∆∽CBE ∆∴BE BCBD AB=∵EBD CBA ∠=∠ ∴BED ∆∽BCA ∆∴11322DEDE AC AC===⇒== 【例3】 如图,ABC △中,60ABC ∠=︒,点P 是ABC △内一点,使得APB BPC CPA ∠=∠=∠,86PA PC ==,,则PB =________.PCBA【解析】120APB BPC ∠=∠=︒,60BAP ABP ABC ABP CBP ∠=︒-∠=∠-∠=∠,故ABP BCP △∽△,2PB PA PC =⋅.【例4】 如图,已知三个边长相等的正方形相邻并排,求EBF EBG ∠+∠.HGFED CB A【答案】45︒ 【解析】连接DF 、CG ,则45EDF EBF DFB ∠=∠+∠=︒,若DFB EBG ∠=∠,则EBF EBG ∠+∠可求,问题的关键是证明BCG FDB △∽△.考点二:相似三角形与边的比例☞考点说明:可运用相似三角形模型,常用A 字形与8字形【例5】 在ABC ∆中,BD CE =,DE 的延长线交BC 的延长线于P , 求证:AD BP AE CP ⋅=⋅.PE D CBA MPED C BA【答案】过C 作CM AB ∥交DP 于M ,∵CM AB ∥,∴PCM PBD ∆∆∽, ∴CM PC BD PB =, ∵CM AB ∥,∴CEM AED ∆∆∽, ∴CM AD CE AE =, ∵BD CE =, ∴CM CM CE BD =, ∴PC AD PB AE=, ∴AD BP AE CP ⋅=⋅【例6】 如图,在ABC ∆的边AB 上取一点D ,在AC 取一点E ,使AD AE =,直线DE 和BC 的延长线相交于P ,求证:BP BDCP CE= PEDCBA4321MPE D CBA【答案】过C 作CM AB ∥交DP 于M ,∵CM AB ∥,∴PCM PBD ∆∆∽, ∴BP BD CP CM =, ∵CM AB ∥, ∴14∠=∠, 又∵AD AE =,∴12∠=∠,∴24∠=∠, ∵23∠=∠, ∴34∠=∠, ∴CM CE = ∴BP BD CP CE= 【例7】 如图,M 、N 为ABC △边BC 上的两点,且满足BM MN NC ==,一条平行于AC 的直线分别交AB 、AM 和AN 的延长线于点D 、E 和F .求证:3EF DE =.F NMED CBAK HF N MG ED CBA【答案】过M ,N 分别作AC 的平行线交AB 于H ,G 两点,NH 交AM 于K ,∵BM MN NC ==, ∴BG GH HA ==,易知12HK GM =,12GM HN =,∴14HK HN =,即13HK KN =,又∵DF HN ∥, ∴13DE HK EF KN ==,即3EF DE =. 考点三:相似三角形与内接矩形☞考点说明:内接矩形问题是相似三角形中比较典型的问题,考查了相似三角形对应高的比等于相似比【例1】 一块直角三角形木板的一条直角边AB 长为1.5米,面积为1.5平方米,工人师傅要把它加工成一个面积最大的正方形桌面,请甲、乙两位同学进行设计加工方案。
人教版九年级数学上相似多边形 课时练习(含答案解析)
北师大版九年级数学上册3.3相似多边形同步练习一、选择题1.用一个2倍放大镜照一个△ABC ,下面说法中错误的是( )A .△ABC 放大后,是原来的2倍B .△ABC 放大后,各边长是原来的2倍C .△ABC 放大后,周长是原来的2倍D .△ABC 放大后,面积是原来的4倍答案:A解析:解答:∵放大前后的三角形相似,∴放大后三角形的内角度数不变,面积为原来的4倍,周长和边长均为原来的2倍. 故本题选A .分析:用2倍的放大镜放大一个△ABC ,得到一个与原三角形相似的三角形;根据相似三角形的性质:相似三角形的面积比等于相似比的平方,周长比等于相似比.可知:放大后三角形的面积是原来的4倍,边长和周长是原来的2倍,而内角的度数不会改变.2.我国国土面积约为960万平方千米,画在比例尺为1:1000万的地图上的面积约是( ) A .960平方千米B .960平方米C .960平方分米D .960平方厘米答案:D解析:解答:169609.610=⨯万平方千米平方厘米,设画在地图上的面积约为x 平方厘米,则1629.61011000x ⨯=:(:万), 解得x=960.则画在地图上的面积约为960平方厘米.故选D .分析:相似多边形的面积比等于相似比的平方,据此求解,注意统一单位.3.如图,一张矩形纸片ABCD 的长AB =a ,宽BC =b .将纸片对折,折痕为EF ,所得矩形AFED 与矩形ABCD 相似,则a :b =( )A .2:1B .2:1C .3:3D .3:2答案:B解析:解答:∵矩形纸片对折,折痕为EF , ∴1122AF AB a ==, ∵矩形AFED 与矩形ABCD 相似, ∴AB AD AD AF =,即12a b b a =, ∴22a b=(), ∴2a b=. 故选B . 分析:根据折叠性质得到1122AF AB a ==,再根据相似多边形的性质得到AB AD AD AF =,即12a b b a =,然后利用比例的性质计算即可. 4.两个相似多边形的一组对分别是3cm 和4.5cm ,如果它们的面积之和是278cm ,那么较大的多边形的面积是( )A .44.8B .42C .52D .54答案:D解析:解答:设较大多边形与较小多边形的面积分别是m ,n .则2344.59n m ==().因而49n m =. 根据面积之和是78cm2.得到4789m m +=. 解得:254m cm =.故选D .分析:根据相似多边形相似比即对应边的比,面积的比等于相似比的平方,即可解决. 5.两个相似多边形的面积之比为1:9,则它们的周长之比为( )A .1:3B .1:9C .1:3D .2:3答案:A解析:解答:∵两个相似多边形的面积之比为1:9,∴两个相似多边形的边长之比是1:3,∴它们的周长之比为1:3.故选A .分析:根据相似多边形的面积之比等于相似比的平方和相似多边形的周长之比等于相似比得出即可.6.如图所示,两个等边三角形,两个矩形,两个正方形,两个菱形各成一组,每组中的一个图形在另一个图形的内部,对应边平行,且对应边之间的距离都相等,那么两个图形不相似的一组是( )A .B .C .D .答案:B解析:解答:由题意得,A 中三角形对应角相等,对应边成比例,两三角形相似; C ,D 中正方形,菱形四条边均相等,所以对应边成比例,又角也相等,所以正方形,菱形相似;而B 中矩形四个角相等,但对应边不一定成比例,所以B 中矩形不是相似多边形故选B .分析:此题考查相似多边形的判定问题,其对应角相等,对应边成比例.7.某块面积为24000m 的多边形草坪,在嘉兴市政建设规划设计图纸上的面积为2250cm ,这块草坪某条边的长度是40m ,则它在设计图纸上的长度是( )A .4cmB .5cmC .10cmD .40cm答案:C解析:解答:设这块草坪在设计图纸上的长度是xcm ,224000m 40000000m =,40m=4000cm , 根据题意得:2400000004000250x=(), 解得:x=10,即这块草坪在设计图纸上的长度是10cm .故选C .分析:首先设这块草坪在设计图纸上的长度是x cm ,根据题意可得这两个图形相似,根据相似图形的面积比等于相似比的平方,可列方程2400000004000250x=(),解此方程即可求得答案,注意统一单位.8.一个多边形的边长分别为2,3,4,5,6,另一个多边形和这个多边形相似,且最短边长为6,则最长边长为( )A .18B .12C .24D .30答案:A解析:解答:设这个多边形的最长边是x,则266x =,解得x=18.故选A.分析:根据题意找出最短边与最长边,然后根据相似多边形对应边成比例列式计算即可.9.若两个相似多边形的面积之比为1:4,则它们的周长之比为()A.1:4B.1:2C.2:1D.4:1答案:B解析:解答:∵两个相似多边形面积比为1:4,∴周长之比为112 4=:.故选:B.分析:根据相似多边形的面积之比等于相似比的平方,周长之比等于相似比,就可求解.10.如果两个相似多边形面积的比为1:5,则它们的相似比为()A.1:25B.1:5C.1:2.5D.15:答案:D解析:解答:∵两个相似多边形面积的比为1:5,∴它们的相似比为15:.故选:D.分析:根据相似多边形的面积的比等于相似比的平方解答.11.对一个图形进行放缩时,下列说法中正确的是()A.图形中线段的长度与角的大小都保持不变B.图形中线段的长度与角的大小都会改变C.图形中线段的长度保持不变、角的大小可以改变D.图形中线段的长度可以改变、角的大小保持不变答案:D解析:解答:根据相似多边形的性质:相似多边形的对应边成比例,对应角相等,∴对一个图形进行收缩时,图形中线段的长度改变,角的大小不变,故选D.分析:根据相似图形的性质得出相似图形的对应边成比例,对应角相等,即可得出答案.12.下面给出了一些关于相似的命题,其中真命题有()(1)菱形都相似;(2)等腰直角三角形都相似;(3)正方形都相似;(4)矩形都相似;(5)正六边形都相似.A.1个B.2个C.3个D.4个答案:C解析:解答:(1)所有菱形的对应角不一定相等,故菱形不一定都相似;(2)等腰直角三角形都相似,正确;(3)正方形都相似,正确;(4)矩形对应边比值不一定相等,不矩形不一定都相似;(5)正六边形都相似,正确,故符合题意的有3个.故选:C.分析:利用相似图形的性质分别判断得出即可.13.如果两个相似多边形的面积比为16:9,那么这两个相似多边形的相似比为()A.16:9B.4:3C.2:3D.256:81答案:B解析:解答:根据题意得:164 93.故选:B.分析:根据两个相似多边形的面积比为16:9,面积之比等于相似比的平方.14.下列判断正确的是()A.所有的直角三角形都相似B.所有的等腰直角三角形都相似C.所有的菱形都相似D.所有的矩形都相似答案:B解析:解答:A、所有的直角三角形只有直角相等,所以不一定都相似,故本选项错误;B、所有的等腰直角三角形都相似正确,故本选项正确;C、所有的菱形只有对应边成比例,对应角不一定相等,所以,不一定相似,故本选项错误;D、所有的矩形对应角相等,对应边不一定成比例,所以不一定相似,故本选项错误.故选B.分析:根据对应边成比例,对应角相等的图形叫做相似图形对各选项分析判断后利用排除法求解.15.如图,用放大镜将图形放大,这种图形的改变是()A.相似B.平移C.轴对称D.旋转答案:A解析:解答:根据相似图形的定义知,用放大镜将图形放大,属于图形的形状相同,大小不相同,所以属于相似变换.故选A.分析:根据轴对称变换、平移变换、旋转变换、相似变换的特点,结合图形即可得出答案.二、填空题16.若两个相似多边形的对应边之比为5:2,则它们的周长比是_____.答案:5:2解析:解答:∵两个相似多边形的对应边的比是5:2,∴这两个多边形的周长比是5:2.故答案为:5:2.分析:根据相似多边形的周长的比等于相似比解答即可.17.图中的两个四边形相似,则x y +=______,a=______.答案:63|85°解析:解答:由于两个四边形相似,它们的对应边成比例,对应角相等,所以18486x y ==:::,解得x =36,y =27,则362763x y +=+=. 360778311585a =︒-︒+︒+︒=︒().故答案为63;85°.分析:根据相似多边形的性质:对应角相等,对应边成比例即可求解.18.若两个相似多边形的面积比是16:25,则它们的周长比等于______.答案:4:5解析:解答:∵两个相似多边形面积的比为16:25,∴两个相似多边形周长的比等于4:5,∴这两个相似多边形周长的比是4:5.故答案为:4:5.分析:直接根据相似多边形周长的比等于相似比,面积的比等于相似比的平方进行解答即可.19.如图,在长8cm ,宽4cm 的矩形中截去一个矩形(阴影部分)使留下的矩形与原矩形相似,那么留下的矩形的面积为______2cm .答案:8解析:解答:设留下的矩形的宽为x,∵留下的矩形与原矩形相似,∴448x=,x=2,∴留下的矩形的面积为:2248cm⨯=()故答案为:8.分析:本题需先设留下的矩形的宽为x,再根据留下的矩形与矩形相似,列出方程即可求出留下的矩形的面积.20.如图,E、F分别是平行四边形ABCD的边AD、BC的中点,若四边形AEFB与四边形ABCD相似,AB=4,则AD的长度为______.答案:42解析:解答:设AE=x,则AD=2x,∵四边形ABCD与矩四边形ABFE是相似的,∴AE AB AB AD=,∴222AB x=,∴24AB x==,∴22x=,∴42AD=,故答案为:42.分析:首先设AE=x,则AD=2x,进而利用四边形ABCD与四边形ABFE是相似的,则AE AB AB AD=,进而求出即可三、解答题21.如图,四边形ABCD 和四边形EFGH 相似,求∠α、∠β的大小和EH 的长度.答案:解答:∵四边形ABCD 和四边形EFGH 相似,∴∠α=∠B=83°,∠D=∠H=118°,360837811881β∠=︒-︒+︒+︒=︒(),EH AD HG DC =::,∴242118EH =, ∴EH =28(cm ).答:∠α=83°,∠β=81°,EH =28cm .解析:分析:观察图形,根据相似多边形的对应角相等可得出∠α=∠B=83°,∠D =∠H =118°,再根据四边形的内角和等于360°可计算求出β的大小,然后根据相似多边形的对应边成比例即可求出EH 的长度.22.两个相似五边形,一组对应边的长分别为3cm 和4.5cm ,如果它们的面积之和是278cm ,则这两个五边形面积各是多少2cm ?答案:解答:设较小五边形与较大五边形的面积分别是2cm x ,2cm y . 则2344.59x y ==(),因而49x y =. 根据面积之和是278cm ,得到4789y y +=, 解得:54y =,则454249x =⨯=. 即较小五边形与较大五边形的面积分别是224cm ,254cm .解析:分析:根据相似多边形相似比即对应边的比,面积的比等于相似比的平方,即可解决.23.把一个长方形(如图)划分成两个全等的长方形.若要使每一个小长方形与原长方形相似,问原长方形应满足什么条件?答案:解答:设AE=ED=a ,AB=b ,∵每一个小长方形与原长方形相似, ∴2a b b a =, ∴222b a =,∵a ,b 均为正数,∴2b a =, ∴2222AD a a AB b a===, ∴原长方形的长与宽之比为21:.解析:分析:设AE=ED=a ,AB =b ,根据每一个小长方形与原长方形相似,可知2a b b a =,再由a ,b 均为正数可知2b a =,故2222AD a a AB b a===,由此即可得出结论. 24.如图,把矩形ABCD 对折,折痕为MN ,矩形DMNC 与矩形ABCD 相似,已知2AD = ,求AB 的长.答案:解答:∵2AD =,∴22MD NC ==, ∵矩形DMNC 与矩形ABCD 相似,∴NC MN AB AD =,即222AB AB =, ∴AB =1.解析:分析:先根据2AD =求出MD 的长,再根据矩形DMNC 与矩形ABCD 相似得出矩形对应边的比例式,求出AB 的长即可. 25.我们通常用到的一种复印纸,整张称为1A 纸,对折一分为二裁开成为2A 纸,再一分为二成为3A 纸,…,它们都是相似的矩形.求这种纸的长与宽的比值(精确到千分位). 答案:1.414解析:解答:设1A 纸的长为a ,宽为b ,2A 纸的长为b ,宽为2a , 由1A 、2A 纸的长与宽对应比成比例,得 12a b b a =, 故2 1.4141a b =≈. 故答案为:1.414.分析:分别设1A 纸的长为a ,宽为b ,2A 纸的长为b ,宽为2a ,再由相似多边形的对应边成比例列出比例式,求出a b的值即可.。
九年级数学上册 第1章 图形的相似 1 相似多边形练习题(新版)青岛版
第一章1练习题一、选择题1.如图,在矩形ABCD中,点E,F分别是AD,BC边的中点,连接EF,假设矩形ABFE与矩形ABCD相似,AB=1,那么矩形ABCD的面积为()C. √2D. 2√2A. 1B. √222.如图,把一个矩形分割成四个全等的小矩形,要使小矩形与原矩形相似,那么原矩形的长与宽之比为()A. 2:1B. 4:1C. √2:1D. 1:23.以下图形中一定是相似形的是()A. 两个等边三角形B. 两个菱形C. 两个矩形D. 两个直角三角形4.五边形ANCDE与五边形A1B1C1D1E1相似,五边形ABCDE的最短边为2,最长边为6,五边形A1B1C1D1E1的最长边是12,那么五边形A1B1C1D1E1的最短边是()A. 4B. 5C. 6D. 85.如图,取一张长为a、宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,假设要使小长方形与原长方形相似,那么原长方形纸片的边a,b应满足的条件是()A. a=√2bB. a=2bC. a=√2bD. a=4b6.以下命题中,真命题是()A. 邻边之比相等的两个平行四边形一定相似B. 邻边之比相等的两个矩形一定相似C. 对角线之比相等的两个平行四边形一定相似D. 对角线之比相等的两个矩形一定相似7.以下说法正确的选项是()A. 菱形都是相似图形B. 矩形都是相似图形欢迎下载C. 等边三角形都是相似圈形D. 各边对应成比例的多边形是相似多边形8.如图,一张矩形纸片沿它的长边AD对折(折痕为EF),得到两个全等的小矩形.假设小矩形与原来的矩形相似,那么原来矩形的长边与短边之比为()A. 1:1B. √2:1C. √3:1D. 2:19.如图,四边形ABCD四边的中点分别为E、F、G、H,对角线AC与BD相交于点O,假设四边形EFGH的面积是3,那么四边形ABCD的面积是()A. 3B. 6C. 9D. 1210.以下各组图形中,一定相似的是()A. 所有矩形B. 所有正方形C. 所有菱形D. 所有平行四边形二、填空题11.如图,矩形ABCD中,AD=2,AB=4,剪去一个矩形AEFD后,余下的矩形EBCF∽矩形BCDA,那么CF的长为______.12.如图,把一个长方形划分成三个全等的长方形.假设要使每个小长方形与原长方形相似,那么原长方形的长与宽的比为.13.把一个矩形的硬纸片剪去一个正方形,假设剩下的矩形与原矩形相似,那么原矩形的长边和短边之比为______.14.假设四边形ABCD与四边形A′B′C′D′是相似的图形,且AB:A′B′=2:3,BC=8,那么B′C′的长为.15.矩形的两边长分别为x和6(x<6),把它按如图方式分割成三个全等的小矩形,每一个小矩形与原矩形相似,那么x=______.16.如图,E,F分别为矩形ABCD的边AD,BC的中点,且矩形ABCD与矩形EABF相似,AB=1,那么BC的长为______.三、解答题17.如图,▱ABCD∽▱AEFB,且AB=3cm,BC=6cm.求:(1)AE的长.(2)▱ABCD与▱ABFE的面积比.18.如图,五边形ABCDE∽五边形FGHIJ.求图中未知的边长x,y和∠H的大小.欢迎下载19.四边形EFGH相似于四边形KLMN,各边长如下图,求∠E,∠G,∠N的度数以及x,y,z的值.。
第四章图形的相似题型专练2021-2022学年数学北师大版九年级上册 (含答案)
2021-2022学年数学北师大版九年级上册第四章图形的相似题型专练1.四条线段a ,b ,c ,d 成比例,其中3b =cm,8c = cm,12d = cm ,则a =( ) A.2 cmB.4 cmC.6 cmD.8 cm2.如图27-2-1-24,在ABC △中,//,932DE BC AD DB CE ===,,, 则AC 的长为( )A.6B.7C.8D.93.如图,在直角坐标系中,矩形OABC 的顶点O 在坐标原点,边OA 在x 轴上,OC 在y 轴上.如果矩形OA B C '''与矩形OABC 关于点O 位似,且矩形OA B C '''与矩形OABC 的相似比为12,那么点B '的坐标是( )A.(2,3)-B.(2,3)-C.(3,2)-或(2,3)-D.(2,3)-或(2,3)-4.下列说法中正确的个数为( ) ①凡正方形都相似; ②凡等腰三角形都相似; ③凡等腰直角三角形都相似;④两个相似多边形的面积比为4:9,则周长的比为16:81. A.1B.2C.3D.45.下列图形中不一定是相似图形的是( ) A.两个含60°角的平行四边形 B.两个含60°角的菱形 C.含60°角的菱形和含120°角的菱形 D.两个正方形6.已知FHB EAD ∽它们的周长分别为30和15,且6FH =,则EA 的长为( )A.3B.2C.4D.57.若线段MN 长为1,点P 是MN 的黄金分割点,则MP 的长是( )D.不能确定8.如图所示,某校数学兴趣小组利用标杆BE 测量建筑物的高度,已知标杆BE 高1.5m ,测得 1.2AB =m,12.8BC = m ,则建筑物CD 的高是( )A.17.5 mB.17 mC.16.5 mD.18 m9.如图,在ABC 中,2AC =,4BC =,D 为BC 边上的一点,且CAD B ∠=∠.若ADC 的面积为a ,则ABD 的面积为( )A.2aB.52a C.3aD.72a 10.如图,在ABC 中,ABC C ∠=∠,将ABC 绕点B 逆时针旋转得到DBE ,点E 在AC 上,若3ED =,1EC =,则EB =( )B.32D.211.如图,直线////a b c ,ABC 的边AB 被这组平行线截成四等份,ABC 的面积为32,则图中阴影四边形DFIG 的面积是( )A.12B.16C.20D.2412.如图,在ABC 中,12AB AC ==,8BC =.正方形DEFG 的顶点E ,F 在ABC 内,顶点D ,G 分别在AB ,AC 上,AD AG =,4DG =,则点F 到BC 的距离为( )A.1B.2C.4D.413.湖南地图出版社首发的竖版《中华人民共和国地图》,将南海诸岛与中国大陆按同比例尺1:6700000表示出来,使读者能够全面、直观地认识我国版图,若在这幅地图上量得我国南北的距离是82.09厘米,则我国南北的实际距离大约是___________千米(结果精确到1千米).14.已知直线//CD EF ,若3,4OC CE ==,则ODOF的值是_________.15.已知111ABC A B C ∽,顶点A 、B 、 C 分别与1A 、1B 、1C 对应,12AC =,118AC =,ABC 的高AD 的长为6,那么111A B C 的高11A D 的长为___________.16.如图,////AB GH CD ,点H 在BC 上,AC 与BD 交于点G ,2,4AB CD ==,则GH 的长为__________.17.如果两个相似三角形的面积之比是9:25,其中小三角形一边上的中线长是12cm ,那么大三角形对应边上的中线长是________cm .18.为了加强视力保护意识,小明要在书房里挂一张视力表.由于书房空间狭小,他想根据测试距离为5 m 的大视力表制作一个测试距离为3 m 的小视力表.如图,如果大视力表中“E”的高度是3.5 cm ,那么小视力表中相应“E”的高度是_____________.19.如图,在矩形ABCD 中,2AD =,5AB =,P 为CD 边上的动点.当ADP 与BCP 相似时,DP =__________.20.如图,∆AOB 三个顶点的坐标分别为(8,0)A ,(0,0)O ,(8,6)B -,点M 为OB 的中点,以点O 为位似中心,把∆AOB 各边缩小为原来的12,得到∆A’OB’,点M '为OB '的中点,则MM '的长为____________.21.如果两个相似三角形的相似比为2:3,两个三角形的周长的和是100 cm ,那么较小的三角形的周长为___________cm.22.如图,ABC 的两条中线AD 和BE 相交于点G ,过点E 作//EF BC 交AD 于点F ,则FGAG=_______________.23.如图,正方形OEFG 和正方形ABCD 是位似图形,且点F 与点C 是对对应点,点F 的坐标是(1,1),点C 的坐标是(4,2),则它们的位似中心的坐标是_____________.24.如图,在正方形ABCD 中,E 是BC 的中点,F 是CD 上一点,且14CF CD =.有下列结论:① 30BAE ∠=︒,②AE EF ⊥,③ABE AEF ,④ADF ECF .其中正确的结论是_______.(填序号)25.已知线段,,a b c 满足0326a b c==≠,且226a b c ++=. (1)求线段,,a b c 的长;(2)若线段x 是线段,a b 的比例中项,求x .26.如图,ABC 中,D 是AC 的中点,E 在AB 上,BD 、CE 交于O 点.已知::1:2OB OD =,求BEAE的值.27.已知,如图27-2-1-23,点,C D 在线段AB 上,PCD △是等边三角形,且1,24AC CD DB ===,.求证:.ACP PDB △△~28.如图,在66⨯的正方形方格中,每个小正方形的边长都为1,顶点都在网格线交点处的ABC 是一个格点三角形.(1)在图①中,请判断ABC 与DEF 是否相似,并说明理由;(2)在图②中,以点O 为位似中心,再画一个格点三角形,使它与ABC 的相似比为2:1;(3)在图③中,请画出所有满足条件的格点三角形,它与ABC 相似,且有一条公共边和一个公共角.29.如图,将一张长、宽之比为的矩形纸ABCD 依次不断对折,可以得到矩形,,,BCEF AEML GMFH LGPN .(1)判断矩形,,,,ABCD BCFE AEML GMFH LGPN 的长、宽之比是否相等,并说明理由; (2)你认为这些大小不同的矩形相似吗?30.如图,在ABCD 中,M 是BC 边的中点,E 是边BA 延长线上的一点,连接EM ,交线段AD 于点F 、AC 于点G .(1)求证:AFG CMG ∽; (2)求证:GF EFGM EM=. 31.如图,在ABC 中,5,3,4,//,AB BC AC PQ AB ===点P 在AC 上(与点A ,C 不重合),点Q 在BC 上.(1)当PQC 的面积与四边形PABQ 的面积相等时,求CP 的长. (2)当PQC 的周长与四边形PABQ 的周长相等时,求CP 的长.32.如图,在ABC 和A B C '''中,D 、D '分别是AB 、''A B 上一点,AD A D AB A B ''=''.(1)当时CD AC ABC D A C A B '''='''=,求证:ABC A B C '''∽. 证明的途径可以用如图所示的框图表示,请填写其中的空格.(2)当CD AC BCC D A C B C '''='''=时,判断ABC 与A B C '''是否相似,并说明理由.答案以及解析1.答案:A解析:四条线段a 、b 、c 、d 成比例,a c b d ∴=,3cm b =,8cm c =12cm d =,8312a ∴=,解得2a =cm.故选A. 2.答案:C解析://,DE BC AD AE DB EC ∴=即9,32AE=6AE ∴=,628.AC AE EC ∴=+=+= 3.答案:D解析:矩形OA B C '''和OABC 关于点O 位似,相似比为12,且点B 的坐标为(4,6)-. 点B '的坐标为(2,3)-或(2,3)-. 4.答案:B解析:①所有正方形的边成比例,角相等,都相似,故①正确;②等腰三角形形状不一定相同,所以不一定相似,故②错误;③所有等腰直角三角形的边成比例,角分别相等,都相似,故③正确;④两个相似多边形的面积比为4:9,则周长的比为2:3,故④错误.所以说法正确的有①③,共2个.故选B. 5.答案:A解析:对于选项A ,两个平行四边形都含60°角,则角分别相等,但边不一定成比例,故不一定相似,故A 符合题意;对于选项B 、C ,两个菱形的角分别相等,边成比例,一定相似,故B 、C 不合题意;对于选项D ,两个正方形一定相似,故D 不合题意.故选A. 6.答案:A 解析:FHB EAD ∽,且FHB 和EAD 的周长分别为30和15,FHB ∴和EAD 的周长比为2:1,FHB EAD ∽,2FH EA ∴=,即62EA=,解得3EA =,故选A. 7.答案:C解析:设MP x =,则1PN x =-.当MP PN PN MN =时,111x xx -=-,解得x =x =(不合题意,舍去).MP 的长也可以为1-=. 8.答案:A解析:EB AC ⊥,DC AC ⊥,//EB DC ∴,ABE ACD ∴∽,AB BEAC CD∴=. 1.5BE =m ,1.2AB =m ,12.8BC =m ,14AC AB BC ∴=+=m ,1.2 1.514DC=,解得17.5DC =m.故选A. 9.答案:C解析:在BAC 和ADC 中,C ∠是公共角,CAD B ∠=∠,BAC ADC ∴∽,2()4ABC DACS BC SAC∴==,又ADC 的面积为a ,ABC ∴的面积为4a ,ABD ∴的面积为3a .10.答案:A解析:由旋转可得ABC DBE ≌,BC BE ∴=,3DE AC ==,C BEC ∴∠=∠.又ABC C ∠=∠,ABC BEC ∴∠=∠,又C C ∠=∠,ABC BEC ∴∽,EC BCBC AC∴=,即2BC CE CA =⋅,BC ∴=,BE ∴=故选A.11.答案:B 12.答案:C解析:如图,作AN BC ⊥于N ,交DG 于M ,交EF 于H .12AB AC ==,AN BC ⊥,8BC =,4BN CN ∴==,AN ∴,AD AG =,AB AC =,ADG AGD ∴∠=∠,B C ∠=∠,2180DAG ADG ∴∠+∠=︒,2180DAG B ∠+∠=︒,ADG B ∴∠=∠,//DG BC ∴,ADG ABC ∴∽,AM DG ⊥,AM DGAN BC ∴=,48=,AM ∴=,MN ∴=,易知四边形MHFG 是矩形,4MH GF DG ∴===,4HN MN MH ∴=-=,点F 到BC 的距离为4.故选C.13.答案:5500解析:设我国南北的实际距离是x 厘米,由题意得82.09:1:6700000x =,解得550003000x =,550003000厘米5500≈千米.14.答案:37解析://,::CD EF OD OF OC OE ∴=.3,4,::3:7OC CE OD OF OC OE ==∴==.15.答案:4解析:111ABC A B C ∽,12AC =,118AC =,相似比为12382=,ABC 的高AD 的长为6,111A B C ∴的高11A D 的长为2643⨯=. 16.答案:43 解析:////AB GH CD ,,GH CH GH BH AB BC CD BC∴==, 1GH GH CH BH AB CD BC BC∴+=+=, 2,4AB CD ==,124GH GH ∴+=,解得43GH =. 17.答案:20解析:两个相似三角形的面积之比是9:25,大三角形的周长:小三角形的周长5:3=.小三角形一边上的中线长是12cm ,大三角形对应边上的中线长是31220(cm)5÷=. 18.答案:2.1 cm 解析:由题意得//CD AB ,ECD EAB ∴∽,CD DE AB BE ∴=. 3.5AB = cm ,5BE = m ,3DE =m ,33.55CD ∴=, 2. 1CD ∴=(cm ). 19.答案:1或4或2.5解析:①当APD PBC 时,AD PD PC BC =,即252PD PD =-,解得1PD =或4PD =. ②当PAD PBC 时,AD PD BC PC =,即225PD PD =-,解得 2.5DP =.综上所述,DP 的长度是1或4或2.5.20.答案:2.5或7.5解析:由A ,B ,O 三点坐标知AOB 为直角三角形,由勾股定理得10OB =,因为M 为OB的中点,所以5OM =.根据题意作AOB 的位似图形A OB '',有两种情况:当位似图形与原图形在位似中心同侧时,点B '与点M 重合,点M '位于OM 的中点, 2.5OM '=,则5 2.5 2.5MM '=-=;当位似图形与原图形在位似中心两侧时,5 2.57.5MM '=+=,所以MM '的长为2.5或7.5.21.答案:40解析:设较小的三角形的周长为x cm ,则较大的三角形的周长为(100)x -cm ,两个相似角形的相似比为2:3,两个相似三角形的周长比为2:3,21003x x ∴=-,解得40x =,即较小的三角形的周长为40 cm.22.答案:14解析:线段AD 、BE 是 ABC 的中线,BD CD ∴=,AE EC =,又//EF BC , EF 是ACD的中位线, AF FD ∴=,1122EF CD BD ==.//EF BC ,EFG BDG ∴∽,12FG EF DG BD ∴==,2DG FG ∴=,3DF AF FG ∴==,4AG FG ∴=,14FG AG ∴=. 23.答案:(2,0)-解析:连接CF 并延长,交x 轴于点H ,则点H 就是位似中心.(1,1)F ,(4,2)C ,1OE ∴=,4OB =,1EF =,2BC =.由图可知,EF x ⊥轴,BC x ⊥轴,//EF BC ∴,HEF HBC ∴∽,HE EF HB BC ∴=,即1142OH OH +=+,解得2OH =,(2,0)H ∴-,即位似中心的坐标是(2,0)-.24.答案:②③解析:在正方形ABCD 中,AB BC =, E 是BC 的中点,11,22BE BE AB AB ∴==, 30BAE ∴∠≠︒,故①错误;E 是BC 的中点,:1:4CF CD =,2AB BE CE CF ∴==,又,B C ABE ECF ∠=∠∴,BAE CEF ∴∠=∠.又90,90BAE AEB AEB FEC ∠+∠=∴∠+∠=︒︒,90AEF ∴∠=︒,即AE EF ⊥,故②正确;,2,AE AB ABE ECF EF EC ∴== AB CE BE AE EF EF∴==,且90ABE AEF ∠=∠=︒, ABE AEF ∴,③正确;2,3,DA DF AD DF CE CF CE CF==∴≠, ADF ∴和ECF 不相似,④错误.综上可知,正确的为②③.25.答案:(1)解:设(0)326a b c k k ===≠ 3,2,6a k b k c k ∴===226a b c ++=34636k k k ∴++=,2k ∴=6,4,12a b c ∴===(2)线段x 是线段,a b 的比例中项,2x ab ∴=.又6,4a b ==,x ∴=(负值舍去).26.答案:如图,取AE 的中点F ,连接DF ,D 是AC 的中点,F 为AE 的中点,DF 为AEC 的中位线,//DF CE ∴.//OE DF ,12BE BO EF OD ∴==, 14BE AE ∴=. 27.答案:证明:PCD △是等边三角形,602PCD PDC PC CD PD ∴∠=∠====,,°120PCA PDB ∴∠=∠=°.14AC BD ==,,11,,22AC PD PC BD ∴== ,AC PD PC BD ∴= .ACP PDB ∴△△~28.答案:(l )如图①所示,ABC 与DEF 相似.理由如下:1,4,AB BC AC DE EF DF ====AB BC AC DE EF DF ∴====ABC ∴与DEF 相似.(2)如图②所示,A B C '''即为所求.(3)如图③所示,ADC 和CEB 即为所求.29.答案:解:(1)矩形, , ,, ABCD BCFE AEML GMFH LGPN 的长、宽之比相等.理由如下: 设矩形纸的宽BC a =,长AB =,则有,,222a BE AE a ME ===,,,24a MF HF a ==,,44a LG LN ==AB BC BC a BE ∴====22AE a ME ==a MF HF ==44LG a LN== ∴五个矩形的长、宽之比相等.(2)这些大小不同的矩形都相似.30.答案:(1)证明://AD BC ,FAG MCG ∴∠=∠.AGF CGM ∠=∠,AFG CMG ∴∽.(2)证明:AFG CMG ∽,GF AF GM CM∴=.//AD BC ,AEF BEM ∴∽,AF EF BM EM∴=. 又由M 是BC 边的中点知CM BM =, AF EF CM EM∴=, GF EF GM EM ∴=. 31.答案:(1)PABQ PQC S S =四边形,:1:2.//,,,,PQC ABC S S PQ AB CPQ CAB CQP CBA PQC ABC ∴=∴∠=∠∠=∠∴222:1:2,14,2PQC ABCPC S S AC PC PC ⎛⎫∴== ⎪⎝⎭∴=⨯∴= (2)PQC 的周长与四边形PABQ 的周长相等, 1()6,26.PC CQ PA AB QB AB BC AC CQ CP ∴+=++=++=∴=- ,CPQ CAB ,CP CQ CA CB ∴=即6,43CP CP -=解得247CP =. 32.答案:(1)CD AC AD C D A C A D '''='''=;A A ∠=∠'. (2)ABC A B C '''∽.理由:如图,分别过点D ,D '作//DE BC ,//D E B C '''',DE 交AC 于点E ,DE''交A C ''于点E './/DE BC ,ADE ABC ∴~,AD DE AE AB BC AC∴==. 同理,A D D E A E A B B CA C '''''''''='''=. r AD A D AB A B '='', DE D E BC B C '''∴'=, DE BC D E B C ∴=''''. 同理,AE A E AC A C ''=''. AC AE A C A E AC A C '''-'∴'='-,即EC E C AC A C ''='', EC AC E C A C ∴=''''. CD AC BC C D A C B C '''=''=', CD DE EC C D D E E C ''='∴'=''. DCE D C E ∴'''∽,CED C E D ∴∠=∠'''.//DE BC ,180CED ACB ∴∠+∠=.同理,180C E D A C B ''''''∠+∠=, ACB A C B ∴∠=∠'''.AC CB A C C B ='''', ABC A B C ∴'''∽.。
九年级上册数学相似图形练习题精选.doc
九年级上册数学相似图形练习题精选姓名:日期:一、 填空题:1、若 AB=1m,CD=25cm,则 AB ∶ CD= ;若线段 AB=m, CD=n,则 AB ∶ CD=.2、若 MN ∶PQ=4∶ 7, 则 PQ ∶ MN= , MN=PQ, PQ=MN。
3、若线段 a,b,c,d成比例 , 其中 a=5 ㎝,b=7 ㎝,c=4 ㎝ , 则 ,d=.4、若 a · b=c · d 则有 a ∶ d=;若 m ∶ x=n ∶ y, 则 x ∶ y=.5、已知 4x - 5y=0, 则( x + y )∶( x - y )的值为 .6、若 x ∶ y ∶z=2∶ 7∶5, 且 x -2y + 3z=6, 则 x=,y=,z=;x y z x+yy+3z7、设 3 = 5 = 7 , 则 y =___, 3y-2z =__ __.8、已知点 C 是线段 AB 的黄金分割点 , 且 AC>BC,则 AC ∶ AB=.9、如图 1,D 、 E 是 ABC 的边 AB 、 AC 上的点 , DE 与 BC 不平行 , 请填上一个你认为合适的条件:使得 ADE ∽ ACB.10、已知: ABC , P 是边 AB 上的一点 , 连结 CP.( 如图 2)(1) 当∠ ACP 满足 条件时 ,ACP ∽ ABC. (2) 当 AC ∶ AP=时 ,ACP ∽ ABC11 、在ABC 和 A ′ B ′ C ′中 ,∠ A=∠ A ′ = 40 °∠ B = 80 °∠ B ′ = 60 °则ABC 和A ′B ′C ′。
( 填“相似”与“不相似” )212、在如图 3 的 ABC 中 ,DE ∥ BC, 且 AD=3 BD,DE = 4cm , 则 BC =。
13、如图 4 在 ABC 中 , DE ∥BC, BC = 6cm, S ADE ∶ S ABC =1 ∶ 4 , 则 DE 的长为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【分析】由∠ACD=∠B结合公共角∠A=∠A,即可证出△ACD∽△ABC,根据相似三角形的性质可得出 =( )2= ,结合△ADC的面积为1,即可求出△BCD的面积.
【解答】解:∵∠ACD=∠B,∠A=∠A,
∴△ACD∽△ABC,
∴ =( )2= .
∵S△ACD=1,
∴S△ABC=4,S△BCD=S△ABC﹣S△ACD=3.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长与面积.
23.如图,Rt△ABC中,∠C=90°,AB=14,AC=7,D是BC上一点,BD=8,DE⊥AB,垂足为E,求线段DE的长.
24.如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且∠APD=∠B.
(1)求证:AC•CD=CP•BP;
(1)求证:△AFE∽△ABC;
(2)若∠A=60°时,求△AFE与△ABC面积之比.
2017年12月12日初中数学的初中数学组卷
参考答案与试题解析
一.选择题(共10小题)
1.已知2x=3y(y≠0),则下面结论成立的是( )
A. = B. = C. = D. =
【分析】根据等式的性质,可得答案.
【解答】解:A、两边都除以2y,得 = ,故A符合题意;
B、两边除以不同的整式,故B不符合题意;
C、两边都除以2y,得 = ,故C不符合题意;
D、两边除以不同的整式,故D不符合题意;
故选:A.
【点评】本题考查了等式的性质,利用等式的性质是解题关键.
2.若△ABC~△DEF,相似比为3:2,则对应高的比为( )
A.3:2B.3:5C.9:4D.4:9
【分析】直接利用相似三角形对应高的比等于相似比进而得出答案.
【点评】此题考查了相似三角形的判断与性质,关键是根据AA证出△CBA∽△CAD,是一道基础题.
8.如图,在四边形ABCD中,AD∥BC,∠ABC=90°,E是AB上一点,且DE⊥CE.若AD=1,BC=2,CD=3,则CE与DE的数量关系正确的是( )
A.CE= DEB.CE= DEC.CE=3DED.CE=2DE
【解答】解:∵D、E分别是AB、AC的中点,
∴AD= AB,AE= AC,DE= BC,
∴△ABC的周长=AB+AC+BC=2AD+2AE+2DE=2(AD+AE+DE)=2×6=12.
故选B.
【点评】本题考查的是三角形的中点的性质和三角形中位线定理,三角形的中位线平行于第三边,并且等于第三边的一半.
8.如图,在四边形ABCD中,AD∥BC,∠ABC=90°,E是AB上一点,且DE⊥CE.若AD=1,BC=2,CD=3,则CE与DE的数量关系正确的是( )
A.CE= DEB.CE= DEC.CE=3DED.CE=2DE
9.如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是( )
A. B. C. D.
【分析】延长FE交AB于点D,作EG⊥BC、作EH⊥AC,由EF∥BC可证四边形BDEG是矩形,由角平分线可得ED=EH=EG、∠DAE=∠HAE,从而知四边形BDEG是正方形,再证△DAE≌△HAE、△CGE≌△CHE得AD=AH、CG=CH,设BD=BG=x,则AD=AH=6﹣x、CG=CH=8﹣x,由AC=10可得x=2,即BD=DE=2、AD=4,再证△ADF∽△ABC可得DF= ,据此得出EF=DF﹣DE= .
6.如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )
A.1:3B.1:4C.1:5D.1:25
【分析】根据相似三角形的判定定理得到△DOE∽△COA,根据相似三角形的性质定理得到 = , = = ,结合图形得到 = ,得到答案.
∴AD=AH,
同理△CGE≌△CHE,
∴CG=CH,
设BD=BG=x,则AD=AH=6﹣x、CG=CH=8﹣x,
∵AC= = =10,
∴6﹣x+8﹣x=10,
解得:x=2,
∴BD=DE=2,AD=4,
∵DF∥BC,
∴△ADF∽△ABC,
∴ = ,即 = ,
解得:DF= ,
则EF=DF﹣DE= ﹣2= ,
15.如图,已知△ABC中,AB=5,AC=3,点D在边AB上,且∠ACD=∠B,则线段AD的长为.
16.如图,在△ABC中,∠BAC=60°,∠ABC=90°,直线l1∥l2∥l3,l1与l2之间距离是1,l2与l3之间距离是2,且l1,l2,l3分别经过点A,B,C,则边AC的长为.
17.若 ,则 =.
【分析】过点D作DH⊥BC,利用勾股定理可得AB的长,利用相似三角形的判定定理可得△ADE∽△BEC,设BE=x,由相似三角形的性质可解得x,易得CE,DE的关系.
【解答】解:过点D作DH⊥BC,
∵AD=1,BC=2,
∴CH=1,
18.如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12m,则旗杆AB的高为m.
19.如图,在△ABC中,AB=5,AC=4,点D在边AB上,∠ACD=∠B,则AD的长为.
20.赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,则学校旗杆的高度为米.
故选C.
【点评】本题考查相似三角形的判定与性质,牢记“相似三角形的面积比等于相似比的平方”是解题的关键.
5.如图,D,E分别是△ABC的边AB,AC上的中点,如果△ADE的周长是6,则△ABC的周长是( )
A.6B.12C.18D.24
【分析】根据线段中点的性质求出AD= AB、AE= AC的长,根据三角形中位线定理求出DE= AB,根据三角形周长公式计算即可.
评卷人
得分
三.解答题(共12小题)
21.如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.
(1)求证:△ACD∽△BFD;
(2)当tan∠ABD=1,AC=3时,求BF的长.
22.如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
故选:C.
【点评】本题主要考查相似三角形的判定与性质、全等三角形的判定与性质及正方形的判定与性质,熟练掌握角平分线的性质和正方形的判定与性质、相似三角形的判定与性质是解题的关键.
4.如图,在△ABC中,点D是AB边上的一点,若∠ACD=∠B,AD=1,AC=2,△ADC的面积为1,则△BCD的面积为( )
6.如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )
A.1:3B.1:4C.1:5D.1:25
7.如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的
∴△DOE∽△COA,又S△DOE:S△COA=1:25,
∴ = ,
∵DE∥AC,
∴ = = ,
∴ = ,
∴S△BDE与S△CDE的比是1:4,
故选:B.
【点评】本题考查的是相似三角形的判定和性质,掌握相似三角形的面积比等于相似比的平方是解题的关键.
7.如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
A. B. C. D.
4.如图,在△ABC中,点D是AB边上的一点,若∠ACD=∠B,AD=1,AC=2,△ADC的面积为1,则△BCD的面积为( )
A.1B.2C.3D.4
5.如图,D,E分别是△ABC的边AB,AC上的中点,如果△ADE的周长是6,则△ABC的周长是( )
A.6B.12C.18D.24
【解答】解:如图,延长FE交AB于点D,作EG⊥BC于点G,作EH⊥AC于点H,
∵EF∥BC、∠ABC=90°,
∴FD⊥AB,
∵EG⊥BC,
∴四边形BDEG是矩形,
∵AE平分∠BAC、CE平分∠ACB,
∴ED=EH=EG,∠DAE=∠HAE,
∴四边形BDEG是正方形,
在△DAE和△HAE中,
∵ ,
∴△DAE≌△HAE(SAS),
1.已知2x=3y(y≠0),则下面结论成立的是( )
A. = B. = C. = D. =
2.若△ABC~△DEF,相似比为3:2,则对应高的比为( )
A.3:2B.3:5C.9:4D.4:9
3.如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,∠BAC,∠ACB的平分线相交于点E,过点E作EF∥BC交AC于点F,则EF的长为( )
12.如图,E为▱ABCD的边AB延长线上的一点,且BE:AB=2:3,连接DE交BC于点F,则CF:AD=.
13.如图,在△ABC中,点D为AC上一点,且 ,过点D作DE∥BC交AB于点E,连接CE,过点D作DF∥CE交AB于点F.若AB=15,则EF=.
14.若两个相似三角形的面积比为1:4,则这两个相似三角形的周长比是.
(1)求证:OD=OE;
(2)求证:四边形ABED是等腰梯形;
(3)若AB=3DE,△DCE的面积为2,求四边形ABED的面积.
27.如图,四边形ABCD、DEFG都是正方形,连接AE、CG,AE与CG相交于点M,CG与AD相交于点N.
求证:(1)AE=CG;(2)AN•DN=CN•MN.
28.如图,已知AD是△ABC的中线,E是AD的中点,CE的延长线交AB于F,求AF:AB的值.
