结构力学静定结构位移计算习题解答
《结构力学》第四章 静定结构的位移计算 (3)

B EI
2
R 1
cos
( FP R
sin
)
Rd
0
EI
d
FPR3
2EI
FPk 1
A
B Bx 2 By 2
B kP
B
A M k M P ds B EI
2
(1)
(FPR sin
)
Rd
0
EI
R
O
FP R2 (
)
EI
(1)梁与刚架
三、结构的外力虚功
作用在结构上的外力可能是单个的集中力、力 偶、均布力,也可能是一个复杂的力系,为了 书写方便,通常将外力系的总虚功记为:
W = Fk × km
其中,Fk为作功的力或力系,称为广义力; km为广义力作功的位移,称为广义位移。 下面讨论几种常见广义力的虚功。
1) 集中力的虚功
Pk
k
M
4EIk
GAl 2
kP
若截面为矩形,则:A bh, I bh3 /12,k 6 l 1, 2
h / l 1 , 10
h/l 1 , 15
则:
Q kP
( h)2
Q
M kP
l
kP 25% kMP
对于粗短杆来说,剪 切变形产生的位移不可忽
Q
kP 1%
1
m
ds
第i根杆件静力状态上的力在位移状态的位移上所 作的虚功:
Vi
s FNk
mds
s FQk mds
s Mk
1
m
ds
整个杆件结构各个截面上的内力在位移状态的位 移上的所作的总虚功:
N
N
N
结构力学-静定结构位移计算

80
32
3m
求图示刚架C铰左右两截面的 相对转动。EI=5×104kN.m
1
m=1
5/8
5m
MP
16
16
M
4m
4m
H
=
M0 C
= 1682
=16kN
f 88
1/8
1/8
H
=
M0 C
=
1m
f8
D
C
=
2 5104
580 2
2 3
5 8
+
580 2
2 3
5 8
+
1 3
-
2532 3
(1)同一结构可用不同的方式撤除多余约束但其超静定次数相同。
X1
X1
X3
X1
X2
X3
X3
X2
X1
X2
X3
(2)撤除一个支座约束用一个多余未知力代替, 撤除一个内部约束用一对作用力和反作用力代替。
(3)内外多余约束都要撤除。 (4)不要把原结构撤成几何
可变或几何瞬变体系
4
3
5 1
外部一次,内部六次 共七次超静定
1
2
不撤能除作支为杆1多后余体系约成束为的瞬变是杆1、2、 5
§9.2 力法的基本概念
1、超静定结构计算的总原则: 欲求超静定结构先取一个基本体系,然后让基本体系在受力方
面和变形方面与原结构完全一样。 力法的特点: 基本未知量——多余未知力; 基本体系——静定结构; 基本方程——位移条件——变形协调条件。
ql 2 8
5 8
l 4
2
+
l-x
结构力学课件 第五章 静定结构位移计算

N P l EA FN FNP
钢筋 混凝土
-4.74FP -1.58
Ab Ab 0.75Ab
Ag 3Ag 2Ag
1.97FPl/AbEb 1.84FPl/AbEb 0 0 0.63FPl/AgEg 0.5FPl/AgEg
CD DE CE
-4.42FP -1.58
0 0
0.263l
0.088l 0.278l
• 结构整体变形和支座移动共同产生的总位移计算
( FN FQ Mk)ds FR K c K
欲求的实际位移
cK
实际发生的已知位移
FN
FQ
M
FR K
虚设单位力作用下产生的力
§5-3 荷载作用下的位移计算
• 计算公式 • 计算步骤 • 各类结构位移计算公式
(M k FN FQ)ds
kFQ FQP FN FN P MMP ds ds ds EI EA GA
欲求的实际位移 M P FNP FQP 实际荷载作用下产生的内力
M
FN
FQ
虚设单位力作用下产生的内力
每一积分式的两个内力若使杆件变形一致,则其乘积取正号, 反之则取负号。
计算结果若 0 若 0
Ay0 EI
ql 2
MP
1
1
M
B
ql 2 ql 2
1
1
1
q
l
ql
l
ql 2
FN P
1
1
FN
FN FNP l FN FNP N ds EA EA
N 1 ql ql 2 N 1 l () M EA 2 2 EA
结构力学位移法题及问题详解
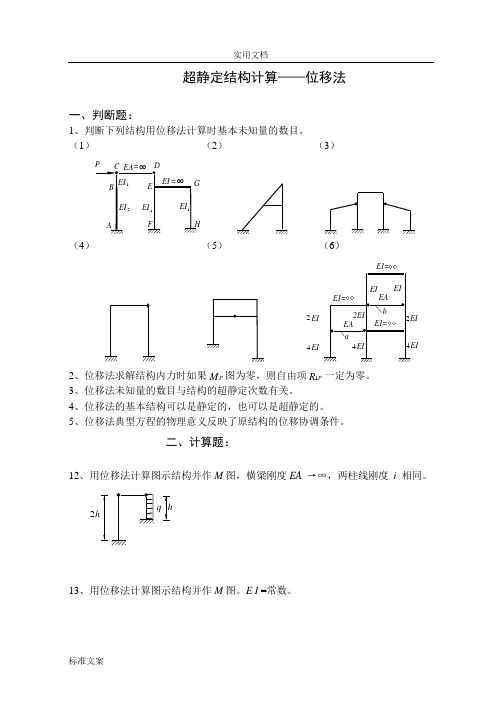
超静定结构计算——位移法一、判断题:1、判断下列结构用位移法计算时基本未知量的数目。
(1) (2) (3)(4) (5) (6)EIEIEIEI 2EI EI EIEIEA EA ab EI=EI=EI=244422、位移法求解结构内力时如果P M 图为零,则自由项1P R 一定为零。
3、位移法未知量的数目与结构的超静定次数有关。
4、位移法的基本结构可以是静定的,也可以是超静定的。
5、位移法典型方程的物理意义反映了原结构的位移协调条件。
二、计算题:12、用位移法计算图示结构并作M 图,横梁刚度EA →∞,两柱线刚度 i 相同。
213、用位移法计算图示结构并作M 图。
E I =常数。
lll/2l/214、求对应的荷载集度q。
图示结构横梁刚度无限大。
已知柱顶的水平位移为()5123/()EI→。
12m12m 8mq15、用位移法计算图示结构并作M图。
EI =常数。
ll l l16、用位移法计算图示结构,求出未知量,各杆EI相同。
4m19、用位移法计算图示结构并作M图。
ql l20、用位移法计算图示结构并作M 图。
各杆EI =常数,q = 20kN/m 。
6m6m23、用位移法计算图示结构并作M 图。
EI =常数。
ll 224、用位移法计算图示结构并作M 图。
EI =常数。
q29、用位移法计算图示结构并作M 图。
设各杆的EI 相同。
qql l /2/232、用位移法作图示结构M 图。
E I =常数。
qql l/2l /2l36、用位移法计算图示对称刚架并作M 图。
各杆EI =常数。
l l38、用位移法计算图示结构并作M 图。
EI =常数。
ql l l l42、用位移法计算图示结构并作M 图。
2m 2m43、用位移法计算图示结构并作M 图。
EI =常数。
lll48、已知B 点的位移∆,求P 。
ll/2/2A∆51、用位移法计算图示结构并作M 图。
q超静定结构计算——位移法(参考答案)1、(1)、4; (2)、4; (3)、9; (4)、5; (5)、7;(6)、7。
结构力学考研《结构力学习题集》4-静定位移

第四章 静定结构位移计算一、是非题1、虚位移原理等价于变形谐调条件,可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下,静定结构不产生内力,但会有位移且位移只与杆件相对刚度有关。
4、用图乘法可求得各种结构在荷载作用下的位移。
5、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图,用图乘法求位移的结果为:()/()ωω1122y y EI +。
Mk M p21y 1y 2**ωω7、图示桁架各杆EA 相同,结点A 和结点B 的竖向位移均为零。
A8、图示桁架各杆EA =常数,由于荷载P 是反对称性质的,故结点B 的竖向位移等于零。
aa9、图示简支梁,当P 11=,P 20=时,1点的挠度为0.01653l EI /,2点挠度为0.0773l EI /。
当P 10=,P 21=时,则1点的挠度为0.0213l EI /。
( )l10、图示为刚架的虚设力系,按此力系及位移计算公式即可求出杆AC 的转角。
C1P11、图示梁AB 在所示荷载作用下的M图面积为ql 3。
lAl /212、图示桁架结点C水平位移不等于零。
13、图示桁架中,结点C 与结点D 的竖向位移相等。
二、选择题1、求图示梁铰C 左侧截面的转角时,其虚拟状态应取:A.;;B.D.M C.=1=1=12、图示结构A 截面转角(设顺时针为正)为:A.22Pa EI / ;B.-Pa EI 2/ ;C.542Pa EI /() ;D.-542Pa EI /() 。
aa3、图示刚架l a >>0 , B 点的水平位移是:A .不定,方向取决于a 的大小;B .向左;C .等于零;D .向右。
4、图示静定多跨粱,当EI 2增大时,D 点挠度:A .不定,取决于EI EI 12;B .减小;C .不变;D .增大。
5、图示刚架中杆长l ,EI 相同,A 点的水平位移为:A.()2302M l EI /→;B.()M l EI 023/→;C.()2302M l EI /←;D.()023M l EI /←。
结构力学-位移法习题

第五章 超静定结构计算——位移法一、是非题1、位移法未知量的数目与结构的超静定次数有关。
2、位移法的基本结构可以是静定的,也可以是超静定的。
3、位移法典型方程的物理意义反映了原结构的位移协调条件。
4、结 构 按 位 移 法 计 算 时 , 其 典 型 方 程 的 数 目 与 结 点 位 移 数 目 相 等 。
5、位移法求解结构内力时如果P M 图为零,则自由项1P R 一定为零。
6、超 静 定 结 构 中 杆 端 弯 矩 只 取 决 于 杆 端 位 移 。
7、位 移 法 可 解 超 静 定 结 构 ,也 可 解 静 定 结 构 。
8、图示梁之 EI =常数,当两端发生图示角位移时引起梁中点C 之竖直位移为(/)38l θ(向下)。
/2/22l l θθC9、图示梁之EI =常数,固定端A 发生顺时针方向之角位移θ,由此引起铰支端B 之转角(以顺时针方向为正)是-θ/2 。
θABl10、用位移法可求得图示梁B 端的竖向位移为ql EI 324/。
q l11、图 示 超 静 定 结 构 , ϕD 为 D 点 转 角 (顺 时 针 为 正), 杆 长 均 为 l , i 为 常 数 。
此 结 构 可 写 出 位 移 法 方 程111202i ql D ϕ+=/。
二、选择题1、位 移 法 中 ,将 铰 接 端 的 角 位 移 、滑 动 支 承 端 的 线 位 移 作 为 基 本 未 知 量 :A. 绝 对 不 可 ;B. 必 须 ;C. 可 以 ,但 不 必 ;D. 一 定 条 件 下 可 以 。
2、AB 杆 变 形 如 图 中 虚 线 所 示 , 则 A 端 的 杆 端 弯 矩 为 :A.M i i i l AB A B AB =--426ϕϕ∆/ ;B.M i i i l AB A B AB =++426ϕϕ∆/ ;C.M i i i l AB A B AB =-+-426ϕϕ∆/ ;D.M i i i l AB A B AB =--+426ϕϕ∆/。
清华大学《结构力学习题集》

清华⼤学《结构⼒学习题集》第三章静定结构的位移计算⼀、判断题:1、虚位移原理等价于变形谐调条件,可⽤于求体系的位移。
2、按虚⼒原理所建⽴的虚功⽅程等价于⼏何⽅程。
3、在⾮荷载因素(⽀座移动、温度变化、材料收缩等)作⽤下,静定结构不产⽣内⼒,但会有位移且位移只与杆件相对刚度有关。
4、求图⽰梁铰C 左侧截⾯的转⾓时,其虚拟状态应取:5、功的互等、位移互等、反⼒互等和位移反⼒互等的四个定理仅适⽤于线性变形体系。
6、已知M p 、M k 图,⽤图乘法求位移的结果为:()/()ωω1122y y EI +。
7、图a 、b 两种状态中,粱的转⾓?与竖向位移δ间的关系为:δ=? 。
8、图⽰桁架各杆E A 相同,结点A 和结点B 的竖向位移均为零。
9、图⽰桁架各杆EA =常数,由于荷载P 是反对称性质的,故结点B 的竖向位移等于零。
⼆、计算题:10、求图⽰结构铰A 两侧截⾯的相对转⾓?A ,EI = 常数。
11、求图⽰静定梁D 端的竖向位移 ?DV 。
EI = 常数,a = 2m 。
12、求图⽰结构E 点的竖向位移。
EI = 常数。
13、图⽰结构,EI=常数,M =?90kN m , P = 30kN 。
求D 点的竖向位移。
14、求图⽰刚架B 端的竖向位移。
15、求图⽰刚架结点C 的转⾓和⽔平位移,EI = 常数。
16、求图⽰刚架中D点的竖向位移。
EI =常数。
17、求图⽰刚架横梁中D点的竖向位移。
EI =常数。
18、求图⽰刚架中D 点的竖向位移。
E I = 常数。
19、求图⽰结构A、B两截⾯的相对转⾓,EI =常数。
20、求图⽰结构A 、B 两点的相对⽔平位移,E I = 常数。
21、求图⽰结构B 点的竖向位移,EI = 常数。
22、图⽰结构充满⽔后,求A 、B 两点的相对⽔平位移。
E I = 常数,垂直纸⾯取1 m 宽,⽔⽐重近似值取10 kN / m 3。
23、求图⽰刚架C 点的⽔平位移 ?CH ,各杆EI = 常数。
04结构力学 第四章 静定结构的位移计算ok

FN , FS , M
FNP , FSP , M P
结构的位移,分别由弯曲变形、剪切变形和轴向变形引起。三种变形, 对位移的贡献各不相同。 上面的计算公式,不仅适用于静定结构,同样适用于超静定结构。
内力符号的规定:
轴力以拉为正; 剪力绕隔离体顺时针为正; 弯矩:规定其乘积的正负号,弯矩在同侧,乘积为正,反之, 乘积为负。 二、各类结构的位移计算公式
直杆
MiM k A EI dx
B
Mk
A
ω
1 EI
B
A
M k xtg dx
B 1 tg x( M k dx ) A EI
x xc
dx
B
y
α
1 1 tg xc yc EI EI
Mi=xtgα Mi yc x
M PM 1 ds EI EI yc
yc=xctgα
-
+1 +2/3 F=1 4m
1/2
3m B
单位力状态
DCV=1.6mm
A C 4m 位移状态 4m
3m B
§4-3
结构位移计算的一般公式
图示结构在某些因素(包括荷载、温度、 支座移动等)作用下,结构发生了变形, 某截面ds段上变形为:
K
DK
K
t1 t2
c2
c1
FR1
du( ds), d , d ( ds)
1cm 位移状态一
位移状态三 1cm 1 DD+1/41cm=0
DD= 0.25cm
位移状态二
单位荷载法求位移:单位力状态,在所求位移方向上施加单位力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6-1 求图示桁架AB 、AC 的相对转角,各杆EA 为常量。
解:(1)实状态桁架各杆的轴力如图(b )所示。
(b)(a)N(d )(c)题6-1N N(2)建立虚设单位力状态如(c )所示,求AB 杆的转角。
1113(2)82i P iAB i i P a P a P a N N l P a a a E A EA EA EA EAϕ⋅⋅⋅⋅-⋅-⋅⋅⋅==++⨯=∑(↺)(3)建立虚设单位力状态如(d )所示,求AC 杆的转角。
113(2)()(72i P i AC i iP a P a N N lPa a E A EA EA EAϕ⋅⋅⋅-⋅-⋅⋅==+⨯=∑(↺)故,AB 、AC 的相对转角为两杆转角之差:8(7(10.414AB AC P P P PEA EA EA EAϕϕϕ+-=-=-==-(夹角减小)6-2 求半圆曲梁中点K 的竖向位移。
只计弯曲变形。
EI 为常数。
方法一 解:(1)荷载作用下的实状态的约束反力如图(a )所示。
以任意半径与水平坐标轴的顺时针夹角为自变量,其弯矩方程为:sin (0)P M θθπ=-≤≤Pr(2)建立虚设单位力状态如(b )所示,其弯矩方程为:[]1cos )(0)2211cos()cos )()222i M πθθππθθθπ⎧≤≤⎪⎪=⎨⎪-=≤≤⎪⎩(r -r r -r (r +r(a)题6-2(3)积分法求半圆曲梁中点K 的竖向位移。
20233220022311cos )(sin )cos )(sin )2211cos )sin cos )sin sin sin 2)sin sin 2)2222cos 2i V Pk Pr Pr M M ds rd rd EIEI EI Pr Pr d d d d EI EI Pr EI πππππππππθθθθθθθθθθθθθθθθθθθ⋅-⋅-⋅∆==+⎡⎤⎡⎤=-⋅+⋅=-+⋅⎢⎥⎢⎥⎣⎦⎣⎦=-∑⎰⎰⎰⎰⎰⎰⎰(r -r (r +r (-(+(-(+(-11320211cos 2)cos cos 2)442Pr EI πππθθθ⎡⎤⎢⎥+-+=-↑⎢⎥⎣⎦()( 方法二:本题也可以只算纵向对称轴左边,再乘2。
题6-2(a)2033220033201sin )(Pr cos )221sin )cos cos sin 2)21sin cos 2)42i VP k M M ds rd EI EIPr Pr d d EI EI Pr Pr EI EI ππππθθθθθθθθθθθ⋅-⋅∆===-⋅=-=-+=-↑∑⎰⎰⎰⎰()(r -r (-(-(1 6-3 求梁的自由端的挠度。
EI 为常数。
方法一 :(积分法) 解:(1)荷载作用的实状态,以及坐标如图(a ),其弯矩方程为:()21(0)2M x qlx qx x l =--≤<(2)建立虚设单位力状态,以及坐标如图(b )所示,其弯矩方程为:()(0)i M x xx l =-≤<(3)积分法求梁自由端的竖向位移VB ∆。
方法二:(图乘法)6-4 求图示梁支座B 左右两侧截面的相对转角。
EI =常数。
题6-4M i (c)(b)M P解:(1)荷载作用的实状态,其弯矩图如图(b )所示。
(2)建立虚设单位力状态, 其弯矩图如图(c )所示。
(3)图乘梁(b )、(c )求自由端的竖向位移VB ∆223121115()38224248i iB y ql ql ql l l EI EI EIωϕ⋅==-⨯⨯⨯-⨯⨯⨯=∑(↺↻) (b)(a)题6-32023043401()()21)21111)3824li V PB l lx qlx qx MM dx dxEIEIq lx x dx EI q ql lx x EI EI -⋅--⋅∆===⋅==+=↓∑⎰⎰⎰()(+()↓题6-3M i 图M P (a)(b)(c)6-5求图示悬臂梁的自由端的挠度。
523.8410kN m EI =⨯⋅。
(a)(c)(m)M i 图(kN ·M P 图(b)解:(1)荷载作用的实状态,其弯矩图如图(b )所示。
(2)建立虚设单位力状态, 其弯矩图如图(c )所示。
(3)图乘梁(b )、(c )求自由端的竖向位移VC ∆3511122112(404(84)480(84)(4044)(4102)22333365606560 5.6910(m) 5.69mm()33 3.8410V i iC y EI EI EI EI EI ω-⋅⎡⎤∆==⨯⨯⨯+-⨯⨯⨯⨯+⨯+⨯⨯-⨯⨯⨯⨯⎢⎥⎣⎦===⨯=↓⨯⨯∑6-6 求简支梁中点K 的竖向位移。
EI =常数。
M i(b)M P题6-64解:(1)荷载作用的实状态,其弯矩图如图(b )所示。
(2)建立虚设单位力状态, 其弯矩图如图(c )所示。
(3)图乘梁(b )、(c )求自由端的竖向位移VK ∆22241311122()()()3164222883232848V i iky ql l l l ql l l ql l ql EI EI EI EI EIω⋅∆==⨯⨯⨯⨯+⨯⨯⨯⨯+⨯⨯⨯⨯=↓∑6-7 求图示刚架结点K 的转角。
E =常数。
题6-7(b)(c)解:(1)荷载作用的实状态,其弯矩图如图(b )所示。
(2)建立虚设单位力状态, 其弯矩图如图(c )所示。
(3)图乘梁(b )、(c )求自由端的竖向位移K ϕ222233333111111121()()()()34422434423438425()96896192192i iK y ql ql ql ql l l l l EI E I EI E I E I ql ql ql ql ql EI EI EI EI EIωϕ⋅==-⨯⨯⨯+⨯⨯⨯+⨯⨯⨯+⨯⨯⨯⨯⋅⋅⋅=-+++=↵∑6-8求图示三铰刚架D 、E 两点的相对水平位移和铰C 两侧截面的相对转角。
EI =常数。
解:(1)荷载作用的实状态,其弯矩图如图(b )所示。
(2)建立虚设单位力状态, 其弯矩图如图(c )、(d )所示。
(3)图乘梁(b )、(c )求自由端的竖向位移HDE ∆241112()()()242864H i iDEy l ql ql l EI EI EIω⋅∆==-⨯⨯⨯⨯⨯⨯=-←→∑(4)图乘梁(b )、(d )求铰C 两侧截面的相对转角C ϕ 方法一:22231112(1)21(1)388388i iC y ql ql ql ql l l l EI EI EI EI EIωϕ⋅==-⨯⨯⨯⨯-⨯⨯⨯+⨯⨯⨯⨯=-∑(↻↺) 方法二:实状态时C 处剪力为零223111(1)2(1)2383828i iC y ql ql l ql l EI EI EI EIωϕ⋅==-⨯⨯⨯⨯-⨯⨯⨯⨯⨯=-∑(↻↺) 6-10 求图示刚架结点K 的竖向位移。
62310kN m EI =⨯⋅。
题6-10解:(1)荷载作用的实状态,其弯矩图如图(b )所示。
(2)建立虚设单位力状态, 其弯矩图如图(c )所示。
(3)图乘梁(b )、(c )求自由端的竖向位移VK ∆3611111221236012618063(6180)9(1806)(1212)(645)93322233231728017280 5.4910() 5.49()310V i i C y EI EI EI E I EI EI m mm EI ω-⋅∆==-⨯⨯⨯-⨯⨯⨯-⨯⨯⨯-⨯⨯⨯⨯⨯-⨯+⨯⨯⨯⨯⋅=-=-=-⨯=-↓⨯∑6-15 求图示组合结构K 的竖向位移。
EA =常数、EI =常数。
(a)12a21(f )12P2IPP 、P2PPa2题6-15212PP221解:(1)荷载作用的实状态如图(a) 所示;用I-I 截面切开三链杆取右边为研究对象如图(b) 所示,并求出此三链杆的轴力;其弯矩图如图(d )所示。
(2)建立虚设单位力状态如图(e) 所示;切开三链杆取右边为研究对象如图(f) 所示,并求出此三链杆的轴力;其弯矩图如图(h )所示。
(3)图乘梁(b )、(c )求自由端的竖向位移VK ∆111()()1122()334i V i i P Ky N N EI EA EI EI EA EA EA EA ω⨯⨯-⨯⨯⨯-⨯⋅⋅∆=+=⨯⨯⨯⨯-⨯⨯⨯⨯+++=-↑∑∑梁式杆链杆222222()()2222P P P a a aPa a Pa a Pa a a6-17图示三铰刚架内部温度升高t o C ,材料的线膨胀率为α。
求中间铰C 的竖向位移。
各杆截面高度h 相同,EI =常数。
题6-17图(b)h解:(1)实状态如图(a)所示,刚架内外侧温度差't t C=o,轴线温度升高02tt=Co(2)建立虚设单位力状态,1124N N N=-==-左右梁, 其弯矩图如图(b)所示。
(3)图乘梁(a)、(b)求中间铰C的竖向位移'2211112()()(22)222424242535335()8888/108i iVC N Mttht t t l l ll l lhtl tl tl tl tlh lααωωαααααααα∆=±±⨯=-⨯⨯⨯⨯-⨯⨯⨯-⨯⨯⨯⨯+⨯⨯⨯=--=--=-↑∑∑6-20 图示桁架中杆件AK在制造时比原设计长度做长了5mm,求由此引起的K点的水平位移。
题6-20图解:(1)实状态如图(a)所示,桁架中AK杆在制造时比原设计长度做长了5mm。
(2)建立虚设单位力状态,先求出反力,再利用结点法求出该状态AK杆的轴力。
(3)图乘梁(a)、(b)求中间铰C的竖向位移5 5.5355()()VC iN∆=±⋅∆==→∑mm6-22 图示刚架支座A发生水平位移1∆、竖向位移2∆及顺时针向转角φ,求由此引起的刚结点K的水平位移。
φ(a)△M解:①实位移状态如图6-22(a )所示。
②沿水平方向虚设单位力1=i P ,虚力状态如图6-22(b )所示。
1()01A A A X Y M l l =←==⨯=(↺)③由刚体的可能功方程,有:110H k A A X M ϕ⋅∆-⋅∆-⋅=1H C l ϕ∆=∆+→()。
