寿险精算学分析
寿险精算学(五)
1 q k 0 4
k 0,1, 2,3
该保单在被保险人死亡年末给付1，年利率6%。
根据净均衡保费原则确定：
（1）在趸缴保费场合，确定在各年期末责任准备金。 （2）在净均衡保费场合，确定在各年期末责任准备金。
例6. 1答案
趸缴保费场合
参照时刻
0
1
2
3
责任准备金
0
0.89
对责任准备金评估工作的监管
责任准备金的过去法计算公式可以对此作出合理
解释，从公式可以看到，责任准备金的评估结果 依赖于所使用的评估方法和评估假设 监管最严格的国家，监管机构会规定适用的准备 金评估方法和评估假设并要求保险公司遵照执行 在监管较松的国家，会规定确定评估假设的程序 和方法，允许精算师在一定范围内选择他自己认 为合适的评估假设。
10001Vx:3， 2Vx:3 1000
例2答案
由后顾公式：
1000 1Vx:3 1000 ( Px:3 x:1 1 k x ) s 1000 2Vx:3 1000 (lx Px:3 (1 i ) d x ) lx 1
1000 [332.511.06 100] 280.51 900 1000 [lx 1 ( Px:3 1Vx:3 )(1 i ) d x 1 ] lx 2 900 (332.51 280.51) 1.06 1000 90] 610.89 810
后顾方法推导
以完全连续n年定期两全保险为例
V ( Ax:n ) Ax s:n s Pax s:n s A1 s:t t Ex s Ax s t:n s t x P[ax s:t t Ex s ax s t:n s t ] A1 s:t Pax s:t t Ex s s tV ( Ax:n ) x
保险精算课程三(寿险精算)
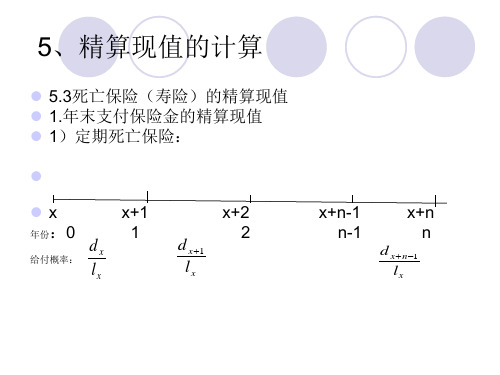
x
xn
x
xh
2.终身寿险的年缴纯保费
h Px
Ax ax:h|
Mx Nx Nxh
3.两全保险的年缴纯保费
P h x：n|
Ax:n| ax:h |
Mx
M xn Dxn Nx Nxh
课堂练习:
1.某人30岁投保20年期，延期10年，5年限期缴费的定期 人寿险,保险金额为100000元，求年缴纯保险费?
N x N x1 Dx
S x N x N x1
(Ia) x
Sx Dx
( Ia) x
S x 1 Dx
( Ia) x:n |
S x 1
S x n1 Dx
nN x n1
作业：
1.某人30岁(女)时投保寿险,约定45岁前死亡给付保险金 150000元,40岁至60岁之间死亡给付保险金为100000 元,60岁以后给付保险金50000元,求趸缴纯保险费?
(In| A)x (IA)1x:n| n|Ax
Rx Rxn nM xn N M xn
Dx
Dx
标准递减也可以看作：
A1 x:n |
A1 x:n 1|
A1 x:n 2|
A1 x:1|
nM x [Rx1 Rxn1 ] Dx
课堂练习
（x）=30，定期寿险保单。第一年死亡给付1000元， 第二年死亡给付1200元，第三年1400元，这样依次按 200元比例递增，n=20，求保险金的精算现值：
x:n |
Dx
Ax:n|
Mx
M xn Dx
Dxn
Ax
Mx Dx
m| Ax
M xm Dx
A1 x :n|
Mx
M Dx
寿险精算学-ch2
未来寿命的生存函数示意图
• t p0 =S0 (t)
• 1 px 简记为 px
特别符号
• t u qx t px tu px
• tu px t px u pxt
未来寿命生存函数的性质
• 定理1： 0 px 1
•
定理2：
d dt
t
px
0
,t 0
•
定理3：
lim
t x
t
px
0
• 由于死亡是必然发生的, 所以还可以得到如下两个引理:
• 在新生婴儿时期寿命的密度函数有一个递减趋势。 这是 因为新生婴儿是脆弱的,各种先天不足都会在刚出生时暴 露, 所以新生婴儿阶段死亡概率是偏高的。 经过医学治疗 和自然淘汰, 婴儿死亡率迅速下降。
• 青少年时期是人一生中死亡率最低的一段时期。 这段时 期是人类的健康黄金期。
• 从40 岁左右开始, 随着年龄的增长, 人的器官逐渐老化, 开 始罹患各种疾病,身体进入失效期, 死亡率开始递增。 60 岁前后进入加速失效期, 80 岁前后达到死亡率的顶峰。
– 中老年时期属于人类的加速失效时期。 在这段时间里, 身体各器 官逐渐老化,开始罹患各种疾病。 通常一种疾病治好了, 不久又会 产生另外一种疾病。 人类进入加速失效期之后, 健康维持成本将 变得越来越大。
例2.5
• 假设某人群每10万个新生婴儿, 能活到40 岁的人数为 97369, 能活到85 岁的人数为33851, 而在85~86 岁这一年 死亡的人数为3758。
• 所以本例中, 40 岁的人在85 岁时未来寿命的密度函数和 死亡力函数（以年为最小计量单位） 为：
f40 (45)
3758 97369
0.0386
保险精算知识点总结
保险精算知识点总结一、保险精算的基本原理保险精算的基本原理主要包括风险评估、定价和赔付计算。
风险评估是指对被保险风险的分析和评估，包括风险的特点、概率、影响程度等，并通过数理统计和概率分析等方法来对风险进行量化和评估。
定价是指根据风险评估的结果来确定保险产品的定价，即保险费率的确定。
赔付计算是指根据保险条款和赔付原则，对保险事故的赔付进行计算和处理。
二、保险精算的技术方法1. 数理统计数理统计是保险精算中最基本的技术方法之一，它涉及到对大量的数据进行分析和处理，通过统计学的方法来评估风险的概率和程度，为保险产品的定价和赔付计算提供依据。
2. 概率分析概率分析是指利用概率论的知识来对风险进行定量的评估和分析，包括风险的概率分布、期望值、方差等。
通过概率分析，可以对不确定性的风险进行量化和评估，为保险精算提供科学的依据。
3. 统计建模统计建模是指将数理统计和概率分析的方法运用到保险精算中，通过建立数学模型来对风险进行评估和定价。
统计建模可以通过回归分析、时间序列分析、生存分析等方法来对不同类型的风险进行建模和预测。
4. 风险管理风险管理是保险精算中非常重要的一个环节，它涉及到对风险的识别、评估、控制和管理。
通过风险管理，可以有效地降低保险公司的风险暴露和损失，提高其经营的安全性和稳定性。
三、保险精算的应用领域保险精算的应用领域非常广泛，包括人寿保险、财产保险、健康保险、再保险等方面。
在人寿保险中，保险精算主要涉及到寿险责任的定价、赔付计算和资金积累的管理；在财产保险中，保险精算主要涉及到财产损失的评估、定价和赔付计算；在健康保险中，保险精算主要涉及到医疗费用的定价和管理等。
此外，再保险领域也是保险精算的重要应用领域，它涉及到对风险的再分担和再定价。
四、保险精算的发展趋势随着信息技术和数据分析的发展，保险精算的方法和技术也在不断地更新和改进。
未来，保险精算将更加注重在对大数据的分析和处理上，通过数据挖掘、机器学习和人工智能等技术手段来提高风险评估和定价的精准度。
保险精算学人寿保险的精算现值
5.3.4 离散型生存年金的精算累积值
对于期初付n年定期生存年金，有
5.4 每年付数次的生存年金
1、终身生存年金
基本公式：
axm
k 0
1
v
k m
m
k m
px
类似于上一节的公式，有
UDD假定下的公式 近似公式（实际操作公式）
2、定期生存年金
UDD假设下的公式
近似公式（实际操作公式）
一年递增无穷次（连续递增）：
对于递增的n年定期寿险，只需将积分上限换成n即可。
2.死亡年度末给付的递增型终身寿险的趸缴纯保 费
相应地，对于n年定期保险，有
4.4.2 递减型寿险 1.立即给付型递减型寿险（n年定期寿险为例）
2. 死亡年末给付型递减型寿险（n年定期寿险为例）
4.4.3 两类精算现值的换算
假定：(x)岁的人，保额1元终身寿险 基本函数关系
vt vt , t 0 bt 1 , t 0
zt btvt vt , t 0
符号： Ax
厘定：
Ax E(zt ) 0 zt fT (t)dt
0
vt
t
pxxt dt
0
e t
t
pxxt dt
方差公式
Var(zt ) E(zt2 ) E(zt )2
由于死亡可能发生在被保险人投保之后的任意时 刻，所以死亡即刻赔付时刻是一个连续随机变量， 它距保单生效日的时期长度就等于被保险人签约 时的剩余寿命。
4.1.1 精算现值的概念
精算现值即趸缴纯保费，未来保险金给付 在签单时的现值，即一次性缴清的纯保费， 它是以预定利率和预定死亡率为基础计算 的。
主要险种的精算现值（趸缴纯保费）的厘定
保险精算学寿险精算现值
1 D x
M
t 0
x t
引进转换函数：Rx M x t
t 0
则 IA x
Rx Dx
根据概率的知识，我们还可以得到
IA x E Z (k 1)v
k 0
k 1 k
qx k Ax
k 0
（2）定期递增寿险
用 IA x:n 表示趸缴净保费，则
631终身寿险年缴净保费死亡年末赔付单位元终身寿险如果规定保费每年一次终身交付这时保险费的现值就是终身生存年金精算现值以表示年缴均衡净保保费在年内缴清632定期寿险年缴净保费在死亡均匀分布的假设下如果被保险人死亡瞬时赔付633两全寿险年缴净保费634延期年金年缴净保费延期年的终身生存年金的年缴净保费设保费的缴付期限为表示年缴净保费
k 0
本节介绍当保险金随保险时期按等差数列变动时的现值表达式。 （1）递增型人寿保险的趸缴净保费 （2）递减型人寿保险的趸缴净保费
（1）标准递增终身寿险
某x岁的人投保，保单规定，若被保险人在第一年死亡，保险金为1单 位元；若被保险人在第二年内死亡，保险金为2单位元 用 IA x 表示这种保险的现值，则
IA x:n IA x:n
1
nAx:n 1
（4） 等值递增n年的终身寿险的趸缴净保费
用 I n A 表示趸缴净保费，则
I A IA
n x t n
x
x
n IA x
t 1 其中， IA ( t n 1) v q x t x n
2 2 2n p v p v n x n x n p xn qx . n 2
Z Z1 Z 2
寿险精算知识点
寿险精算知识点寿险精算是指利用数学、统计学和金融学等理论与方法，对寿险业务进行风险评估、保费定价、赔付准备金计提等工作的过程。
它是寿险行业中的核心技术之一，具有重要的意义。
本文将从寿险精算的基本概念、核心任务以及一些常见的精算方法等方面进行介绍。
我们来了解一下寿险精算的基本概念。
寿险精算是指寿险公司通过对历史数据进行分析和建模，利用数学和统计学的方法，对寿险业务进行风险评估和保费定价的过程。
它主要包括风险评估、保费定价、赔付准备金计提以及风险管理等方面的工作。
寿险精算的核心任务之一是风险评估。
风险评估是指对寿险业务的风险进行测算和评估，主要包括寿险产品的死亡率、残疾率、疾病率等指标的测算和预测。
通过对风险的评估，可以帮助寿险公司合理确定保费水平，确保寿险公司的盈利能力和偿付能力。
保费定价是寿险精算的另一个核心任务。
保费定价是指根据寿险产品的风险特征和市场需求，确定合理的保费水平。
在进行保费定价时，需要考虑到寿险公司的风险承受能力、保险产品的竞争力以及客户的支付能力等因素。
通过合理的保费定价，可以保证寿险公司的盈利能力和可持续发展。
赔付准备金计提是寿险精算的另一个重要任务。
赔付准备金是指寿险公司为支付未来赔款而预先计提的资金。
在进行赔付准备金计提时，需要考虑寿险产品的赔付率、赔付期限、赔付模式等因素。
通过合理的赔付准备金计提，可以确保寿险公司的偿付能力，保障客户的权益。
在寿险精算的实践中，还存在一些常见的精算方法。
例如，死亡率分析是寿险精算中常用的方法之一。
通过对历史死亡率数据的分析和建模，可以预测未来的死亡率，从而为保费定价和赔付准备金计提提供依据。
此外，寿险精算还可以运用生命表、经验法、模型法等方法进行风险评估和保费定价。
寿险精算是寿险行业中的核心技术之一，它通过利用数学、统计学和金融学等理论与方法，对寿险业务进行风险评估、保费定价、赔付准备金计提等工作。
寿险精算的核心任务包括风险评估、保费定价、赔付准备金计提以及风险管理等方面的工作。
寿险精算电子教案分析
寿险精算教案第二章利息的度量及基本计算★本章教学目的：通过本章学习，要求学生能准确理解利息的基本概念，掌握利息度量标准和有关计算。
★本章重点与难点：利率与贴现率、现值与终值的比较；单利与复利、单贴现与复贴现的比较；实际利息率与名义利息率、实际贴现率与名义贴现率的比较；利息理论的核心问题的理解。
★本章教学内容：主要介绍利息理论中的有关利息的基本概念和度量方法，以及利息的有关计算。
§2.1 利息的度量一、利息的相关概念1．利息：是资金的价格，指借款者向贷款者所支付的使用资金的代价。
2．利息的几种来源:(1)节欲论(2)时差利息论(3)流动偏好论(4)劳动价值论二、现值函数与终值函数1．本金、利息和积累值（终值）的关系：2．终值函数与总量函数（1）终值函数：a（t）（2）总量函数：A（t）3．现值函数：1()a t-三、利息的度量1．利息率（1）实际利息率 i（2）名义利息率()m i2．贴现率（1）实际贴现率 d（2）名义贴现率()md3．息力（1）利息力定义：()()()() td dA t a tdt dtA t a t δ==（2）贴息力定义：1'1()() tda tdta t δ--=-§2.2 等值方程及其求解一、可比点（日）二、等值方程（等价值式）三、建立等值方程的一般步骤1．画时间轴2．选择可比日3．建立等值方程4．解等值方程第三章 确定年金★本章教学目的：通过本章学习，要求学生理解确定年金的概念及相互关系，特别是年金给付期与利息结算期之间的关系。
正确掌握确定年金的计算原理和方法。
★本章重点与难点：年金的概念与分类、年金给付期不等于利息结算期时的确定年金是采取什么样的方法进行计算？变额年金的现值与终值的计算。
★本章教学内容：主要介绍利息理论中有关确定年金的基本概念，年金现值和年金终值的计算方法。
§3.1 每期支付一次的等额确定年金一、 期末付年金 1．21nnn v a v v v i-=+++=2．1(1)11(1)(1)nn n i S i i i-+-=+++++=3．有关ni a 和n i S 的关系式二、期初付年金1．2111n n n v a v vvd--=+++=2．2(1)1(1)(1)(1)n nn i S i i i d+-=+++++=三、延付年金1．m m ni n m n m a v a a a +==- 2．mm ni n m n m a v a a a +==- 四、永久年金1．11v a v i ∞==- 2．111a v d∞==-§3.2 每期支付m 次的等额确定年金一、 期末付年金1．现值：12()()11(...)m n nm m m mm nv a v v v m i-=+++=2．终值：121()()1(1)1[1(1)(1)...(1)]m n nm m m mm n i S i i i m i -+-=+++++++=二、期初付年金1．现值：()()1n m m nv a d-=2．终值：()()(1)1n m m ni Sd+-=三、期末付年金与起初付年金的关系 四、延付年金1．()()()()m f m m m f n n n f f a v a a a +==- 2．()()()()m f m m m f nn n ffa v a a a +==-五、永久年金1．()()1m m a i ∞=2．()()1m m a d∞=§3.3 每k 期支付一次的等额确定年金一、 期末付年金1．现值：21()...(1)1n n k kkkI k v PV v vvi -=+++=+- 2．终值：(1)1()(1)1n I ki AV i +-=+-二、 期末付年金3．现值：(1)21()1...1n n k kkkD k v PV v vvv--=++++=- 4．终值：(1)1()1n D ki AV v +-=-§3.4 变额年金一、 按等差数列变化的变额年金 （一）期末付年金： 1．递增年金：（1） 现值：23()23...nnn n a nv Ia v v v nv i-=++++=（2） 终值：()(1)()nn n n S n IS i Ia i-=+=2．递减年金：（1） 现值：23()(1)(2)...nnn n a Da nv n v n v v i-=+-+-++=（2） 终值：(1)()(1)()n nnn n n i S DS i Da i+-=+=（二）期初付年金： 1．递增年金：（1） 现值：21()123...nn n n a nv Ia v v nv d--=++++=（2） 终值：()(1)()nn n n S n IS i Ia d-=+=2．递减年金：（1） 现值：21()(1)(2)...n nn n a Da n n v n v vd--=+-+-++=（2） 终值：(1)()(1)()n n nnn n i S DS i Da d+-=+=二、 按等比数列变化的变额年金第四章 生命函数★本章教学目的：通过本章学习，要求学生清楚的知道构成生命表中的原始生存人数和它们的死亡率是计算的基础，而生命表中的其它项目均是由它们派生而来的生命函数，且都为随机变量。
保险精算学6-寿险责任准备金
• 在常数利息力与常数死力假设下，有：
v e , t px eut
Ax
0
vt
t
px
xt dt
et eut dt
0
0.04 e dt (0.060.04)t 0.04 10 0.4 0
ax
1 Ax
10
And we can show :
Axt Ax 0.4, a xt ax 10 tV ( Ax ) Axt P( Ax ) a xt 0
– 责任准备金是已付保费积累值与保险成本积累 值（accumulated cost of insurance）之差。
公式推导：以 Vt x:n 为例
（1）保费差公式
Vt x:n
A xt:nt
P x:n
a xt:nt
A
xt:nt
a xt:nt
P x:n
a xt:nt
P xt:nt
P x:n
a x
h
tV
( Ax:n
)
Axt:nt Axt:nt
h P( Ax:n ) a xt:ht ht n
1 t n
h年限期缴费 n年生存保险
h
1
tV ( Ax:n
)
Ax
1 t:nt
Ax
1 t:nt
1
h P( Ax:n ) axt:ht ht n
1 t n
th
th
m年递延 生存年金
tV (m
ax)
50
0.5508
60
0.8214
4、其他评估方法
• 从未来法推导：
– 保费差公式（premium-difference formula）
• 责任准备金等于剩余缴费期内保费差的精算现值。
《寿险精算学》课件
寿险精算学的未 来发展趋势包括 大数据、人工智 能、区块链等新 技术的应用，以 及与金融、医学、 心理学等学科的 交叉融合。
市场变化：人口老龄化、医 疗技术进步等社会变化将对 寿险精算产生影响
技术发展：人工智能、大数 据等新技术的应用将提高精 算效率和准确性
监管政策：政府对保险行业 的监管政策将影响寿险精算
风险转移：通过保险合同 将风险转移给其他主体
风险监测：定期监测风险 状况，及时调整风险管理 和控制策略
风险报告：定期向管理层 和监管机构报告风险管理 和控制情况
人工智能和大数据 技术的应用：提高 精算效率和准确性
互联网保险的发展： 推动精算师需求增 加
老龄化社会的挑战： 精算师需要应对长 寿风险和养老保障 需求
,
01 单 击 添 加 目 录 项 标 题 02 寿 险 精 算 学 概 述 03 寿 险 精 算 学 的 原 理 和 方 法 04 寿 险 精 算 学 的 模 型 和 工 具 05 寿 险 精 算 学 的 风 险 管 理 和 控 制 06 寿 险 精 算 学 的 未 来 发 展
定义：寿险精算 学是研究寿险公 司经营风险和财 务风险的学科， 包括风险评估、 定价、准备金评
生命表：描述人口死亡率和 生存率的统计表
精算模型：用于计算保险费、 准备金等精算指标的数学模
型
精算软件：用于精算分析和 计算的专业软件，如Excel、
SPSS等
模型：生命表、利率模型、死亡 率模型等
应用：评估寿险产品的风险、定 价、投资等
添加标题
添加标题
添加标题
添加标题
工具：Excel、SPSS、R等统计 分析软件
风险识别：识别 可能影响寿险公 司经营的各种风 险
寿险精算学分析102页PPT
51、没有哪个社会可以制订一部永远 适用的 宪法， 甚至一 条永远 适用的 法律。 ——杰 斐逊 52、法律源于人的自卫本能。——英 格索尔
53、人们通常会发现，法律就是这样 一种的 网，触 犯法律 的人， 小的可 以穿网 而过， 大的可 以破网 而出， 只有中 等的才 会坠入 网中。 ——申 斯通 54、法律就是法律它是一座雄伟的大 夏，庇 护着我 们大家 ；它的 每一块 砖石都 垒在另 一块砖 石上。 ——高 尔斯华 绥 55、今天的法律未必明天仍是法律。 ——罗·伯顿
6、最大的骄傲于最大的自卑都表示心灵的最软弱无力。——斯宾诺莎 7、自知之明是最难得的知识。——西班牙 8、勇气通往天堂，怯懦通往地狱。——塞内加 9、有时候读书是一种巧妙地避开思考的方法。——赫尔普斯 10、阅读一切好书如同和过去最杰出的人谈话。——笛卡儿
Thanபைடு நூலகம் you
保险精算学3li
保险精算学引言保险精算学是一门涉及风险管理和保险预测的学科。
它利用统计学、概率论和数学方法来评估和预测保险风险，并为保险公司提供相关的决策依据。
保险精算学的应用范围广泛，涵盖了保险产品设计、保费定价、准备金计提等方面，在保险行业中起着重要的作用。
保险精算的意义与作用保险精算学在保险行业中的作用不可无视。
首先，保险精算学可以通过对保险风险的评估和预测，提供应保险公司有关保险产品设计与定价的决策依据。
其次，保险精算学可以帮助保险公司合理计提准备金，确保公司具备足够的偿付能力。
此外，保险精算学还可以为保险公司提供风险管理的手段，帮助公司防范风险、躲避损失。
保险精算的根本方法保险精算学主要依靠统计学、概率论和数学方法来进行分析和预测。
以下是保险精算学中常用的根本方法：1.损失频率和损失严重程度分析：保险精算师通过对历史数据的分析，计算出损失发生的频率和损失的严重程度，从而评估保险风险的大小。
2.预测模型的建立：保险精算师可以利用统计学方法建立预测模型，预测未来的损失发生情况和保险风险的变化趋势。
3.经验法那么和风险分级：保险精算师可以根据历史数据和经验法那么，将保险风险进行分类和分级，以便更好地进行风险评估和定价。
4.模拟和蒙特卡洛方法：保险精算师可以利用模拟和蒙特卡洛方法，对保险风险的不确定性进行模拟和评估，从而为保险公司决策提供更科学的依据。
保险精算的应用领域保险精算学在各个保险行业领域都有广泛的应用。
以下是一些常见的应用领域：1.车险精算：保险精算师通过对车险保单数据的分析，评估和预测车险风险，确定车险产品的保费定价和准备金计提。
2.人寿险精算：保险精算师通过对人寿险保单数据的分析，评估和预测人寿险风险，确定人寿险产品的保费定价和准备金计提。
3.健康险精算：保险精算师可以通过对健康险保单数据的分析，评估和预测健康险风险，为保险公司提供有关健康险产品设计和定价的建议。
4.再保险精算：再保险精算主要关注保险公司对大额风险进行转移的过程和原那么，通过对再保险合同和再保险市场的分析，评估再保险风险，并为保险公司提供再保险方案的建议。
保险精算原理与实务 第五章 人寿保险
9
生存保险
1
：n年纯生存保险精算现值。
1 定义： n年纯生存保险是以满期被保险人仍然存活为给 付条件的生存保险。
10
两全保险
1
：对(x)的1单位元n年两全保险精算现值。
1定义：对(x)的1单位元n年两全保险，是对(x)的n年定 期寿险和n年纯生存保险的合险。
14
标准递增变额寿险
从标准递增定期寿险的意义出发，可以得出另外两个不同的公式：
1n年标准递增的两全保险：是n年定期递增寿险精算现值与n年n 单位元纯生存保险现值之和。其精算现值为，
15
标准递减变额年金
1定义：变额寿险当bK+1=n-k时，称为标准递减的定期寿险。
1
：标准递减的定期寿险精算现值。
16
1定义：对(x)的1单位元延期m年n年定期寿险是从x+m 岁起到 x+m+n年的定期寿险。
13
标准递增变额寿险
1 定义：标准递增的变额寿险，是赔付额bK+1=k+1 ，k是 从投保开始到死亡时存活的整数年数的变额寿险。
1 (IA)x ：标准递增的终身寿险的精算现值。
1
：标准递增的n年定期寿险的精算现值。
2
定期寿险
1 均衡保费定期寿险简称为定期寿险，保险费在约定的 缴费期内均衡缴付，通常缴费期与保险期相同。
1 递增保费定期寿险的保险费在缴费期内递增，在实践 中常见的递增保费定期寿险是每年更新定期寿险。
1 保额递减定期寿险的死亡赔付金额随着已投保时期的 延长而降低，保险费通常采取均衡方式。实践中最常 见的保额递减寿险是以抵押贷款余额为死亡赔付额， 以还款期为保险期的定期保险。
寿险精算第一讲：生命分布理论
生存分布理论（寿险精算课程I ）学习重点：掌握生存函数及其相互关系、了解三种常用非整数年存活函数估计方法和几个死亡时间的解析分布、掌握生命表基本函数及其相互关系“如果算命先生能算出人的寿命，那么还要精算师干什么？”“既然‘天有不测风云、人有旦夕祸福’，那么精算师能算出人的寿命吗？” “算一个人的寿命‘不可能’，算一群人的寿命‘可能’”人寿保险是以人的生命为保险标的，以被保险人在指定时期的生存或死亡作为保险金给付条件。
因此，被保险人的寿命分布状况，也就是被保险人能存活多久，他在各年龄段上的死亡率有多大的是保险人所关心的问题。
寿险公司的承保对象是数以万计的保险人，如此众多的人的生存（死亡）率，必定存在着某种统计规律，这就是所谓“大数法则”。
寿险精算就是要利用这种大数法则，从概率论和数理统计的角度来研究和揭示这些统计规律性，用以解决寿险精算中的实际问题。
一、寿命的分布函数、生存函数和密度函数 1、寿命的分布函数一个人的寿命是从出生到死亡的时间长度，它是无法事先确定的，这在概率论中称为随机变量，记为)0(>X X 。
人的寿命总是有限的，假设人的寿命极限为ω，则ω<<X 0。
寿命随机变量X 的分布函数为：)()(x X P x F r ≤=，0≥x)(x F 在统计中称为累积分布函数，它的概率意义是随机变量X 小于等于一个给定值x 的概率。
在此，X 表示一个0岁的人将来的寿命，)(x F 可以理解为0岁的人在x 之前死亡的概率。
显然有：0)0(=F ，1)(=ωF 。
2、寿命的生存函数寿命随机变量X 的生存函数为：)()(x X P x S r >=，0≥x在此，X 表示一个0岁的人将来的寿命，)(x S 可以理解为0岁的人能活过x 岁的概率。
或者说一个人寿命大于x 岁的概率。
生存函数与分布函数具有如下补函数关系：)(1)(1)()(x F x X P x X P x S r r -=≤-=>= 显然有：1)0(=S ，0)(=ωS 。
《寿险精算》学习指南
迄今为止，国内外对精算尚未达成完全统一的定义。不过，大多采用如下方 式来描述。所谓精算，就是运用数学、统计学、金融学、保险学及人口学等多学 科的知识和原理，定量解决金融保险等领域中有关问题，进而为决策提供科学依 据的一门应用型学科。精算与保险的结合形成保险精算，保险精算是精算的重要 组成部分。保险精算一般被描述为：运用数学、统计学、金融学、保险学及人口 学等学科的知识和原理，去解决商业保险与各种社会保障业务中有关项目，如死 亡率的测定、生命表的构造、费率的厘定、准备金的计提、利源分析、盈余分配、 偿付能力管理等，以此保证保险经营的稳定性和安全性。
4
叉和边缘学科。
§1.2 寿险精算的起源
寿险精算是从寿险经营的窘境中应运而生的一门新兴学科。寿险的前身是欧 洲中世纪的基尔特（Guild）制定。据记载，世界上最早的寿险保单之一，是在 16 世纪末，由一群海上保险承保人在伦敦对 William Gibbon 签发的，一年保险 期限，保险金额为 382.68 镑的定期保单。
18 世纪中期以前，英国早期的寿险组织、资格最老的要数于 1706 年在伦敦 特许成立的协和保险社。1721 年经特许成立的皇家交易保险公司和伦敦保险公 司开始经营寿险业务。此外，还有一些捐助团体以及联盟协会也经营寿险业务。 这些互助协会、保险公司以及其他团体经营寿险业务，这些业务概括起来，具有 如下几个特点：（1）寿险仅为火险、海险的副产品，尚未大规模独立地经营寿险。 （2）寿险业务所承保的对象限制较多。互助协会承保会员人数有限，主要局限 于商人、企业合伙人；特许保险公司经营的寿险，将病人、老年人及天花病人等 一概拒之门外。（3）寿险的保险费采用赋课式，未将年龄大小、死亡率高低等与 保险费挂钩。（4）寿险经营缺乏严密的科学基础，表现在有关计算单一、粗糙， 考虑因素较少。这样的寿险经营导致的是寿险业的不景气，保险技术的停滞不前。 也正是在这种经营思想的指导下，协和保险社在 1756 年以詹姆斯·道森（James Dodson）年龄偏大（那时 Dodson 实际年龄仅 46 岁）为由，拒绝吸收其为保险 社成员，其结果成为寿险精算兴起的导火线。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
趸缴纯保费的厘定
按照净均衡原则，趸缴纯保费就等于
E( zt )
第二节
死亡即刻赔付 趸缴纯保费的厘定
1、死亡即刻赔付(payable at the moment of death)
死亡即刻赔付的含义
死亡即刻赔付就是指如果被保险人在保障期内发生
保险责任范围内的死亡 ，保险公司将在死亡事件发 生之后，立刻给予保险赔付。它是在实际应用场合， 保险公司通常采用的理赔方式。 由于死亡可能发生在被保险人投保之后的任意时刻， 所以死亡即刻赔付时刻是一个连续随机变量，它距 保单生效日的时期长度就等于被保险人签约时的剩 余寿命。
被保障人群的大数性(large number of the insured)
这就意味着，保险公司可以依靠概率统计的原理计算出
平均赔付并可预测将来的风险。
4、趸缴纯保费的厘定
4.1假定条件(assumptions)
假定一：同性别、同年龄、同时参保的被保险人
的剩余寿命是独立同分布的。 假定二：被保险人的剩余寿命分布可以用经验生 命表进行拟合(fitting)。 假定三：保险公司可以预测将来的投资受益（即 预定利率）。
net single premium paid at the monent of death
死亡年末赔付保险趸缴纯保费的厘定
net single premium paid at the end of the year of death
递归方程 recursion equations 计算基数 commutation functions
2、主要险种的趸缴纯保费的厘定
n年期定期寿险n-year term life insurance 终身寿险whole life insurance 延期m年的终身寿险m-year deferred whole life insurance n年期生存保险n-year pure endowment n年期两全保险n-year endowment 延期m年的n年期的两全保险m-year deferred nyear endowment 递增终身寿险increasing whole life insurance 递减n年定期寿险decreasing n-year term insurance
非延期保险non-deferred
insurance 两全保险 endowment insurance
保障期是否有限
定期寿险 term year
insurance 延期保险 deferred insurance
insurance 终身寿险whole life insurance
第二章中英文单词对照一
Net single premium 趸缴纯保费 Actuarial present value 精算现时值 死亡即刻赔付保险 Insurances payable at the moment of death Insurances payable at the 死亡年末给付保险 end of the year of death Level benefit insurance
定额受益保险
第二章中英文单词对照二
定期人寿保险 终身人寿保险 两全保险 生存保险
延期保险 变额受益保险
Term life insurance Whole life insurance Endowment insurance Pure endowment insurance Deferred insurance Varying benefit insurance
Acturial Mathematics(寿险精算学)
第三章
Net Single Premium of Life Insurance
人寿保险趸缴纯保费的厘定
本章结构
人寿保险趸缴纯保费厘定原理 the principal of net single premiun 死亡即刻纯保费厘定的原理
1、人寿保险简介
什么是人寿保险
狭义的人寿保险是以被保险人在保障期是否死亡
作为保险标的的一种保险。 广义的人寿保险是以被保险人的寿命作为保险标 的的一种保险。它包括以保障期内被保险人死亡 为标的的狭义寿险，也包括以保障期内被保险人 生存为标底的生存保险和两全保险。
3、人寿保险的性质
保障的长期性(long term )
这使得从投保到赔付期间的投资受益（利息）成为不容
忽视的因素。
保险赔付金额和赔付时间的不确定性(uncertain of the size and time of payment)
人寿保险的赔付金额和赔付时间依赖于被保险人的生命
状况。被保险人的死亡时间是一个随机变量。这就意味 着保险公司的赔付额也是一个随机变量，它依赖于被保 险人剩余寿命分布。
4、趸缴纯保费的厘定
4.3基本符号
—— 的人。 ( x 投保年龄 ) ——人的极限年龄 ——保险金给付函数。 t —— 贴现函数。 v t ——保险给付金在保单生效时的现时值 t
b
z
x
zt bt vt
4、趸缴纯保费的厘定
趸缴纯保费的定义
在保单生效日一次性支付将来保险赔付金的期望现时值
2、人寿保险的分类
受益金额是否恒定
定额受益保险 level benefit insurance 变额受益保险varying benefit insurance
保障标的的不同
人寿保险life insurance 生存保险pure endowment
保单签约日和保障期期 始日是否同时进行
4、趸缴纯保费的厘定
4.2厘定原则
保费净均衡原则 解释 所谓净均衡原则(it is net because it has not been loaded)， 即保费收入的期望现时值正好等于将来的保险赔付金 的期望现时值(expectation of the present value of the net premium equals expectation of the present value of the payment)。它的实质是在统计意义上的收支平衡。是 在大数场合下，收费期望现时值等于支出期望现时值