航带法空中三角测量详解
合集下载
摄影测量学航带法空中三角测量

2447132 2447132
2450136 2450136
2449233 2449233 2449233
2448233 2448233 2448233
2447083 2447083
B655
2450082 2450082
2449136 2449136 2449136
B653
B653
2450013 2450013
2464
2465
2466
2467
1
3
Y
5
V
2
X
8 6 7
Y
U
X
1 1 V ... 1 X1 X2 ... Xn Y1 Y2 ... Yn X1 X2 ... Xn
2 2 2
a 0 l x1 X 1Y1 a1 l x 2 X 2Y2 a 2 l x 3 ... a3 ... X nYn a l 4 xn
v u 1 0 0 U 0 1 0 V v v v w 0 0 1 W
W 0 U
0 W V
U X 0 lu X l Y 0 R 0 V Y 0 v W Z 0 l w Z
B655
B655 B655
2448143 2448143 2448143
B658
2448017 2448017 2448017
B658
2450001 2450001 2450001
B654
B654
2449
2467101
2448
2447
航带解析空中三角测量

▪ 三、航带模型的概略定向
▪ 类似于单元模型的概略定向,把航带模型作为一个整体, 通过空间相似变换来实现。引用式(9-55),此处的符号 为:
X Y
=R
U V
X G
YG
Z
W ZG
▪ 式中 为模型点经空间相似变换后所取得重心化地面参考
坐标;ΔXG、ΔYG、ΔZG为航带模型重心平移值,误差方程
2
3
2
Z c0 c1 X c2Y c3 X c4 XY c5 X c6 X Y
▪ 式中:ΔX、ΔY、ΔZ为航带模型经概略绝对定向后模型点
的非线性变形坐标改正值;
▪ X、Y、Z 为航带模型经概略绝对定向后模型点重心化概略 坐标;
▪ ai、bi、ci为非线性变形多项式的系数。 ▪ 使用上列多项式进行运算时,对X、Y、Z坐标改正可以分
2
▪ 单航带空中三角测量是把航带中每个像对经连续像对 相对定向构成一个航带模型,然后根据航带内地面控制 点进行航带模型的绝对定向,以取得加密点的地面坐标 。由于在建立航带模型的过程中不可避免地有误差存在 ,即使在构网前对每张像片的像点坐标已作了系统误差 的改正,在构网中航带模型还要受到偶然误差累积的影 响,致使航带模型产生非线性变形,需要根据地面控制 点按其规律加以改正,最终求出各加密点的地面坐标。
式可写成:
18
v 0 W V U 1 0 0 l
U
v V
W
0
U
V 0 1 0
U
l
V
vW
V
U
0W
0
0
1
dX
G
lW
dYG
dZG
▪ 其中:
(10-7)
l
航带法解析空中三角测量

X 2Y2 Y22 Y2 vQ N 2 ( Z 2 ) N 2 X 2 N 2 Bx Bx Q Z2 Z2 Z2
特别注意: • 模型中的定向点只建立VQ方程 • 模型间的连接点需建立VQ, V P方程 • 对于模型间的连接点建立误差方程时,常数项中的 N1 X1, N1 Y1 , N1 Z1必须用前一模型中的N2 X2, N2 Y2 , N2 Z2
二、构建自由航带网
(2、带模型连接条件的连续法相对定向) 摄站坐标
X s 2 X s1 mBx Ys 2 Ys1 mBy Z s 2 Z s1 mBz
非连接点的模型坐标
X p X s1 mN1 X 1 1 Y p (Ys1 mN1Y1 Ys 2 mN2Y2 ) 2 Z p Z s1 mN1式曲 面拟合航带网复 杂的变形曲面, 使该曲面经过航 带网已知点时, 所求得坐标变形 值与它们实际的 变形值相等或使 其残差的平方和 为最小
1、二次多项式
X A0 A1 X A2Y A3 X 2 A4 XY Y B0 B1 X B2Y B3 X 2 B4 XY Z C0 C1 X C2Y C3 X 2 C4 XY
连接点的模型坐标
X p X s 2 mN2 X 2 Y p Ys 2 mN2Y2 Z p Z s 2 mN2 Z 2
N2
a a N2 Z 2 Bz
Z2
二、构建自由航带网(2、连续法相对定向)
Z Z B
b 1 a 2 a z
a
3 1 5
4 2 6
b
3 1 5
4
2
非独立累积性误差:随模型个数的增加而增大其影响
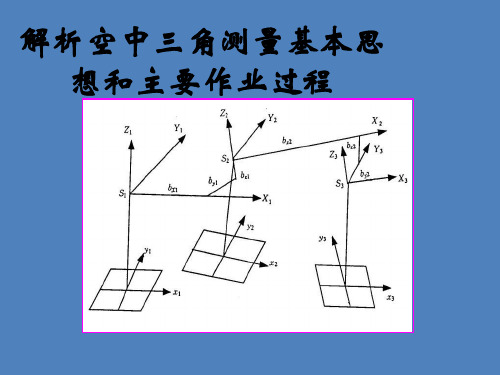
解析空中三角测量基本思想和主要作业过程
解析空中三角测量>概述
§1-1 解析空中三角测量概述
知识点:
◇ 解析空中三角测量的定义 ◇解析空中三角测量的意义 ◇解析空中三角测量的目的 ◇解析空中三角测量的分类
解析空中三角测量>概述
§1-1 解析空中三角测量概述
◇ 解析空中三角测量的定义
利用计算的方法,根据航摄像片上 所量测的像点坐标以及少量的地面控制 点求出地面加密点的物方空间坐标,称 之为解析空中三角测量。俗称摄影测量加
解析空中三角测量>光束法区域网空三
§1-4光束法区域网空中三角测量
知识点: ◇ 基本思想与流程
解析空中三角测量>光束法区域网空三
§1-4光束法区域网空中三角测量
◇ 基本思想与流程
以一张像片组成的一束光线作为一 个平差单元,以中心投影的共线方程作 为平差的基础方程,通过各光线束在空 间的旋转和平移,使模型之间的公共点 的光线实现最佳交会,将整体区域最佳 地纳入到控制点坐标系中,从而确定加 密点的地面坐标及像片的外方位元素
解析空中三角测量基本思 想和主要作业过程
解析空中三角测量>重要回顾
上节课重点
主要知识点: ◇ 解析法相对定向 ◇ 模型点坐标计算 ◇ 解析法绝对定向 ◇ 光束法严密解法(一步定向法)
基本要求:理解像对解析相对定向的概念、相 对定向元素解算过程。掌握模型解析绝对定向 目的和过程;了解光束法双像解析摄影测量。
密
解析空中三角测量的信息
○
○ ○
○
○
像片上 量测的 像点坐 标
少 量 地 面 点 坐 标
Z
Y X
S
S
待定点 高程控制点 平高控制点
平高 控制点
⊙ 高程 控制点
空中三角测量

正变换:由大地坐标系到(地面)摄影测 量坐标系的坐标变换
X p
Yp
sin cos
cos Xt
sin
Yt
b a
a Xt
b
Yt
Z p Zt
Yp Xt
Xp
1
Yt
a
X pYt
X
2 t
YpX t Yt2
b
X
pX t YpYt
X
2 t
Yt2
a2 b2
X
2 p
Y
2 p
X
2 t
Yt2
航带法空三是以一条航带作为平差的基本单元,将模型点 的摄影测量作为观测值,根据地面控制点的摄影测量坐标 和地面坐标应相等以及相邻航带公共点坐标应相等为条件 ,用平差解求航带网的非线性变形改正系数,从而求出各 加密点的地面坐标。
独立模型法是以单元模型为平差单元以模型坐标为观测值 ,根据地面控制点的摄影测量坐标和地面坐标应相等以及 相邻模型公共点、公共摄站点的摄影测量坐标应相等为条 件,确定每一个单元模型的旋转、平移和缩放参数,从而 求出各加密点的地面坐标
量
三、空中三角测量的分类
按阶段可以分为模拟空中三角测量、解析空三 和数字空三。模拟的采用图解法或光学机械法, 在全能型立体测图仪上根据摄影过程的几何反 转原理建立航带模型,实现控制点的加密。解 析的是利用计算机,根据人工观测方法在坐标 量测仪或解析测图仪上量测的像点坐标,采用 一定的数学模型计算出待定点的地面坐标。数 字的又称自动空三,它不需要模拟的或解析的 坐标量测仪器,而是直接在计算机屏幕显示的 数字影像上,自动或半自动地采集加密点的像 点坐标,进而计算出待定点的地面坐标。当前, 数字空三已成为主流的作业方式,但数字空三 仍然沿用解析空三的数学模型。
X p
Yp
sin cos
cos Xt
sin
Yt
b a
a Xt
b
Yt
Z p Zt
Yp Xt
Xp
1
Yt
a
X pYt
X
2 t
YpX t Yt2
b
X
pX t YpYt
X
2 t
Yt2
a2 b2
X
2 p
Y
2 p
X
2 t
Yt2
航带法空三是以一条航带作为平差的基本单元,将模型点 的摄影测量作为观测值,根据地面控制点的摄影测量坐标 和地面坐标应相等以及相邻航带公共点坐标应相等为条件 ,用平差解求航带网的非线性变形改正系数,从而求出各 加密点的地面坐标。
独立模型法是以单元模型为平差单元以模型坐标为观测值 ,根据地面控制点的摄影测量坐标和地面坐标应相等以及 相邻模型公共点、公共摄站点的摄影测量坐标应相等为条 件,确定每一个单元模型的旋转、平移和缩放参数,从而 求出各加密点的地面坐标
量
三、空中三角测量的分类
按阶段可以分为模拟空中三角测量、解析空三 和数字空三。模拟的采用图解法或光学机械法, 在全能型立体测图仪上根据摄影过程的几何反 转原理建立航带模型,实现控制点的加密。解 析的是利用计算机,根据人工观测方法在坐标 量测仪或解析测图仪上量测的像点坐标,采用 一定的数学模型计算出待定点的地面坐标。数 字的又称自动空三,它不需要模拟的或解析的 坐标量测仪器,而是直接在计算机屏幕显示的 数字影像上,自动或半自动地采集加密点的像 点坐标,进而计算出待定点的地面坐标。当前, 数字空三已成为主流的作业方式,但数字空三 仍然沿用解析空三的数学模型。
16-解析空中三角测量(概述)

五、解析空中三角测量所需信息
3、解析空中三角测量中的像点
控制点、定向点、待求点和连接点 航 带 区 域 网 平 差 实 例
控制点---平高点、高程点、平面点
定向点---相对定向和绝对定向点 待求点---为满足测图而需要求解地 面坐标的点 连接点---被相邻像片、相邻模型、相邻航线共用且参与平差的 点,由于起到连接像片、模型或航线的作用,故称为连接点。 注意:在解析空中三角测量中参加平差的点是控制点和连接点
解析空中三角测量
(Analytical Aerial Triangulation)
解析空中三角测量(篇) §1 解析空中三角测量概述 §2 像点坐标的系统误差及其改正 §3 单航带空中三角测量 §4 航带法区域网平差 §5 模型法区域网平差 §6 光束法区域网平差
一、解析空中三角测量的目的
内 容 安 排 二、解析空中三角测量的定义 三、解析空中三角测量的特点
(点定位)+(测图)
摄影定位理论与方法
三、解析空中三角测量的特点
• 不接触被测目标即可测定其位置和形状,对 被测目标是否可以接触无特别要求。 • 可以快速地在大范围内实施点位的测定,节省 大量的野外测量工作。 • 凡从空中摄站可摄取的目标,均可测定其点位, 不受地面通视条件的限制。 • 区域网平差的精度高,内部精度均匀,且不受 区域大小的限制。
该技术又称为解析空中三角测量。 (Analytical Aerial Triangulation )
二、解析空中三角测量的定义
美国摄影测量协会专业术语委员会的定义:
Analytical Aerial Triangulation An aerial triangulation procedure in which the spatial solution is obtained by computational routines. When performed with aerial photographs, the procedure is referred as analytical aero-triangulation.
航带法空中三角测量

摄站坐标
X s 2 X s1 mBx Ys 2 Ys1 mBy Z s 2 Z s1 mBz
Bx B B R 0 y Bz 0
模型坐标
X p X s1 mX 新 Y p Ys1 mY新 Z p Z s1 mZ新
Fy
Fy Bx
Bx
Fy B y
B y
Fy Bz
Bz 0
Fx Fx Fx Fx B x
2 2 N2 X 2 N2Z2
N 2 X 2Y2
2 N 2Y22 N 2 Z 2
N 2 X 2Y2 N 2Y2 Z 2 Z 2
连接点的模型坐标
X p X s 2 mN2 X 2 Y p Ys 2 mN2Y2 Z p Z s 2 mN2 Z 2
绝对定向的计算步骤 步1 :绝对定向的定向控制点的地面测量坐标经正旋转 后,所得到的地面摄测坐标与摄测坐标的轴系的夹角 为小角,比例尺也比较接近,坐标原点一致。因此, 七个绝对定向元素的初始值可以取 X 0 Y0 Z0 0; 0 0 k0 0, 0 1 步2:根据确定的初始值,逐点计算出误差方程的常数 项 步3:逐点组成误差方程式的系数矩阵 步4: 根据逐点组成的误差方程式,逐点进行法化,即 组成法方程系数矩阵和常数项矩阵。 步5:定向点未组完时重复2~4步,直到组完所有定向 点。
13 17
×
5
9
×
G 10 H 11 I
A
2 B 3 C 4
D
J
M
18 N 19 O
×
6
×
14 K
E ×
7 F
X s 2 X s1 mBx Ys 2 Ys1 mBy Z s 2 Z s1 mBz
Bx B B R 0 y Bz 0
模型坐标
X p X s1 mX 新 Y p Ys1 mY新 Z p Z s1 mZ新
Fy
Fy Bx
Bx
Fy B y
B y
Fy Bz
Bz 0
Fx Fx Fx Fx B x
2 2 N2 X 2 N2Z2
N 2 X 2Y2
2 N 2Y22 N 2 Z 2
N 2 X 2Y2 N 2Y2 Z 2 Z 2
连接点的模型坐标
X p X s 2 mN2 X 2 Y p Ys 2 mN2Y2 Z p Z s 2 mN2 Z 2
绝对定向的计算步骤 步1 :绝对定向的定向控制点的地面测量坐标经正旋转 后,所得到的地面摄测坐标与摄测坐标的轴系的夹角 为小角,比例尺也比较接近,坐标原点一致。因此, 七个绝对定向元素的初始值可以取 X 0 Y0 Z0 0; 0 0 k0 0, 0 1 步2:根据确定的初始值,逐点计算出误差方程的常数 项 步3:逐点组成误差方程式的系数矩阵 步4: 根据逐点组成的误差方程式,逐点进行法化,即 组成法方程系数矩阵和常数项矩阵。 步5:定向点未组完时重复2~4步,直到组完所有定向 点。
13 17
×
5
9
×
G 10 H 11 I
A
2 B 3 C 4
D
J
M
18 N 19 O
×
6
×
14 K
E ×
7 F
第十一章区域网解析空中三角测量

N1T2
0
0
N 22
N
T 23
0
N 23
N 33
N
T 34
0
X
2
U 2
N N
34 44
X X
3 4
U U
3 4
(11-12)
(四)、法方程的解算
式(11-12)的法方程为一个带状矩阵,可采用 高斯约化法求解。逐步约化使系数阵变为一个上 三角矩阵,其相应常数项进行同样约化,然后求 解最后一组未知数,再从下而上回代,解求出全 部未知数。
(三)、法方程式的组成及特点 由误差方程式(11-8),可得相应的法方程式:
BTPBX-BTPL=O
法方程的系数矩阵为4×4的矩阵块,每块为 5×5的方阵。内容为:
B1Tc
B1c
1 2
B1T下
B1下
-
1 2
B2T上
B1下
BT
PB
0
0
-
1 2
B1T下 B2上
BT2c B2c
1 2
B2T上 B2上
X
tP
X tPgi
X
a0 j
a1 j
X
a2 j Y
a3 j
2
X
a4 j XY
YtP
YtPgi
Y
b0 j
b1 j X
b2 j Y
b3 j
2
X
b4 j X Y
2
ZtP ZtPgi Z c0 j c1 j X c2 j Y c3 j X c4 j X Y
(11-15)
1 2
B2T下 B2下
-
1 2
B3T上
B2下
0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
模型连接的实质:求出相邻模型之间的比
例尺规划系数k,后一模型中每一模型点 的空间辅助坐标以及基线分量BXBYBZ均乘 以规划系数k,就可获得与前一模型比例 尺一致的坐标。 将航带中所有的摄站点、模型点的坐标都 纳入到全航带统一的摄影测量坐标系中。
二、构建自由航带网(连续法相对定向)
摄站坐标
解析法空中三角测量
定义:在一条航线十几个像对中,甚至在若
干条航线构成的区域中,只布设少量野外实 测的地面控制点,在室内用电算方法加密出 测图所需的控制点(一般不少于每像对4个)。 野外布点:航带:1、平坦地区 品字形
2、丘陵山地 五点法 3、高山地 六点法 区域布点:九点法
一、解析空中三角测量的意义
0 y
Fx F F F F F x x x Bx x B y x Bz 0 Bx B y Bz Fy
X s 2 X s1 kmBx Ys 2 Ys1 kmBy Z s 2 Z s1 kmBz
模型坐标
X p X s1 k mN1 X 1 Yp 1 (Ys1 k mN1Y1 Ys 2 k mN2Y2 ) 2 Z p Z s1 k mN1 Z1
P215
相对控制条件 湖面等高 平面 圆周
共线
五、影像连接点的类型与设置 • • • 人工转刺点 仪器转刺点 标志点
•
•
明显地物点
数字影像相关转点
转刺点
标志点
明显地物点
B:航带法空中三角测量
主要内容
一、基本思想与流程
二、自由航带网的构建
三、单航带空中三角测量 四、航带法区域网平差
航带法解析空中三角测量研究的对象是一条航 带的模型。把一个航带模型视为一个单元模 型进行解析处理,因此这种方法首先把许多 立体像对构成的单个模型连结成航带模型。 在单个模型连成航带模型的过程中,各单个 模型中偶然误差和残余的系统误差会传递到 下一个模型中,由于这些误差传递累积的结 果使航带模型产生扭曲变形,所以航带模型 经绝对定向以后还需作模型的非线性改正, 才能得到所需的结果,这便是航带法解析空 中三角测量的基本原理。
•
不触及被量测目标即可测定其位置和几 何形状
• •
•
可快速地在大范围内同时进行点位测定 ,以节省野外测量工作量 不受通视条件限制
区域内部精度均匀,且不受区域大小限 制
二、解析空中三角测量的目的 • 为测绘地形图提供定向控制点和像 片定向参数
•
• •
测定大范围内界址点的统一坐标
单元模型中大量地面点坐标的计算 解析近景摄影测量和非地形摄影测 量
《摄影测量学》
第3章
航带法空中三角测量
A:解析空中三角测量概述 主要内容
一、解析空中三角测量的意义
二、解析空中三角测量的目的
三、解析空中三角测量的分类 四、解析空中三角测量的信息 五、影像连接点的类型与设置
概论
在双像解析摄影测量中,每个像对都要在野外测 求四个地面控制点。这样外业工作量太大效率 不高。能否只要在一条航带十几个像对中,或 几条航带构成的一个区域网中,测少量外业控 制点,在内业用解析摄影测量的方法加密出每 个像对所要求的控制点,然后用于测图呢?回 答是肯定的,解析法空中三角测量就是为解决 这个问题而提出的方法。
Z
si si-1
Y
Bx
si+1
By
Bz
X
Fx Z 2 ( N1 X 1 Bx ) X 2 ( N1 Z1 Bz ) 0 Fy Z 2 ( N1Y1 B y ) Y2 ( N1 Z1 Bz ) 0
二、构建自由航带网
(带模型连接条件的连续法相对定向)
Fx Fx0 Fy F
• 航带模型绝对定向
• 航带模型非线性改正
• 加密点向)
Z Z B
b 1 a 2 a z
a
3 1 5
4 2 6
b
3 1 5
4
2
6
归化系数
a Z2 B za k2 Z1b
Z Y
s3 s2
Z1b
a Z2
s1
X
1 k (k 2 k 4 k 6 ) 3
摄站坐标
X s 2 X s1 mBx Ys 2 Ys1 mBy Z s 2 Z s1 mBz
Bx B B R 0 y Bz 0
模型坐标
X p X s1 mX 新 Y p Ys1 mY新 Z p Z s1 mZ新
二、构建自由航带网(单独法相对定向)
a
3 1 5 4 2 6
b
3 1 5
4
2
6
s3 s2
X X X s2 Y R Y Y s2 Z 2 Z 1 Z s2
a b a
s1
二、构建自由航带网(单独法相对定向)
三、解析空中三角测量的分类
航带法 独立模型法 光线束法
按数学模型
按平差范围
单模型法 航带法 区域网法
四、解析空中三角测量的信息
摄影测量信息: 像片上量测的像点坐标
非摄影测量信息:
大地测量观测值 距离 角度 天文经纬度 局部坐标
像片外方位元素 高差仪记录 摄站坐标 像片姿态 摄站坐标差
X X X s2 Y R Y Y s2 Z 新 Z Z s2
前
二、构建自由航带网
(带模型连接条件的连续法相对定向) a
3 1 5 4 2 6
b
3 1 5
4
2
6
X2 Y2 Z2 N1 X 1 Bx N1Y1 B y N1 Z1 Bz
一、基本思想与流程 基本思想
把许多立体像对构成的单个模型连结 成一个航带模型,将航带模型视为单 元模型进行解析处理,通过消除航带 模型中累积的系统误差,将航带模型 整体纳入到测图坐标系中,从而确定 加密点的地面坐标。
一、基本思想与流程
基本流程
• 像点坐标系统误差预改正 • 立体像对相对定向
• 模型连接构建自由航带网
