航带法解析空中三角测量
合集下载
几种空中三角测量的比较

• 光束法是最严密的一步解法,误差方程式直接对原 始观测值列出,能最方便地顾及影像系统误差的影像 ,最便于引入非摄影测量附加观测值,如导航数据和 地面量测数据。它还可以严密地处理非常规摄影以及 非量测相机的影像数据。目前光束法已广泛应用于各 种高精度解析空三和点位实际生产中。
• 与前两种方法相比,光束法也有其缺点。首先像点 坐标所描述的像点坐标和各未知数的关系是非线性的 ,因此必须建立线性化的误差方程式和提供未知数的 初始值。其次光束法未知数多、计算量大、计算速度 相对较慢。此外它不能将平面高程分开处理,只能三 维网平差。
• 光束法是从实现摄影过程的几何反转出发,基于摄 影成像时像点、物点和摄影中心三点共线的特点而提 出的。这种方法最初提出时,由于受当时计算机水平 和计算技术的限制,未能广泛应用。但随着摄影测量 技术的发展和计算机水平的提高,这种最严密的平差 方法得到广发应用,并已成为解析空三加密的主流。
• 光束法的数学模型是共线方程,平差单元是单个光 束,每幅影像的像点坐标为原始观测值,未知数是各 影像的外方位元素和所有加密点的地面坐标。通过各 个光束在空间的旋转和平移(6个定向参数)使同名 光线最佳地交会,并最佳地纳入到地面控制系统中。
• 航带法产生于计算机问世之初,是一种分步的近似平差方法。 首先通过单个像对的相对定向和模型连接建立自由航带,然后 在进行每条航带多项式非线性改正时,顾及航带间公共点条件 和区域内的控制点。
• 独立模型法源于单元模型空间相似变换。影像坐标经过相对定 向求出独立模型坐标,通过各单元模型在空间的平移、旋转和 缩放,使得模型公共点有尽可能相同的坐标,并通过地面控制 点,使整个空中三角测量网最佳纳入到规定的坐标系中。
• 光束法是从实现摄影过程的几何反转出发,基于摄影成像时像 点、物点和摄影中心三点共线的特点而提出的,以共线方程作为 其理论基础。光束法区域网平差首先进行区域网概算,确定区 域中各像片外方位元素的近似值和各加密点坐标的近似值,然 后依据共线条件列出控制点和加密点的误差方程式,在全区域 范围内,统一进行平差处理,联立解算出各像片的外方位元素 和加密点的地面坐标。
第六章-解析法空中三角测量-参考更改版

m
n-m-q
N11
N12
N13
N22
N23
N33
t1
t2
t3
l1
l2
l3
带状法方程的循环分块解法
上移
N ’22
消元后仍具有带状阵的特征, 用相同的算法继续消元
q
m-q
m
n-m-q
N11
N12
N13
N22
N23
N33
t1
t2
t3
l1
l2
l3
边法化边消元 达到只进行必要的计算, 只占最少的内存的目的
转
置
对
项
称
带宽
航带数
垂直于航带方向编号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
1,2,…,20 待定点名 A,B,…,O 像片名 高程控制点 平高控制点
×
×
×
×
×
×
×
×
改化法方程
×
1
2
3
4
5
6
7
8
9
10
11
12
13
14
×
×
×
×
×
×
×
×
未知数个数 15×6+20×3=150
多余观测数 234 - 150 =84
n-m-q
N11
N12
N13
N22
N23
N33
t1
t2
t3
l1
l2
l3
带状法方程的循环分块解法
上移
N ’22
消元后仍具有带状阵的特征, 用相同的算法继续消元
q
m-q
m
n-m-q
N11
N12
N13
N22
N23
N33
t1
t2
t3
l1
l2
l3
边法化边消元 达到只进行必要的计算, 只占最少的内存的目的
转
置
对
项
称
带宽
航带数
垂直于航带方向编号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
1,2,…,20 待定点名 A,B,…,O 像片名 高程控制点 平高控制点
×
×
×
×
×
×
×
×
改化法方程
×
1
2
3
4
5
6
7
8
9
10
11
12
13
14
×
×
×
×
×
×
×
×
未知数个数 15×6+20×3=150
多余观测数 234 - 150 =84
解析空中三角测量基本思想和主要作业过程
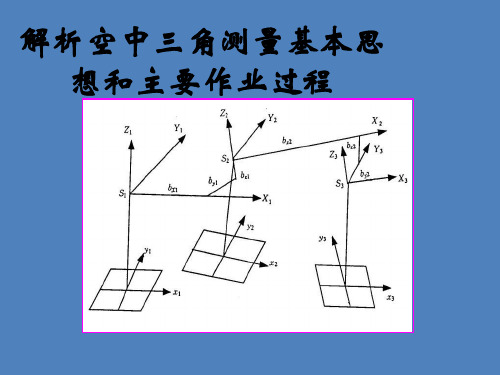
解析空中三角测量>概述
§1-1 解析空中三角测量概述
知识点:
◇ 解析空中三角测量的定义 ◇解析空中三角测量的意义 ◇解析空中三角测量的目的 ◇解析空中三角测量的分类
解析空中三角测量>概述
§1-1 解析空中三角测量概述
◇ 解析空中三角测量的定义
利用计算的方法,根据航摄像片上 所量测的像点坐标以及少量的地面控制 点求出地面加密点的物方空间坐标,称 之为解析空中三角测量。俗称摄影测量加
解析空中三角测量>光束法区域网空三
§1-4光束法区域网空中三角测量
知识点: ◇ 基本思想与流程
解析空中三角测量>光束法区域网空三
§1-4光束法区域网空中三角测量
◇ 基本思想与流程
以一张像片组成的一束光线作为一 个平差单元,以中心投影的共线方程作 为平差的基础方程,通过各光线束在空 间的旋转和平移,使模型之间的公共点 的光线实现最佳交会,将整体区域最佳 地纳入到控制点坐标系中,从而确定加 密点的地面坐标及像片的外方位元素
解析空中三角测量基本思 想和主要作业过程
解析空中三角测量>重要回顾
上节课重点
主要知识点: ◇ 解析法相对定向 ◇ 模型点坐标计算 ◇ 解析法绝对定向 ◇ 光束法严密解法(一步定向法)
基本要求:理解像对解析相对定向的概念、相 对定向元素解算过程。掌握模型解析绝对定向 目的和过程;了解光束法双像解析摄影测量。
密
解析空中三角测量的信息
○
○ ○
○
○
像片上 量测的 像点坐 标
少 量 地 面 点 坐 标
Z
Y X
S
S
待定点 高程控制点 平高控制点
平高 控制点
⊙ 高程 控制点
航带法空中三角测量详解

模型连接的实质:求出相邻模型之间的比
例尺规划系数k,后一模型中每一模型点 的空间辅助坐标以及基线分量BXBYBZ均乘 以规划系数k,就可获得与前一模型比例 尺一致的坐标。 将航带中所有的摄站点、模型点的坐标都 纳入到全航带统一的摄影测量坐标系中。
二、构建自由航带网(连续法相对定向)
摄站坐标
解析法空中三角测量
定义:在一条航线十几个像对中,甚至在若
干条航线构成的区域中,只布设少量野外实 测的地面控制点,在室内用电算方法加密出 测图所需的控制点(一般不少于每像对4个)。 野外布点:航带:1、平坦地区 品字形
2、丘陵山地 五点法 3、高山地 六点法 区域布点:九点法
一、解析空中三角测量的意义
0 y
Fx F F F F F x x x Bx x B y x Bz 0 Bx B y Bz Fy
X s 2 X s1 kmBx Ys 2 Ys1 kmBy Z s 2 Z s1 kmBz
模型坐标
X p X s1 k mN1 X 1 Yp 1 (Ys1 k mN1Y1 Ys 2 k mN2Y2 ) 2 Z p Z s1 k mN1 Z1
P215
相对控制条件 湖面等高 平面 圆周
共线
五、影像连接点的类型与设置 • • • 人工转刺点 仪器转刺点 标志点
•
•
明显地物点
数字影像相关转点
转刺点
标志点
明显地物点
B:航带法空中三角测量
主要内容
一、基本思想与流程
二、自由航带网的构建
三、单航带空中三角测量 四、航带法区域网平差
航带法解析空中三角测量研究的对象是一条航 带的模型。把一个航带模型视为一个单元模 型进行解析处理,因此这种方法首先把许多 立体像对构成的单个模型连结成航带模型。 在单个模型连成航带模型的过程中,各单个 模型中偶然误差和残余的系统误差会传递到 下一个模型中,由于这些误差传递累积的结 果使航带模型产生扭曲变形,所以航带模型 经绝对定向以后还需作模型的非线性改正, 才能得到所需的结果,这便是航带法解析空 中三角测量的基本原理。
航带法空中三角测量

( i 1 )
V S k Mbv
i
( i 1 )
(W ) S
( i 1 )
(W ) S k Mbw
i
W (W ) S
( i 1 )
2、航带模型绝对定向
2370 2369 B596 2368 B595 B594 2367
B602 B603
将航带辅助坐标系中的坐标(U,V,W)纳入到地面摄影测量坐标 系统中,获得模型点的地面摄影测量坐标值(X,Y,Z)。
二、像点坐标的系统误差及改正
摄影机的系统误差 底片变形 航摄飞机带来的系统误差 大气折光误差 地球曲率的影响 摄影处理与底片复制中的系统误差 观测系统误差
1、像片系统误差预改正(摄影材料变形)
• 四个框标位于像片的四个角隅时 可用仿射变换
x a0 a1x a2 y y b0 b1x b2 y
B653
B653
2450013 2450013
B655
B655 B655
B658
2448017 2448017 2448017
B658
2450001 2450001 2450001
B654
B654
2449
2467101
2448
2447
245 0 2450136 2449233
244 9 2450136
三维空间相似变换基本关系式: (1)
重心化的变换关系式:
(2)
2450
2449
2448
2447
3、航带模型的非线性改正
2464 2465 2466 2467
航线方向
2464
2465
16-解析空中三角测量(概述)

五、解析空中三角测量所需信息
3、解析空中三角测量中的像点
控制点、定向点、待求点和连接点 航 带 区 域 网 平 差 实 例
控制点---平高点、高程点、平面点
定向点---相对定向和绝对定向点 待求点---为满足测图而需要求解地 面坐标的点 连接点---被相邻像片、相邻模型、相邻航线共用且参与平差的 点,由于起到连接像片、模型或航线的作用,故称为连接点。 注意:在解析空中三角测量中参加平差的点是控制点和连接点
解析空中三角测量
(Analytical Aerial Triangulation)
解析空中三角测量(篇) §1 解析空中三角测量概述 §2 像点坐标的系统误差及其改正 §3 单航带空中三角测量 §4 航带法区域网平差 §5 模型法区域网平差 §6 光束法区域网平差
一、解析空中三角测量的目的
内 容 安 排 二、解析空中三角测量的定义 三、解析空中三角测量的特点
(点定位)+(测图)
摄影定位理论与方法
三、解析空中三角测量的特点
• 不接触被测目标即可测定其位置和形状,对 被测目标是否可以接触无特别要求。 • 可以快速地在大范围内实施点位的测定,节省 大量的野外测量工作。 • 凡从空中摄站可摄取的目标,均可测定其点位, 不受地面通视条件的限制。 • 区域网平差的精度高,内部精度均匀,且不受 区域大小的限制。
该技术又称为解析空中三角测量。 (Analytical Aerial Triangulation )
二、解析空中三角测量的定义
美国摄影测量协会专业术语委员会的定义:
Analytical Aerial Triangulation An aerial triangulation procedure in which the spatial solution is obtained by computational routines. When performed with aerial photographs, the procedure is referred as analytical aero-triangulation.
航带法空中三角测量
摄站坐标
X s 2 X s1 mBx Ys 2 Ys1 mBy Z s 2 Z s1 mBz
Bx B B R 0 y Bz 0
模型坐标
X p X s1 mX 新 Y p Ys1 mY新 Z p Z s1 mZ新
Fy
Fy Bx
Bx
Fy B y
B y
Fy Bz
Bz 0
Fx Fx Fx Fx B x
2 2 N2 X 2 N2Z2
N 2 X 2Y2
2 N 2Y22 N 2 Z 2
N 2 X 2Y2 N 2Y2 Z 2 Z 2
连接点的模型坐标
X p X s 2 mN2 X 2 Y p Ys 2 mN2Y2 Z p Z s 2 mN2 Z 2
绝对定向的计算步骤 步1 :绝对定向的定向控制点的地面测量坐标经正旋转 后,所得到的地面摄测坐标与摄测坐标的轴系的夹角 为小角,比例尺也比较接近,坐标原点一致。因此, 七个绝对定向元素的初始值可以取 X 0 Y0 Z0 0; 0 0 k0 0, 0 1 步2:根据确定的初始值,逐点计算出误差方程的常数 项 步3:逐点组成误差方程式的系数矩阵 步4: 根据逐点组成的误差方程式,逐点进行法化,即 组成法方程系数矩阵和常数项矩阵。 步5:定向点未组完时重复2~4步,直到组完所有定向 点。
13 17
×
5
9
×
G 10 H 11 I
A
2 B 3 C 4
D
J
M
18 N 19 O
×
6
×
14 K
E ×
7 F
X s 2 X s1 mBx Ys 2 Ys1 mBy Z s 2 Z s1 mBz
Bx B B R 0 y Bz 0
模型坐标
X p X s1 mX 新 Y p Ys1 mY新 Z p Z s1 mZ新
Fy
Fy Bx
Bx
Fy B y
B y
Fy Bz
Bz 0
Fx Fx Fx Fx B x
2 2 N2 X 2 N2Z2
N 2 X 2Y2
2 N 2Y22 N 2 Z 2
N 2 X 2Y2 N 2Y2 Z 2 Z 2
连接点的模型坐标
X p X s 2 mN2 X 2 Y p Ys 2 mN2Y2 Z p Z s 2 mN2 Z 2
绝对定向的计算步骤 步1 :绝对定向的定向控制点的地面测量坐标经正旋转 后,所得到的地面摄测坐标与摄测坐标的轴系的夹角 为小角,比例尺也比较接近,坐标原点一致。因此, 七个绝对定向元素的初始值可以取 X 0 Y0 Z0 0; 0 0 k0 0, 0 1 步2:根据确定的初始值,逐点计算出误差方程的常数 项 步3:逐点组成误差方程式的系数矩阵 步4: 根据逐点组成的误差方程式,逐点进行法化,即 组成法方程系数矩阵和常数项矩阵。 步5:定向点未组完时重复2~4步,直到组完所有定向 点。
13 17
×
5
9
×
G 10 H 11 I
A
2 B 3 C 4
D
J
M
18 N 19 O
×
6
×
14 K
E ×
7 F
第十一章区域网解析空中三角测量
N1T2
0
0
N 22
N
T 23
0
N 23
N 33
N
T 34
0
X
2
U 2
N N
34 44
X X
3 4
U U
3 4
(11-12)
(四)、法方程的解算
式(11-12)的法方程为一个带状矩阵,可采用 高斯约化法求解。逐步约化使系数阵变为一个上 三角矩阵,其相应常数项进行同样约化,然后求 解最后一组未知数,再从下而上回代,解求出全 部未知数。
(三)、法方程式的组成及特点 由误差方程式(11-8),可得相应的法方程式:
BTPBX-BTPL=O
法方程的系数矩阵为4×4的矩阵块,每块为 5×5的方阵。内容为:
B1Tc
B1c
1 2
B1T下
B1下
-
1 2
B2T上
B1下
BT
PB
0
0
-
1 2
B1T下 B2上
BT2c B2c
1 2
B2T上 B2上
X
tP
X tPgi
X
a0 j
a1 j
X
a2 j Y
a3 j
2
X
a4 j XY
YtP
YtPgi
Y
b0 j
b1 j X
b2 j Y
b3 j
2
X
b4 j X Y
2
ZtP ZtPgi Z c0 j c1 j X c2 j Y c3 j X c4 j X Y
(11-15)
1 2
B2T下 B2下
-
1 2
B3T上
B2下
0
摄影测量学第六章航带法空中三角测量PPT课件
03
航带法空中三角测量技术还可以用于生态保护和环境监测,为环境保护和治理 提供数据支持。
军事侦察与情报获取
军事侦察与情报获取是航带法空中三角测量的重要应用之一。该技术可以用于获 取敌方阵地、军事设施和战略要地的详细信息,为军事决策和行动提供重要支持 。
航带法空中三角测量技术还可以用于情报分析和反情报工作,为维护国家安全提 供重要的数据保障。
摄影测量学第六章航 带法空中三角测量
ppt课件
目录
• 航带法空中三角测量的基本概念 • 航带法空中三角测量的基本原理 • 航带法空中三角测量的数据处理流程
目录
• 航带法空中三角测量的实践应用案例 • 航带法空中三角测量的未来发展与挑战
01
航带法空中三角测量的基 本概念
定义与特点
定义
航带法空中三角测量是一种摄影测量技术,通过在航带上 布设多个相机,获取地面目标的多角度影像,然后利用这 些影像进行空间几何建模和定位。
三维重建
利用多张相片之间的几何 关系,解算出地面点的空 间坐标,构建三维模型。
精度分析
对重建结果进行精度评估 和分析,确保满足工程或 应用需求。
03
航带法空中三角测量的数 据处理流程
数据准备与预处理
原始数据检查
格式转换
坐标系统转换
辐射校正
确保所收集的像片、控 制点等数据完整、准确,
无缺失或损坏。
高效性
通过在航带上布设多个相机,可以快速获取大量地面影像 ,提高测量效率。
高精度
航带法空中三角测量能够获取高精度的空间几何信息,为 地形测绘、城市规划、资源调查等需求调整航带布局和相 机数量,以满足不同规模和精度要求的项目需求。
航带法空中三角测量的应用领域
第六章 空中三角测量
内 容 安 排
一、单航带解析空三的基本思想
二、单航带解析空中三角测量的 基本过程 三、航带网法空中三角测量的建 网过程
一、单航带解析空三的基本思想
• 研究对象:
一条航带模型,即将整个航带视为一个平差单元。
• 思路:
• 单个模型连接成航带模型。 • 绝对定向。 • 非线性改正。 由于在单个模型连成航带模型的过程中,各单个 模型的偶然误差和残余的系统误差,将传递到下一 个模型中,这些误差传递累积的结果,使航带模型 产生扭曲变形,因此航带模型经绝对定向后,还需 作模型的非线性改正。
X A0 A1 X A2Y A3 X 2 A4 XY Y B0 B1 X B2Y B3 X 2 B4 XY Z C 0 C 1 X C 2Y C 3 X 2 C 4 XY
X X T X Y YT Y Z Z T Z
二、单航带解析空中三角测量的基本过程
1、量测像点坐标 2、像点坐标系统误差的改正
3、在一定的基准坐标系中,建立单模型
4、模型连接——利用模型间的公共连接点,进行模型连接, 将各单模型连接成统一比例尺的整条航线模型 5、航带模型的绝对定向。利用少量地面控制点, 对整条航带模型进行绝对定向 6、航带模型的非线性改正。改正航带模型的累积误差, 从而求得加密点的地面坐标和高程
1、建立航带模型
3、模型的连接,统一比例尺
计算第二个模型比例尺缩放系数k2?
S1 S2 S2 S3
当两个模型比例尺一致时,模型连接 点的高程有如下关系:
4 2 6 1 5 3
h ( Z s 2 w2 )1 (Z s 2 w1 ) 2 ( w2 )1 ( w1 ) 2 ( N 2 w2 )1 ( N1 w1 ) 2 ( N1 w1 bw )1 ( N1 w1 ) 2
一、单航带解析空三的基本思想
二、单航带解析空中三角测量的 基本过程 三、航带网法空中三角测量的建 网过程
一、单航带解析空三的基本思想
• 研究对象:
一条航带模型,即将整个航带视为一个平差单元。
• 思路:
• 单个模型连接成航带模型。 • 绝对定向。 • 非线性改正。 由于在单个模型连成航带模型的过程中,各单个 模型的偶然误差和残余的系统误差,将传递到下一 个模型中,这些误差传递累积的结果,使航带模型 产生扭曲变形,因此航带模型经绝对定向后,还需 作模型的非线性改正。
X A0 A1 X A2Y A3 X 2 A4 XY Y B0 B1 X B2Y B3 X 2 B4 XY Z C 0 C 1 X C 2Y C 3 X 2 C 4 XY
X X T X Y YT Y Z Z T Z
二、单航带解析空中三角测量的基本过程
1、量测像点坐标 2、像点坐标系统误差的改正
3、在一定的基准坐标系中,建立单模型
4、模型连接——利用模型间的公共连接点,进行模型连接, 将各单模型连接成统一比例尺的整条航线模型 5、航带模型的绝对定向。利用少量地面控制点, 对整条航带模型进行绝对定向 6、航带模型的非线性改正。改正航带模型的累积误差, 从而求得加密点的地面坐标和高程
1、建立航带模型
3、模型的连接,统一比例尺
计算第二个模型比例尺缩放系数k2?
S1 S2 S2 S3
当两个模型比例尺一致时,模型连接 点的高程有如下关系:
4 2 6 1 5 3
h ( Z s 2 w2 )1 (Z s 2 w1 ) 2 ( w2 )1 ( w1 ) 2 ( N 2 w2 )1 ( N1 w1 ) 2 ( N1 w1 bw )1 ( N1 w1 ) 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
X 2Y2 Y22 Y2 vQ N 2 ( Z 2 ) N 2 X 2 N 2 Bx Bx Q Z2 Z2 Z2
特别注意: • 模型中的定向点只建立VQ方程 • 模型间的连接点需建立VQ, V P方程 • 对于模型间的连接点建立误差方程时,常数项中的 N1 X1, N1 Y1 , N1 Z1必须用前一模型中的N2 X2, N2 Y2 , N2 Z2
二、构建自由航带网
(2、带模型连接条件的连续法相对定向) 摄站坐标
X s 2 X s1 mBx Ys 2 Ys1 mBy Z s 2 Z s1 mBz
非连接点的模型坐标
X p X s1 mN1 X 1 1 Y p (Ys1 mN1Y1 Ys 2 mN2Y2 ) 2 Z p Z s1 mN1式曲 面拟合航带网复 杂的变形曲面, 使该曲面经过航 带网已知点时, 所求得坐标变形 值与它们实际的 变形值相等或使 其残差的平方和 为最小
1、二次多项式
X A0 A1 X A2Y A3 X 2 A4 XY Y B0 B1 X B2Y B3 X 2 B4 XY Z C0 C1 X C2Y C3 X 2 C4 XY
连接点的模型坐标
X p X s 2 mN2 X 2 Y p Ys 2 mN2Y2 Z p Z s 2 mN2 Z 2
N2
a a N2 Z 2 Bz
Z2
二、构建自由航带网(2、连续法相对定向)
Z Z B
b 1 a 2 a z
a
3 1 5
4 2 6
b
3 1 5
4
2
非独立累积性误差:随模型个数的增加而增大其影响
n n1 (n 1) 2 n
四、航带网的误差传播
S’1 S0 dbz1 S1 S’2 S’3
S2
S3
Z
0’ 0 X 1 1’ 2 2’ 3
X 3
Z 3
3’
Z1 Z 2 Z 3
X 1 X 2 X 3
一、基本思想与流程 基本流程
• 像点坐标系统误差预改正 • 立体像对相对定向
• 模型连接构建自由航带网
• 航带网的概略绝对定向
• 航带模型非线性改正
• 加密点坐标计算
二、构建自由航带网
(1、带模型连接条件的连续法相对定向) a
3 1 5 4 2 6
b
3 1 5
4
2
6
X2 Y2 Z2 N1 X 1 Bx N1Y1 B y N1 Z1 Bz
a b a
a
3 1 5
4 2 6
b
3 1 5
4
2
6
已知值 s1
X X Y R Y Z 2 Z 1
a b
s3 s2
二、构建自由航带网(3、单独法相对定向)
摄站坐标
X s 2 X s1 mBx Ys 2 Ys1 mBy Z s 2 Z s1 mBz
Bx B B R 0 y Bz 0
模型坐标
X p X s1 mX新 Y p Ys1 mY新 Z p Z s1 mZ新
X X X s2 Y R Y Y s2 Z 新 Z Z s2
6
a Bz 为模型a的相对定向元素
归化系数
a Z2 B za k2 Z1b
Z Y
s3 s2
Z1b
a Z2
s1
X
1 k (k 2 k 4 k 6 ) 3
二、构建自由航带网(2、连续法相对定向)
摄站坐标
X s 2 X s1 k mBx Ys 2 Ys1 k mBy Z s 2 Z s1 k mBz
Z
si si-1
Y
Bx
si+1
By
Bz
X
Fx Z 2 ( N1 X 1 Bx ) X 2 ( N1 Z1 Bz ) 0 Fy Z 2 ( N1Y1 B y ) Y2 ( N1 Z1 Bz ) 0
二、构建自由航带网
(1、带模型连接条件的连续法相对定向)
2 X2 X Y X v P ( Z 2 ) N 2 2 2 N 2 Y2 N 2 2 Bx Bx P Z2 Z2 Z2
b b a
三、自由航带网的概略绝对定向
获取控制点的地面摄影测量坐标 Xtp , Ytp , Ztp
计算重心化坐标 求相似变换参数 计算各模型点的地面摄影测量坐标
四、航带网的误差传播
系统误差 偶然误差
独立累积性误差:不随模型个数的增加而增大其影响
n 1 2 n
模型坐标
X p X s1 k mN1 X 1 Yp 1 (Ys1 k mN1Y1 Ys 2 k mN2Y2 ) 2 Z p Z s1 k mN1 Z1
二、构建自由航带网(3、单独法相对定向)
X X X s2 Y R Y Y s2 Z 2 Z 1 Z s2
《摄影测量学》(上)第六章
航带法空中三角测量
主要内容
一、基本思想与流程 二、自由航带网的构建 三、单航带空中三角测量 四、航带法区域网平差
一、基本思想与流程 主要思想
把许多立体像对构成的单个模型连结 成一个航带模型,将航带模型视为单 元模型进行解析处理,通过消除航带 模型中累积的系统误差,将航带模型 整体纳入到测图坐标系中,从而确定 加密点的地面坐标
X tp X X Ytp Y Y Z tp Z Z
五、航带模型非线性改正
2、二次正形变换多项式
X a0 a1 X a2Y a3 X 2 a4 XY a5Y 2 a6 X 3 a7 X 2Y a8 XY 2 a9Y 3 Y b0 b1 X b2Y b3 X 2 b4 XY b5Y 2 b6 X 3 b7 X 2Y b8 XY 2 b9Y 3
