模拟退火算法.ppt
很经典的模拟退火算法PPT

Simulated Annealing
22
其他的问题(2/4) 其他的问题(2/4)
价值函数(Cost Function) 价值函数(Cost Function) – Hard Constraints 在不违背合适解的条件下,所提出的强制规定. 在不违背合适解的条件下,所提出的强制规定. – Soft Constraints 无论这种解是否违背条件,都算是合适解. 无论这种解是否违背条件,都算是合适解. – HardConstraints会给一个很大的weight HardConstraints会给一个很大的weight – SoftConstraints则是情况给予不同的weight SoftConstraints则是情况给予不同的weight
Simulated Annealing
26
算法修正(1/2) 算法修正(1/2)
可接受的机率(Acceptance Probability) 可接受的机率(Acceptance Probability)
P(E) =1 (E / t)
– 少计算exponential会加快速度 少计算exponential会加快速度 – 建立一个可查询各种值的table 建立一个可查询各种值的table 冷却(Cooling) 冷却(Cooling) – 花一些时间找寻最佳温度(包括最终温度,温差)
19
机率函(3/3)
当 T越高或 f越小时,则 p(X ' ) 越大,相对的扰动解被接受成新解的机 越大, 率越高. 因此会随着迭代次的增加而逐渐下,所以较差的扰动解被接受成 因此 T 新解的机会也随着 T 的下而越越小. 所以当迭代到最后因为温度 T 已到达低点,这时系统只会接受较佳的 扰动解为新解. 而扰动解 f (X ' ) 若小于目前解 f (X )则一定接受为新解,但若是 f ( X ' ) > f ( X ) 则接受为新解的机率随着f 的变大而越小.
模拟退火算法

Keynote:尤志强
背景
模拟退火算法是Kirkpatrick提出,应组合优化问题而产生的,主要解决的是NP-hard问题。 优化问题可以分为:函数优化问题和组合优化问题两大类
1、函数优化问题: 可以描述为:令S为上的有界子集(即变量的定义域),f:S—>R为n维实值函数,所谓函数f在S域上全局最 小化就是寻求点XminS使得f(Xmin)在S域上全局最小,即X S:f(Xmin)<=f(X)
pr exp[(E j Ei ) / kt]
大于[0,1)区间内的随机数则仍旧接受新状态j为当前状态,若不成立则保留i为当前状态,其中k为 Boltzmann常数。 这种重要性采样过程在高温下可接受与当前状态能量差较大的新状态,而在低温下基本只接受与当 前能量差较小的新状态,而且当温度趋于零时,就不能接受比当前状态能量高的新状态。
背景
计算复杂度
由于某些优化算法所需的计算时间和存储空间难以承受,因此算法可解的问题在实践中不 一定可解。如TSP问题,可能的路径有n!,暴力求解显然是不行的。所以只有了解了研究 问题的复杂性,才能有针对性地设计算法,进而提高优化效率。
算法的时间和空间复杂性对计算机求解非常重要。问题的时间复杂性是指求解该问题的所 有算法中时间复杂性最小的算法的时间复杂性,同理,空间复杂性也有类似定义。这样, 按照计算复杂性理论研究问题求解的难易程度,可把问题分为P类、NP类和NP完全类。
背景
4、基于系统动态演化算法
将优化过程转化为系统动态的演化过程,基于系统动态的演化来实现优化,如神经网络和混沌 搜索等。
5、混合型算法 上述算法从结果或者操作上相混合而产生的各类算法
模拟退火算法
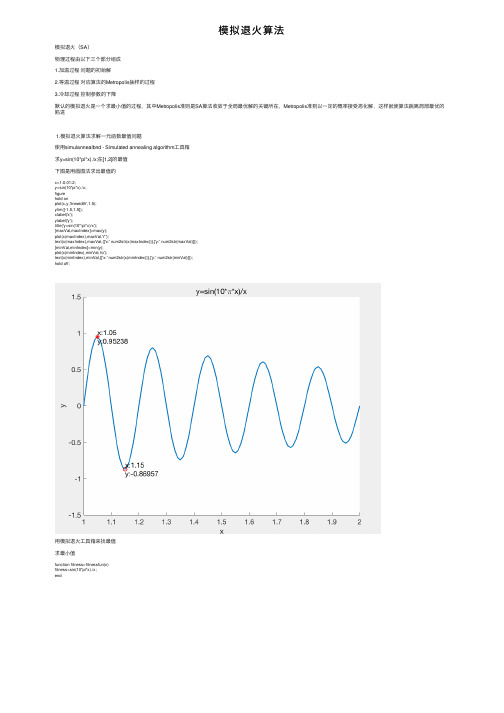
模拟退⽕算法模拟退⽕(SA)物理过程由以下三个部分组成1.加温过程问题的初始解2.等温过程对应算法的Metropolis抽样的过程3.冷却过程控制参数的下降默认的模拟退⽕是⼀个求最⼩值的过程,其中Metropolis准则是SA算法收敛于全局最优解的关键所在,Metropolis准则以⼀定的概率接受恶化解,这样就使算法跳离局部最优的陷进1.模拟退⽕算法求解⼀元函数最值问题使⽤simulannealbnd - Simulated annealing algorithm⼯具箱求y=sin(10*pi*x)./x;在[1,2]的最值下图是⽤画图法求出最值的x=1:0.01:2;y=sin(10*pi*x)./x;figurehold onplot(x,y,'linewidth',1.5);ylim([-1.5,1.5]);xlabel('x');ylabel('y');title('y=sin(10*\pi*x)/x');[maxVal,maxIndex]=max(y);plot(x(maxIndex),maxVal,'r*');text(x(maxIndex),maxVal,{['x:' num2str(x(maxIndex))],['y:' num2str(maxVal)]});[minVal,minIndex]=min(y);plot(x(minIndex),minVal,'ro');text(x(minIndex),minVal,{['x:' num2str(x(minIndex))],['y:' num2str(minVal)]});hold off;⽤模拟退⽕⼯具箱来找最值求最⼩值function fitness=fitnessfun(x)fitness=sin(10*pi*x)./x;end求最⼤值function fitness=fitnessfun(x)fitness=-sin(10*pi*x)./x;endOptimization running.Objective function value: -0.9527670052175917Maximum number of iterations exceeded: increase options.MaxIterations.⽤⼯具箱求得的最⼤值为0.95276700521759172.⼆元函数优化[x,y]=meshgrid(-5:0.1:5,-5:0.1:5);z=x.^2+y.^2-10*cos(2*pi*x)-10*cos(2*pi*y)+20;figuremesh(x,y,z);hold onxlabel('x');ylabel('y');zlabel('z');title('z=x^2+y^2-10*cos(2*\pi*x)-10*cos(2*\pi*y)+20');maxVal=max(z(:));[maxIndexX,maxIndexY]=find(z==maxVal);%返回z==maxVal时,x和y的索引for i=1:length(maxIndexX)plot3(x(maxIndexX(i),maxIndexY(i)),y(maxIndexX(i),maxIndexY(i)),maxVal,'r*');text(x(maxIndexX(i),maxIndexY(i)),y(maxIndexX(i),maxIndexY(i)),maxVal,{['x:' num2str(x(maxIndexX(i)))] ['y:' num2str(y(maxIndexY(i)))] ['z:' num2str(maxVal)] }); endhold off;function fitness=fitnessfun(x)fitness=-(x(1).^2+x(2).^2-10*cos(2*pi*x(1))-10*cos(2*pi*x(2))+20);endOptimization running.Objective function value: -80.50038894455415Maximum number of iterations exceeded: increase options.MaxIterations.找到的最⼤值:80.500388944554153.解TSP问题(⽤的数据和前⼏天⽤遗传算法写TSP问题的数据⼀致,但是结果⽐遗传算法算出来效果差很多,不知道是不是我写错了,怀疑⼈⽣_(:з」∠)_中。
局部搜索最优算法之模拟退火

模拟退火(SAA)起源
❖ 模拟退火最早由Metropolis等人提出,由 Kirkpatrick等人和Cerny应用于优化问题的求解。
❖ SAA是一种基于Metropolis迭代求解法的启发式随 机收索算法。
❖ SAA是基于金属退火的机理而建立起的一种全局最 优化方法,它能够以随机搜索技术从概率意义上找 出目标函数的最优解。
盲目搜索
1. 广度搜索 2. 深度搜索 3. 双向性搜索 4. 分支定界
模拟退火算法(流程)
1. 任选一个初始状态解x0,即有此时初始温度T (0),令xbest=x0,设定;
2. 令T=T(0),以T和xbest调用Metropolis抽样 法,返回的解x作为本算法的当前最优解xi=x ;
3. 按一定方式将T降温,即 T=Ti+1,Ti+1<Ti,i=i+1;模退火(Metropolis准则)
Metropolis抽样准则: 1.令i=0时的当前解为x0=x,在T下进行以下各步; 2.在当前解xi邻域,随机取一个新的状态x作为当前候选解,
并计算△E=E(x’)-E(x); 3.若△E<0,则接受x为下一个当前最优解;
若△E>0,则按概率exp(- △ E/kT)接受x为下一个当前最 优解;
局部搜索最优算法之 模拟退火
退火优化过程演变
搜索算法
❖确定性搜索(启发式搜索):可以使算 法收敛于性能优良的解;
❖盲目性搜索:使算法能够跳出局 部最优解。按照预定的控制策略实 行搜索,在搜索过程中获取的中间 信息不用来改进控制策略。
启发式搜索
1. 贪婪算法 2. 模拟退火算法 3. 遗传算法 4. 粒子群算法 5. 蚁群算法……
模拟退火算法

模拟退火算法模拟退火是一种通用概率算法,目的是在固定时间内在一个大的搜寻空间内寻求给定函数的全局最优解。
它通常被用于离散的搜索空间中,例如,旅行商问题。
特别地,对于确定的问题,模拟退火算法一般是优于穷举法。
这是由于我们一般只需得到一个可接受的最优解,而不是精确的最优解。
退火一词来源于冶金学。
退火(见图1)是将材料加热后再经特定速率冷却,目的是增大晶粒的体积,并且减少晶格中的缺陷。
材料中的原子原来会停留在使内能有局部最小值的位置,加热使能量变大,原子会离开原来位置,而随机在其他位置中移动。
退火冷却时速度较慢,使得原子有较多可能可以找到内能比原先更低的位置。
因此,我们将热力学的理论应用到统计学上,将搜寻空间内每一点想象成空气内的分子;分子的能量,就是它本身的动能;而搜寻空间内的每一点,也像空气分子一样带有“能量”,以表示该点对命题的合适程度。
而模拟退火算法先以搜寻空间内一个任意点作起始:每一步先选择一个“邻居”,然后再计算从现有位置到达“邻居”的概率。
模拟退火原理最早是 S. Kirkpatrick, C. D. Gelatt 和 M. P. Vecchi 在1983年所创造的。
而 V . Černý 在1985年也独立发明了此算法。
1. 问题描述数学上的最优化问题一般描述为如下形式:()()minimize()g 0,1,2,,subject to 0,1,2,,i i f x x i m h x i p≤=⎧⎪⎨==⎪⎩ 其中,():R n f x R →称作问题的目标函数,()g 0i x ≤称作问题的不等式约束条件,()0i h x =称作问题的等式约束条件。
寻求上述问题的最优解的过程就类似于从热动力系统的任意一个初始状态向内能最小的状态转移的过程,即退火过程。
2. 模拟退火算法基本思想模拟退火算法来源于固体退火原理,将固体加温至充分高,再让其徐徐冷却,加温时,固体内部粒子随温升变为无序状,内能增大,而徐徐冷却时粒子渐趋有图1 物理退火原理图序,在每个温度都达到平衡态,最后在常温时达到基态,内能减为最小。
《模拟退火算》课件

模拟退火算法的优缺点分析
1 优点
能够全局搜索,不容易陷入局部最优解。
2 缺点
运行时间较长,需要合理选择参数和策略。
模拟退火算法的改进
1 多种调节参数方法
通过改变各个参数的值来优化算法的性能。
2 算法复杂度分析
对模拟退火算法的复杂度进行分析,提出改进措施。
结语
算法总结
通过学习模拟退火算法,我们可以更好地应对各种优化问题。
《模拟退火算法》PPT课 件
欢迎大家参加今天的课程!本课程将介绍模拟退火算法的概念、原理、应用 以及优缺点分析。让我们一起探索这个优秀的优化算法吧!
概述
模拟退火算法(SA)是一种优化算法,其灵感来源于固体退火原理。通过模 拟固体物质的退火过程,以一定的概率接受差解,从而在搜索空间中寻找到 全局最优解。
模拟退火算法的实现步骤
1
初始化
设置初始状态和温度。
2
生成新解
通过随机移动改变当前解。
3
判断新解是否接受
根据能量差和概率判断是否接受新解。
4
更新状态
根据降温策略和接受准则更新状态,循环迭代直到满足停止条件。
模拟退火算法的优化
1 降温策略
选择合适的降温方式,平 衡全局搜索和局部搜索的 能力。
2 解的表示方法
3 种子的选择
选择适当的解的表示方法, 提高搜索效率。
合理选择初始化的种子解, 减少搜索空间。
模拟退火算法的应用
旅行商问题
通过模拟退火算法解决旅行 商问题,寻找最短路径。
图像匹配问题
利用模拟退火算法进行图像 匹配,实现图像识别和辨识。
近似最优化问题
应用于一些实际生活中的近 似最优化问题,如资源分配 等。
模拟退火算法
目录
搜索算法简介
模拟退火算法的原理
模拟退火算法的应用
英文文献介绍
参考文献
搜索问题
最小最优解的搜索
局部最优
除对当 前的位 置外, 对环境 无任何 感知。
全局最优
搜索算法
• 盲目搜索与启发式搜索 • 按照预定的控制策略实行搜索,在搜索过程中 获取的中间信息不用来改进控制策略,称之为 盲目搜索,反之,称为启发式搜索。 • 盲目搜索
文献讲解——问题描述
• 如图,为一个二维运输网,由供应商,直接转运设施与用 户组成,本文做出以下相关假设,约束条件方便建模。
文献讲解——算法应用
• 退火算法流程 所示如图
• 求新解的方法 1.改变货物的顺序 2.改变进入车的顺序 3.改变出去车的顺序
文献讲解——计算与结论
• 通过设置不同的参数(S/C/D/Fmax) • 文中设置了两个例子分析:单产品,单卡车模型与多产品 多卡车模型。
外文文献讲解[2]
• 文献题目:Simulated annealing approach for transportation problem of cross-docking network design • 译名:使用模拟退火方法解决运输问题中的直接转运网的 设计 • 2014年,Uludag 大学,第二届世界商业经济管理大会 • 研究背景:在产品供应链管理中,运输效率是一个重要因 素,高效的运输既满足了顾客的需求,也降低了成本。直 接转运策略降低了储存成本加速了产品流通,而直接转运 网的设计与优化是一个研究热点。 • 研究目的:设计二维的直接转运网络,设计卡车载运计划 与货物的流通路径来实现最低的运输费用。
《模拟退火算法》课件
03
可能陷入局部最优 解
在某些情况下,模拟退火算法可 能无法跳出局部最优解,导致无 法找到全局最优解。
未来研究的方向和挑战
要点一
算法改进
针对模拟退火算法的缺陷,研究改进算法以提高其性能和 适用性。
要点二
并行化与分布式实现
研究如何利用并行计算和分布式技术加速模拟退火算法的 执行。
未来研究的方向和挑战
总结词
优化分类和聚类
详细描述
模拟退火算法在机器学习中用于优化分类和聚类算法的性能,通过优化参数和搜索空间 ,提高分类和聚类的准确性和稳定性。
06
总结与展望
Chapter
模拟退火算法的优势与局限性
全局优化
模拟退火算法在搜索过程中能够跳出局部最 优解,寻找全局最优解。
适用范围广
模拟退火算法适用于解决连续和离散优化问 题,尤其在处理大规模、复杂问题时表现出 色。
模拟退火算法的优势与局限性
• 灵活性高:算法参数可根据具体 问题进行调整,以适应不同场景 的需求。
模拟退火算法的优势与局限性
01
计算量大
模拟退火算法需要大量的计算资 源,尤其在问题规模较大时更为 明显。
02
参数设置困难
算法参数如初始温度、降温速率 等对算法性能影响较大,但合理 设置这些参数较为困难。
算法的参数敏感性分析
初始温度
模拟退火算法的初始温度对算法的性能有很大影响。初始温度过高可能导致算法陷入局部最优解,而初始温度过低则 可能导致算法收敛速度过慢。因此,需要根据问题特性和需求合理设置初始温度。
冷却率
冷却率决定了算法在退火过程中的温度下降速度。冷却率过高可能导致算法在最优解附近“振荡”,而冷却率过低则 可能导致算法收敛速度过慢。因此,需要根据问题特性和需求合理设置冷却率。
模拟退火算法ppt课件
.
10
3) 如果ΔE <0,则xbest = xnew; 4) 如果ΔE >0,则p = exp(- ΔE /T(i));
1) 如果c = random[0,1] < p, xbest = xnew; 否则xbest = xbest。 5) End for 4) i = i + 1; 5) End Do 6) 输出当前最优点,计算结束。
.
7
SA算法的思想为: ➢ 由初始解i和控制参数初值t开始,对当前解重复
产生新解 →计算目标函数差 →接受或舍弃
的迭代, ➢ 并逐步衰减t值, ➢ 算法终止时的当前解即为所得近似最优解, ➢ 这是基于蒙特卡罗迭代求解法的一种启发式随机搜索过程。
.
8
SA算法与其它搜索方法相比,具有如下的特点: ➢ 以一定的概率接受恶化解; ➢ 引进算法控制参数; ➢使用对象函数值进行搜索; ➢ 隐含并行性; ➢搜索复杂区域。
.
4
2、SA算法的起源
SA算法起源于对固体退火过程的模拟。简单而言,在固体退火时, 先将固体加热使其温度充分高,再让其徐徐冷却,其物理退火过程由 以下三部分组成:加温过程、等温过程、冷却过程。
.
5
SA算法就是模仿上述物理系统徐徐退火过程的一种通用随机搜索技术。 模拟退火算法与物理退火过程的相似关系
.
13
5、SA算法应用范围与一般要求
冷却进度表是指从某一高温状态T0向低温状态冷却时的降温管理表。
假设时刻t的温度用T(t)来表示,则经典模拟退火算法的降温方式为: T(t) T0 lg(1t)
而快速模拟退火算法的降温方式为: T (t) T0 1 t
模拟退火算法
模拟退火算法
模拟退火算法(simulated annealing,简称 SA)的思想最早是由Metropolis等(1953)提 出的,1983年Kirkpatrick等将其用于组合 优化。SA算法是基于Monte Carlo迭代求 解策略的一种随机寻优算法,其出发点 是基于物理中固体物质的退火过程与一 般组合优化问题之间的相似性。
降低温度Tk的方法有以下两种: Tk+1=Tk*r,其中r∈(0.95-0.99) Tk+1=Tk-ΔT
模拟退火算法流程图
开始 产生 i
S
k 0, Tk T0
设定 n T 外循环 产生 计算
n 1
f i
j
T k 8
模拟退火算法的应用
(3)
注释: 1.① ②无条件转移; 2.在③中,停在3-1-4-2状态,目标值仍为92; SA没有历史最优,不会终止在最优解,故算 法一定要保持历史最优。
Tk
模拟退火算法的应用
0-1背包问题 一个旅行者有一个最多能装M公斤的背 包,现在有N件物品, 它们的重量分别是W1,W2,...,Wn, 它们的价值分别为P1,P2,...,Pn. 若每种物品只有一件。 求旅行者能获得的最大总价值。
总结
模拟退火是一种贪心算法,但是它的搜 索过程引入了随机因素。模拟退火算法 以一定的概率来接受一个比当前解要差 的解,因此有可能会跳出这个局部的最 优解,达到全局的最优解。 模拟退火算法也是一种随机算法,并不 一定能找到全局的最优解,可以比较快 的找到问题的近似最优解。
模拟退火算法的应用
1. 问题的提出
单机极小化总流水时间的排序问题 四个工作:P1=8,P2=18,P3=5,P4=15,求 min∑Fi的最优顺序。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
流 程 图
5、SA算法应用范围与一般要求
SA算法是近年来备受重视的一类软计算方法,能解决传统的非线性 规划方法难于解决的某些问题,在VLSI、生成调度、控制工程、机器学 习、神经网络、图像处理、函数优化等许多领域得到广泛的研究。
最优解 设定初温 Metropolis采样过程 控制参数的下降 目标函数
物理退火 粒子状态 能量最低态 熔解过程 等温过程
冷却 能量
3、SA算法的基本思想
在搜索最优解的过程中,SA算法除了可以接受优化解外,还基 于随机接受准则(Metropolis准则)有限度地接受恶化解,并且接 受恶化解的概率慢慢趋向于0。(这使得算法有可能从局部最优中 跳出,尽可能找到全局最优解,并保证了算法的收敛)
SA的思想最早是由Metropolis等在1953年提出的,Metropolis 等 提出了重要性采样法,即以概率接受新状态。
SA算法的思想为: ➢ 由初始解i和控制参数初值t开始,对当前解重复
产生新解 →计算目标函数差 →接受或舍弃
的迭代, ➢ 并逐步衰减t值, ➢ 算法终止时的当前解即为所得近似最优解, ➢ 这是基于蒙特卡罗迭代求解法的一种启发式随机搜索过程。
xn1 xn nf (xn )
然而以速降法为代表的传统算法具有共同的缺点,它们都不 保证求得全局极小,只能保证收敛到一个由初值决定的局部极小 点。每次都鼠目寸光的选择一个当前最优解,因此只能搜索到局 部的最优值。模拟退火其实也是一种贪心算法,但是它的搜索过 程引入了随机因素。模拟退火算法以一定的概率来接受一个比当 前解要差的解,因此有可能会跳出这个局部的最优解,达到全局 的最优解。
SA算法的应用需满足如下三个方面的要求: (1)对问题的简明形式的描述即数学模型,由解空间、目标函数和 初始解三部分构成; (2)新解的产生和接受机制; (3)冷却进度表。
5、SA算法应用范围与一般要求
冷却进度表是指从某一高温状态T0向低温状态冷却时的降温管理表。
假设时刻t的温度用T(t)来表示,则经典模拟退火算法的降温方式为: T (t) T0 lg(1 t)
模拟退火算法
(Simulated Annealing)
1、引子 2、SA算法的起源 3、SA算法的基本思想 4、SA算法的步骤 5、SA算法应用范围与一般要求 6、SA算法的优缺点
1、引子
在科学与工程计算中,经常发生的一个问题是在Rn中或 者是在一个有界区域上求某个非线性函数f(x)的极小点。在f(x)可 导时,一个最基本的算法就是最速下降法。这一方法从某一选定 的初值开始,利用如下公式进行迭代,即
1) for j = 1~k 2) 对当前最优解xbest按照某一邻域函数,产生一新的解xnew。计算
新的目标函数值E(xnew) ,并计算目标函数值的增量ΔE = E(xnew) - E(xbest) 。
3) 如果ΔE <0,则xbest = xnew; 4) 如果ΔE >0,则p = exp(- ΔE /T(i));
而快速模拟退火算法的降温方式为: T (t) T0 1 t
这两种方式都能够使得模拟退火算法收敛于全局最小点。
5、SA算法应用范围与一般要求
初始温度T0的设定: 实验表明,初温越大,获得高质量解的几率越大,但花费的计算时 间将增加。因此,初温的确定应折衷考虑优化质量和优化效率,常用方 法包括:
(1) 均匀抽样一组状态,以各状态目标值的方差为初温。 (2) 随机产生一组状态,确定两两状态间的最大目标值差|Δmax|,然 后依据差值,利用一定的函数确定初温。比如,t0=-Δmax/pr,其中pr为初 始接受概率。
缺点:由于要求较高的初始温度、较慢的降温速率、较低的终止温 度,以及各温度下足够多次的抽样,因此其收敛速度慢,执行时间长, 算法性能与初始值有关及参数敏感等缺点。
Hale Waihona Puke (3) 利用经验公式给出。
5、SA算法应用范围与一般要求
算法终止准则,常用的包括: (1) 设置终止温度的阈值; (2) 设置外循环迭代次数; (3) 算法搜索到的最优值连续若干步保持不变; (4) 检验系统熵是否稳定。
6、SA算法的优缺点
与同类方法相比,SA算法具有以下优缺点: 优点:高效,灵活,通用,初值鲁棒性强,适用于并行处理,可用 于求解复杂的非线性优化问题。
SA算法与其它搜索方法相比,具有如下的特点: ➢ 以一定的概率接受恶化解; ➢ 引进算法控制参数; ➢使用对象函数值进行搜索; ➢ 隐含并行性; ➢搜索复杂区域。
4、SA算法的基本步骤
1) 随机产生一个初始解x0,令xbest= x0并计算目标函数值E(x0); 2) 设置初始温度T(0)=To,迭代次数i = 1; 3) Do while T(i) > Tmin
2、SA算法的起源
SA算法起源于对固体退火过程的模拟。简单而言,在固体退火时, 先将固体加热使其温度充分高,再让其徐徐冷却,其物理退火过程由 以下三部分组成:加温过程、等温过程、冷却过程。
SA算法就是模仿上述物理系统徐徐退火过程的一种通用随机搜索技术。 模拟退火算法与物理退火过程的相似关系
模拟退火 解
