有限元的MATLAB解法
MATLAB有限元分析与应用精选全文完整版

%SpringElementForces This function returns the element nodal force
%
vector given the element stiffness matrix k
%
and the element nodal displacement vector u.
2019/11/28
§2-1 弹簧元
u1=U(1:2); f1=SpringElementForces(k1,u1);
f1 = -15.0000 15.0000
u2=U(2:3); f2=SpringElementForces(k2,u2);
f2 = -15.0000 15.0000
12
§3-1 弹簧元
%
modulus of elasticity E, cross-sectional
%
area A, and length L. The size of the
%
element stiffness matrix is 2 x 2.
y = [E*A/L -E*A/L ; -E*A/L E*A/L];
2019/11/28
3.1 单元刚度矩阵的形成
function y = SpringElementStiffness(k)
%SpringElementStiffness This function returns the element stiffness %matrix for a spring with stiffness k. %The size of the element stiffness matrix is 2 x 2.
电磁场有限元Matlab解法

nel=n1;
%总网格数
%******************定义各个单元的常量和矩阵************************ K=zeros(ndm,ndm); %定义 K 矩阵 Ke=zeros(3,3); %单元 Ke 矩阵 s=0.5/(Jmax*Jmax); %单元面积 b=zeros(ndm,1); %b 矩阵 be=1:3; %单元 be 矩阵 eps=1:nel; rho=1:nel; %定义 ε 和 ρ 数组 for n=1:2*Jmax*Imax %定义上下两部分的 ε 和 ρ 值,,两部分的 ε 分别 为 9 和 1,ρ 都为 0 eps(n)=eps1; rho(n)=rho1; end for n=2*Jmax*Imax+1:nel eps(n)=eps2; rho(n)=rho2; end %****************计算系统的[K][b]矩阵************************* for n=1:nel for i=1:3 n1=NE(1,n); n2=NE(2,n); n3=NE(3,n); %给每个单元的点进行编号 bn(1)=Y(n2) - Y(n3); bn(2)=Y(n3) - Y(n1); bn(3)=Y(n1) - Y(n2); cn(1)=X(n3) - X(n2); cn(2)=X(n1) - X(n3); cn(3)=X(n2) - X(n1); for j=1:3 Ke(i,j)=eps(n)*(bn(i)*bn(j)+cn(i)*cn(j))/(4*s); be(i)=s*rho(n)/3; %计算每个单元的 Ke 和 be 矩阵 end end for i=1:3 for j=1:3 K(NE(i,n),NE(j,n))=K(NE(i,n),NE(j,n))+Ke(i,j); b(NE(i,n))=b(NE(i,n))+be(i); %把 Ke 和 be 分别相加求总矩阵 end end end
有限元MATLAB
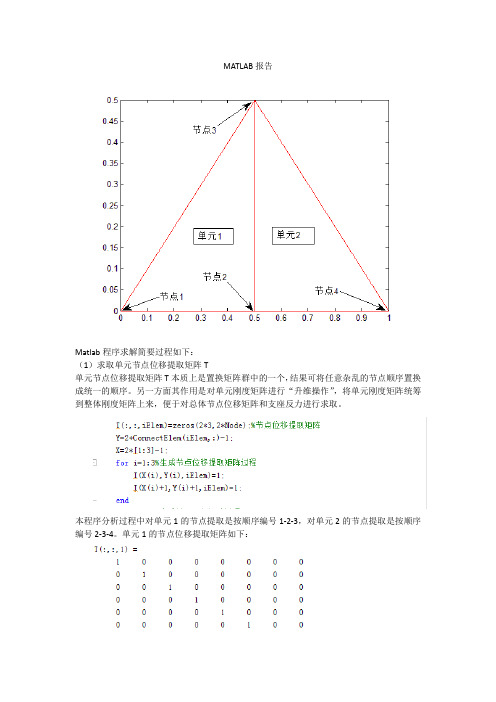
MATLAB报告Matlab程序求解简要过程如下:(1)求取单元节点位移提取矩阵T单元节点位移提取矩阵T本质上是置换矩阵群中的一个,结果可将任意杂乱的节点顺序置换成统一的顺序。
另一方面其作用是对单元刚度矩阵进行“升维操作”,将单元刚度矩阵统筹到整体刚度矩阵上来,便于对总体节点位移矩阵和支座反力进行求取。
本程序分析过程中对单元1的节点提取是按顺序编号1-2-3,对单元2的节点提取是按顺序编号2-3-4。
单元1的节点位移提取矩阵如下:单元2的节点位移提取矩阵如下:(2)求取单元几何矩阵B单元1的节点按编号顺序1-2-3分别进行对几何函数矩阵或算子矩阵的bi逆时针操作,对ci顺时针操作;单元2的节点按编号顺序2-3-4分别进行对几何函数矩阵的bi顺时针操作,对ci逆时针操作.在MATLAB程序中通过mod()取模函数来达到对节点的顺时针或逆时针循环操作。
单元1的几何矩阵如下:单元2的几何矩阵如下:(3)求取应力矩阵S单元应力矩阵满足S=D*B,其中D为弹性矩阵,B为单元几何矩阵各单元的弹性矩阵如下:单元1的应力矩阵如下:单元2的应力矩阵如下:(4)求取单元刚度矩阵K单元刚度矩阵K满足公式K=B’*D*B*t*A,其中t为平面板的厚度,A为单元面积,且单元刚度矩阵为对称矩阵。
单元1的刚度矩阵如下:单元2的刚度矩阵如下:(5)求取总体刚度矩阵sumKK由上述步骤求得的单元刚度矩阵K利用单元虚功原理和刚度方程可导出K’*δ=f,其中δ为单元节点位移列阵,f为单元等效节点载荷列阵,为了能将各个单元刚度方程统一到一个整体,便需要步骤(1)的单元节点提取矩阵对单元刚度方程进行变换,将两个变换结果联立便得到总体刚度方程,其中也可得到总体刚度矩阵sumKK,且总体刚度矩阵可由sumKK=Σ T’*K*T 求得。
总体刚度矩阵如下:(6)求取总体节点位移矩阵和支座反力利用上述步骤提到的总体刚度方程sumKK*delta=F,其中delta为总体节点位移矩阵,F为总体等效节点载荷列阵。
第三章MATLAB有限元分析与应用

第三章MATLAB有限元分析与应用有限元分析(Finite Element Analysis, FEA)是一种工程计算方法,用于解决结构力学和流体力学等问题。
它将一个复杂的结构分割成多个简单的离散单元,通过建立数学模型和求解方程组,得到结构的力学、热力学和流体力学等性能参数。
MATLAB是一种功能强大的数学计算软件,具有直观的用户界面和丰富的工具箱,可以方便地进行有限元分析。
本章将介绍在MATLAB中进行有限元分析的基本步骤和方法,以及一些常见的应用例子。
首先,进行有限元分析需要将结构进行离散化。
常用的离散化方法有节点法和单元法。
节点法是将结构的几何形状划分为小的节点,并在节点上进行计算。
单元法是将结构划分为多个小的单元,并在每个单元内进行计算。
在MATLAB中,可以通过创建节点和单元的矩阵来描述结构和单元的关系。
例如,创建一个2D结构形式的节点矩阵:nodes = [0 0; 1 0; 0 1; 1 1];然后,通过创建描述节点连接关系的矩阵,来定义结构的单元:elements = [1 2 3; 2 4 3];这里的每一行代表一个单元,数字表示节点的编号。
接下来,需要定义材料的力学参数和边界条件。
材料的力学参数包括弹性模量、泊松比等。
边界条件包括支座约束和加载条件。
在MATLAB中,可以通过定义力学参数和边界条件的向量来描述。
例如,定义弹性模量和泊松比的向量:E=[200e9200e9];%弹性模量nu = [0.3 0.3]; % 泊松比定义支座约束的向量(1表示固定,0表示自由):constraints = [1 1; 0 0; 0 1; 0 1];定义加载条件的向量(包括点力和面力):最后,通过求解方程组得到结构的应力和位移等结果。
在MATLAB中,可以利用有限元分析工具箱中的函数进行计算。
例如,可以使用“assem”函数将节点和单元的信息组装成方程组,并使用“solveq”函数求解方程组。
matlab中fvtool用法

matlab中fvtool用法fvtool是MATLAB中的一个非常有用的工具,用于对有限元方法(Finite Element Method,FEM)进行设计和分析。
它可以创建二维和三维有限元模型,并对其进行模拟和分析。
下面详细介绍如何使用fvtool。
首先,需要打开MATLAB并进入命令行界面。
然后,可以通过以下命令来启动fvtool:fvtool这会打开一个新的图形窗口,在这个窗口中可以创建和编辑有限元模型。
创建新的有限元模型:1.在fvtool窗口中,选择“File”菜单,然后选择“New” -> “Model”。
这会创建一个新的有限元模型。
2.在新模型中,可以通过选择“Mesh”菜单来添加网格。
网格是有限元模型的基础,它定义了模型的形状和大小。
可以手动添加网格,也可以通过导入外部文件来添加网格。
3.添加完网格后,可以通过选择“Elements”菜单来添加有限元。
有限元是用来描述物理行为的数学模型。
例如,可以选择“Linear”元素来添加线性元素。
4.添加完有限元后,可以通过选择“Properties”菜单来为有限元分配物理属性,如弹性模量、泊松比等。
对有限元模型进行模拟和分析:1.在创建和编辑完有限元模型后,可以通过选择“Solution”菜单来定义模拟条件和求解方法。
例如,可以选择“Static” -> “力和位移”来模拟静态条件下的力和位移。
2.然后,可以通过选择“Solve”菜单来求解有限元模型。
求解器会根据定义的模拟条件和求解方法来计算模型的响应。
3.最后,可以通过选择“Results”菜单来查看和分析计算结果。
结果可以包括位移、应力、应变等。
可以使用图形和图表来可视化结果,也可以将结果导出到其他工具中进行进一步分析。
此外,fvtool还提供了很多高级功能,如创建自定义元素、定义材料非线性等。
这些功能可以根据具体需求进行使用。
总之,fvtool是一个强大的有限元分析工具,它可以帮助用户创建和模拟有限元模型,并分析模型的响应。
matlab有限元法

matlab有限元法
有限元法是一种常用的工程数值计算方法,广泛应用于结构力学、流体力学、热传导等领域。
它通过将复杂的连续体分割成有限个简单的单元,利用单元之间的相互关系来近似描述整个问题的解。
在工程实践中,有限元法已经成为一种不可或缺的分析工具。
有限元法的基本步骤包括建立数学模型、离散化、确定边界条件、求解方程、后处理等。
首先,需要将实际工程问题转化为数学模型,确定问题的几何形状、材料特性和载荷条件。
然后,将问题离散化,即将结构分割成有限个简单的单元,并确定单元之间的连接关系。
接下来,需要确定边界条件,即给定结构的边界约束和外部载荷。
然后,通过求解离散化后的方程组,得到问题的数值解。
最后,进行后处理,分析和展示结果。
有限元法的优点在于能够处理复杂的几何形状和边界条件,可以模拟各种不同的物理现象,并且具有较高的精度和可靠性。
它能够帮助工程师更好地理解和设计结构,提高工程的可靠性和安全性。
然而,有限元法也存在一些局限性。
首先,离散化过程会引入一定的误差,尤其是在模型中存在较大的变形或应力集中的情况下。
其次,求解大规模的方程组需要较高的计算资源和时间。
此外,有限元法对材料的本构关系和边界条件的设定要求较高,需要进行合理的模型假设和参数选择。
总的来说,有限元法是一种强大而灵活的工程分析方法,能够帮助工程师解决各种复杂的工程问题。
通过合理的模型建立和边界条件设定,以及精确的计算和后处理,可以得到准确可靠的结果,为工程设计和优化提供有力支持。
有限元方法步骤-MATLAB的简略使用指南

第1章引言这个简短的引言分为两部分,第一部分是对有限元方法步骤的概括介绍,第二部分是MATLAB的简略使用指南。
1.1 有限元方法的步骤有许多关于有限元分析的优秀教材,比如在参考文献[1-18]中列出的那些书目。
因此,本书不准备对有限元理论或有限元方程进行详细地阐述和推导。
每一章只总结概括主要的方程,这些章节都附有示例来说明这些方程。
此外,全书只讨论线弹性结构力学的问题。
有限元方法用于解决工程问题的数值计算过程。
本书假定所有的行为都是线弹性行为。
虽然本书的问题都与结构工程相关,但有限元方法也同样适用于工程的其他领域。
本书中使用有限元方法解决问题共包括6个步骤。
对有限元分析的6个步骤阐述如下:(1) 离散化域——这个步骤包括将域分解成单元和节点。
对于像桁架和刚架这类离散系统,已经离散化,这一步就不需要了。
此处获得的结果应该已经是精确的。
然而,对于连续系统,如板壳,这一步就变得至关重要,因为它只能得到近似的结果。
因此解决方案的精确度取决于所使用的离散化方法。
本书中,我们将手动完成这一步(对连续系统)。
(2) 写出单元刚度矩阵(element stiffness matrices)——写出域内每个单元的单元刚度矩阵。
在本书中,这个步骤通过MATLAB实现。
(3) 集成整体刚度矩阵(global stiffness matrices)——这一步用直接刚度法(direct stiffness approach)实现。
在本书中,该步骤借助于MATLAB实现。
(4) 引入边界条件——诸如支座(supports)、外加载荷(applied loads)和位移(displacements)等。
本书中手动实现这一步骤。
(5) 解方程——这一步骤分解整体刚度矩阵并用高斯消去法求解方程组。
在本书中,在用高斯消去法实现求解部分的时候需要手动分解矩阵。
(6) 后处理——得到额外的信息,如支反力、单元节点力和单元应力。
本书中这一步骤通过MATLAB实现。
有限元数值解法在MATLAB中的实现及可视化

有限元数值解法在MATLAB中的实现及可视化摘要:偏微分方程的数值解法在数值分析中占有很重要的地位,很多科学技术问题的数值计算包括了偏微分方程的数值解问题。
在学习初等函数时,总是先画出它们的图形,因为图形能帮助我们了解函数的性质。
而对于偏微分方程,画出它们的图形并不容易,尤其是没有解析解的偏微分方程,画图就显得更加不容易了。
为了从偏微分方程的数学表达式中看出其所表达的图形、函数值与自变量之间的关系,通过MATLAB编程,用有限元数值解法求解了偏微分方程,并将其结果可视化。
关键词:偏微分方程;MATLAB;有限元法;可视化1 引言(Introduction)偏微分方程的数值解法在数值分析中占有很重要的地位,很多科学技术问题的数值计算包括了偏微分方程的数值解问题。
近三十多年来,它的理论和方法都有了很大的发展,而且在各个科学技术的领域中应用也愈来愈广泛。
例如,核武器的研制要有理论设计和核试验。
但核反应和核爆炸的过程是在高温高压的条件下进行的,而且巨大的能量在极短的时间内释放出来,核装置内部的细致反应过程及各个物理量的变化是根本不能用仪器测量出来的,核试验只是提供综合的数据。
而描述核反应和爆炸物理过程的数学模型是一个很复杂的非线性偏微分方程组,也根本没有办法得到这个方程组理论上的精确解。
所以发展核武器的国家都在计算机上对核反应过程进行数值模拟,这也称为“数值核实验”,它可以大大减少核试验的次数,节约大量的经费,缩短研制的周期[1]。
在学习初等函数时,总是先画出它们的图形,因为图形能帮助我们了解函数的性质。
而对于偏微分方程,画出它们的图形并不容易,尤其是没有解析解的偏微分方程,画图就显得更加不容易了。
所以本文主要研究如何用MATLAB数值求解偏微分方程,并将其数值解绘制成三维图形的形式,从而可以从复杂的数学表达式中看出其所表达的图像、函数值与自变量之间的关系[2]。
2 有限元法(Finite element method)2.1 有限元法概述有限元法的基本思想是将结构离散化,用有限个容易分析的单元来表示复杂的对象,单元之间通过有限个节点相互连接,然后根据变形协调条件综合求解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有限元的MATLAB解法1.打开MATLAB。
2.输入“pdetool”再回车,会跳出PDE Toolbox的窗口(PDE意为偏微分方程,是partial differential equations的缩写),需要的话可点击Options菜单下Grid命令,打开栅格。
3.完成平面几何模型:在PDE Toolbox的窗口中,点击工具栏下的矩形几何模型进行制作模型,可画矩形R,椭圆E,圆C,然后在Set formula栏进行编辑并(如双脊波导R1+R2+R3改为RI-R2-R3,设定a、b、s/a、d/b的值从而方便下步设定坐标)用算术运算符将图形对象名称连接起来,若还需要,可进行储存,形成M文件。
4.用左键双击矩形进行坐标设置:将大的矩形left和bottom都设为0,width是矩形波导的X轴的长度,height是矩形波导的y轴的长度,以大的矩形左下角点为原点坐标为参考设置其他矩形坐标。
5.进行边界设置:点击“Boundary”中的“Boundary Mode”,再点击“Boundary”中的“Specify Boundary Conditions”,选择符合的边界条件,Neumann为诺曼条件,Dirichlet为狄利克雷条件,边界颜色显示为红色。
6.进入PDE模式:点击"PDE"菜单下“PDE Mode”命令,进入PDE 模式,单击“PDE Specification”,设置方程类型,“Elliptic”为椭圆型,“Parabolic”为抛物型,“Hyperbolic”为双曲型,“Eigenmodes”为特征值问题。
7.对模型进行剖分:点击“Mesh”中“Initialize Mesh”进行初次剖分,若要剖的更细,再点击“Refine Mesh”进行网格加密。
8.进行计算:点击“Solve”中“Solve PDE”,解偏微分方程并显示图形解,u值即为Hz或者Ez。
9.单击“Plot”菜单下“Parameters”选项,打开“Plot Selection”对话框。
选中Color,Height(3-D plot)和Show mesh三项,然后单击“Plot”按钮,显示三维图形解。
10.如果要画等值线图和矢量场图,单击“Plot”菜单下“Parameters”选项,打开“Plot Selection”对话框。
选中Contour和Arrows两项,然后单击Plot按钮,可显示解的等值线图和矢量场图。
11.将计算结果条件和边界导入MATLAB中:点击“Export Solution”,再点击“Mesh”中“Export Mesh”。
12.在MATLAB中将编好的计算程序导入,按F5运行。
备注:Property(属性)用于画图时选用相应的绘图类型u 方程的解abs(grad(u)) 每个三角形的中心的▽u的绝对值abs(c*grad(u)) 每个三角形的中心的c·▽u的绝对值- grad(u) u的负梯度-▽u我们也可以用MATLAB程序求解PDE问题,同时显示解的图形;一个长直接接地金属矩形槽,其侧壁与底面电位均为0,顶盖电位为100V,求槽内的电位分布:100V0V0V0V(1)画出剖分图(尺寸与书上一样);(2)标出各剖分点坐标值;(3)求出各点电位值(用有限差分);(4)画出等电位图。
解:(1)编写以下程序得:x=0:5y=0:5[X,Y]=meshgrid(x,y)plot(X,Y)hold onplot(Y,X)for i=0:5s=i:5t=0:(5-i)plot(s,t)plot(t,s)end得到剖分图如下:(2)用有限元法编写程序如下:Nx=6;Ny=6;Xm=5;Ym=15;Np=5;Nq=5; for i=1:Nxfor j=1:NyN(i,j)=(i-1)*Ny+j; /i列j行的节点编号/ X(N(i,j))=(i-1)*Xm/Np;/节点横坐标/Y(N(i,j))=(j-1)*Ym/Nq;/节点纵坐标/ endendfor i=1:2*Xmfor j=1:Ymif rem(i,2)==1L(i,j)=(i-1)*Nq+j;p(i,j)=2*(i-1)*Ny/2+Ny+j+1;q(i,j)=p(i,j)-Ny;r(i,j)=q(i,j)-1;else rem(i,2)==0L(i,j)=(i-1)*Ny+j;p(i,j)=(2i-2)*Ny/2+j;q(i,j)=p(i,j)+Ny;r(i,j)=q(i,j)+1;endendendfor i=1:2*Xmfor j=1:Ymb(p(i,j))=Y(q(i,j))-Y(r(i,j));b(q(i,j))=Y(r(i,j))-Y(p(i,j));b(r(i,j))=Y(p(i,j))-Y(q(i,j));c(p(i,j))=X(r(i,j))-X(q(i,j));c(q(i,j))=X(p(i,j))-X(r(i,j));c(r(i,j))=X(q(i,j))-X(p(i,j));area(i,j)=(b(p(i,j))*c(q(i,j))-b(q(i,j))*c(p(i,j)))/2;K=zeros(Nx*Ny);Kpp(i,j)=(b(p(i,j))^2+c(p(i,j))^2)/(2*area(i,j));Kpq(i,j)=(b(p(i,j))*b(q(i,j))+c(p(i,j))*c(q(i,j)))/(2*area(i,j)); Kpr(i,j)=(b(p(i,j))*b(r(i,j))+c(p(i,j))*c(r(i,j)))/(2*area(i,j)); Kqp(i,j)=Kpq(i,j);Kqq(i,j)=(b(q(i,j))^2+c(q(i,j))^2)/(2*area(i,j));Kqr(i,j)=(b(q(i,j))*b(r(i,j))+c(q(i,j))*c(r(i,j)))/(2*area(i,j)); Krp(i,j)=Kpr(i,j);Krq(i,j)=Kqr(i,j);Krr(i,j)=(b(r(i,j))^2+c(r(i,j))^2)/(2*area(i,j));endendfor i=1:2*Xmfor j=1:YmK(p(i,j),p(i,j))=Kpp(i,j)+K(p(i,j),p(i,j));K(p(i,j),q(i,j))=Kpq(i,j)+K(p(i,j),q(i,j));K(p(i,j),r(i,j))=Kpr(i,j)+K(p(i,j),r(i,j));K(q(i,j),p(i,j))=Kqp(i,j)+K(q(i,j),p(i,j));K(q(i,j),q(i,j))=Kqq(i,j)+K(q(i,j),q(i,j));K(q(i,j),r(i,j))=Kqr(i,j)+K(q(i,j),r(i,j));K(r(i,j),p(i,j))=Krp(i,j)+K(r(i,j),p(i,j));K(r(i,j),q(i,j))=Krq(i,j)+K(r(i,j),q(i,j));K(r(i,j),r(i,j))=Krr(i,j)+K(r(i,j),r(i,j));endendfor i=1:11K(i,:)=0;K(i,i)=1;endfor i=1:11:111 K(i,:)=0;K(i,i)=1;endfor i=111:121 K(i,:)=0;K(i,i)=1;endfor i=11:11:121 K(i,:)=0;K(i,i)=1;endB=zeros(121,1); for i=11:11:121 B(i,1)=100; endU=K\B;b=1;XX=zeros(11,11)for j=1:11for i=1:11XX(i,j)=U(b,1);b=b+1;endendsubplot(1,2,1),mesh(XX)axis([0,11,0,11,0,100])subplot(1,2,2),contour(XX,15)hold on(3)由上面的程序得到节点电位:V1=0 0 0 0 00 7.1429 9.8214 7.1429 00 18.7500 25.0000 18.7500 00 42.8571 52.6786 42.8571 00 100.0000 100.0000 100.0000 0(4)由程序得到的电场分布图及等位线图如下:4.用有限元法求矩形波导(b/a=0.45)的:(1)电场分布图;(2)求TE模式下的主模、第一、二高次模的截止波长(5次),画出截至波长图;(3)求TM模式下的主模、第一、二高次模的截止波长(5次),画出截至波长图。
解:利用MATLAB中的PDE工具箱:取矩形波导的宽边尺寸为a,窄边尺寸为0.45a。
(1)主模的电场分布图如下:在Neumann边界条件下:在Dirichlet边界条件下:(2)在TE模式下设置边界条件为Neumann条件,使用编制好的程序计算出主模的截止波长为 1.9988a,第一高次模为0.9977a,第二高次模为0.8972a,截止波长图如下:单模TE10区λ时截止模区λ(3)在TM模式下设置边界条件为Dirichlet条件,使用编制好的程序计算出主模的截止波长为0.8179a,第一高次模为0.6655a,第二高次模为0.5315a,截止波长图如下:高次模区单模TM11区截止模区λ5.用时域有限差分求解上述4题中的前两问。
解:(1)根据时域有限差分编写的程序可画出主模的电场分布图如下:在Neumann 边界条件下:在Dirichlet 边界条件下:(2)根据时域有限差分编写的程序可画出频谱图和场结构图,从左图中可以读出主模截止频率c f 值,主模81.499610c f ,根据01/()ccof ,其中128.8510,-601.256630610,从而计算出主模截至波长2.0273ca 。
