四年级数学下册认识三角形和四边形知识点及测试题(精品)
四年级数学下册认识三角形和四边形知识点及测试题

第二单元:认识三角形和四边形知识点及测试题1.图形分为:立体图形和平面图形。
2.平面图形:a、圆(由曲线围成的图形)b、三角形、四边形、多边形(由线段围成的图形)3.三角形内角和是180°。
锐角:小于90°的角是锐角。
钝角:大于90°的角是钝角。
直角:等于90°的角是直角。
平角=180°;周角=360°4.等腰三角形相等的两条边叫做腰。
等腰三角形两腰间的夹角叫顶角。
腰与底边的夹角叫底角。
5.等腰三角形包含:等腰三角形、等边三角形(又叫正三角形)、等腰直角三角形。
等边三角形是特殊的等腰三角形,它的每个内角都是60°。
6.三角形不易变形具有稳定性。
四边形易变形具有不稳定性.直角三角形(有一个直角两个锐角)按角分锐角三角形(三个角都是锐角)钝角三角形(有一个钝角两个锐角)7 .三角形(有三条边)等边三角形(三条边都相等)是对称图形,有三条对称轴按边分等腰三角形(有两条边相等)是对称图形,有一条对称轴不等边三角形(三条边都不相等)8.三角形任意两边之和大于第三边。
9.由四条线段围成的封闭图形叫四边形四边形内角和是360°。
10.正方形是特殊的长方形。
长方形和正方形是特殊的平行四边形。
11.平行四边形:两组对边分别平行且相等的四边形。
12.梯形:只有一组对边平行的四边形。
13.平行的两条边叫做梯形的底边,上面的一条叫上底,下面一条叫下底。
14.梯形的周长:上底+下底+腰+腰梯形的面积:(上底+下底)×高÷215..根据三角形的边长判定三角形的类型:较小两边的平方和小于最长边的平方钝角三角形较小两边的平方和等于最长边的平方直角三角形较小两边的平方和大于最长边的平方钝角三角形16.. 等腰三角形的两个底角相等。
等边三角形是特殊的等腰三角形。
一般平行四边形平行四边形: 长方形(两组对边分别平行且相等的四边形) 正方形 17. 四边形 一般四边形: (有四条边) (两组对边都不平行的四边形) 一般梯形梯形: 等腰梯形:两条腰相等,同一底上的两个底角相等。
北师大版小学四年级数学下册第二单元认识三角形和四边形知识点、经典例题与单元检测试题(附答案)

【专题讲义】北师大版小学四年级数学下册第二单元认识三角形和四边形知识点、经典例题与单元检测精讲(学生版)【知识点归纳总结】1. 四边形的特点、分类及识别1.四边形的特点:四边形就是四条线段围成的图形,有四条边,四个角,且内角和是360°.2.四边形的分类:任意四边形:图形没有平行的边平行四边形:图形两组平行的边梯形:图形只有一组平行的边3.四边形的识别:根据分类特地进行识别即可.【经典例题】例1:把符合要求的图形序号填在横线里.A、正方形B、长方形C、平形四边形D、梯形①两组对边分别平行,有四个直角.②只有一组对边平行.③两组对边分别平行,没有直角.页1例2:正方形、长方形是特殊的平行四边形..(判断对错)2. 平行四边形的特征及性质平行四边形的概念:1.两组对边分别平行的四边形叫做平行四边形.平行四边形用符号“ABCD”,如平行四边形ABCD记作“ABCD”.(1)平行四边形属于平面图形.(2)平行四边形属于四边形.(3)平行四边形中还包括特殊的平行四边形:矩形,正方形和菱形等.(4)平行四边形属于中心对称图形.2.平行四边形的性质:主要性质(矩形、菱形、正方形都是特殊的平行四边形.)(1)如果一个四边形是平行四边形,那么这个四边形的两组对边分别相等.(简述为“平行四边形的两组对边分别相等”)(2)如果一个四边形是平行四边形,那么这个四边形的两组对角分别相等.(简述为“平行四边形的两组对角分别相等”)(3)夹在两条平行线间的平行线段相等.(4)平行四边形的面积等于底和高的积.(可视为矩形)(5)过平行四边形对角线交点的直线,将平行四边形分成全等的两部分图形.(6)平行四边形是中心对称图形,对称中心是两对角线的交点.页2(7)平行四边形不是轴对称图形,矩形和菱形是轴对称图形.注:正方形,矩形以及菱形也是一种特殊的平行四边形,三者具有平行四边形的性质.【经典例题】例1:两组对边分别平行没有直角的图形是()A、长方形B、平行四边形C、梯形例2:一个长方形的框架,如果把它拉成一个平行四边形,它的周长和面积()A、周长不变,面积变大B、周长不变,面积也不变C、周长变小,面积变小D、周长不变,面积变小3. 长方形的特征及性质长方形:是一种平面图形,长方形的四个角都是直角,同时长方形的对角线相等.长方形的性质:1.长方形的4个内角都是直角;2.长方形对边相等;3.长方形既是轴对称图形,也是中心对称图形(对称轴是任何一组对边中点的连线),它至少有两条对称轴.对称中心是对角线的交点.4.长方形是特殊的平行四边形,长方形具有平行四边形的所有性质长方形的判定:①定义:有一个角是直角的平行四边形是长方形页3②定理1:有三个角是直角的四边形是长方形矩形的面积:S矩形=长×宽=ab.黄金长方形:宽与长的比是(√5-1)/2(约为0.618)的矩形叫做黄金长方形.黄金长方形给我们一协调、匀称的美感.世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计.如希腊的巴特农神庙等.【经典例题】例:如图中甲的周长与乙的周长相比()A、甲长B、乙长C、同样长4. 正方形的特征及性质1.概念:有一组邻边相等且一个角是直角的平行四边形叫做正方形.2.性质:(1)边:两组对边分别平行;四条边都相等;相邻边互相垂直(2)内角:四个角都是90°;(3)对角线:对角线互相垂直;对角线相等且互相平分;每条对角线平分一组对角;(4)对称性:既是中心对称图形,又是轴对称图形(有四条对称轴).(5)正方形具有平行四边形、菱形、矩形的一切性质.页4(6)特殊性质:正方形的一条对角线把正方形分成两个全等的等腰直角三角形,对角线与边的夹角是45°;正方形的两条对角线把正方形分成四个全等的等腰直角三角形.(7)正方形是特殊的长方形.【经典例题】例:四个角都是直角的四边形一定是正方形..(判断对错)5.梯形的特征及分类1.概念:梯形是指一组对边平行而另一组对边不平行的四边形.2.分类:(1)直角梯形:有一个角为直角的梯形为直角梯形(2)等腰梯形:两腰相等的梯形叫做等腰梯形(3)一般梯形.【经典例题】例1:只有一组对边平行的四边形是()A、三角形B、长方形C、平行四边形D、梯形例2:两个完全一样的直角梯形,一定不能拼成()A、平行四边形B、长方形C、三角形6.三角形的特性页5三角形具有稳定性.三内角之和等于180度,根据角可以分为锐角三角形(每个角小于90°),直角三角形(有一个角等于90°),钝角三角形(有一个角大于90°).任意两边之和大于第三边,任意两边之差小于第三边.【经典例题】例1:可以围成一个三角形的三条线段是.()A、 B 、C、例2:下面图形是用木条钉成的支架,其中最不容易变形的是()A、 B、 C、页67.三角形的分类1.按角分判定法一:锐角三角形:三个角都小于90°.直角三角形:可记作Rt△.其中一个角必须等于90°.钝角三角形:有一个角大于90°.判定法二:锐角三角形:最大角小于90°.直角三角形:最大角等于90°.钝角三角形:最大角大于90°.其中锐角三角形和钝角三角形统称为斜三角形.2.按边分不等边三角形;等腰三角形;等边三角形.页7【经典例题】例:一个三角形,三个内角的度数比是2:3:4,这个三角形为()A、锐角三角形B、直角三角形 C、钝角三角形D、不能确定【同步测试】一.选择题(共8小题)1.四条边相等,四个角是直角的四边形是()A.正方形B.长方形C.梯形2.将一个平行四边形沿高剪开,不可能得到()A.一个三角形和一个梯形B.一个平行四边形和一个梯形C.两个三角形3.如图是个四边形,但被挡住了一部分.被挡住的角一定是()A.锐角B.直角C.钝角4.正方形是特殊的()A.三角形B.圆C.平行四边形D.梯形页85.下面三句话中,说法错误的是()A.梯形的上底与下底互相平行B.梯形的两腰相等C.平行四边形的两组对边分别互相平行6.下列几组长度能拼成三角形的是()A.4cm、5cm、9cmB.3cm、6cm、10cmC.4cm、6cm、5cm7.下列各图表示的关系正确的个数有()A.0个B.1个C.2个D.3个8.当一个四边形只有一组对边平行时,它是()A.正方形B.长方形C.平行四边形D.梯形二.填空题(共7小题)页99.数学书相邻的两条边互相,上下的两条边互相.10.两腰相等的梯形叫做.11.张红用一根40厘米长的铁丝围成了一个平行四边形,这个平行四边形的一条边长是15厘米,与它相邻的另一条边是厘米.12.小红用一根14cm长的铁丝围成了一个三边长都为整厘米数的三角形,它的边长可能是6cm、cm、cm.13.和都是特殊的平行四边形.14.如图是长方形,如果宽不变,长减少厘米,长方形就变成正方形;如果长不变,宽增加厘米,长方形也变成正方形.15.等边三角形每个角都是度,它按角分又是三角形.三.判断题(共5小题)16.把一个锐角三角形顺时针旋转90°,它就变成了直角三角形.(判断对错)17.这样的四根小棒可以围成许多不同的平行四边形.(判断对错)页1018.梯形的两条腰一定不平行..(判断对错)19.四条边都相等的图形不一定是正方形.(判断对错)20.两组对边相等的四边形一定是长方形..(判断对错)四.计算题(共1小题)21.计算下面图形的周长.五.应用题(共2小题)22.一块平行四边形菜地,它的两条相交的边的长度分别是28.5米和46米,围这块菜地需要篱笆多少米?页1123.一个三角形2边的长度如图,第三边最短是几厘米?最长是几厘米?(取整厘米数)页12六.操作题(共1小题)24.在点子图上按要求画图形.七.解答题(共4小题)25.用一张长10厘米,宽6厘米的长方形纸折成一个最大的正方形,正方形的边长是多少厘米?页1326.选择正确的番号填空.27.一根27厘米长的铁丝,可以围成边长是几厘米的等边三角形?28.一个等腰三角形的周长是36厘米,底比腰多3厘米,它的腰长是多少厘米?底长是多少厘米?页14【专题讲义】北师大版小学四年级数学下册第二单元认识三角形和四边形知识点、经典例题与单元检测精讲(解析版)一.选择题(共8小题)1.【分析】根据正方形的特征及性质可知:具有四条边都相等且四个角都是直角的四边形为正方形,据此判断即可.【解答】解:四条边相等,四个角是直角的四边形是正方形;故选:A.【点评】本题主要考查正方形的特征及性质.2.【分析】沿平行四边形钝角所在的一个顶点,向对边做垂线,这样的高有两条,沿这两条高剪开,都能得到一个三角形和一个梯形;如图2这样剪开,得到两个梯形,且是直角梯形.如图三特殊的一点的平行四边形沿高剪开可以得到两个直角三角形.【解答】解:由以上图形可以看出,将一个平行四边形沿高剪开,可能得到一个三角形和一个梯形、两个梯形或两个直角三角形.故选:C.【点评】本题属于简单的图形切割,在练习本上画一画就可以得到答案.页153.【分析】根据长方形、正方形的特征,长方形的对边平行且相等,4个角都是直角;正方形的4条边的长度都相等,4个角都是直角.据此解答即可.【解答】解:这个四边形是长方形,所以挡住的角一定是直角;故选:B.【点评】此题考查的目的是理解掌握长方形、正方形的特征及应用.4.【分析】根据平行四边形的特征,两组对边分别平行且相等的四边形是平行四边形,因为正方形的对边分别平行且相等,所以正方形是特殊的平行四边形.据此解答.【解答】解:由分析得:正方形是特殊的平行四边形.故选:C.【点评】此题考查的目的是理解掌握平行四边形、正方形的特征及应用,明确:长方形、正方形都是特殊的平行四边形.页165.【分析】根据梯形的特征,梯形的上、下底互相平行.A说法正确.等腰梯形的两腰相等,一般梯形的两腰不相等.B说法错误.根据平行四边形的特征,平行四边形再组对边平行且相等.C说法正确.【解答】解:A、梯形的上底与下底互相平行.此种说法正确;B、梯形的两腰相等.此种说法错误;C、平行四边形的两组对边分别互相平行.此种说法正确.故选:B.【点评】此题主要考查梯形、平行四边形的特征.6.【分析】根据三角形的特性:两边之和大于第三边,三角形的两边的差一定小于第三边;进行解答即可.【解答】解:A、4+5=9,所以不能围成三角形;B、3+6=9<10,所以不能围成三角形;C、4+5=9>6,所以能围成三角形;故选:C.【点评】解答此题的关键是根据三角形的特性进行分析、解答即可.页177.【分析】根据三角形按角可以分为锐角三角形、直角三角形、钝角三角形;按边可以分为:不等腰三角形和等腰三角形,其中等边三角形属于等腰三角形;四边形可以分为一般四边形和长方形,其中正方形是长方形的一种特殊情况;由此解答即可.【解答】解:下列各图表示的关系正确的个数有0个;故选:A.【点评】灵活掌握三角形的分类、四边形的分类,是解答此题的关键.8.【分析】根据平行四边形和图形的定义:两组对边分别平行的四边形叫平行四边形,正方形和长方形都是特殊的平行四边形;只有一组对边平行的四边形叫梯形,即可解答.【解答】解:当一个四边形只有一组对边平行时,它是梯形;故选:D.【点评】此题考查了平行四边形和梯形的定义.页18二.填空题(共7小题)9.【分析】数学书的封面是长方形,根据长方形的特征,对边平行且相等,4个角都是直角.由此解答.【解答】解:根据长方形的特征,对边平行且相等,4个角都是直角.因此,数学书的封面相邻的两条边互相垂直,上下的两条边互相平行.故答案为:垂直,平行.【点评】此题主要考查长方形的特征,对边平行且相等,4个角都是直角,据此解决问题.10.【分析】根据梯形的分类可知:两腰相等的梯形是等腰梯形,由此填空.【解答】解:两腰相等的梯形叫做等腰梯形.故答案为:等腰梯形.【点评】此题考查了等腰梯形的定义.页1911.【分析】根据平行四边形的周长=邻边之和×2,可得邻边之和=周长÷2,由此先求得邻边之和,再减去15厘米即可得解.【解答】解:40÷2﹣15=20﹣15=5(厘米)答:与它相邻的另一条边是5厘米.故答案为:5.【点评】本题主要考查了平行四边形的周长公式的灵活运用.12.【分析】根据三角形的特性:两边之和大于第三边,三角形的两边的差一定小于第三边;进行解答即可.【解答】解:3+5+6=14,3+5>6,符合构成三角形的条件,所以,它的三边长可能是6cm,3cm,5cm.故答案为:3,5.(答案不唯一)【点评】解答此题的关键是根据三角形的特性进行分析、解答即可.页2013.【分析】根据平行四边形的特征:两组对边平行且相等;则得出:长方形、正方形两组对边平行且相等,有四个角是直角,所以是特殊的平行四边形.【解答】解:长方形和正方形都是特殊的平行四边形;故答案为:长方形,正方形.【点评】此题考查了正方形和长方形与平行四边形的关系,应注意基础知识的积累.14.【分析】根据正方形的特征“四条边都相等”可知:如果宽不变,则长和宽相等时,该长方形变成正方形,即长减少:6﹣4=2厘米;同理,如果长不变,宽增长到和长相等时,长方形也变成正方形,即宽增加:6﹣4=2厘米;由此解答即可.【解答】解:长减少:6﹣4=2(厘米),宽增加:6﹣4=2(厘米);故答案为:2,2.【点评】解答此题应根据正方形的特征进行解答.页2115.【分析】等边三角形又叫做正三角形,其三个内角都相等,即每个内角都是60度,又因为三个角都是锐角,根据锐角三角形的含义得出结论.【解答】解:等边三角形每个角都是60度,它按角分又是锐角三角形.故答案为:60,锐角.【点评】解答此题应结合题意,并根据等边三角形的特征和锐角三角形的含义进行解答.三.判断题(共5小题)16.【分析】根据旋转的特征,一个图形绕某点顺时针旋转90°,某点的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形,即旋转后形状、大小不变,只是位置发生变化.【解答】解:一个图形绕某一点顺时针旋转90°,其大小、形状不变,位置发生变化,原题的说法是错误的.故答案为:×.【点评】此题是考查旋转的特征.图形平移、旋转后形状、大小不变,只是位置发生变化.页2217.【分析】依据平行四边形的意义,即两组对边分别平行或相等的四边形,叫做平行四边形;据此可知:只要是两组对边相等,就能围成一个平行四边形;据此判断即可.【解答】解:如图的四根小棒,因为两组分别相等,所以可以围成平行四边形,因为平行四边形具有易变形的性质,所以能围成许多不同的平行四边形,所以本题说法正确;故答案为:√.【点评】此题关键是根据四边形的特征进行分析、解答.18.【分析】只有一组对边平行的四边形是梯形,平行的这组对边叫做梯形的底,不平行的对边叫做梯形的腰,由此可知:梯形的两条腰一定不平行;由此判断即可.【解答】解:根据梯形的特征可知:梯形的两条腰一定不平行,如果延长,可以相交,所以本题说法正确;故答案为:√.【点评】此题考查梯形的特征及同一平面内两条直线的位置关系的灵活应用.页2319.【分析】如果一个四边形为正方形,必须保证四条边都相等,四个角都是直角,两个条件缺一不可.【解答】解:四条边相等的图形,四个角不一定都是直角,所以原题说法正确.故答案为:√.【点评】此题主要利用正方形的性质:正方形的四条边都相等,四个角都是直角进行判定.20.【分析】根据平行四边形的性质:两组对边平行且相等;可以得出:两组对边相等的四边形一定是平行四边形,但不一定是长方形,因为长方形的四个角都是直角;进而判断即可.【解答】解:两组对边相等的四边形一定是长方形,说法错误,因为两组对边相等的四边形一定是平行四边形,但不一定是长方形,因为长方形的四个角都是直角.故答案为:×【点评】此题考查了长方形的辨析,应注意基础知识的积累.页2421.【分析】根据周长的意义,围成平面图形所有边长的和叫做这个平面图形的周长.(1)根据加法的意义,把围成这个多边形的4条边的长度合并起来即可.(2)已知正六边形的边长是5分米,根据正六边形的周长=边长×6,据此列式解答.【解答】解:(1)33+17+(15+35)=50+50=100(厘米);答:它的周长是100厘米.(2)5×6=30(分米);答:这个正六边形的周长是30分米.【点评】此题考查的目的是理解掌握周长的意义,以及多边形周长的计算方法及应用.页2522.【分析】由题意得:四周的篱笆的长度等于平行四边形的四条边的长度之和,因为平行四边形对边长度相等,所以平行四边形周长=邻边长度之和×2.据此解答即可.【解答】解:(28.5+46)×2=74.5×2=149(米).答:围这个菜地需要149米长的篱笆.【点评】此题主要考查利用平行四边形的周长=邻边的和×2进行解决实际问题.23.【分析】根据三角形的两边之和大于第三边,两边之差小于第三边,进行分析解答即可.【解答】解:12﹣8<第三边<12+8,所以4<第三边<20,即第三边在4厘米~20厘米之间但不包括4厘米和20厘米,已知第三边长度是整厘米数,那么第三条边最短5厘米,最长19厘米.【点评】解答此题的关键是根据三角形的特性进行分析、解答即可.页2624.【分析】在三角形中,其中有一个角为钝角的三角形为钝角三角形;三个角都为锐角的三角形为锐角三角形;其中两条边都相等的三角形为等腰三角形;两组对边分别平行的四边形叫平行四边形;只有一组对边平行的四边形叫梯形,根据他们的意义画图即可.【解答】解:【点评】此题主要考查了常见的几种简单图形的定义以及画法.七.解答题(共4小题)25.【分析】长方形中最大的正方形的边长应等于长方形的宽,长方形的宽已知,由此得解.【解答】解:因为长方形中最大的正方形的边长应等于长方形的宽,所以正方形的边长为6厘米;答:正方形的边长是6厘米.【点评】解答此题的关键是明白:长方形中最大的正方形的边长应等于长方形的宽.页2726.【分析】根据角对三角形分类的方法:三个角都是锐角,这个三角形是锐角三角形;有一个角是钝角的三角形是钝角三角形;有一个角是直角的三角形是直角三角形,等腰三角形是有两条边相等的三角形;三条边都相等的三角形是等边三角形;解答即可.【解答】解:【点评】此题考查了根据角对三角形分类的方法:三个角都是锐角,这个三角形是锐角三角形;有一个角是钝角的三角形是钝角三角形;有一个角是直角的三角形是直角三角形,有两条边相等的三角形叫做等腰三角形.三条边都相等的三角形叫做等边三角形.27.【分析】依据等边三角形的性质可知,等边三角形的三条边相等,因此用27除以3就是这个等边三角形的边长.据此解答.【解答】解:27÷3=9(厘米);答:这个三角形的边长是9厘米的等边三角形.【点评】本题主要考查了学生对等边三角形三条边都相等知识的掌握.页2828.【分析】根据等腰三角形的特征可知:等腰三角形两腰相等,设腰长为x厘米,则底为(x+3)厘米,由此根据三角形的周长是36列出方程,解答即可.【解答】解:设腰长为x厘米,则底为(x+3)厘米,2x+(x+3)=362x+x+3=36x=1111+3=14(厘米)答:它的腰长是11厘米,底长是14厘米.【点评】此题根据等腰三角形的特征进行解答即可.页29页30。
2021年北师大版数学四下第二单元《认识三角形和四边形》章节知识点、达标训练附解析
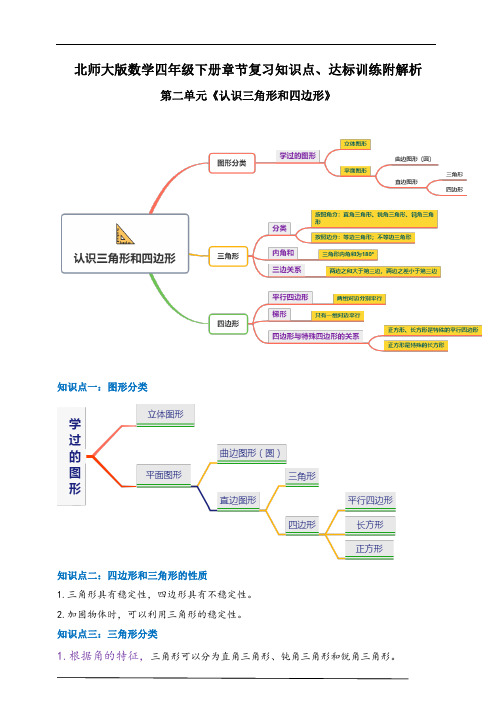
北师大版数学四年级下册章节复习知识点、达标训练附解析第二单元《认识三角形和四边形》知识点一:图形分类知识点二:四边形和三角形的性质1.三角形具有稳定性,四边形具有不稳定性。
2.加固物体时,可以利用三角形的稳定性。
知识点三:三角形分类1.根据角的特征,三角形可以分为直角三角形、钝角三角形和锐角三角形。
2.根据边的特征,三角形可以分为不等边三角形和等腰三角形。
3. 等腰三角形是两条边相等的三角形,等边三角形是三条边都相等的三角形,所以可以说所有的等边三角形都是等腰三角形,但不能说所有的等腰三角形都是等边三角形。
知识点四:三角形内角和1. 所有三角形的内角和都是180°。
每个三角形的所有内角都能拼成一个平角。
2. 已知三角形两个角的度数可以求出另外一个角的度数,进而确定三角形的形状。
3.已知三角形中一个角的度数,根据三角形内角和等于180°,可以求出另外两个角的度数和,并根据每个角的大小来判断这个三角形可能是什么三角形。
知识点五:三角形三边的关系1.三角形边的关系:三角形任意两边之和大于第三边。
2.判断三条线段能否围成三角形最简捷的方法:只要把较短的两条线段的和与最长的线段进行比较即可。
知识点六:四边形的分类1.四边形的分类:平行四边形、梯形和一般的四边形。
2.两组对边分别平行的四边形是平行四边形。
只有一组对边平行的四边形是梯形。
3. 正方形、长方形都是特殊的平行四边形;正方形是特殊的长方形。
一、精挑细选(共5题;每题3分,共15分)1. 两个完全相同的梯形一定能拼成一个()。
A. 梯形B. 长方形C. 平行四边形2. 一个三角形最多有()个钝角。
A. 1B. 2C. 33. 一个等腰三角形的一个角是30°,其它两个角分别是()。
A. 30°和120°B. 75°和75°C. 以上两种情况均有可能4. 如果三角形最小的一个内角大于45°,这个三角形一定是()三角形。
北师大四年级数学下册二 认识三角形和四边形1 图形分类试题(附答案)

二认识三角形和四边形
1 图形分类
重点导学
知识点:对已经学过的一些图形进行整理分类,了解这些图形的类别特征。
例题:给下面的图形分类。
点拨:进行图形分类的时候,我们既可以按照图形是否是平面图形来分,也可以按照图形是否由线段围成来分,还可以按照围成图形的边数来分。
【轻松通关】
一、把下面的图形进行分类。
(填序号)
1.平面图形有()。
2.立体图形有()。
3.由四条边围由成的图形有()。
4.由三条边围成的图形有()。
二、精挑细选。
(将正确答案的序号填在括号里)
1.四边形具有()的特性,三角形具有()的特性。
A.稳定
B.容易变形
2.下面的图形中,“最坚固”的图形是()。
A.长方形
B.正方形
C.三角形
D.梯形
三、想一想,连一连。
【能力晋级】
四、在下面的图形中任意画一条线段,使原来的图形变成两个三角形。
五、解决问题。
1.电线杆上的支架为什么要做成三角形?
2.学校的伸缩门为什么要做成平行四边形?
参考答案
一、1.①③⑤⑥⑦⑨⑩ 2. ②④⑧ 3.①③⑥⑨⑩ 4.⑦
二、1.BA 2.C
三、
四、略。
五、1. 因为三角形很稳定。
2.因为平行四边形容易变形,有伸缩性。
北师大版数学四年级下册-《认识三角形和四边形》达标测试卷

认识三角形和四边形一、填一填。
(每空1分,共18分)1.两条边相等的三角形是( )三角形,有一个角是90°的三角形是( )三角形。
2.红领巾,按角分属于( )三角形,按边分属于( )三角形。
3.用四个完全一样的等边三角形拼成一个大三角形,这个大三角形的内角和是( )。
4.( )和( )都是特殊的平行四边形。
5.将房屋的屋架做成三角形,是因为三角形具有( )。
6.在一个等腰三角形中,顶角的度数是90°,底角的度数是( )。
7.一个三角形三条边的长度分别为3厘米、3厘米、4厘米,按照边来分这是一个( )三角形,围成这个三角形需要( )厘米长的绳子。
8.一个三角形的两条边长分别是8厘米和5厘米,第三条边长必须比( )厘米大,比( )厘米小。
9.在直角三角形中,较大锐角的度数是较小锐角的2倍,两锐角分别是( )和( )。
10.一个等腰三角形的两条边的长度分别是3厘米和8厘米,这个等腰三角形的周长是( )厘米。
11.在一个三角形中,最多有( )个钝角,最少有( )个锐角。
二、选一选。
(每题2分,共12分)1.三个小朋友分别测量一个等腰三角形的边长,你能发现谁量错了吗?( )A.媛媛:腰长为2.5 cm,底边为5.5 cm。
B.君君:腰长为3.2 cm,底边为6 cm。
C.璐璐:腰长为4.7 cm,底边为6.2 cm。
2.在锐角三角形中,任意两个锐角的和一定( )90°。
A.小于B.等于C.大于3.一个三角形,如果它的两个内角的度数之和小于第三个内角的度数,那么它是( )三角形。
A.锐角B.直角C.钝角4.两个完全相同的梯形一定能拼成一个( )。
A.梯形B.平行四边形C.长方形5.把一个等边三角形平均分成两个直角三角形,其中一个直角三角形中的两个锐角分别是( )。
A.45°和45° B.60°和60° C.30°和60°6.一个三角形的下部被一张纸遮住了(如图),只露出了一个角,这个三角形是( )三角形。
数学四年级(下)认识三角形和四边形知识点总结练习题

数学四年级(下)认识三角形和四边形知识点总结练习题
认识三角形和四边形知识点总结+练习题
1、图形分类
2、三角形的特性
1、三角形内角和等于180。
2、三角形任意两边之和大于第三边。
3、三角形具有稳定性。
三、平行四边形、梯形的定义
平行四边形:两组对边分别平行的四边形叫平行四边形。
梯形:只有一组对边平行的四边形叫梯形。
四、四边形的特性
1、四边形不具有稳定性。
2、四边形内角和等于360。
五、等边三角形、等腰三角形、等腰直角三角形的关系
六、正方形、长方形、平行四边形的关系
七、练习题
1、算出下面各角的度数。
2、爸爸给小红买了一个等腰三角形的风筝,它的一个底角是70度,它的顶角是多少度?
3、把下面这个三角形沿虚线剪成两个小三角形,每个小三角形的内角和是多少度?
4、在能拼成三角形的各小组小棒下面画√(单位cm)。
5、下面的哪种篱笆更牢固为什么?
6、在点子图上按要求画图。
7、在下面各图中画一条直线。
能分成两个直角三角形的是图()
能分成两个钝角三角形的试图()
能分成一个直角三角形和一个锐角三角形的是图()
8、下面图形各是什么三角形?
9、下面哪组小棒能摆成等腰三角形?单位:cm。
北师大四年级数学下册《认识三角形和四边形》试题附答案(全套)

二认识三角形和四边形1 图形分类重点导学知识点:对已经学过的一些图形进行整理分类,了解这些图形的类别特征。
例题:给下面的图形分类。
点拨:进行图形分类的时候,我们既可以按照图形是否是平面图形来分,也可以按照图形是否由线段围成来分,还可以按照围成图形的边数来分。
【轻松通关】一、把下面的图形进行分类。
(填序号)1.平面图形有()。
2.立体图形有()。
3.由四条边围由成的图形有()。
4.由三条边围成的图形有()。
二、精挑细选。
(将正确答案的序号填在括号里)1.四边形具有()的特性,三角形具有()的特性。
A.稳定B.容易变形2.下面的图形中,“最坚固”的图形是()。
A.长方形B.正方形C.三角形D.梯形三、想一想,连一连。
【能力晋级】四、在下面的图形中任意画一条线段,使原来的图形变成两个三角形。
五、解决问题。
1.电线杆上的支架为什么要做成三角形?2.学校的伸缩门为什么要做成平行四边形?参考答案一、1.①③⑤⑥⑦⑨⑩ 2. ②④⑧ 3.①③⑥⑨⑩ 4.⑦二、1.BA 2.C三、四、略。
五、1. 因为三角形很稳定。
2.因为平行四边形容易变形,有伸缩性。
二认识三角形和四边形2 三角形分类重点导学知识点:会对三角形进行分类,并在分类中感受各类三角形之间的关系。
例题:把下面的图形进行分类。
(填序号)点拨:分类的时候,需要熟练掌握直角三角形、锐角三角形、钝角三角形、等腰三角形和等边三角形的特点。
【轻松通关】一、想一想,填一填。
1.三角形有()个角,()条边。
2.三角形按边分类可分为()三角形、()三角形、()三角形。
3.三角形按角分类可分为()三角形、()三角形、()三角形。
4.等边三角形又叫()三角形,它的三条边都(),三个角也(),每个角都是()度。
二、判断是非。
(对的画“√”,错的画“×”)1.由三条直线围成的图形叫做三角形。
()2.所有的等腰三角形都是锐角三角形。
()3.等腰三角形都是等边三角形。
()4.所有等边三角形都是等腰三角形而且都是锐角三角形。
第二单元 认识三角形和四边形(易错梳理)-四年级下册数学单元复习讲义 北师大版

认识三角形和四边形知识盘点知识点1:图形的分类立体图形圆(由曲线围成) 平面图形 三角形(3条边) 三角形、四边形 平行四边形(由线段围成) 四边形(4条边) 长方形正方形知识点2:三角形的认识1、 直角三角形:三个角都是锐角的三角形是锐角三角形 按角分 锐角三角形:有一个角是直角的三角形是直角三角形 三角形分类 钝角三角形:有一个角是钝角的三角形是钝角三角形 等腰三角形:有两条边相等的三角形是等腰三角形按边分 等边三角形:三条边都相等的三角形是等边三角形任意三角形 2、三角形内角和及三边关系① 任意一个三角形内角和等于180度。
② 三角形任意两边之和大于第三边。
已知两条边的长度,那么第三边的长度要大于已知两边之差小于两边只差。
知识点3:四边形的认识由四条线段围成的封闭图形叫作四边形。
四边形中有两组对边分别平行的四边形是平行四边形。
只由一组对边平行的四边形是梯形。
长方形、正方形是特殊的平行四边形。
正方形是特殊的长方形。
⭐注意易错集合易错点1:四边形的概念典例 判断:由四条线段组成的图形就是四边形。
( ) 解析 误认为只要四条线段组成的图形就是四边形,忽略了四条线段需要首尾相连。
解答 ×✨针对练习1你能解释为什么吗?易错点2:三角形的分类典例 猜一猜被遮挡住的可能是什么三角形?解析 直角三角形和钝角三角形都有两个锐角,可以根据露出的这个角是直角或钝角来判断是直角三角形还是钝角三角形;当露出来的角是锐角时,则无法直接断定是什么三角形。
解答 直角三角形 钝角三角形 可能是锐角三角形或直角三角形或钝角三角形⭐点拨 由四条线段首位顺次连接组成的封闭图形叫作四边形。
⭐点拨 四边形具有不稳定性,三角形具有稳定性。
✨针对练习2将下面的三角形进行分类(填写序号)锐角三角形有( );直角三角形有( );钝角三角形有( ); 等腰三角形有( );等边三角形( )。
易错点3:三角形的内角和问题 典例 求出图中三角形未知角的度数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一般平行四边形
17. 四边形
平行四边形:
长方形
(两组对边分别平行且相等的四边形) 正方形
特殊的平行四边形
一般四边形:
正方形是特殊的长方形
(有四条边)
(两组对边都不平行的四边形)
一般梯形
等腰梯形是轴对称图形
梯形: 等腰梯形:两条腰相等,同一底上的两个底角相等。
三个内角,那么这个三角形一定是(
)三角形。如果一个三角形两个内角的和等于第
三个内角,那么这个三角形一定是(
)三角形;如果一个三角形两个内角的和大于第
三个内角,那么这个三角形一定是(
)三角形
12.在一个三角形中,∠1=42°,∠2=29°,∠1=( )°。这是一个( )三角形。
13.在一个三角形的三个内角中,一个角是 50 度,一个角是 80 度,另一个角是(
直角三角形(有一个直角两个锐角) 按角分 锐角三角形(三个角都是锐角)
钝角三角形(有一个钝角两个锐角)
按边分
等边三角形(三条边都相等)是对称图形,有三条对称轴 等腰三角形(有两条边相等)是对称图形,有一条对称轴 不等边三角形(三条边都不相等)
8.三角形任意两边之和大于第三边。
9.由四条线段围成的封闭图形叫四边形 四边形内角和是 360°。
第二单元:认识三角形和四边形知识点及测试题
1.图形分为:立体图形和平面图形。
2.平面图形:a、圆(由曲线围成的图形)b、三角形、四边形、多边形(由线段围成的图 形)
3.三角形内角和是 180°。锐角:小于 90°的角是锐角。钝角:大于 90°的角是钝角。直角: 等于 90°的角是直角。 平角=180°; 周角=360°
3.三角形中三个角都相等的是( ( ),每个角都是( )度。
)三角形,又叫(
)三角形。它的三天边都
4.三角形按角分可以分为(
)(
)(
);按边分可以分为(
)
(
)(
)。三角形是(
)图形,圆球是( )图形。
5.三角形最多有( )直角,最多有( )钝角,最多有( )锐角,至少有( )个锐角。
6.( )条边相等的三角形是等腰三角形,( )条边都相等的三角形是等边三角形。
(只有一组对边平行的四边形) 直角梯形:一条腰垂直于的的梯形。
第二单元认识三角形和四边形测试题
一、 填空:
1.有一个角是直角的三角形是(
)有一个角是钝角的三角形是(
),三个角是
锐角的三角形是(
)。任何三角形都有( )个角,( )条边,( )顶角。
2.等腰三角形相等的两条边叫( 上的两个角叫( )。
),另一条边叫( );两腰的夹角叫( ),底边
能是(
)分米。B、一个三角形两条边的长度分别是 6 厘米和 9 厘米,那么第三条边
的长小于(
)厘米,大于(
)厘米。C、一个等腰三角形,三边之和是 24 分
米,那么它的一条边的长度是(
)分米。D、一个等腰三角形的底边和一条腰数位长
度分别是 4 厘米和 7 厘米,它的周长是(
)厘米。
17.由四条线段围成的图形叫( 四边形;(
);(
)叫梯形。
)叫平行
18.有一组邻边相等并且有一个角是直角的平行四边形叫做(
)
19.正方形的四个角都是(
),四条边都( )。正方形是特殊的( );(
)
(
)是特殊的平行四边形。
20.两个完全一样的三角形可以拼成一个(
个(
);拼一个长方形最少要(
(
)个相同的三角形。
),两个完全一样的梯形可以拼成一 )个相同的三角形,拼一个梯形最少要
10.正方形是特殊的长方形。 长方形和正方形是特殊的平行四边形。
11.平行四边形:两组对边分别平行且相等的四边形。
12.梯形:只有一组对边平行的四边形。
13.平行的两条边叫做梯形的底边,上面的一条叫上底,下面一条叫下底。
14.梯形的周长:上底+下底+腰+腰 梯形的面积:(上底+下底)×高÷2
1
15..根据三角形的边长判定三角形的类型: 较小两边的平方和小于最长边的平方 钝角三角形 较小两边的平方和等于最长边的平方 直角三角形 较小两边的平方和大于最长边的平方 钝角三角形
3
二、判断: 1.钝角三角形只有一个内角是钝角。( )等腰三角形一定是钝角三角形。( ) 2.有一个角是直角的三角形一定是直角三角形。( ) 3.四边形只包括长方形、正方形、梯形和平行四边形。( ) 4.等边三角形一定是锐角三角形。( ) 5.任意一个三角形中最少有两个锐角。( ) 6.等边三角形是特殊的等腰三角形。等边三角形都是等腰三角形。( ) 7.用 5 厘米、12 厘米和 7 厘米长的三条线段可以围成一个三角形。( ) 8.只有一组对边平行的四边形叫梯形。( ) 9.正方形是特殊的长方形,正方形和长方形是特殊的平行四边形。( ) 10.如果一个三角形两个内角的和小于第三个内角,这个三角形一定是钝角三角形( ) 11.一个三角形中最多有一个直角或钝角。( ) 12.用三根不一样长的小棒一定能围成一个三角形。( ) 13.平行四边形和梯形都是轴对称图形。平行四边形是特殊的长方形。( ) 14.所有的三角形内角和都一样。平行四边形的四个内角和等于 360 度。( ) 15.有一个角是锐角的三角形就是锐角三角形。( ) 16.房间的门都是长方形是因为平行四边形具有稳定性。( ) 17.有一个角是 60 度的等腰三角形是等边三角形。( ) 18.等腰三角形有可能是直角三角形。( )梯形中最多有两锐角,( ) 19.钝角三角形的两个锐角之和一定小于 90 度。( ) 20.梯形也是特殊的平行四边形。梯形中互相平行的一组对边相等。( ) 21.平行四边形的四个内角和等于 360 度。( ) 22.三角形最长的一条边有可能等于其他两边的和( )
4.等腰三角形相等的两条边叫做腰。等腰三角形两腰间的夹角叫顶角。腰与底边的夹角叫底 角。
5.等腰三角形包含:等腰三角形、等边三角形(又叫正三角形)、等腰直角三角形。
等边三角形是特殊的等腰三角形,它的每个内角都是 60°。
6.三角形不易变形具有稳定性。四边形易变形具有不稳定性.
7 .三角形 (有三条边)
2
7.三角形具有(
)性,而(
)易变形。
8.三角形的内角和是( ( )度,周角是(
)度,四边形的内角和是( )度。
)度。直角是( )度,平角是
9.小于 90°的角叫( ),大于 90°的角叫( ),等于 90°的角叫( )
10.等腰三角形的一个底角是 40°,它的顶角是(
)°。
11.一个直角与一个锐角的和一定是一个( )角。如果一个三角形两个内角的和小于第
)
度;这个三角形按角分是(
)三角形,按边分是( )三角形。
14.一个直角三角形,其中一个锐角是 35 度,另一个锐角是( )度。
15.三角形(
)大于第三边。5cm、5cm、6cm 的木棒围成的三角形是()三角形;
6cm、6cm、6cm 的木棒围成的一个三脚架,其中两条边的长分别是 4 分米和 6 分米,第三边的长度可
