勾股定理知识点+对应类型
勾股定理知识点归纳和题型归类

勾股定理知识点归纳和题型归类一.知识归纳1.勾股定理:直角三角形两直角边的平方和等于斜边的平方;表示方法:如果直角三角形的两直角边分别为a ,b ,斜边为c ,那么222a b c += 2.勾股定理的证明勾股定理的证明方法很多,常见的是拼图的方法,用拼图的方法验证勾股定理的思路是: ①图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理常见方法如下:方法一:4EFGH S S S ∆+=正方形正方形ABCD ,2214()2ab b a c ⨯+-=,化简可证. 方法二:四个直角三角形的面积与小正方形面积的和等于大正方形的面积. 四个直角三角形的面积与小正方形面积的和为221422S ab c ab c =⨯+=+ 大正方形面积为222()2S a b a ab b =+=++,所以222a b c += 方法三:1()()2S a b a b =+⋅+梯形,2112S 222ADE ABE S S ab c ∆∆=+=⋅+梯形,化简得证 3.勾股定理的适用范围勾股定理揭示了直角三角形三条边之间所存在的数量关系,它只适用于直角三角形,对于锐角三角形和钝角三角形的三边就不具有这一特征,因而在应用勾股定理时,必须明了所考察的对象是直角三角形4.勾股定理的应用①已知直角三角形的任意两边长,求第三边在ABC ∆中,90C ∠=︒,则c,b =,a②知道直角三角形一边,可得另外两边之间的数量关系③可运用勾股定理解决一些实际问题5.勾股定理的逆定理如果三角形三边长a ,b ,c 满足222a b c +=,那么这个三角形是直角三角形,其中c 为斜边①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状,在运用这一定理时,可用两小边的平方和22a b +与较长边的平方2c 作比较,若它们相等时,以a ,b ,c 为三边的三角形是直角三角形;若222a b c +<,时,以a ,b ,c 为三边的三角形是钝角三角形;若222a b c +>,时,以a ,b ,c 为三边的三角形是锐角三角形;c b a H G F E D C B A b a c b a c c a b c a b abc c b a E D C B A②定理中a ,b ,c 及222a b c +=只是一种表现形式,不可认为是唯一的,如若三角形三边长a ,b ,c 满足222a c b +=,那么以a ,b ,c 为三边的三角形是直角三角形,但是b 为斜边③勾股定理的逆定理在用问题描述时,不能说成:当斜边的平方等于两条直角边的平方和时,这个三角形是直角三角形6.勾股数①能够构成直角三角形的三边长的三个正整数称为勾股数,即222a b c +=中,a ,b ,c 为正整数时,称a ,b ,c 为一组勾股数②记住常见的勾股数可以提高解题速度,如3,4,5;6,8,10;5,12,13;7,24,25等 ③用含字母的代数式表示n 组勾股数:丢番图发现的:式子n m n m mn n m >+-(,2,2222的正整数)毕达哥拉斯发现的:122,22,1222++++n n n n n (1>n 的整数)柏拉图发现的:1,1,222+-n n n (1>n 的整数)7.勾股定理的应用勾股定理能够帮助我们解决直角三角形中的边长的计算或直角三角形中线段之间的关系的证明问题.在使用勾股定理时,必须把握直角三角形的前提条件,了解直角三角形中,斜边和直角边各是什么,以便运用勾股定理进行计算,应设法添加辅助线(通常作垂线),构造直角三角形,以便正确使用勾股定理进行求解.8..勾股定理逆定理的应用勾股定理的逆定理能帮助我们通过三角形三边之间的数量关系判断一个三角形是否是直角三角形,在具体推算过程中,应用两短边的平方和与最长边的平方进行比较,切不可不加思考的用两边的平方和与第三边的平方比较而得到错误的结论.9.勾股定理及其逆定理的应用勾股定理及其逆定理在解决一些实际问题或具体的几何问题中,是密不可分的一个整体.通常既要通过逆定理判定一个三角形是直角三角形,又要用勾股定理求出边的长度,二者相辅相成,完成对问题的解决.题型一:直接考查勾股定理例1.在ABC ∆中,90C ∠=︒.⑴已知6AC =,8BC =.求AB 的长⑵已知17AB =,15AC =,求BC 的长题型二:应用勾股定理建立方程例2.⑴在ABC ∆中,90ACB ∠=︒,5AB =cm ,3BC =cm ,CD AB ⊥于D ,CD = ⑵已知直角三角形的两直角边长之比为3:4,斜边长为15,则这个三角形的面积为 ⑶已知直角三角形的周长为30cm ,斜边长为13cm ,则这个三角形的面积为例3.如图ABC ∆中,90C ∠=︒,12∠=∠, 1.5CD =, 2.5BD =,求AC 的长 21E DCBA例4.如图Rt ABC ∆,90C ∠=︒3,4AC BC ==,分别以各边为直径作半圆,求阴影部分面积题型三:实际问题中应用勾股定理例5.如图有两棵树,一棵高8cm ,另一棵高2cm ,两树相距8cm ,一只小鸟从一棵树的树梢飞到另一棵数的树梢,至少飞了 m 。
初二数学下册勾股定理知识点及常考题型

初二数学下册勾股定理知识点及常考题型《勾股定理》知识点1:勾股定理直角三角形两直角边a、b的平方和等于斜边c的平方。
即:a²+b²=c²要点诠释:勾股定理反映了直角三角形三边之间的关系,是直角三角形的重要性质之一。
其主要应用:(1)已知直角三角形的两边求第三边;(2)已知直角三角形的一边与另两边的关系,求直角三角形的另两边; (3)利用勾股定理可以证明线段平方关系的问题。
2:勾股定理的逆定理如果三角形的三边长:a、b、c,则有关系a²+b²=c²,那么这个三角形是直角三角形。
要点诠释:勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状。
运用这一定理时应注意:(1)首先确定最大边,不妨设最长边长为:c;(2)验证c2与a2+b2是否具有相等关系,若c²=a²+b²,则△ABC是以∠C 为直角的直角三角形(若c²>a²+b²,则△ABC是以∠C为钝角的钝角三角形;若c²<a²+b²,则△ABC为锐角三角形)。
3:勾股定理与勾股定理逆定理的区别与联系区别:勾股定理是直角三角形的性质定理,而其逆定理是判定定理;联系:勾股定理与其逆定理的题设和结论正好相反,都与直角三角形有关。
4:互逆命题的概念如果一个命题的题设和结论分别是另一个命题的结论和题设,这样的两个命题叫做互逆命题。
如果把其中一个叫做原命题,那么另一个叫做它的逆命题。
5:勾股定理的证明勾股定理的证明方法很多,常见的是拼图的方法用拼图的方法验证勾股定理的思路是:①图形经过割补拼接后,只要没有重叠,没有空隙,面积不会改变;②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理。
《勾股定理》常考题1、用对称法求平面中最短问题如图,在正方形ABCD中,AB边上有一点E,AE=3,EB=1,在AC上有一点P,使EP+BP最短,求EP+BP的最短长度.解:如图,连接BD交AC于O,连接ED与AC交于点P,连接BP.已知BD⊥AC,且BO=OD,∴BP=PD,则BP+EP=ED,此时最短.∵AE=3,AD=1+3=4,由勾股定理得ED2=AE2+AD2=32+42=25=52∴ED=BP +EP=5.2、用平移法求平面中最短问题如图是一个三级台阶,它的每一级的长、宽和高分别是50 cm,30 cm,10 cm,A和B是这个台阶的两个相对的端点,A点上有一只壁虎,它想到B点去吃可口的食物,请你想一想,这只壁虎从A点出发,沿着台阶面爬到B点,至少需爬几厘米?将台阶面展开,连接AB,如图,线段AB即为壁虎所爬的最短路线.∵BC=30×3+10×3=120(cm),AC=50 cm,在Rt△ABC中,根据勾股定理,得AB2=AC2+BC2=16 900,∴AB=130 cm.所以壁虎至少爬行130 cm.3、利用勾股定理证明线段之间的平方关系如图,∠C=90°,AM=CM,MP⊥AB于点P.求证:BP2=BC2+AP2.证明:如图,连接BM.∵PM⊥AB,∴△BMP和△AMP均为直角三角形.∴BP2+PM2=BM2,AP2+PM2=AM2.同理可得BC2+CM2=BM2.∴BP2+PM2=BC2+CM2.又∵CM=AM,∴CM2=AM2=AP2+PM2.∴BP2+PM2=BC2+AP2+PM2.∴BP2=BC2+AP2.。
勾股定理知识点+对应类型
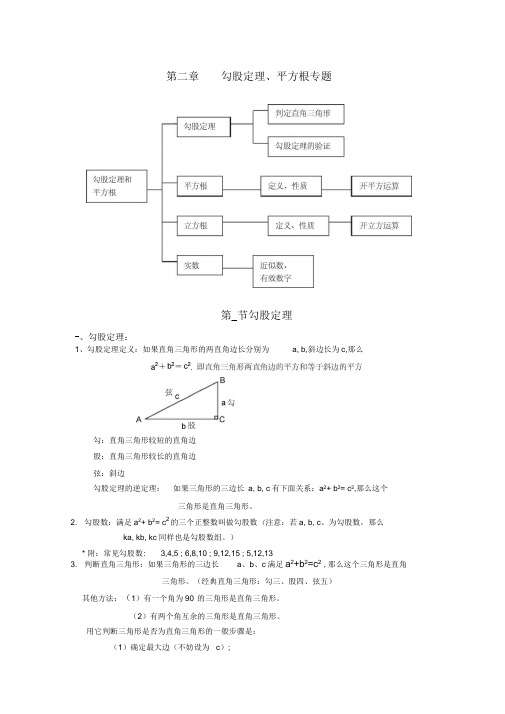
第二章勾股定理、平方根专题第_节勾股定理-、勾股定理:1、勾股定理定义:如果直角三角形的两直角边长分别为a, b,斜边长为c,那么勾:直角三角形较短的直角边股:直角三角形较长的直角边弦:斜边勾股定理的逆定理:如果三角形的三边长a, b, c有下面关系:a2+ b2= c2,那么这个三角形是直角三角形。
2. 勾股数:满足a2+ b2= c2的三个正整数叫做勾股数(注意:若a, b, c、为勾股数,那么ka, kb, kc同样也是勾股数组。
)* 附:常见勾股数: 3,4,5 ; 6,8,10 ; 9,12,15 ; 5,12,133. 判断直角三角形:如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形。
(经典直角三角形:勾三、股四、弦五)其他方法:(1)有一个角为90°的三角形是直角三角形。
(2)有两个角互余的三角形是直角三角形。
用它判断三角形是否为直角三角形的一般步骤是:(1)确定最大边(不妨设为c);(2) 若c2= a2+ b2,则^ ABC是以Z C为直角的三角形;若a2 + b2v c2,则此三角形为钝角三角形(其中c为最大边);若a2 + b2> c2,则此三角形为锐角三角形(其中c为最大边)4. 注意:(1)直角三角形斜边上的中线等于斜边的一半(2)在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的(3) 在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°。
5. 勾股定理的作用:(1) 已知直角三角形的两边求第三边。
(2) 已知直角三角形的一边,求另两边的关系。
(3) 用于证明线段平方关系的问题。
(4) 利用勾股定理,作出长为际的线段二、平方根:(11——19的平方)1、平方根定义:如果一个数的平方等于a,那么这个数就叫做a的平方根。
(也称为二次方根),也就是说如果x2=a,那么x就叫做a的平方根。
勾股定理知识点与常见题型总结

勾股定理复习一.知识归纳 1.勾股定理内容:直角三角形两直角边的平方和等于斜边的平方;表示方法:如果直角三角形的两直角边分别为a ,b ,斜边为c ,那么222a b c += 2.勾股定理的证明勾股定理的证明方法很多,常见的是拼图的方法 用拼图的方法验证勾股定理的思路是①图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变 ②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理 常见方法如下: 方法一:4EFGHS S S ∆+=正方形正方形ABCD ,2214()2ab b a c ⨯+-=,化简可证.方法二:四个直角三角形的面积与小正方形面积的和等于大正方形的面积.四个直角三角形的面积与小正方形面积的和为221422S ab c ab c =⨯+=+大正方形面积为222()2S a b a ab b =+=++ 所以222a b c +=方法三:1()()2S a b a b =+⋅+梯形,2112S 222ADE ABE S S ab c ∆∆=+=⋅+梯形,化简得证3.勾股定理的适用范围勾股定理揭示了直角三角形三条边之间所存在的数量关系,它只适用于直角三角形, 4.勾股定理的应用①已知直角三角形的任意两边长,求第三边在ABC ∆中,90C ∠=︒,则c,b =,a ②知道直角三角形一边,可得另外两边之间的数量关系 ③可运用勾股定理解决一些实际问题 5.勾股定理的逆定理如果三角形三边长a ,b ,c 满足222a b c +=,那么这个三角形是直角三角形,其中c 为斜边 ① 勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法, ② 若222a b c +<,时,以a ,b ,c 为三边的三角形是钝角三角形; ③ 若222a b c +>,时,以a ,b ,c 为三边的三角形是锐角三角形; 6.勾股数①能够构成直角三角形的三边长的三个正整数称为勾股数,即222a b c +=中,a ,b ,c 为正整数时,称a ,b ,c 为一组勾股数②记住常见的勾股数可以提高解题速度,如3,4,5;6,8,10;5,12,13;7,24,25等 ③用含字母的代数式表示n 组勾股数:cba HG F EDCBA bacba c ca bcab a bc c baE D CBA221,2,1n n n -+(2,n ≥n 为正整数); 2221,22,221n n n n n ++++(n 为正整数) 2222,2,m n mn m n -+(,m n >m ,n 为正整数)7.勾股定理的应用勾股定理能够帮助我们解决直角三角形中的边长的计算或直角三角形中线段之间的关系的证明问题. 8..勾股定理逆定理的应用勾股定理的逆定理能帮助我们通过三角形三边之间的数量关系判断一个三角形是否是直角三角形9.勾股定理及其逆定理的应用勾股定理及其逆定理在解决一些实际问题或具体的几何问题中,是密不可分的一个整体.通常既要通过逆定理判定一个三角形是直角三角形,又要用勾股定理求出边的长度,二者相辅相成,完成对问题的解决. 常见图形:题型一:直接考查勾股定理 例1.在ABC ∆中,90C ∠=︒.⑴已知6AC =,8BC =.求AB 的长 ⑵已知17AB =,15AC =,求BC 的长题型二:应用勾股定理建立方程例2.⑴在ABC ∆中,90ACB ∠=︒,5AB =cm ,3BC =cm ,CD AB ⊥于D ,CD = ⑵已知直角三角形的两直角边长之比为3:4,斜边长为15,则这个三角形的面积为 ⑶已知直角三角形的周长为30cm ,斜边长为13cm ,则这个三角形的面积为 2cm例3.如图ABC ∆中,90C ∠=︒,12∠=∠, 1.5CD =, 2.5BD =,求AC 的长例 4.如图Rt ABC ∆,90C ∠=︒3,4AC BC ==,分别以各边为直径作半圆,求阴影部分面积ABC30°DCB A ADBCCB DA21EDCBA题型三:实际问题中应用勾股定理例5.如图有两棵树,一棵高8cm ,另一棵高2cm ,两树相距8cm ,一只小鸟从一棵树的树梢飞到另一棵数的树梢,至少飞了 m题型四:应用勾股定理逆定理,判定一个三角形是否是直角三角形例6.已知三角形的三边长为a ,b ,c ,判定ABC ∆是否为Rt ∆ ① 1.5a =,2b =, 2.5c = ②54a =,1b =,23c =题型五:勾股定理与勾股定理的逆定理综合应用例8.已知ABC ∆中,13AB =cm ,10BC =cm ,BC 边上的中线12AD =cm ,求证:AB AC =勾股定理练习一.填空题:1. 在Rt △ABC 中,∠C=90°(1)若a=5,b=12,则c=________; (2)b=8,c=17,则S △ABC =________。
勾股定理(知识点+题型分类练习)

ABCabc弦股勾勾股定理(知识点)【知识要点】1. 勾股定理的概念:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么 a2+b2=c2. 即直角三角形两直角边的平方和等于斜边的平方。
常用关系式由三角形面积公式可得:AB·CD=AC·BC2. 勾股定理的逆定理:如果三角形的三边长a,b,c有下面关系:a2+b2=c2,那么这个三角形是直角三角形,其中c为斜边。
3. 勾股数:①满足a2+b2=c2的三个正整数叫做勾股数(注意:若a,b,c、为勾股数,那么ka,kb,kc同样也是勾股数组。
)②记住常见的勾股数可以提高解题速度,如3,4,5;6,8,10;5,12,13;7,24,25;8,15,17等③用含字母的代数式表示n组勾股数:221,2,1n n n -+(2,n ≥n 为正整数); 2221,22,221n n n n n ++++(n 为正整数)2222,2,m n mn m n -+(,m n >m ,n 为正整数)4.判断直角三角形:(1)有一个角为90°的三角形是直角三角形。
(2)有两个角互余的三角形是直角三角形。
(3)如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
(4)如果三角形的三边长a 、b 、c 满足a 2+b 2=c 2 ,那么这个三角形是直角三角形。
(经典直角三角形:勾三、股四、弦五)用勾股定理逆定理判断三角形是否为直角三角形的一般步骤是: (1)确定最大边(不妨设为c );(2)若c 2=a 2+b 2,则△ABC 是以∠C 为直角的三角形;若a 2+b 2<c 2,则此三角形为钝角三角形(其中c 为最大边); 若a 2+b 2>c 2,则此三角形为锐角三角形(其中c 为最大边)5.直角三角形的性质(1)直角三角形的两个锐角互余。
可表示如下:∠C=90°⇒∠A+∠B=90°B(2)在直角三角形中,30°角所对的直角边等于斜边的一半。
勾股定理知识点与常见题型总结

第18章 勾股定理复习一.知识归纳1.勾股定理内容:直角三角形两直角边的平方和等于斜边的平方;表示方法:如果直角三角形的两直角边分别为a ,b ,斜边为c ,那么222a b c +=勾股定理的由来:勾股定理也叫商高定理,在西方称为毕达哥拉斯定理.我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.早在三千多年前,周朝数学家商高就提出了“勾三,股四,弦五”形式的勾股定理,后来人们进一步发现并证明了直角三角形的三边关系为:两直角边的平方和等于斜边的平方2.勾股定理的证明勾股定理的证明方法很多,常见的是拼图的方法用拼图的方法验证勾股定理的思路是①图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理常见方法如下:方法一:4EFGH S S S ∆+=正方形正方形ABCD ,2214()2ab b a c ⨯+-=,化简可证. c ba HG FEDCB A方法二:b ac b a cca b c a b四个直角三角形的面积与小正方形面积的和等于大正方形的面积. 四个直角三角形的面积与小正方形面积的和为221422S ab c ab c =⨯+=+ 大正方形面积为222()2S a b a ab b =+=++所以222a b c +=方法三:1()()2S a b a b =+⋅+梯形,2112S 222ADE ABE S S ab c ∆∆=+=⋅+梯形,化简得证a b ccb a E DCB A3.勾股定理的适用范围勾股定理揭示了直角三角形三条边之间所存在的数量关系,它只适用于直角三角形,对于锐角三角形和钝角三角形的三边就不具有这一特征,因而在应用勾股定理时,必须明了所考察的对象是直角三角形 4.勾股定理的应用①已知直角三角形的任意两边长,求第三边在ABC ∆中,90C ∠=︒,则c,b =,a②知道直角三角形一边,可得另外两边之间的数量关系③可运用勾股定理解决一些实际问题5.勾股定理的逆定理如果三角形三边长a ,b ,c 满足222a b c +=,那么这个三角形是直角三角形,其中c 为斜边①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状,在运用这一定理时,可用两小边的平方和22a b +与较长边的平方2c 作比较,若它们相等时,以a ,b ,c 为三边的三角形是直角三角形;若222a b c +<,时,以a ,b ,c 为三边的三角形是钝角三角形;若222a b c +>,时,以a ,b ,c 为三边的三角形是锐角三角形;②定理中a ,b ,c 及222a b c +=只是一种表现形式,不可认为是唯一的,如若三角形三边长a ,b ,c 满足222a c b +=,那么以a ,b ,c 为三边的三角形是直角三角形,但是b 为斜边③勾股定理的逆定理在用问题描述时,不能说成:当斜边的平方等于两条直角边的平方和时,这个三角形是直角三角形6.勾股数①能够构成直角三角形的三边长的三个正整数称为勾股数,即222a b c +=中,a ,b ,c 为正整数时,称a ,b ,c 为一组勾股数②记住常见的勾股数可以提高解题速度,如3,4,5;6,8,10;5,12,13;7,24,25等③用含字母的代数式表示n 组勾股数:221,2,1n n n -+(2,n ≥n 为正整数);2221,22,221n n n n n ++++(n 为正整数)2222,2,m n mn m n -+(,m n >m ,n 为正整数)7.勾股定理的应用勾股定理能够帮助我们解决直角三角形中的边长的计算或直角三角形中线段之间的关系的证明问题.在使用勾股定理时,必须把握直角三角形的前提条件,了解直角三角形中,斜边和直角边各是什么,以便运用勾股定理进行计算,应设法添加辅助线(通常作垂线),构造直角三角形,以便正确使用勾股定理进行求解.8..勾股定理逆定理的应用勾股定理的逆定理能帮助我们通过三角形三边之间的数量关系判断一个三角形是否是直角三角形,在具体推算过程中,应用两短边的平方和与最长边的平方进行比较,切不可不加思考的用两边的平方和与第三边的平方比较而得到错误的结论.9.勾股定理及其逆定理的应用勾股定理及其逆定理在解决一些实际问题或具体的几何问题中,是密不可分的一个整体.通常既要通过逆定理判定一个三角形是直角三角形,又要用勾股定理求出边的长度,二者相辅相成,完成对问题的解决. 常见图形:A B C 30°D CB A AD B CCB D A题型一:直接考查勾股定理例1.在ABC ∆中,90C ∠=︒.⑴已知6AC =,8BC =.求AB 的长⑵已知17AB =,15AC =,求BC 的长分析:直接应用勾股定理222a b c +=解:⑴10AB⑵8BC ==题型二:应用勾股定理建立方程例2.⑴在ABC ∆中,90ACB ∠=︒,5AB =cm ,3BC =cm ,CD AB ⊥于D ,CD =⑵已知直角三角形的两直角边长之比为3:4,斜边长为15,则这个三角形的面积为⑶已知直角三角形的周长为30cm ,斜边长为13cm ,则这个三角形的面积为分析:在解直角三角形时,要想到勾股定理,及两直角边的乘积等于斜边与斜边上高的乘积.有时可根据勾股定理列方程求解解:⑴4AC , 2.4AC BC CD AB⋅== DB A C⑵设两直角边的长分别为3k ,4k ∴222(3)(4)15k k +=,3k ∴=,54S =⑶设两直角边分别为a ,b ,则17a b +=,22289a b +=,可得60ab =1302S ab ∴==2cm 例3.如图ABC ∆中,90C ∠=︒,12∠=∠, 1.5CD =, 2.5BD =,求AC 的长21DCBA分析:此题将勾股定理与全等三角形的知识结合起来解:作DE AB ⊥于E ,12∠=∠,90C ∠=︒∴ 1.5DE CD ==在BDE ∆中90,2BED BE ∠=︒=Rt ACD Rt AED ∆≅∆AC AE ∴=在Rt ABC ∆中,90C ∠=︒222AB AC BC ∴=+,222()4AE EB AC +=+3AC ∴=例4.如图Rt ABC ∆,90C ∠=︒3,4AC BC ==,分别以各边为直径作半圆,求阴影部分面积答案:6题型三:实际问题中应用勾股定理例5.如图有两棵树,一棵高8cm ,另一棵高2cm ,两树相距8cm ,一只小鸟从一棵树的树梢飞到另一棵数的树梢,至少飞了 mAB CD E分析:根据题意建立数学模型,如图8AB =m ,2CD =m ,8BC =m ,过点D 作DE AB ⊥,垂足为E ,则6AE =m ,8DE =m在Rt ADE ∆中,由勾股定理得10AD =答案:10m题型四:应用勾股定理逆定理,判定一个三角形是否是直角三角形例6.已知三角形的三边长为a ,b ,c ,判定ABC ∆是否为Rt ∆ ① 1.5a =,2b =, 2.5c = ②54a =,1b =,23c = 解:①22221.52 6.25a b +=+=,222.5 6.25c ==∴ABC ∆是直角三角形且90C ∠=︒ ②22139b c +=,22516a =,222bc a +≠ABC ∴∆不是直角三角形 例7.三边长为a ,b ,c 满足10a b +=,18ab =,8c =的三角形是什么形状? 解:此三角形是直角三角形 理由:222()264a b a b ab +=+-=,且264c =222a b c ∴+= 所以此三角形是直角三角形题型五:勾股定理与勾股定理的逆定理综合应用例8.已知ABC ∆中,13AB =cm ,10BC =cm ,BC 边上的中线12AD =cm ,求证:AB AC =证明:D CB AAD 为中线,5BD DC ∴==cm在ABD ∆中,22169AD BD +=,2169AB =222AD BD AB ∴+=, 90ADB ∴∠=︒,222169AC AD DC ∴=+=,13AC =cm ,AB AC ∴=。
八年级数学《勾股定理》知识点

八年级数学《勾股定理》知识点一、勾股定理:1、勾股定理定义:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2. 即直角三角形两直角边的平方和等于斜边的平方ABCabc弦股勾勾:直角三角形较短的直角边股:直角三角形较长的直角边弦:斜边勾股定理的逆定理:如果三角形的三边长a,b,c有下面关系:a2+b2=c2,那么这个三角形是直角三角形。
2. 勾股数:满足a2+b2=c2的三个正整数叫做勾股数(注意:若a,b,c、为勾股数,那么ka,kb,kc同样也是勾股数组。
)*附:常见勾股数:3,4,5; 6,8,10; 9,12,15; 5,12,133. 判断直角三角形:如果三角形的三边长a、b、c满足a2+b2=c2 ,那么这个三角形是直角三角形。
(经典直角三角形:勾三、股四、弦五)其他方法:(1)有一个角为90°的三角形是直角三角形。
(2)有两个角互余的三角形是直角三角形。
用它判断三角形是否为直角三角形的一般步骤是:(1)确定最大边(不妨设为c);(2)若c2=a2+b2,则△ABC是以∠C为直角的三角形;若a2+b2<c2,则此三角形为钝角三角形(其中c为最大边);若a2+b2>c2,则此三角形为锐角三角形(其中c为最大边)4.注意:(1)直角三角形斜边上的中线等于斜边的一半(2)在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
(3)在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°。
5. 勾股定理的作用:(1)已知直角三角形的两边求第三边。
(2)已知直角三角形的一边,求另两边的关系。
(3)用于证明线段平方关系的问题。
(4)利用勾股定理,作出长为n的线段1。
勾股定理知识点与常见题型总结

勾股定理复习一.知识归纳1.勾股定理内容:直角三角形两直角边的平方和等于斜边的平方;表示方法:如果直角三角形的两直角边分别为a ,b ,斜边为c ,那么222a b c +=勾股定理的由来:勾股定理也叫商高定理,在西方称为毕达哥拉斯定理.我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.早在三千多年前,周朝数学家商高就提出了“勾三,股四,弦五”形式的勾股定理,后来人们进一步发现并证明了直角三角形的三边关系为:两直角边的平方和等于斜边的平方2.勾股定理的证明勾股定理的证明方法很多,常见的是拼图的方法用拼图的方法验证勾股定理的思路是①图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理常见方法如下:方法一:4EFGH S S S ∆+=正方形正方形ABCD ,2214()2ab b a c ⨯+-=,化简可证. c ba HG FEDCB A方法二:b ac b a cca b c a b四个直角三角形的面积与小正方形面积的和等于大正方形的面积. 四个直角三角形的面积与小正方形面积的和为221422S ab c ab c =⨯+=+ 大正方形面积为222()2S a b a ab b =+=++所以222a b c +=方法三:1()()2S a b a b =+⋅+梯形,2112S 222ADE ABE S S ab c ∆∆=+=⋅+梯形,化简得证a b ccb a E DCB A3.勾股定理的适用范围勾股定理揭示了直角三角形三条边之间所存在的数量关系,它只适用于直角三角形,对于锐角三角形和钝角三角形的三边就不具有这一特征,因而在应用勾股定理时,必须明了所考察的对象是直角三角形 4.勾股定理的应用①已知直角三角形的任意两边长,求第三边在ABC ∆中,90C ∠=︒,则c,b =,a②知道直角三角形一边,可得另外两边之间的数量关系③可运用勾股定理解决一些实际问题5.勾股定理的逆定理如果三角形三边长a ,b ,c 满足222a b c +=,那么这个三角形是直角三角形,其中c 为斜边①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状,在运用这一定理时,可用两小边的平方和22a b +与较长边的平方2c 作比较,若它们相等时,以a ,b ,c 为三边的三角形是直角三角形;若222a b c +<,时,以a ,b ,c 为三边的三角形是钝角三角形;若222a b c +>,时,以a ,b ,c 为三边的三角形是锐角三角形;②定理中a ,b ,c 及222a b c +=只是一种表现形式,不可认为是唯一的,如若三角形三边长a ,b ,c 满足222a c b +=,那么以a ,b ,c 为三边的三角形是直角三角形,但是b 为斜边③勾股定理的逆定理在用问题描述时,不能说成:当斜边的平方等于两条直角边的平方和时,这个三角形是直角三角形6.勾股数①能够构成直角三角形的三边长的三个正整数称为勾股数,即222a b c +=中,a ,b ,c 为正整数时,称a ,b ,c 为一组勾股数②记住常见的勾股数可以提高解题速度,如3,4,5;6,8,10;5,12,13;7,24,25等③用含字母的代数式表示n 组勾股数:221,2,1n n n -+(2,n ≥n 为正整数);2221,22,221n n n n n ++++(n 为正整数)2222,2,m n mn m n -+(,m n >m ,n 为正整数)7.勾股定理的应用勾股定理能够帮助我们解决直角三角形中的边长的计算或直角三角形中线段之间的关系的证明问题.在使用勾股定理时,必须把握直角三角形的前提条件,了解直角三角形中,斜边和直角边各是什么,以便运用勾股定理进行计算,应设法添加辅助线(通常作垂线),构造直角三角形,以便正确使用勾股定理进行求解.8..勾股定理逆定理的应用勾股定理的逆定理能帮助我们通过三角形三边之间的数量关系判断一个三角形是否是直角三角形,在具体推算过程中,应用两短边的平方和与最长边的平方进行比较,切不可不加思考的用两边的平方和与第三边的平方比较而得到错误的结论.9.勾股定理及其逆定理的应用勾股定理及其逆定理在解决一些实际问题或具体的几何问题中,是密不可分的一个整体.通常既要通过逆定理判定一个三角形是直角三角形,又要用勾股定理求出边的长度,二者相辅相成,完成对问题的解决. 常见图形:A B C 30°D CB A AD B CCB D A题型一:直接考查勾股定理例1.在ABC ∆中,90C ∠=︒.⑴已知6AC =,8BC =.求AB 的长⑵已知17AB =,15AC =,求BC 的长分析:直接应用勾股定理222a b c +=解:⑴10AB⑵8BC ==题型二:应用勾股定理建立方程例2.⑴在ABC ∆中,90ACB ∠=︒,5AB =cm ,3BC =cm ,CD AB ⊥于D ,CD =⑵已知直角三角形的两直角边长之比为3:4,斜边长为15,则这个三角形的面积为⑶已知直角三角形的周长为30cm ,斜边长为13cm ,则这个三角形的面积为分析:在解直角三角形时,要想到勾股定理,及两直角边的乘积等于斜边与斜边上高的乘积.有时可根据勾股定理列方程求解解:⑴4AC , 2.4AC BC CD AB⋅== DB A C⑵设两直角边的长分别为3k ,4k ∴222(3)(4)15k k +=,3k ∴=,54S =⑶设两直角边分别为a ,b ,则17a b +=,22289a b +=,可得60ab =1302S ab ∴==2cm 例3.如图ABC ∆中,90C ∠=︒,12∠=∠, 1.5CD =, 2.5BD =,求AC 的长21E DCBA分析:此题将勾股定理与全等三角形的知识结合起来解:作DE AB ⊥于E ,12∠=∠,90C ∠=︒∴ 1.5DE CD ==在BDE ∆中90,2BED BE ∠=︒=Rt ACD Rt AED ∆≅∆AC AE ∴=在Rt ABC ∆中,90C ∠=︒222AB AC BC ∴=+,222()4AE EB AC +=+3AC ∴=例4.如图Rt ABC ∆,90C ∠=︒3,4AC BC ==,分别以各边为直径作半圆,求阴影部分面积答案:6题型三:实际问题中应用勾股定理例5.如图有两棵树,一棵高8cm ,另一棵高2cm ,两树相距8cm ,一只小鸟从一棵树的树梢飞到另一棵数的树梢,至少飞了 mAB CD E分析:根据题意建立数学模型,如图8AB =m ,2CD =m ,8BC =m ,过点D 作DE AB ⊥,垂足为E ,则6AE =m ,8DE =m在Rt ADE ∆中,由勾股定理得10AD ==答案:10m题型四:应用勾股定理逆定理,判定一个三角形是否是直角三角形例6.已知三角形的三边长为a ,b ,c ,判定ABC ∆是否为Rt ∆ ① 1.5a =,2b =, 2.5c = ②54a =,1b =,23c = 解:①22221.52 6.25a b +=+=,222.5 6.25c ==∴ABC ∆是直角三角形且90C ∠=︒ ②22139b c +=,22516a =,222bc a +≠ABC ∴∆不是直角三角形 例7.三边长为a ,b ,c 满足10a b +=,18ab =,8c =的三角形是什么形状? 解:此三角形是直角三角形 理由:222()264a b a b ab +=+-=,且264c =222a b c ∴+= 所以此三角形是直角三角形题型五:勾股定理与勾股定理的逆定理综合应用例8.已知ABC ∆中,13AB =cm ,10BC =cm ,BC 边上的中线12AD =cm ,求证:AB AC =证明:D CB AAD 为中线,5BD DC ∴==cm在ABD ∆中,22169AD BD +=,2169AB =222AD BD AB ∴+=, 90ADB ∴∠=︒,222169AC AD DC ∴=+=,13AC =cm ,AB AC ∴=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章勾股定理、平方根专题第一节勾股定理一、勾股定理:1、勾股定理定义:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2. 即直角三角形两直角边的平方和等于斜边的平方ABCabc弦股勾勾:直角三角形较短的直角边股:直角三角形较长的直角边弦:斜边勾股定理的逆定理:如果三角形的三边长a,b,c有下面关系:a2+b2=c2,那么这个三角形是直角三角形。
2. 勾股数:满足a2+b2=c2的三个正整数叫做勾股数(注意:若a,b,c、为勾股数,那么ka,kb,kc同样也是勾股数组。
)*附:常见勾股数:3,4,5; 6,8,10; 9,12,15; 5,12,133. 判断直角三角形:如果三角形的三边长a、b、c满足a2+b2=c2 ,那么这个三角形是直角三角形。
(经典直角三角形:勾三、股四、弦五)其他方法:(1)有一个角为90°的三角形是直角三角形。
(2)有两个角互余的三角形是直角三角形。
用它判断三角形是否为直角三角形的一般步骤是:(1)确定最大边(不妨设为c);(2)若c 2=a 2+b 2,则△ABC 是以∠C 为直角的三角形; 若a 2+b 2<c 2,则此三角形为钝角三角形(其中c 为最大边); 若a 2+b 2>c 2,则此三角形为锐角三角形(其中c 为最大边)4.注意:(1)直角三角形斜边上的中线等于斜边的一半(2)在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
(3)在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°。
5. 勾股定理的作用:(1)已知直角三角形的两边求第三边。
(2)已知直角三角形的一边,求另两边的关系。
(3)用于证明线段平方关系的问题。
(4)利用勾股定理,作出长为n 的线段二、平方根:(11——19的平方)1、平方根定义:如果一个数的平方等于a ,那么这个数就叫做a 的平方根。
(也称为二次方根),也就是说如果x 2=a ,那么x 就叫做a 的平方根。
2、平方根的性质:①一个正数有两个平方根,它们互为相反数;一个正数a 的正的平方根,记作“a ”,又叫做算术平方根,它负的平方根,记作“—a ”,这两个平方根合起来记作“±a ”。
( a 叫被开方数, “”是二次根号,这里“”,亦可写成“2”)②0只有一个平方根,就是0本身。
算术平方根是0。
③负数没有平方根。
3、 开平方:求一个数的平方根的运算叫做开平方,开平方和平方运算互为逆运算。
4、(1) 平方根是它本身的数是零。
(2)算术平方根是它本身的数是0和1。
(3)()()()().0,0,0222<-=≥=≥=a a a a a a a a a(4)一个数的两个平方根之和为0三、立方根:(1——9的立方)1、立方根的定义:如果一个数的立方等于a ,那么这个数就叫做a 的立方根。
(也称为二次方根),也就是说如果x 3=a ,那么x 就叫做a 的立方根。
记作“3a ”。
2、立方根的性质:①任何数都有立方根,并且只有一个立方根,正数的立方根是正数,负数的立方根是负数,0的立方根是0. ②互为相反数的数的立方根也互为相反数,即3a -=3a - ③a a a ==3333)(3、开立方:求一个数的立方根的运算叫做开立方,开立方与立方运算为互逆运算,开立方的运算结果是立方根。
4、立方根是它本身的数是1,0,-1。
5、平方根和立方根的区别:(1)被开方数的取值范围不同:在±a 中,a ≥0,在a 3中,a 可以为任意数值。
(2)正数的平方根有两个,而它的立方根只有一个;负数没有平方根,而它有一个立方根。
6、立方根和平方根:不同点:(1)任何数都有立方根,正数和0有平方根,负数没有平方根;即被开方数的取值范围不同:±a 中的被开方数a 是非负数;3a 中的被开方数可以是任何数.(2)正数有两个平方根,任何数都有惟一的立方根;(3)立方根等于本身的数有0、1、—1,平方根等于本身的数只有0. 共同点:0的立方根和平方根都是0. 四、实数:1、定义:有理数和无理数统称为实数无理数:无限不循环小数称(包括所有开方开不尽的数,∏)。
有理数:有限小数或无限循环小数注意:分数都是有理数,因为任何一个分数都可以化为有限小数或无限循环小数的形式 2、实数的分类:实数有理数正有理数零负有理数有限小数或无限循环小数无理数正无理数负无理数无限不循环小数⎧⎨⎪⎩⎪⎫⎬⎪⎪⎭⎪⎪⎧⎨⎪⎩⎪⎫⎬⎪⎭⎪⎧⎨⎪⎪⎪⎪⎩⎪⎪⎪⎪实数的性质:①实数的相反数、倒数、绝对值的意义与在有理数范围内的意义是一样的。
②实数同有理数一样,可用数轴上的点表示,且实数和数轴上的点一一对应。
③两个实数可以按有理数比较大小的法则比较大小。
④实数可以按有理数的运算法则和运算律进行运算。
实数3、近似数:由于实际中常常不需要用精确的数描述一个量,甚至在更多情况下不可能得到精确的数,用以描述所研究的量,这样的数就叫近似数。
取近似值的方法——四舍五入法4、有效数字:对一个近似数,从左边第一个不是0的数字起,到末位数字止,所有的数都称为这个近似数的有效数字 5、科学记数法:把一个数记为做科学记数法。
是整数)的形式,就叫其中n ,10a 1(10a n<≤⨯ 6、实数和数轴:每一个实数都可以用数轴上的点来表示;反过来,数轴上每一个点都表示一个实数。
实数与数轴上的点是一一对应的。
勾股定理:(一)结合三角形:1.已知∆ABC 的三边a 、b 、c 满足0)()(22=-+-c b b a ,则∆ABC 为 三角形 2.在∆ABC 中,若2a =(b +c )(b -c ),则∆ABC 是 三角形,且∠ ︒90 3.在∆ABC 中,AB=13,AC=15,高AD=12,则BC 的长为1.已知2512-++-y x x 与25102+-z z 互为相反数,试判断以x 、y 、z 为三边的三角形的形状。
2.已知:在∆ABC 中,三条边长分别为a 、b 、c ,a =12-n ,b =2n ,c =12+n (n >1) 试说明:∠C=︒90。
3.若∆ABC 的三边a 、b 、c 满足条件2a c b a c b 26241033822++=+++,试判断∆ABC 的形状。
4.已知,0)10(8262=-+-+-c b a 则以a 、b 、c 为边的三角形是(二)、实际应用:1. 梯子滑动问题:(1)一架长2.5m 的梯子,斜立在一竖起的墙上,梯子底端距离墙底0.7m (如图),如果梯子的顶端沿墙下滑0.4m ,那么梯子底端将向左滑动 米(2)如图,一个长为10米的梯子,斜靠在墙面上,梯子的顶端距地面的垂直距离为8米,如果梯子的顶端下滑1米,那么,梯子底端的滑动距离 1米,(填“大于”,“等于”,或“小于”)(3)如图,梯子AB 斜靠在墙面上,AC ⊥BC ,AC=BC ,当梯子的顶端A 沿AC 方向下滑x 米时,梯足B 沿CB 方向滑动y 米,则x 与y 的大小关系是( )A. y x =B. y x >C. y x <D. 不能确定(4)小明想知道学校旗杆的高度,他发现旗杆上的绳子吹到地面上还多1 m ,当他把绳子的下端拉开5米后,发现绳子下端刚好触到地面,试问旗杆的高度为 米86ACB2. 直角边与斜边和斜边上的高的关系:直角三角形两直角边长为a ,b ,斜边上的高为h ,则下列式子总能成立的是( ) A. 2b ab = B. 2222h b a =+ C.h b a 111=+ D. 222111hb a =+ 变:如图,在Rt △ABC 中,∠ACB=90°,CD ⊥AB 于D ,设AB=c ,AC=b ,BC=a ,CD=h 。
求证:(1)222111h b a =+ (2)h c b a +<+(3)以h c h b a ++,,为三边的三角形是直角三角形DABC试一试:(1)只需证明1)11(222=+b a h ,从左边推到到右边 (2)()()22h c b a +<+(3)()()222h c h h a +=++,注意面积关系ch ab =的应用3. 爬行距离最短问题:1.如图,一个无盖的正方体盒子的棱长为10cm ,得到1C 处有一只昆虫甲,在盒子的内部有一只昆虫乙(盒壁的 忽略不计)(1)假设昆虫甲在顶点1C 处静止不动,如图a ,在盒子的内部我们先取棱1BB 的中点E ,再连结AE 、1EC ,昆虫乙如果沿途径1C E A →→爬行,那么可以在最短的时间内捕捉到昆虫甲,仔细体会其中的道理,并在图b 中画一条路径,使昆虫乙从顶点A 沿这条路爬行,同样可以在最短的时间内捕捉到昆虫甲。
(2)如图b ,假设昆虫甲从点1C 以1 厘米/秒的速度在盒子的内部沿C C 1向下爬行,同时昆虫乙从顶点A 以2厘米/秒的速度在盒壁上爬行,那么昆虫乙至少需要多少时间才能捕捉到昆虫甲?试一试:对于(2),当昆虫甲从顶点1C 沿棱C C 1向顶点C 爬行的同时,昆虫乙可以沿不同的路径爬行,利用勾股定理建立时间方程,通过比较得出昆虫乙捕捉到昆虫甲的最短时间图b图aADCBA1B1C1D1D1C1B1A1BCDA2.如图,一块砖宽AN=5㎝,长ND=10㎝,CD 上的点F 距地面的高FD=8㎝,地面上A 处的一只蚂蚁到B 处吃食,要爬行的最短路线是 cm3.如图,是一个三级台阶,它的每一级的长、宽、高分别为20dm 、3dm 、2dm ,A 和B是这个台阶两相对的端点,A 点有一只昆虫想到B 点去吃可口的食物,则昆虫沿着台阶爬到B 点的最短路程是 分米? 4. 如图,一只蚂蚁沿边长为a 的正方体表面从点A 爬到点B ,则它走过的路程最短为( ) A.a 3 B. ()a 21+ C. a 3 D.a 5BAQNMP4.折叠问题:1.如图,有一张直角三角形纸片,两直角边AC=6,BC=8,将△ABC 折叠,使点B 与点A 重合,折痕为DE ,则CD 等于( ) A.425 B. 322 C. 47D. 35ABCE D1. 小明和爸爸妈妈十一登香山,他们沿着45度的坡路走了500米,看到了一棵红叶树,这棵红叶树离地面的高度是 米。
2. 如图,山坡上两株树木之间的坡面距离是43米,则这两株树之间的垂直距离是____________米,水平距离是 米。
3. 如图,一根12米高的电线杆两侧各用15米的铁丝固定,两个固定点之间的距离是 。
4. 如图,欲测量松花江的宽度,沿江岸取B 、C 两点,在江对岸取一点A ,使AC 垂直江岸,测得BC =50米,∠B =60°,则江面的宽度为 。
