河北省定州市第二中学_学年高二数学上学期寒假作业3理【含答案】
河北省定州市第二中学高二数学上学期寒假作业13 文

高二数学文 寒假作业13一、选择题1.若函数322()f x x ax bx a =+++在1x =时有极值10,则实数,a b 的值是( )A .33a b =-⎧⎨=⎩B .411a b =⎧⎨=-⎩C .33a b =-⎧⎨=⎩或411a b =⎧⎨=-⎩D .311a b =-⎧⎨=-⎩或43a b =⎧⎨=⎩2.若函数m mx mx x x f 3)(23++-=在)1,0(内有极大值,无极小值,则A. 0<mB.3<mC.3>mD.30<<m3.设)(x f 是可导函数,且='=∆-∆-→∆)(,2)()2(lim 0000x f xx f x x f x 则( ) A .21 B .-1 C .0 D .-2 4.已知函数742)(23---=x x x x f ,其导函数为)(x f '.①)(x f 的单调减区间是⎪⎭⎫ ⎝⎛2,32;②)(x f 的极小值是15-;④函数)(x f 有且只有一个零点.其中真命题的个数为 ( )A .1个B .2个C .3个D .0个5.曲线x x yln =在点()e e ,处的切线方程为( ) A.e x y-=2 B.e x y --=2 C.e x y +=2 D.1--=x y6.若函数2)(3-+=ax x x f 在区间),1(+∞内是增函数,则实数a 的取值范围是A.),3(+∞B. ),3[+∞-C. ),3(+∞-D.)3,(--∞二、填空题7.已知函数f(x)=mx 2+lnx -2x 在定义域内是增函数,则实数m 的取值范围为________.8.若x e x f 1)(=,则0(12)(1)lim t f t f t→--=________. 9.设二次函数()22f x ax bx a =++的导函数为()f x ',对任意x R ∈,不等式()()'f x f x ≥恒成立,则22b a 的最大值为______. 10.若函数f(x)=x 3-mx 2+2m 2-5的单调递减区间为(-9,0),则m =______三、解答题11.设()32112.32f x x x ax =-++ (Ⅰ)若()f x 在2,3⎛⎫+∞ ⎪⎝⎭上存在单调递增区间,求a 取值范围;(Ⅱ)当2a 0<<时,()f x 在[]4,1上的最小值为163-,求()f x 在该区间上的最大值.12.已知函数322()1(f x x mx m x m =+-+为常数,且0)m >有极大值9,求m 的值及()f x 的极小值.参考答案131.B 2.C 3.B 4.B 5.A 6.B7.1,2⎡⎫+∞⎪⎢⎣⎭ 8.e 2 9.4. 10.-272 11.解:(I )知()3211232f x x x ax =-++,()2'2f x x x a ∴=-++ 函数()f x 在2,3⎛⎫+∞ ⎪⎝⎭上存在单调递增区间,即导函数在2,3⎛⎫+∞ ⎪⎝⎭上存在函数值大于零的部分,2222'()()()20333f a ∴=-++>∴19a >-(Ⅱ)因为()f x 取到最小值163-,而()2'2f x x x a =-++的图像开口向下,且对称轴12x =, 22'(1)11220,'(4)4422120f a a f a a =-++=>=-++=-<则必有一点[],4,10∈x 使得0'()0=f x 此时函数()f x 在0[1,]x 上单调递增,在0[,4]x 单调323211(1)11203211(4)4480324016(4)8133=⨯+⨯+>∴=⨯+⨯+<∴=-+=-∴=f a f a f a a , 此时,由200000'()202,1()=-++=∴==-舍去f x x x x x , 所以函数max 10()(2)3==f x f 考点:导数在研究函数中的运用.12.x m =-时有极大值()9f m -= ,2m =。
河北省定州市第二中学2019-2020学年高二寒假作业数学(理)试题(3) Word版含答案

高二理数 寒假作业3命题人:韩成群 学生训练日期:1.一个口袋中装有形状和大小完全相同的3个红球和2个白球,甲从这个口袋中任意摸取2个球, 则甲摸得的2个球恰好都是红球的概率是( )A .103B .52C .53D . 32 2.同时抛两枚硬币,则一枚朝上一枚朝下的事件发生的概率是( )A.1/2B. 1/3C.1/4D.2/33.同时投掷两个骰子,则向上的点数之差的绝对值为4的概率是( ) A.181 B.121 C.91 D.61 4.容量为20的样本数据,分组后的频数如下表:则样本数据落在区间[10,40)的频率为( )(A )0.35 (B )0.45 (C )0.55 (D )0.655.掷两颗骰子得两数,则事件“两数之和大于4”的概率为( )A .61B .21C .32D .65 6.从2名男生和2名女生中,任意选择两人在星期六、星期日参加某公益活动,每天一人,则星期六安排一名男生、星期日安排一名女生的概率为( ) A.13 B.512 C.12 D.7127.如图,长方体ABCD —A 1B 1C 1D 1,有一动点在此长方体内随机运动,则此动点在三棱锥A —A 1BD 内的概率为.8.右图的茎叶图是甲、乙两人在4次模拟测试中的成绩,其中一个数字被污损,则甲的平均成绩不超过乙的平均成绩的概率为.9.从长度分别为2,3,4,5的四条线段中任意取出三条,则以这三条线段为边可以构成三角形的概率是________.10.集合A ={x|x 2-3x -10<0,x ∈Z},从集合A 中任取两个元素a 、b 且a·b≠0,则方程22x y a b+=1表示焦点在x 轴上的椭圆的概率为________.11.对关于x 的一元二次方程22960x ax b ++=……()*,解决下列两个问题: (1)若a 是从1,2,3三个数中任取的一个数,b 是从0,1,2三个数中任取的一个数,求方程()*有两个不相等实根的概率;(2)若a 是从区间[13],任取的一个数,b 是从区间[02],任取的一个数,求方程()*有两个不相等实根的概率.12.在一次商贸交易会上,商家在柜台开展促销抽奖活动,甲、乙两人相约同一天上午去该柜台参与抽奖.(1)若抽奖规则是从一个装有2个红球和4个白球的袋中无放回地取出2个球,当两个球甲乙 88 5 3 9 9 2 1 ● 5同色时则中奖,求中奖概率;(2)若甲计划在9:00~9:40之间赶到,乙计划在9:20~10:00之间赶到,求甲比乙提前到达的概率.理数寒假作业3参考答案1.A 2.A 3.C 4.B 5.D 6.A 7.168.0.3 9.3410.31011.设事件A 为“方程22960x ax b ++=有两个不相等实根”.当0a >且0b ≥时,要方程22960x ax b ++=有两个不相等实根,需a b >.(1)基本事件共9个:(10)(11)(12)(20)(21)(22)(30)(31)(32),,,,,,,,,,,,,,,,,.其中第一个数表示a 的取值,第二个数表示b 的取值.事件A 中包含6个基本事件(1,0),(2,0),(2,1),(3,0),(3,1),(3,2),则事件A 发生的概率为62()93P A ==. (2)试验的全部结果所构成的区域为{}()|130 2.a b a b ≤≤≤≤,,.构成事件A 的区域为{}()|1302a b a b a b ≤≤≤≤≥,,,(如图示). 则所求的概率为2122172228⨯-⨯==⨯. 12.(1)记“取到同色球”为事件A ,则其概率为157)(=A P . (2)设甲乙到达的时刻分别为x,y ,则131,320≤≤≤≤y x,甲乙到达时刻(x,y)为图中正方形区域,甲比乙先到则需满足y x <,为图中阴影部分区域,设甲比乙先到为事件B ,则8732323131211)(=⨯⨯⨯-=B P。
高二(理)上学期数学寒假作业3 含答案

1、数列{}n a 的前n 项和为n S ,若1(1)na n n =+,则19S 等于( )A .1819B .2019C .1920D .21202、设n S 是等差数列{}n a 的前n 项和,若==5935,95S S a a 则( ) A .1 B .1- C .2 D .213、在数列{}n a 中,12a =, 11ln(1)n n a a n+=++,则n a =( )A .2ln n +B .2(1)ln n n +-C .2ln n n +D .1ln n n ++ 4、 设n S 为等差数列{}n a 的前项和,若36324S S ==,,则9a =( )A. 15B. 45C. 192D. 27 5、已知{}n a 是等比数列,a n>0,且a 4a 6+2a 5a 7+a 6a 8=36,则a 5+a 7等于 ( )A .6B .12C .18D .24 6、两个等差数列{}{},,n n b a ,327......2121++=++++++n n b b b a a a n n 则55b a=___________7、数列{}n a 的前n项的和S n=3n 2+ n +1,则此数列的通项公式 .8、设n S 是等差数列{}n a 的前n 项和,且8765S S S S >=< ,则下列结论一定正确的有(1).0<d(2).07=a(3)59S S > (4)01<a (5).6S 和7S 均为n S 的最大值9.在等比数列{a n }中,a 1+a n =66,a 2·a n -1=128,且前n 项和S n =126,求n 及公比q .10、已知:等差数列{n a }中,4a =14,前10项和18510=S .(1)求n a ;(2)将{n a }中的第2项,第4项,…,第n2项按原来的顺序排成一个新数列,求此数列的前n 项和n G .11.已知数列{}n a 是等差数列,且.12,23211=++=a a a a(1)求数列{}n a 的通项公式;(2)令).(R x x a b nn n ∈=求数列{}n b 前n 项和的公式.12、 在数列{}n a 中,11a =,2112(1)n n a a n+=+⋅.(Ⅰ)证明数列2{}n a n 是等比数列,并求{}n a 的通项公式;(Ⅱ)令112n n n b a a +=-,求数列{}n b 的前n 项和n S ;(Ⅲ)求数列{}n a 的前n 项和n T .答案1—5CCAAA6、12657、a n =⎩⎨⎧≥-=2,261,5n n n 8(1)(2)(5)、 9、 [解析] ∵a 1a n =a 2a n -1=128,又a 1+a n =66,∴a 1、a n 是方程x 2-66x +128=0的两根,解方程得x 1=2,x 2=64,∴a 1=2,a n =64或a 1=64,a n =2,显然q ≠1.若a 1=2,a n =64,由a 1-a n q 1-q =126得2-64q =126-126q ,∴q =2,由a n =a 1q n -1得2n -1=32,∴n =6.若a 1=64,a n =2,同理可求得q =12,n =6.综上所述,n 的值为6,公比q =2或12.10、解析:(1)由41014185a S =⎧⎨=⎩ ∴11314,1101099185,2a d a d +=⎧⎪⎨+⋅⋅⋅=⎪⎩ 153a d =⎧⎨=⎩ 由23,3)1(5+=∴⋅-+=n a n a n n(2)设新数列为{n b },由已知,2232+⋅==n n n a b.2)12(62)2222(3321n n G n n n +-=+++++=∴Λ *)(,62231N n n G n n ∈-+⋅=∴+11、解:设数列}{n a 公差为d ,则 ,12331321=+=++d a a a a 又.2,21=∴=d a所以.2n a n =(Ⅱ)解:令,21n n b b b S +++=Λ则由,2nn n n nx x a b ==得,2)22(4212n n n nx x n x x S +-++=-Λ①,2)22(42132++-+++=n n n nx x n x x xS Λ②当1≠x 时,①式减去②式,得 ,21)1(22)(2)1(112++---=-++=-n n n nn nx xx x nxx x x S x Λ所以.12)1()1(212xnxx x x S n n n ----=+当1=x 时, )1(242+=+++=n n n S n Λ,综上可得当1=x 时,)1(+=n n S n当1≠x 时,.12)1()1(212x nx x x x S n n n ----=+ 12解:(Ⅰ)由条件得1221(1)2n n a a n n +=⋅+,又1n =时,21n a n =, 故数列2{}n a n 构成首项为1,公式为12的等比数列.从而2112n n a n -=,即212n n n a -=.(Ⅱ)由22(1)21222n n n n n n n b ++=-=得23521222nnn S +=+++L , 231135212122222n n n n n S +-+⇒=++++L ,两式相减得 :23113111212()222222n n n n S ++=++++-L , 所以 2552n n n S +=-.(Ⅲ)由231121()()2n n n S a a a a a a +=+++-+++L L 得1112n n n n T a a T S +-+-= 所以11222n n n T S a a +=+-2146122n n n -++=-.。
河北省定州市第二中学高二数学上学期寒假作业4文

高二数学文 寒假作业4一、选择题1 )A 2.从{2,3,4}中随机选取一个数a ,从{2,3,4}中随机选取一个数b ,则b a > 的概率是A 3.下列命题:①将一枚硬币抛两次,设事件M :“两次出现正面”,事件N :“只有一次出现反面”,则事件M 与N 互为对立事件. ②若事件A 与B 互为对立事件,则事件A 与B 为互斥事件. ③若事件A 与B 为互斥事件,则事件A 与B 互为对立事件. ④若事件A 与B 互为对立事件,则事件A +B 为必然事件. 其中,真命题是 ( ) A .①②④ B. ②④ C. ③④ D. ①②4.高三毕业时,甲、乙、丙、丁四位同学站成一排照相留念,已知甲乙相邻,则甲丙相邻的概率为( )5.如图,向边长为2的正方形中随机投入一粒黄豆,若圆C 则黄豆落入阴影部分的概率为( )6内任意取一点),(y x P ,则122>+y x 的概率是A .二、填空题7.将十进制数51化成二进制数为 .8.已知样本9,10,11,,x y 的平均数是10,标准差是9.一箱产品中有正品4件,次品3件,从中任取2件,其中事件:①恰有1件次品和恰有2件次品 ②至少有1件次品和全是次品③至少有1件正品和至少1件次品 ④至少有1件次品和全是正品其中互斥事件为__________.10.从1,2,3,6这4个数中一次随机地取2个数,则所取2个数的乘积为6的概率是________.三、解答题11.先后随机投掷2枚正方体骰子,其中x 表示第1枚骰子出现的点数,y 表示第2枚骰子出现的点数),(y x P .(Ⅰ)求点),(y x P 在直线上的概率;(Ⅱ)求点),(y x P 满足的概率。
12.袋中有12个小球,分别为红球、黑球、黄球、绿球,从中任取一球,得到红球的概率绿球的概率各是多少?参考答案41.D 2.C 3.B 4.A 5.B. 6.C7.)2(1100118.96 xy .9.①④1011.(1)(2)12.。
河北省定州市第二中学2019-2020学年高二寒假作业数学(理)试题(8) Word版含答案

高二理数 寒假作业8命题人:韩成群 学生训练日期:1.已知 215()sin(),'()42f x x x f x π=++为()f x 的导函数,则 '()y f x =的图象大致是( )2.函数3()3f x x x =-在区间(1,1)-上( )A .有最大值,但无最小值B .有最大值,也有最小值C .无最大值,但有最小值D .既无最大值,也无最小值.3.曲线x y e =在点(0,1)处的切线斜率为( )A .1B .2C .eD .1e4.函数f(x)的定义域为R ,f(-1)=2,对任意x ∈R ,f ′(x)>2,则f(x)>2x+4的解集为( )A .(-1,1)B .(-1,+∞)C .(-∞,-1)D .(-∞,+∞)5.已知函数在区间[-1,2]上是减函数,那么b+c( ) A .有最大值B .有最大值- C .有最小值D .有最小值-6.若0,0>>b a ,且函数224)(23+--=bx ax x x f 在1=x 处有极值,则ab 的最大值为。
7.曲线2l o g y x =与曲线以及x 轴所围成的图形的面积 . 8.设.若曲线与直线所围成封闭图形的面积为,则______.9.圆心在曲线3(0)y x x=->上,且与直线3430x y -+=相切的面积最小的圆的方程是. 10.点P 是曲线2ln y x x =-上任意一点,则点P 到直线2y x =-的距离的最小值是11.在区间[0,1]上给定曲线2y x =,试在此区间内确定点t 的值,使图中所给阴影部分的面积1S 与2S 之和最小.12.若函数f(x)=-12()22x -+blnx 在(1,+∞)上是减函数,求实数b 的取值范围.理数寒假作业8参考答案1. A 2.D3. A4. B 5.B6.97.. 8.9.223(x 2)(y )92-++=10.2 11.设10≤≤t 当t x =时,2t y =∴303222013231()(t x x t dx x t S tt=-=-⎰=3132)(232212+-=-⎰=t t dx t x S t ∴阴影部分的面积为3134)(2321--==+t t t f S S )10(≤≤t t t t f 24)(2-=',令0)(='t f 可得01=t 或212=t 由31)0(=f , 32)1(=f 41)21(=f 可知当21=t 时,12S S +有最小值4112.由f(x)=-12()22x -+blnx ,得f ′(x)=-(x -2)+b x ,由题意,知f ′(x)≤0即-()2x -+b x ≤0在(1,+∞)上恒成立,∴b≤()min 2x x -⎡⎤⎣⎦,当x∈(1,+∞)时,()2x x -⎡⎤⎣⎦∈(1,+∞),∴b ≤1.。
河北省定州市第二中学高二上学期数学(文)寒假作业3 Word版含答案

高二数学文 寒假作业3 命题人:李英欣 审核人:李英欣 训练日期: 一、 选择题 1.一枚硬币连掷2次,只有一次出现正面的概率为( )A .32B .41C .31D .21 2.两个事件对立是两个事件互斥的( )A.充分非必要条件B.必要非充分条件C.充要条件D.既不充分又不必要条件3.如图,是由一个圆、一个三角形和一个长方形构成的组合体,现用红、蓝两种颜色为其涂色,每个图形只能涂一种颜色,则三个形状颜色不全相同的概率为( )A .43B .83C .41 D .814.甲、乙、丙三名同学站成一排,甲站在中间的概率是( )A .61B .21C .31D .325.若将一个质点随机投入如图所示的长方形ABCD 中,其中AB=2,BC=1,则质点落在以AB 为直径的半圆内的概率是( )(A )2π (B )4π (C )6π (D )8π 6.在区间上随机取一个数x ,的值介于0到之 间的概率为( ). A .31 B .π2 C .21 D .32二、填空题7.已知多项式函数f (x )=2x 5-5x 4-4x 3+3x 2-6x+7,当x=5时由秦九韶算法v 0=2 v 1=2×5-5=5 则v 3= ________.8.设P 在[0]5,上随机地取值,则关于x 的方程210x px ++=有实数根的概率为 .9.甲、乙两人下棋,则甲获胜的概率是 . 10.在区间[2,1]-上随机取一个实数x ,则x 使不等式1|1|x -≤成立的概率为____.三、解答题11.某射手在一次射击中射中10环、9环、8环、7环, 7环以下的概率分别为0.24,0.28,0.19,0.16,0.13,计算这个射手在一次射击中:(1)射中10环或9环的概率;(2)至少射中7环的概率;(3)射中环数不是8环的概率。
12.(本小题13分)已知关于x 的一元二次函数2()1f x ax bx =-+,分别从集合P 和Q 中随机取一个数a 和b 得到数列(,)a b 。
数学-高二-河北省定州市第二中学高二上学期数学(文)寒假作业(1-6)

高二数学文 寒假作业1命题人:李英欣 审核人:李英欣 训练日期:一、选择题1.阅读如图所示的程序框图,运行相应的程序.若输出的S 为1112,则判断框中填写的内容可以是( )A .6n =B .6n <C .6n ≤D .8n ≤2.用秦九韶算法求多项式234561235879653f x x x x x x x =+++++()-在4x =-,4v 的值为( )A .-57B .220C .-845D .33923.根据我国古代数学名著《九章算术》中的“更相减损术”.求得144,28的最大公约数为 ( )A .4B .2C .0D .144.下列各进制数中值最小的是( )A .()885B .()6210C .()2111111D .()410005.雅礼中学教务处采用系统抽样方法,从学校高三年级全体1000名学生中抽50名学生做学习状况问卷调查.现将1000名学生从1到1000进行编号,求得间隔数k=20,即分50组每组20人.在第一组中随机抽取一个号,如果抽到的是17号,则第8组中应取的号码是()A.177 B.157 C.417 D.3676.某校有行政人员、教学人员和教辅人员共200人,其中教学人员与教辅人员的比为10:1,行政人员有24人,现采取分层抽样容量为50的样本,那么行政人员应抽取的人数为()A.3 B.4 C.6 D.8二、填空题7.如图是某学校一名篮球运动员在10场比赛中所得分数的茎叶图,则该运动员在这10场比赛中得分的中位数为.8.有一个简单的随机样本: 10, 12,9,14,13,则样本平均数x= ,样本方差2s= .9.一个容量为20的样本数据,分组后,组距与频数如下:(]20,10,2;(]30,20,3;(]40,30,4;(]50,40,5;(]60,50,4 ;(]70,60,2.则样本在区间(]70,50上的频率为.10.已知样本9,10,11,x,y的平均数是10,方差是2,则xy= .三、解答题(题型注释)11.某校200位学生期末考试物理成绩的频率分布直方图如图所示,其中成绩分组区间是:[)80,90、[]70,80、[)50,60、[)60,70、[)90,100.(1)求图中a的值;(2)根据频率分布直方图,估计这200名学生物理成绩的平均值和中位数.12.下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据x3456y2.5344.5(1221,ni iiniix y nx yb a y b xx nx∧∧∧==-==--∑∑)(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程ˆy bx a=+;(2)已知该厂技术改造前100吨甲产品能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?高二数学文寒假作业2命题人:李英欣审核人:李英欣训练日期:一、选择题1.执行如图所示的程序框图,则输出的S值是()A.﹣1 B. C. D.42.计算机执行右边的程序段后,输出的结果是A .3,1B .1,4C .2,4-D .2,1-3.下列各进制数中值最小的是( )A .()885B .()6210C .()2111111D .()410004.三个数390, 455, 546的最大公约数是 ( ) A.65 B.91 C.26 D.135.已知x ,y 的取值如下表示:若y 与x 线性相关,且0.95y x a =+,则a=( )A .2.2B .2.6C .2.8D .2.96.已知x 、y 之间的一组数据如下:则线性回归方程bx a y+=ˆ所表示的直线必经过点A .(1.5,5)B .(5,1.5)C .(2,5)D .(1.5,4)二、填空题7.有下面的程序运行该程序,要使输出的结果30,在“ ”处应添加的条件是______________.s=0i=2DOs=s+ii= i+2LOOP UNTILPRINT sEND8.生活中常用的十二进位制,如一年有12个月,时针转一周为12个小时,等等,就是逢12进1的计算制,现采用数字0~9和字母A、B共12个计数符号,这些符号与十进制的数的对应关系如下表:十二进制0123456789A B十进制01234567891011例如用十二进位制表示A+B=19,照此算法在十二进位制中运算A×B= .9.如图是某学校一名篮球运动员在10场比赛中所得分数的茎叶图,则该运动员在这10场比赛中得分的中位数为.10.有一个简单的随机样本:10,12,9,14,13,则样本平均数x= ,样本方差2s= .三、解答题11.从高三抽出50名学生参加数学竞赛,由成绩得到如下的频率分布直方图.由于一些数据丢失,试利用频率分布直方图求:(1)这50名学生成绩的众数与中位数.(2)这50名学生的平均成绩.12.假设关于某设备的使用年限x和所支出的维修费用y(万元)有如下的统计资料:使用年限x23456维修费用y 2.2 3.8 5.5 6.5 7.0(1)画出散点图;(2)若线性相关,则求出回归方程a bx y+=ˆ; (3)估计使用年限为10年时,维修费用是多少?高二数学文 寒假作业3命题人:李英欣 审核人:李英欣 训练日期:一、 选择题1.一枚硬币连掷2次,只有一次出现正面的概率为( ) A .32 B .41 C .31 D .212.两个事件对立是两个事件互斥的( ) A.充分非必要条件 B.必要非充分条件 C.充要条件D.既不充分又不必要条件3.如图,是由一个圆、一个三角形和一个长方形构成的组合体,现用红、蓝两种颜色为其涂色,每个图形只能涂一种颜色,则三个形状颜色不全相同的概率为( )A .43B .83C .41 D .814.甲、乙、丙三名同学站成一排,甲站在中间的概率是( ) A .61 B .21 C .31 D .325.若将一个质点随机投入如图所示的长方形ABCD 中,其中AB=2,BC=1,则质点落在以AB 为直径的半圆内的概率是( )(A )2π (B )4π (C )6π (D )8π6.在区间上随机取一个数x ,的值介于0到之间的概率为( ). A .31 B .π2 C .21 D .32二、填空题7.已知多项式函数f (x )=2x 5-5x 4-4x 3+3x 2-6x+7,当x=5时由秦九韶算法v 0=2 v 1=2×5-5=5 则v 3= ________.8.设P 在[0]5,上随机地取值,则关于x 的方程210x px ++=有实数根的概率为 . 9.甲、乙两人下棋,两人下成和棋的概率是21,乙获胜的概率是31,则甲获胜的概率是 . 10.在区间[2,1]-上随机取一个实数x ,则x 使不等式1|1|x -≤成立的概率为____. 三、解答题11.某射手在一次射击中射中10环、9环、8环、7环, 7环以下的概率 分别为0.24,0.28,0.19,0.16,0.13,计算这个射手在一次射击中: (1)射中10环或9环的概率; (2)至少射中7环的概率; (3)射中环数不是8环的概率。
河北省定州市第二中学高二寒假作业数学(理)试题(9)
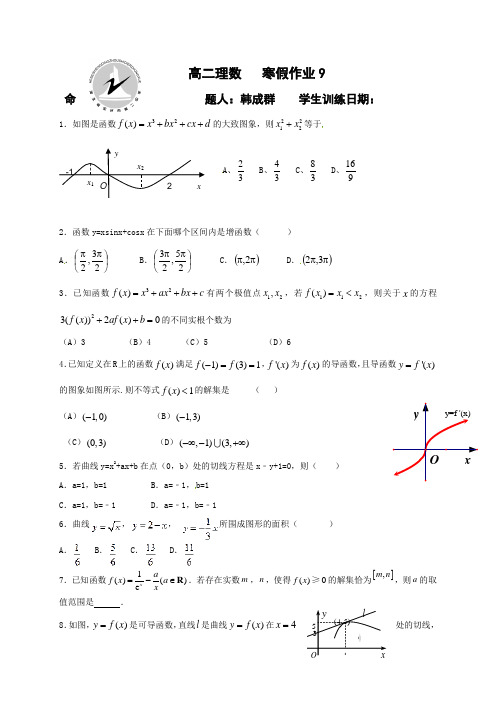
高二理数 寒假作业9命题人:韩成群 学生训练日期:1.如图是函数32()f x x bx cx d =+++的大致图象,则2212x x +等于A 、23B 、43C 、83D 、1692.函数y=xsinx+cosx 在下面哪个区间内是增函数( ) A .⎪⎭⎫⎝⎛ππ23,2 B .⎪⎭⎫⎝⎛ππ25,23 C .()ππ2, D .()ππ3,2 3.已知函数32()f x x ax bx c =+++有两个极值点12,x x ,若112()f x x x =<,则关于x 的方程23(())2()0f x af x b ++=的不同实根个数为(A )3 (B )4 (C )5 (D )64.已知定义在R 上的函数()f x 满足(1)(3)1f f -==,'()f x 为()f x 的导函数,且导函数'()y f x =的图象如图所示.则不等式()1f x <的解集是 ( ) (A )(1,0)- (B )(1,3)- (C )(0,3) (D )(,1)(3,)-∞-+∞5.若曲线y=x 2+ax+b 在点(0,b )处的切线方程是x ﹣y+1=0,则( ) A .a=1,b=1 B .a=﹣1,b=1 C .a=1,b=﹣1 D .a=﹣1,b=﹣1 6.曲线,, 所围成图形的面积( )A .B .C .D .7.已知函数1()()e x a f x a x=-∈R .若存在实数m ,n ,使得()0f x ≥的解集恰为[],m n ,则a 的取值范围是 .8.如图,()y f x =是可导函数,直线l 是曲线)(x f y =在4=x 处的切线,y y=f '(x)Ox-1Ox 1 x 22xyl(4,5)xy4O53令()()f x g x x=,则(4)g '= . 9.如图,△OAB 是边长为2的正三角形,记△OAB 位于直线)<20(≤=t t x 左侧的图形的面积为)(t f ,则(1)函数)(t f 的解析式为_______;(2)函数)(t f y =的图像与直线t t 、2=轴围成的图形面积为______.10.如图是()y f x =的导函数的图像,现有四种说法: ①()f x 在(3,1)-上是增函数;②1x =-是()f x 的极小值点; ③()f x 在(2,4)上是减函数,在(1,2)-上是增函数; ④2x =是()f x 的极小值点;以上正确的序号为________. 11.已知函数f(x)=ln x -ax.(1)当a>0时,判断f(x)在定义域上的单调性; (2)f(x)在上的最小值为32,求实数a 的值; (3)试求实数a 的取值范围,使得在区间(1,+∞)上函数y =x 2的图象恒在函数y =f(x)图象的上方.12.已知函数2()2()3xf x e x a =--+,a ∈R .(1)若函数()y f x =的图象在0x =处的切线与x 轴平行,求a 的值;(2)若0x ≥,()0f x ≥恒成立,求a 的取值范围.理数寒假作业9参考答案1.D 2.B 3.A 4.B 5.A 6.C 7.1(0,).e 8.316-9.(1)223,012()33(2),122t t f t t t ⎧<≤⎪⎪=⎨⎪--<≤⎪⎩(2)3 10.② 11.(1)f′(x)=1x +2a x =2x a x +(x>0),当a>0时,f′(x)>0恒成立, 故f(x)在(0,+∞)上是单调递增函数. (2)由f′(x)=0得x =-a ,①当a≥-1时,f′(x)≥0在上恒成立,f(x)在上为增函数. f(x)min =f(1)=-a =32得a =-32(舍).②当a≤-e 时,f′(x)≤0在上恒成立,f(x)在上为减函数. 则f(x)min =f(e)=1-a e=32得a =-2e (舍). ③当-e<a<-1时,由f′(x)=0得x 0=-a . 当1<x<x 0时,f′(x)<0,f(x)在(1,x 0)上为减函数; 当x 0<x<e 时,f′(x)>0,f(x)在(x 0,e)上为增函数. ∴f(x)min =f(-a)=ln(-a)+1=32,得a =-e . 综上知:a =-e .(3)由题意得:x 2>ln x -a x在(1,+∞)上恒成立,即a>xln x -x 3在(1,+∞)上恒成立.设g(x)=xln x -x 3(x>1),则g′(x)=ln x -3x 2+1.令h(x)=ln x -3x 2+1,则h′(x)=1x -6x .当x>1时,h′(x)<0恒成立.∴h(x)=g′(x)=ln x -3x 2+1在(1,+∞)上为减函数,则g′(x)<g′(1)=-2<0.所以g(x)在(1,+∞)上为减函数, ∴g(x)<g(1)<-1,故a≥-112.(1)()2()x f x e x a '=-+ 因为()y f x =在0x =处切线与x 轴平行,即在0x =切线斜率为0即(0)2(1)0f a '=+=,∴1a =-.(2)()2()x f x e x a '=-+, 令()2()x g x e x a =-+,则()2(1)0x g x e '=-≥, 所以()2()x g x e x a =-+在[)0,+∞内单调递增,(0)2(1)g a =+(i )当2(1)0a +≥即1a ≥-时,()2()(0)0x f x e x a f ''=-+≥≥,()f x 在[)0,+∞内单调递增,要想()0f x ≥只需要2(0)50f a =-≥,解得a ≤≤,从而1a -≤≤ (ii )当2(1)0a +<即1a <-时,由()2()x g x e x a =-+在[)0,+∞内单调递增知, 存在唯一0x 使得000()2()0x g x e x a =-+=,有00x e x a =-,令()0f x '>解得0x x >,令()0f x '<解得00x x ≤<,从而对于()f x 在0x x =处取最小值,0200()2()3x f x e x a =--+,又00x x e a =+0()f x 000022()3(1)(3)x x x x e e e e =-+=-+-,从而应有0()0f x ≥,即030x e -≤,解得00ln 3x <≤,由00x e x a =-可得00x a x e =-,有ln331a -≤<-,综上所述,ln 33a -≤≤。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高二数学 寒假作业31.某市有大型超市200家、中型超市400家、小型超市1400家,为掌握各类超市的营业情况,现按分层抽样方法抽取一个容量为100的样本,应抽取中型超市( )A. 70家B.50家C.20家D.10家2.某校开展“爱我海西、爱我家乡”摄影比赛,9位评委为参赛作品A 给出的分数如下图所示.记分员在去掉一个最高分和一个最低分后,算得平均分为91.复核员在复核时,发现有一个数字(茎叶图中的x)无法看清.若记分员计算无误,则数字x 应该是( ).A.1B.2C.3D.43.某防疫站对学生进行身体健康调查,欲采用分层抽样的办法抽取样本.某中学共有学生2000名,抽取了一个容量为200的样本,已知样本中女生比男生少6人,则该校共有女生( ) A .1030人 B .97人 C .950人 D .970人4.已知方程y =bx +a 是两个具有线性相关关系的变量的一组数据(x 1,y 1),(x 2,y 2),…,(x 10,y 10)的回归方程,则“1210010x x x x +++=,1210010y y y y +++=”是“(x 0,y 0)满足线性回归方程y =bx +a ”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件5.在一次实验中,测得()x y ,的四组值分别是(12)(23)(34)(45)A B C D ,,,,,,,,则y 与x 之间的回归直线方程为( )A .21y x =+B .2y x =+C .1y x =+D .1y x =-6.2013年湖北省宜昌市为了创建国家级文明卫生城市,采用系统抽样方法从960人中抽取32人做问卷调查,为此将他们随机编号为001,002,…,960,分组后在第一组采用简单随机抽样的方法抽到的号码为9,抽到的32人中,编号落入区间[1,450]的人做问卷A ,编号落入区间[451,750]的人做问卷B ,其余的人做问卷C ,则抽到的人中,做问卷B 的人数为( )A .20B .19C .10D .97.某工厂生产A 、B 、C 三种不同型号的产品,产品数量之比为3∶4∶7,现在用分层抽样的方法抽出容量为n 的样本,样本中A 型号产品有15件,那么样本容量n 为( )A .50B .60C .70D .808.某学校为调查高三年级的240名学生完成课后作业所需时间,采取了两种抽样调查的方式:第一种由学生会的同学随机抽取24名同学进行调查;第二种由教务处对高三年级的学生进行编号,从001到240,抽取学号最后一位为3的同学进行调查,则这两种抽样方法依次为 ( )A .分层抽样,简单随机抽样B .简单随机抽样,分层抽样C .分层抽样,系统抽样D .简单随机抽样,系统抽样9.某班级有50名学生,现要采取系统抽样的方法在这50名学生中抽出10名学生,将这50名学生随机编号1~50号,并分组,第一组1~5号,第二组6~10号,…,第十组46~50号,若在第三组中抽得号码为12的学生,则在第八组中抽得号码为 的学生.10.甲校有3600名学生,乙校有5400名学生,丙校有1800名学生.为统计三校学生某方面的情况,计划采用分层抽样法,抽取一个样本容量为90人的样本,则应在甲校抽取的学生数是___________.11.已知y 与x 之间具有很强的线性相关关系,现观测得到),(y x 的四组观测值并制作了右边的对照表,由表中数据粗略地得到线性回归直线方程为60y bx =+,其中b 的值没有写上.当x 等于5-时,预测y 的值为 .12.一组数据2,,4,6,10x 的平均值是5,则此组数据的标准差是 .13.甲、乙两名运动员参加“选拔测试赛”,在相同条件下,两人5次测试的成绩(单位:分)记录如下:甲 86 77 92 72 78乙 78 82 88 82 95(1)用茎叶图表示这两组数据;.(2)现要从中选派一名运动员参加比赛,你认为选派谁参赛更好?说明理由(不用计算);(3)若从甲、乙两人的5次成绩中各随机抽取一个,求甲的成绩比乙高的概率.14.某商场经营一批进价是30元/台的小商品,在市场试验中发现,此商品的销售单价x(x 取整数)元与日销售量y(1)画出散点图,并判断y 与(2)求日销售量y 对销售单价x 的线性回归方程;(3)设经营此商品的日销售利润为P 元,根据(1)写出P 关于x 的函数关系式,并预测当销售单价x 为多少元时,才能获得最大日销售利润.寒假作业3参考答案1.C试题分析:∵1002004001400400x =++,∴20x =. 考点:分层抽样. 2.A 【解析】当x ≥4时,当x <4时,∴x =1.选A 3.D 试题分析:抽样比为2001200010=,设样本中女生有x 人,则x +(x 6200+=), 所以,97x =,该校共有女生97970110=人,考点:分层抽样. 4.A 试题分析:因为回归直线必过样本中心点,所以点()00,x y 满足线性回归方程y bx a =+;而()00,x y 不一定是这一组数据中的点,因此为充分不必要条件.考点:回归分析、充分必要条件.5.C中心点是(2.5,3.5),把样本中心点代入四个选项中,只有y=x+1成立,考点:线性回归方程.6.C 试题分析:采用系统抽样方法从960人中抽取32人,将整体分成32组,每组30人,即30l =,第k 组的号码为30(1)9k -+,令45130(1)9750k ≤-+≤,而k Z ∈,解得1625k ≤≤,则满足1625k ≤≤的整数k 有10个.考点:系统抽样.7.C 试题分析:依题意可得153347n =++,解得70n =。
故C 正确。
考点:分层抽样。
8.D 试题分析:第一种强调的是随机抽取故属于简单随机抽样;第二种强调抽取的是学号最后一位为3的同学,属系统抽样。
故D 正确。
考点:统计中的抽样方法。
9.37试题分析:由题设知第八组的号码数比第三组的号码数大(8﹣3)×5,由此能求出结果.解:这50名学生随机编号1~50号,并分组,第一组1~5号,第二组6~10号,…,第十组46~50号,在第三组中抽得号码为12的学生,则在第八组中抽得号码为12+(8﹣3)×5=37.故答案为:37.点评:抽样选用哪一种抽样形式,要根据题目所给的总体情况来决定,若总体个数较少,可采用抽签法,若总体个数较多且个体各部分差异不大,可采用系统抽样,若总体的个体差异较大,可采用分层抽样.10.30试题分析:分层抽样时样本容量与总体容量成正比.考点:分层抽样.11.70 试题分析:由已知, 1813101104x ++-==,24343864404y +++==, 所以401060,2b b =+=-, 260y x =-+,当5x =-时,70y =,答案为70.考点:回归直线方程及其应用12.试题分析:因为一组数据2,,4,6,10x 的平均值是5,所以3x =.因此方差为1[941125]8,5++++=标准差是注意审题.考点:数据分析相关知识 13.(1)茎叶图见解析;(2)乙;(3)725. 试题分析:(1)茎叶图是将数组中的数按位数进行比较,将数的大小基本不变或变化不大的位作为一个主干(茎),将变化大的位的数作为分枝(叶),列在主干的后面,这样就可以清楚地看到每个主干后面的几个数,每个数具体是多少。
在制作茎叶图时,重复出现的数据要重复记录,不能遗漏,特别是“叶”部分,同一数据出现几次,就要在图中体现几次;(2)可计算出两人的平均成绩,方差(以说明他的稳定性),最高成绩等数据,然后比较得出结论;(3)甲乙两人各5个数据,因此各抽取一个,可以用列举法列出所有情形,共25个,然后在其中观察计数甲比乙大的组合,有7个,那么所求概率为725. 试题解析:(1)茎叶图 6257882287298乙甲 3分(2)由图可知,乙的平均成绩大于甲的平均成绩,且乙的方差小于甲的方差,且乙的最高分高于甲的最高分,因此应选派乙参赛更好. 6分(3)记事件A : 甲的成绩比乙高从甲、乙两人5次的成绩中各随机抽取一个成绩,所有的基本事件如下:{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}86,78,86,82,86,88,86,82,86,9577,78,77,82,77,88,77,82,77,9592,78,92,82,92,88,92,82,92,9572,78,72,82,72,88,72,82,72,9578,78,78,82,78,88,78,82,78,95共25个. 9分事件A 包含的基本事件有{}{}{}{}{}{}{}86,78,86,8286,82,92,78,92,82,92,88,92,82,共7个 11分 ∴7()25P A = 13分 考点:(1)茎叶图;(2)样本数据的特征;(3)古典概型.14.(1)见解析 (2) y =-3x +161.5 (3) 销售单价为42元时,能获得最大日销售利润【解析】解:(1)散点图如图所示,从图中可以看出这些点大致分布在一条直线附近,因此两个变量线性相关.(2)∵x =14×(35+40+45+50)=42.5. y =14×(56+41+28+11)=34. 41i ii x y =∑=35×56+40×41+45×28+50×11=5 410. 421i i x=∑=352+402+452+502=7 350. ∴b =41422144i ii i i x y x y xx ==-⋅⋅-⋅∑∑=25410442.5347350442.5-⨯⨯-⨯=370125-≈-3. ∴a =y -b x =34-(-3)×42.5=161.5.∴y =-3x +161.5.(3)依题意有P =(-3x +161.5)(x -30)=-3x 2+251.5x -4 845=-3(x -251.56)2+2251.512-4 845. ∴当x =251.56≈42时,P 有最大值,约为426. 即预测销售单价为42元时,能获得最大日销售利润.方法点评:该题属于线性回归问题,解答本类题目的关键首先应先通过散点图(或相关性检验求相关系数r)来分析两变量间的关系是否相关,然后再利用求回归方程的公式求解回归方程,在此基础上,借助回归方程对实际问题进行分析.。
