第二章 状态方程的解
2_状态方程求解

4) (t2 t1 ) (t1 t0 ) (t2 t0 )
e At e Bt e( A B )t 5)当且仅当AB=BA时
状态转移矩阵的基本性质
1) (t ) A (t ) (t ) A
2) (0) I
3)
(t )1 1 (t ) (t )
5 线性系统的脉冲响应矩阵
6 线性连续系统方程的离散化
7 线性离散系统的运动分析 8 用MATLAB求解系统方程
2.1
线性定常系统齐次状态方程的解
x (t ) Ax (t )
(1)
线性定常系统齐次状态方程为 这时系统的输入为零 先考察标量齐次微分方程的幂级数解法
x ax
假设其解为一幂级数
如果 [ sI A]为非奇异
[ sI A] x ( s) x (0)
1
x(s) [sI A]1 x(0) [sI A]1 x(0)
(10)
x (t ) L
1
{[sI A]1 x(0)} L
1
由微分方程解的唯一性
(t ) e At L
[sI A]1
而 b0 x(0) (4)
则解为 x(t ) (1 at 因为
1 2 2 1 a t a k t k ) x(0) e at x(0) 2! k!
1 2 2 1 a t akt k 2! k!
e at 1 at
模仿标量齐次微分方程的解法,假设线性定常系统齐次状态方程 (1)的解为 (5) x b0 b1t b2t 2 b3t 3 bk t k 将(5)式代入(1)式
e
Jt
现代控制理论第二章

= α n −1 (t ) An −1 + α n − 2 (t ) An − 2 + ⋯ + α1 (t ) A + α 0 (t ) I
【例2-5】见板书
(3)α i (t )的计算公式 A的特征值互异时 α 0 (t ) 1 λ1 α1 (t ) 1 λ2 ⋮ = ⋮ ⋮ α (t ) 1 λ n −1 n
λ λ λ
பைடு நூலகம்
2 1 2 2
⋮
2 n
⋯ λ e λ1t λ2 t ⋯ λ e ⋮ ⋮ λn t n −1 ⋯ λn e
At
2.变换A为约旦标准型 (1)A特征根互异 Λ = T −1 AT 有
例2-2 ,同例2-1
e At = Te ΛtT −1
(2)A特征值有重根
J = T AT e At = Te JtT −1
0 1 0 [例2 - 3]已知A = 0 0 1 , 求e At 2 - 5 4
若
σ ω A= −ω σ
则
cos ωt sin ωt σt e = Φ(t ) = e − sin ωt cos ωt
At
2.2.4 计算
1.根据 e At 或 Φ (t ) 的定义直接计算
1 2 2 1 33 1 n n e = I + At + A t + A t ⋯ A t + ⋯ 2! 3! k! 1 0 [例2 - 1]已知A = , 求e At − 2 − 3
现代控制理论基础第二章习题答案

第二章 状态空间表达式的解3-2-1 试求下列矩阵A 对应的状态转移矩阵φ(t )。
(1) ⎥⎦⎤⎢⎣⎡-=2010A (2) ⎥⎦⎤⎢⎣⎡-=0410A (3) ⎥⎦⎤⎢⎣⎡--=2110A (4) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=452100010A (5)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0000100001000010A (6)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=λλλλ000100010000A 【解】:(1) (2) (3) (4)特征值为:2,1321===λλλ。
由习题3-1-7(3)得将A 阵化成约当标准型的变换阵P 为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=421211101P ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=-1211321201P线性变换后的系统矩阵为:(5)为结构四重根的约旦标准型。
(6)虽然特征值相同,但对应着两个约当块。
或}0100010000{])[()(1111----⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------=-=Φλλλλs s s s L A sI L t 3-2-2 已知系统的状态方程和初始条件 (1)用laplace 法求状态转移矩阵; (2)用化标准型法求状态转移矩阵; (3)用化有限项法求状态转移矩阵; (4)求齐次状态方程的解。
【解】:(1) (2)特征方程为: 特征值为:2,1321===λλλ。
由于112==n n ,所以1λ对应的广义特征向量的阶数为1。
求满足0)(11=-P A I λ的解1P ,得:0110000000312111=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--P P P ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0011P 再根据0)(22=-P A I λ,且保证1P 、2P 线性无关,解得:对于当23=λ的特征向量,由0)(33=-P A I λ容易求得: 所以变换阵为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-==110010001321P P P P ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=-1100100011P 线性变换后的系统矩阵为:(3)特征值为:2,1321===λλλ。
第二章流体的P-V-T关系与状态方程

2.2.3 立方型状态方程
2.2.3.1 Van der Waals (vdW)范德华方程
RT a pVbV2
体积修正项, b为有效分子体 积,斥力参数
压力修正项, a为引力参数
vdW方程的优点:
1)1873年范德华在其著名的论文“关于气态和液态的连 续性”中提出,是第一个有实用意义的状态方程。1910年 曾获诺贝尔奖。
方程两边乘以 (V b ) P
得:
RT a(Vb)
VbPP1 T/2VVb
V k 1R P TbPa 1T /2 V V k k V b kb
初值取
1.875107
理想气体EOS只适合压力非常低的气体, 不适合真实气体。
2.2.2 气体的非理想性
真实气体分子有大小、分子间有相互作用力是造成气体非理 想性的原因。 真实气体对理想气体的偏离程度可以用压缩因子Z来表达:
Z PV V RT Vig
分子间吸引力促使Z<1; 分子间排斥力使Z>1; 吸引力和排斥力的平衡暗指Z=1。
方程在P →0 时,应变为:PV = RT
2. 低压下的气体(特别是难液化的N2,H2,CO,CH4,…), 在工程设计中,在几十个大气压(几个MPa)下,仍可按 理想气体状态方程计算P、V、T: 而对较易液化的气体,如NH3,CO2,C2H4(乙炔)等,在 较低压力下,也不能用理想气体状态方程计算。
对方程的引力项进行修正,以使计算的V减小, 提高计算的准确性,是真正实用的EOS。
R-K 方程中的常数a,b 的求取
•用同于vdW方程的方法得到常数a,b值, •即临界等温线在临界点的条件得到:
a 0 .42748
R
2T
2.5 c
第2章 控制系统状态空间表达式的解

其必满足方程(2-1),将上式代入方程(2-1)可得 比较可得:
b1 2b2 t 3b3t 2 A( b0 b1t b2 t 2 )
1 1 2 1 1 3 1 k b1 Ab0,b2 Ab1 A b0,b3 Ab2 A b0, ,bk A b0, 2 2 3 3! k!
1 k k 1 t 1 k k k! e1t 1 t k 0 k! 1 T 1 1 T T T T ( )T k 0 1 k k ent 1 k k k! nt nt k 0 k!
1 2 2 1 3 3 At x( t ) ( I At A t A t )x0 e x0 2! 3!
线性定常系统零输入响应的几点说明: l如果t取某个固定值,零输入响应就是状态空间中由初始状态 x0 经线性 变换阵 e At 所导出的一个变换点。系统的自由运动就是由初始状态 x0 出 发,并由各个时刻的变换点 x0 所组成的一条轨线。
§2-1 线性定常齐次状态方程的解(自由解)
而
e J it
1 k 1 J1 t k 1 k 0 k! k 0 k! i
i 1
tk
k
1 0 it e 0 0
1 2 1 t t t i 1 2! ( i 1)! 1 1 t t i 2 ( i 2)! 0 0 t 0 0 1
ቤተ መጻሕፍቲ ባይዱ
1 1 a 0 ( t ) a ( t ) 1 1 2 2 n 1 a n1 ( t ) 1 n n n
现代控制理论(第二章)讲解

sI
A 1
s 2
s3
1 1 s 3
(s
1)(s 2
2)
(s 1)(s 2)
1
(s
1)(s s
2)
(s 1)(s 2)
s3
e At
L1
(s
1)( s 2
2)
(s 1)(s 2)
EAST CHINA INSTITUTE OF TECHNOLOgy
第二章 控制系统状态空间表达式的解
2.1 线性定常齐次状态方程的解(自由解) 2.2 矩阵指数函数——状态转移矩阵 2.3 线性定常系统非齐次方程的解 2.4 * 线性时变系统的解 2.5 * 离散时间系统状态方程的解 2.6* 连续时间状态空间表达式的离散化
(s
1)( s 2
2)
(s 1)(s 2)
1
(s
1)( s s
2)
(s 1)(s 2)
eAt L1
sI A 1
2et e2t 2et 2e2t
et e2t
et
2e2t
et
2e2t
例2-6,利用凯莱-哈密顿定理— -----------------自学! 例2-3与例2-7也请注意自学!
EAST CHINA INSTITUTE OF TECHNOLOgy
2.3 线性定常系统非齐次方程的解
现在讨论线性定常系统在控制作用 方程为非齐次矩阵微分方程:
第二章 状态方程的解

例1:设系统的状态方程为 :
ɺ x1 0 1 x1 = ɺ x2 0 0 x2
试求状态转移矩阵. 试求状态转移矩阵
解:求状态转移矩阵为
1 22 1 k k Φ(t ) = e = I + At + A t + ⋯ + A t + ⋯ 2! k!
e
At
矩阵,称矩阵指数。 为n×n矩阵,称矩阵指数。
于是, 于是,齐次状态方程的解为
x(t ) = e x(0)
At
若初始时刻 t0 ≠0 ,对应的初始状态为 x(t0 ) ,则 齐次状态方程的解为
x(t ) = e
A ( t −t0 )
x(t0 )
Φ (t ) = e
At
状态转移矩阵具有以下性质: 状态转移矩阵具有以下性质:
λk +1 , λk + 2 ,⋯ , λn 互异,则 A 的 (n − k) 个互异特征值均满足系统方程,得到 (n − k) 个代数方程。
eλit = α0 (t ) + α1 (t )λi + ⋯ + αn−1 (t )λin−1 , i = k + 1, k + 2,⋯, n
对于 A 的 k 重特征根,则有下列 k 个代数方程。 将 λ1 代入系统方程,得
Φ(t ) = e At = I + At + 1 22 1 A t + ⋯ + Ak t k + ⋯ 2! k!
n −1
= α0 (t ) I + α1 (t ) A + ⋯ + αn−1 (t ) A
= ∑αk (t ) Ak
k =0
系统的状态空间模型
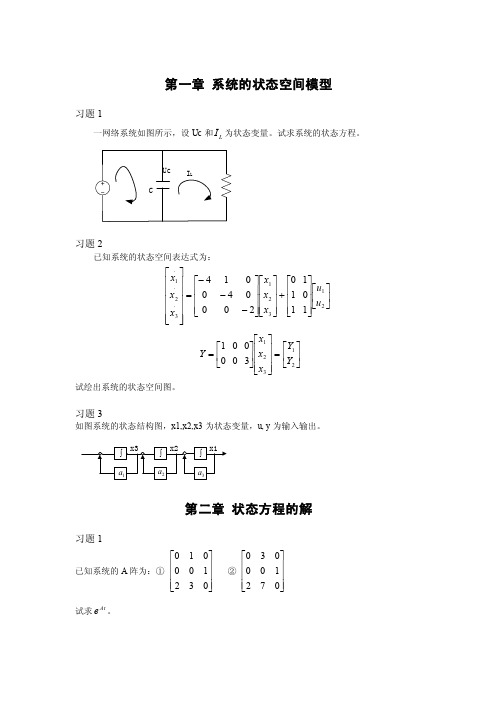
第一章 系统的状态空间模型习题1一网络系统如图所示,设Uc 和L I 为状态变量。
试求系统的状态方程。
习题2已知系统的状态空间表达式为:⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡21321.3.2.1101110200040014u u x x x x x x⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=21321300001Y Y x x x Y 试绘出系统的状态空间图。
习题3如图系统的状态结构图,x1,x2,x3为状态变量,u, y 为输入输出。
第二章 状态方程的解习题1已知系统的A 阵为:① ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡032100010 ②⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡072100030 试求At e 。
习题2F= ⎥⎦⎤⎢⎣⎡--5610 G=⎥⎦⎤⎢⎣⎡11 试求系统当u (k )=3的解。
第三章 能控性和能观性习题1能控且能观的两个系统1S ,2S : 1S :11111.u b x A x +=, 111x c y = 其中,⎥⎦⎤⎢⎣⎡--=43101A ,⎥⎦⎤⎢⎣⎡=101b ,[]121=c ,2S :22222.u b x A x +=,222x c y = 12-=A ,12=b ,12=c① 试求对于⎥⎦⎤⎢⎣⎡=21x x x 的状态方程。
② 考察图中系统得能控性及能观性。
③ 求关于1S ,2S 这两个子系统得传递函数,并验证②。
习题2直流电动机系统如下:RL① 以w 为输出时的状态能控性及输出能观性;② 以转角θ为输出时系统的能观性。
第四章 动态系统的确定性分析习题1⎪⎩⎪⎨⎧--==2.31.22.1x x x x x 试确定e x 的稳定性。
习题2⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=⎥⎥⎦⎤⎢⎢⎣⎡21.2.1211x x K x x试用李雅普诺夫理论求系统稳定时K 的取值范围 第五章 极点配置与观测器设计习题1试为下面系统设计一个全阶观测器,使闭环极点配置在-4和-5上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
or y(t)= Cx(t) = Cϕ (t ) x(0) + C ∫ ϕ (t ) Bu(τ )dτ t ≥ 0
(a) 设 n × n 矩阵 A 的特征值 λ1 , λ 2 ,⋯ λ n 是两两相异的,则
eλit = α0 (t ) + α1 (t )λi + ⋯ + αn−1 (t )λin−1 , i = 1, 2,⋯, n
因而,计算 α i ( t ) 的关系式为:
α 0 (t ) 1 λ1 α (t ) 1 = 1 λ2 ⋮ ⋮ ⋮ α n −1 (t ) 1 λn
举例 P69
kλ1 ⋯
(n − 1)⋯ (n − k + 1) n − k λ1 α (t) (k − 1)! 0 ⋮ α1 (t) (n − 1)(n − 2) n −3 α 2 (t) λ1 2! ⋮ (n − 1)λ1n − 2 α k −1 (t) λ1n −1 α k (t) λkn+−11 ⋮ α n −1 (t) ⋮ n −1 λn
第二章 状态方程的解
本章重点讨论在给定系统的输入信号和初始状 态下状态空间表达式的求解, 态下状态空间表达式的求解,并在此基础上定 义状态转移矩阵, 义状态转移矩阵,讨论状态转移矩阵的性质和 计算方法。状态空间表达式的求解, 计算方法。状态空间表达式的求解,有助于直 观地了解和分析系统, 观地了解和分析系统,获得描述系统所需的全 部信息。 部信息。
Φ(t ) = e At = I + At + 1 22 1 A t + ⋯ + Ak t k + ⋯ 2! k!
n −1
= α0 (t ) I + α1 (t ) A + ⋯ + αn−1 (t ) A
= ∑αk (t ) Ak
k =0
n −1
式中α 0 ( t ),α 1 ( t ),α 2 ( t ),⋯ ,α n−1 ( t ) 为 t 的函数。
1. 线性定常系统状态方程的零输入响应
(1)齐次状态方程的解 (1)齐次状态方程的解
齐次微分方程
ɺ x = Ax
方程的解为
(1)
x (t ) = b0 + b1t + b2t 2 + ⋯ + bk t k + ⋯ (2)
b 式中, 均为列向量。 式中, i ( i = 0 ,1, 2 ⋯ ) 均为列向量。
由状态转移方程,代入系统的输出方程, 由状态转移方程,代入系统的输出方程, 就可以得到系统在初始状态x(t , 就可以得到系统在初始状态 0),输入 作用为u(t)时,系统输出响应: 作用为 时 系统输出响应:
y(t)= Cx(t) = Cϕ (t − t0 ) x(t0 ) + C ∫ ϕ (t − t0 ) Bu(τ )dτ t ≥ t0
At
可以写出方程解为
0 1 2 0 0 3 n 其中 A = , A = A = ⋯ = A = 0 0 0 0 1 0 0 t 1 t Φ (t ) = + 0 0 = 0 1 0 1
x1 ( t ) 1 = x2 (t ) 0
λ12 ⋯ λ1n −1 λ22 ⋯ λ2n −1
⋮ ⋯
−1
λn2
⋮ ⋯ λnn −1
eλ1t λ2t e ⋮ λnt e
, 其 余 (n − k) 个 特 征 值
(b)
设
n× n
的矩阵 A 有 k 重特征值
λ1 = λ2 = ⋯ = λk
−1
1 1 − s +1 s + 2 −1 2 + s +1 s + 2
将上式进行拉氏反变换
2e−t − e−2t e−t − e−2t eAt = L−1[(sI− A)−1] = −t −2t −t −2t − e + 2e − 2e + 2e
状态方程之解为
k Akt
= Φ ( kt )
(2) 状态转移矩阵的计算 一、根据定义计算 二、应用拉氏变换法求解
ɺ x (t ) = Ax (t )
sX (s) − x0 = AX (s)
(3) (4)
X ( s ) = ( sI − A) x0
拉氏反变换后得到
−1
−1
x (t ) = L [( sI − A) ] x0
e
At
矩阵,称矩阵指数。 为n×n矩阵,称矩阵指数。
于是, 于是,齐次状态方程的解为
x(t ) = e x(0)
At
若初始时刻 t0 ≠0 ,对应的初始状态为 x(t0 ) ,则 齐次状态方程的解为
x(t ) = e
A ( t −t0 )
x(t0 )
Φ (t ) = e
At
状态转移矩阵具有以下性质: 状态转移矩阵具有以下性质:
将 x ( t ) 代入方程(1),得
b1 + 2b2t +⋯+ kbkt
b1 = Ab0 =
k −1
+⋯= A(b0 + b1t +⋯+ bkt +⋯)
k
方程两边系数必相等, 即
1 Ab0 1! 1 1 2 1 2 b2 = Ab1 = A b0 = A b0 2 2 2! 1 1 3 1 b3 = Ab2 = A b0 = A3b0 3 3× 2 3! ⋮ bk = 1 k A b0 k!
(3) 非齐次状态方程的解
非齐次方程
ɺ x (t ) = Ax (t ) + Bu (t )
改写为
ɺ x ( t ) − Ax ( t ) = Bu ( t )
用e
−At
左乘等式两边
e
− At
d − At ɺ [ x (t ) − Ax (t )] = [e x (t )] = e − At Bu (t ) dt
ɺ 1. Φ (t ) = AΦ (t ) 2. Φ (0) = I 3. Φ ( −t ) = e
− At
= ( e ) = Φ (t )
At −1
−1
4. Φ (t 2 − t1 )Φ (t1 − t0 ) = Φ (t 2 − t0 ) 5. Φ (t1 + t 2 ) = Φ (t1 )Φ (t 2 ) 6. [Φ (t )] = e
−t −2t 2e−t − e−2t e − e x1 (0) At x(t) = e x(0) = −t −2t −t −2t x2 (0) − e + 2e − 2e + 2e
三、应用凯莱-哈密顿定理 应用凯莱-
1.Calay-Hamilton 定理 . 设 n × n 系统矩阵 A 的特征多项式为:
λk +1 , λk + 2 ,⋯ , λn 互异,则 A 的 (n − k) 个互异特征值均满足系统方程,得到 (n − k) 个代数方程。
eλit = α0 (t ) + α1 (t )λi + ⋯ + αn−1 (t )λin−1 , i = k + 1, k + 2,⋯, n
对于 A 的 k 重特征根,则有下列 k 个代数方程。 将 λ1 代入系统方程,得
将t=0代入(2)式得 t=0代入(2)式得 代入(2)
x (0) = b0
因此,齐次状态方程的解为 因此,
1 22 1 k k x(t ) = ( I + At + A t + ⋯ + A t + ⋯) x(0) 2! k!
仿照标量指数函数 exp( at ) ,我们定义
e
At
1 2 2 1 K k = I + At + A t + ⋯ + A t +⋯ 2! k!
t0 t
上式通常又称为线性定常系统的状态转移方程。 上式通常又称为线性定常系统的状态转移方程。 其中, 其中,等式右边第一项是输入作用为零时的状态 转移,称为系统零输入的状态转移 系统零输入的状态转移; 转移,称为系统零输入的状态转移;第二项是系 统初始状态为零对应输入作用的状态转移, 统初始状态为零对应输入作用的状态转移,称为 系统零状态的状态转移。 系统零状态的状态转移。
在区间[0 t]上积分,得
e − At x(t ) = x(0) + ∫ e − Aτ Bu (τ )dτ
0t x(0) + ∫ e A( t −τ ) Bu (τ )dτ
可改写为
0
t
t
x (t ) = Φ (t ) x (0) + ∫ Φ (t − τ ) Bu (τ ) dτ
(3)
总共 n 个代数方程,写成向量矩阵形式为:
1 0 1 t k −1eλ1t 0 ⋯ (k − 1)! ⋮ ⋮ 1 2 λ1t 0 0 1 3λ1 te 2! λ1t = 0 1 2λ1 te λ12 eλ1t 1 λ1 1 λ λk2+1 eλk+1t k +1 ⋮ ⋮ ⋮ ⋮ λn2 eλn t 1 λn
f (λ ) = λ n + a1λ n −1 + ⋯ + an −1λ + an = 0 ,则 A 满足它自身的特征方程,
即方阵 A 的特征多项式是 A 的零化多项式。
f ( A) = An + a1 An −1 + ⋯ + an −1 A + an I = 0
