第六章 解线性方程组的迭代法 习题六 1 A 零矩阵 故 2 方 …
第六章 解线性方程组的迭代法 习题六 1 A 零矩阵 故 2 方 …
第六章解线性方程组的迭代法习题六
1.证明对于任意的矩阵A，序列
2. 方程组
J法与GS法均收敛。
具有严格对角占优，故
（2）J法得迭代公式是
取
证明解此方程的Jacobi迭代法与Gauss-Seidel迭代法同时收敛或发散
解：Jacobi迭代为
，而Gauss-Seide 迭代法为
其迭代矩阵
解：Jacobi法的迭代矩阵是
即
5. 设
得GS法收敛得充要条件是
7当
若取
第
对上题求出SOR迭代法的最优松弛因子及渐近收敛速，题第
度，并求J法与GS法的渐近收敛速度.若要使
，故
J法收敛速度
72`*+b数
各a K＝15
对于GS法
，取K＝5
8. 填空题
(1)
7则解此方程组的Jacobi迭代法是否收敛（）.它的渐近收敛速度R(B)=（）.
(3) 设方程组Ax=b,其中
(4) 用GS法解方程组
,a为实数.当a满足（），且0＜ω＜2时SOR迭代法收敛.
答:
(1)
(3)J法迭代矩阵是
(4)
(5)。
数值分析课后习题与解答
课后习题解答第一章绪论习题一1.设x>0,x*的相对误差为δ，求f(x)=ln x的误差限。
解：求lnx的误差极限就是求f(x)=lnx的误差限，由公式()有已知x*的相对误差满足，而，故即2.下列各数都是经过四舍五入得到的近似值，试指出它们有几位有效数字，并给出其误差限与相对误差限。
解：直接根据定义和式()(1.2.3)则得有5位有效数字，其误差限，相对误差限有2位有效数字，有5位有效数字，3.下列公式如何才比较准确？〔1〕〔2〕解：要使计算较准确，主要是避免两相近数相减，故应变换所给公式。
〔1〕〔2〕4.近似数x*=0.0310,是 3 位有数数字。
5.计算取，利用：式计算误差最小。
四个选项：第二、三章插值与函数逼近习题二、三1. 给定的数值表用线性插值与二次插值计算ln0.54的近似值并估计误差限. 解：仍可使用n=1与n=2的Lagrange插值或Newton插值,并应用误差估计〔5.8〕。
线性插值时，用0.5与0.6两点，用Newton插值误差限，因，故二次插值时，用0.5，0.6，0.7三点，作二次Newton插值误差限，故2. 在-4≤x≤4上给出的等距节点函数表，若用二次插值法求的近似值，要使误差不超过，函数表的步长h 应取多少?解：用误差估计式〔5.8〕，令因得3. 若，求和.解：由均差与导数关系于是4. 若互异，求的值，这里p≤n+1.解：，由均差对称性可知当有而当P＝n＋1时于是得5. 求证.解：解：只要按差分定义直接展开得6. 已知的函数表求出三次Newton均差插值多项式，计算f(0.23)的近似值并用均差的余项表达式估计误差.解：根据给定函数表构造均差表由式(5.14)当n=3时得Newton均差插值多项式N3(x)=1.0067x+0.08367x(x-0.2)+0.17400x(x-0.2)(x-0.3) 由此可得f(0.23) N3(0.23)=0.23203由余项表达式(5.15)可得由于7. 给定f(x)=cosx的函数表用Newton等距插值公式计算cos 0.048与cos 0.566的近似值并估计误差解：先构造差分表计算，用n=4得Newton前插公式误差估计由公式〔5.17〕得其中计算时用Newton后插公式〔 5.18)误差估计由公式〔5.19〕得这里仍为0.5658．求一个次数不高于四次的多项式p(x),使它满足解：这种题目可以有很多方法去做，但应以简单为宜。
数值分析--第6章 解线性方程组的迭代法
数值分析--第6章解线性方程组的迭代法第6章 解线性方程组的迭代法直接方法比较适用于中小型方程组。
对高阶方程组，即使系数矩阵是稀疏的，但在运算中很难保持稀疏性，因而有存储量大，程序复杂等不足。
迭代法则能保持矩阵的稀疏性，具有计算简单，编制程序容易的优点，并在许多情况下收敛较快。
故能有效地解一些高阶方程组。
1 迭代法概述迭代法的基本思想是构造一串收敛到解的序列，即建立一种从已有近似解计算新的近似解的规则。
由不同的计算规则得到不同的迭代法。
迭代法的一般格式(1)()(1)()(,,,),0,1,k k k k m kF k +--==x x x x式中(1)k +x 与()(1)(),,,k k k m --x x x 有关，称为多步迭代法。
若(1)k +x 只与()k x 有关，即(1)()(),0,1,k k kF k +==x x称为单步迭代法。
再设kF 是线性的，即(1)(),0,1,k kk kk +=+=x B x f式中n nk ⨯∈B R ，称为单步线性迭代法。
kB 称为迭代矩阵。
若k B 和kf 与k 无关，即(1)(),0,1,k k k +=+=x Bx f称为单步定常线性迭代法。
本章主要讨论具有这种形式的各种迭代方法。
1.1 向量序列和矩阵序列的极限由于nR 中的向量可与nR 的点建立——对应关系，由点列的收敛概念及向量范数的等价性，可得到向量序列的收敛概念。
定义6.1 设(){}k x 为n R 中的向量序列，nx R ∈，如果()lim 0k k x x →∞-=其中为向量范数，则称序列(){}k x 收敛于x ，记为()lim k k x x →∞=。
定理6.1 nR 中的向量序列(){}k x 收敛于nR 中的向量x 当且仅当()lim (1,2,,)k i i k x x i n →∞==其中()()()()1212(,,,),(,,,)k k k k T Tnnx x x x x x x x ==。
第六章 回归问题——线性方程组求解的迭代法
第六章回归问题——线性方程组求解的迭代法6.1 回归问题6.1.1 问题的引入在数理统计中，把研究对象的全体称为总体，而把组成总体的每个单元称为个体，要了解总体的规律性，必须对其中的个体进行统计观测。
但若对全部个体进行观测，这样能对总体有充分的了解，但实际上行不通，而且也不经济。
所以对整体进行随机抽样观测，再根据抽样观察的结果来推断总体的性质成为一种重要的方法。
许多数理统计建模的实际问题中，一个随机变量与另一个随机变量的关系不是线性关系，而是曲线关系，那么如何确定回归方程呢？下表给出了某种产品每件平均单价y（元）与批量x（件）之间的关系的一组数据，试确定y与x的函数关系。
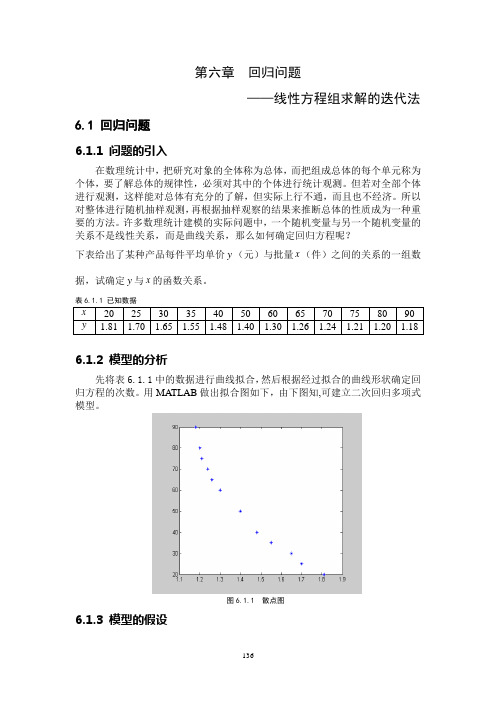
表6.1.1 已知数据6.1.2 模型的分析先将表6.1.1中的数据进行曲线拟合，然后根据经过拟合的曲线形状确定回归方程的次数。
用MATLAB做出拟合图如下，由下图知,可建立二次回归多项式模型。
图6.1.1 散点图6.1.3 模型的假设假设上表给出的数据是真实的，且以上数据是随机抽取的可以较准确地推断单位与批量的关系，假设单价与批量的函数关系是一个多项式函数，可用多项回归来建立模型。
6.1.4 模型的建立根据模型的分析，可以建立多项式模型22012,(0,)y x x N βββεεδ=+++ ，令212,x x x x ==，则回归方程可写成2201121,(0,)y x x N βββεεδ=+++ ，这是一个二元线性回归模型。
且()T T X X X Y β=，其中：120400 1.18125625 1.70130900 1.651351225 1.551401600 1.481502500 1.40 1603600 1.301654225 1.261704900 1.241755625 1.211806400 1.201908100 1.18X Y ⎡⎤⎡⎢⎥⎢⎢⎥⎢⎢⎥⎢⎢⎥⎢⎢⎥⎢⎢⎥⎢⎢⎥⎢⎢⎥⎢==⎢⎥⎢⎢⎥⎢⎢⎥⎢⎢⎥⎢⎢⎥⎢⎢⎥⎢⎢⎥⎢⎢⎥⎢⎥⎣⎦⎣012 =ββββ⎤⎥⎥⎥⎥⎥⎥⎥⎡⎤⎥⎢⎥⎥⎢⎥⎥⎢⎥⎣⎦⎥⎥⎥⎥⎥⎢⎥⎢⎥⎦ 6.2 线性方程组迭代法概述迭代法：即用某种极限过程逐步逼近线性方程组精确解的方法。
第6章 线性方程组迭代解法 参考答案
第6章 线性方程组迭代解法 参考答案一、选择题（15分，每小题3分)1、(3)2、(4)3、(4)4、(1)5、(2)二、填空题（15分，每小题3分）1、1a <；2、2a <；3、1a <；4；5、Ax b − 三、（9分）解： (1) 19.01<=B ，∴迭代法f Bx x k k +=−1的收敛；--------------------（3分）(2) B 的特征值8.0,5.1=λ，15.1)(>=B ρ，∴迭代法f Bx x k k +=−1发散；（6分）(3) B 的特征值19.0)(<=B ρ，∴迭代法f Bx x k k +=−1收敛。
---------（9分）四、（14分）解：（1）Jacobi 迭代法的分量形式1123121313121222012322()()()()()()()()();,,,k k k k k k k k k x x x x x x k x x x +++⎧=−+⎪=−−=⎨⎪=−−⎩L ----------------------------------（2分） Gauss-Seidel 迭代法的分量形式1123112131113121222012322()()()()()()()()();,,,k k k k k k k k k x x x x x x k x x x ++++++⎧=−+⎪=−−=⎨⎪=−−⎩L ---------------------------------（4分） （2）Jacobi 迭代法的迭代矩阵为1022101220()B D L U −−⎡⎤⎢⎥=+=−−⎢⎥⎢⎥−−⎣⎦， --------------------------------（6分） 1230λλλ===，01()B ρ=<，Jacobi 迭代法收敛 ------------------------（8分） Gauss-Seidel 迭代法的迭代矩阵为1022023002()G D L U −−⎡⎤⎢⎥=−=−⎢⎥⎢⎥⎣⎦， --------------------------------（10分） 12302,λλλ===，21()B ρ=>，Gauss-Seidel 迭代法发散------------------（12分）（3）SOR 迭代法的分量形式1112311221311133120515122051520120515322()()()()()()()()()()()()..()..();,,,..()k k k k k k k k k k k k x x x x x x x x k x x x x ++++++⎧=−+−+⎪=−+−−=⎨⎪=−+−−⎩L ----------------------（14分） 五、（10分）证明：由**x Bx g =+与(1)()k k xBx g +=+相减得()(1)*()*k k x x B x x +−=− 反复递推得 ()(1)*1(0)*k k x x B x x ++−=− ---------------------------------（4分）设矩阵B 的对应于特征值λ的特征向量为y ，若取初始向量(0)*x x y =+，则(1)*11k k k x x B y y λ+++−== --------------------------------（6分）从而有 1(1)*k k xx y λ++−= --------------------------------（8分） 因为1λ<，所以(1)*lim 0k k x x +→∞−=，即(1)k x +收敛到*x 。
12 第六章解线性代数方程组的迭代方法
13
( k 1)
r 设有简单迭代法X
( k 1)
r BX
(k )
r g,现 将 迭 代
矩 阵 B ( b ij ) n n 分 解 为 B L U , 其 中 b1 n 0 0 b1 2 L b21 0 0 L b2 n ,U L M M O O M 0 0 bn1 bn 2 L r r r r ( k 1) (k ) (k ) 则X LX UX g ( k 0,1, 2, L ) 现将其修改为 : r r r ( k 1) ( k 1) X LX UX r g
15 代 的 分 量 形 式 : xi
( k 1)
b
j 1
i 1
ij
xj
( k 1)
j i 1
n
b ij x j
(k)
gi
( i 1, 2, L , n ; k 0,1, 2, L )
S ei d el 迭 代 的 矩 阵 形 式 : r r ( k 1) 1 (k ) 1 r X (I L) UX (I L) g
20
松驰法的分量形式为 : xi
( k 1)
(1 ) x i
(k )
i 1 ( k 1) b ij x j j 1
j i 1
n
b ij x j
(k)
gi
( i 1, 2, L , n ; k 0,1, 2, L )
5 0.9890 2.0114
6 1.0032 1.9922
7 0.9981 2.0023
数值分析第六章线性方程组迭代解法
数值分析第六章线性方程组迭代解法线性方程组是数值分析中的重要内容之一，其求解方法有很多种。
其中一种常用的方法是迭代解法，即通过不断迭代逼近方程组的解。
本文将介绍线性方程组迭代解法的基本思想和常用方法。
线性方程组可以用矩阵形式表示为Ax=b，其中A是系数矩阵，b是常数向量，x是未知向量。
线性方程组的解可以是唯一解，也可以是无穷多个解。
迭代解法的基本思想是通过不断迭代，并利用迭代序列的极限，逼近线性方程组的解。
迭代解法适用于大型的线性方程组，而直接求解法则适用于小型的线性方程组。
常用的迭代解法有雅可比迭代法、高斯-赛德尔迭代法和逐次超松弛迭代法。
雅可比迭代法是最简单的线性方程组迭代解法之一、它的基本思想是将线性方程组的每个方程都单独表示为未知数x的显式函数，然后通过不断迭代求解。
雅可比迭代法的迭代公式为：x(k+1)=D^(-1)(b-(L+U)x(k))其中，D是A的对角元素构成的对角矩阵，L是A的下三角矩阵，U 是A的上三角矩阵，x(k)是第k次迭代的解。
高斯-赛德尔迭代法是雅可比迭代法的改进版。
它的基本思想是将每个方程的解带入到下一个方程中，而不是等到所有方程都迭代完毕后再计算下一组解。
高斯-赛德尔迭代法的迭代公式为：x(k+1)=(D-L)^(-1)(b-Ux(k))其中，D是A的对角矩阵，L是A的下三角矩阵（除去对角线），U是A的上三角矩阵（除去对角线），x(k)是第k次迭代的解。
逐次超松弛迭代法是对高斯-赛德尔迭代法的改进。
它引入了松弛因子w，通过调节松弛因子可以加快收敛速度。
逐次超松弛迭代法的迭代公式为：x(k+1)=(D-wL)^(-1)[(1-w)D+wU]x(k)+w(D-wL)^(-1)b其中，D是A的对角矩阵，L是A的下三角矩阵（除去对角线），U是A的上三角矩阵（除去对角线），w是松弛因子，x(k)是第k次迭代的解。
线性方程组迭代解法需要设置迭代停止准则，通常可以设置迭代次数上限或者设置一个精度要求。
第六章解线性方程组的迭代法
a11
A
a22
0
-
a21
0
ann
an1
an2
D LU
x M 1Nx M 1b
这样，可构造迭代法：
0 a12
-
0
0
a1n
a2n
0
取x(0)为初始向量
x(k
1)
Bx(k )
f
(k 0,1,
)
其中：B M 1N M 1(M A) I M 1A, f M 1b, 称 B I M 1A
为迭代法的迭代矩阵，选取 M 阵，就得到解 Ax b 的各
种迭代法。
6.2 基本迭代法
设 aii 0(i 1, 2, , n) ，并将 A 写为三部分：
Jacobi迭代法的分量表示
记 x(k) (x1(k) , , xi(k) , , xn(k) )T 由Jacobi迭代公式可得：Dx(k1) (L U )x(k) b ，写成分量
i1
n
形式即为：aii xi(k1) aij x(jk)
aij
x(k) j
13 15
例：用迭代法求解线性方程组：
9x1 x2 x3 7 x1 10x2 x3 8
x1 x2 15x3 13
记为：Ax b，其中：
9 1 1 x1 7
A
1
10
1 ,
x
x2
数值分析分章复习(第六章线性方程组迭代解法)
第六章 线性方程组迭代解法要点：（1）线性方程组迭代格式：Jacobi 迭代，G-S 迭代 （2）矩阵范数计算，矩阵谱半径计算（3）线性方程组迭代格式(1)()k k x Bx f +=+的收敛性判断（4）Jacobi 迭代，G-S 迭代收敛的判断 （5）线性方程组的性态 复习题：1、已知线性方程组为123211*********x x x -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦（1）写出Jacobi 迭代格式和Seidel 迭代格式； （2）写出Jacobi 迭代矩阵和Seidel 迭代矩阵； （3）判别这两种迭代法的收敛性。
解：(1) Jacobi 迭代格式： (1)()()123(1)()()213(1)()()312111222311122k k k k k k k k k x x x x x x x x x +++⎧=-+⎪⎪⎪=--+⎨⎪⎪=+-⎪⎩Gauss-Seidel 迭代格式：(1)()()123(1)(1)()213(1)(1)(1)312111222311122k k k k k k k k k x x x x x x x x x ++++++⎧=-+⎪⎪⎪=--+⎨⎪⎪=+-⎪⎩（2）Jacobi 迭代矩阵：111022()10111022J B D L U -⎛⎫- ⎪ ⎪=+=-- ⎪ ⎪⎪⎝⎭Gauss-Seidel 迭代矩阵：11102211()0221002GS B D L U -⎛⎫- ⎪ ⎪⎪=-=-- ⎪ ⎪⎪- ⎪⎝⎭ （3） 35||4J I B λλλ-=+，得J B的特征值为12,30, 2λλ==±()12J B ρ=>， 可见Jacobi 迭代格式不收敛另外， 21||()2GS I B λλλ-=+，得GS B 的特征值为12,310, 2λλ==-1()12GS B ρ=<， 可见Gauss-Seidel 迭代格式收敛2、设方程组1312123879897x x x x x x x -+=⎧⎪-+=⎨⎪--=⎩试问，是否可以适当调整方程的排列顺序，使得用Gauss-Seidel 迭代法求解时收敛？说明收敛原因解：可通过方程顺序交换，等价为以下方程组1231213979887x x x x x x x --=⎧⎪-+=⎨⎪-+=⎩这样，系数矩阵911190108--⎛⎫⎪- ⎪ ⎪-⎝⎭为严格对角占优矩阵，对该方程组使用Jacobi 迭代和Gauss-Seidel 迭代均收敛3、对方程组⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡43132121x x ，验证Jacobi 迭代法的收敛性，若发散，则说明理由， 并调整方程顺序使得Jacobi 迭代收敛。
第6章 线性方程组的迭代法
( 0) ( 0) ( 0) X 0 ( x1 , x2 ,, xn ),
雅可比迭代法公式的分量形式为：
( k 1) 1 (k ) (k ) (k ) (b1 a12 x 2 a13 x 3 a1n x n ) x1 a11 ( k 1) 1 (k ) (k ) (k ) x ( b a x a x a x 2 2 21 1 23 3 2n n ) a 22 1 ( k 1) (k ) (k ) (k ) x ( b a x a x a x n n1 1 n2 2 n n 1 n 1 ) n a nn
x( k 1) x( k ) 10m
这种方法称为迭代法。
2016/11/19
接下来的问题就是迭代矩阵 G 的构造法。
5
§6.2 雅可比（Jacobi）迭代法
考察一般的 n元线性方程组
a11 x1 a12 x 2 a1n x n b1 a x a x a x b 21 1 22 2 2n n 2 a n1 x1 a n 2 x 2 a nn x n bn
或 构造方程组的等价方程组
x1 x1 x2 3 x2 2 x1 4 x2 3
Jacobi迭代公式。
(k ) ( k 1) 3 x2 x 1 2 2 (k ) 3 2 x ( k 1) 1 x2 5 5
据此建立迭代公式
第六章 解线性方程组的迭代法
1. 雅可比（Jacobi）迭代法 2. 高斯-塞德尔(Gauss-Seidel)迭代法
3. 超松弛迭代法（SOR方法）
4. 迭代法的收敛性
第6章 解线性方程组的迭代法
有 lim || Ak x || 0.所以就有定理的右边成 立。
k
反之，若定理的右边成 立，取x为第j个坐标向量e j， 则 lim Ak e j 0, 表示Ak的第j列元素极限均为零，当
k
j 1,2, , n时就证明了lim Ak 0，证毕。
k
给出的迭代法
( ( x1( k 1) (3x2k ) 2 x3k ) 20) / 8 ( k 1) (k ) (k ) x2 (4 x1 x3 33) / 11 的收敛性。 ( ( x3k 1) (6 x1( k ) 3x2k ) 36) / 12
第6章
解线性代数方程组的迭代法
§1 引言
考虑线性方程组
a11x1 a12 x2 a1n xn b1 a x a x a x b 21 1 22 2 2n n 2 an1x1 an2 x2 ann xn bn
(1.4)
即
x(k+1)=B0x(k)+f， (k=0,1,2,„)
x (10 ) (3.0000321.999838 0.9998813T , , , ) ε
(10 )
0.000187其中ε ,
(k )
(10 )
x
(10 )
x *.
从此例可以看出，由迭 代法产生的向量 序列x 逐步逼近此方程的精确 解。
3 8
0
3 12
2 8 1 11 0
20 x1 8 x 33 . 2 11 x3 36 12
任取初值,如x(0)=(0,0,0)T,代入(1.3)得到x(1)= (2.5,3,3)T. 反复迭代
(数值分析)第六章 解线性方程组的迭代法
华长生制作
1
定义1 设 中的向量序列，若有向 k n x 量 x R ，使 lim x x 0 ，则称 k lim x x 收敛于 x ，记为 k
x
k
是R
n
(k)
k
nn A R 定义2 设 是 中的矩阵序列，若有矩 n n lim A A 0 A A R 阵 ，使 ，则称 lim A A 收敛于A，记为
k 1 k x B x f
华长生制作
17
定理5.
设 方 程 x = B x + f 有 惟 一 解 x , 若 B 1 , 则 由
简 单 迭 代 法 产 生 的 向 量 序 列 x 满 足
x x
(k )
x x
B 1 B B
k
k
x( k ) x( k 1) x1 x 0
( 0 ) 取初始向量 x ,代入 ( 2 ), 可得
( 1 ) ( 0 ) x Bx f
依此类推
华长生制作 11
(2 ) ( 1 ) x Bx f
(k) x(k1) Bx f
--------(3)
( k 0 , 1 , 2 , )
这种方式就称为迭代法 ,以上过程称为迭代过程
k
k n l i m Ax 0 , x R 0 的 充要条件是
lim Ak 0.
k
R 定理 4 设矩阵 B ，则 k 的充分 m a x B B . 必要条件是 B 的谱半径 (B) 1 ，其中 i 1 i n
( n n )
第六章 解线性方程组的迭代法-2
j= 1 j=i i− 1 n
21
(2) 如 p > p0 则 0 ← p 果 p
(3) xi ←xi + p
6. 输 p0 出 7. 如 p0 <eps 则 出k,ω,x, 停 果 输 机
8. 如 k< N0 则 3 果 转
A 11 A 21 A= M A q1 A 12 A 22 M A2 q L Aq A 1 11 L Aq 2 , D= M L A qq A 22 , O A qq
24
0 −A 21 L= M −A q1
0 M −A 2 q
0 − A 12 0 , U = O L 0
L −Aq 1 L −A q 2 . O M 0
q
n , , 且 A (i =1 2,L q) 为 ni ×ni非奇异矩阵， ∑ i =n. ii
i= 1
对 x及 b同样分块
aii ≥ ∑ aij
1 j= j ≠i n
(i =1 2,L n). , ,
弱对角占优阵. 弱对角占优阵 且上式至少有一个不等式严格成立，称 A为弱对角占优阵
1
定义4 (可约与不可约矩阵) 设 A = (aij )n×n (n ≥ 2) , 定义4 如果存在置换阵 P使
A P AP = 11 0
之根. 记
λa 11 λa21 C ≡λ(D−L)−U = M λa n1
λa22
M λan2
a 12
an 1 L a2n , M L λann L
迭代解法(全章)讲解ppt课件
10/18/2023
第六章 线性方程组的迭代解法
21
§3 常用的三种迭代解法
一、 Jacobi迭代法
对于线性方程组 Ax=b
(1)
设 det(A)≠ 0 ，aii ≠ 0,i=0,1,2,…,n ，按照如下方式对A
进行分裂：
A=L+D+U
(2)
10/18/2023
第六章 线性方程组的迭代解法
22
则由 Ax=b 得到 (L+D+U) x=b >D x=-(L+U)x+b
或 向量序列 {x(k)} 收敛于向量 x* ，当且仅当它的每一 个分量序列收敛于x* 的对应分量，即
10/18/2023
第六章 线性方程组的迭代解法
7
二、矩阵的范数
矩阵范数是反映矩阵“大小”的一种度量，具体定义如下。 定义6.3 设||·||是以n阶矩阵为变量的实值函数，且满足 条件：
(1) || A ||≥0，且|| A ||＝0时，当且仅当A＝0
矩阵1-范数：
列和
矩阵2-范数：
矩阵∞-范数：
行和
以上三种范数都满足矩阵范数的条件，通常将这三种 矩阵范数统一表示为||A ||p，P＝1 ，2 ，∞。
10/18/2023
第六章 线性方程组的迭代解法
9
例6.2 设矩阵
求矩阵A的范数||A ||p，P＝1 ，2 ，∞ 。 解 根据定义
由于 则它的特征方程为:
25
对于 n 元线性方程组 其一般式为：
从中解出：
得Jacobi迭代格式
通过|| x(k+1)-x(k)||<ε 控制迭代次数。
10/18/2023
第6章 线性方程组迭代解法
第6章 线性方程组迭代解法一、选择题（四个选项中仅有一项符合题目要求，每小题3分，共计15分)1、设Ax b =的系数矩阵122111221A −⎡⎤⎢⎥=−−⎢⎥⎢⎥−−⎣⎦，若用雅可比法和高斯-赛德尔法求解，则下列说法正确的是（ ）（1）两者都收敛；（2）两者都发散；（3）前者收敛，后者发散；（4）前者发散，后者收敛。
2、用一般迭代法(1)()k k x Bx g +=+求解方程组Ax b =的解，则当（ ）时，迭代收敛。
（1）方程组系数矩阵A 对称正定；（2）方程组系数矩阵A 严格对角占优；（3）迭代矩阵B 严格对角占优；（4）迭代矩阵B 的谱半径()1B ρ<。
3、设求解方程组Ax b =的迭代格式为(1)()811717071088k k x x +⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦，其系数矩阵为711160107A −−−⎡⎤⎢⎥=−−⎢⎥⎢⎥−−⎣⎦，迭代矩阵为811170108B ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦，则下列说法正确的是（ ）。
（1）方程组系数矩阵A 严格对角占优，故此迭代收敛于方程组的解；（2）迭代矩阵B 严格对角占优，故此迭代收敛于方程组的解；（3）1101B B ∞==>，故此迭代发散；（4）迭代矩阵B 的谱半径()1B ρ>，故此迭代发散。
4、若线性代数方程组Ax b =的系数矩阵A 为严格对角占优阵，若用雅可比法和高斯-赛德尔法求解，则下列说法正确的是（ ）（1）两者都收敛；（2）两者都发散；（3）前者收敛，后者发散；（4）前者发散，后者收敛。
5、若线性代数方程组Ax b =的系数矩阵A 为对称正定矩阵，则下列说法正确的是（ ） （1）雅可比法收敛；（2）高斯-赛德尔法收敛；（3）雅可比法和高斯-赛德尔法均收敛；（4）SOR 迭代法收敛。
二、填空题（每小题3分，共计15 分）1、设10102a A ⎡⎤⎢⎥=⎢⎥⎣⎦，要使lim 0k k A →∞=，a 应满足的条件是________ __。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第六章解线性方程组的迭代法习题六
1.证明对于任意的矩阵A，序列
2. 方程组
J法与GS法均收敛。
具有严格对角占优，故
（2）J法得迭代公式是
取
证明解此方程的Jacobi迭代法与Gauss-Seidel迭代法同时收敛或发散
解：Jacobi迭代为
，而Gauss-Seide 迭代法为
其迭代矩阵
解：Jacobi法的迭代矩阵是
即
5. 设
得GS法收敛得充要条件是
7当
若取
第
对上题求出SOR迭代法的最优松弛因子及渐近收敛速，题第
度，并求J法与GS法的渐近收敛速度.若要使
，故
J法收敛速度
72`*+b数
各a K＝15
对于GS法
，取K＝5
8. 填空题
(1)
7则解此方程组的Jacobi迭代法是否收敛（）.它的渐近收敛速度R(B)=（）.
(3) 设方程组Ax=b,其中
(4) 用GS法解方程组
,a为实数.当a满足（），且0＜ω＜2时SOR迭代法收敛.
答:
(1)
(3)J法迭代矩阵是
(4)
(5)。