小学一年级数学 奥数名师精编试题 枚举法(扫描版)
枚举算法经典例题
枚举算法经典例题一、以下哪个问题适合使用枚举算法解决？A. 查找一个无序数组中的最大值B. 求解旅行商问题（TSP）的最短路径C. 生成一个集合的所有子集D. 对一个有序数组进行二分查找（答案）C二、在使用枚举算法生成一个长度为n的二进制串的所有可能组合时，时间复杂度为多少？A. O(n)B. O(n!)C. O(2n)D. O(n2)（答案）C三、枚举算法在解决以下哪个问题时，可能会因为问题规模过大而变得不实际？A. 找出一个字符串中的所有字符排列B. 计算一个数的阶乘C. 验证一个数是否为素数D. 求解一个50x50的棋盘上的骑士周游问题（答案）D四、以下哪个不是枚举算法的特点？A. 简单易实现B. 适用于所有问题C. 可能产生大量计算D. 通常用于小规模问题（答案）B五、在使用枚举算法解决排列问题时，如果要对n个元素进行排列，总共会有多少种不同的排列方式？A. nB. n!C. 2nD. n2（答案）B六、以下哪个问题不适合直接使用枚举算法解决，因为其解空间太大？A. 找出一个数组中所有元素的和B. 求解一个密码的所有可能组合（密码长度为10，字符集为大小写字母和数字）C. 找出一个字符串中的最长回文子串D. 计算一个数的平方根（精确到小数点后10位）（答案）B七、枚举算法在解决组合问题时，如果要从n个元素中选出k个元素，总共会有多少种不同的组合方式？A. nkB. k!C. C(n, k) = n! / (k!(n-k)!)D. 2n（答案）C八、以下哪个场景是枚举算法的典型应用？A. 大规模数据的排序B. 图的遍历C. 查找一个数是否在有序数组中D. 生成并检查所有可能的解以找到满足条件的解（答案）D。
小学奥数 加法原理之分类枚举(一) 精选练习例题 含答案解析(附知识点拨及考点)
1.使学生掌握加法原理的基本内容；2.掌握加法原理的运用以及与乘法原理的区别；3.培养学生分类讨论问题的能力，了解分类的主要方法和遵循的主要原则．加法原理的数学思想主旨在于分类讨论问题，教授本讲的目的也是为了培养学生分类讨论问题的习惯，锻炼思维的周全细致．一、加法原理概念引入 生活中常有这样的情况，就是在做一件事时，有几类不同的方法，而每一类方法中，又有几种可能的做法．那么，考虑完成这件事所有可能的做法，就要用加法原理来解决．例如:王老师从北京到天津，他可以乘火车也可以乘长途汽车，现在知道每天有五次火车从北京到天津，有4趟长途汽车从北京到天津．那么他在一天中去天津能有多少种不同的走法？分析这个问题发现，王老师去天津要么乘火车，要么乘长途汽车，有这两大类走法，如果乘火车，有5种走法，如果乘长途汽车，有4种走法．上面的每一种走法都可以从北京到天津，故共有5+4=9种不同的走法．在上面的问题中，完成一件事有两大类不同的方法．在具体做的时候，只要采用一类中的一种方法就可以完成．并且两大类方法是互无影响的，那么完成这件事的全部做法数就是用第一类的方法数加上第二类的方法数．二、加法原理的定义一般地，如果完成一件事有k 类方法，第一类方法中有1m 种不同做法，第二类方法中有2m 种不同做法，…，第k 类方法中有k m 种不同做法，则完成这件事共有12 k N m m m =+++……种不同方法，这就是加法原理．加法原理运用的范围：完成一件事的方法分成几类，每一类中的任何一种方法都能完成任务，这样的问题可以使用加法原理解决．我们可以简记为：“加法分类，类类独立”．分类时，首先要根据问题的特点确定一个适合于它的分类标准，然后在这个标准下进行分类；其次，分类时要注意满足两条基本原则：① 完成这件事的任何一种方法必须属于某一类；② 分别属于不同两类的两种方法是不同的方法．只有满足这两条基本原则，才可以保证分类计数原理计算正确．运用加法原理解题时，关键是确定分类的标准，然后再针对各类逐一计数．通俗地说，就是“整体等于局部之和”．三、加法原理解题三部曲知识要点教学目标7-1-1.加法原理之分类枚举（一）2、每类找种数（每类的一种情况必须是能完成该件事）；3、类类相加枚举法：枚举法又叫穷举法，就是把所有符合条件的对象一一列举出来进行计数．分类讨论的时候经常会需要把每一类的情况全部列举出来，这时的方法就是枚举法．枚举的时候要注意顺序，这样才能做到不重不漏．例题精讲模块一、分类枚举——数出来的种类【例1】小宝去给小贝买生日礼物，商店里卖的东西中，有不同的玩具8种，不同的课外书20本，不同的纪念品10种，那么，小宝买一种礼物可以有多少种不同的选法？【考点】加法原理之分类枚举【难度】2星【题型】解答【关键词】分类讨论思想【解析】小宝买一种礼物有三类方法：第一类，买玩具，有8种方法；第二类，买课外书，有20种方法；第三种，买纪念品，有10种方法．根据加法原理，小宝买一种礼物有8+20+10=38种方法．【答案】38【巩固】有不同的语文书6本，数学书4本，英语书3本，科学书2本，从中任取一本，共有多少种取法？【考点】加法原理之分类枚举【难度】2星【题型】解答【关键词】分类讨论思想【解析】根据加法原理，共有6+4+3+2=15种取法．【答案】15【巩固】阳光小学四年级有3个班，各班分别有男生18人、20人、16人．从中任意选一人当升旗手，有多少种选法？【考点】加法原理之分类枚举【难度】2星【题型】解答【关键词】分类讨论思想【解析】解决这个问题有3类办法：从一班、二班、三班男生中任选1人，从一班18名男生中任选1人有18种选法：同理，从二班20名男生中任选1人有20种选法；从三班16名男生中任意选1人有16种选法；根据加法原理，从四年级3个班中任选一名男生当升旗手的方法有：18201654++=种．【答案】54【例2】和为15的两个非零自然数共有对。
小学数学《常规应用题的解法——枚举法》练习题(含答案)
小学数学《常规应用题的解法——枚举法》练习题(含答案)小学数学《常规应用题的解法——枚举法》练习题(含答案)在小学数学中，常规应用题是我们在学习数学的过程中经常会遇到的一种题型。
而枚举法则是解决常规应用题的一种常见方法。
本文将通过一系列练习题，帮助小学生们更好地理解和掌握枚举法的解题技巧。
练习题一：小明买苹果小明从超市买了6个苹果，每个苹果的重量都不相同。
他想从中选择两个苹果，使得这两个苹果的重量之和恰好等于10克。
请问小明有多少种选择的可能性？解法：首先我们需要列举出所有的可能情况：(1, 9), (2, 8), (3, 7), (4, 6), (5, 5)共有5种选择的可能性。
练习题二：小华的生日礼物小华过生日了，他爸爸送给他3个盒子作为礼物，里面分别装着红、黄、蓝三种颜色的贴纸。
小华每次可以从一个或多个盒子中任意选择贴纸，但是每种颜色的贴纸只能拿一次，问小华一共有多少种选择的方式？解法：对于每个盒子，小华可以选择拿或不拿，所以对于三个盒子就有2^3种选择的方式。
但是，每个盒子至少要拿一个贴纸，所以我们需要减去只拿空盒子的情况，剩下的就是不同选择的方式。
2^3 - 1 = 7小华一共有7种选择的方式。
练习题三：买水果小明去水果店买水果，他买了6个苹果，4个橙子和3个香蕉。
他打算把这些水果分给他的两个朋友，每人至少分到一个水果，并且每个人分到的水果数目不能相同。
请问他有多少种分法？解法：首先，我们先找出所有可能的分法。
(1, 1, 6, 4, 3)(1, 2, 5, 4, 3)(1, 2, 6, 3, 4)(1, 3, 4, 2, 6)(1, 3, 4, 6, 2)(1, 3, 6, 2, 4)(1, 4, 3, 2, 6)(1, 4, 3, 6, 2)共有8种分法。
练习题四：座位安排现在有6个小朋友，他们要坐在一张圆桌周围，每个位置只能坐一个人。
其中小明和小华是好朋友，他们希望他们之间至少有一个空位。
小学奥数题目及解析分类枚举
小学奥数题目及解析：分类枚举分类枚举，就是依据一定的标准把题目的答案分为几种类型，一一列举出来。
分类枚举的方法主要用来解决一些排列组合的问题，列举时要有序分类，保证答案既不遗漏又不重复，其中分类标准的确定是解题的关键，同一题因标准不同可能有不同的分类方法，好的分类方法会使解题过程变得更加简单。
学会分类枚举，不仅可以解决本讲的问题，遇到更复杂问题时，我们也可以用列举的方法找出部分答案，然后在已有答案中发现规律，从而进一步寻求解题方案。
【题目】：把10只鸽子关在3个同样的笼子里，使得每个笼子里都有鸽子，可以有多少种不同的放法？【解析】：这里笼子都是同样的，因此3只笼子是无序的。
因为10÷3=3……1，根据题中条件，可得鸽子最少的那个笼子里的鸽子不多于3只，不少于1只，我们可以这样分为三类：一、鸽子最少的那个笼子里有1只鸽子，共有4种放法：①1只、1只、8只；②1只、2只、7只；③1只、3只、6只；④1只、4只、5只。
二、鸽子最少的那个笼子里有2只鸽子，共有3种放法：①2只、2只、6只；②2只、3只、5只；③2只、4只、4只。
三、鸽子最少的那个笼子里有3只鸽子，共有1种放法：①3只、3只、4只。
所以共有放法：4+3+1=8（只）。
【题目】：有一架天平和三只重量分别为1克，3克，6克的砝码，你知道用这架天平和这些砝码共能称出多少种重量吗？【解析】：这一题要在孩子学习了三上第三单元，认识了常见的称和质量单位后，再学习比较合适。
如果超前完成，需要对孩子介绍一下天平的用法。
因为1克+3克+6克=10克，所以这架天平最重能称出10克，最轻能称出1克。
因此这架天平最多能称出1克到10克之间的10种不同重量的物体，然后我们再对这10类情况进行验证：①天平左边：物体右边：1克砝码能称出1克重的物体；②天平左边：物体+1克砝码右边：3克砝码能称出2克重的物体；③天平左边：物体右边：3克砝码能称出3克重的物体；④天平左边：物体右边：3克砝码+1克砝码能称出4克重的物体；⑤天平左边：物体+1克砝码右边：6克砝码能称出5克重的物体；⑥天平左边：物体右边：6克砝码能称出6克重的物体；⑦天平左边：物体右边：6克砝码+1克砝码能称出7克重的物体；⑧天平左边：物体+1克砝码右边：6克砝码+3克砝码能称出8克重的物体；⑨天平左边：物体右边：6克砝码+3克砝码能称出9克重的物体；⑩天平左边：物体右边：6克砝码+3克砝码+1克砝码能称出10克重的物体。
奥数-枚举法
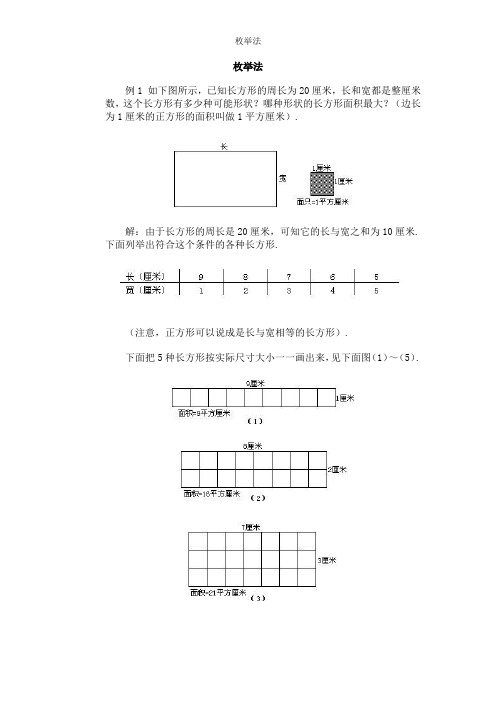
枚举法例1 如下图所示，已知长方形的周长为20厘米，长和宽都是整厘米数，这个长方形有多少种可能形状？哪种形状的长方形面积最大？（边长为1厘米的正方形的面积叫做1平方厘米）.解：由于长方形的周长是20厘米，可知它的长与宽之和为10厘米.下面列举出符合这个条件的各种长方形.（注意，正方形可以说成是长与宽相等的长方形）.下面把5种长方形按实际尺寸大小一一画出来，见下面图（1）～（5）.例2 如右图所示，ABCD是一个正方形，边长为2厘米，沿着图中线段从A到C的最短长度为4厘米.问这样的最短路线共有多少条？请一一画出来.解：将各种路线一一列出，可知共6条，见下图.注意，如果题中不要求将路径一一画出，可采用如右图所示方法较为便捷.图中交点处的数字表示到达该点的路线条数，如O点处的数字2，表示由A到O有2条不同的路径，见上图中的（1）和（2）；又H点处的数字3的意义也如此，见上图中的（1）、（2）、（3）可知有3条路径可由A到H.仔细观察，可发现各交点处的数字之间的关系，如O点的2等于F点和E点的数字相加之和，即1+1=2，又如，C点的6等于G点和H点的数字相加之和，即3+3=6.例3 在10和31之间有多少个数是3的倍数？解：由尝试法可求出答案：3×4=12 3×5=15 3×6=18 3×7=213×8=24 3×9=27 3×10=30可知满足条件的数是 12、15、18、21、24、27和30共7个.注意，倘若问10和1000之间有多少个数是3的倍数，则用上述一一列举的方法就显得太繁琐了，此时可采用下述方法：10÷3=3余1，可知10以内有3个数是3的倍数；1000÷3=333余1，可知1000以内有333个数是3的倍数；333-3=330，则知10～1000之内有330个数是3的倍数.由上述这些例题可体会枚举法的优点和缺点及其适用范围.例4 两个整数之积为144，差为10，求这两个数？解：列出两个数积为144的各种情况，再寻找满足题目条件的一对出来：1 2 3 4 6 8 9 12144 72 48 36 24 18 16 12可见其中差是10的两个数是8和18，这一对数即为所求.例5 12枚硬币的总值是1元，其中只有5分和1角的两种，问每种硬币各多少个？解：列举出两种硬币的可能搭配：可见满足题目要求的搭配是：四个5分币，八个1角币.例6 小虎给4个小朋友写信.由于粗心，在把信纸装入信封时都给装错了.4个好朋友收到的都是给别人的信.问小虎装错的情况共有多少种可能？解：把4封信编号：1，2，3，4.把小朋友编号，友1，友2，友3，友4.并假定1号信是给友1写的，2号信是给友2写的，3号信是给友3的，4号信是给友4写的：再把各种可能的错装情况列成下表：说明：如第一种错收情况是友1得2号信，友2得了1号信，友3得了4号信，友4得了3号信.。
小学奥数精讲与测试目录
第1讲比一比第2讲几与第几第3讲简单分类第4讲认识图形第5讲数与数数第6讲变与不变第7讲位置与顺序第8讲找规律填数第9讲数图形第10讲图形填数第11讲找规律画图形第12讲图形的拼搭第13讲玩火柴棒第14讲单数与双数第15讲简单推理第16讲排列与搭配第17讲数的大小与多少第18讲有趣的排队第19讲简单应用第20讲趣味问题第1讲混合运算第2讲等式的加减法第3讲速算与巧算第4讲比长短第5讲找规律填数第6讲找规律填图第7讲位置与顺序第8讲横式迷第9讲时间问题第10讲简单的周期问题第11讲年龄问题第12讲简单推理第13讲数数与计数第14讲一笔画第15讲两步计算应用题第16讲用尝试法解题第17讲利用图形解题第18讲巧解应用题第19讲火柴棒游戏第20讲数学趣题奥数精讲与测试（三年级）第1讲速算与巧算第2讲平均数第3讲简单数列求和第4讲植树问题第5讲方阵问题第6讲年龄问题第7讲消元问题第8讲逆推问题第9讲简单的逻辑推理问题第10讲奇数与偶数第11讲除法与余数第12讲数线段第13讲数图形第14讲巧求周长第15讲定义新运算第16讲混合运算与应用题第17讲归一问题第18讲盈亏问题第19讲最大与最小第20讲幻方奥数精讲与测试（四年级）第1讲速算与巧算第2讲和倍问题第3讲差倍问题第4讲和差问题第5讲年龄问题第6讲相遇问题第7讲追击问题第8讲火车行程问题第9讲流水问题第10讲植树问题第11讲鸡兔同笼问题第12讲数阵图第13讲长方形的面积第14讲数谜问题第15讲图形的拼切与面积计算第16讲巧算24点第17讲逻辑问题第18讲定义新运算第19讲加法原理与乘法原理第20讲奇数与偶数奥数精讲与测试（五年级）第1讲小数的巧算与大小比较第2讲等差数列第3讲列方程解应用题第4讲平均数第5讲鸡兔同笼问题第6讲平面图形的周长与面积第7讲等积变形第8讲图形的割补与切拼第9讲数的整除特征第10讲质数与合数第11讲分解质因数第12讲最大公约数与最小公倍数第13讲数阵问题第14讲周期问题第15讲盈亏问题第16讲完全平方数第17讲相遇和追击问题第18讲流水行船问题第19讲有余数的除法第20讲长方体和正方体THANKS !!!致力为企业和个人提供合同协议，策划案计划书，学习课件等等打造全网一站式需求欢迎您的下载，资料仅供参考。
小学数学《常规应用题的解法——枚举法》练习题(含答案)
小学数学《常规应用题的解法——枚举法》练习题（含答案）知识要点我们在课堂上遇到的数学问题，有一些需要计算总数或种类的趣题，因其数量关系比较隐蔽，很难利用计算的方法解决。
我们可以抓住对象的特征，按照一定的顺序，选择恰当的标准，把问题分为不重复、不遗漏的有限种情形，通过一一列举或计数，最终达到解决目的。
这就是枚举法，也叫做列举法或穷举法。
解题指导11.枚举法在数字组合中的应用。
按照一定的组合规律，把所有组合的数一一列举出来。
【例1】用数字1，2，3组成不同的三位数，分别是哪几个数？【思路点拨】根据百位上的数字的不同分为3类。
第一类：百位上为1的有：123 132第二类：百位上为2的有：213 231第三类：百位上为3的有：312 321答：可以组成123，132，213 ，231，312 ，321六个数。
【变式题1】用0、6、7、8、9这五个数字组成各个数位上数字不相同的两位数共有多少个？解题指导22.骰子中的点数掷骰子是生活中常见的游戏玩法，既可以掷一个骰子，比较掷出的点数大小，也可以掷两个骰子，把两个骰子的点数相加，再比较点数的大小。
一个骰子只有6个点数，而两个骰子的点数经过组合最小是2，最大是12。
在解决有关掷两个骰子的问题时，要全面考虑所有出现的点数情况。
【例2】小明和小红玩掷骰子的游戏，共有两枚骰子，一起掷出。
若两枚骰子的点数和为7，则小明胜；若点数和为8，则小红胜。
试判断他们两人谁获胜的可能性大。
【思路点拨】将两枚骰子的点数和分别为7与8的各种情况都列举出来，就可得到问题的结论。
用a＋b表示第一枚骰子的点数为a，第二枚骰子的点数是b的情况。
出现7的情况共有6种，它们是：1＋6，2＋5，3＋4，4＋3，5＋2，6＋1。
出现8的情况共有5种，它们是：2＋6，3＋5，4＋4，5＋3，6＋2。
所以，小明获胜的可能性大。
注意，本题中若认为出现7的情况有1＋6，2＋5，3＋4三种，出现8的情况有2＋6，3＋5，4＋4也是三种，从而得“两人获胜的可能性一样大”，那就错了。
小学奥林匹克数学(一年级)
小学奥林匹克数学思维方法训练大全九龙坡区教师进修校邓永富编给读者的话在人生漫长的学习过程中有几个重要的分化期，其中小学阶段，尤其是小学三四年级是第一个也是最重要的一个分化期。
如果说智慧是成功大厦的基石，数学则是开启智慧大门的金钥匙。
愿每一位小朋友用奥林匹克的拼搏精神,从一年级开始学好数学的思维方法, 亲自动手摆一摆，认真动脑想一想,开启智慧大门,成为一个聪明的人！目录第一讲摆一摆想一想 (1)第二讲折一折分一分 (3)第三讲速算与巧算 (5)第四讲统计与计数 (7)第五讲身边数学 (10)第六讲数字游戏 (12)第七讲火柴棍游戏（一） (14)第八讲火柴棍游戏（二） (16)第九讲找出不同 (18)第十讲寻找规律 (20)第十一讲小发明家 (22)第一讲摆一摆想一想例1 用两根火柴棍，摆成一个锐角、一个直角、一个钝角。
用两根火柴棍，你还能摆出一个什么？例2 用四根火柴棍摆出两条平行直线，再摆出两条相交直线。
用四根火柴棍，你还能摆出一个什么？例3 用火柴棍摆出一个三角形、一个正方形、一个菱形、一个长方形、一个平行四边形、一个等腰梯形、一个五边形、一个六边形、一个八边形。
你还能摆出什么图形？例4 用三根火柴棍可以摆出一个三角形，如图。
（1）再加两根火柴棍，摆出两个三角形（2）再加两根，摆出三个三角形来。
（3）再加两根，摆出五个三角形来。
（1）（2）（3）说一说：你发现了什么？1习题一1.用两根小木棍，摆成一个很小的锐角，然后慢慢地挪动一根，使锐角渐渐变大。
如果继续转动小棍，将会出现什么角？2．如右图所示，用火柴棍摆了五个三角形。
（1）拿掉哪三根，就可以变成一个三角形？（2）拿掉哪两根，就可变成两个三角形？（3）拿掉哪一根，就可变成三个三角形？3．如右图所示，用火柴棍摆了五个正方形。
（1）请你拿掉两根，剩下三个正方形。
（2）请你拿掉两根，剩下两个正方形。
4．如图所示，用火柴棍摆了六个三角形。
如果拿掉三根火柴棍就变成了三个三角形，应该拿掉哪三根？试试看。
算法实例-枚举法
ppt课件
1
枚举法
把各种可能的情况都考虑到，并对全部可能 结果逐一进行判断，过滤掉那些不符合要求 的，保留符合要求的结果，这种方法叫枚举 算法（Enumerat推算
一张单据上有一个5位数的编号，其百位数 和十位数已经变得模糊不清，但是知道这个 5位数是37或67的倍数。现在要求设计一个 算法，找出所有满足这些条件的5位数，并 统计这些5位数的个数。
提示：本题关键在问题的转化 设定冠军为X(1<=X<=6) 甲乙丙丁四个人的话可以用逻辑表达式表示 如下： 甲：X=1 OR X=2 乙：X<>3 丙：X<=3 丁：X>=4
ppt课件
7
此课件下载可自行编辑修改，此课件供参考！ 部分内容来源于网络，如有侵权请与我联系删除！感谢你的观看！
A，B，C，D，E，F 6人参加跳高决赛，甲 乙丙丁4人猜测谁是冠军： 甲说：“冠军不是A，就是B。” 乙说：“冠军决不是C” 丙说：“DEF都不可能是冠军。” 丁说：“冠军可能是DEF中的一个” 比赛成绩公布时发现，这4个人所说的话中， 只有一句话是对的。你能断定谁是冠军吗？
ppt课件
6
学生练习
NO.25**6
ppt课件
3
例1－流程图
ppt课件
4
例1－程序
c=0
For j = 0 To 99
n = 25006 + j * 10
If n Mod 37 = 0 Or n Mod 67 = 0 Then
c=c+1
Print n
End If
Next
Print c
ppt课件
5
学生练习－猜冠军
奥数-08枚举法+答案
枚举法我们在课堂上遇到的数学问题，一般都可以列出算式，然后求出结果，但在数学竞赛或生活中却经常会遇到一些有趣的题目，由于找不到计算它们的算式，似乎无从下手。
但是，如果题目所述的情况或满足题目要求的对象能够被一一列举出来，或能被分类列举出来，那么问题就可以通过枚举法获得解决。
所谓枚举法（或称穷举法），就是根据题目要求，将符合要求的结果不重复、不遗漏地一一列举出来，从而找到解决问题的方法。
当可能的结果较少时，可以直接枚举，即将所有结果一一列举出来；当可能的结果较多时，就需要分类枚举。
分类一定要包括所有可能的结果，这样才能不遗漏，并且类与类之间不重叠，这样才能做到不重复。
枚举法的分类：简单枚举法——将各种可能的情况或对象一一列举出来。
字典枚举法——对象已经确定，把对象按顺序进行不同的排列组合。
图形计数枚举法——先按不同的类型进行分类，再进行统计。
数字拆分枚举法——先将对象拆分成若干份，再进行排列组合。
画枚举树枚举法——将各种可能的情况画成树状图形，再进行统计。
【例 1】有一天，丽丽去天天家，而从丽丽家到天天家不能直接到达，必须要经过公园或丁丁家(如右图)，找一找，从丽丽家到天天家共有几条路可以走？（简单枚举法）解析：为了便于统计，我们先给每一条线路编号。
采用简单枚举方法——将各种可能的线路一一列举出来，再进行计数。
1＋8 2＋8 3＋5 3＋63＋7 4＋5 4＋6 4＋7从丽丽家到天天家共有8条路可走。
练习一1、某人要去日本旅游，从家到上海去可以选择的交通工具有地铁、公交和自驾，从上海到日本既可以乘游轮也可以坐飞机，那么他到日本去有几种方案可以选择？2、用0、2、3、4、7、8组成不同的两个三位数，每个数字只能用一次，使它们的和最小。
【例 2】用分别写着7、8、9、0的卡片各一张，可以组成多少个不同的四位数？（字典枚举法）解析：对象已经确定是数字7、8、0、9，然后按顺序进行不同的排列组合，先确定千位上的数字，再确定百位上的数字，以此类推。
枚举法经典例题
一、选择题1.题目：一个骰子有六个面，每个面上的点数分别为1、2、3、4、5、6。
现在投掷这个骰子一次，问出现点数为偶数的概率是多少？A.1/6B.1/3C.1/2（正确答案）D.2/32.题目：一个密码箱有4个数字转盘，每个转盘上有0-9共10个数字。
若某人只记得密码是由不同的数字组成，但不记得具体顺序，问此人最多需尝试多少次才能确保打开密码箱？A.10000B.5040（正确答案）C.2400D.1203.题目：某班级有10名学生，需要选出3名学生参加学校的数学竞赛。
如果甲和乙两名学生不能同时被选上，那么一共有多少种不同的选法？A.108B.112C.120（正确答案）D.1404.题目：一个正方体有6个面，每个面上分别写有数字1、2、3、4、5、6。
现在将这个正方体任意投掷，问出现数字小于4的面的概率是多少？A.1/2（正确答案）B.1/3C.1/4D.2/35.题目：从1到100的自然数中，任取一个数，求取到的数是7的倍数或者含有7的数字的概率是多少？A.0.14B.0.19（正确答案）C.0.21D.0.266.题目：一个足球队有11名队员，其中包括队长和副队长。
现在要从这11名队员中选出3名队员参加一个访谈节目，要求队长和副队长不能同时被选上，问有多少种不同的选法？A.140B.150C.160D.165（正确答案）7.题目：一个口袋中有5个红球和3个白球，从中任意摸出一个球，记下颜色后放回，再摸出一个球。
问两次都摸到红球的概率是多少？A.1/4B.9/16C.25/64（正确答案）D.5/88.题目：某班级有8名学生，需要分成两组进行辩论，每组4人。
如果甲和乙两名学生必须分在同一组，那么一共有多少种不同的分组方法？A.30B.35（正确答案）C.40D.45。
一年级上册奥数试题-第10讲你有几种答案.精英班.教师解析版
第十讲你有几种答案？(教师解析版)本节课主要选择有多种答案的习题，让学生在解这些题的过程中找不同的方法，把所学的知识融会贯通，同时也拓展学生的思维．让学生从不同的角度来思考问题，并且意识到有些题的答案有多种，我们要全面的来考虑．在解答问题的过程中，学生往往容易疏漏，老师要引导学生去思考．1、教学点为各位老师提供了本节课挂图．第十讲你有几种答案？猜数字：“体育彩票”有一期的中奖号码是0，2，4，6，7，10这六个数．这一期有三位叔叔都中了奖．这三位叔叔说了一句同样的话：“在这六个数中有一个数与众不同，这个与众不同的数就是我的幸运数字．”这三位叔叔的幸运数字都不一样，你能帮他们找出来吗？【教学思路】（1）因为在0，2，4，6，7，10中，只有7是单数，所以7是与众不同的，是一位叔叔的幸运数字．（2）因为在0，2，4，6，7，10中，只有10是两位数，所以10是与众不同的，是另一位叔叔的幸运数字．（3）因为在0，2，4，6，7，10中，只有0表示没有，所以0是与众不同的，是最后一位叔叔的幸运数字．所以0，7，10分别是三位叔叔的幸运数字．通过这个题的训练，让学生发现从不同的角度去思考问题，得出的答案就不相同．小朋友们，我们在解答数学问题时，得到的答案往往不一定是唯一的，有时会出现几种不同的结果．遇到这样的问题，就需要小朋友们仔细思考，尽可能的把问题考虑周全，从而提高我们灵活运用知识的能力，聪明的小朋友，跟我一起来挑战吧！小寿星阳阳切蛋糕，如果只切2刀可以把这块蛋糕切成几份呢？你有几种不同的切法，请画出来．【教学思路】把一个蛋糕切2刀，切的方法非常多，但是只能切成3块或者是4块．如下图：12名同学到北海公园去划船，一共租了三条小船，每条小船限坐4人，上船前有3名同学因临时有事情离开了．你能帮剩下的几个同学分配一下怎样乘船吗？【教学思路】原来有12名同学参加活动，现在走了3名，这样就只剩下了9名同学．现在这9名同学来分配这3条船，每条小船最多只能坐4人．有以下三种方法：方法一：3条船，每条船上都坐3人，3339++=（人）方法二：一条船上坐4人，一条船上坐3人，一条船上坐2人．4329++=（人）方法三：一条船上坐4人，一条船上坐4人，一条船上坐1人．4419++=（人）下面这张方格纸是由一些大小完全一样的小正方形组成的．马老师想沿格子线剪成形状相同且大小相等的两块分给两个同学，你能找出几种不同的方法？请在方格纸上画一画．【教学思路】我们可以找到以下4种不同的分法：下面的四个图形，哪些是这个长方体上的面？【教学思路】长方体有6个面，通过观察上图的长方体我们发现，第一个长方形是长方体上面的面；第二个长方形是长方体前面的面；第四个长方形是长方体右面的面．只有第三个正方形不是长方体的面．【教学思路】三徒弟射的是结有4个苹果的那根树枝，只需要一根箭，射断树枝，自然苹果也掉下来了.小明家、小红家、学校在同一条街道的一侧，小明家离学校45米，小红家离学校55米，请你猜一猜小明和小红的家各在哪里？从小明家到小红家要走多少米？请你在图上画一画．一天，弓箭手带着三个徒弟经过一片果实累累的果园。
小学奥数枚举法题及答案【三篇】
小学奥数枚举法题及答案【三篇】导读：本文小学奥数枚举法题及答案【三篇】，仅供参考，如果觉得很不错，欢迎点评和分享。
【篇一】枚举法问题在一个圆周上放了1个红球和1994个黄球。
一个同学从红球开始，按顺时针方向，每隔一个球，取走一个球；每隔一个球，取走一个球；……他一直这样操作下去，当他取到红球时就停止。
你知道这时圆周上还剩下多少个黄球吗？答案与解析：根据题中所说的操作方法，他在第一圈的操作中，取走的是排在黄球中第2、4、6、……1994位置上的黄球，这时圆周上除了一个红球外，还剩下1994÷2=997个黄球。
在第二圈操作时，他取走了这997个黄球中，排在第1、3、5、7、……995、997位置上的黄球，这时圆周上除了一个红球外，还剩下997—(997+1)÷2=498个黄球。
他又要继续第三圈操作了，他隔过红球，又取走了这498个黄球中，排在第1、3、5、……495、497的位置上的黄球，这时圆周上除了一个红球外，还剩下498÷2=249个黄球。
因为在上一圈操作时，排在这498个黄球中最后一个位置上的黄球没有被取走，所以他再进行操作时，第一个被取走的就是那个红球，这时，他的操作停止，圆周上剩下249个黄球。
【篇二】在一个圆周上放了1个红球和1994个黄球。
一个同学从红球开始，按顺时针方向，每隔一个球，取走一个球;每隔一个球，取走一个球;……他一直这样操作下去，当他取到红球时就停止。
你知道这时圆周上还剩下多少个黄球吗? 答案与解析：根据题中所说的操作方法，他在第一圈的操作中，取走的是排在黄球中第2、4、6、……1994位置上的黄球，这时圆周上除了一个红球外，还剩下1994÷2=997个黄球。
在第二圈操作时，他取走了这997个黄球中，排在第1、3、5、7、……995、997位置上的黄球，这时圆周上除了一个红球外，还剩下997—(997+1)÷2=498个黄球。
小学奥数枚举法解析：分类枚举知识点讲解
小学奥数枚举法解析：分类枚举知识点讲解小芳数钱，用的就是分类枚举的方法。
这是一种很重要的数学思考方法，在很多问题的思考过程中都发挥了很大的作用。
下面就让我们跟###一起来看看它的本领吧！经典试题例[1] 下图中有多少个三角形？分析我们能够根据图形特征将它分成3类：第一类：有6个；第2类：有6个；第3类：有3个；解 6+6+3=15（个）图中有15个三角形。
例[2]下图中有多少个正方形？分析根据正方形边长的大小，我们将它们分成4类。
第1类：由1个小正方形组成的正方形有24个；第2类：由4个小正方形组成的正方形有13个；第3类：由9个小正方形组成的正方形有 4个；第4类：由16个小正方形组成的正方形有1个。
解 24+13+4+1=42。
图中有42个正方形。
例[3] 在算盘上，用两粒珠子能够表示几个不同的三位数：分别是哪几个数？分析根据两粒珠子的位置，我们可将它们分成3类：第1类：两粒珠子都在上档，能够组成505，550；第2类：两粒珠子都在下档，能够组成101，110，200；第3类：一粒在上档，另一粒在下档，能够组成510，501，150，105，600。
解能够表示101，105，110，150，200，501，505，510，550，600共10个三位数。
例[4] 用数字7，8，9能够组成多少个不同的三位数？分别是哪几个数？分析根据百位上数字的不同，我们能够将它们分成三类：第1类：百位上的数字为7，有789，798；第2类：百位上的数字为8，有879，897；第3类：百位上的数字为9，有978，987。
解能够组成789，798，879，897，978，987共6个三位数。
例[5] 往返于南京和上海之间的沪宁高速列车沿途要停靠常州、无锡、苏州三站。
问：铁路部门要为这趟车准备多少种车票？分析我们能够根据列车的往与反把它们分成两大类（注：为了方便，我们将上述地点简称为宁、常、锡、苏、沪）：在第一大类中，我们又能够根据乘客乘车时所在起点站的不同分成4类。
小学数学枚举法练习题
小学数学枚举法练习题一、填空题：1. 用1、2、3三个数字组成不能重复的三位数，一共有_____种可能。
2. 小明有5支彩色笔，他要用其中的2支笔组合成不同的颜色。
一共有_____种组合方式。
3. 一架飞机有3个旅客座位，共有_____种不同的乘客排列方式。
二、选择题：1. 用A、B、C三个字母组成的两位数中，满足以下条件的数是：A. 取出的字母不可重复B. 数字不能是奇数C. 数字不能大于50D. 都满足以上条件的数2. 一台音乐播放器有4首歌曲，小明想按照特定顺序播放其中的2首歌曲。
一共有多少种不同的播放方式？A. 4B. 6C. 8D. 12三、计算题：1. 某手机密码锁的密码是4位数，且每位数均为1、2、3、4四个数字中的一个，密码不可重复。
共有多少种可能的密码组合方式？2. 某班级有5个男生和4个女生，老师要选择3个同学参加学校的演讲比赛。
如果要求至少有一个男生参赛，一共有多少种不同的选择方式？四、解答题：1. 小明的学校每天上午举行升旗仪式，共有6个学生按摩运动，其中3名男生和3名女生。
老师要选择3位学生升旗。
请列出所有可能的组合方式。
2. 用A、B、C、D四个字母中的任意三个字母组成三位数，且数字不可重复。
请列出所有可能的数。
3. 一组合页有三个数字按钮，按钮的数字为1、2、3、4、5、6六个数字中的三个，数字不可重复。
请列出所有可能的组合。
以上是我为你准备的小学数学枚举法的练习题。
通过这些题目的练习，希望能够帮助你掌握数学枚举法的思维和方法，提高你的数学能力。
祝你学习进步！。
小学生奥数枚举法练习题五篇
【导语】在进⾏归纳推理时，如果逐个考察了某类事件的所有可能情况，因⽽得出⼀般结论，那么这结论是可靠的，这种归纳⽅法叫做枚举法。
以下是整理的《⼩学⽣奥数枚举法练习题五篇》相关资料，希望帮助到您。
1.⼩学⽣奥数枚举法练习题 1、⽤两个3，⼀个1，⼀个2可组成种种不同的四位数，这些四位数共有（）个。
2、甲、⼄、丙、丁四个同学排成⼀排，从左往右数，如果甲不排在第⼀的位置上，⼄不排在第⼆的位置上，丙不排在第三的位置上，丁不排在第四的位置上，那么不同的排法共有（）种。
3、某⼈射击8枪，命中4枪，命中4枪中恰好有3枪连在⼀起的情况的种数是（）。
4、把10个苹果分给甲、⼄、丙三⼈，要求是：甲⾄少得到3个苹果，⼄⾄少得到2个苹果，丙最多得到3个苹果，符合这样要求的分配⽅案共有（）种。
5、⽤红⾊或绿⾊的7颗珠⼦串成⼀条环⾏的⼿链，那么⼀共可得到（）条不同的⼿链（通过旋转和翻转能重合的只能算是同⼀种）。
2.⼩学⽣奥数枚举法练习题 1、⼀个长⽅形的周长是22⽶，如果它的长和宽都是整⽶数，问： ①这个长⽅形的⾯积有多少可能值？ ②⾯积的长⽅形的长和宽是多少？ 2、三个⾃然数的乘积是24，问由这样的三个数所组成的数组有多少个？如（1，2，12）就是其中的⼀个，⽽且要注意数组中数字相同但顺序不同的算作同⼀数组，如（1，2，12）和（2，12，1）是同⼀数组。
3、⼩虎给3个⼩朋友写信，由于粗⼼，把信装⼊信封时都给装错了，结果3个⼩朋友收到的都不是给⾃⼰的信，请问⼩虎错装的情况共有多少种可能？ 4、⼀个学⽣假期往a、b、c三个城市游览。
他今天在这个城市，明天就到另⼀个城市。
假如他第⼀天在a市，第五天⼜回到a市。
问他的游览路线共有⼏种不同的⽅案？ 5、五个学⽣友1，友2，友3，友4，友5⼀同去游玩，他们将各⾃的书包放在了⼀处。
分⼿时友1带头开了个玩笑，他把友2⼩朋友的书包拿⾛了，后来其他的⼩朋友也都拿了别⼈的书包。
试问在这次玩笑中故意错拿书包的情形有多少种不同⽅式？3.⼩学⽣奥数枚举法练习题 印刷⼯⼈在排印⼀本书的页码时共⽤1890个数码，这本书有多少页？（适于四年级程度） 解：（1）数码⼀共有10个：0、1、2……8、9。
枚举法解题
枚举法解题摘要：一、枚举法的概念二、枚举法的分类1.完全枚举法2.条件枚举法三、枚举法的应用1.应用场景2.实际案例分析四、枚举法的优缺点1.优点2.缺点五、总结正文：一、枚举法的概念枚举法是一种求解问题的方法，它通过列举所有可能的解决方案来寻找问题的答案。
这种方法适用于问题范围明确，可以通过穷举所有可能来求解的情况。
二、枚举法的分类1.完全枚举法完全枚举法指的是对问题的所有可能解决方案进行逐一列举，直到找到满足条件的解决方案为止。
这种方法适用于问题范围较小，可以通过列举所有可能性来求解的情况。
2.条件枚举法条件枚举法是在完全枚举法的基础上，对问题进行一定程度的筛选，只保留满足某一条件的解决方案进行列举。
这种方法适用于问题范围较大，但可以通过限定条件来缩小搜索范围的情况。
三、枚举法的应用1.应用场景枚举法广泛应用于数学、物理、化学等自然科学领域，以及计算机科学、逻辑学等社会科学领域。
例如，在组合数学中求解排列组合问题，在计算机科学中寻找算法最优化解等。
2.实际案例分析以组合数学中的“百鸡百钱”问题为例，假设鸡和钱的总数为100，需要找到所有可能的鸡和钱数量组合。
这个问题可以通过枚举法来求解。
首先列举所有可能的鸡的数量（1-100），然后针对每个鸡的数量，列举所有可能的钱的数量（1-100），直到找到满足条件的鸡和钱数量组合为止。
四、枚举法的优缺点1.优点枚举法能够针对问题进行全面的分析，不容易遗漏解题思路。
对于某些问题，通过枚举法可以找到唯一的解，避免了其他方法可能出现的近似解或多种解的情况。
2.缺点枚举法的缺点在于，当问题范围较大时，需要列举的数量会非常庞大，导致计算量过大，甚至无法得到结果。
此外，枚举法对于一些具有规律的问题，可能无法发现和利用规律，降低了解题效率。
五、总结枚举法作为一种求解问题的方法，在一定范围内具有较好的适用性。
枚举法——精选推荐
枚举法⼀，枚举算法的思想：1，枚举算法的定义：在进⾏归纳推理时，如果逐个考察了某类事件的所有可能情况，因⽽得出⼀般结论，那么该结论是可靠的，这种归纳⽅法叫做枚举法。
2，枚举算法的思想是：将问题的所有可能的答案⼀⼀列举，然后根据条件判断此答案是否合适，保留合适的，舍弃不合适的。
3，使⽤枚举算法解题的基本思路如下：（1）确定枚举对象、范围和判定条件。
（2）逐⼀枚举可能的解并验证每个解是否是问题的解。
4，枚举算法步骤：（1）确定解题的可能范围，不能遗漏任何⼀个真正解，同时避免重复。
（2）判定是否是真正解的⽅法。
（3）为了提⾼解决问题的效率，使可能解的范围将⾄最⼩，5，枚举算法的流程图如下所⽰：⼆，枚举算法实例例⼀：百钱买⽩鸡1，问题描述：公鸡每只5元，母鸡每只3元，三只⼩鸡1元，⽤100元买100只鸡，问公鸡、母鸡、⼩鸡各多少只？2，算法分析：利⽤枚举法解决该问题，以三种鸡的个数为枚举对象,分别设为mj,gj和xj，⽤三种鸡的总数（mj+gj+xj=100）和买鸡钱的总数（1/3*xj+mj*3+gj*5=100）作为判定条件，穷举各种鸡的个数。
例⼆：使⽤枚举法解决“填写运算符问题”1，问题描述：在下⾯的算式中，添加“+”、“-”，“*”，“/”,4个运算符，使得这个式⼦成⽴。
5 5 5 5 5=52，算法分析：上述式⼦左侧有5个数字，⼀共需要4个运算符。
根据题⽬要求，两个数字之间的运算符只能有4中选择。
在具体编程时，可以通过循环来填⼊各种运算符，然后再判断算式左侧的值是否等于右侧的值。
并保证，当填⼊的是除号时，则右侧的数不能为0，并且乘除的优先级⾼于加减的优先级。
三，算法实现：例⼀：百钱买⽩鸡1. #include<iostream>2. using namespace std;3. int main()4. {5. int mj=0, gj=0, xj=0; //定义变量分别表⽰母鸡、公鸡、⼩鸡并初始化6. for (gj = 0; gj <= 20; gj++) //公鸡最多可买20个7. {8. for (mj = 0; mj <= 33; mj++) //母鸡最多可买33个9. {10. xj = 100 - gj - mj; // 三种鸡的总数是100只11. if (xj % 3 == 0 && 5 * gj + 3 * mj + xj / 3 == 100) // 总花费为100元。
枚举法
4+3+2+1=10（种）
答：一共有10种分法。
• 3：张奶奶从超市里买了10包果冻，分别装在3个 塑料袋里，每袋至少一包，那么张奶奶一共有多 少种不同的装果冻的方法？
• 分析：先判断是否有序，没有说每袋分别分给谁， 1+2+7，2+1+7,7+1+2这三种算是同一种分法， 是无序的；再判断范围，每袋至少一包，所以最 小是1，最大是8
练习题
• 1、有一些三位数的各位数字都不是0，且各位数 字之和为7，这样的3位数有多少个？
• 分析：先看有无次序之分，因为是一个三位数， 有个位、十位、百位之分，所以是有次序的，再 确定范围，各位数字都不为0，各位数字之后为7， 所以最小为1，最大为5，则应用字典排列法解题 如下。
• 解：当首位为1时，有以下5种情况 115,124,133,142,151 当首位为2时，有以下4种情况 214,223,232,241
汤姆有1颗，即首位为1，有以下6种情况 116,125,134,143, 152,161. 汤姆有2颗，即首位为2，有以下5种情况 215,224,233,242,251. 汤姆有3颗，即首位为3，有以下4种情况 314,323,332,341. 汤姆有4颗，3种情况 313,322,331 当首位为4时，有以下2种情况 411,421 当首位为5时，有以下1种情况 511 5+4+3+2+1=15（个） 答：这样的三位数共有15个
• 2、费叔叔买来6个苹果，分给小悦、东东、 阿奇三个人，每人至少一个，那么一共至 少有多少种分法。
• 分析：在3堆蚂蚁中，每堆至少有2只，一共有12只，因此 每堆蚂蚁至少有2只，至多有8只。同样为了方便解题，我 们先假设是有次序的，然后再去掉重复的。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
二年级奥数题及答案：枚举法
二年级奥数题及答案：枚举法
1.一个长方形的周长是22米，如果它的长和宽都是整米数，问：
①这个长方形的面积有多少可能值?
②面积最大的长方形的长和宽是多少?
2.有四种不同面值的硬币各一枚，它们的形状也不相同，用它们共能组成多少种不同钱数?
3.三个自然数的乘积是24，问由这样的三个数所组成的数组有多少个?如(1，2，12)就是其中的一个，而且要注意数组中数字相同但顺序不同的算作同一数组，如(1，2，12)和(2，12，1)是同一数组.
4.小虎给3个小朋友写信，由于粗心，把信装入信封时都给装错了，结果3个小朋友收到的都不是给自己的信，请问小虎错装的情况共有多少种可能?
5.一个学生假期往A、B、C三个城市游览.他今天在这个城市，明天就到另一个城市.假如他第一天在A市，第五天又回到A市.问他的游览路线共有几种不同的方案?
6.下图中有6个点，9条线段，一只甲虫从A点出发，要沿着某几条线段爬到F点.行进中甲虫只能向右、向下或向右下方运动.问这只甲虫有多少种不同的走法?
7.小明有一套黄色数字卡片、、，有一套蓝色数字卡片、、.一天他偶然用卡片做了下面的游戏：把不同色的卡片交叉配对，一次配成3对，然后把每对卡片上的黄蓝数字相乘之后再相加求和，你知道他共找到了多少种配对相乘求和的方式吗?比如说下面是其中一种：
黄蓝黄蓝黄蓝
8.五个学生友1，友2，友3，友4，友5一同去游玩，他们将各自的书包放在了一处.分手时友1带头开了个玩笑，他把友2小朋友的书包拿走了，后来其他的小朋友也都拿了别人的书包.试问在这次玩笑中故意错拿书包的情形有多少种不同方式?
习题解答
1.解：这个长方形的长和宽之和是22÷2=11(米)，由长方形的面积=长×宽，可知：
由上表可见面积最大的长方形的长是6米、宽是5米，面积是30平方米.
猜想：由本讲的例1和习题1这两题来看，周长一定的所有长方形中，长和宽相等或相近那个长方形面积最大.这是有名的“等周问题”的特例.
2.解：把各种不同的组合及其对应的钱数列表枚举如下：
数一数可知，能组成15种不同的钱数.注意它们是从1到15的15个自然数：1，2，3，4，5，6，7，8，9，10，11，12，13，14，15.
3.解：不计数组中数的顺序，所有乘积为24的三个数所组成的数组共有6组，枚举如下：
(1，1，24)，(1，2，12)，(1，3，8)，
(1，4，6)，(2，2，6)，(2，3，4).
4.解：把三封信编号为1号、2号、3号;
把三个小朋友编号为友1、友2、友3;1号、2号、3号信应该分别发给友1、友2、友3。
按题意，友1没有收到给自己的1号信，他只可能收到2号或3号信.
当友1收到2号信时，友2只可能收到3号信，则友3收到1号信;
当友1收到3号信时，友2只可能收到1号信，则友3收到2号信.
可见共有2种可能的错装情况，列表更为清楚，
5.解：请看下面的树形图.
可见他第五天回到A市的不同游览路线共有6种，分别是：
①A→B→A→B→A ④A→C→A→B→A
②A→B→A→C→A ⑤A→C→A→C→A
③A→B→C→B→A ⑥A→C→B→C→A.
6.解：经过E点的有3条路线，不经过E点的有2条路线，共有5条不同的路线，见下图.
7.解：可以按下面的方法找出所有不同的配对相乘求和方式：
可见共有6种不同的配对相乘求和方式，其中第①种情况(可叫做同序配对)各乘积之和最大，第⑥种情况(可叫做逆序配对)各乘积之和最小.
如果你感兴趣，可以进一步问，这个结果有普遍性吗?我们再进一步探讨一下：
结果和上述相同.
2.假如黄蓝卡片各有4张，不同的配对方式有很多.
(4×3×2×1=24种，这点同学们以后就会明白!)
我们找几种情况试一试：
①同序配对：
②逆序配对
③交叉配对
交叉配对
交叉配对
可见：同序配对，各乘积之和最大：30
逆序配对，各乘积之和最小：20
交叉配对，各乘积之和居中：大于20小于30.
猜想：两个项数相同的数列配对相乘积之和，同序配对时最大，逆序配对时最小，交叉配对时在最小值和最大值之间.
8.解：设友1、友2、友3、友4、友5的书包分别是1号、2号、3号、4号、5号.因为友1拿了2号书包，那么友2就有拿1号、3号、4号和5号书包的四种可能.如果友2拿了1号书包，友3拿了4号书包，友4拿了5号书包，友5拿了3号书包，这就是一种错拿方式.其他方式看如下的树形图.
数一数，共有11种不同的错拿方式.。