§4-1材料力学的任务 §4-2 杆件变形的基本形式
材料力学的基本任务

第一章绪论1.1 材料力学的基本任务各种机械、设备和结构物在使用时,组成它们的每个构件,都要受到从相邻构件或从其它构件传递来的外力(即载荷)的作用。
材料力学是一门研究各种构件的抗力性能的科学,它的主要任务就是从保证所有构件能够正常工作的要求出发,帮助设计者合理地选择构件的适当材料和形状,确定所需要的几何尺寸;判断已有的构件是否能合乎正常地使用,并考虑如何改造它们,使之能够适应新任务的要求。
为了使所有构件在各种实际工作的考验中不至于丧失应有的效能,这些构件必须具备下列三项基本条件:1)具有足够的强度就是能够安全地承受所担负的载荷,不至于发生断裂或产生严重的永久变形。
例如,冲床的曲轴,在工作冲压力作用下不应折断。
又如,储气罐或氧气瓶,在规定压力下不应爆破。
可见,所谓强度是指构件在载荷作用下抵抗破坏的能力。
2)具有足够的刚度在载荷作用下,构件的最大变形不超过实际使用中所能容许的数值。
某些结构的变形,不能超过正常工作允许的限度。
以机床的主轴为例,即使它有足够的强度,若变形过大时(图1-1a),将使轴上的齿轮啮合不良,并引起轴承的不均匀磨损(图l-1b)。
因而,所谓刚度是指构件在外力作用下抵抗变形的能力。
3)具有足够的稳定性当受力时能够保持原有的平衡形式,不至于突然偏侧而丧失承载能力。
有些细长杆,如内燃机中的挺杆、千斤顶中的螺杆等(图1-2 a、b),在压力作用下,有被压弯的可能。
为了保证其正常工作.要求这类杆件始终保持直线形式.亦即要求原有的直线平衡形态保持不变。
所以,所谓稳定性是指构件保持其原有平衡状态的能力。
图1-1 图1-2若构件的截面尺寸过小,或截面形状不合理,或材料选用不当,在外力作用下将不能满足上述要求,从而影响机械或工程结构的正常工作。
反之,如构件尺寸过大,材料质量太高,虽满足了上述要求,但构件的承载能力难以充分发挥。
这样,既浪费了材料.又增加了成本和重量。
材料力学的任务就是在满足强度、刚度和稳定性的要求下,以最经济的代价,为构件确定合理的形状和尺寸,选择适宜的材料,为构件设计提供必要的理论基础和计算方法。
杆件变形的基本形式

课后作业
把四种基本变形的名称以及受力特点,变 形特点抄写在作业本上
谢谢观看
轴向拉伸与压缩
轴向拉伸:杆的变 轴向压缩:杆的变形
形是轴向伸长,横 是轴向缩短,横向伸
Байду номын сангаас
向缩短。
长。
F
F
轴向拉伸
F
F
轴向压缩
剪切
在一对相距很近、大小相等、方向相反的横
向外力作用下,杆件的主要变形是横截面沿
外力作用方向发生错动,这种变形方式称为
剪切。
F
F
剪切
F F
受力特点:反向外 力垂直于杆件轴线 并相互平行且相距 很近。
变形特点:两外力间 的截面沿外力方向产 生相对错动。
课堂小结
轴向拉伸
F
F
轴向压缩
F
F
剪切
F
F
课后作业
把这两种基本变形的名称以及受力特 点,变形特点抄写在作业本上
扭转
在一对大小相等、方向相反、位于垂直于杆轴线的 两平面内的外力偶作用下,杆的任意横截面将绕轴 线发生相对转动,而轴线仍维持直线,这种变形称 为扭转。
项目二 杆件的基本变形
2.1 杆件变形的基本形式
杆件变形的基本形式
轴向拉伸与压缩 剪切 扭转 弯曲
轴向拉伸与压缩
轴向拉伸与压缩由大小相等,方向相反,作用线与杆 件轴线重合的一对力所引起的,表现为杆件长度的伸 长或压缩。
拉伸与压缩的受力特点:外 力的合力作用线与杆的轴线 完全重合。
拉伸与压缩的变形特点:杆 的变形主要是轴向伸缩,伴 随横向缩扩。
M
M
扭转
受力特点:由垂直于杆轴 线平面内的力偶作用引起 的。
杆件的基本变形

计算简图
计算简图
阳台
阳台梁是受弯构件
内力及其截面法
一、内力的概念
1、外力:其它物体对构件作用的力。例如支座反力,荷载等。
2、内力:固有内力--分子内力,它是由构成物体的材料的
物理性质所决定的。
附加内力—由于外力作用而引起的受力构件内部各质
点间相互作用力的改变量。
材料力学研究----附加内力 (简称内力)
随外力产生或消失 随外力改变而改变
但有一定限度
截面法
步骤: 1、切开
根据空间任意力系的六个平衡方程
X0 Y 0 Z 0 Mx 0 My 0 Mz 0
求பைடு நூலகம்内力分量
2、代替 3、平衡
注意:
用截面法求内力和取分离体求约束反力的方法本质 相同。这里取出的研究对象不是一个物体系统或一个完 整的物体,而是物体的一部分。
螺 栓
连 接 键
销钉
螺 栓
扭转变形
受力特点:由垂直于杆轴线平面内的力偶作用引起的
变形特点:相邻横截面绕杆轴产生相对旋转变形。
对称扳手拧紧镙帽 自 行 车 中 轴 受 扭
桥 体 发 生 扭 转 变 形
弯曲变形
受力特点:是由垂直于杆件轴线的横向力或作用 在杆件的纵向平面内的力偶引起的
变形特点:杆轴由直变弯,杆件的轴线变成曲线。
必须指出:用截面法之前 ⑴ 一般不允许用力的可传性原理。
⑵ 不允许用合力来代替力系的作用。
⑶ 不允许把力偶在物体上移动。
拉伸
压缩
变形特点:杆轴沿外力方向伸长或缩短, 主要变形是长度的改变
屋 架 结 构 中 的 拉 压 杆
塔 式 结 构 中 的 拉 压 杆
桥 梁 结 构 中 的 拉 杆
杆件的基本变形形式

杆件的基本变形形式
杆件的基本变形形式有以下几种:
1. 拉伸和压缩:当杆件受到沿其轴向的力时,杆件会发生拉伸或压缩变形。
拉伸时杆件长度增加,压缩时杆件长度减小。
2. 剪切:当杆件受到垂直于其轴向的力时,杆件会发生剪切变形。
剪切变形表现为杆件的横截面发生相对错动。
3. 扭转:当杆件受到绕其轴线的力矩时,杆件会发生扭转变形。
扭转变形使得杆件的横截面绕轴线旋转。
4. 弯曲:当杆件受到垂直于其轴线的横向力时,杆件会发生弯曲变形。
弯曲变形导致杆件的轴线发生弯曲。
这些基本变形形式是杆件在不同加载条件下的主要响应方式。
在工程和力学领域中,了解杆件的基本变形形式对于设计和分析结构非常重要。
通过对这些变形形式的研究,可以确定杆件在负载下的应力、应变分布以及可能的破坏模式。
需要注意的是,实际工程结构中的杆件可能同时受到多种变形形式的组合作用。
例如,在一个梁的设计中,可能同时存在弯曲和剪切变形。
因此,在分析杆件的变形和应力时,需要综合考虑各种变形形式的影响。
希望这些信息对你有所帮助!如果你有其他问题,请随时提问。
材料力学 杆件的变形计算
例题4-2: 已知:l = 54 mm ,di = 15.3 mm,E=200 GPa, ν = 0.3,拧紧后,△l =0.04 mm。 试求:(a) 螺栓横截面上的正应力 σ (b) 螺栓的横向变形△d
解:1) 求横截面正应力 :
ε=
∆l 0.04 = = 7.41×10-4 l 54
l = 54 mm ,di = 15.3 mm, E=200 GPa, ν = 0.3, △l =0.04 mm
∆ac = a ′c′ − ac
∆ac ε′ = ac
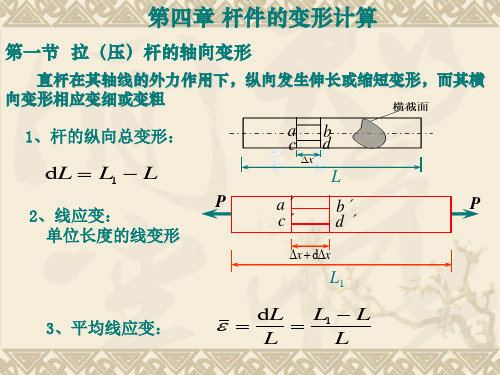
二、拉压杆的弹性定律 1、等内力拉压杆的弹性定律 P P
PL NL dL = = EA EA
PL dL ∝ A
2、变内力拉压杆的弹性定律
N(x) N(x)
x dx dx 内力在n段中分别为常量时 内力在 段中分别为常量时
※“EA”称为杆的抗拉压刚度。 ※“ ”称为杆的抗拉压刚度。
C1
C点总位移: 点总位移:
∆C = ∆C y + ∆C x = 1.47mm
2 2
C0
Cx
(此问题若用圆弧精确求解) 此问题若用圆弧精确求解)
∆C x = 0.278mm ∆C y = 1.44mm
第二节 圆轴的扭转变形及相对扭转角
为 dx 的两个相邻截面之间有相对转角dϕ 的两个相邻截面之间有相对转角d
800 π × 0.04 4 80 ×109 32 = 0.03978rad / m
综合两段, 综合两段,最大单位扭转角应在BC 段 为 0.03978 rad/m
例4-5 图示一等直圆杆, 图示一等直圆杆,已知 d =40mm a =400mm G =80GPa, ϕ DB=1O , 求 : 1) 最大切应力 2)ϕ AC
材料力学-整理笔记

材料力学第1章绪论1.1材料力学的任务构件应满足以下基本要求:强度,刚度,稳定性要求1.2材料力学的基本假设连续性,均匀性,各向同性假设1.3杆件的基本变形形式拉伸或压缩,剪切,扭转,弯曲1.4内力一截面法1.5应力平均应力-p:应力p:应力,切应力,正应力:1.6应变1.棱边长度的改变(原长为△x,变形后成为△x+△u)该点处沿x方向的线应变:2.棱边间夹角的改变切应变:y。
切应变的单位为rad第2章拉伸压缩与剪切2.1拉压杆的内力及应力2.1.1轴力、轴力图Fn=FFn即为横截面n—n上的内力。
由于F的作用线与杆轴线重合,故称为轴力。
规定拉伸的轴力为正,压缩为负。
2.1.2轴力图2.1.3拉压杆横截面上的应力轴向载荷作用下杆件是否破坏,不仅与轴力的大小有关,还与横截面面积有关。
正应力:。
拉应力为正,压应力为负。
2.1.4斜截面上的应力斜面上的全应力Pa:将全应力Pa分解为沿斜面法向的正应力和沿切向的切应力思考:a=0/45/90°时,正应力,切应力大小2.2拉压杆的变形2.2.1 轴向与横向变形轴向线应变为:。
以伸长为正,缩短为负。
横向线应变为:。
正负号与轴向线应变相反。
材料的泊松比u(量纲一):2.2.2 拉压胡克定律当应力o未超过某一极限值时,拉压杆的轴向变形与外力F及杆的原长l 成正比,与横截面面积A成反比。
引进比例常数E,则有胡克定律公式:E为材料的弹性模量,其量纲为ML^-1T^-2。
EA反映了杆件抵抗拉压变形的能力,称为杆件的抗拉(压)刚度。
由Fn/A=正应力,△l/l=线应力,故。
(在弹性范围内,正应力与线应变成正比。
)2.3金属拉压时的力学性能2.3.1低碳钢拉伸时的力学性质1.在拉伸过程中,标距l的伸长量与试件所受载荷F之间的关系曲线F—△l 称为拉伸曲线。
工程应力:将纵坐标值F除以原始的横截面面积A,即为正应力=F/A工程应变:将横坐标值除以原始的标距长度l,即为线应变=△l /l将拉伸曲线F—△l变为应力应变曲线(消除试件尺寸的影响)(1)弹性阶段Ob:弹性阶段的应力最高限称为材料的弹性极限(用符号6e表示)。
材料力学总复习与例题

剪力图有突变,P力向下,
Q 图向下变,变化值=P x -
a P l
值;弯矩图有折角。
M
Pab l
+ x
RA A
m
a
C
b
RB
B
内力图特征: 在集中力偶作用的地方,
l Q +
m l x 变,m逆时针转,M图向上
剪力图无突变;弯矩图有突 变,变化值=m值。
M
+
a m l
-
x
b m l
RA
q
RB
B
A
a Q
§3–1 扭转的概念和实例
扭 转
扭矩和扭矩图
§3–2 外力偶矩的计算
§3–3 纯剪切 §3–4 圆轴扭转时的应力 §3–5 圆轴扭转时的变形
§3–7 非圆截面杆扭转的概念
扭转时的内力——扭矩 m
m
T x
m 构件受扭时,横截面上的内力为力偶,称为扭矩,记作“T”。 扭矩的正负规定: 以右手螺旋法则,沿截面外法线方向为正,反之为负。
m
m B
弯矩M
RB
P Q
M C RB
内力的正负规定: ①剪力Q: 左上右下为正;反之为负。 Q Q
左上右下为正
Q
+
Q Q
+
Q
Q - Q
Q Q
Q
Q
-
②弯矩M:使梁变成上凹下凸的为正弯矩;反之为负弯矩。
M
M
M (+)
MM (+)
M
M
M
M
(–)
MM
(–)
M
a
P
C
b
B
A
第六讲 杆件变形的基本形式

有缘学习更多+谓ygd3076或关注桃报:奉献教育 (店铺)
§1.5 杆件变形的基本形式
杆件的基本变形: 拉伸(压缩)、剪切、扭转、弯曲 2、弯曲(bending)
M
M
杆受一对大小相等,方向相反的力偶,力偶的作用线是包含轴线的纵向面。
§1.5 杆件变形的基本形式
图中杆件所受外力的形式是怎么样的?
§1.5 杆件变形的基本形式
杆件的基本变形: 拉伸(压缩)、剪切、扭转、弯曲 1、拉伸或压缩(tension and compression)
F
FF
F
杆受一对大小相等,方向相反的纵向力,力的作用线与杆轴线重合。
§1.5 杆件变形的基本形式
杆件的基本变形: 拉伸(压缩)、剪切、扭转、弯曲 2、弯曲(bending)
4剪切shear15杆件变形的基本形式数学物理学理论力学其他入门材料力学材料力学是一门很重要的技术基础课它与机械土建航空交通水利等工程密切相关他在基础课和专业课之间起着桥梁作用
1.5 杆件变形的基本形式
§1.5 杆件变形的基本形式
杆件的基本变形: 拉伸(压缩)、剪切、扭转、弯曲 1、拉伸或压缩(tension and compression)
有缘学习更多+谓ygd3076或关注桃报:奉献教育(店铺)
材料力学是一门很重要的技术基础课,它与机械、土建、航空、交 通水利等工程密切相关,他在基础课和专业课之间起着桥梁作用。
入门
数学
物理学
理论力学
其他
材料力学
新
建
结
弹
机
机
其
型
筑
构
性械械来自他材结
力
力
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏省技工院校
教案首页
课题:§4-1材料力学的任务§4-2 杆件变形的基本形式
教学目的要求:1、明确材料力学研究的对象是有一定承载能力的变形固体
2、了解材料力学的基本任务和杆件变形的四种基本形式
3、初步建立起构件的强度、刚度、稳定性的概念
教学重点、难点:重点:杆件变形的四种基本形式
难点:对于稳定性、剪切概念的理解
授课方法:讲授法,作图法
教学参考及教具(含电教设备):工程力学教学参考书,绘图工具
授课执行情况及分析:
板书设计或授课提纲
受力特点和变形特点②剪切
受力特点和变形特点③扭转
受力特点和变形特点④弯曲
受力特点和变形特点。
