信号系统习题解答3版-4
信号与系统课后习题与解答第三章
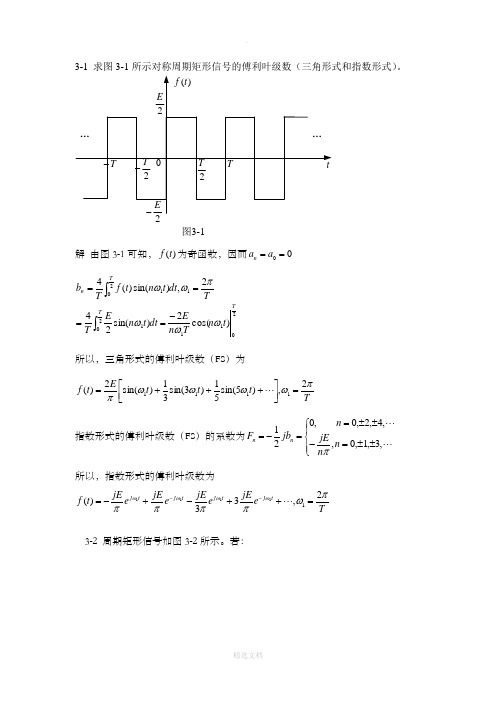
3-1 求图3-1所示对称周期矩形信号的傅利叶级数(三角形式和指数形式)。
图3-1解 由图3-1可知,)(t f 为奇函数,因而00==a a n2112011201)cos(2)sin(242,)sin()(4T T T n t n T n Edt t n E T T dt t n t f T b ωωωπωω-====⎰⎰所以,三角形式的傅利叶级数(FS )为T t t t E t f πωωωωπ2,)5sin(51)3sin(31)sin(2)(1111=⎥⎦⎤⎢⎣⎡+++=指数形式的傅利叶级数(FS )的系数为⎪⎩⎪⎨⎧±±=-±±==-= ,3,1,0,,4,2,0,021n n jE n jb F n n π所以,指数形式的傅利叶级数为Te jE e jE e jEe jEt f t j t j t j t j πωππππωωωω2,33)(11111=++-+-=--3-2 周期矩形信号如图3-2所示。
若:图3-22τT-2τ-重复频率kHz f 5= 脉宽 s μτ20= 幅度 V E 10=求直流分量大小以及基波、二次和三次谐波的有效值。
解 对于图3-2所示的周期矩形信号,其指数形式的傅利叶级数(FS )的系数⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛====⎰⎰--22sin 12,)(1112212211τωττωππωττωωn Sa T E n n E dt Ee T T dt e t f T F tjn TT t jn n则的指数形式的傅利叶级数(FS )为∑∑∞-∞=∞-∞=⎪⎭⎫⎝⎛==n tjn n tjn ne n Sa TE eF t f 112)(1ωωτωτ其直流分量为T E n Sa T E F n ττωτ=⎪⎭⎫ ⎝⎛=→2lim100 基波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-2sin 2111τωπEF F 二次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-22sin 122τωπEF F 三次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-23sin 32133τωπE F F 由所给参数kHz f 5=可得s T s rad 441102,/10-⨯==πω 将各参数的值代入,可得直流分量大小为V 110210201046=⨯⨯⨯--基波的有效值为())(39.118sin 210101010sin 210264V ≈=⨯⨯⨯- πππ二次谐波分量的有效值为())(32.136sin 251010102sin 21064V ≈=⨯⨯⨯- πππ三次谐波分量的有效值为())(21.1524sin 32101010103sin 2310264V ≈=⨯⨯⨯⨯- πππ3-3 若周期矩形信号)(1t f 和)(2t f 的波形如图3-2所示,)(1t f 的参数为s μτ5.0=,s T μ1= ,V E 1=; )(2t f 的参数为s μτ5.1=,s T μ3= ,V E 3=,分别求:(1))(1t f 的谱线间隔和带宽(第一零点位置),频率单位以kHz 表示; (2))(2t f 的谱线间隔和带宽; (3))(1t f 与)(2t f 的基波幅度之比; (4))(1t f 基波与)(2t f 三次谐波幅度之比。
信号系统(第3版)习题解答

信号系统(第3版)习题解答《信号与系统》(第3版)习题解析高等教育出版社目录第1章习题解析 (2)第2章习题解析 (6)第3章习题解析 (16)第4章习题解析 (23)第5章习题解析 (31)第6章习题解析 (41)第7章习题解析 (49)第8章习题解析 (55)第1章习题解析1-1 题1-1图示信号中,哪些是连续信号?哪些是离散信号?哪些是周期信号?哪些是非周期信号?哪些是有始信号?(c) (d)题1-1图解 (a)、(c)、(d)为连续信号;(b)为离散信号;(d)为周期信号;其余为非周期信号;(a)、(b)、(c)为有始(因果)信号。
1-2 给定题1-2图示信号f ( t ),试画出下列信号的波形。
[提示:f ( 2t )表示将f ( t )波形压缩,f (2t )表示将f ( t )波形展宽。
] (a) 2 f ( t - 2 )(b) f ( 2t )(c) f ( 2t ) (d) f ( -t +1 )题1-2图解 以上各函数的波形如图p1-2所示。
图p1-21-3 如图1-3图示,R 、L 、C 元件可以看成以电流为输入,电压为响应的简单线性系统S R 、S L 、S C ,试写出各系统响应电压与激励电流函数关系的表达式。
题1-3图解 各系统响应与输入的关系可分别表示为)()(t i R t u R R ⋅= tt i L t u L L d )(d )(= ⎰∞-=t C C i Ct u ττd )(1)(1-4 如题1-4图示系统由加法器、积分器和放大量为-a 的放大器三个子系统组成,系统属于何种联接形式?试写出该系统的微分方程。
S R S L S C题1-4图解 系统为反馈联接形式。
设加法器的输出为x ( t ),由于)()()()(t y a t f t x -+=且)()(,d )()(t y t x t t x t y '==⎰故有 )()()(t ay t f t y -='即)()()(t f t ay t y =+'1-5 已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|,试判定该系统是否为线性时不变系统?解 设T 为系统的运算子,则可以表示为)()]([)(t f t f T t y ==不失一般性,设f ( t ) = f 1( t ) + f 2( t ),则)()()]([111t y t f t f T ==)()()]([222t y t f t f T ==故有)()()()]([21t y t f t f t f T =+=显然)()()()(2121t f t f t f t f +≠+即不满足可加性,故为非线性时不变系统。
《信号与系统(第三版)习题解析》勘误表

《信号与系统(第三版)习题解析》勘误表1谷源涛2012年3月25日一、可能影响理解的错误1、 第12页,第3行“(t −π4)”改为“(t +π4)”,即把减号改成加号2、 第291页,第10行“=Wal2{[(i −1)⊕j ]+1,t]”改为“=Wal2{[(i −1)⊕j ]+1,t }”,即最后一个中括号改成大括号3、 第297页,第7行行末“πA 28δ(ω+1800)”改为“πA 28[δ(ω+1800)”并移至第8行行首,注意改动是插入方括号4、 第311页,倒数第6行“cos (ωc T −ωc t )+sin (ωc T −ωc t )”改成“cos (ωc T −ωc t )−sin (ωc T −ωc t )”,即加号改成减号5、 第311页,倒数第5行“cos (ωc t )−sin (ωc t )”改成 “cos (ωc t )+sin (ωc t )”,即减号改成加号6、 第391页,倒数第4行“DFT[x (n )]=X (k )”改为“DFT[x (n )]=X (k )”,即去掉x 和X 上的黑体;将“IDFT[X ](k )=x (n )”改为“IDFT[X (k )] =x (n )”,即一方面去掉黑体,另一方面将(k )移到方括号之内7、 第434页,第7行“0.739”改为“2.825”8、 第434页,倒数第3行“0.739”改为“2.825”9、 第455页,倒数第4行“,代价是增大了主瓣宽度和过渡带宽度”删掉10、 第460页,第9行“在∞有一个四阶零点,”删掉11、 第469页,第6行“ℒ[KΘ(t )]”改为“ℒ[Kθ(t )]”,即大写Θ改成小写θ,注意花体的ℒ还用原来的样子12、 第472页,倒数第3、4行“在PI 控制跟踪阶跃信号稳态误差不为零的情况下,”删掉13、 第472页,倒数第3行“可以改善”改为“可以提高系统稳定性,改善”14、 第486页,最后一行,分母“e jw −12”改成“e jω−12”,即把w 改成omega15、 第521页,第5行“|000−100006232−200−3|”改为“[000−100006232−200−3]”,即把绝对值号改为方括号 1 已将本勘误表交给出版社;希望这些问题能在第二次印刷中更正。
计算机网络吴功宜(第三版)课后习题解答(第1-4章)

计算机网络-清华版_吴功宜(第三版)课后习题解答(第1-4 章)第一章计算机网络概论P421. 请参考本章对现代Internet 结构的描述,解释“三网融合”发展的技术背景。
答:基于Web的电子商务、电子政务、远程医疗、远程教育,以及基于对等结构的P2P网络、3G/4G与移动Internet 的应用,使得Internet 以超常规的速度发展。
“三网融合”实质上是计算机网络、电信通信网与电视传输网技术的融合、业务的融合。
2. 请参考本章对Internet 应用技术发展的描述,解释“物联网”发展技术背景。
答:物联网是在Internet 技术的基础上,利用射频标签、无线传感与光学传感等感知技术自动获取物理世界的各种信息,构建覆盖世界上人与人、人与物、物与物的智能信息系统,促进了物理世界与信息世界的融合。
3. 请参考本章对于城域网技术特点的描述,解释“宽带城域网”发展技术背景。
答:宽带城域网是以IP 为基础,通过计算机网络、广播电视网、电信网的三网融合,形成覆盖城市区域的网络通信平台,以语音、数据、图像、视频传输与大规模的用户接入提供高速与保证质量的服务。
4. 请参考本章对WPAN技术的描述,举出 5 个应用无线个人区域网络技术的例子。
答:家庭网络、安全监控、汽车自动化、消费类家用电器、儿童玩具、医用设备控制、工业控制、无线定位。
5.. 请参考本章对于Internet 核心交换、边缘部分划分方法的描述,举出身边 5 种端系统设备。
答:PDA、智能手机、智能家电、无线传感器节点、RFID 节点、视频监控设备。
7. 长度8B与536B的应用层数据通过传输层时加上了20B的TCP报头, 通过网络层时加上60B 的IP 分组头,通过数据链路层时加上了18B 的Ethernet 帧头和帧尾。
分别计算两种情况下的数据传输效率。
(知识点在:P33)解:长度为8B的应用层数据的数据传输效率:8/(8+20+60+18) ×100%=8/106×100%=7.55%长度为536B的应用层数据的数据传输效率:536/(536+20+60+18) ×100%=536/634×100%=84.54%8. 计算发送延时与传播延时。
信号与线性系统复习课用习题

第三、四章自测题解答一、 填空题:1、(1))(1t f 的参数为VA s T s 1,1,5.0===μμτ,则谱线间隔为__1000__kHz, 带宽为___2000__kHz 。
(2))(2t f 的参数为V A s T s 3,3,5.1===μμτ,则谱线间隔为___333__kHz, 带宽为_666__kHz 。
(3))(1t f 与)(2t f 的基波幅度之比为___1:3____。
(4))(1t f 的基波幅度与)(2t f 的三次谐波幅度之比为__1:1___。
2、由于周期锯齿脉冲信号的傅里叶级数的系数具有收敛性,因此,当k →∞时,k a =0。
3、信号x (t)的频带宽度为B ,x(2t)的频带宽度为 ,x(t/2)的频带宽度为 .3、根据尺度变化性质,可得x(2t)的频带宽度为2B ,可得x(t/2)的带宽为B/2。
6、设f (t)的傅里叶变换为)(ωj F ,则)(jt F 的傅里叶变换为2f ()πω-。
7、单个矩形脉冲的频谱宽度一般与其脉宽τ有关,τ越大,则频谱宽度 越窄 。
8、矩形脉冲通过RC 低通网络时,波形的前沿和后沿都将产生失真,这种失真的一个主要的原因是RC 低通网络不是理想低通滤波器,脉冲中的高频成分被削弱 。
9、为满足信号无失真,传输系统应该具有的特性(1)H(j )ω=;(2)h(t)= 。
9、(1)0j t Ke ω-(K 为常数),(2)0K (t-t )δ(0t 为常数) 10、已知某个因果连续时间LTI 系统的频率响应为H(j )ω,则该系统对输入信号tj t j e a e a E t x 0011)(ωω--++=的响应为 . 10、系统对输入信号t j t j e a e a E t x 0011)(ωω--++=的响应为)()()0()(010100ωωωωj H e a j H e a j EH t y t j t j -++=--。
信号与系统第二版课后习题解答(3-4)奥本海姆

Chap 33.1 A continuous-time periodic signal x(t) is real value and has a fundamental period T=8. The nonzero Fourier series coefficients for x(t) arej a a a a 4,2*3311====--.Express x(t) in the form)cos()(0k k k k t A t x φω+=∑∞=Solution:Fundamental period 8T =.02/8/4ωππ==00000000033113333()224434cos()8sin()44j kt j t j t j t j tk k j t j t j t j tx t a e a e a e a e a e e e je je t t ωωωωωωωωωππ∞----=-∞--==+++=++-=-∑A discrete-time periodic signal x[n] is real valued and has afundamental period N=5.The nonzero Fourier series coefficients for x[n] are10=a ,4/2πj e a --=,4/2πj e a =,3/*442πj e a a ==- Express x[n] in the form)sin(][10k k k k n A A n x φω++=∑∞=Solution:for, 10=a , 4/2πj ea --= , 4/2πj ea = ,3/42πj e a --=,3/42πj e a =n N jk k N k e a n x )/2(][π∑>=<=n j n j n j n j e a e a e a e a a )5/8(4)5/8(4)5/4(2)5/4(20ππππ----++++=n j j n j j n j j n j j e e e e e e e e )5/8(3/)5/8(3/)5/4(4/)5/4(4/221ππππππππ----++++=)358cos(4)454cos(21ππππ++++=n n)6558sin(4)4354sin(21ππππ++++=n nFor the continuous-time periodic signal)35sin(4)32cos(2)(t t t x ππ++= Determine the fundamental frequency 0ω and the Fourier seriescoefficients k a such thattjk k kea t x 0)(ω∑∞-∞==.Solution:for the period of )32cos(t πis 3=T , the period of )35sin(t πis 6=Tso the period of )(t x is 6, i.e. 3/6/20ππ==w )35sin(4)32cos(2)(t t t x ππ++=)5sin(4)2cos(21200t t ωω++=0000225512()2()2j t j t j t j t e e j e e ωωωω--=++-- then, 20=a , 2122==-a a , j a 25=-, j a 25-=3.5 Let 1()x t be a continuous-time periodic signal with fundamental frequency1ω and Fourier coefficients k a . Given that211()(1)(1)x t x t x t =-+-How is the fundamental frequency2ω of 2()x t related to? Also,find a relationship between the Fourier series coefficients k b of2()x t and the coefficients k a You may use the properties listed inTable 3.1. Solution:(1). Because )1()1()(112-+-=t x t x t x , then )(2t x has the same period as )(1t x , that is 21T T T ==, 12w w =(2). 212111()((1)(1))jkw t jkw t k TT b x t e dt x t x t e dt T --==-+-⎰⎰ 111111(1)(1)jkw t jkw t TTx t e dt x t e dt T T --=-+-⎰⎰111)(jkw k k jkw k jkw k e a a e a e a -----+=+=Suppose given the following information about a signal x(t): 1. x(t) is real and odd.2. x(t) is periodic with period T=2 and has Fourier coefficients k a .3. 0=k a for 1||>k .4 1|)(|21202=⎰dt t x .Specify two different signals that satisfy these conditions. Solution:0()j kt k k x t a e ω∞=-∞=∑while: )(t x is real and odd, then k a is purely imaginary and odd , 00=a , k k a a --=,.2=T , then 02/2ωππ==and0=k a for 1>kso0()j kt k k x t a e ω∞=-∞=∑00011j t j t a a e a e ωω--=++)sin(2)(11t a e ea t j tj πππ=-=-for12)(2121212120220==++=-⎰a a a a dt t x∴ j a 2/21±=∴)sin(2)(t t x π±=3 Consider a continuous-time LTI system whose frequency response is⎰∞∞--==ωωωω)4sin()()(dt e t h j H t jIf the input to this system is a periodic signal⎩⎨⎧<≤-<≤=84,140,1)(t t t x With period T=8,determine the corresponding system output y(t). Solution:Fundamental period 8T =.02/8/4ωππ==0()j kt k k x t a e ω∞=-∞=∑∴ 00()()jk t k k y t a H jk e ωω∞=-∞=∑0004, 0sin(4)()0, 0k k H jk k k ωωω=⎧==⎨≠⎩ ∴ 000()()4jkw t k k y t a H jk e a ω∞=-∞==∑Because 48004111()1(1)088T a x t dt dt dt T ==+-=⎰⎰⎰另:x(t)为实奇信号,则a k 为纯虚奇函数,也可以得到a 0为0。
数字信号处理课后答案+第4章(高西全丁美玉第三版)

6*. 按照下面的IDFT算法编写MATLAB语言 IFFT程 序, 其中的FFT部分不用写出清单, 可调用fft函数。 并分 别对单位脉冲序列、 矩形序列、 三角序列和正弦序列进行 FFT和IFFT变换, 验证所编程序。
解: 为了使用灵活方便, 将本题所给算法公式作为函 数编写ifft46.m如下: %函数ifft46.m %按照所给算法公式计算IFET function xn=ifft46(Xk, N) Xk=conj(Xk); %对Xk取复共轭 xn=conj(fft(Xk, N))/N; %按照所给算法公式计算IFFT 分别对单位脉冲序列、 长度为8的矩形序列和三角序列 进行FFT, 并调用函数ifft46计算IFFT变换, 验证函数 ifft46的程序ex406.m如下:
快速卷积时, 需要计算一次N点FFT(考虑到H(k)= DFT[h(n)]已计算好存入内存)、 N次频域复数乘法和 一次N点IFFT。 所以, 计算1024点快速卷积的计算时间Tc 约为
Fs <
1024 = 15 625 次 /秒 65536 × 10−6
Fs 15625 = = 7.8125 kHz 2 2
1 x ( n) = IDFT[ X ( k )] = [DFT[ X * ( k )]]* N
%程序ex406.m %调用fft函数计算IDFT x1n=1; %输入单位脉冲序列x1n x2n=[1 1 1 1 1 1 1 1]; %输入矩形序列向量x2n x3n=[1 2 3 4 4 3 2 1]; %输入三角序列序列向量x3n N=8; X1k=fft(x1n, N); X2k=fft(x2n, N); X3k=fft(x3n, N); %计算x1n的N点DFT %计算x2n的N点DFT %计算x3n的N点DFT
信号与系统课后习题答案

习 题 一 第一章习题解答基本练习题1-1 解 (a) 基频 =0f GCD (15,6)=3 Hz 。
因此,公共周期3110==f T s 。
(b) )30cos 10(cos 5.0)20cos()10cos()(t t t t t f ππππ+==基频 =0f GCD (5, 15)=5 Hz 。
因此,公共周期5110==f T s 。
(c) 由于两个分量的频率1ω=10π rad/s 、1ω=20 rad/s 的比值是无理数,因此无法找出公共周期。
所以是非周期的。
(d) 两个分量是同频率的,基频 =0f 1/π Hz 。
因此,公共周期π==01f T s 。
1-2 解 (a) 波形如图1-2(a)所示。
显然是功率信号。
t d t f TP T TT ⎰-∞→=2)(21lim16163611lim 22110=⎥⎦⎤⎢⎣⎡++=⎰⎰⎰∞→t d t d t d T T T W(b) 波形如图1.2(b)所示。
显然是能量信号。
3716112=⨯+⨯=E J (c) 能量信号 1.0101)(lim101025=-===⎰⎰∞∞---∞→T t ttT e dt edt eE J(d) 功率信号,显然有 1=P W1-3 解 周期T=7 ,一个周期的能量为 5624316=⨯+⨯=E J 信号的功率为 8756===T E P W 1-5 解 (a) )(4)2()23(2t tt δδ=+; (b) )5.2(5.0)5.2(5.0)25(5.733-=-=----t e t e t et tδδδ(c) )2(23)2()3sin()2()32sin(πδπδπππδπ+-=++-=++t t t t 题解图1-2(a) 21题解图1-2(b) 21(d) )3()3()(1)2(-=----t e t t et δδε。
1-6 解 (a) 5)3()94()3()4(2-=+-=+-⎰⎰∞∞-∞∞-dt t dt t t δδ(b) 0)4()4(632=+-⎰-dt t t δ(c) 2)]2(2)4(10[)]42(2)4()[6(63632=+++-=+++-⎰⎰--dt t t dt t t t δδδδ(d)3)3(3)(3sin )(1010=⋅=⎰⎰∞-∞-dt t Sa t dt ttt δδ。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4章习题答案4-2 已知系统微分方程相应的齐次方程为(1)22d ()d ()22()0d d y t y t y t t t ++=(2)22d ()d ()2()0d d y t y t y t tt ++= 两系统的起始条件都是:(0)1, (0)2y y --'==,试求两系统的零输入响应zi ()y t ,并粗略画出波形。
解:(1)0222=++ααj j --=+-=1121ααt e C t e C e A e A t y t t t t h cos sin )(212121--+=+=αα1)0(2==+C y2cos sin sin cos )0(2102211,=-=---==----+C C t e C t e C t e C t e C y t t t t t ⎩⎨⎧==1321C C0cos sin 3)(≥+=--t te t e t y tth(2) 0122=++αα1121-=-=ααt t h te A e A t y --+=21)(t t t h te A e A e A t y ----+-=221,)( ⎩⎨⎧=+-=21211A A A ⎩⎨⎧==3121A A 03)(≥+=--t tee t y tthty h (t)π/2π1ty h (t)2/33e -2/34-3 给定系统微分方程、起始状态及激励信号分别如下,试判断系统在起始点是否发生跳变,并据此写出()(0)k +y 的值。
(1)d ()d ()2()3d d y t x t y t t t+= (0)0y -=,()()x t u t = (2)22d ()d ()d ()234()d d d y t y t x t y t t tt ++= (0)1y -=,(0)1y -'=,()()x t u t =*(3)22d ()d ()d ()234()()d d d y t y t x t y t x t t t t ++=+(0)1y -=,(0)1y -'=,()()x t t δ=解:(1) )(3)(2)(t t y t y dtdδ=+因为方程在t =0时,存在冲激作用,则起始点会发生跳变设:代入方程⎪⎩⎪⎨⎧=+=)()()()()(t au t y t bu t a t y dtdδ得:a =3, 3)0(3)0(=+-+y y =(2) )()(4)(3)(222t t y t y dtdt y dt d δ=++因为方程在t =0时,存在冲激作用,则起始点会发生跳变设:代入方程⎪⎩⎪⎨⎧=+=)()()()()(22t au t y dt d t bu t a t y dt d δ得:a =0.5, ⎩⎨⎧==5.1)0(5.0)0(1)0()0(,,=+=-+-+y y y y(3) )()(')(4)(3)(222t t t y t y dtd t y dt d δδ+=++ 因为方程在t =0时,存在冲激和冲激偶作用,则起始点会发生跳变设:代入方程⎪⎪⎩⎪⎪⎨⎧=+=++=)()()()()()()()()('22t au t y t bu t a t y dtdt cu t b t a t y dt d δδδ⎩⎨⎧-4/12/1==b a ⎩⎨⎧=+=4/3)0()0(2/3)0()0(,,=+=-+-+y b y y a y4-4 给定系统微分方程为 22d ()d ()d ()32()3()d d d y t y t x t y t x t t tt ++=+ 若激励信号与起始状态为以下二种情况时,分别求它们的全响应。
并指出其零输入响应、零状态响应、自由响应和强迫响应各分量(应注意在起始点是否发生跳变)。
(1)()()x t u t =,(0)1y -=,(0)2y -'= (2)3()e ()t x t u t -=,(0)1y -=,(0)2y -'=解:(1))(3)()(2)(3)(22t u t t y t y dt dt y dtd +=++δ0232=++αα 2121-=-=αα齐次解:tt h e A e A t y 221)(--+= 特解:2/3)(=t y p完全解:2/3)(221++=--t t e A e A t y 因为方程在t =0时,存在冲激作用,则起始点会发生跳变设:代入方程⎪⎩⎪⎨⎧=+=)()()()()(22t au t y dt d t bu t a t y dt d δ 得:a =1, ⎩⎨⎧==3)0(1)0(1)0()0(,,=+=-+-+y y y y 则:2/523212/3212121-⎩⎨⎧--++====A A A A A A完全解:023252)(2≥+-=--t e e t y t t设零输入响应为:tzi t zi zi e A e A t y 221)(--+= 342)0(21)0(21,2121-⎩⎨⎧--=+--=====zi zi zi zi zi zi A A y A A y A A则:034)(2≥-=--t e e t y tt zi05.15.02)()()(2≥++-=-=--t e e t y t y t y t t zi zs自由响应:t te e25.22---;强迫响应:1.5。
(2)微分方程右边为:)()(3)()(3333t t u e t e t u e t t t δδ=++----原方程为:)()(2)(3)(22t t y t y dtdt y dt d δ=++由上述微分方程可知,t>0后方程右边没有输入,因此,系统没有强迫响应,完全响应和自由响应相同,零输入和零状态响应的形式均为齐次解形式,且零输入响应同(1),为:034)(2≥-=--t e e t y tt zi零状态响应的形式为:tzs t zs zs e A e A t y 221)(--+=设:代入方程⎪⎩⎪⎨⎧=+=)()()()()(22t au t y dt d t bu t a t y dt d δ得:a =1, ⎩⎨⎧=--1)0()0(0)0()0(,,a y y y y ==-+-+ 11120212121-⎩⎨⎧--+====A A Azs Azs A A zs zs则:0)(2≥-=--t e e t y tt zs045)()()(2≥-=+=--t e e t y t y t y tt zs zi4-6 一线性时不变系统在相同的起始状态下,当输入为()x t 时,全响应为(2e cos2)()t t u t -+;当输入为2()x t 时,全响应为(e 2cos2)()t t u t -+,求输入为4()x t 时的全响应。
解:系统的零状态响应为:)()2cos ()2cos 2()2cos 2()()()(12t u t e t e t e t y t y t y tttzs +-=+-+=-=---当输入为4x (t )时,系统的全响应为:)()2cos 4()()(3)(1t u e t t y t y t y t zs --=+=)(3)()()(1t u e t y t y t y t zs zi -=-=4-7 系统的微分方程由下列各式描述,分别求系统的冲激响应与阶跃响应。
(1)d ()2()()d y t y t x t t+=解:(1)首先求阶跃响应,原方程变为:)()(2)(t u t g t g dtd=+ 方程右边没有冲激作用,则起始点不会发生跳变,0)0()0(==-+g g 特征方程:02=+α2-=α齐次解:th e A t g 21)(-= 特解:B =0.5则:5.0)(21+=-t e A t g ,代入初始值,05.01=+A 系统的阶跃响应为:)()5.05.0()(21t u et g t+-=-系统的冲激响应为:)()()(2t u e t g dtd t h t-==*4-12 一线性时不变系统,当激励信号为1()()x t t δ=时,全响应为1()()e ()t y t t u t δ-=+;当激励信号为2()()x t u t =时,全响应为2()3e ()t y t u t -=。
求系统的冲激响应()h t (两种激励下,起始状态相同)。
解:)2()1()(3)()()()()()()()(21⎪⎩⎪⎨⎧=+=+=+=-∞--⎰t u e t y d h t y t u e t t y t h t y tzi t tzi ττδ 式(1) – 式(2)得:)(2)()()(t u e t d h t h t t-∞--=-⎰δττ上式求导:)(2)(2)()()(''t u e t t t h t h t-+-=-δδ设:)()()(t u Be t A t h t-+=δ代入上式:''()()()()()()2()2()t t t A t B t Be u t A t Be u t t t e u t δδδδδ---+---=-+方程两边函数相等:1,1-==B A)()()(t u e t t h t --=δ4-13 试求下列各函数1()f t 与2()f t 的卷积12()()()s t f t f t =* (1)1()()f t u t =,2()()f t u t =(3)1()(1)[()(1)]f t t u t u t =+--,2()(1)(2)f t u t u t =---解:(1))()()(1t t u dtd t f dt d δ== )()()(1)()(002t tu t u t t u d d u d f t tt t=⋅===⎰⎰⎰∞-∞-τττττ1212()()()()()()()()t s t f t f t d f t f d dtt tu t tu t ττδ-∞=*=*=*=⎰ (3)a)1()0t S t -∞<<=时12211b)12()(1)(0.5)(1)02t t t S t d t ττττ--≤<=+=+=-⎰时τf 1(τ)1210τf 2(t-τ)t-1t-21τ121t-121<≤t 0τ12t-232<≤t 0tS (t )1222113c)23()(1)(0.5)222t t S t d t t t ττττ-≤<=+=+=-++-⎰时d)3()0t S t ≤<+∞=时*4-14 对图题4-14所示的各组信号,求二信号的卷积12()()()s t f t f t =*,并绘出()s t 的波形。
