希尔伯特变换
希尔伯特(Hilbert)变换

希尔伯特(Hilbert)变换希尔伯特(Hilbert)变换是一种信号处理中常用的数学工具之一,主要用于将实数信号转化为复数信号,并提取出复信号的包络和瞬时相位等信息。
本文将对希尔伯特变换的基本概念、性质以及在信号处理中的应用进行介绍。
一、基本概念1. 复信号的生成在信号处理中,我们往往需要将一个实数信号变为一个复数信号,这可以通过对信号进行“解析”的方式来实现。
具体地,我们将实数信号x(t)通过一个信号处理器H(t)(即称为系统传递函数)得到一个复数信号X(t),即:X(t) = H(t) * x(t)其中,符号“*”表示对那些对应时间点处的信号进行点乘,即乘上相应的复数模长e^(jw),其中w为角频率,j为单位复数。
2. 复信号的包络和瞬时相位由于复数信号包含实部和虚部两个分量,其中实部和虚部分别表示原信号的信号值和90度相位移的信息。
因此,我们可以通过分别从复数信号中提取出它的实部和虚部,来获得原始信号的包络和瞬时相位两个信息。
具体的,假设我们有一个复数信号X(t) = x(t) + j*y(t),其中x(t)为实部,y(t)为虚部,则:信号的包络:A(t) = sqrt(x^2(t) + y^2(t))其中,atan2(y(t), x(t))表示y(t)/x(t)的反正切,但与通常的反正切最大的区别在于,它不仅考虑了y(t)/x(t)的值,而且也考虑了x(t)的符号,从而在所有象限范围内都具有唯一性。
3. 希尔伯特变换希尔伯特变换是一种用于从实数信号中构造复数信号的技术。
具体地,假设我们有一个实数信号x(t),那么它的希尔伯特变换y(t)定义如下:y(t) = H[x(t)] = P.\ I.C.\ \lim_{\varepsilon \to 0} \frac{1}{\pi}\int_{-\infty}^\infty \frac{x(t')}{t-t'-j\varepsilon} dt'其中,P和I.C.分别表示柯西主值和积分常数项。
证明希尔伯特变换是正交的

证明希尔伯特变换是正交的希尔伯特变换的正交性在信号处理中有着非常重要的应用。
通过对其进行研究和证明,我们可以更好地了解希尔伯特变换的性质以及在信号处理中的实际应用。
下面,我们将为大家介绍证明希尔伯特变换是正交的详细过程。
首先,我们需要明确什么是希尔伯特变换。
希尔伯特变换是一种线性运算,用于将一个信号转换为其复解析信号,即在傅里叶变换的基础上,将实部和虚部的信号分别反转并取相反数,用于分析信号在时域和频域中的行为。
那么,如何证明希尔伯特变换是正交的呢?步骤一:定义内积首先,我们需要定义内积。
内积是在函数空间中定义的一种运算,用于度量两个函数相似程度的大小。
对于两个实函数f(x)和g(x),其内积定义如下:( f , g )= ∫f(x)g(x)dx对于两个复函数,其内积定义如下:(f , g)= ∫f*(x)g(x)dx其中,f*(x)是f(x)的共轭复数。
步骤二:证明正交性根据内积的定义,我们可以证明希尔伯特变换是正交的。
首先,我们需要证明希尔伯特变换是有限范围内的,即其信号在无穷远处趋于0。
根据奇偶性,我们可以证明实部和虚部对应的傅里叶变换值分别关于频率轴对称,因此,它们的线性组合即希尔伯特变换的傅里叶变换值也是关于频率轴对称的,这就保证了其在无穷远处趋于0。
接下来,我们需要证明希尔伯特变换的内积等于零。
我们可以将希尔伯特变换的实部和虚部表示为:h(x)=f(x)cos(wx)-g(x)sin(wx)h*(x)=f(x)cos(wx)+g(x)sin(wx)其中,f(x)和g(x)是两个实函数,w是一个常数。
我们可以将希尔伯特变换的内积表示为:(h , h*)= ∫[f(x)cos(wx)-g(x)sin(wx)][f(x)cos(wx)+g(x)sin(wx)]dx将其展开,得到:(h , h*)= ∫[f(x)^2+g(x)^2]cos^2(wx)dx +∫[f(x)^2+g(x)^2]sin^2(wx)dx根据三角函数的性质,cos^2(wx)+sin^2(wx)=1,因此,上式可以简化为:(h , h*)= ∫[f(x)^2+g(x)^2]dx由于f(x)和g(x)都是实函数,因此其和的平方和是非负的,即(h , h*)≥ 0。
第十六讲希尔伯特变换和过程介绍

补充二希尔伯特变换及其应用课件

希尔伯特变换定义
02
对控制系统的传递函数进行希尔伯特变换,得到系统的频域响
应。
应用场景
03
在控制系统分析和设计中,希尔伯特变换用于系统的稳定性分
析和控制性能优化。
05
希尔伯特变换的优缺点分析
希尔伯特变换的优点
线性性
实时性
希尔伯特变换是线性的,对于多个输入信 号的组合,其变换结果等于各个输入信号 变换结果的线性组合。
对于非线性和非平稳信号,希尔伯特变换可能无法得到准确的结果。
对初始条件敏感
对于某些类型的信号,如果初始条件选择不当,希尔伯特变换的结果 可能会产生较大的误差。
对计算精度要求高
对于高精度的信号处理,希尔伯特变换需要较高的计算精度。
希尔伯特变换的改进方向
研究更鲁棒的算法
针对希尔伯特变换对噪声和初始条件 敏感的问题,研究更鲁棒的算法是未 来的一个重要方向。
信号同步
利用希尔伯特变换对通信 信号进行同步处理,可以 提高通信系统的可靠性和 稳定性。
信道均衡
通过希尔伯特变换对通信 信道进行均衡处理,可以 消除信道失真对信号的影 响,提高通信质量。
03
希尔伯特变换的数学推导
希尔伯特变换的推导过程
希尔伯特变换是基于傅里叶变换 的一种扩展,它能够将实数信号 转换为复数信号,从而揭示信号
信号的边缘检测
希尔伯特变换可以用于信号的边缘检测,通过分析信号的 相位变化,可以检测出信号的突变点,从而提取出信号的 边缘信息。
信号去噪
利用希尔伯特变换对信号进行去噪处理,可以通过分析信 号的相位和幅度信息,去除噪声干扰,提高信号的纯净度 。
在控制系统中的应用
系统稳定性分析
通过希尔伯特变换,可以对控制 系统的稳定性进行分析,判断系
希尔伯特变换性质

R d
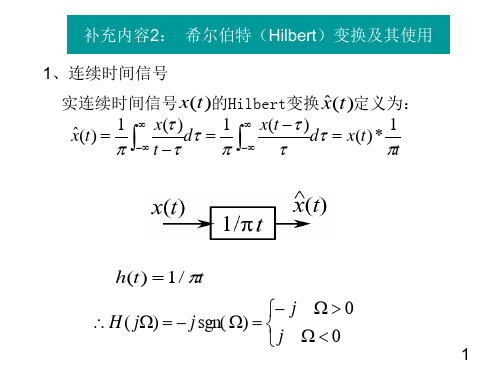
根据实部、虚部对应相等,可得: 1 X R( ) d , X 1
R d
因果系统的系统函数,其实部与虚部之间满足 一定的约束关系。实部(虚部)包含全部信息。
第 8 页
H.T.关系: f t f R t j f R t 实信号(或虚信号)才定义H.T。 定理:乘积调制信号的H.T. 定理:调幅信号的H.T. 定理:最小相位信号的幅度和相位的Bode关系式。 参考书:
– 《信号分析与处理》 – 《信号重构理论及应用》
X
1 1 H H 2 j
X
第 3 页
1 1 R jX R 2 2
注 非 H(j)
X d
意 应 H()
X 1 j 2 2
j sgn
ˆ t f ˆ F
jF ˆ ˆ F f t F F j sgn jF
0 0
具有系统函数为 j sgn 的网络是一个使相位滞 后 弧度的宽带相移全通网络。
其傅里叶变换:
即: ht 0, t 0
假设 H ( ) H e j R jX ( ) 则: 1 1 R jX R( ) jX 2 j 1 1 j 1 R X X R 2 2
X
四.希尔伯特变换的等价系统
f t F
第 6 页
ht
j sgn
ˆ t f ˆ F
加窗希尔伯特(hilbert)变换

加窗希尔伯特(hilbert)变换窗口化希尔伯特(Hilbert)变换是在时间序列数据中提取幅度和相位特征的一种有效方法。
该方法将希尔伯特变换应用于一个带有窗函数的时间序列,可以使其具有高分辨率和可靠性,而且能够广泛应用于信号处理、图像处理、控制理论、模式识别等领域。
希尔伯特变换是一种常用于信号处理和通信系统的数学工具。
经常出现在音频、图像和视频信号处理等领域。
希尔伯特变换将一个信号分解成两个部分,一个是原始信号,另一个是原始信号的希尔伯特变换。
希尔伯特变换对于信号的幅度和相位特征进行分离并对它们进行量化,同时在信号处理中还可用于边缘检测、波形变形和调制识别等任务。
希尔伯特变换可以表示为一个固定的线性变换,其傅里叶变换是复共轭对称的。
给定一个信号f(t),希尔伯特变换产生一个新信号h(t),使得h(t)与f(t)的傅里叶变换有以下关系:H(f) = \begin{cases} i\cdot F(f),& f>0 \\ 0, & f=0 \\ -i\cdot F(f), & f<0 \end{cases}在窗口化希尔伯特变换中,我们将信号f(t)与一个窗函数w(t)进行卷积,产生新信号g(t):g(t) = f(t) * w(t)然后对于信号g(t)进行希尔伯特变换得到h(t):h(t) = \mathcal{H}\{g(t)\}h(t)包含了f(t)的幅度和相位信息。
通常幅度用于表示信号的能量或大小,而相位用于表示信号随时间的变化。
希尔伯特变换可以实现幅度谱和相位谱的分离,因此可以用于各种情况下的信号处理任务。
窗口化希尔伯特变换在信号处理中应用广泛。
例如,用于检测和分类呼吸和睡眠状态,以及研究心脏疾病和脑电信号。
它还可以用于分析和模拟语音和音乐信号,进行图像处理和分割以及模式识别和机器学习等任务。
总之,窗口化希尔伯特变换是一种强大而灵活的信号处理技术,它可以从时域和频域两方面提供相当优异的表现。
希尔伯特变换

§5.6 希尔伯特(Hilbert )变换• 希尔伯特变换的引入•可实现系统的网络函数与希尔伯特变换一.由傅里叶变换到希尔伯特变换 已知正负号函数的傅里叶变换根据对称性得到则假设系统函数为则冲激响应系统框图:系统的零状态响应利用卷积定理具有系统函数为 - 的网络是一个使相位滞后 弧度的宽带相移全通网络同理可得到: 假设系统冲激响应为()[]ωj t F 2sgn =()jt 221sgn ⋅↔-πω()ωπ-↔sgn 1j t()为奇函数ωsgn ()ωπsgn 1j t -↔()⎩⎨⎧<>--=-=090 0 90sgn )(00ωωωωj j j j H ()()[]tj H F t h πω11==-()()ωF t f ˆˆ ()()ωF t f ()ωsgn j -()()()()t t f t h t f t f π1ˆ*=*=()[]()()()[]()()⎩⎨⎧<>-=-⋅== 0 0 sgn ˆˆωωωωωωωjF jF j F F t f F ()t t h π1-=2π()ωsgn j其网络的系统函数为该系统框图为输出信号利用卷积定理具有系统函数为 的网络是一个使相位滞后 弧度的宽带相移全通网络希尔伯波特变换二. 可实现系统的网络函数与希尔伯特变换 可实现系统是因果系统,其冲激响应 ()[]()⎩⎨⎧<->===090 0 90 sgn )(00ωωωωj j j t h FH ()()ωt f ()(ωF t f ˆˆ ()ωsgn j ()()()()⎪⎪⎭⎫ ⎝⎛-*=*=t t f t h t f t f π1ˆˆ()()()()()⎩⎨⎧<->=⋅= 0 0 sgn ˆωωωωωωωjF jF j FF 2π()ωsgn j ()[]()()τττπd 1ˆ⎰∞∞--==t f t f tf H ()()t t f t fπ1ˆ*=()[]()()τττπd 1ˆ1⎰∞∞----==t f t f tf H ()()⎪⎪⎭⎫⎝⎛-*=t t f t f π1ˆ即:其傅里叶变换又则根据实部与实部相等,虚部与虚部相等,解得因果系统系统函数 的实部与虚部满足希尔伯特变换约束关系三.常用希尔伯特变换对 作为一种数学工具在通信系统中得到了广泛的应用()()()t u t h t h ⋅=()00<=t t h ()()()⎥⎦⎤⎢⎣⎡+*=ωωπδωπωj j H j H 121()()())()(ωωωωωϕj jX j R e j H j H j +==()ωωj jX j R +)(()()[]()⎥⎦⎤⎢⎣⎡+*+=ωωπδωωπj j jX j R 121()()⎥⎦⎤⎢⎣⎡*+=ωωωππ121j X j R ()()⎥⎦⎤⎢⎣⎡*-+ωωωππ12j R j X j ()()()()⎥⎦⎤⎢⎣⎡-+=+∴⎰∞∞-λλωλπωωωd 2121j X j R j jX j R ()()⎥⎦⎤⎢⎣⎡--+⎰∞∞-λλωλπωd 212j R j X j ()λλωλπωd 1)(⎰∞∞--=j X j R ()()λλωλπωd 1⎰∞∞---=j R j X )(ωj H例5-6-1用三种方法求解此题:方法1 :方法2:则希尔伯特变换的频谱函数为即:方法3:直接用希尔伯特变换定义式例5-6-2因为即系统函数式中实部虚部[]的实部与虚部满足希尔,证明已知)()()(thFtueth tα-=().ˆtft的希尔伯特变换ω()()弧度,即滞后比希尔伯特变换2ˆπtftf()()[]tttfHtfsin4cosˆωπω=⎪⎭⎫⎝⎛-==()[]()()cosωωπδωωπδωω-++==tFF因()()()[]()()()sgnˆωωπδωωπδωωω--++=-⋅=jjjFF()()()[]()ttfjFsinˆˆωωωδωωδπω=↔--+=[]tttHsindcos1cosωτττωπω=-=⎰∞∞-()[][]ωααjtueFthF t+==-1)(()()()ωωωαωωααωjjXjRjjH+=+-+=2222()22ωααω+=jR()22ωαωω+-=jX现在求 的希尔伯特变换可求出各分式系数 则()ωj X ()[]()λλωλπωd 1⎰∞∞--=j X j X H ()()λλωαλλπd 122⎰∞∞-=+-=()()λωαλαλλωαλλ-+++-==+-Cj B j A 22令22,21,21αωωαωαω+=+-=--=C j B j A ()[]()()()()()()λωλαωωαλαωαλαωπωd 2121122⎰∞∞-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-++++-+---=j j j j j X H ()[]()()()()()()λωλαωωαλαωαλαωπωd 2121122⎰∞∞-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-++++-+---=j j j j j X H ()λωλωαλωλααωπd 122222⎰∞∞-⎥⎦⎤⎢⎣⎡-++-+=()λωλωαλωλαλααωπd 12222222⎰∞∞-⎥⎦⎤⎢⎣⎡-++-++=()()()∞∞-⎥⎦⎤⎢⎣⎡-++-+=ωλωαλαωαλααωπln ln arctg 12222()⎥⎦⎤⎢⎣⎡+-⎪⎭⎫ ⎝⎛++=0022122ππααωπ22αωα+=()ωR =例5-6-3试分析下面系统可以产生单边带信号已知信号 是带限信号,其频谱函数为图中系统函数 载频由调制定理可知 为带通信号 其频谱函数是 的希尔伯特变换信号其频谱则其频谱函数即输出信号其频谱为()t y 2mm ()t g ()ωG ()()ωωsgn j j H -=m ωω>>0()()t t g t y 01cos ω=()[]()()()00112121ωωωωω-++==G G Y t y F ()t gˆ()t g ()[]()()()ωωωsgn ˆˆj jG G t gF -==()()()t t g t y 02sin ˆω-⋅=()[]()()()()[]0022ˆ21ωωδωωδπωπω+--*==j G Y t y F ()()()()[]0000sgn sgn 2ωωωωωωωω+++---=jG jG j()()()()()00002sgn 21sgn 21ωωωωωωωωω++---=G G Y ()()()t y t y t y 21+=()()()ωωω21Y Y Y +=频谱图如下所示是带通信号〔上边带调幅信号〕的频谱00m 0m 000m 0m 0()ωY。
补充二希尔伯特变换及其应用ppt课件
• z=sqrt(rx.*rx+ix.*ix);%求信号x的包络
• %z=sqrt(abs(x).^2+abs(y).^2);
• subplot(222);
• plot(z);
1
1.5
• thet=atan(ix./rx);%求信0.5号x的瞬时相位
1
• subplot(223);
0
• plot(thet);
h(n) 1 H (e j )e jnd 1 0 je jnd 1 je jnd
2
2
2 0
h(n) 1 (1)n
n
0
2
n
n为偶数 n为奇数
1
Hilbert变换与解析信号
∴ x(n)的Hilbert变换 xˆ(n)为:
xˆ(n) x(n)*h(n) 2 x(n 2m 1)
t
Xˆ ( j) X ( j)H ( j)
X ( j)[ j sgn( )] jX ( j)sgn( )
X ( j) j sgn( )Xˆ ( j)
由此可得:Hilbert反变换的公式
x(t) 1 * xˆ(t) 1 xˆ( )d
解析信号 t
t
设xˆ(t)为x(t)的Hilbert变换,定义 z(t) x(t) jxˆ(t)
1
amp
单道地震信号数值模拟
3. 瞬时属性的分辨率及地质意义
通过单道信号的瞬时属性的分析,可知利用瞬时属性可以反映同相轴的 局部或细微变换,但其分辨率也是有限的,而且不同瞬时属性反映的信息也 不同。
属性类别 物理意义
主要地质意义
瞬时振幅 地震反射波强度 的量度
瞬时相位 瞬时频率
同相轴连续性的 量度
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
希尔伯特变换
一物理可实现系统其传递函数为一解析函数,而其冲激响应必为因果函数(即时,冲击响应为0)。
也就是说时域的因果性与频域得解析性是等效的。
我们来证明,物理可实现系统的传递函数的实部与虚部之间存在某种相互制约的联系。
对于物理可实现系统而言,其冲激响应为
其中为单位阶跃函数,系统传递函数为
F (4.3-3)
由频域卷积定理可知
(4.3-4)
由式(4.3-3)、(4.3-4)可得
(4.3-5)
(4.3-6)
由式(4.3-5)、(4.3-6)可知,物理可实现系统的传递函数其实部与虚部之间存在对应的确定关系。
通常把这一对关系式称为希尔伯特变换对,式(4.3-5)称为希尔伯特变换,而式(4.3-6)称为希尔伯特反变换。
希尔伯特滤波器,它实质上是一个宽带相移网络,对中的任意频率分量均相移。
