沪教版八年级上册-几何证明讲义
沪教版(五四学制)八年级上册第十九章几何证明:1线段的垂直平分线课件
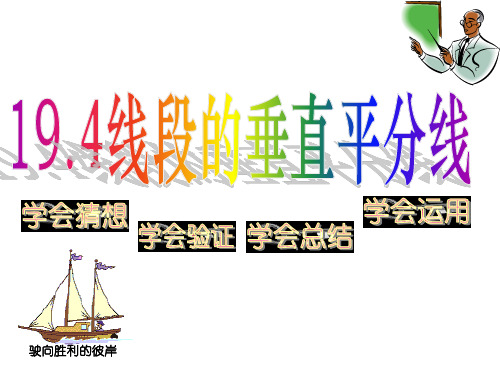
∴PA=PB(全等三角形的对应边相等)
N
总结
线段垂直平分线的性质:线段垂直平分线上的任意一点 到这条线段两个端点的距离相等。
∵点P在线段AB的垂直平分线上(已知) ∴PA=PB (线段垂直平分线上的任意一点到这条线 段两个端点的距离相等。 )
A
M P
B
N
猜想
定理:线段垂直平分线上的任意一点到这条线段 两个端点的距离相等。
=14cm.
有没有什么体会和大家分享?
运用3
练习1. 已知:如图, 在△ ABC中,AB=AC , DE是AB边
的垂直平分线交AC于点E,CBE 30o
求:A 多少度?
A
x
及时反思?
D
合理设参数,引入方程 求角度。
E
x 30o x 30o
B
C
运用4
例题2. 已知:如图,ΔABC中,BA=BC,边AB,BC的垂直平 分线交于P.
求:∠B等于多少度?
A
50°
D 50° E
B
C
学会运用
作图2,七宝镇政府打算修建一个体育中心.在选址 过程中,有人建议该体育中心所在位置到三个中学 (如图中P,Q,R表示)的距离相等.
P●
(1) Q●
R●
P● Q●
R● (2)
(1)根据上述建议,试在图(1)中画出体育中心G的位置;
(2)如果这三个中学的位置如图(2)所示,∠RPQ是一个钝 角,那么根据上述建议,体育中心G应在什么位置?
三角形的三条边的垂直平分线相交于一点
驶向胜利的彼岸
思考:证明线段相等的方法有哪些?
点P在线 段AB的垂 直平分线 上
线段垂直平分线的性质
PA=PB
沪教版八年级数学上册《几何证明》教案及教学反思

沪教版八年级数学上册《几何证明》教案及教学反思一、教学目标1.了解几何证明的基本概念和方法;2.掌握基本的几何证明方法,如等腰三角形的性质、直角三角形的性质等;3.能够灵活运用所学的几何证明方法解决问题;4.培养学生的证明思维和可视化能力。
二、教学重难点重点1.等腰三角形的性质;2.直角三角形的性质;3.证明思维的培养。
难点1.多边形内部角和公式的证明;2.解决实际问题的证明方法。
三、教学内容1. 等腰三角形的性质知识点1.等腰三角形的定义;2.等腰三角形的性质:两底角相等,两腰相等;3.等腰三角形的判定方法。
教学过程1. 引入教师以生活中的实例引入,如城门上的双旗筒、音响演奏时的对称等,引导学生思考等腰三角形的性质。
2. 讲解教师通过图像和实例详细讲解等腰三角形的定义、性质和判定方法。
特别是两底角相等是等腰三角形最基本、最重要的性质,要重点讲解,让学生深刻理解。
3. 训练教师提供一些较为简单的练习题,让学生掌握等腰三角形的判定方法,培养学生发现、解决问题的能力。
2. 直角三角形的性质知识点1.直角三角形的定义;2.直角三角形的性质:勾股定理;3.直角三角形的判定方法。
教学过程1. 引入教师以勾股定理在实际应用中的例子引入,让学生认识到直角三角形的重要性。
2. 讲解教师通过图像和实例讲解直角三角形的定义、性质和判定方法。
特别是勾股定理是解决直角三角形问题的基本方法,要重点讲解,让学生深刻理解。
教师提供一些较为简单的练习题,让学生掌握勾股定理的应用,培养学生运用所学知识解决问题的能力。
3. 多边形内部角和公式的证明知识点1.多边形内部角和公式的定义;2.多边形内部角和公式的证明。
教学过程1. 引入教师以正多边形为例,引导学生思考如何计算它的内部角和。
通过引入正十二边形、正二十边形等一些例子,让学生感受到探究的乐趣。
2. 讲解教师通过推理、证明等方法讲解多边形内部角和公式的证明过程。
特别是对于较为困难的证明,要逐步分析,在保证理解的基础上进行深入探究。
沪教版(五四学制)八年级上册第十九章几何证明:1证明举例(第1课时)课件
求证:EF∥AC
分析:
A
要证明EF ∥AC,只要证明 ∠DFE=∠FDC
又已知∠DFE=∠A ,因此只要
﹖ 证明 ∠A=∠FDC ,而这由
E D
﹖ 已知条件DF∥AB得到的。
B
C
F
例2 已知:如图,点D,E,F分别是AC、AB、BC 上的点,DF∥AB, ∠DFE=∠A
求证:EF∥AC
分析:
要证明EF ∥AC,只要证明 ∠A+∠AEF=1800
平行?
平行线的判定定理: (1)同位角相等,两直线平行; (2)内错角相等,两直线平行; (3)同旁内角互补,两直线平行;
平行线的传递性:平行于同一条直线的两条
直线也平行;
例1 已知:如图,AB∥CD, ∠B+ ∠D=180O 求证:CB∥DE
分析: 要证明CB∥DE,只要证
A
. C ﹖B
明 ∠C+ ∠D=180O ,已知 ∠B+ ∠D=1800 ,因此只要证
(3) 若GP、HN分别平分∠BGF、∠EHD, 探索:GP、HN具有怎样的位置关系?
必做题:练习册 习题19.2(1) 选做题:提高题
又已知∠DFE=∠A ,因此只要 证明 ∠DFE+∠AEF=1800 , 而这由已知条件DF∥AB得到的。 B
A
﹖E ﹖D C F
例2变式练习: 已知:如图,DF∥AB, EF∥AC
求证: ∠DFE=∠A
﹖A
E
D
﹖ B
C
F
练习1 已知:如图,∠1=∠B, ∠2=∠D 求证:AB∥CD
A
B
E1
F
2
C
D
练习2 已知:如图,∠C=∠1, ∠B=∠D
沪教版(五四学制)八年级上册第十九章几何证明:1命题和证明课件

第三段因果关系: 因:“∠1+∠2=∠2+∠3”; 果:“∠1=∠3”;“根据”是“等量减等量,差相等”.
再尝试说一说“三角 E
A
F
形内角和”证明过程中
的因果关系.
B
C
注意:寻找因果关系可以从条件出发找到由条件能够 直接得到的结果,也可以从结论出发去寻找得到这个 结论所需要的条件,同时还要注意导致这个结果的原 因往往不止一个,需要从前面的段落中去寻找.
得 ∠1+∠2=∠2+∠3(等量代换). 所以∠1=∠3(等量减等量,差相等).
辩一辩
这三种方法中,哪一种最可靠,最有说服力?
像上述第三种方法,我们运用演绎推理的方法得到 “对顶角相等”这个结论,演绎推理的过程就是演绎证 明.
演绎证明:从已知的概念、条件出发,根据已被 确认的事实和公认的逻辑规则,推导出某结论为正 确的过程.
D 3
2 1
E C
其中,因: BE平分∠ABC 证明:因为 BE平分∠ABC(已知);
果:∠1=∠2.
所以 ∠1=∠2(角平分线的意义).
因: BD=DE
因为 BD=DE(已知) ;
果:∠2=∠3.
所以 ∠2=∠3(等边对等角);
因:∠1=∠2, ∠2=∠3
所以 ∠1=∠3(等量代换);
果:∠1=∠3.
Hale Waihona Puke 演绎推理是数学证明的一种常用的、完全可靠的方 法.演绎证明是一种严格的数学证明.
在本书中,演绎证明简称证明. 学习演绎证明可以使我们的思维严格、缜密,其表 达条理清楚、无可辩驳 .
沪教版(上海)八年级第一学期 第十九章 第1讲 几何证明

例
逆命题:如果一个角是钝角,那么这个角是两个钝角的和.
4
逆命题:直角三角形其中一边上中线等于这边的一半.
逆命题:如果两个三角形关于某点成中心对称,那么这两个三角形全等. 逆命题:如果两个三角形全等,那么其中两边及第三边上的高对应相等.
逆命题:如果两个角不相等,那么这两个角不是对顶角.
例 5
例
逆命题:如果三角形两腰上的中线相等,那么这个三角形是等腰三角形.
第一讲
几何证明
命题 可以判断正误的陈述句
滚出去! 站起来.
命题的组成
如果两条直线互相平行, 那么这两条直线被第三条直线所截得的内错角相等.
如果一个人骑着白马,那么他一定是唐僧。
对顶角相等.
逆命题
原命题: 如果两条直线互相平行, 那么这两条直线被第三条直线所截得的内错角相等.
逆命题: 如果两条直线被第三条直线所截得的内错角相等, 那么这两条直线互相平行.
l
例 6
例 6
例 6
例 7
例 7
例 8
练 习 1
练 习 2
练 习 3练 习 4练 习 5练 习 6
对顶角相等.
相等的角是对顶角.
如果一个人骑着白马,那么他一定是唐僧。
如果一个人是唐僧,那么他骑着白马。
例 1
例 1
例 2
例 2
如果一个四边形有三个角是直角,那么这个四边形是矩形.
如果两个角是同一个角的补角,那么这两个角相等.
如果两个数都是无理数,那么他们的积是无理数.
例 3
例 3
例 4
5
逆命题:两直线平行,内错角相等. 逆命题:等角对等边.
逆命题:如果两条直线被第三条直线所截得的同旁内角的角平分线互相垂直,那么这两条直线平行. 逆命题:如果 a+b 为奇数,那么a,b两数一奇一偶.
沪教版(五四制)八年级数学上册 第十九章几何证明提高讲义【无答案】

几何证明提高学生姓名 授课日期 教师姓名授课时长【本讲内容】通过“倍长中线”、“截长补短”、“图形旋转”等添加辅助线的方法,构造全等三角形,实现边与角的转化及转移,最终得到证明结果。
【重点难点】添加合适的辅助线,解决证明问题知识梳理1.倍长中线法几何是初中数学的重要组成部分,在中考中占有相当的比例,在证明举例中,主要学习了以下几种题型:题型一:证明两条线段相等;(等腰三角形,三角形全等) 题型二:证明两线平行;(利用两条直线平行的判定定理) 题型三:证明两线垂直(证明角90度);题型四:证明两角相等(等腰三角形,三角形全等); 题型五:证明线段或角的和差倍;有一部分题目,只要应用我们的一些定理公理即可证明,但有部分题需要做出辅助线才能完成。
有的时候,做不出恰当的辅助线,或者做不出辅助线,就没有办法完成该题的解答。
为了能够更好的让学生在做几何题时得心应手,现在将八年级数学中几何题的辅助线添加方法总结如下。
倍长中线法:1.线段的中点:把一条线段分成两条相等线段的点,叫做这条线段的中点。
2.若点C 是线段AB 的中点,则:① 从线段来看:12AC BC AB ==;② 从点与点的相对位置来看:点C 在点A B 、之间,且点A B 、关于点C 对称。
3.三角形的中线:连接三角形的一个顶点和它所对的边的中点所得的线段叫做三角形的中线。
① 一个三角形有三条中线; ② 每条中线平分三角形的面积;③ 三角形的三条中线交于一点,每条中线被该点(重心)分成1:2的两段;④ 三角形的三条中线把三角形分成六个面积相等的小三角形。
如何延长三角形的中线 1.延长1倍的中线:如图,线段AD 是ABC ∆的中线,延长线段AD 至E ,使DE AD =(即延长1倍的中线),再连接BE CE 、。
①总的来说,就可以得到一个平行四边形ABCD 和两对(中心选转型)全等三角形ABD ECD ∆≅∆、ACD EBD ∆≅∆,且每对全等三角形都关于点D 中心对称;②详细地说,就是可以转移角:BAD CED ∠=∠,CAD BED ∠=∠,ABD ECD ∠=∠,ACD EBD ∠=∠,ADB ECD ∠=∠,ADC EDB ∠=∠;可以移边:AB EC =,AC EB =;可以构造平行线:AB ∥EC ,AC ∥EB ;可以构造边长与AB 、AC 、AD 有关的三角形:ABE ∆、ACE ∆。
几何证明(4个概念2个性质3个判定2个定理2个应用2种思想方法1个轨迹)八年级数学上册沪教版

2 个性质3个判定
考点05 线段的垂直平分线
7.在锐角三角形ABC内一点P,,满足PA=PB=PC,则点P是△ABC
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点
(D )
8.已知: 如图,QA=QB.
求证: 点Q在线段AB的垂直平分线上.
(2)区别:定义、公理、定理都是真命题,都可以作为进一步判断其
他命题真假的依据,只不过公理是最原始的依据;而命题不一定是真
命题,因而不能作为进一步判断其他命题真假的依据.
考点04 互逆定理
6. [2022·江苏无锡宜兴市二模]下列命题的逆命题成立的是
①同旁内角互补,两直线平行
①④ .
②等边三角形是锐角三角形
证明:过点Q作MN⊥AB,垂足为点C,
故∠QCA=∠QCB=90°.
在Rt△QCA 和Rt△QCB中,
∵QA=QB,QC=QC,
∴Rt△QCA≌Rt△QCB(H.L.).
∴AC=BC.
∴点Q在线段AB的垂直平分线上.
你能根据分析
中后一种添加辅
助线的方法,写
出它的证明过程
吗?
考点06 角 平 分 线
AB=CB,
∴Rt△ABE≌Rt△CBF(HL).
15.如图,点B,E,F,C在同一条直线上,AE⊥BC,DF⊥BC,
AB=DC,BE=CF.试判断AB与CD的位置关系,并证明.
A
解:AB//CD,理由如下:
∵AE⊥BC,DF⊥BC,
∴∠AEB=∠DFC=90°
B
F
∵在Rt△ABE和Rt△DCF中, AB=DC,
沪教版八年级数学上册《几何证明》说课稿

沪教版八年级数学上册《几何证明》说课稿一、教材分析《几何证明》是沪教版八年级数学上册中的一篇重要的知识点。
在这个单元中,学生将学习如何进行几何证明,从而培养他们的逻辑思维能力和分析问题的能力。
本单元主要包括以下内容:1.基本概念:学生将回顾和巩固几何中的基本概念,如线段、角度、旁征博引和同位角等。
2.三角形的性质:学生将学习三角形的内角和、外角和的性质,并掌握七类常见的特殊三角形。
3.平行线与相交线的性质:学生将探究平行线与相交线之间的性质,如同位角、内错角、对应角等,并学习如何运用这些性质进行证明。
4.四边形的性质:学生将学习四边形的性质,如平行四边形、矩形、菱形和正方形等,并重点讲解这些四边形的性质和特征。
二、教学目标知识目标•熟悉几何中的基本概念,并能正确应用它们进行证明。
•掌握三角形的内角和、外角和的性质,并能应用于具体问题。
•理解平行线与相交线之间的关系,包括同位角、内错角、对应角等,并能进行几何证明。
•熟练掌握平行四边形、矩形、菱形和正方形等四边形的性质。
能力目标•培养学生的逻辑思维和分析问题的能力。
•培养学生的几何证明能力,提高其解决实际问题的能力。
•培养学生的合作探究和团队合作能力。
情感目标•培养学生对几何学科的兴趣和探究精神。
•培养学生的思维习惯和解决问题的耐心和毅力。
三、教学重点与难点教学重点:1.如何利用基本几何概念进行证明。
2.三角形的内角和、外角和的性质。
3.平行线与相交线之间的性质及其应用。
4.平行四边形、矩形、菱形和正方形等四边形的性质。
教学难点:1.如何运用已有的几何定理和性质进行证明。
2.如何通过合理的推理和思考解决综合性的几何问题。
四、教学过程及设计第一步:导入与激发兴趣(5分钟)通过问题、情境等导入的形式,激发学生的学习兴趣,引导学生思考和提出问题。
第二步:知识讲解与示范(15分钟)1.回顾和讲解几何中的基本概念,如线段、角度、旁征博引和同位角等,明确其定义和性质。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
DEF
第二种:FB =CE ,AC =DF 添加 ③∠ACB =∠DFE
证明:因为FB =CE ,所以BC =EF ,又∠ACB =∠DFE AC =EF ,所以ABC ≅DEF 所以∠ABC =∠DEF 所以AB//ED
精讲名题
例1、已知:如图所示,∆A B C 中,∠=︒===C AC BC AD DB AE CF 90,,,。
求证:DE =DF 证明:连结CD
A C
B C
A B
A C
B A D D B
C
D B D A D D C B B A
A E C F A D C
B A D
C D
=∴∠=∠∠
=︒=∴==∠=∠=∠=∠=∠=90,,,,
∴≅∴=∆∆A D E C D F D E D F
说明:在直角三角形中,作斜边上的中线是常用的辅助线;在等腰三角形中,作顶角的平分线或底边上的中线或高是常用的辅助线。
例2、已知:如图所示,AB =CD ,AD =BC ,AE =CF 。
求证:∠E =∠F 证明:连结AC 在∆A B C 和∆C D A
中, AB CD BC AD AC CA ABC CD A SSS B D AB CD AE CF
BE D F
===∴≅∴∠=∠==∴=,,,∆∆()
在∆B C E 和∆D A F 中,
BE D F
B D B
C
D A BC
E D A
F SAS E F
=∠=∠=⎧⎨⎪
⎩
⎪∴≅∴∠=∠∆∆()
说明:利用三角形全等证明线段求角相等。
常须添辅助线,制造全等三角形,这时应注意: (1)制造的全等三角形应分别包括求证中一量; (2)添辅助线能够直接得到的两个全等三角形。
例3、已知:如图所示,AB =AC ,∠,,A A E B F B D D C =︒==90。
求证:FD ⊥ED 证明一:连结AD
AB AC BD D C
D A
E D AB
BAC BD D C
BD AD
B D AB D AE
==∴+=︒==︒=∴=∴==,∠∠,∠∠∠,∠∠∠129090
在∆A D E 和∆B D F 中,
A E
B F B D A E A D B D
A D E
B D F
F D E D
===∴≅∴∠=∠∴∠+∠=︒∴⊥,∠∠,∆∆31
3290
说明:有等腰三角形条件时,作底边上的高,或作底边上中线,或作顶角平分线是常用辅助线。
证明二:如图所示,延长ED 到M ,使DM =ED ,连结FE ,FM ,BM
B
C
A E
F
D M
图5
B D D C
B D M
C
D
E D M D E B D M C D E C E B M C C B M
B M A C
A A
B M A A B A
C B F A E A F C E B M
=∠=∠=∴≅∴=∠=∠∴∠=︒∴∠=︒=∠==∴==,,,∆∆//9090
E
A B C
D
例4、已知:如图所示在∆A B C 中,∠=︒B 60,∠BAC 、∠BCA 的角平分线AD 、CE 相交于O 。
求证:AC =AE +CD
分析:在AC 上截取AF =AE 。
易知∆∆A E O A F O ≅,∴∠=∠12。
由∠=︒
B 60,知∠+∠=︒∠=︒∠+∠=︒566016023120,,。
∴∠=∠=∠=∠=︒123460,得:∆∆F O CD O
C F C
D C
≅∴=, 证明:在AC 上截取AF =AE
()
∠=∠=∴≅∴∠=∠B A D C A D A O A O
A E O A F OS A S ,∆∆42
又∠=︒
B 60 ∴∠+∠=︒
∴∠=︒
∴∠+∠=︒∴∠=∠=∠=∠=︒∴≅∴=566016023120123460∆∆FOC DOC AAS FC DC
()
即A C A E C D =+
备选例题
例1、 已知:在⊿ABC 中,AB=AC ,延长AB 到D ,使AB=BD ,E 是AB 的中点。
求证:CD=2CE 。
证明:延长CE 到F ,使EF=CE ,连结BF 易证△AEC ≌△FEB ,(SAS ) ∴BF=AC ,∠A=∠FBE 因为AB=AC=BD
∴∠ABC=∠ACB ,BF=BD 因为∠FBC=∠ABC+∠FBE ∠DBC=∠A+∠ACB ∴∠FBC=∠DBC (等量代换) 所以易证△BCD ≌△BCF (SAS ) ∴CF=CD
∴∠EGB=∠B
∴BE=EG ∴BE=CF
6、已知等腰直角三角形△ABC 中,∠BAC=0
90,BD 是角平分线,CE ⊥BE ,交BD 延长线于点E ,求证:BD=2CE 。
证明:延长CE 、BA 交于点F A
因为∠BAC=0
90,CE ⊥BE D E 所以∠F+∠ACF=0
90,∠F+∠ABD=0
90 D
所以∠ACF=∠ABD , B C 易得△ABD ≌△ACF 所以BD=CF
因为BD 是角平分线,∠BEC=∠BEF=0
90 所以△BCE ≌△BFE 所以CF=FE ,即BD=2CE
自我测试
1、下列语句中是命题的是( C )
A .过点
B 作直线B
C B .线段BC C .π是无理数
D .画正方形
2、 如图,下列判断:①∠A 与∠1是同位角;②∠A 与∠B 是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角.其中正确的是…………………………………( A ) A .①、②、③ B .①、②、④ C .②、③、④ D .①、②、③、④
3、 下列命题正确的是( A )
A .等边对等角
B .面积相等的三角形全等
C .线段有两条对称轴
D .等腰三角形高是它的对称轴。
4、 下列命题中是真命题的是( B )
A .同位角相等
B .对顶角相等
C .相等的角是对顶角
D .同旁内角互补
5、已知线段AC 与BD 相交于点O ,联结AB 、DC ,E 为BO 的中点,F 为OC 的中点,联结EF , (1)添加条件∠A=∠D ,∠OEF=∠OFE ,求证:AB=DC ;
(2)分别将“∠A=∠D”记为①,“∠OEF=∠OFE”记为②,“AB=DC”记为③,添加条件①、③,以②为结论构成的命题1;添加条件②、③,以①为结论构成命题2。
命题1是 命题,命题2是 命题。
A D (1) 提示:要证AB=DC ,只需证明△ABO ≌△DCO O (2) 真、假 E F
B C
6、已知:如图所示,∆A B C 中,∠=︒C 90,D 是AB 上一点,DE ⊥CD 于D ,交BC 于E ,且有A C A D C E
==。
求证:DE CD =1
2
证明:取CD 的中点F ,连结AF
3
E
A
D
41
C
B
F
A C A D
A F C D
A F C C D E =∴⊥∴∠=∠=︒
90 ∴∠=∠=∴≅∴=∴=431
2
A C C E
A C F C E D A S A C F E D
D E C D
∆∆() 又∠+∠=︒∠+∠=︒14901390,。
