统计学第八章时间数列
第八章 时间序列
华南理工大学精品课程
13
8.2.3 指数平滑法
指数平滑法模型：
Ft 1 Yt (1 ) Ft （ 8-2）
式中Ft+1——t+1期时间序列的预测值； Yt——t期时间序列的实际值； Ft——t期时间序列的预测值； α——平滑常数（0≤α≤1）。
华南理工大学精品课程 14
8.2.3 指数平滑法
时间序列的 四种独立成分
趋势
华南理工大学精品课程
循环
季节
不规则
3
8.1.1 趋势成分
在一段较长的时间内，时间序列往往呈现逐渐 增加或减少的总体趋势。时间序列逐渐转变的 性态称为时间序列的趋势。
趋势通常是长期因素影响的结果，如人口总量 的变化、方法的变化等等
长期 影响因素
时间序列的 长期动向
趋势成分
季节因素引起的一年内 有规则的运动
季节成分
华南理工大学精品课程
6
8.1.3 季节成分
• 例如，一个游泳池制造商在秋季和冬季各月有 较低的销售活动，而在春季和夏季各月有较高 的销售量。 • 铲雪设备和防寒衣物的制造商的销售却正好相 反。
华南理工大学精品课程
7
8.1.3 季节成分
季节成分的扩展 • 季节成分也可用来描述任何持续时间小于一年 的、有规则的、重复的运动。 • 例如，每天的交通流量资料显示在一天内的 “季节”情况，在上、下班拥挤时刻出现高峰， 在一天的休息时刻和傍晚出现中等流量，在午 夜到清晨出现小流量。
长期 线性 趋势 数列
不稳定，随时间 呈现持续增加 或减少的形态
趋势推测法可行
平滑法不合适
华南理工大学精品课程
18
8.3 利用趋势推测法进行预测
第八章时间序列分析
第⼋章时间序列分析第⼋章时间序列分析与预测【课时】6学时【本章内容】§ 时间序列的描述性分析时间序列的含义、时间序列的图形描述、时间序列的速度分析§ 时间序列及其构成分析时间序列的构成因素、时间序列构成因素的组合模型§ 时间序列趋势变动分析移动平均法、指数平滑法、模型法§ 时间序列季节变动分析[原始资料平均法、趋势-循环剔除法、季节变动的调整§ 时间序列循环变动分析循环变动及其测定⽬的、测定⽅法本章⼩结【教学⽬标与要求】1.掌握时间序列的四种速度分析2.掌握时间序列的四种构成因素3.掌握时间序列构成因素的两种常⽤模型4.掌握测定长期趋势的移动平均法5.了解测定长期趋势的指数平滑法6.；7.掌握测定长期趋势的线性趋势模型法8.了解测定长期趋势的⾮线性趋势模型法9.掌握分析季节变动的原始资料平均法10.掌握分析季节变动的循环剔出法11.掌握测定循环变动的直接法和剩余法【教学重点与难点】1.对统计数据进⾏趋势变动分析，利⽤移动平均法、指数平滑法、线性模型法求得数据的长期趋势；2.对统计数据进⾏季节变动分析，利⽤原始资料平均法、趋势－循环剔除法求得数据的季节变动；3.对统计数据进⾏循环变动分析，利⽤直接法、剩余法求得循环变动。
【导⼊】；很多社会经济现象总是随着时间的推移不断发展变化，为了探索现象随时间⽽发展变化的规律，不仅要从静态上分析现象的特征、内部结构以及相互关联的数量关系，⽽且应着眼于现象随时间演变的过程，从动态上去研究其发展变动的过程和规律。
这时需要⼀些专门研究按照时间顺序观测的序列数据的统计分析⽅法，这就是统计学中的时间序列分析。
通过介绍⼀些时间序列分析的例⼦，让同学们了解时间序列的应⽤，并激发学⽣学习本章知识的兴趣。
1.为了表现中国经济的发展状况，把中国经济发展的数据按年度顺序排列起来，据此来研究。
2.公司对未来的销售量作出预测。
这种预测对公司的⽣产进度安排、原材料采购、存货策略、资⾦计划等都⾄关重要。
第八章 时间数列分析
值的比重） 两个时点数列之比（每万人口中大专以上学历
人口数） 时期数列和时点数列之比（商品流转次数=商品
销售额/商品库存量）
1/8/2020
13
1月 2月
3月
4月
5月
6月
7月
销售额 11.2 11.6 11.5
15
12
13
14.2
（万元）
平均库存 7 （吨）
1/8/2020
24
2、连续但是不等间隔
日期 1-3 4-5 6-9 10
职工人数 450 458 452 466
间隔日期 3 2 4 1
af 1350 916 1808 466
a
af f
454人
1/8/2020
25
3、不连续登记，间隔相同
例：某公司2006年第二季度对职工出勤情况进行抽查，结 果如下表所示，请计算该公司2006年第二季度的平均人数
26
第二季度平均每月的职工人数：
460 466 466 484 484 506
2
2
2 478人
3
因此计算公式可写为：
a (a0 a1) / 2 (a1 a2 ) / 2 (an1 an ) / 2 n
a0 / 2 a1 an1 an / 2 n
年份 1994 1995 1996 1997 1998 1999 2000
人均支出 0.71 0.88 （万元）
0.98
1.15
1.25
1.48
1.98
相对数时间数列与平均数时间数列的关系： 相似点：不具有可加性；
统计学罗文宝主编 第八章时间序列分析单选题多选题参考答案
第八章 时间序列分析二、单项选择题1.根据时期数列计算序时平均数应采用（ C ）。
A 、几何平均法 B.加权算术平均法 C.简单算术平均法 D.首末折半法2.间隔相等的时点数列计算序时平均数应采用（D ）。
A.几何平均法B.加权算术平均法C.简单算术平均法D.首末折半法3.数列中各项数值可以直接相加的时间数列是（B ）。
A.时点数列B.时期数列C.平均指标动态数列D.相对指标动态数列4.时间数列中绝对数列是基本数列，其派生数列是（D ）。
A. 时期数列和时点数列B. 绝对数时间数列和相对数时间数列C. 绝对数时间数列和平均数时间数列D.相对数时间数列和平均数时间数列5.下列数列中哪一个属于动态数列（ D ）。
A.学生按学习成绩分组形成的数列B.工业企业按地区分组形成的数列C.职工按工资水平高低排列形成的数列D.出口额按时间先后顺序排列形成的数列6.已知某企业1月、2月、3月、4月的平均职工人数分别为190人、195人、193人和201人。
则该企业一季度的平均职工人数的计算方法为（B ）。
7.说明现象在较长时期内发展的总速度的指标是（C ）。
A 、环比发展速度 B.平均发展速度 C.定基发展速度 D.环比增长速度8.已知各期环比增长速度为2%、5%、8%和7%，则相应的定基增长速度的计算方法为（A ）。
A.（102%×105%×108%×107%）-100%B. 102%×105%×108%×107%C. 2%×5%×8%×7%D. （2%×5%×8%×7%）-100%4201193195190+++、A 3193195190++、B 1422011931952190-+++、C 422011931952190+++、D9.平均发展速度是（ C ）。
A.定基发展速度的算术平均数B.环比发展速度的算术平均数C.环比发展速度的几何平均数D.增长速度加上100%10.若要观察现象在某一段时期内变动的基本趋势,需测定现象的（ C ）。
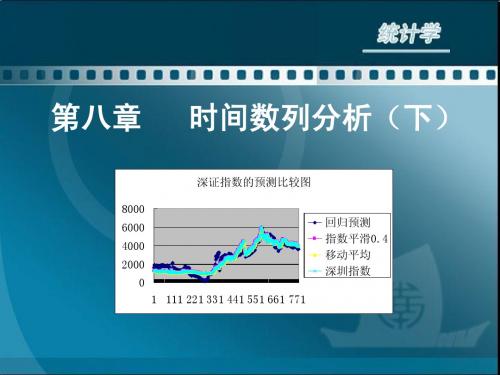
第八章 时间数列分析(下)
不规则变动(I) 不规则变动(I)
不规则变动是指由意外的偶然性因素引 不规则变动是指由意外的偶然性因素引 是指由意外的偶然性因素 起的，突然发生的、无周期的随机波动。 起的，突然发生的、无周期的随机波动。 例如，地震、 例如，地震、水、旱、风、虫灾害和原 因不明所引起的各种变动。 因不明所引起的各种变动。
Y-T=S+C+I
其次，将时间数列中的实际数据减去季节变动值， 其次，将时间数列中的实际数据减去季节变动值，测定循环变 动和不规则变动的绝对额。 动和不规则变动的绝对额。
Y-T-S=C+I
再次，将循环变动和不规则变动绝对额进行移动平均， 再次，将循环变动和不规则变动绝对额进行移动平均，剔除不 规则变动影响，测定循环变动绝对额。 规则变动影响，测定循环变动绝对额。将时间数列中的实际数 据减去长期趋势、季节变动、循环变动， 据减去长期趋势、季节变动、循环变动，其差额就是不规则变 也可用循环、不规则变动减去循环变动计算不规则变动。 动。也可用循环、不规则变动减去循环变动计算不规则变动。
作用： 消除较小时距单位内偶然因素的影响， 作用：—消除较小时距单位内偶然因素的影响，显 示现象变动的基本趋势
y1 y2 y1 + y2 + y3 y = y1 + y2 + y3 2 3 y3 y4 y4 + y5 + y6 y4 + y5 + y6 y = y5 5 3 y6 y7 yn − 2 + yn − 1 + yn y = 3 M yn − 2 + y n − 1 + yn n − 1 yn
应用时距扩大法时需要注意以下几个问题： 应用时距扩大法时需要注意以下几个问题： 1、扩大的时距多大为宜取决于现象自身 的特点。对于呈现周期波动的动态数列， 的特点。对于呈现周期波动的动态数列，扩大 的时距应与波动的周期相吻合； 的时距应与波动的周期相吻合；对于一般的动 态数列，则要逐步扩大时距， 态数列，则要逐步扩大时距，以能够显示趋势 变动的方向为宜。时距扩大太大， 变动的方向为宜。时距扩大太大，将造成信息 的损失。 的损失。 扩大的时距要一致， 2、扩大的时距要一致，相应的发展水平 才具有可比性。 才具有可比性。
应用统计学时间数列分析
应用统计学时间数列分析时间数列分析是统计学中的一项重要内容，通过对时间序列数据进行分析，可以揭示数据之间的内在关联和规律。
本文将探讨时间数列分析在实际应用中的重要性和方法。
什么是时间数列分析时间数列（Time Series）指的是按时间顺序排列的一系列数据观测值。
时间数列分析是指根据时间数列数据进行的统计分析方法，旨在发现数据中存在的趋势、季节性、周期性等规律，以便进行预测和决策。
时间数列分析的重要性时间数列分析在许多领域都有广泛的应用，包括经济学、金融、医学、气象等。
通过时间数列分析，我们可以：•发现数据中的趋势和规律•预测未来数据走势•制定决策和策略•检验模型的有效性•揭示不同变量之间的关联时间数列分析方法1. 平稳性检验平稳性是时间数列分析的前提条件之一，可以通过单位根检验、ADF检验等方法来判断时间数列是否平稳。
如果时间数列不平稳，需要进行差分处理或其他转换方法使其平稳化。
2. 自相关性分析自相关性分析是检验数据是否存在自相关性（即相邻数据之间的相关性）的方法，可以通过自相关图和偏自相关图来判断数据中的自相关性程度。
3. 移动平均法移动平均法是一种基本的时间数列预测方法，通过计算一定窗口内的数据均值来平滑数据曲线，以便更好地观察数据走势和预测未来走向。
4. 季节性调整在时间数列分析中，常常需要对数据进行季节性调整，以消除季节性影响，使预测结果更为准确。
应用实例1. 股票价格预测时间数列分析在金融领域有着广泛的应用。
通过分析股票价格的时间数列数据，可以预测股价的未来走势，指导投资决策。
2. 气象预测气象数据也是时间数列数据的一种，通过对气象数据进行时间数列分析，可以预测未来的气候变化和天气情况，为灾害预警和农业生产提供依据。
3. 经济指标分析经济数据的时间数列分析可以揭示经济增长趋势、波动周期等信息，帮助政府和企业做出相应决策。
结语时间数列分析是统计学中一个重要的分析方法，通过对时间序列数据进行分析，可以揭示数据之间的规律、趋势和关联。
统计学时间数列分析指标
43
▪ 按照几何平均法所确定的平均发展速度，所推算最末一年的发展水平，与实际资料 最末一年的发展水平相同。
▪ 按方程按照方程式法所确定的平均发展速度，所推算全期各年发展水平的总和与全 期各年的实际发展水平的总和相同。
44
三、计算和运用速度指标注意的问题
个发展水平。
▪ 最初水平，最末水平，中间各项水平（中间水平）。
5
（二）平均发展水平
▪
平均发展水平是时间数列中各不同时期发展水平计算的平均数，又称序时平
均数或时间平均数。
1、绝对数时间数列的序时平均数
2、相对数时间数列＆平均数时间的序时平均数
6
1、绝对数时间数列的序时平均数
（1）由时期数列计算序时平均数
▪ 用符号表示为：
a1 , a2 , a3 ,, an
a0 a0 a0
a0
26
2.环比发展速度
环比发展速度
报告期水平 前一期水平
▪ 用符号表示为：
a1 , a2 , a3 ,, an
a0 a1 a2
an1
27
3. 定基发展速度与环比发展速度的关系。
a1 a2 a3 an an
a0 a1 a2
增长速度 平均增长速度
动 态 平 均 指 标
46
某企业产值与月初职工人数资料
a.产值（万元） b.月初职工人数（人）
７月 750 870
８月 830 910
９月 800 900
１0月 … 920
18
▪ 二、增长量与平均增长量
（一）增长量 ▪ 也称增减量，其计算公式为：
▪ 增长量=报告期水平–基期水平
《统计学原理与应用》课件第08章 时间数列分析
时间
1月底
3月底
8月底
12月底
固定资产原值（万元） 230
238
229
240
Fundamentals of Statistics
统计学基础
第八章 时间数列 （二）相对指标时间数列 （三）平均指标时间数列
相对指标和平均指标时间数列的形成—都需要分子和分母
时期数列 时期数列
时点数列 时点数列
例如
月份
生产工人劳动生产率
一、发 展 水 平 二、平均发展水平 三、增长量 四、平均增长量
Fundamentals of Statistics
统计学基础
第八章 时间数列
一、发 展 水 平
发展水平就是动态数列中的每一项具体指标数值。 其数值可以表现为绝对数、相对数或平均数。 用符号表示为：
a0，a1，a2，a3，a4，…an-1，an
Fundamentals of Statistics
统计学基础
第八章 时间数列
第一节 时间数列的意义和种类
一、时间数列的意义 二、时间数列的种类 三、编制时间数列的原则
Fundamentals of Statistics
统计学基础
第八章 时间数列
第一节 时间数列的意义和种类
一、时间数列的意义
2.分子和分母都为时点数列时，(有16个公式) 常用的有：
c
a
a1 2
a2
a3
an1
an 2
b
b1 2
b2
b3
bn1
bn 2
Fundamentals of Statistics
统计学基础
(二第八)章由时相间数对列指标或平均指标动态数列计算序时 平均数
统计学第八章课后题及答案解析
第八章一、单项选择题1．时间数列的构成要素是（）A．变量和次数 B．时间和指标数值C．时间和次数 D．主词和时间2．编制时间数列的基本原则是保证数列中各个指标值具有（）A．可加性 B．连续性C．一致性 D．可比性3．相邻两个累积增长量之差，等于相应时期的（）A．累积增长量 B．平均增长量C．逐期增长量 D．年距增长量4．统计工作中，为了消除季节变动的影响可以计算（）A．逐期增长量 B．累积增长量C．平均增长量 D．年距增长量5．基期均为前一期水平的发展速度是（）A．定基发展速度 B．环比发展速度C．年距发展速度 D．平均发展速度6．某企业2003年产值比1996年增长了1倍，比2001年增长了50%，则2001年比1996年增长了（）A．33% B．50%C．75% D．100%7．关于增长速度以下表述正确的有（）A．增长速度是增长量与基期水平之比 B．增长速度是发展速度减1C．增长速度有环比和定基之分 D．增长速度只能取正值8．如果时间数列环比发展速度大体相同，可配合（）A．直线趋势方程 B．抛物线趋势方程C．指数曲线方程 D．二次曲线方程二、多项选择题1．编制时间数列的原则有（）A．时期长短应一致 B．总体范围应该统一C．计算方法应该统一 D．计算价格应该统一E．经济内容应该统一2．发展水平有（）A．最初水平 B．最末水平C．中间水平 D．报告期水平E．基期水平3．时间数列水平分析指标有（）A．发展速度 B．发展水平C．增长量 D．平均发展水平E．平均增长量4．测定长期趋势的方法有（）A．时距扩大法 B．移动平均法C．序时平均法 D．分割平均法E．最小平方法三、填空题1．保证数列中各个指标值的_______是编制时间数列的最主要规则。
2．根据采用的基期不同，增长量可以分为逐期增长量和_______增长量两种。
3．累积增长量等于相应的_______之和。
两个相邻的_______之差，等于相应时期的逐期增长量。
统计学第八章时间数列
2020/1/19
增长速度growth rate 表明现象的增长程度
某现 基象 期报 水 告 平 报期 告 基的 期 期 基 增 水 水 期 长 平 平 发 水 量 展 平 1速
环比增长速度=环比发展速度-1 定基增长速度=定基发展速度-1
2020/1/19
增 1长 的 % 绝 环 对 逐 比 期 增 1 值 增 0 长 0上 长 1速 0 期 量 0度 水平
n 1
n 1
（5）间隔不相等不连续时点的时点数列
2020/1/19
aa1 2a2t1a2 2a3t2an12 antn1 t1t2tn1
增长量和平均增长量 •增长量growth amount
总量指标报告期水平与基期水平之差，表明 该指标在一定时期内增加或减少的绝对数量。
社会经济现象以若干年为周期的 涨落起伏相同或基本相同的一种 波浪式的变动
随机变动（I）
客观社会经济现象由于天灾、人 祸、战乱等突发事件或偶然因素 引起是无周期性波动
2020/1/19
一般模型 加法模型
Y=T+S+C+I
乘法模型 Y=T×S×C×I
分解方法
加法模型 T=Y-（S+C+I）
乘法模型
2020/1/19
✓水平法（几何平均法）
n
X
n
Xi
i1
n
an a0
适用：水平指标的平均发展速度计算
2020/1/19
✓方程法（累计法）
a 0 x a 0 x 2 a 0 x 3 a 0 x n a i
xx2x3xnai a0
适用：侧重于考察中长期间的累计总量
平均增长速度 = 平均发展速度-100% 表明现象在一个较长时期中逐期平均增长变化的程度
《统计基础》(第二版)课件、答案 第八章
目标要求
能力（技能）目标
知识目标
会计算平均发展水平
会计算定基发展速度 与环比发展速度
会计算增长量、增长 速度
会进行趋势分析与预 测
会用Excel测定动态趋 势并预测
了解时间数列概念、种类 及编制原则
掌握现象发展水平指标和 现象发展速度指标的计算
掌握直线趋势测定的各种 方法
掌握用时间数列预测的方 法
一、时间数列趋势分析的意义
时间数列中各期发展水平的变化，是由许多复杂因素共同作 用的结果，归纳起来大体有四类：
在较长的时间 内,由于持续的 决定性的 因素 作用,现象发展 呈某种趋势与 规律。
现象在一年内 随时序的更换, 呈周期性变动, 变动原因有自 然因素也有人 为因素。
现象发生周期 比较长的涨落 起伏的变动
现象受偶 然因素引起非 周期非趋势的 随机变动
（一）时距扩大法
它是指合并原动态数列中若干时期的数 据资料，得出扩大间隔的较大时距单位 的新动态数列，消除由于时距较短而受 偶然因素影响所引起的不规则变动。 注：时距扩大法也称为间隔扩大法，是 测定长期趋势最原始、最简单的方法。
（二）移动平均法
根据动态数列资料，将原时间数列的 时间间隔扩大，并按选定的时间长度，采 用逐次递移的方法对原时间数列计算一系 列的序时平均数。
（二）平均增减量
平均增减量是逐期增减量的序时
平均数，用于描述现象在观察期内 平均每期增减的数量。计算公式：
平均增长量
逐期增长量之和 逐期增长量项数
累积增长量 指标项数-1
第三节 时间数列的速度指标
一、发展速度
两个不同时期发展水平对比，说明报告期水平已发展到基 期水平的几分之几或若干倍，表明现象发展的相对程度。
统计学第八章 时间数列分析试题及答案
第八章时间数列分析(二) 单项选择题1、组成动态数列的两个基本要素是(A )。
A、时间和指标数值B、变量和次数（频数）C、主词和宾词D、水平指标和速度指标2、下列数列中哪一个属于动态数列（ C ）A、学生按学习成绩分组形成的数列B、职工按工资水平分组形成的数列C、企业总产值按时间顺序形成的数列D、企业按职工人数多少形成的分组数列3、下列属于时点数列的是( C )。
A、某工厂各年工业总产值；B、某厂各年劳动生产率；C、某厂历年年初固定资产额D、某厂历年新增职工人数。
3、时间数列中，各项指标数值可以相加的是( A )。
A、时期数列B、相对数时间数列C、平均数时间数列D、时点数列5、工人劳动生产率时间数列，属于( C )。
A、时期数列B、时点数列C、相对数时间数列D、平均数时点数列6、在时点数列中，称为“间隔”的是( C )。
A、最初水平与最末水平之间的距离；B、最初水平与最末水平之差；C、两个相邻指标在时间上的距离；D、两个相邻指标数值之间的距离。
7、对时间数列进行动态分析基础指标是( A )。
A、发展水平；B、平均发展水平；C、发展速度；D、平均发展速度。
8、计算序时平均数与一般平均数的资料来源是（ D）A、前者为时点数列，后者为时期数列B、前者为时期数列，后者为时点数列C、前者为变量数列，后者为时间数列D、前者为时间数列，后者为变量数列9、根据时期数列计算序时平均数应采用（ B ）A、首尾折半法B、简单算术平均法C、加权算术平均法D、几何平均法10、某企业某年1-4月初的商品库存额如下表：（单位：万元）月份 1 2 3 4月初库存额 20 24 18 22则第一季度的平均库存额为（ C ）A、（20+24+18+22）/4B、（20+24+18）/3C、（10+24+18+11）/3D、（10+24+9）/311、上题中如果把月初库存额指标换成企业利润额，则第一季度的平均利润额为（ B ）A、（20+24+18+22）/4B、（20+24+18）/3C、（10+24+18+11）/3D、（10+24+9）/312、某企业某年一季度的利润额为150万元，职工人数120人，则一季度平均每月的利润额和平均每月的职工人数分别为：（ B ）A、50万元，40人B、 50万元，120人C、150万元，120人D、以上全错13、定基增长量和环比增长量的关系是( B )。
08第八章 时间序列分析
某地10月份上旬中午12点平均室外温度：
20.5 21 23 19 20 21.5 23 22 . 5 24 23 . 5 连续时点数列 y 10 （简单平均法） o 21.8 C
2014-3-30
第八章 时间序列分析
19
2.2 平均发展水平
【例8-4】 某企业2007年11月份在册职
注意：
—要根据不同数列（时期、时点、相 对数、 平均数）采用不同的计算公式 计算！
2014-3-30
第八章 时间序列分析
12
2.2 平均发展水平
序时平均数与一般平均数的不同点
序时平均数
依据 时间数列
对象 不同时间指标值平均 性质 动态平均数 不同类型数列采用不 方法 同计算公式
2014-3-30
一般平均数
【例 8-6】某企业 2007年四个季 度 一 二 三 四 计划完成（%） 95 120 110 105 度的产品产量计划完成情况如下表 实际完成（件） 3 800 4 800 5 500 5 250 所示，求该企业全年的平均计划完 计划任务（件） 4 000 4 000 5 000 5 000 实际完成数 成程度。 该企业全年平均计划完成百分数： 根据：计划任务数
2014-3-30
第八章 时间序列分析
21
2.2 平均发展水平
间隔相等的时点数列
y1
y3
y2
y n 1
yn
y 0 y1 y1 y 2 y n 1 y n y0 2 2 2 y n
y4
y 0 y1 y1 2
2014-3-30
0
1
y1 y 2 y2 2
间隔不等的时点数列
统计学_第八章__时间序列分析
1978—2003年GDP和最终消费（亿元） 140000 120000 100000 80000 60000 40000 20000 0
年 份 1979 1981 1983 1985 1987 1989 1991 1993 1995 1997 1999 2001
GDP 最终消费
4、二者关系 （1）各逐期增长量之和等于相应的累计增长量
an a0 (a1 a0 ) (a2 a1 ) (a3 a2 ) (an an1 )
（2）相邻两期的逐期增长量之和等于相应的 累计增长量；相邻两期的累计增长量之差等于 相应的逐期增长量
（二）平均增长量 1、概念 一段时期内平均每期增加或者减少的绝 对数量。或者说是逐期增长量的序时平均数。 2、计算公式
a0 a1 a 2 a n 或 a n 1
af a f
B、如果是间断时点数列，计算方法为： 『两个假设条件： 一是假设上期期末水平等于本期期初水平； 二是假设现象在间隔期内数量变化是均匀的。』 Ⅰ、间隔期相等的时点数列，采用“首尾（首末）折半 法”计算。 先计算各间隔期的平均数；然后再将这些平均数进行 简单算术平均。例如：
第一节
时间序列分析概述
一、时间序列的概念和作用
（一）、概念： 1、时间序列：将不同时间的某一统计指标数据按照 时间的先后顺序排列起来而形成的统计序列，也称时间 数列或动态数列。 2、基本构成要素（从形式上看）： 一是时间顺序（现象所属的时间）。可以是年份、季 度、月份或其他任何时间，称时间要素（常用t表示）； 二是不同时间的统计数据（现象在不同时间上的观察 值）。可以是绝对数、相对数、平均数，称数据要素 （常用小写的英文字母a、b、c表示）。
第一节 时间序列的对比分析
y yy y y yi 1 , 2 ,, n ⒉ i 0 i 10 i i 1
《统计学》第八章 时间序列分析
年距增长量
本期发展水平与去年同期水平之 差，目的是消除季节变动的影响
年 距 y y L 41 或 2 ； i 1 , 2 , , n i L i 增 长 量
y y 3 4 2
y y y y y y 2 3 n 1 n 1 2 f f f 1 2 n 1 2 2 2 一 般 有 ： f f f 1 2 n 1
《统计学》第八章 时间序列分析
【例】 某地区2005年社会劳动者人数资料如下
单位：万人 时间 社会劳动者 人数 1 月 1日 362 5月31日 390 8月31日 416 12月31日 420
计算的，后者则是根据时间数列计算的； 说明的内容不同：前者表明总体内部各 单位的一般水平，后者则表明整个总体在 不同时期内的一般水平。
《统计学》第八章 时间序列分析
序时平均数的计算方法
⒈计算绝对数时间数列的序时平均数 ⑴由时期数列计算，采用简单算术平均法
y
1
y
2
y
n 1
y
n
a
y y 1 y 2 n y i1 n n
平均增长量
逐期增长量的序时平均数
平 均 增 长 量
( y y )
i 1 i i 1
n
n
y y n 0 n
《统计学》第八章 时间序列分析
平均发展水平
又叫序时平均数，是把时 间数列中各期指标数值加 以平均而求得的平均数
一般平均数与序时平均数的区别：
计算的依据不同：前者是根据变量数列
统计学第八章
第八章 时间数列分析一、单项选择题1.时间序列与变量数列( )A 都是根据时间顺序排列的B 都是根据变量值大小排列的C 前者是根据时间顺序排列的，后者是根据变量值大小排列的D 前者是根据变量值大小排列的，后者是根据时间顺序排列的 2.时间序列中，数值大小与时间长短有直接关系的是( )A 平均数时间序列B 时期序列C 时点序列D 相对数时间序列 3.发展速度属于( )A 比例相对数B 比较相对数C 动态相对数D 强度相对数 4.计算发展速度的分母是( )A 报告期水平B 基期水平C 实际水平D 计划水平 5.某车间月初工人人数资料如下：则该车间上半年的平均人数约为( )A 296人B 292人C 295 人D 300人6.某地区某年9月末的人口数为150万人，10月末的人口数为150．2万人，该地区10月的人口平均数为( )A 150万人B 150．2万人C 150．1万人D 无法确定 7.由一个9项的时间序列可以计算的环比发展速度( ) A 有8个 B 有9个 C 有10个 D 有7个 8.采用几何平均法计算平均发展速度的依据是( )A 各年环比发展速度之积等于总速度B 各年环比发展速度之和等于总速度C 各年环比增长速度之积等于总速度D 各年环比增长速度之和等于总速度9.某企业的科技投入，2010年比2005年增长了58．6％，则该企业2006—2010年间科技投入的平均发展速度为( )A 5%6.58B 5%6.158C 6%6.58D 6%6.15810.根据牧区每个月初的牲畜存栏数计算全牧区半年的牲畜平均存栏数，采用的公式是( ) A 简单平均法 B 几何平均法 C 加权序时平均法 D 首末折半法 11.在测定长期趋势的方法中，可以形成数学模型的是( )A 时距扩大法B 移动平均法C 最小平方法D 季节指数法 12.动态数列中，每个指标数值相加有意义的是（ ）。
A.时期数列 B.时点数列 C.相对数数列 D.平均数数列 13.按几何平均法计算的平均发展速度侧重于考察现象的（ ） A.期末发展水平 B.期初发展水平C.中间各项发展水平D.整个时期各发展水平的总和14.累计增长量与其相应的各逐期增长量的关系表现为（ ） A.累计增长量等于相应各逐期增长量之和 B.累计增长量等于相应各逐期增长量之差 C.累计增长量等于相应各逐期增长量之积 D.累计增长量等于相应各逐期增长量之商15.已知某地区2010年的粮食产量比2000年增长了1倍，比2005年增长了0.5倍，那么2005年粮食产量比2000年增长了（ ）。
统计学第8章 时间序列分析
a n 1
a0
（二）增长速度（增减速度）
增长速度=
增减量 基期水平
报告期水平 基期水平 基期水平
报告期水平 基期水平 1
发展速度1
环比增长速度= an an1 an 1
an1
an1
=环比发展速度 - 100%
定基增长速度= an a0 an 1
a0
a0
=定基发展速度 - 100%
例题：
时间序列的构成要素与模型
（构成要素与测定方法）
时间序列的构成要素
长期趋势
季节变动
循环波动 不规则波动
线性趋势 非线性趋势
按月(季)平均法
移动平均法
二次曲线 指数曲线
趋势剔出法
半数平均法
修正指数曲线
最小平方法
Gompertz曲线 Logistic曲线
剩余法
线性趋势
一、移动平均法
(Moving Average Method)
移动平均法(趋势图)
200
汽 150
车
产 100
量
（万辆）50
产量 五项移动平均趋势值 五项移动中位数
0
1981
1985
1989
1993
1997
（年份）
图11-1 汽车产量移动平均趋势图
移动平均法特点
1、对原数列有修匀作用，移动项数越大，修匀 作用越强。
2、移动平均时，项数为奇数时，只需一次移动 平均，其平均值作为移动平均项中间一期； 当为偶数时，需再进行一次相邻两平均值的 移动平均。
年份
销售额 逐 期 增 减 量 环比发展速度 定基增长速
（万元） （万元）
（%）
度（%）
第八章时间序列分析
第八章 时间序列分析第一部分 习题一、单项选择题1．编制时间数列，要求在时间间隔方面( )。
A.必须相等B.必须不相等C.可相等也可不相等D.不需要考虑 2．动态数列中各项指标数值可以相加的是( )。
A.相对数动态数列B.绝对数动态数列C.时期数列D.时点数列3．以1980年0a 为最初水乎，2005年n a为最末水平，在计算钢产量的年平均发展速度时，需要开( )。
A.24次方B.25次方C.26次方D.27次方 4．对长度不同的各时期产值资料计算平均发展速度应采用( )。
A.简单算术平均 B.加权算术平均 C.简单几何平均 D.加权几何平均 5．由两个时期数列相应项对比所形成的相对数动态数列算序时平均数的基本公式是（ ）。
A.n aa ∑=B.n cc ∑=C.∑--++++++=ff a a f a a f a a a n n n 11232121222 D.∑∑=b a c 6．间隔不等的间断时点数列的序时平均数的计算公式是（ ）。
A.n a a ∑=B.12121121-++++=-n a a a a a n nC.∑--++++++=ff a a f a a f a a a n n n 11232121222 D.∑∑=f af a7．根据现象在不同时间上的指标数值而计算的平均数是（ ）。
A.算术平均数B.序时平均数C.调和平均数D.静态平均数 8．累计增长量与逐期增长量的关系是（ ）。
A.逐期增长量之和等于累计增长量B.逐期增长量之积等于累计增长量C.累计增加量之和等于逐期增长量D.两者没有直接关系 9．环比发展速度与定基发展速度之间的关系是（ ）。
A.定基发展速度等于环比发展速度之和 B.环比发展速度等于定基发展速度的平方根 C.环比发展速度的连乘积等于定基发展速度 D.环比发展速度等于定基发展速度减110．某现象前期水平为1600万吨，本期水平为2000万吨，则增长1%的绝对值为( )。
统计学第八章时间数列
＝（报告期水平－前一期水平）/前一期水平 ＝环比发展速度－1（或100％）
发展速度与增长速度
2、定基增长速度。 定基增长速度是报告期的累计增长量与 某一固定基期水平之比，说明现象在较 长时间内总的增长速度。公式如下：
定基增长速度＝累计增长量/某一固定期水平 ＝报告期水平－某一固定期水平）/某一固定期 水平 ＝定基发展速度－1（或100％）
1、移动平均法。 移动平均法是对原时间数列逐项求 序时平均数，平均项数固定，并逐 项移动得出由这些平均数构成的新 数列，它可以消除某些因素及随机 因素的影响，显示出现象的长期趋 势。
测定长期趋势的方法
设时间数列的水平顺次为： a1，a2，a3， an 若取三项平均移动平均形成的新数 列为：
a1 a 2 a 3 a 2 a3 a 4 a2 ， a3 ， 3 3
第八章 时间数列
第一节 第二节 第三节 第四节 时间数列概述 时间数列的水平指标 时间数列的速度指标 动态数列的因素分析
第八章 时间数列
第一节 时间数列概述 一、时间数列的概念及作用 二、时间数列的种类 三、编制时间数列的原则
时间数列的概念及作用
一）时间数列的概念
时间数列亦称动态数列，是将反映某现象的 统计指标在不同时间上的数值，按时间先后 顺序排列而形成的一种数列；如：
动态数列影响因素及其分解 模型
3、循环变动(以C表示) 循环变动是指现象以若干年为一周 期，近乎规律性的盛衰交替变动。 如经济危机就是循环变动，每一循 环周期都要经历危机、萧条、复苏 和高涨四个阶段。
动态数列影响因素及其分解 模型
4、随机变动(以I表示) 随机变动亦称不规则变动或剩余变 动，是动态数列除了上述三种变动 之外剩余的一种变动，是偶然因素 引起的一种随机波动。如自然灾害、 战争等无法预见的因素引起的波动。
统计学8章
三、平均发展水平
又称序时平均数或动态平均数，是时间数 列中各项指标值的平均数。它将现象在不同时 间上的数量差异抽象化，从动态上反映现象在 一段时间内的一般发展水平。 现象在不同时间上的发展变化总是不平衡 的，在动态分析中序时平均数可以用来修匀时 间数列，消除现象在短时间内的波动，使时间 数列能更明显更集中地反映出现象的发展变化 方向、程度和趋势。序时平均数还广泛用于对 比不同单位，不同地区，不同部门乃至不同国 家在某一时间内发展变化的一般水平。
（二）相对指标时间数列
是由不同时间上的同类相对数按先后顺 序排列而成的动态数列，用来说明现象之间 的数量对比关系或相互联系的发展变化过程， 能更清晰地表明某些现象数量对比关系的发 展变化及规律性。 各个指标都是相对数，其计算基础不同， 不能直接相加。
（三）平均指标时间数列
是由不同时间上的同类平均指标按先后 顺序排列而成的动态数列，可用以分析某一 现象的一般水平的变化过程和发展趋势。
（2）当已知分子数列和相对指标时间 数列时，应采用加权调和平均法。
a a 由于 c ， 则： b c b
而 所以
a a c b b
a c a c
2. 分子数列、分母数列都是时点数列
如果分子数列和分母数列都是时点数列， 当两个时点数列的资料是逐日记录的，以日 为间隔依次排列时，就可视为连续的时点数 列，可用简单算术平均法分别计算分子数列 和分母数列的序时平均数，再求得相对指标 时间数列的序时平均数。
动态平均数所组成的时间数列。由于这两种
时间数列性质不同，计算序时平均数的方法 也不同。
1. 根据一般平均数所组成的时间数列 计算序时平均数
由于该种时间数列中每个指标都是平均 数，不能直接相加，必须求出分子数列的序 时平均数和分母数列的序时平均数，用两者 对比，才可求出一般平均数时间数列的序时 平均数。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
绝对数时间数列
a
ai
n
相对数时间数列
ca b
（1）时期数列
a i n
（2）间隔相等连续时点的时点数列
a
i
n
（3）间隔不等连续时点的时点数列
a iti ti
ti —与现象各期水平相应的时间距离
（4）间隔相等不连续时点的时点数列
a
a1 a2 2
a2
a3 2
a n-1 a n 2
1 2
a1
编制方法和原则
➢总体范围应一致 ➢指标内容应相同 ➢时期数列的时期长短应一致，时期数列和时点数 列的间隔力求一致。 ➢指标的计算方法、计算价格和计量单位应一致。
动态数列分析指标 1. 水平指标
序时平均数
动态平均数、平均发展水平，是对时间 数列中各期发展水平的平均，表明现象在一 段时期的一般水平。
逐期增长量 环比增长速度100
上期水平 100
年距发展速度
报告期某月水平 上年同月水平
年距增长速度
年距增长量 上年同月水平
年距发展速度
1
时间数列中的指标值为0或负数时，不宜计算速度 速度指标与发展水平指标要结合使用
平均发展速度average growth rate
环比发展速度的平均数，表明现象在一个 较长时期中逐期平均发展变化的程度。
逐期增长量的平均数，表明总量指标在一段 时期内平均每期增减的绝对数量。
✓水平法 适用：多期增长量平稳变化的数列
平均增长量
逐期增长量之和 逐期增长量个数
（a1 a0）（a 2 a1） （a n an1） an a0
n
n
✓总和法
a0 a0 2 a0 n ai
△ 2(at a0 ) n(n 1)
逐期增长量 累计增长量
a1 a0 , a2 a1, an an1 a1 a0 , a2 a0 , an a0
注：
★ ①累计增长量=∑逐期增长量 ②两个相邻累计增长量之差=相应的逐期增长量 ③增长量是一个时期指标 ④年距增长量=报告期某月（季）水平 - 上年某
月（季）水平
•平均增长量average growth amount
各期水平 某一固定基期水平
a1 , a2 , , an
a0 a0
a0
表明现象在一段时间内总的发展程度
增长速度growth rate
表明现象的增长程度
某现象报告期的增长量
基期水平
报告期水平 基期水平 基期水平
发展速度 1
环比增长速度=环比发展速度-1 定基增长速度=定基发展速度-1
增长1%的绝对值
a2
an1
1 2
an
n 1
n 1
（5）间隔不相等不连续时点的时点数列
a
a1 a2 an1 an 2
t n1
t1 t 2 t n1
增长量和平均增长量 •增长量growth amount
总量指标报告期水平与基期水平之差，表明 该指标在一定时期内增加或减少的绝对数量。
适用：各期增长变化较大的数列
2、速度指标
发展速度development 百分数、倍数
rate报基告期期水水平平
>100%，现象在增长 <100%，现象在下降
✓环比发展速度
各期水平 前一期水平
a1 , a2 , , an
a0 a1
an1
表明现象逐期发展的程度
✓定期发展速度（定基发展速度、总速度）
数
季度 季末人数
某商场2004年各季度末销售员人数
1季度
2季度
3季度
83.0
93.3
时间数列的种类与编制方法
概念 时间序列、动态数列，把反映某种现象的同一
指标，在不同时间上的指标数值，按时间先后顺序 编排所形成的数列。
基本要素
现象所属的时间 反映在现象所属时间的发展水平
——统计指标数值
种类
指标 形式
绝对数时间数列 相对数时间数列
时期数列 时点数列
平均数时间数列
数据 性质
纯随机型时间数列 确定型时间数列
时距扩大法
简单长期趋势分析法 序时平均法
移动平均法 直线配合法 长期趋势的数字模型 指数曲线趋势模型
简单长期趋势分析法——时距扩大法
把时间数列中各期指标数值按较长的时距加 以归并，形成一个新的简化了的时间数列，以消 除原数列中的季节变动和各种偶然因素的影响， 显现出长期趋势。
例：P301 表8-8
计算和应用平均速度指标应注意的问题
计算平均发展速度的基本方法：几何平均法、 高次方程法，但注意选择合适的方法 根据事物的发展状态,应用分段平均发展速度 来补充说明整个时期的总平均发展速度
在应用几何平均法计算平均发展速度时,还要 注意与环比发展速度结合进行分析 注意平均速度指标与原时间数列的发展水平、 增长量、平均水平等指标的结合应用,以便对研 究现象做出比较确切和全面的认识。
随机变动（I）
客观社会经济现象由于天灾、人 祸、战乱等突发事件或偶然因素 引起是无周期性波动
一般模型 加法模型
Y=T+S+C+I
乘法模型 Y=T×S×C×I
分解方法
加法模型 T=Y-（S+C+I）
乘法模型 T=Y/（S×C×I）
1、长期趋势（Trend）测定 概念 某种现象在相当长的时期内，发展过程表现为不断 增长或不断下降的总趋势 随手法
变动因素
长期趋势 （T）
时间数列的测定
客观社会经济现象在一个相当长的 时期内，由于受某种基本因素的影 响所呈现出来的一种基本走势
季节变动（S）
由于自然条件、社会条件的影响， 社会经济现象在一年内或更短的时 间内，随着季节的转变而引起的周 期性变动
循环变动 （C）
社会经济现象以若干年为周期的 涨落起伏相同或基本相同的一种 波浪式的变动
★对于时距究竟扩大到何种程度为宜，应依据 现象和原动态数列的特点而定，以明显反映现象 的发展趋势为宜。
简单长期趋势分析法——序时平均法
例：某商场2004年各月末销售员人数
月份 上年12 1月 2月 3月 4月 5月 6月 7月 8月 9月 10 11 12
月
月月月
月末人 85 75 81 101 87 93 99 85 105 99 97 103 107
✓水平法（几何平均法）
n
X
n
i 1
Xi
n
an a0
适用：水平指标的平均发展速度计算
✓方程法（累计法）
a 0 x a 0 x 2 a 0 x 3 a 0 x n ai
x x 2 x 3 x n ai a0
适用：侧重于考察中长期间的累计总量
平均增长速度 = 平均发展速度-100% 表明现象在一个较长时期中逐期平均增长变化的程度