第一节 集合的概念与运算
第一讲 集合的概念和运算
。
解析：对于新定义题，关键是读懂题目， 弄清概念的含义，准确运用。 ∵n=4, ∴ Sn {1, 2,3, 4}, ，则X可取 ,{1}, {2}, {3},
{4}, {1,2}, {1,3}, {1,4}, {2,3}, {2,4}, {3,4}, {2,4}, {1,2,3}, {1,2,4}, {1,3,4}, {2,3,4}.不是偶子集有{1}，
A B 0,1,2,4,16
则a的值为（ A. 0 答案：D. B. 1
） C. 2 D. 4
a4 解析：抓住并集中的元素，由此知 a 2 16 2
a 4 或 ，∴选D。 a 16
变式题：含有三个实数的集合可表示为{a,b,lg(ab)},也可 表示为{|a|,b,0},则 a 2015 b2015 的值等于 。
7.特别提醒的几点：
①．注意区分几种常见集合
研究一个集合，首先要看集合中的代表元素，然 后再看元素的限制条件，当集合用描述法表示时，注 意弄清其元素表示的意义是什么.
集合 {x|f(x)＝0} {x|f(x)＞0} {x|y＝f(x)} {y|y＝f(x)} {(x，y)|y＝f(x)}
集合的意义 方程f(x)＝0的解源自 不等式f(x)＞0的解集 函数y＝f(x)的定义域 函数y＝f(x)的值域 函数y＝f(x)图象上的点集
⑶
无序性
。
5.集合中元素和集合、集合与集合的关系： ⑴元素和集合的关系：若元素a 是集合A的元素， A”。 记作：a A ，否则“a
⑵集合与集合的关系：包含和不包含关系。包含关系又 分为真包含和相等关系。符号为“ ”，“＝”， ”，“ “ ”，“ ” .
特别提醒：规定空集是 空集是
第1章 第1节 集合的概念与运算
B＝{x|－2≤x≤2}，则如图所表示阴影部分所示的集合为( )
A．{x|－2≤x<4}
B．{x|x≤2 或 x≥4}
C．{x|－2≤x≤－1}
D．{x|－1≤x≤2}
解析： 依题意得 A＝{x|x<－1 或 x>4}，因为∁RA＝{x|－1≤x≤4}，题中的
阴影部分所表示的集合为(∁RA)∩B＝{x|－1≤x≤2}． 答案： D
返回
[同类练]
1．(2017·天津卷)设集合 A＝{1,2,6}，B＝{2,4}，C＝{x∈R|－1≤x≤5}，则(A
∪B)∩C＝( )
A．{2}
B．{1,2,4}
C．{1,2,4,6}
D．{x∈R|－1≤x≤5}
解析： 因为 A＝{1,2,6}，B＝{2,4}，所以 A∪B＝{1,2,4,6}，又 C＝{x∈R| －1≤x≤5}，所以(A∪B)∩C＝{1,2,4}．
返回
2．判断集合关系的三种方法 (1)一一列举观察． (2)集合元素特征法：首先确定集合的元素是什么，弄清集合元素的特征，再 利用集合元素的特征判断集合关系． (3)数形结合法：利用数轴或 Venn 图．
返回
考向·分层突破
考向一 集合的基本概念 自主练透型
1．已知集合 A＝{0,1,2}，则集合 B＝{(x，y)|x≥y，x∈A，y∈A}中元素的个
(2)∵B⊆A，
∴①若 B＝∅，则 2m－1<m＋1，此时 m<2.
②若 B≠∅，则2mm＋－11≥≥－m2＋，1， 2m－1≤5.
注意集合的分类 讨论问题
解得 2≤m≤3.
由①、②可得，符合题意的实数 m 的取值范围为 m≤3.
答案： (1)D (2)(－∞，3]
1-1_集合的概念与运算课件
补集： 补集：∁UA＝{x|x∈U且x∉A}． ＝ ∈ 且 ∉ ． U为全集，∁UA表示 相对于全集 的补集． 为全集， 表示A相 于全集U的 表示 (2)集合的运算性质 集合的运算性质 集合的运算性 ①A∪B＝A⇔B⊆A，A∩B＝A⇔ A⊆B ∪ ＝ ⇔ ⊆ ， ＝ ⇔ ⊆ ②A∩A＝A，A∩∅＝ ∅ ； ＝ ， ∅ ③A∪A＝A，A∪∅＝A； ∪ ＝ ， ∪ ； ④A∩∁UA＝∅，A∪∁UA＝U，∁U(∁UA)＝A. ∁ ＝ ∪ ＝ ， ∁ ＝ ；
考基联动
考向导析
规范解答
限时规范训练
②若 B≠∅，
m＋1≤2m－1， 则－2≤m＋1， 2m－1≤5.
(2)若 A⊆B，
解得 2≤m≤3.由①②得，m 的取值范围是(－∞，3]．
2m－5.
∴m 的取值范围是[3,4]．
第 1 讲 集合的概念与运算
1．了解集合的含义、元素与集合的“属于”关系，能用自然语言、图形语言、 ．了解集合的含义、元素与集合的“属于”关系，能用自然语言、图形语言、 集合语言(列举法或描述法 描述不同的具体问题 集合语言 列举法或描述法)描述不同的具体问题，理解集合之间包含与相等 列举法或描述法 描述不同的具体问题， 的含义，能识别给定集合的子集，在具体情境中，了解全集与空集的含义． 的含义，能识别给定集合的子集，在具体情境中，了解全集与空集的含义． 2．理解两个集合的并集与交集的含义，会求两个简单集合的并集与交集，理解 ．理解两个集合的并集与交集的含义，会求两个简单集合的并集与交集， 在给定集合中一个子集的补集的含义，会求给定子集的补集， 在给定集合中一个子集的补集的含义，会求给定子集的补集，能使用韦恩图 (Venn)表达集合的关系及运算． 表达集合的关系及运算． 表达集合的关系及运算
第1章 第1节 集合的概念与运算
服/务/教/师
免/费/馈/赠
返回菜单
数学·新课标(文科)山东专用
对点训练
(1)(2014· 深圳模拟)已知集合 A＝{1,2,3,4,5}，B＝ )
{(x，y)|x∈A，y∈A，x－y∈A}，则 B 中所含元素的个数为( A．3 B．6 C．8 D．10
(2)已知集合 A＝{x|ax2－3x＋2＝0}，若 A＝∅，则实数 a 的取 值范围为________．
服/务/教/师
免/费/馈/赠
返回菜单
数学·新课标(文科)山东专用
【解析】 (1)因为 A＝{1,2,3,4,5}，所以集合 A 中的元素都为 正数，若 x－y∈A，则必有 x－y＞0，即 x＞y. 当 y＝1 时，x 可取 2,3,4,5，共有 4 个数； 当 y＝2 时，x 可取 3,4,5，共有 3 个数； 当 y＝3 时，x 可取 4,5，共有 2 个数； 当 y＝4 时，x 只能取 5，共有 1 个数； 当 y＝5 时，x 不能取任何值． 综上，满足条件的实数对(x，y)的个数为 4＋3＋2＋1＝10，即 集合 B 中的元素共有 10 个，故选 D.
2 所以 a 的取值集合是－1，0，3 . 2 【答案】 (1)D (2)－1，0，3
服/务/教/师 免/费/馈/赠
数学·新课标(文科)山东专用
抓 住 3 个 基 础 知 识 点
第一章 集合与常用逻辑用语
第一节 集合的概念与运算
挖 掘 1 大 技 法
掌 握 3 个 核 心 考 向
课 堂 限 时 检 测
服/务/教/师
免/费/馈/赠
返回菜单
数学·新课标(文科)山东专用
[考情展望]
1.给定集合，直接考查集合的交、并、补集的
集合与常用逻辑用语高考考点梳理及真题分类解析(2022年高考备考版)
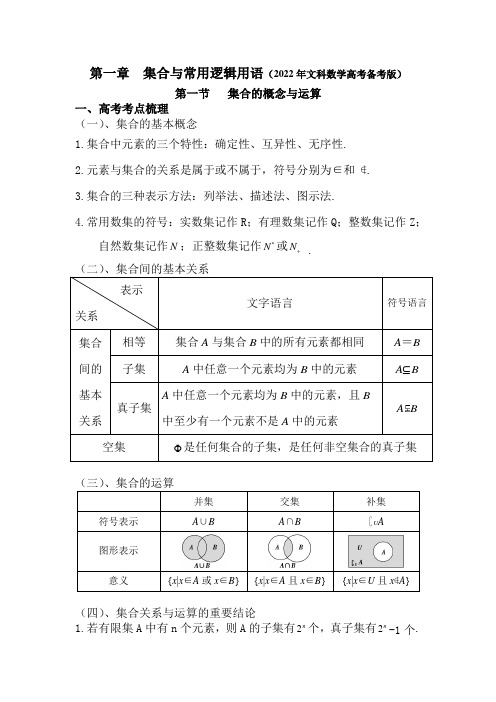
第一章集合与常用逻辑用语（2022年文科数学高考备考版）第一节集合的概念与运算一、高考考点梳理（一）、集合的基本概念1.集合中元素的三个特性：确定性、互异性、无序性.2.元素与集合的关系是属于或不属于，符号分别为∈和∉.3.集合的三种表示方法：列举法、描述法、图示法.4.常用数集的符号：实数集记作R；有理数集记作Q；整数集记作Z；自然数集记作N；正整数集记作*N或N .+A B（四）、集合关系与运算的重要结论1.若有限集A中有n个元素，则A的子集有个，真子集有-1个.n2n22.传递性：A ⊆B ，B ⊆C ，则A ⊆C .3.A ∪B ＝A ⇔B ⊆A ； A ∩B ＝A ⇔A ⊆B .4.∁U (A ∪B )＝(∁U A )∩(∁U B )；∁U (A ∩B )＝(∁U A )∪(∁U B ) . 二、历年高考真题题型分类突破题型一 集合的基本概念【例1】（2021全国甲卷） 设集合{}{}1,3,5,7,9,27M N x x ==>，则MN =（ ）A. {}7,9B. {}5,7,9C. {}3,5,7,9D. {}1,3,5,7,9解析：∵7,2N ⎛⎫=+∞ ⎪⎝⎭，∴MN ={}5,7,9，故选：B .【例2】（2020全国Ⅰ卷）已知合集{}2340A x x x =--<，{}4,1,3,5B =-，则A B =（ ）A.{}4,1-B. {}1,5C. {}3,5D. {}1,3解析：∵{}2340A x x x =--<＝{ x |－1＜ x ＜4}，∴A ∩B ＝{1,3}，故选D . 【例3】（2013全国Ⅰ卷）已知集合A ＝{1,2,3,4}，},|{2A n n x x B ∈==， 则=B A ( )．A ．}4,1{B ．}3,2{C ．}16,9{D ．}2,1{ 解析：∵B ＝{x |x ＝n 2，n ∈A }＝{1,4,9,16}，∴A ∩B ＝{1,4}，故选A .题型二 集合间的关系【例4】（2021全国乙卷） 已知全集{}1,2,3,4,5U =，集合{}{}1,2,3,4M N ==，则∁U (M ∪N ) ＝（ ） A. {}5B. {}1,2C. {}3,4D. {}1,2,3,4解析：由题意可得：{}1,2,3,4MN =，则∁U (M ∪N ) ＝{}5. 故选：A .【例5】（2020全国Ⅲ卷） 已知集合{}1,2,3,5,7,11A =，{}|315B x x =<<，则A B中元素的个数为（ ）A. 2B. 3C. 4D. 5解析：根据题意，得A ∩B ＝{5,7,11}，故选B .【例6】（2017全国Ⅰ卷）已知集合A ={}|2x x <，B ={}|320x x ->，则（ ）．A ．AB =3|2x x ⎧⎫<⎨⎬⎩⎭ B ．A B =∅ C ．AB 3|2x x ⎧⎫=<⎨⎬⎩⎭D ．AB=R解析：由B ={}|320x x ->，得B 3|2x x ⎧⎫=<⎨⎬⎩⎭，因为A ={}|2x x <，所以A B =3|2x x ⎧⎫<⎨⎬⎩⎭，故选A .题型三 集合的运算【例7】（2020全国Ⅱ卷）已知集合A={}3,x x x Z <∈，B={}1,x x x Z >∈，则A B =（ ）A. ∅B. {}3,2,2,3--C. {}2,0,2-D. {}2,2-解析：由以知，得A ＝{x |－3＜ x ＜3，x ∈Z}，B ＝{x |x ＜－1或x ＞1，x ∈Z}， 所以A ∩B ＝{-2,2}，故选D .【例8】（2019全国Ⅰ卷）已知集合U ＝{1，2，3，4，5，6，7}，A ＝{2，3，4，5}，B ＝{2，3，6，7}，则B ∩∁U A ＝（ ）．A ．{1，6}B ．{1，7}C ．{6，7}D ．{1，6，7}解析：∵U ＝{1，2，3，4，5，6，7}，A ＝{2，3，4，5}，B ＝{2，3，6，7}， ∴∁U A ＝{1，6，7}，则B ∩∁U A ＝{6，7}，故选C ．第二节 命题及其关系、充分条件与必要条件一、高考考点梳理 （一）、命题的定义可以判断真假用文字或符号表述的语句叫做命题。
高考数学一轮复习 1.1 集合的概念与运算
2.如果集合 A 中含有 n 个元素,则集合 A 有 2n 个子集,2n-1 个真子集. 3.正确理解交、并、补集的含义是解决集合的运算问题的关键.数轴和 Venn 图是进行集合交、并、补运算的有力工具.
12
核心考点
(4)空集: 不含任何元素的集合
叫做空集,记作: ⌀
.
规定:空集是 任何集合的子集 .
4
知识梳理
双击自测
知识梳理
-5-
3.集合的基本运算
并集
符号 表示
A∪B
图形 表示
交集 A∩B
补集
设全集为 U,集合 A 的 补集∁UA
含义
A∪
B={x|x∈A,或 x∈B}
A∩B={x|x∈A,且 x∈B}
∁UA={x|x∈U,且 x∉ A}
-13-
考点一
考点二
考点三
考点一集合的基本概念
1.设集合 A={1,2,3},B={4,5},M={x|x=a+b,a∈A,b∈B},则 M 中元素的
个数为( )
A.3
B.4
C.5
D.6
关闭
由题意知 x=a+b,a∈A,b∈B,则 x 的可能取值为 5,6,7,8.因此,集合 M 共有 4 个元素.故选 B.
关闭
B
13 解析 答案
核心考点
-14-
考点一
考点二
考点三
2.若集合 A={x∈R|ax2+ax+1=0}中只有一个元素,则 a=( )
(6)设全集为 R,函数 y= 1-������2的定义域为 M,则∁RM={x|x>1,或 x<1}.( )
高考数学总复习 第一章 第一节集合的概念与运算课件 理
第十七页，共35页。
考点(kǎo 集合(jíhé)的基本关系及空集的妙用 diǎn)三
【例3】 设集合A＝{x|x2－3x－10≤0}，B＝{x|m＋1≤x≤2m －1}，若B⊆A，求实数(shìshù)m的取值范围．
思路点拨：考查集合间的包含、相等关系，关键搞清A，B两 集合谁是谁的子集．若B⊆A，说明B是A的子集，即集合B中元素 都在集合A中，注意B是∅的情况；同样若A⊆B，说明A是B的子集， 此时注意B是不是∅；若A＝B，说明两集合元素完全相同．
A．A＝B B．B＝C C．C＝E D．B＝E
思路点拨：要注意分辨各集合的代表元素是什么，如果性质 相同，但代表元素不同，则它们所表示的集合也是不一样的．因此 对于集合问题(wèntí)，要首先确定它属于哪类集合(数集、点集或某 类图形)．
第十五页，共35页。
解析：集合 A 是用列举法表示，它只含有一个元 素，即函数 y＝x2＋2，集合 B，C，E 中的元素都是数， 即这三个集合都是数集，集合 B 表示的是函数 y＝x2 ＋2 的值域2，＋∞，集合 C 表示的是函数 y＝x2＋2 的 定 义 域 R， 集 合 E 是不 等 式 x － 2≥0 的 解集 2，＋∞，集合 D 的元素则是平面上的点，此集合是 函数 y＝x2＋2 的图象上所有点所组成的集合．故只有 B＝E.故选 D.
第七页，共35页。
2．并集． (1)定义： 由所有属于集合A或集合B的元素组成的集合，称 为(chēnɡ w集éi)合__(_j_íh_é_)_A_与__集__合__(_j_íh的é)并B集，记作___A__∪__B_____(读作 “A并B”)．即 A∪B＝{ x|x∈A，或x∈B}. (2)性质：
第1讲集合的概念和运算
第1讲 集合的概念和运算必记考点1．集合的基本概念(1)集合元素的三个特征： 、 、 ． (2)元素与集合的关系是属于或不属于关系，用符号 或 表示． (3)集合的表示法：列举法、描述法、图示法、区间法．(4)常用数集： N ； N *(或N ＋) ； Z ；Q ； R . (5)集合的分类：按集合中元素个数划分，集合可以分为有限集、无限集、 . 2．集合间的基本关系(1)子集： ，则A ⊆B (或B ⊇A )． (2)真子集： 则A B (或B A )．若集合A 中含有n 个元素，则A 的子集有2n 个，A 的真子集有2n －1个．(3)空集：空集是 的子集，是 的真子集．即∅⊆A ，∅B (B ≠∅)．(4)集合相等：若 ，则A ＝B . 3．集合的基本运算及其性质(1)并集：A ∪B ＝ ． (2)交集：A ∩B ＝ ．(3)补集：∁U A ＝ ，U 为全集，∁U A 表示A 相对于全集U 的补集． (4)集合的运算性质①A ∪B ＝A ⇔B ⊆A ，A ∩B ＝A ⇔A ⊆B ； ②A ∩A ＝A ，A ∩∅＝∅； ③A ∪A ＝A ，A ∪∅＝A ；④A ∩∁U A ＝∅，A ∪∁U A ＝U ，∁U (∁U A )＝A .考向一 集合的基本概念【例1】►已知a ∈R ，b ∈R ，若⎩⎨⎧⎭⎬⎫a ，b a ，1＝{a 2，a ＋b,0}，则a 2 014＋b 2 014＝________.【训练1】集合⎩⎨⎧⎭⎬⎫x ∈N *⎪⎪12x∈Z 中含有的元素个数为( )．考向二 集合间的基本关系【例2】已知集合A ＝{x |0<x ≤4}，B ＝(－∞，a )，若A ⊆B ，则实数a 的取值范围是________.【训练2】已知集合A ＝{x |－2≤x ≤7}，B ＝{x |m ＋1<x <2m －1}，若B ⊆A ，求实数m 的取值范围．考向三 集合的基本运算【例3】►(1)(2012·安徽)设集合A ＝{x |－3≤2x －1≤3}，集合B 为函数y ＝lg(x －1)的定义域，则A ∩B ＝( )．A ．(1,2)B ．[1,2]C ．[1,2)D ．(1,2](2)(2012·山东)已知全集U ＝{0,1,2,3,4}，集合A ＝{1,2,3}，B ＝{2,4}，则(∁U A )∪B 为( )． A ．{1,2,4} B ．{2,3,4} C ．{0,2,4}D ．{0,2,3,4}(3)设全集U ＝{1,2,3,4,5,6}，集合A ＝{1,2,4}，B ＝{3,4,5}，则图中的阴影部分表示的集合为( )．A ．{5}B ．{4}C．{1,2} D．{3,5}基础演练1.已知集合A＝{x|x2－x－2<0}，B＝{x|－1<x<1}，则()．A．A B B．B AC．A＝B D．A∩B＝∅2．设全集U＝{1,2,3,4,5,6}，集合P＝{1,2,3,4}，Q＝{3,4,5}，则P∩(∁U Q)＝()．A．{1,2,3,4,6} B．{1,2,3,4,5}C．{1,2,5} D．{1,2}3．设集合U＝{x|x<5，x∈N*}，M＝{x|x2－5x＋6＝0}，则∁U M＝()．A．{1,4} B．{1,5}C．{2,3} D．{3,4}4.若集合A＝{x||x|>1，x∈R}，B＝{y|y＝2x2，x∈R}，则(∁R A)∩B＝()．A．{x|－1≤x≤1} B．{x|x≥0}C．{x|0≤x≤1} D．∅5．设集合A＝{－1,1,3}，B＝{a＋2，a2＋4}，A∩B＝{3}，则实数a＝________. 6．集合A＝{x∈R||x－2|≤5}中的最小整数为________．7．若集合A＝{－1,3}，集合B＝{x|x2＋ax＋b＝0}，且A＝B，求实数a，b.第2讲函数及其表示必记考点1．函数的概念一般地，设A，B是两个非空数集，如果按照某种确定的对应关系f，使对于集合A中的任意一个数x，在集合B中都有唯一确定的数f(x)与之对应；那么就称：f：A→B为从集合A到集合B 的一个函数．记作.2．函数的三要素函数由、、三个要素构成，对函数y＝f(x)，x∈A，其中(1)定义域：．(2)值域：．(3)两个函数就相同: .3．函数的表示方法表示函数的常用方法有：解析法、图象法、列表法．4．分段函数若函数在其定义域内，对于定义域内的不同取值区间，有着不同的对应法则，这样的函数通常叫做分段函数．分段函数虽然由几部分组成，但它表示的是一个函数．考向一函数的定义【例1】(1)下列各图形中是函数图象的是()．2．下列各组函数表示相同函数的是()．A．f(x)＝x2，g(x)＝(x)2B．f(x)＝1，g(x)＝x2C．f(x)＝⎩⎪⎨⎪⎧x，x≥0，－x，x<0，g(t)＝|t|D．f(x)＝x＋1，g(x)＝x2－1x－1考向二 求函数的定义域、值域【例2】►(1) 函数y ＝x ＋1x 的定义域为________．(2)函数y ＝x －3x ＋1的值域为________．(3) 设函数f (x )＝41－x ，若f (a )＝2，实数a ＝________.考向三 分段函数及其应用【例3】(1) 设函数f (x )＝⎩⎪⎨⎪⎧x 2＋1，x ≤1，2x ，x >1，则f (f (3))＝( )．A.15 B ．3 C.23D.139(2)设f (x )＝⎩⎪⎨⎪⎧1，x >0，0，x ＝0，－1，x <0，g (x )＝⎩⎪⎨⎪⎧1，x 为有理数，0，x 为无理数，则f (g (π))的值为( )．A ．1B ．0C ．－1D ．π(3)已知函数f (x )＝⎩⎪⎨⎪⎧2x＋1，x ＜1，x 2＋ax ，x ≥1，若f (f (0))＝4a ，则实数a 等于( )．A.12 B.45 C ．2 D ．9基础演练1．函数f (x )＝11－x ＋lg(1＋x )的定义域是( )．A ．(－∞，－1)B ．(1，＋∞)C ．(－1,1)∪(1，＋∞)D ．(－∞，＋∞)2.下列各组函数中，表示同一函数的是( )． A ．f (x )＝x ，g (x )＝(x )2 B ．f (x )＝x 2，g (x )＝(x ＋1)2 C ．f (x )＝x 2，g (x )＝|x |D ．f (x )＝0，g (x )＝x －1＋1－x3．设函数f (x )＝⎩⎨⎧x ，x ≥0，－x ，x <0，若f (a )＋f (－1)＝2，则a ＝( )．A ．－3B ．±3C ．－1D ．±14．函数f (x )＝lg 1－x 2的定义域为________．5．(2013·皖南八校联考)已知f (x )＝⎩⎪⎨⎪⎧2－x，x ≤0，log 2x ，x >0，则f ⎣⎡⎦⎤f ⎝⎛⎭⎫－12＝________. 6.已知f (x )是二次函数，若f (0)＝0，且f (x ＋1)＝f (x )＋x ＋1.求函数f (x )的解析式.第3讲 函数的性质必记考点 1．函数的单调性 (1)单调函数的定义设函数f (x )的定义域为I ，如果对于定义域I 内某个区间D 上的任意两个自变量x 1，x 2，当x 1＜x 2时，①若 ，则f (x )在区间D 上是增函数；②若 ，则f (x )在区间D 上是减函数．(2)单调区间的定义若函数f (x )在区间D 上是 或 ，则区间D 叫做f (x )的单调区间．(3)用定义判断函数单调性的步骤: . 2. 函数的奇偶性(1)定义：如果对于函数f (x )的定义域内任意一个x ，都有 ，那么函数f (x )就叫做偶函数．如果对于函数f (x )的定义域内任意一个x ，都有 ，那么函数f (x )就叫做奇函数．(2)性质:奇函数的图象关于 对称;偶函数的图象关于 对称．考向一 确定函数的单调性或单调区间【例1】(1)下列函数中，在区间(0，＋∞)上为增函数的是( )．A ．y ＝ln(x ＋2)B ．y ＝－x ＋1C ．y ＝⎝⎛⎭⎫12xD ．y ＝x ＋1x(2)函数y ＝－x 2＋2x －3(x <0)的单调增区间是( )．A ．(0，＋∞)B ．(－∞，1]C ．(－∞，0)D ．(－∞，－1]考向二 函数单调性的应用【例2】(1)若函数f (x )＝4x 2－mx ＋5在[－2，＋∞)上递增，在(－∞，－2]上递减，则f (1)＝________. (2) 函数y ＝f(x)在R 上为增函数，且f(2m)>f(－m ＋9)，则实数m 的取值范围是 .考向三 求函数的最值【例3】函数f (x )＝2xx ＋1在[1,2]上的最大值和最小值分别是________．考向四 判断函数的奇偶性【例4】判断下列函数的奇偶性： (1)f (x )＝x 3－2x ；(2)f (x )＝x 2－1＋1－x 2；(3)f (x )＝(x －1)－ 1＋x1－x.考向五 函数奇偶性的应用【例5】(1)函数f (x )＝(x ＋a )(x －4)为偶函数，则实数a ＝________.(2) 设函数f (x )＝(x ＋1)(x ＋a )x 为奇函数，则a ＝________. (3) 设f (x )为定义在R 上的奇函数．当x ≥0时，f (x )＝2x＋2x ＋b (b 为常数)，则f (－1)＝ ．基础演练1．定义在R 上的函数f (x )对任意两个不相等的实数a ，b ，总有f (a )－f (b )a －b>0，则必有( )．A ．函数f (x )先增后减B ．f (x )是R 上的增函数C ．函数f (x )先减后增D ．函数f (x )是R 上的减函数2．函数y ＝f (x )在R 上为减函数，且f (2m )>f (－m ＋9)，则实数m 的取值范围是 .3．下列函数中，在(0，＋∞)上单调递增的函数是( )．A ．y ＝1xB ．y ＝|x |＋1C ．y ＝－x 2＋1D ．y ＝－2x ＋14．已知f (x )＝x 2－2mx ＋6在(－∞，－1]上是减函数，则m 的范围为________．5．已知函数f (x )为定义在区间[－1,1]上的增函数，则满足f (x )<f ⎝⎛⎭⎫12的实数x 的取值范围为________． 6.下列函数是偶函数的是( )．A ．y ＝xB ．y ＝2x 2－3C ．y ＝1xD ．y ＝x 2，x ∈[0,1]7. 设偶函数f (x )的定义域为R ，当x ∈[0，＋∞)时，f (x )是增函数，则f (－2)，f (π)，f (－3)的大小关系是 .8. 设f (x )是定义在R 上的奇函数，当x ≤0时，f (x )＝2x 2－x ，则f (1)＝________.9．已知函数y ＝f (x )是偶函数，其图象与x 轴有四个交点，则方程f (x )＝0的所有实根之和是________． 10．若f (x )＝x 2＋bx ＋c ，且f (1)＝0，f (3)＝0.(1)求b 与c 的值；(2)试证明函数f (x )在区间(2，＋∞)上是增函数．第4讲 指数与指数函数必记考点1．指数与指数运算 (1)根式的概念若x n ＝a ，则x 叫 ，.式子na 叫做根式，这里n 叫做根指数，a 叫做被开方数．即x n＝a ⇒⎩⎨⎧x ＝n a (当n 为奇数且n ∈N *时)，x ＝±n a (当n 为偶数且n ∈N *时).(2)根式的性质①(na )n ＝ .②当n 为奇数时，na n＝ ；当n 为偶数时，na n＝|a |＝⎩⎪⎨⎪⎧a (a ≥0)－a (a <0).(3)分数指数幂的含义正分数指数幂a m n ＝na m (a >0，m ，n ∈N *，n >1)．负分数指数幂a －m n ＝1a m n ＝1na m (a >0，m ，n ∈N *，n >1)．(4)幂指数的运算性质a r ·a s ＝ rs aa= (a r )s ＝ (ab )r ＝2．指数函数的图象与性质考向一 指数幂的化简与求值【例1】化简下列各式： (1)[(0.06415)－2.5]23－ 3338－π0；(2) 2132a b ·(－31132a b )÷156613a b(3)a ·3a 25a ·3a考向二 指数函数的性质【例2】(1)方程2x －2＋x ＝0的解的个数是________． (2) 下列各式比较大小正确的是( )． A ．1.72.5>1.73 B ．0.6－1>0.62C ．0.8－0.1>1.250.2 D ．1.70.3<0.93.1(3)已知函数f (x )＝2x －12x ＋1，①讨论f (x )的奇偶性；②讨论f (x )的单调性．⎝⎛⎭⎫21412－⎝⎛⎭⎫－350－⎝⎛⎭⎫827－13＝________. 已知函数f (x )＝4＋a x －1(a ＞0且a ≠1)的图象恒过定点P ，则点P 的坐标是( )．函数y ＝1－3x 的定义域为________。
集合的概念与运算
分配律
定义
对于任意三个集合A、B和C，如果A∪(B∩C)=(A∪B)∩(A∪C)和 A∩(B∪C)=(A∩B)∪(A∩C)，则称集合的运算满足分配律。
解释
分配律意味着并集和交集运算可以分配给括号内的并集和交集运算。 即，括号内的并集和交集运算的结果可以与外部的并集和交集运算 的结果进行交换。
伍 集合的应用
集合的元素
元素可以是具体的， 如苹果、汽车等；也 可以是抽象的，如数 字、图形等。 元素是构成集合的基 本单位，可以是任何 对象或实体。
并集
并集是将两个集合中 的所有元素合并到一 个新的集合中。 并集运算可以用符号 “∪”表示。
交集
交集运算可以用符号“∩”表示。 交集是两个集合中共有的元素组成的集合。
壹
集合的概念与运算
目录 CONTENTS
0 1 集合的基本概念
0 4 集合的应用
0 2 集合的运算
0 5 集合运算的注意事项
0 3 集合运算的性质
贰 集合的基本概念
集的定义
集合中的元素具有确定性、 互异性和无序性。 集合是由确定的、互不相 同的元素所组成的总体。
集合的表示方法
将集合中的元素一一列举出 来，用大括号括起来。 列举法 通过描述集合中元素的共同 特征，用大括号括起来。 描述法
交集是指两个或多个集合中共有的元素的集合，即同时属于A和B的元素组成的集合。 交集的表示方法为A∩B，其中A和B为两个集合。 交集的性质包括交换律、结合律和分配律。
差集
差集是指属于A但不属于B的元素的集合，即所有属于A但不属于B的元素组成的集合。 差集的表示方法为A−B，其中A和B为两个集合。 差集的性质包括反身律、对称律和传递律。
解释
离散数学 第1章 集合的基本概念和运算
B A ( x) ( x B x A)
例：设A={1,2,3,4,5,6,}, B={2,4,5,}及C={1，2，3，4，5} 定义3.1.2（外延性原理）设A，B为集合，如果B⊆A且A⊆B， 则称A与B相等，记作A=B。相等的符号化表示为
x 则 x A B或x A C ， A且x B或x A且x C ，即 x A且x B C, 于是x A ( B C ) 所以 ( A B) ( A C ) A ( B C ) 因此 ( A B) ( A C ) A ( B C )
离散数学
第一章 集合的基本集合的基本概念和运算
1.1 1.2 1.3 1.4 集合的基本概念 集合的基本运算 集合中元素的计数 笛卡尔乘积
1.1 集合的基本概念
集合是不能精确定义的基本的数学概念，直观地讲，集合是 由某些可以相互区别的事物汇集在一起所组成的整体。对于给定 的集合和事物，应该可以断定这个特定的事物是否属于这个集合。 如果属于，就称它为这个集合的元素。 集合通常用大写的英文字母来表示。 集合有两种表示方法：枚举法和谓词表示法。前一种方法是 将集合中的所有元素罗列出来，元素之间用逗号隔开，并把它们 用花括号括起来。例如 A {a, b, c} ， {1, 2, 3, ...}， {春， 秋， }，都是合法的表示。 C 夏， 冬 B 谓词表示法是用谓词来概括集合中元素的属性，例如 2 } F D {x | x是学生 ， {x | x是整数 ， {x | x R x 1 0} } E 一般的 A={x︱R(x)} R(x)表示x具有性质R，表示任何谓词 集合的元素是彼此不同的，如果同一个元素在集合中多次出现 应该认为是一个元素。集合的元素也是无序的，元素的排列顺序 对集合没有影响。
1、集合的概念与运算(一)
诸城繁华中学高三数学文科第一轮复习讲义1 第一章《集合与简易逻辑》§1.1 集合的概念和运算（一）【复习目标】1． 了解集合中元素的三种特性，正确使用集合的符号和语言表达数学问题；2． 分清集合中的两种关系，即元素与集合关系、集合与集合的关系；3． 了解空集的意义，在解题中强化空集的意识。
【重点难点】集合语言的正确、准确理解；熟练进行集合的基本运算【知识回顾】1、基本概念：集合、元素；有限集、无限集；空集、全集；2、集合的表示法： 、 、 .3、集合元素的特征： 、 、 .4、集合与元素的关系： 。
【课前预习】1． 数0与空集φ的关系是 （ ）A ．0φ∈B ．0φ=C ．{0}φ=D ．0φ∉2． 集合M=8|,,3y y x y Z x ⎧⎫=∈⎨⎬+⎩⎭的元素个数是 （ ） A ．2个 B ．4个 C ．6个 D ．8个 3． 用适当符号（,,,,∈∉=刭）填空： π Q ；{3.14} Q ；N N *；{|21,}x x k k Z =+∈ {|21,}x x k k Z=-∈； *{|21,}x x k k N =+∈ *{|21,}x x k k N =-∈. 4． 用描述法表示下列集合（1） 由直线y=x+1上所有点的坐标组成的集合 ；（2） {0，－1，－4，－9，－16，－25，－36，－49} ；5． 设集合M=1{|,}24k x x k Z =+∈，N=1{|,}42k x x k Z =+∈，则 （ ） A ．M=N B ．M ØN C ．M ÙN D ．M ⋂N=φ6． 若A ⋂B=B ，，则A B （填,⊆⊇）；若A ⋃B=B ，则A B. 【典型例题】例1 已知集合M={|3,}x x n n Z =∈，N={|31,}x x n n Z =+∈，P={|31,}x x n n Z =-∈，且,,a M b N c P ∈∈∈，设d a b c =-+，则A ．d M ∈B ．d N ∈C ．d P ∈D ．以上都不正确第1课：§1.1 集合的概念和运算（一）- 2 - 例2 已知集合2{|210,,}x ax x a R x R ++=∈∈（1） 若A 中只有一个元素，求a 的值；（2） 若A 中至多有一个元素，求a 的取值范围。
总复习《第01讲 集合的概念与运算》
设A={1，2}，B={0，2}，则 A B 的 所有元素之和为 .
高中数学总复习
第1讲 集合的概念与运算
浙江省嵊州长乐中学
一.概念的理解
集合符号
A x p ( x)
yx
. .
的理解.
研究对象
对象满足的条件
例题1.已知A={y| 则A∩B= 变式1.若A={(x,y)| 则A∩B= 变式2.若A={ y| y 则A∩B=
}, B={y| y
x
},
y x }, B={(x,y)| y x }, x
二.重视空集的“参与”.
例题3. 作业第10题(2)和第7题.
A= 3,5
B x ax 1 0
问题1. 集合B有几个元素？
问题2. 满足
B A 的集合B有几种情况？
三.集合创新题.
例题4. 定义集合运算：
A B z z xy, x A, y B
}, B={ x| 合符号
A x p ( x)
x y
的理解.
研究对象
对象满足的条件
例题2. 讲义P2例1（2）.
x
y
0
1 1
2 2 1
0
0
1 2
1 0
2 1 0
一.概念的理解
2. 子集、真子集和空集.
(1) A中有n个元素： A的子集有 2n 个； A的真子集有 2n-1 个； A的非空真子集有 2n-2 个； (2) 空集是任何集合的子集. 空集是任何非空集合的真子集.
高中数学中集合的概念与运算的解题归纳
高中数学中集合的概念与运算的解题归纳-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN§1.1 集合的概念与运算一、知识导学1.集合：一般地，一定范围内某些确定的、不同的对象的全体构成一个集合.2.元素：集合中的每一个对象称为该集合的元素，简称元.3.子集：如果集合A 的任意一个元素都是集合B 的元素（若A a ∉则B a ∈），则称 集合A 为集合B 的子集，记为A ⊆B 或B ⊇A ；如果A ⊆B ，并且A ≠B ，这时集合A 称为集合B 的真子集，记为A B 或B A.4.集合的相等：如果集合A 、B 同时满足A ⊆B 、B ⊇A ，则A=B.5.补集：设A ⊆S ，由S 中不属于A 的所有元素组成的集合称为S 的子集A 的补集，记为 A C s .6.全集：如果集合S 包含所要研究的各个集合，这时S 可以看做一个全集，全集通常 记作U.7.交集：一般地，由所有属于集合A 且属于B 的元素构成的集合，称为A 与B 的交集，记作A ⋂B.8.并集：一般地，由所有属于集合A 或者属于B 的元素构成的集合，称为A 与B 的并 集，记作A ⋃B.9.空集：不含任何元素的集合称为空集，记作Φ.10.有限集：含有有限个元素的集合称为有限集.11.无限集：含有无限个元素的集合称为无限集.12.集合的常用表示方法：列举法、描述法、图示法（Venn 图）.13.常用数集的记法：自然数集记作N ，正整数集记作N +或N *，整数集记作Z ，有理数集记作Q ，实数集记作R .二、疑难知识导析1.符号⊆，，⊇，，=，表示集合与集合之间的关系，其中“⊆”包括“”和“=”两种情况，同样“⊇”包括“”和“=”两种情况.符号∈，∉表示元素与集合之间的关系.要注意两类不同符号的区别.2.在判断给定对象能否构成集合时，特别要注意它的“确定性”，在表示一个集合时，要特别注意它的“互异性”、“无序性”.3.在集合运算中必须注意组成集合的元素应具备的性质.4.对由条件给出的集合要明白它所表示的意义，即元素指什么，是什么范围．用集合表示不等式（组）的解集时，要注意分辨是交集还是并集，结合数轴或文氏图的直观性帮助思维判断．空集是任何集合的子集，但因为不好用文氏图形表示，容易被忽视，如在关系式中，B =Φ易漏掉的情况.5.若集合中的元素是用坐标形式表示的，要注意满足条件的点构成的图形是什么，用数形结合法解之.6.若集合中含有参数，须对参数进行分类讨论，讨论时既不重复又不遗漏.7.在集合运算过程中要借助数轴、直角坐标平面、Venn 图等将有关集合直观地表示出来.8.要注意集合与方程、函数、不等式、三角、几何等知识的密切联系与综合使用.9.含有n 个元素的集合的所有子集个数为：n 2，所有真子集个数为：n 2-1三、经典例题导讲[例1] 已知集合M={y |y =x 2＋1,x∈R },N={y|y =x ＋1,x∈R }，则M∩N=（ ）A ．（0，1），（1，2）B ．{（0，1），（1，2）}C ．{y|y=1,或y=2}D ．{y|y≥1}错解：求M∩N 及解方程组⎩⎨⎧+=+=112x y x y 得⎩⎨⎧==10y x 或 ⎩⎨⎧==21y x ∴选B错因：在集合概念的理解上，仅注意了构成集合元素的共同属性，而忽视了集合的元素是什么．事实上M 、N 的元素是数而不是实数对(x,y )，因此M 、N 是数集而不是点集,M 、N 分别表示函数y =x 2＋1(x∈R )，y =x ＋1(x∈R )的值域，求M∩N 即求两函数值域的交集．正解：M={y |y =x 2＋1,x∈R }={y |y ≥1}， N={y|y=x ＋1,x∈R }={y|y∈R }．∴M∩N={y |y ≥1}∩{y|(y∈R)}={y |y ≥1}, ∴应选D ．注：集合是由元素构成的，认识集合要从认识元素开始，要注意区分{x |y =x 2＋1}、{y |y =x 2＋1,x ∈R }、{(x ,y )|y =x 2＋1,x ∈R }，这三个集合是不同的．[例2] 已知A={x |x 2－3x ＋2=0},B={x |ax －2=0}且A∪B=A，求实数a 组成的集合C ． 错解：由x 2－3x ＋2=0得x =1或2．当x =1时，a =2， 当x =2时，a=1．错因：上述解答只注意了B 为非空集合，实际上，B=时，仍满足A∪B=A .当a =0时，B=，符合题设，应补上，故正确答案为C={0，1，2}．正解：∵A∪B=A ∴B A 又A={x |x 2－3x ＋2=0}={1，2}∴B=或{}{}21或 ∴C={0，1，2}[例3]已知m ∈A,n ∈B, 且集合A={}Z a a x x ∈=,2|，B={}Z a a x x ∈+=,12|，又C={}Z a a x x ∈+=,14|，则有： （ ）A ．m +n ∈A B. m +n ∈B C.m +n ∈C D. m +n 不属于A ，B ，C 中任意一个错解：∵m ∈A ，∴m =2a ,a Z ∈,同理n =2a +1,a ∈Z, ∴m +n =4a +1,故选C错因是上述解法缩小了m +n 的取值范围.正解：∵m ∈A, ∴设m =2a 1,a 1∈Z , 又∵n B ∈,∴n =2a 2+1,a 2∈ Z ,∴m +n =2(a 1+a 2)+1,而a 1+a 2∈ Z , ∴m +n ∈B, 故选B.[例4］ 已知集合A={x|x 2－3x －10≤0}，集合B={x|p ＋1≤x≤2p－1}．若BA ，求实数p 的取值范围．错解：由x 2－3x －10≤0得－2≤x≤5． 欲使B A ，只须3351212≤≤-⇒⎩⎨⎧≤-+≤-p p p ∴ p 的取值范围是－3≤p≤3.错因：上述解答忽略了"空集是任何集合的子集"这一结论，即B=时，符合题设． 正解：①当B≠时，即p ＋1≤2p－1p≥2.由B A 得：－2≤p＋1且2p －1≤5.由－3≤p≤3.∴ 2≤p≤3②当B=时，即p ＋1>2p －1p ＜2.由①、②得：p≤3.点评：从以上解答应看到：解决有关A∩B=、A∪B=，A B 等集合问题易忽视空集的情况而出现漏解，这需要在解题过程中要全方位、多角度审视问题．[例5] 已知集合A={a,a ＋b,a ＋2b}，B={a,ac,ac 2}．若A=B ，求c 的值．分析：要解决c 的求值问题，关键是要有方程的数学思想，此题应根据相等的两个集合元素完全相同及集合中元素的确定性、互异性，无序性建立关系式．解：分两种情况进行讨论．（1）若a ＋b=ac 且a ＋2b=ac 2，消去b 得：a ＋ac 2－2ac=0，a=0时，集合B 中的三元素均为零，和元素的互异性相矛盾，故a≠0．∴c 2－2c ＋1=0，即c=1，但c=1时，B 中的三元素又相同，此时无解．（2）若a ＋b=ac 2且a ＋2b=ac ，消去b 得：2ac 2－ac －a=0，∵a≠0，∴2c 2－c －1=0，即(c －1)(2c ＋1)=0，又c≠1，故c=－21． 点评：解决集合相等的问题易产生与互异性相矛盾的增解，这需要解题后进行检验. [例6] 设A 是实数集，满足若a∈A，则a -11∈A ，1≠a 且1∉A. ⑴若2∈A，则A 中至少还有几个元素？求出这几个元素.⑵A 能否为单元素集合？请说明理由.⑶若a∈A，证明：1－a1∈A. ⑷求证：集合A 中至少含有三个不同的元素. 解：⑴2∈A ⇒ －1∈A ⇒21∈A ⇒ 2∈A∴ A 中至少还有两个元素：－1和21 ⑵如果A 为单元素集合，则a ＝a -11 即12+-a a ＝0该方程无实数解，故在实数范围内，A 不可能是单元素集⑶a∈A ⇒ a -11∈A ⇒ a --1111∈A ⇒111---a a ∈A ，即1－a 1∈A ⑷由⑶知a∈A 时，a-11∈A， 1－a 1∈A .现在证明a,1－a 1, a -11三数互不相等.①若a=a -11,即a2-a+1=0 ，方程无解，∴a ≠a-11 ②若a=1－a 1，即a 2-a+1=0，方程无解∴a ≠1－a1 ③若1－a 1 =a -11，即a2-a+1=0，方程无解∴1－a 1≠a -11. 综上所述，集合A 中至少有三个不同的元素.点评：⑷的证明中要说明三个数互不相等，否则证明欠严谨.[例7] 设集合A={a |a =12+n ,n ∈N +}，集合B={b |b =542+-k k ,k ∈N +}，试证：A B ．证明：任设a ∈A，则a =12+n =(n ＋2)2－4(n ＋2)＋5 (n ∈N +), ∵ n∈N*，∴ n ＋2∈N*∴ a∈B 故 ①显然，1{}*2,1|Nn n a a A ∈+==∈，而由 B={b |b =542+-k k ,k ∈N +}={b |b =1)2(2+-k ，k ∈N +}知1∈B，于是A≠B②由①、② 得A B ．点评：（1）判定集合间的关系，其基本方法是归结为判定元素与集合之间关系．（2）判定两集合相等，主要是根据集合相等的定义．四、典型习题导练1．集合A={x|x 2－3x －10≤0，x ∈Z}，B={x|2x 2－x －6＞0， x ∈ Z}，则A ∩B 的非空真子集的个数为（ ）A ．16B ．14C ．15D ．322．数集{1，2，x 2－3}中的x 不能取的数值的集合是（ ）A ．{2，-2 }B ．{－2，－5 }C ．{±2，±5 }D ．{5，－5}3. 若P={y|y=x 2,x∈R}，Q={y|y=x 2＋1,x∈R}，则P∩Q 等于（ ）A ．PB ．QC ．D ．不知道4. 若P={y|y=x 2,x∈R}，Q={(x ，y)|y=x 2,x∈R}，则必有（ ）A ．P∩Q=B ．P QC ．P=QD ．PQ5．若集合M ＝｛11|<xx ｝，N ＝{x |2x ≤x }，则M N ＝ （ ） A ．}11|{<<-x x B ．}10|{<<x xC ．}01|{<<-x xD ．∅6.已知集合A={x|x 2＋(m ＋2)x ＋1=0,x∈R }，若A∩R ＋=，则实数m 的取值范围是_________．7.（06高考全国II 卷）设a R ∈，函数2()22.f x ax x a =--若()0f x >的解集为A ，{}|13,B x x A B φ=<<≠，求实数a 的取值范围。
第一节 集合概念及其运算
第一章 集合与常用逻辑用语【知识导读】【方法点拨】1. 集合蕴涵着一种数学思想即对应的思想，数学的统一靠集合的语言，语言的形式化、符号化为现代数学的逻辑结构及相互关系提供了较好的表达、组织方式．在复习中应强调渗透和运用集合的语言、思想和方法．2. 逻辑体现了一种数学思想，即转化的思想．命题的转化有等价和不等价的，主要依据四个命题的关系和充分性、必要性．3.已知简单命题的真假而判断由其构成的复合命题的真假，主要是依据真值表而不是命题的具体内容，这种判断实际上是一种命题演算，是抽象的判断，而不是经验的判断． 4. 判断全称命题是假命题，只要在限定的集合M 中找到一个0x x =使)(0x p 不成立；要判断一个特称命题是真命题，只要在限定的集合M 中至少找到一个0x x =使)(0x p 为真．全称量词的否定是存在量词，存在量词的否定是全称量词；全称命题的否定是特称命题，特称命题的否定是全称命题．第1课 集合的概念及运算【考点导读】1. 了解集合的含义，体会元素与集合的属于关系；能选择自然语言，图形语言，集合语言描述不同的具体问题，感受集合语言的意义和作用．2. 理解集合之间包含与相等的含义，能识别给定集合的子集；了解全集与空集的含义．3. 理解两个集合的交集与并集的含义，会求两个集合的交集与并集；理解在给定集合中一个子集补集的含义，会求给定子集的补集；能使用文氏图表达集合的关系及运算，体会直观图示对理解抽象概念的作用．4. 集合问题常与函数，方程，不等式有关，其中字母系数的函数，方程，不等式要复杂一些，综合性较强，往往渗透数形思想和分类讨论思想． 【基础练习】1.集合{(,)02,02,,}x y x y x y Z ≤≤≤<∈用列举法表示{(0,0),(0,1),(1,0),(1,1),(2,0),(2,1)}．2.设集合{21,}A x x k k Z ==-∈，{2,}B x x k k Z ==∈，则A B ⋂=∅．3.已知集合{0,1,2}M =，{2,}N x x a a M ==∈，则集合M N ⋂=____________． 4.设全集{1,3,5,7,9}I =，集合{1,5,9}A a =-，{5,7}I A =ð，则实数a 的值为____8或2___．5. 已知集合[1,4)A =,(,)B a =-∞，若A B A ⋂=，则实数a 的取值范围____________． 6. 已知集合{|10}M x x =+<,1{|0}N x x=>，则图中【范例解析】例1. 设,a b R ∈，集合{1,,}{0,,}ba b a b a+=，求b a -的值.分析：利用集合中元素互异性和集合相等性质，得到集合中对应元素的关系.解：由题知，0a ≠， 0a b +=，则1b a =-，所以 1baa b ⎧=⎪⎨⎪=⎩，解得11a b =-⎧⎨=⎩，所以2b a -=.点评：本题以集合中元素的性质为载体，考察学生对条件的把握分析能力，以寻找解题的突破口. 例2.已知集合{026}A x ax =<+≤，{124}B x x =-<≤.（1） 若A B A ⋂=，求实数a 的取值范围；（2） 集合A ，B 能否相等？若能，求出a 的值；若不能，请说明理由. 分析：（1）对a 进行分类讨论，利用数轴求a 的取值范围. 解： {124}B x x =-<≤1{2}2x x =-<≤，{026}A x ax =<+≤{24}x ax =-<≤. ①当0a =时，A R =，所以A B ⊆不可能；第6题{0,2} [4,)+∞②当0a >时，24{}A x x a a =-<≤，若A B ⊆，则21,24 2.a a ⎧-≥-⎪⎪⎨⎪≤⎪⎩解得4a ≥.③当0a <时，42{}A x x a a =≤<-，若A B ⊆，则41,22 2.a a⎧>-⎪⎪⎨⎪-≤⎪⎩解得8a <-.综上所得，a 的取值范围为(,8)[4,)-∞-⋃+∞.(2)分析一：求出满足B A ⊆时a 的取值范围，再与（1）取交集.解法一：①当0a =时，A R =，所以B A ⊆成立；②当0a >时，24{}A x x a a =-<≤，若B A ⊆，则21,24 2.a a ⎧-≤-⎪⎪⎨⎪≥⎪⎩解得02a <≤.③当0a <时，42{}A x x a a =≤<-，若B A ⊆，则41,22 2.a a⎧≤-⎪⎪⎨⎪->⎪⎩解得10a -<<.综上，B A ⊆时，12a -<≤.A B A B =⇔⊆ 且B A ⊆，∴若A B =，则(1,2]a ∈-且(,8)[4,)a ∈-∞-⋃+∞，矛盾.所以，集合A 与B 不可能相等.分析二：利用两个相等集合中元素的对应关系，建立等量关系. 解法二：①当0a =时，A R =，所以B A ≠；②当0a >时，24{}A x x a a =-<≤，若B A =，则21,24 2.a a⎧-=-⎪⎪⎨⎪=⎪⎩无解.③当0a <时，42{}A xx a a=≤<-，若B A =，显然不成立. 综上，集合A 与B 不可能相等.点评：在解决两个数集关系问题时，应合理运用数轴帮助分析与求解.另外，在解含参数的不等式（方程）时，要对参数进行分类讨论，分类时要遵循不重不漏的分类原则，然后对每一类情况都要给出问题的解答.例3.（1）已知R 为实数集，集合2{320}A x x x =-+≤.若R B A R ⋃=ð，{01R B A x x ⋂=<<ð或23}x <<，求集合B ；（2）已知集合{,0}M a =，2{30,}N x x x x Z =-<∈，且{1}M N ⋂=，记P M N =⋃，写出集合P的所有子集.分析：（1）先化简集合A ，由R B C A R ⋃=可以得出A 与B 的关系；最后，由数形结合，利用数轴直观地解决问题.（2）求出N ，由{1}M N ⋂=，可知1M ∈，解得a ，进而求出P .解：（1）{12}A x x =≤≤ ，{1R C A x x ∴=<或2}x >.又R B C A R ⋃=，R A C A R ⋃=，可得A B ⊆. 而{01R B C A x x ⋂=<<或23}x <<，∴{01x x <<或23}x <<.B ⊆ 借助数轴可得B A =⋃{01x x <<或23}x <<{03}x x =<<.（2）由230x x -<，得03x <<；又x Z ∈，故{1,2}N =.由{,0}M a =且{1}M N ⋂=，可得1a =.{1,0}M ∴=，故P 的子集为：∅，{0}，{1}，{2}，{0,1}，{0,2}，{1,2}，{0,1,2}.点评：（1）研究数集的相互关系时，可通过数轴示意，借助直观性探求，易于理解.（2）含有n 个元素的集合，共有2n 个子集，21n-个真子集.另注意空集的情况.例4.已知函数2()f x x px q =++，集合{()}A x f x x ==，集合{[()]}B x f f x x ==. （1）求证：A B ⊆；（2）若{1,3}A =-，求集合B .分析：（1）要证明A B ⊆，根据定义，只要证A 中任一元素都是B 中的元素即可； （2）由{1,3}A =-，可以求出p ，q 的值，从而求出B .解：（1）设0x 是集合A 中的任一元素，即0x A ∈. {()}A x f x x ==，∴ 00()x f x =， 即有000[()]()f f x f x x ==.∴0x B ∈.故A B ⊆.（2） {1,3}A =-2{}x x px q x =++=，1∴-，3是方程2(1)0x p x q +-+=的两个根，∴1(1)(1)0,9(1)30,p q p q +-⋅-+=⎧⎨+-⋅+=⎩1,3.p q =-⎧∴⎨=-⎩2() 3.f x x x ∴=-- 因为集合B 中的元素是方程[()]f f x x =的根，也就是222(3)(3)3x x x x x ------=的根.方程整理得22(23)(3)0x x x ---=，解得1x =-{1B =-.点评：本题考查集合语言与集合思想在解决方程问题时的运用，在解答过程中，应脱去集合符号和抽象函数符号的“外衣”，显出本质的数量关系，要不断实施各种数学语言间的相互转换. 【反馈演练】1．设全集U =R ，集合M ={x | x >1}，P ={x | x 2>1}，则下列关系中正确的是（ C ） A ．M ＝P B ．P ÜM C ．M ÜP D ．U M P =∅ ð2．设集合{}2,1=A ，{}3,2,1=B ，{}4,3,2=C ，则()C B A =_________． 3．设P ，Q 为两个非空实数集合，定义集合P +Q =},5,2,0{},,|{=∈∈+P Q b P a b a 若}6,2,1{=Q ，则P +Q 中元素的个数是____8___个．4．已知集合A ＝{－1，3，2m －1}，集合B ＝{3，2m }．若B ⊆A ，则实数m ＝ 1 ． 5．若集合M ＝{0，l ，2}，N ＝{(x ，y )|x －2y ＋1≥0且x －2y －1≤0，x ，y ∈M }，则N 中元素的个数为 ______4____个．6．设f (n )＝2n ＋1(n ∈N )，P ＝{1，2，3，4，5}，Q ＝{3，4，5，6，7}，记P ∧＝{n ∈N |f (n )∈P }，Q ∧＝{n ∈N |f (n )∈Q }，则(P ∧∩N ðQ ∧)∪(Q ∧∩N ðP ∧)＝_____________. 7．若集合131,11,2,01A y y x x B y y x x ⎧⎫⎧⎫⎪⎪==-≤≤==-<≤⎨⎬⎨⎬⎩⎭⎪⎪⎩⎭，则A ∩B 等于[]1,1-．8．已知集合}1≤-=a x x A ，{}0452≥+-=x x x B ，若φ=B A ，则实数a 的取值范围是 .9．已知A ，B ，C 为三个集合，若C B B A ⋂=⋃，给出下列结论：①C A ⊆；②A C ⊆；③C A ≠；④φ=A ． 其中正确结论的有_______①______．提示：由A B B C = 知，,A B B A B C A B C ⊆⊆∴⊆⊆ ．10．已知集合2{20}A x x x =+-≤，{214}B x x =<+≤，2{0}C x x bx c =++>，若集合A ，B ，C满足()A B C ⋃⋂=∅，()A B C R ⋃⋃=，求b ，c 的值.解：由题知：{(1)(2)0}A x x x =-+≤{21}x x =-≤≤，{13}B x x =<≤.{23}A B x x ∴⋃=-≤≤.()A B C ⋃⋂=∅，()A B C R ⋃⋃=，()R C A B ∴=⋃ð.{2C x x ∴=<-或3}x >.又2{0}C x x bx c =++>，∴20x bx c ++=的两根为2-和3，即有420,930.b c b c -+=⎧⎨++=⎩解得1b =-，6c =-．11．设集合2{60}P x x x =--<，{23}Q x a x a =≤≤+.（1）若P Q P ⋃=，求实数a 的取值范围； （2）若P Q ⋂=∅，求实数a 的取值范围；{}4,2,1 {0,3} (2,3)（3）若{03}P Q x x ⋂=≤<，求实数a 的值.解：（1）由题意知：{23}P x x =-<<， P Q P ⋃=，Q P ∴⊆. ①当Q =∅时，得23a a >+，解得3a >．②当Q ≠∅时，得2233a a -<≤+<，解得10a -<<． 综上，(1,0)(3,)a ∈-⋃+∞．（2）①当Q =∅时，得23a a >+，解得3a >；②当Q ≠∅时，得23,3223a a a a ≤+⎧⎨+≤-≥⎩或，解得3532a a ≤-≤≤或．综上，3(,5][,)2a ∈-∞-⋃+∞．（3）由{03}P Q x x ⋂=≤<，则0a =．12．设集合2{40}A x x x =+=，22{2(1)10}B x x a x a =+++-=．（1）若A B B ⋂=，求a 的值； （2）若A B B ⋃=，求a 的值． 解：由题知：{0,4}A =-． （1）A B B ⋂= ，B A ∴⊆．①当B =∅时，224(1)4(1)0a a ∆=+--<，解得1a <-；②当{0}B =或{4}-时，224(1)4(1)0a a ∆=+--=，解得1a =-，此时，{0}B =，满足B A ∴⊆；③当{0,4}B =-时，22224(1)4(1)0,10,168(1)10.a a a a a ⎧∆=+-->⎪-=⎨⎪-++-=⎩综上所述，实数a 的取值范围是1a =或1a ≤-．（2）A B B ⋃= ，A B ∴⊆，故{0,4}B =-．即22224(1)4(1)0,10,168(1)10.a a a a a ⎧∆=+-->⎪-=⎨⎪-++-=⎩，解得1a =．。
第1讲 集合的概念与运算学生(新高一培优十六讲系列)
第1讲 集合的概念与运算[玩前必备]1.元素与集合的概念(1)集合：研究的对象统称为元素，把一些元素组成的总体叫作集合. (2)集合元素的特性：确定性、互异性. 2.元素与集合的关系(1)空集：不含任何元素的集合，记作∅.(2)非空集合：①有限集：含有有限个元素的集合. ②无限集：含有无限个元素的集合. 4.常用数集的表示符号 把有限集合中的所有元素都列举出来，写在花括号“{__}”内表示这个集合的方法. 6.描述法(1)集合的特征性质如果在集合I 中，属于集合A 的任意一个元素x 都具有性质p (x )，而不属于集合A 的元素都不具有性质p (x )，则性质p (x )叫做集合A 的一个特征性质. (2)特征性质描述法集合A 可以用它的特征性质p (x )描述为{x ∈I |p(x )}，它表示集合A 是由集合I 中具有性质p (x )的所有元素构成的.这种表示集合的方法，叫做特征性质描述法，简称描述法. 7.集合间的基本关系A B(或B A)8.集合的运算(1)如果一个集合包含了我们所要研究的各个集合的全部元素，这样的集合就称为全集，全集通常用字母U表示；[玩转典例]题型一集合的基本概念例1(大纲全国，1) 设集合A＝{1，2，3}，B＝{4，5}，M＝{x|x＝a＋b，a∈A，b∈B}，则M中元素的个数为()A.3B.4C.5D.6例2 已知集合A＝{m＋2,2m2＋m}，若3∈A，则m的值为________．[玩转跟踪]1.(新课标全国，1)已知集合A＝{1，2，3，4，5}，B＝{(x，y)|x∈A，y∈A，x－y∈A}，则B 中所含元素的个数为()A.3B.6C.8D.102.已知集合A是由a－2,2a2＋5a,12三个元素组成的，且－3∈A，求实数a.3.(探究与创新)设A 为实数集，且满足条件：若a ∈A ，则11－a∈A (a ≠1).求证： (1)若2∈A ，则A 中必还有另外两个元素； (2)集合A 不可能是单元素集.题型二 集合的表示方法例3 下面三个集合：A ＝{x |y ＝x 2＋1}；B ＝{y |y ＝x 2＋1}；C ＝{(x ，y )|y ＝x 2＋1}. 问：(1)它们是不是相同的集合？ (2)它们各自的含义是什么？例4 已知集合A ＝{x ∈R |ax 2＋2x ＋1＝0}，其中a ∈R .若1是集合A 中的一个元素，请用列举法表示集合A .[玩转跟踪]1.已知x ，y 为非零实数，则集合M ＝⎩⎨⎧m |m ＝x |x |＋y |y |＋⎭⎬⎫xy |xy |为( )A.{0,3}B.{1,3}C.{－1,3}D.{1，－3}2.(探究与创新)已知集合A ＝{x |ax 2－3x －4＝0，x ∈R }： (1)若A 中有两个元素，求实数a 的取值范围； (2)若A 中至多有一个元素，求实数a 的取值范围.题型三 集合间的基本关系例5 (2013·江苏，4)集合{－1，0，1}共有________个子集.例6 设集合⎭⎬⎫⎩⎨⎧∈+==Z k k x x M ，412|，⎭⎬⎫⎩⎨⎧∈+==Z k k x x N ，421|，则( ) A ．N M =B ．NM C ．MN D ．=N M I例7 已知集合A ＝{x |－3≤x ≤4}，B ＝{x |2m －1＜x ＜m ＋1}，且B ⊆A . 求实数m 的取值范围.[玩转跟踪]1.设M 为非空的数集，M ⊆{1,2,3}，且M 中至少含有一个奇数元素，则这样的集合M 共有( ) A ．6个B ．5个C ．4个D ．3个2.(2016·山东北镇中学、莱芜一中、德州一中4月联考)定义集合A －B ＝{x |x ∈A 且x ∉B },若集合M ＝{1,2,3,4,5},集合N ＝{x |x ＝2k －1,k ∈Z },则集合M －N 的子集个数为( ) A.2 B.3C.4D.无数个3.已有集合A ＝{x |x 2－4x ＋3＝0}，B ＝{x |mx －3＝0}，且B ⊆A ，求实数m 的集合.题型四 集合的基本运算例8 (2016·全国Ⅰ,1)设集合A ＝{x |x 2－4x ＋3<0},B ＝{x |2x －3>0},则A ∩B ＝( ) A.⎝⎛⎭⎫－3，－32 B.⎝⎛⎭⎫－3，32 C.⎝⎛⎭⎫1，32 D.⎝⎛⎭⎫32，3 例9 (2015·四川,1)设集合A ＝{x |(x ＋1)(x －2)＜0},集合B ＝{x |1＜x ＜3},则A ∪B ＝( ) A ．{x |－1＜x ＜3} B ．{x |－1＜x ＜1} C ．{x |1＜x ＜2} D ．{x |2＜x ＜3} 例10 (1)设全集U ＝R ，A ＝{x |x (x ＋3)<0}，B ＝{x |x <－1}，则图中阴影部分表示的集合为( )A ．{x |－3<x <－1}B ．{x |－3<x <0}C ．{x |－1≤x ＜0}D ．{x |x <－3}(2).(2011·江西，2)若集合A ＝{x |－1≤2x ＋1≤3}，B ＝⎩⎨⎧⎭⎬⎫x ⎪⎪x －2x ≤0，则A ∩B ＝( )A.{x |－1≤x ＜0}B.{x |0<x ≤1}∅C.{x |0≤x ≤2}D.{x |0≤x ≤1}例11 已知A ＝{x |2a ≤x ≤a ＋3}，B ＝{x |x ＜－1，或x ＞5}，若A ∩B ＝∅，求实数a 的取值范围.[玩转跟踪]1.(2016·安徽安庆市第二次模拟)若集合P ＝{x ||x |＜3,且x ∈Z },Q ＝{x |x (x －3)≤0,且x ∈N },则P ∩Q 等于( )A.{0,1,2}B.{1,2,3}C.{1,2}D.{0,1,2,3}2.如图，I 是全集，M 、P 、S 是I 的3个子集，则阴影部分所表示的集合是( )A.(M ∩P )∩SB.(M ∩P )∪SC.(M ∩P )∩(∁I S )D.(M ∩P )∪(∁I S )3.(探究与创新)已知集合A ＝{x |－2≤x ≤5}，B ＝{x |2a ≤x ≤a ＋3}，若A ∪B ＝A ，求实数a 的取值范围.[玩转练习]1．已知集合A ＝{y |y ＝|x |－1，x ∈R }，B ＝{x |x ≥2}，则下列结论正确的是( ) A ．－3∈A B ．3∉B C ．A ∩B ＝BD ．A ∪B ＝B2．设集合M ＝{－1,1}，N ＝⎩⎨⎧⎭⎬⎫x ⎪⎪1x<2，则下列结论中正确的是( ) A ．N M B ．M N C ．N ∩M ＝∅D ．M ∪N ＝R3．(2018·全国Ⅱ)已知集合A ＝{(x ，y )|x 2＋y 2≤3，x ∈Z ，y ∈Z }，则A 中元素的个数为() A ．9 B ．8 C ．5 D ．44.(2018·济南模拟)设全集U ＝R ，集合A ＝{x |x －1≤0}，集合B ＝{x |x 2－x －6<0}，则右图中阴影部分表示的集合为( )A ．{x |x <3}B ．{x |－3<x ≤1}C ．{x |x <2}D ．{x |－2<x ≤1}5．(2018·潍坊模拟)设集合A ＝N ，B ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪x x －3≤0，则A ∩B 等于( )A ．[0,3)B ．{1,2}C ．{0,1,2}D ．{0,1,2,3}6．(2017·全国Ⅱ)设集合A ＝{1,2,4}，B ＝{x |x 2－4x ＋m ＝0}．若A ∩B ＝{1}，则B 等于( ) A ．{1，－3} B ．{1,0} C ．{1,3} D ．{1,5}7．已知集合A ＝{x |－1<x <0}，B ＝{x |x ≤a }，若A ⊆B ，则a 的取值范围为( ) A ．(－∞，0] B ．[0，＋∞) C ．(－∞，0)D ．(0，＋∞)8.满足{a ，b }∪B ＝{a ，b ，c }的集合B 的个数是________.9.设集合A ＝{－1,1,3}，B ＝{a ＋2，a 2＋4}，A ∩B ＝{3}，则实数a 的值为________. 10.已知集合M ＝{－2,3x 2＋3x －4，x 2＋x －4}，若2∈M ，则满足条件的实数x 组成的集合为________.11.已知全集I ＝{2,3，a 2＋2a －3}，若A ＝{b,2}，∁I A ＝{5}，求实数a ，b .12.已知A ＝{x |x 2－3x ＋2＝0}，B ＝{x |ax －2＝0}，且A ∪B ＝A ，求实数a 组成的集合C .13.设全集为R ，集合A ＝{x |3≤x ＜6}，B ＝{x |2＜x ＜9}. (1)分别求A ∩B ，(∁R B )∪A ；(2)已知C ＝{x |a ＜x ＜a ＋1}，若C ⊆B ，求实数a 的取值构成的集合.14.已知集合A ＝{x |0＜x －a ≤5}，B ＝{x |－a2＜x ≤6}.(1)若A∩B＝A，求a的取值范围；(2)若A∪B＝A，求a的取值范围.。
高考数学总复习第1讲 集合的概念与运算
D．{1,2,3,4,6}
解：因为 A∪B＝{1,2,6}∪{2,4}＝{1,2,4,6}， 所以(A∪B)∩C＝{1,2,4,6}∩{1,2,3,4}＝{1,2,4}．
ห้องสมุดไป่ตู้
答案：B
4．(2017·北京卷)已知全集 U＝R，集合 A＝{x|x＜
－2 或 x＞2}，则∁UA＝(
)
A．(－2,2)
B．(－∞，－2)∪(2，＋∞)
点评：(1)用描述法表示集合，首先要搞清集合中代表 元素的含义，再看元素的限制条件，分清是数集、点集还 是其他类型的集合．
(2)解决含有参数的集合问题时，要注意集合中元素的 特征，并注意用互异性进行检验．
(3)分类讨论的思想方法常用于解决集合问题．
【变式探究】
1．(1)若集合 A＝{x∈R|ax2＋ax＋1＝0}中只有一个元素，
则 a 等于( )
A．4
B．2
C．0
D．0 或 2
(2)已知集合 A＝{m＋2,2m2＋m}，若 3∈A，则 m 的值
为
.
解：(1)当 a＝0 时，方程化为 1＝0，无解， 集合 A 为空集，不符合题意； 当 a≠0 时，由 Δ＝a2－4a＝0，解得 a＝4.
解：(2)因为 3∈A，所以 m＋2＝3 或 2m2＋m＝3， 若 m＋2＝3，解得 m＝1，此时 A＝{3,3}与集合中元素的 互异性矛盾，所以 m＝1，不符合题意； 若 2m2＋m＝3，解得 m＝1(舍去)或 m＝－23. 检验知 m＝－32满足题意． 故所求 m 的值为－32.
3．注意空集∅的特殊性，在解题时，若未能指明集合
非空时，要考虑空集的可能性，如 A⊆B，则有 A＝∅或 A≠∅
两种可能，解题时常常遗漏对空集的讨论，这一点应引起 重视．
第一讲 集合与命题
第一讲 集合与命题第一节 集合的概念与运算一、知识梳理1、集合：把某些能够确切指定的对象看作一个整体，这个整体就叫做集合，简称集。
集合中的各个对象叫做这个集合的元素。
2、集合元素的特征：确定性、互异性、无序性3、子集：对于两个集合A 和B ，如果集合A 中任何一个元素都属于B ，那么集合A 叫作集合B 的子集，记作A B ⊆，或B A ⊇4、真子集：对于两个集合A 和B ，如果A B ⊆，并且集合B 中至少有一个元素不属于集合A ，那么集合A 叫作集合B 的真子集，记作A B Ü，或B A Ý5、相等集：对于两个集合A 和B ，如果A B ⊆，且B A ⊆，那么集合A 与B 相等，记作A B =6、空集：不含任何元素的集合，记∅。
空集是任何集合的子集，是任何非空集合的真子集。
7、交集：由集合A 和集合B 的所有公共元素组成的集合，叫作A 与B 的交集，记作{}A B x x A x B =∈∈ 且8、并集：由所有属于集合A 或者属于集合B 的元素组成的集合，叫作A 与B 的并集，记作{}A B x x A x B =∈∈ 或9、补集：记U 为全集，A 是U 的子集，则由U 中所有不属于A 的元素组成的集合，叫作A 在全集U 中的补集，记作{}U A x x U x A =∈∉且ð10、对于含有n 个元素的有限集合{}12,,,n A a a a = ，其子集的个数为2n个，其真子集的个为21n -个，其非空子集的个数为21n -个，其非空真子集的个数为22n-个 11、集合的表示方法：列举法、描述法、文氏图法 12、德·摩根公式：()U UU A B A B = 痧?，()U UU A B A B =痧?二、学法点拨1、理解集合的概念，掌握集合的三种表示方法，领会集合中元素的确定性、互异性、无序性（确定性和无序性主要用于列式，互异性主要用于检验），以及元素与集合的“属于”或“不属于”关系。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
限时规范训练(限时练·夯基练·提能练)A级基础夯实练1．(2019·全国卷Ⅱ)设集合A＝{x|x2－5x＋6＞0}，B＝{x|x－1＜0}，则A∩B＝() A．(－∞，1)B．(－2，1)C．(－3，－1) D．(3，＋∞)解析：选A.A∩B＝{x|x2－5x＋6>0}∩{x|x－1<0}＝{x|x<2或x>3}∩{x|x<1}＝{x|x<1}．故选A.2．(2019·浙江卷)已知全集U＝{－1，0，1，2，3}，集合A＝{0，1，2}，B＝{－1，0，1}，则(∁U A)∩B＝()A．{－1} B．{0，1}C．{－1，2，3} D．{－1，0，1，3}解析：选A.∵U＝{－1，0，1，2，3}，A＝{0，1，2}，∴∁U A＝{－1，3}．又∵B＝{－1，0，1}，∴(∁U A)∩B＝{－1}．故选A.3．设集合M＝{x|x＜4}，集合N＝{x|x2－2x＜0}，则下列关系中正确的是()A．M∩N＝M B．M∪(∁R N)＝MC．N∪(∁R M)＝R D．M∪N＝M解析：选D.由题意可得，N＝(0，2)，M＝(－∞，4)，N⊆M所以M∪N＝M.故选D.4．已知集合A＝{0}，B＝{－1，0，1}，若A⊆C⊆B，则符合条件的集合C的个数为() A．1 B．2C．4 D．8解析：选C.由题意得，含有元素0且是集合B的子集的集合有{0}，{0，－1}，{0，1}，{0，－1，1}，即符合条件的集合C共有4个．故选C.5．设全集U＝R，集合A＝{x∈N|x2<6x}，B＝{x∈N|3<x<8}，则如图所示的阴影部分表示的集合是()A ．{1，2，3，4，5}B ．{1，2，3，6，7}C ．{5，4}D ．{4，5，6，7}解析：选B.因为A ＝{x ∈N|x 2＜6x }＝{x ∈N|0<x <6}＝{1，2，3，4，5}，B ＝{x ∈N|3<x <8}＝{4，5，6，7}，所以图中阴影部分表示的集合是{1，2，3，6，7}，故选B.6．集合A ＝⎩⎨⎧⎭⎬⎫x ⎪⎪2x >1，B ＝{x |x 2＋x －2>0}，则A ∩(∁R B )＝( )A ．(0，2)B ．(0，1]C ．(0，1)D ．[0，2]解析：选B.解法一：解不等式2x >1，得0<x <2，即A ＝{x |0<x <2}．解不等式x 2＋x －2>0，得x <－2或x >1，即B ＝{x |x <－2或x >1}，所以∁R B ＝{x |－2≤x ≤1}，所以A ∩(∁R B )＝{x |0＜x ≤1}，故选B.解法二：取x ＝1，知1∈A ，1∈∁R B ，则1∈A ∩(∁R B )，排除C ；取x ＝32，则32∈A ，32∉(∁R B )，则32∉A ∩(∁R B )，排除A ，D ，选B.7．(2019·广州模拟)已知集合A ＝{4，a }，B ＝{x ∈Z|x 2－5x ＋4≥0}，若A ∩(∁Z B )≠∅，则实数a 的值为( )A ．2B ．3C ．2或4D ．2或3解析：选D.因为B ＝{x ∈Z|x 2－5x ＋4≥0}，所以∁Z B ＝{x ∈Z|x 2－5x ＋4＜0}＝{2，3}，又集合A ＝{4，a }，若A ∩(∁Z B )≠∅，则a ＝2或a ＝3，故选D.8．(2019·河北六校联考)已知全集U ＝R ，集合M ＝{x |x ＋2a ≥0}，N ＝{x |log 2(x －1)＜1}，若集合M ∩(∁U N )＝{x |x ＝1或x ≥3}，那么a 的取值为( )A ．a ＝12B ．a ≤12C ．a ＝－12D ．a ≥12解析：选C.∵log 2(x －1)＜1，∴⎩⎪⎨⎪⎧x －1＞0，x －1＜2，即1＜x ＜3，则N ＝{x |1＜x ＜3}，∵U ＝R ，∴∁U N ＝{x |x ≤1或x ≥3}，又∵M ＝{x |x ＋2a ≥0}＝{x |x ≥－2a }，M ∩(∁U N )＝{x |x ＝1或x ≥3}，∴－2a ＝1，解得a ＝－12.故选C.9．已知集合A ＝{1，2}，B ＝{a ，a 2＋3}．若A ∩B ＝{1}，则实数a 的值为________．解析：∵B ＝{a ，a 2＋3}，A ∩B ＝{1}， ∴a ＝1或a 2＋3＝1，∵a ∈R ，∴a ＝1. 经检验，满足题意． 答案：110．(2019·汕头模拟)已知集合A ＝{1，2，3，4}，集合B ＝{x |x ≤a ，a ∈R}，A ∪B ＝(－∞，5]，则a 的值是________．解析：因为集合A ＝{1，2，3，4}，集合B ＝{x |x ≤a ，a ∈R}，A ∪B ＝(－∞，5]，所以a ＝5.答案：5B 级 能力提升练11．集合M ＝{x |2x 2－x －1<0}，N ＝{x |2x ＋a >0}，U ＝R.若M ∩(∁U N )＝∅，则a 的取值范围是( )A ．(1，＋∞)B ．[1，＋∞)C ．(－∞，1)D ．(－∞，1]解析：选B.由集合M ＝{x |2x 2－x －1＜0}，N ＝{x |2x ＋a >0}，可得M ＝⎝⎛⎭⎫－12，1，∁U N ＝⎝⎛⎦⎤－∞，－a 2.要使M ∩(∁U N )＝∅，则－a 2≤－12，解得a ≥1，故选B. 12．(2019·西安三模)已知全集U ＝{x ∈N|－1≤x ≤9}，集合A ＝{0，1，3，4}，集合B ＝{y |y ＝2x ，x ∈A }，则(∁U A )∩(∁U B )＝( )A ．{5，7}B ．{－1，5，7，9}C ．{5，7，9}D ．{－1，1，2，3，4，5，6，7，8，9}解析：选C.解法一：因为U ＝{x ∈N|－1≤x ≤9}，所以U ＝{0，1，2，3，4，5，6，7，8，9}．因为集合A ＝{0，1，3，4}，集合B ＝{y |y ＝2x ，x ∈A }，所以B ＝{0，2，6，8}．所以∁U A ＝{2，5，6，7，8，9}，∁U B ＝{1，3，4，5，7，9}，所以(∁U A )∩(∁U B )＝{5，7，9}，故选C.解法二：因为U ＝{x ∈N|－1≤x ≤9}，所以U ＝{0，1，2，3，4，5，6，7，8，9}．因为集合A ＝{0，1，3，4}，集合B ＝{y |y ＝2x ，x ∈A }，所以B ＝{0，2，6，8}．所以A ∪B ＝{0，1，2，3，4，6，8}，所以(∁U A )∩(∁U B )＝∁U (A ∪B )＝{5，7，9}，故选C.13．(2019·杭州模拟)已知集合A ＝{0，1，2m }，B ＝{x |1<22－x <4}，若A ∩B ＝{1，2m }，则实数m 的取值范围是( )A.⎝⎛⎭⎫0，12 B ．⎝⎛⎭⎫12，1 C.⎝⎛⎭⎫0，12∪⎝⎛⎭⎫12，1 D ．(0，1)解析：选C.因为B ＝{x |1<22－x <4}，所以B ＝{x |0<2－x <2}＝{x |0<x <2}．观察选项，取m ＝14，则A ＝⎩⎨⎧⎭⎬⎫0，1，12，因为B ＝{x |0<x <2}，所以A ∩B ＝⎩⎨⎧⎭⎬⎫1，12，所以m ＝14符合题意，排除B ；取m ＝12，则A ＝{0，1，1}，这与集合中元素的互异性相矛盾，所以m ≠12，排除D ；取m ＝34，则A ＝⎩⎨⎧⎭⎬⎫0，1，32，因为B ＝{x |0<x <2}，所以A ∩B ＝⎩⎨⎧⎭⎬⎫1，32，所以m ＝34符合题意，排除A.故选C.14．已知集合A ＝{x |－1<x <3}，B ＝{x |－m <x <m }，若B ⊆A ，则m 的取值范围为________． 解析：当m ≤0时，B ＝∅，显然B ⊆A . 当m ＞0时，∵A ＝{x |－1<x <3}．当B ⊆A 时，在数轴上标出两集合，如图，∴⎩⎪⎨⎪⎧－m ≥－1，m ≤3，－m ＜m .∴0＜m ≤1. 综上所述m 的取值范围为(－∞，1]． 答案：(－∞，1]C 级 素养加强练15．对于非空数集A ＝{a 1，a 2，a 3，…，a n }(n ∈N *)，其所有元素的算术平均数记为E (A )，即E (A )＝a 1＋a 2＋a 3＋…＋a nn.若非空数集B 满足下列两个条件：①B ⊆A ；②E (B )＝E (A )．则称B 为A 的一个“保均值子集”．据此，集合{1，2，3，4，5}的“保均值子集”有( )A ．4个B ．5个C ．6个D ．7个解析：选D.因为集合{1，2，3，4，5}中所有元素的算术平均数E (A )＝1＋2＋3＋4＋55＝3，所以由新定义可知，只需找到其非空子集B 满足E (B )＝3即可．据此分析易知，集合{1，2，3，4，5}，{1，2，4，5}，{1，3，5}，{2，3，4}，{1，5}，{2，4}，{3}都符合要求．故集合{1，2，3，4，5}的“保均值子集”有7个．故选D.16．(2019·苏州模拟)设A ，B 是非空集合，定义A ⊗B ＝{x |x ∈(A ∪B )且x ∉(A ∩B )}．已知集合A ＝{x |0＜x ＜2}，B ＝{y |y ≥0}，则A ⊗B ＝________．解析：由已知A ＝{x |0＜x ＜2}，B ＝{y |y ≥0}，又由新定义A ⊗B ＝{x |x ∈(A ∪B )且x ∉(A ∩B )}，结合数轴得A ⊗B ＝{0}∪[2，＋∞)．答案：{0}∪[2，＋∞)17．当两个集合中一个集合为另一个集合的子集时，称这两个集合构成“全食”，当两个集合有公共元素，但互不为对方子集时，称这两个集合构成“偏食”．对于集合A ＝⎩⎨⎧⎭⎬⎫－1，12，1，B ＝{x |ax 2＝1，a ≥0}，若A 与B 构成“全食”或构成“偏食”，则a 的取值集合为________．解析：当a ＝0时，B 为空集，满足B ⊆A ，此时A 与B 构成“全食”；当a ＞0时，B ＝⎩⎨⎧⎭⎬⎫1a ，－1a ，由题意知1a ＝1或1a ＝12，解得a ＝1或a ＝4.故a 的取值集合为{0，1，4}．答案：{0，1，4}。