高等数学(方桂英,崔克俭主编)思维导图
《高等数学习题全解与学习指导 上册 》读书笔记思维导图

第二章 一元函数微分学及其应用
1
一、知识结构
2
二、归纳总结
3
三、例题解析
4
四、习题详解
5
章节测试二
习题2-1 导数的概念 及基本求导公式
习题2-2 导数的计算 法则
习题2-3 微分的概念 与应用
习题2-4 微分中值定 理与应用
习题2-6 函数的性 质与图形
习题2-5 泰勒中值 定理
习题2-7 微分学的 实际应用
习题3-7 定积分的几 何应用与物理应用
习题3-8 反常积分
第四章 微分方程
1
一、知识结构
2
二、归纳总结
3
三、例题解析
4
四、习题详解
5
章节测试四
习题4-1 微分方程的 基本概念
习题4-2 一阶微分方 程
习题4-3 二阶微分方 程
习题4-4 微分方程的 实际案例
感谢观看
读
书
笔
记
第一章 函数、极限与连续
一、知识结构
2
二、归纳总结
3
三、例题解析
4
四、习题详解
5
章节测试一
习题1-1 集合与函数
习题1-2 数列极限的 定义与计算
习题1-3 函数极限的 定义与计算
习题1-4 极限的证明 与性质
习题1-6 无穷小与 无穷大
习题1-5 两个重要 极限
习题1-7 函数的连 续性及其性质
05 第四章 微分方程
《高等数学习题全解与学习指导》分上、下两册。上册内容为函数与极限,一元函数微学分,一元函数积分 学,常微分方程配套习题讲解。书中各章节的主要内容都配有精心选取的例题和习题,着重训练读者对定义与概 念的理解、对定理与方法的应刚能力,培养读者解决问题的逻辑心维方法和创新能力。
2023高等数学考试大纲思维导图,脑图
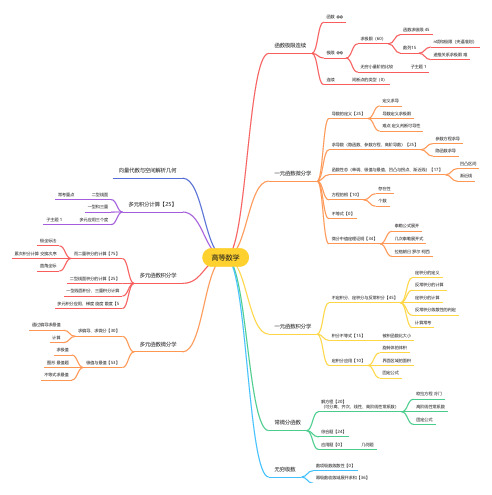
高等数学函数极限连续函数极限求极限(60)函数求极限 45数列15n项和极限(夹逼准则)递推关系求极限 难无穷小量阶的比较子主题 1连续间断点的类型(0)一元函数微分学导数的定义【25】定义求导导数定义求极限难点 定义判断可导性求导数(隐函数、参数方程、高阶导数)【25】参数方程求导隐函数求导函数性态(单调、极值与最值、凹凸与拐点、渐近线)【17】凹凸区间渐近线方程的根【10】存在性个数不等式【0】微分中值定理证明【34】泰勒公式展开几次泰勒展开式拉格朗日 罗尔 柯西一元函数积分学不定积分、定积分与反常积分【45】定积分的定义反常积分的计算定积分的计算反常积分敛散性的判定计算常考积分不等式【15】被积函数比大小定积分应用【10】旋转体的体积界面区域的面积固定公式常微分函数解方程【20】(可分离、齐次、线性、高阶线性常系数)欧拉方程 冷门高阶线性常系数固定公式综合题【24】应用题【0】几何题无穷级数数项级数敛散性【0】幂级数收敛域展开求和【36】向量代数与空间解析几何多元积分计算【25】二型线面常考重点一型和三重多元应用三个度子主题 1多元函数积分学而二重积分的计算【75】极坐标法累次积分计算 交换次序直角坐标二型线面积分的计算【25】一型线面积分、三重积分计算多元积分应用、梯度 旋度 散度【5多元函数微分学求偏导、求微分【30】通过偏导求最值计算极值与最值【53】求极值图形 最值题不等式求最值。
考研高等数学思维导图

则在开区间(a,b)内至少有一点 ξ,使f (ξ ) = 0.
③ 设函数f (x)在闭区间[a,b]上连续,且在这区间的端点取不同的函数值,f (a) = A, f (b) = B,
则对于A与B之间的任意一个数C,在开区间(a,b)内至少有一点ξ,使得f (ξ) = C(a < ξ < b).
可去间断点:(1)=(2)≠(3) 跳跃间断点:(1)≠(2)
第二类间断点,(1)、(2)至少有一个不存在 无穷间断点、振当间断点都属于第二类
常考:无定义点一定是间断点;分段点可能是间断点
渐近线 水平渐近线、铅直渐近线、斜渐近线
1/31
① 在闭区间上连续的函数在该区间上有界且一定能取得它的最小值和最大值
数列极限总结 ........................................................................ 3
第六章 定积分的应用 ....................................................................17
④ ∀ε > 0, ∃δ > 0,当0 < x − x0 < δ时,有 f (x) − A < ε ⇔ lim f (x) = A x→ x0
第二章 导数与微分.......................................................................... 5
第八章 向量代数与空间解析几何(数一).....................................20
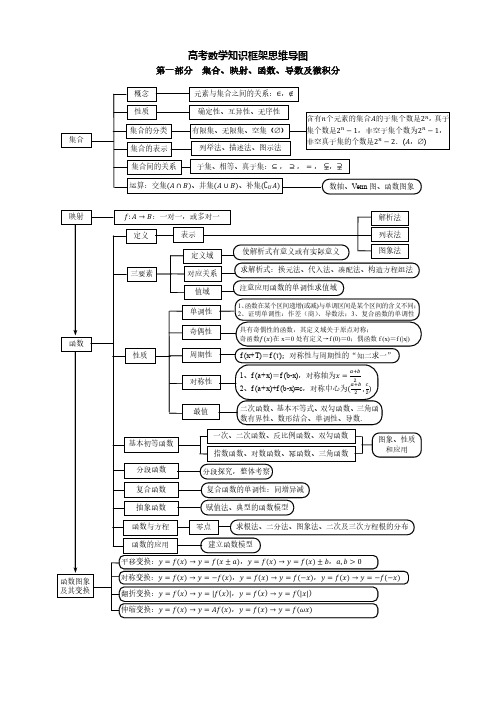
高中数学知识框架思维导图(整理版)
柯西不等式
第四部分
位置关系
截距
解析几何
斜率公式、倾斜角的变化与斜率的变化: = tan , =
倾斜角和斜率
重合
A1B2-A2B1=0,C1B2-C2B1=0
平行
A1B2-A2B1=0,C1B2-C2B1≠0
相交
A1B2-A2B1≠0
垂直
直线的方程
z 的几何意义:
过可行域内一点(, )
向直线 = , = 作
复合函数
函数与方程
2
二次函数、基本不等式、双勾函数、三角函
数有界性、数形结合、单调性、导数.
基本初等函数
分段函数
, )
零点
求根法、二分法、图象法、二次及三次方程根的分布
建立函数模型
平移变换: = () → = ( ± ), = () → = () ± ,, > 0
对称性
y=Asin(x+)+b
化简、求值、
证明(恒等变形)
)
值域
图象
对称轴(正切函数除外)经过函数图象
的最高(或低)点且垂直 x 轴的直线,
对称中心是正余弦函数图象的零点,正
切函数的对称中心为( ,0)(k∈Z).
最值
2
①图象可由正弦曲线经过平移、伸缩得到,但要注意先平移后伸缩与先伸缩后平移不同;
2.
3.
分组求和法
2
=
1
−
−1)(2+1 −1)
2 −1
+1
1 1
1
= (
2 (+2)2
(−1) ∙4
4 2
(2−1)(2+1)
1
2+1 −1
大学高数常微分方程思维导图_高等数学各章节知识点框架常微分方程.pdf

⼤学⾼数常微分⽅程思维导图_⾼等数学各章节知识点框架常微分⽅程.pdf【微信公众号:给⼒考研资料】免费分享常微分⽅程1.概念,2.⼀阶微分⽅程求解3.⾼阶微分⽅程求解4.应⽤题1.概念(7个概念,了解即可)微分⽅程—含有未知函数的导数或者微分的⽅程常微分⽅程—未知函数为⼀元函数的微分⽅程偏微分⽅程—未知函数为多元函数的微分⽅程微分⽅程的阶—未知函数的导数的最⾼阶数为⽅程的阶数微分⽅程的解—将函数代⼊⽅程,为恒等式,则该函数为解微分⽅程的通解与特解—通解—解中独⽴常数的个数等于⽅程的阶数,特解—解中没有任何常数初始条件(定解条件)—确定通解中的常数的条件2.⼀阶微分⽅程求解⼀阶⽅程(4个)1.可分离变量型(两边直接积分)2.可化成可分离变量型形如y'=f(ax+by+c)型 (令u=ax+by+c,相应对x求导,则化成可分离变量)⻬次型—形如y'=f(y/x) (令p=y/x,相应求导,则可化为分离变量型)Note :1.对于式⼦中出现lnu中u不知正负,则要带上绝对值,除过⼀阶线性2.对于⼀阶线性⽅程,不⽤带绝对值(18版18讲P217有分析)3.所求的通解可以不是全部解(线性:通解=全部解,⾮线性:通解不等于全部解)4.在求通解中,⼀定要带上对独⽴常数C的限定5.若出现不属于⼀阶⽅程四种类型,则考虑调换x ,y的地位6.能写成显⽰解就写要写成显⽰解3.⼀阶线性⽅程(要掌握推导解的公式,利⽤求导公式逆⽤法)—形如y'+p(x)y=q(x)4.伯努利⽅程(这⾥可以将其化成⼀阶线性,利⽤恒等变形中三种⽅法中换元)形如y'+p(x)y=q(x)yn(令y1-n=u ,相应求导,化成⼀阶线性)5.全微分⽅程利⽤积分与路径⽆关的性质,⽤折线法来求原函数=C⼆阶可降阶⽅程1.形如y''=f(x,y') 缺y型——将y斩草除根(令y'=u,y''=u',化成了⼀阶)2.形如y''=f(y,y')缺x型——将x斩尽杀绝(令y'=u,y'=udu/dy,化成⼀阶)要注意两种类型不同的处理⽅法Note :还有⼀种可降阶的n阶⽅程,连续求导即可3.⾼阶微分微分⽅程的求解(2~4阶)⼆阶线性微分⽅程的概念(详⻅18讲P218)1.⻬次与⾮⻬次2.变系数与常系数注意若真的出现了变系数⼆阶,要想到换元,化成⼆阶(或者是欧拉⽅程)解的结构与解的性质(各2个)(详⻅⾼数18讲P218)1.⼆阶常系数⻬次线性微分⽅程的通解结构(两个线性⽆关的解(通俗理解就是相除不为常数)可以构成起通解)2.⾮⻬次的解的结构——⻬次的特解+⾮⻬次的特解3.两个⾮⻬次的特解相加为⼀个全新⾮⻬次的特解(叠加原理)【微信公众号:给⼒考研资料】免费分享4.两个⾮⻬次的特解相减为其⻬次的⼀个解⼆阶常系数⻬次线性微分⽅程求解(背公式)⾮⻬次的特解(背公式)n阶常系数线性⻬次微分⽅程求解(背公式)注意特征⽅程的特征根各种情况(四种情况)4.欧拉⽅程(仅数⼀)(18讲259)形如x2y''+pxy'+qy=f(x)换元:当x⼤于0当x⼩于04.应⽤题:1.背景公平——信息给予2.翻译成数学表达式Note :注意⽐例系数应是正号,或负号,应根据题意主动添上。
