2020届江苏高考数学专题复习隐形圆问题

高三数学隐形圆练习题

高三数学隐形圆练习题隐形圆是高中数学中一个重要的概念，理解隐形圆的性质和应用对于解决相关的几何问题至关重要。

本文将提供一些高三数学隐形圆练习题，帮助学生巩固对该概念的理解和运用能力。

练习题1：已知在平面直角坐标系中，圆心为O(-2, 3)，半径为5。

请回答以下问题：1. 圆的方程是什么？2. 过圆心的直径的方程是什么？3. 过由圆心和横坐标为1的点的直线的方程是什么？解答：1. 圆的方程可以表示为：(x+2)² + (y-3)² = 25。

2. 过圆心的直径的方程可以表示为：x + 2y - 10 = 0。

3. 过由圆心和横坐标为1的点的直线的方程可以表示为：2y - x - 5 = 0。

练习题2：已知在平面直角坐标系中，直线方程为2x + 3y - 6 = 0。

请回答以下问题：1. 该直线与y轴的交点是什么？2. 该直线与x轴的交点是什么？3. 该直线是否与圆心为(1, -2)、半径为4的圆相切？解答：1. 该直线与y轴的交点可以通过令x=0来求解，得到点(0, 2)。

2. 该直线与x轴的交点可以通过令y=0来求解，得到点(3, 0)。

3. 该直线不与圆心为(1, -2)、半径为4的圆相切。

通过将直线方程带入圆的方程进行判别，得到：(1+2)² + (m+2)² = 16。

化简得到m² + 4m + 5 = 0，该二次方程没有实根，因此直线与圆不相切。

练习题3：已知在平面直角坐标系中，直线L₁的方程为3x - 4y - 5 = 0，直线L₂过点A(3, 2)且与直线L₁垂直。

请回答以下问题：1. 直线L₂的方程是什么？2. 直线L₁与直线L₂的交点是什么？3. 直线L₂与圆心为(1, -1)、半径为3的圆是否相切？解答：1. 直线L₁的斜率为3/4，垂直于L₁的直线L₂的斜率为-4/3。

过点A(3, 2)且斜率为-4/3的直线方程可以表示为：y - 2 = (-4/3)(x - 3)，化简可得y = (-4/3)x + 14/3，即直线L₂的方程为y = (-4/3)x + 14/3。

2020年九年级数学中考专题复习：隐形圆求最值问题(含答案)

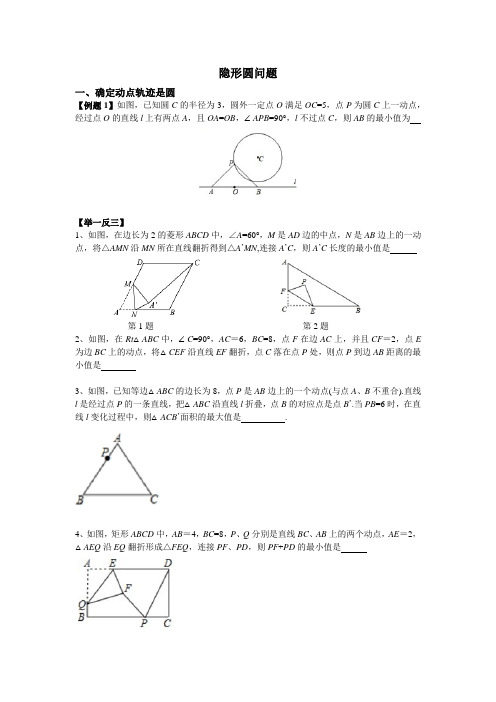
隐形圆问题一、确定动点轨迹是圆【例题1】如图，已知圆C的半径为3，圆外一定点O满足OC=5，点P为圆C上一动点，经过点O的直线l上有两点A，且OA=OB，∠APB=90°，l不过点C，则AB的最小值为【举一反三】1、如图，在边长为2的菱形ABCD中，∠A=60°，M是AD边的中点，N是AB边上的一动点，将△AMN沿MN所在直线翻折得到△A’MN,连接A’C，则A’C长度的最小值是第1题第2题2、如图，在Rt△ABC中，∠C=90°，AC＝6，BC=8，点F在边AC上，并且CF＝2，点E 为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是3、如图，已知等边△ABC的边长为8，点P是AB边上的一个动点(与点A、B不重合).直线l是经过点P的一条直线，把△ABC沿直线l折叠，点B的对应点是点B’.当PB=6时，在直线l变化过程中，则△ACB’面积的最大值是.4、如图，矩形ABCD中，AB＝4，BC=8，P、Q分別是直线BC、AB上的两个动点，AE＝2，△AEQ沿EQ翻折形成△FEQ，连接PF、PD，则PF+PD的最小值是二、定边对直角知识回顾:直径所对的圆周角是直角构造思路:一条定边所对的角始终为直角，则直角顶点轨迹是以定边为直径的圆或圆弧.图形释义:若AB是一条定线段，且∠APB-90°，则P点轨迹是以AB为直径的圆【例题1】已知正方形ABCD边长为2，E、F分别是BC、CD上的动点，且满足BE＝CF，连接AE、BF，交点为P点，则PC的最小值为【举一反三】1、如图，E、F是正方形ABCD的边AD上的两个动点，满足AE＝DF，连接CF交BD于点G，连接BE交AG于点H，若正方形边长为2，则线段DH长度的最小值是2、如图，Rt△ABC中，AB⊥BC，AB=6，BC＝4，P是△ABC内部的一个动点，且满足∠P AB ＝∠PBC，则线段CP长的最小值是3、如图，AB是半圆O的直径，点C在半圆O上，AB＝5，AC＝4.D是弧BC上的一个动点，连接AD，过点C作CE⊥AD于E，连接BE.在点D移动的过程中，BE的最小值为4、如图，在Rt△ABC中，∠BAC=90°，AC＝12，AB＝10，点D是AC上的一个动点，以AD为直径作圆O，连接BD交圆O于点E，则AE的最小值为5、如图，正方形ABCD的边长为4，动点E、F分別从点A、C同时出发，以相同的速度分别沿AB、CD向终点B、D移动，当点E到达点B时，运动停止，过点B作直线EF的垂线BG，垂足为点G，连接AG，则AG长的最小值为【辅助圆+将军饮马】如图，正方形ABCD的边长是4，点E是AD边上一动点，连接BE，过点A作AF⊥BE于点F，点P是AD边上另一动点，则PC+PF的最小值为【辅助圆+相切】如图，在Rt△ABC中，∠ACB=90°，∠B=30°，AB＝4，D是BC上一动点，CE⊥AD于E，EF⊥AB交BC于点F，则CF的最大值是三、定边对定角在“定边对直角”问题中，依据“直径所对的圆周角是直角”，关键性在于寻找定边、直角，而根据圆周角定理:同圆或等圆中，同弧或等弧所対的圆周角都相.定边必不可少，而直角则可一般为定角.例如，AB为定值，∠P为定角，则P点轨迹是一个圆.当然，∠P度数也是特殊角，比如30°、45°、60°、120°，下面分别作对应的轨迹圆若∠P＝30°，以AB为边，同侧构造等边三角形AOB，O即为圆心若∠P＝45°，以AB为斜边，同侧构造等腰直角三角形AOB，O即为圆心.若∠P＝60°，以AB为底，同侧构造顶角为120°的等腰三角形AOB，O即为圆心.若∠P＝120°，以AB为底，异侧为边构造顶角为120°的等腰三角形AOB，O即为圆心.【例题1】如图，等边△ABC边长为2，E、F分別是BC、CA上两个动点，且BE=CF，连接AE、BF，交点为P点，则CP的最小值为【举一反三】1、如图，△ABC为等边三角形，AB=3，若P为△ABC内一动点，且满足∠P AB＝∠ACP，则线段PB长度的最小值为2、在△ABC中，AB＝4，∠C＝60°，∠A>∠B，则BC的长的取值范围是3、如图，AB是圆O的直径，M、N是弧AB(异于A、B)上两点，C是弧MN上一动点，∠ACB 的角平分线交圆O于点D，∠BAC的平分线交CD于点E，当点C从点M运动到点N时，则C、E两点的运动路径长的比是。

2020高考数学热点难点微专题隐圆问题(29张)

热点难点微专题五 “隐圆”问题
热点难点微专题五 “隐圆”问题
第1页
专题综述典型例题课后作业
热点难点微专题五 “隐圆”问题
专课题时综作述业
江苏省高考考试说明中圆的方程是 C 级考点，近几年在各地模考和高考的填空题和解答题中都有出现且频率较高，难度为中档题．在题设中没有明确给出圆的相关信息，而是隐含在题目中的，要通过分析、转化，发现圆(或圆的方程)，从而最终利用圆的知识来求解，我们称这类问题为“隐圆”问题．
第14页
专题综述典型例题课后作业
热点难点微专题五 “隐圆”问题
则点 C 的运动轨迹是以点 P 为圆心，1 为半径的圆，而|O→P|＝ 6，则|O→C|的取值范围为[ 6－1， 6＋1]．
第15页
专题综述典型例题课后作业
热点难点微专题五 “隐圆”问题
3. 在平面直角坐标系 xOy 中，点 A(1,0)，B(4,0)．若直线 x－y＋m＝0 上存在点 P
第12页
专题综述典型例题课后作业
热点难点微专题五 “隐圆”问题
课后时作业
1. 已知点 M(a，b)在圆 O：x2＋y2＝4 外，则直线 ax＋by＝4 与圆 O 的位置关系是 ________．
相交解析：因为点 M(a，b)在圆 O：x2＋y2＝4 外，所以 a2＋b2>4，圆心 O(0,0) 到直线 ax＋by＝4 的距离为 d＝ a24＋b2<2＝r，故直线 ax＋by＝4 与圆 O 的位置关系是相交．
第18页
专题综述典型例题课后作业
热点难点微专题五 “隐圆”问题
解法二：A→M·A→B＝|A→M||A→B|cos∠MAB＝12|A→B|2＝2，|A→B|＝c＝2，又 AC2＋3BC2＝4 即 b2＋3a2＝4 得 a2＝4－3b2，cosA＝b2＋2cb2c－a2＝b23＋b 2.

2020年九年级数学中考专题复习：隐形圆求最值问题(含答案)

隐形圆问题一、确定动点轨迹是圆【例题1】如图，已知圆C的半径为3，圆外一定点O满足OC=5，点P为圆C上一动点，经过点O的直线l上有两点A，且OA=OB，∠APB=90°，l不过点C，则AB的最小值为【举一反三】1、如图，在边长为2的菱形ABCD中，∠A=60°，M是AD边的中点，N是AB边上的一动点，将△AMN沿MN所在直线翻折得到△A’MN,连接A’C，则A’C长度的最小值是第1题第2题2、如图，在Rt△ABC中，∠C=90°，AC＝6，BC=8，点F在边AC上，并且CF＝2，点E 为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是3、如图，已知等边△ABC的边长为8，点P是AB边上的一个动点(与点A、B不重合).直线l是经过点P的一条直线，把△ABC沿直线l折叠，点B的对应点是点B’.当PB=6时，在直线l变化过程中，则△ACB’面积的最大值是.4、如图，矩形ABCD中，AB＝4，BC=8，P、Q分別是直线BC、AB上的两个动点，AE＝2，△AEQ沿EQ翻折形成△FEQ，连接PF、PD，则PF+PD的最小值是二、定边对直角知识回顾:直径所对的圆周角是直角构造思路:一条定边所对的角始终为直角，则直角顶点轨迹是以定边为直径的圆或圆弧.图形释义:若AB是一条定线段，且∠APB-90°，则P点轨迹是以AB为直径的圆【例题1】已知正方形ABCD边长为2，E、F分别是BC、CD上的动点，且满足BE＝CF，连接AE、BF，交点为P点，则PC的最小值为【举一反三】1、如图，E、F是正方形ABCD的边AD上的两个动点，满足AE＝DF，连接CF交BD于点G，连接BE交AG于点H，若正方形边长为2，则线段DH长度的最小值是2、如图，Rt△ABC中，AB⊥BC，AB=6，BC＝4，P是△ABC内部的一个动点，且满足∠P AB ＝∠PBC，则线段CP长的最小值是3、如图，AB是半圆O的直径，点C在半圆O上，AB＝5，AC＝4.D是弧BC上的一个动点，连接AD，过点C作CE⊥AD于E，连接BE.在点D移动的过程中，BE的最小值为4、如图，在Rt△ABC中，∠BAC=90°，AC＝12，AB＝10，点D是AC上的一个动点，以AD为直径作圆O，连接BD交圆O于点E，则AE的最小值为5、如图，正方形ABCD的边长为4，动点E、F分別从点A、C同时出发，以相同的速度分别沿AB、CD向终点B、D移动，当点E到达点B时，运动停止，过点B作直线EF的垂线BG，垂足为点G，连接AG，则AG长的最小值为【辅助圆+将军饮马】如图，正方形ABCD的边长是4，点E是AD边上一动点，连接BE，过点A作AF⊥BE于点F，点P是AD边上另一动点，则PC+PF的最小值为【辅助圆+相切】如图，在Rt△ABC中，∠ACB=90°，∠B=30°，AB＝4，D是BC上一动点，CE⊥AD于E，EF⊥AB交BC于点F，则CF的最大值是三、定边对定角在“定边对直角”问题中，依据“直径所对的圆周角是直角”，关键性在于寻找定边、直角，而根据圆周角定理:同圆或等圆中，同弧或等弧所対的圆周角都相.定边必不可少，而直角则可一般为定角.例如，AB为定值，∠P为定角，则P点轨迹是一个圆.当然，∠P度数也是特殊角，比如30°、45°、60°、120°，下面分别作对应的轨迹圆若∠P＝30°，以AB为边，同侧构造等边三角形AOB，O即为圆心若∠P＝45°，以AB为斜边，同侧构造等腰直角三角形AOB，O即为圆心.若∠P＝60°，以AB为底，同侧构造顶角为120°的等腰三角形AOB，O即为圆心.若∠P＝120°，以AB为底，异侧为边构造顶角为120°的等腰三角形AOB，O即为圆心.【例题1】如图，等边△ABC边长为2，E、F分別是BC、CA上两个动点，且BE=CF，连接AE、BF，交点为P点，则CP的最小值为【举一反三】1、如图，△ABC为等边三角形，AB=3，若P为△ABC内一动点，且满足∠P AB＝∠ACP，则线段PB长度的最小值为2、在△ABC中，AB＝4，∠C＝60°，∠A>∠B，则BC的长的取值范围是3、如图，AB是圆O的直径，M、N是弧AB(异于A、B)上两点，C是弧MN上一动点，∠ACB 的角平分线交圆O于点D，∠BAC的平分线交CD于点E，当点C从点M运动到点N时，则C、E两点的运动路径长的比是。

2020届高考数学江苏省二轮课件：微专题6 隐性圆问题

a2 1
14 或a≥ 14 .
2
2
栏目索引
题型二与相交弦有关的隐性圆
例2 (2019南通通州、海门联考,13)在平面直角坐标系xOy中,已知点A(1,1),
B,C为圆O:x2+y2=4上的两动点,且BC=2
3
,若圆O上存在点高考P,导使航得uAuBur
uuur
+ AC
=m
uuur
OP,m>0,则正数m的取值范围为
∴|m-1|≤ 2 ≤m+1,又m>0,
∴ 2 -1≤m≤ 2 +1.
栏目索引高考导航
栏目索引
【方法归纳】当直线与圆相交时,特征三角形(由弦心距、半弦、半径构成)的应用是最普遍的,在特征三角形中应用边角关系求出动点的条件是解题
高考导航
的关键.
栏目索引
2-1 已知A,B是圆O:x2+y2=1上的动点,满足AB= 3,P是圆C:(x-3)2+(y-4)2=1上
uur
PA+
uuur PB
|∈[7,13].
栏目索引
2-2 已知A,B是圆O:x2+y2=9上的动点,且直线AB过定点M(2,0),P是圆C:(x-3)2+
uur uuur
(y-4)2=1上的动点,则| PA+ PB |的取值范围是
.
高考导航
答案 [4 5 -4,4 5 +4]
解析设AB的中点为Q,连接OQ,则OQ⊥QM,即点Q在以OM为直径的圆上,
.
答案 [ 2 -1, 2 +1]
解析如图,取BC的中点M,连接OM.
∵BC=2 3 ,∴O到BC的距离OM=1,

专题58 隐形圆问题-2020年江苏省高考数学考点探究(解析版)

专题58 隐形圆问题专题知识梳理隐形圆也就是题目中给出的条件不是给出一个圆，而是要通过设点、列式、化简得到动点的轨迹是一个圆.本专题分四个方面讲了隐形圆问题.1．利用圆的定义：在平面内到定点的距离等于常数，则这个点的轨迹是一个圆.解决这类问题只要抓住两个关键词：定点，定长.然后再化归为圆中的有关问题去解.2．是利用几何特征，直径所对的圆周角是直角，得到了隐形圆，有时两个定点所张的角也不一定是90o，可以是其他的定角，则动点的轨迹是两段圆弧.3．动点到两个定点的距离的平方和是定值，则这个点的轨迹也是一个圆，当然这个定值会有一定的范围，否则轨迹不存在，如果在某一距离前加其他系数也可以.4．是著名的阿波罗尼斯圆：到两个定点的距离之比是一个不为1的定值，这类题可能给出的背景也不在解析几何中，是要自己建系后，才能看出点的轨迹.所以在解题时要当心给出的条件.5．化归思想在本专题的作用很重要，因为给出的条件不是圆，是需要大家在解题分析得出的，另外得到圆以后，要合理用好点与圆、直线与圆、圆与圆的位置关系.考点探究【例1】(1)已知圆O ：x 2＋y 2＝1，圆M ：(x －a )2＋(y －a ＋4)2＝1.若圆M 上存在点P ，过点P 作圆O 的两条切线，切点为A ，B ，使得∠APB ＝60°，则a 的取值范围为____．(2)如果圆(x －2a )2＋(y －a －3)2＝4上总存在两个点到原点的距离为1，则实数a 的取值范围是____．【解析】（1）连OP ，则30OPA ∠=o，∵1OA =，∴2OP =，即P 点的轨迹方程为224x y +=，又点P在圆M 22()(4)1x a y a -+-+=上，∴两圆有交点，即221(4)9a a ≤+-≤，解得：2222a -≤≤+．（2）到原点的距离为1的点的轨迹方程为221x y +=，如果圆(x －2a )2＋(y －a －3)2＝4上总存在两个点到原点的距离为1等价于两圆相交，即2214(3)9a a ≤++≤，解得605a -≤≤．【例2】(1)已知圆C ：(x －3)2＋(y －4)2＝1和两点A (－m ，0)，B (m ，0) 0m >，若圆上存在点P ，使得∠APB ＝90°，则m 的取值范围是____．(2)（2019·南通一模）在平面直角坐标系xOy 中，已知B ，C 为圆x 2＋y 2＝4上两点，点A (1，1)，且AB ⊥AC ，则线段BC 的长的取值范围为_ ___．【解析】（1）∵∠APB ＝90°，∴点P 在以AB 为直径的圆上，其方程为222x y m +=，又点P 在圆C ：(x－3)2＋(y －4)2＝1上，且有两个，∴两圆相交，即11m m -≤+，解得46m ≤≤.（2）∵AB ⊥AC ，设D 为AB 的中点，D 点坐标为(,)x y ，BC 的长为2m ，∴DA m =，在三角形OCD 中，有224m OD +=，即2222(1)(1)4x y x y -+-++=，化简得22113()()222x y -+-=，∴DA 的取值范围为,22．∴BC 的取值范围为．【例3】在平面直角坐标系xOy 中，已知点(2,0)A ，直线:4l y x =-，圆C 的半径为1，圆心在l 上．若圆C 上存在点M ,使2210MA MO +=,求圆心C 的横坐标a 的取值范围．【解析】设(,)M x y ，∵2210MA MO +=，∴2222(2)10x y x y -+++=，即2223x y x +-=，又圆C 的半径为1，圆心在l 上，∴圆C 的方程为22()(4)1x a y a -+-+=．∵点M也在圆C 上，∴两圆有交点，即221(1)(4)9a a ≤-+-≤，∴2540a a -+≥或250a a -≤，解得4a ≥或1a ≤或05a ≤≤，综上横坐标a 的取值范围为45a ≤≤或01a ≤≤．【例4】已知点A(-2,0)，B(4,0),圆C: 16)4(22=++y x ,P 为圆C 上任意一点，问是否存在常数λ，使λ=PBPA，若存在，求出常数λ的值，若不存在，请说明理由．【解析】假设存在，设P 的坐标为(,)x y ，∵λ=PB PAλ=， ∴22222(2)[(4)]x y x y λ++=-+，即222222(1)(1)(48)4160x y x λλλλ-+-+++-=，又∵P 为圆C 上任意一点，∴16)4(22=++y x ，即228x y x +=-，∴22(164)4160x λλ-+-=对于圆上的任意一点均成立，∴21640λ-=，即12λ=．题组训练1.(2018·扬州一模)已知ABC ∆是边长为3的等边三角形，点P 到点A 的距离为1，点Q 满足2133AQ AP AC =+u u u r u u u r u u u r，则BQ uuu r 的最小值为．【解析】以BC 所在的直线为x 轴，BC 的垂直平分线为y 轴，建立直角坐标系，则33(,0),(,0),22B C A -，∵点P 到点A 的距离为1，∴2200(1x y +=，设00(,),(,)Q x y P x y ，∵2133AQ AP AC =+u u u r u u u r u u u r ，∴00213(,)(,(,232322x y x y -=-+-，则00333,242x x y y =-=，∴2214()(29x y -+=，令212cos ,sin 323x y αα=+=∴33(,(,(,)2222BQ BA AQ x y x y =+=+-=+u u u r u u u r u u u r ，∴BQ ==u u u r23≥=. 2.已知直线l ：x －2y ＋m ＝0上存在点M 满足与两点A (－2，0)，B (2，0)连线的斜率之积为－1，则实数m 的取值范围是____．【解析】[]－25，25设点(,)M x y ，∵点M 满足与两点A (－2，0)，B (2，0)连线的斜率之积为－1，∵122y yx x ⋅=-+-，∵224x y +=（2x ≠±），又点M 在直线l ：x －2y ＋m ＝0上，∵2≤，即m -≤≤3.已知点(2,2),(0,2)A B -，若直线3x ＋4y －m ＝0上一动点P 满足224PA PB +=，则实数m 的取值范围是________．【解析】设点(,)P x y ，由题意知2222(2)(2)(2)4x y x y ++-++-=，化简得222440x y x y ++-+=，又点P 在直线3x ＋4y －m ＝0上，即直线与圆有公共点，∴3815m-+-≤，解得010m ≤≤．4.（2008·江苏卷）在△ABC 中，2AB =，AC =，则△ABC 面积的最大值是 .【解析】以AB 所在的直线为x 轴，AB 的垂直平分线为y 轴，建立平面直角坐标系，则(1,0),(1,0)A B -，设(,)C x y，∵AC ==即2222(1)2(1)2x y x y ++=-+，22(3)8x y -+=，∴点C 到x轴距离的最大值为3+，则△ABC面积的最大值是12332⨯⨯+=+5.在平面直角坐标系xOy 中，圆C 的方程为x 2＋y 2－8x ＋15＝0，若直线y ＝kx －2上至少存在一点，使得以该点为圆心，1为半径的圆与圆C 有公共点，则k 的最大值是____．【解析】∵圆C 方程为22(4)1x y -+=，∴圆心为(4,0)，半径为1，若直线y ＝kx －2上至少存在一点，使得以该点为圆心，1为半径的圆与圆C 有公共点，即两圆有公共点，2≤，化简得2340k k -≤，解得403k ≤≤，∴k 的最大值为43403k ≤≤6.在平面直角坐标系xOy 中，已知点(0,2)A -，(1,1)B -，P 为圆222x y +=上一动点，则PBPA的最大值为．【解析】设(,)P x y ，PBt PA =t =，化简得222222(1)(24)2(24)240t x t y x t y t -+-++-+-=， ∵222x y +=，∴22(12)230x t y t --+-=， ∴圆心(0,0)O到直线的距离d =≤，∵0t >，∴02t <≤，即PBPA的最大值为2．7.已知圆C ：(x －2)2＋y 2＝4，线段EF 在直线l ：y ＝x ＋1上运动，点P 为线段EF 上任意一点，若圆C 上存在两点A 、B ，使得PA →·PB →≤0，则线段EF 长度的最大值是___．【解析】设点P 的坐标为(x ，y )，则x 2+y 2=50，∴=(－12－x ，－y )，=(－x ，6－y )，∴=x 2+12x +y 2－6y =12x －6y +50≤20，即2x －y ≤－5，直线2x －y =－5与圆x 2+y 2=50的交点坐标为M (－5，－5)，N (1，7)，圆x 2+y 2=50与x 轴负半轴的交点坐标为(，0)，∴点P 的横坐标的取值范围是≤x ≤1，故答案为.8.设P 在圆O ：224x y +=上运动，点(4,0)A ，直线:1l y kx =+上总存在点Q ，使Q 恒为AP 的中点，求实数k 的取值范围.【解析】设P (,)x y ，11(,)Q x y ，则114,2,2x x y y +⎧=⎪⎪⎨⎪=⎪⎩∵点Q 在直线:1l y kx =+上，∴4122y x k +=+，即(4)2y k x =++，代入224x y +=中得：22(42)4x kx k +++=，即222(1)2(42)16160k x k k x k k +++++=，∴22224(42)4(1)(1616)0k k k k k ∆=+-++≥，即2340k k +≤，403k -≤≤. ∴实数k 的取值范围为：403k -≤≤. 9.在平面直角坐标系xoy 中，直线02:1=+-y kx l 与直线02:2=-+ky x l 相交于点P ，则当实数k 变化时，点P 到直线04=--y x 距离的最大值为___________.【解析】设P (,)x y ，∵直线1:20l kx y -+=与直线02:2=-+ky x l 垂直，且直线02:1=+-y kx l 过定点(0,2)，直线2:20l x ky +-=过定点(2,0)，∴P 点轨迹方程为22(1)(1)2x y -+-=， ∴点P 到直线04=--y x=10. (2018·苏北四市期末)已知A ，B 是圆C 1：x 2＋y 2＝1上的动点，AB，P 是圆C 2：(x －3)2＋(y －4)2＝1上的动点，则PA PB +u u u r u u u r的取值范围为________．【解析】因为A ，B 是圆C 1：x 2＋y 2＝1上的动点，AB ＝3，所以线段AB 的中点H 满足221122AB OH ⎛⎫=-= ⎪⎝⎭,∴H 在圆O ：x 2＋y 2＝41上，且2PA PB PH +=u u u r u u u r u u u r 因为点P 是圆C 2：(x －3)2＋(y－4)2＝1上的动点，所以335522PH -≤≤+u u u r ，即71322PH ≤≤u u ur ，所以7213PH ≤≤u u u r ，从而PA PB +u u u r u u u r 的取值范围是[7,13]．。

2020高考数学热点难点微专题“隐圆”问题典型试题(3页)

2020高考数学热点难点微专题“隐圆”问题典型试题1. 已知点M (a ，b )在圆O ：x 2＋y 2＝4外，则直线ax ＋by ＝4与圆O 的位置关系是________．2. 已知|OA →|＝|OB →|＝2，且OA →·OB →＝1，若点C 满足|OA→＋OB →|＝1，则|OC→|的取值范围是________．3. 在平面直角坐标系xOy 中，点A (1,0)，B (4,0)．若直线x －y＋m ＝0上存在点P 使得P A ＝12PB ，则实数m 的取值范围是________．4. 已知两定点A (－3,0)，B (1,0)，如果直线l ：x ＋ay －2＝0上一点M 满足MA 2＋MB 2＝16，那么实数a 的取值范围是________．5. 已知△ABC 中，M 为线段BC 上一点，AM ＝BM ，AM→·AB →＝2，AC 2＋3BC 2＝4，则△ABC 的最大值为________．6. 已知点A (0,1)，B (1,0)，C (t,0)，点D 是直线AC 上的动点，若AD ≤2BD 恒成立，则最小正整数t 的值为________．7. 设直线x ＝－y ＋a 与圆C ：x 2＋y 2－2x ＋4y ＋a ＝0相交于A ，B 两点，若CA→·CB →<0，则实数a 的取值范围为________．8. 已知A ，B 为圆O ：x 2＋y 2＝5上的两个动点，AB ＝4，M 为线段AB 的中点，点P 为直线l ：x ＋y －6＝0上一动点，则PM→·PB →的最小值为________．9. 在平面直角坐标系xOy 中，已知点A (－4,0)，B (0,4)，从直线AB 上一点P 向圆x 2＋y 2＝4引两条切线PC ，PD ，切点分别为C ，D .设线段CD 的中点为M ，则线段AM 长的最大值为________．10. 在平面直角坐标系xOy 中，已知点A (0，－2)，点B (1，－1)，P 为圆x 2＋y 2＝2上一动点，则PB P A 的最大值是________．。

2020江苏高考数学(理)(提高版)大一轮复习课件：微难点10 “隐圆”问题(共31张PPT)

(4) A，B 是两个定点，动点 P 满足P→A·P→B＝l(l 为常数)确定隐圆(如变式)； (5) A，B 是两个定点，动点 P 满足 PA＝λPB(λ＞0 且 λ≠1)确定隐圆(阿波罗尼斯圆)； (6) 由圆周角的性质确定隐圆等．
解类题 ·融会贯通
1.(2017·海安期末)在平面直角坐标系 xOy 中，已知点 P(－1，0)，Q(2,1)，直线 l：ax＋by＋c＝0，其中实数 a，b，c 成等差数列，若点 P 在直线 l 上的射影为 H，则线段 QH 的取值范围是__[__2_，__3__2_]__．
【思维引导】(1)过点 B 作圆 M 的直径 BD，求点 D 的轨迹．(2)将 PB＝2PA 利用坐标法得到点 P 的轨迹，从而得到隐圆．(3)两条直线均过定点，交点在以两个定点间线段为直径的圆周上，从而问题转化为求圆上的点到直线 x－y－4＝0 距离的最大值．
ቤተ መጻሕፍቲ ባይዱ
【解析】方法一：如图，过点 B 作圆 M 的直径 BD，连接 DA，DP，
方法二：设 A(x，y)，则 B(2x－a,2y)．因为点 B 在圆 M 上，所以(2x－a－1)2＋(2y－4)2＝4，即x－a＋2 12＋(y－2)2＝1(*)，这表明点 A 在方程(*)表示的圆上，又点 A 在圆 M 上，因此这两个圆有公共点，
所以 2－1≤ 2 5]．
a＋2 1－12＋2－42≤1＋2，解得 a 的取值范围是[1－2 5，1＋
得 x2＋y2－2x－3≤0，则圆 C：x2＋y2＋2x－1＝0 与圆 C′：x2＋y2－2x－3＝0 有公共点，将两圆方程相减可得两圆公共弦所在直线方程为 x＝－12，代入 x2＋y2－2x－3≤0，可得－ 27≤y≤ 27，所以点 M 的纵坐标的取值范围是－ 27， 27.

江苏省2020届高三数学二轮复习第10讲 “隐形圆”问题(共50张PPT)

因为圆C 上存在点M ，满足MA2 MO2 10，
所以两圆有公共点，所以2 1 a2 a 32 2 1，
所以0 a 3．
变式 1：已知两定点 A3,0， B1,0，若直线l ：
x ay 2 0上的一点P满足PA2 PB2 16，则实数 a 的取值范围是___________．
O B
可得OP 2 ，所以d 3 2 ，
a2 1
解得a2 7 ，所以a 14 或a 14 ．
2
2
2
解：②OA AP， AB OP，
② AB 3
由等积法可得 SOAPB
OA
AP
1 2
OA 1, AB 3, AP OP2 1，
D O
B
所以 OP2 1 1 3 OP，解得OP2 4，
2
2
所以2 2 m 2 2 ．
变式 1：在平面直角坐标系中，已知点 A0,2，
B1,1， P 为圆 x2 y2 2上一动点，则 PB 的最大
PA 值是________．
解：设P x, y，则x2 y2 2，
PB
2
PA
x 12 y 12 x2 y 22
x2 y2 2x 2y 2 x2 y2 4y 4
________．
A P
O B
A
解：由APB 60 可得APO 30 ，
P
由OA 1可得OP 2，所以点P在以 O 为圆心，OP 为半径的圆上，
O B
其方程为 x2 y2 4．
又点P在直线l ：ax y 3上，故直线l与圆x2 y2 4
有公共点，
所以d 3 2， a2 1
2 2x 2y 2 x y 2，
2 4y 4
2y 3

高三数学隐形圆例练习题

高三数学隐形圆例练习题隐形圆是数学中的一个重要概念，它在几何形状的判断和计算中起到了关键作用。

为了帮助高三学生更好地理解和掌握隐形圆的相关知识，本文将提供一些隐形圆的例练习题，并附有解答，供大家参考和实践。

1. 问题描述：已知平面上一圆心为P，点A、B、C分别位于这个平面上的圆周上。

如果角ABC为锐角，且角ABC的度数为30°，则这个圆的方程是什么？解答：首先根据题意，可以知道角ABC为锐角，所以弧AB小于半圆，也即弧AB的度数小于180°。

由题意可知角ABC的度数为30°，所以弧AB的度数也应为30°。

而根据圆的定义，半圆对应的弧度为π，所以弧AB的弧度应为π/6。

由于P为圆心，所以PA、PB、PC为半径，可以用r表示。

根据三角函数的定义，可以得到：cos(π/6) = (PC - PA) / r根据余弦函数的性质，可以知道cos(π/6)等于根号3/2，将其代入上式，得到：根号3/2 = (PC - PA) / r由于PB为半径，所以PA和PC的长度都应等于半径r，所以上式可以转化为：根号3/2 = (r - r) / r化简后可得：根号3/2 = 0 / r根据数学中的定义，当等式两边的值相等时，这个等式为恒等式，即对于任意的r都成立。

因此，这个圆的方程是恒等式。

2. 问题描述：已知平面上一圆心为O，点A、B、C分别位于这个平面上的圆周上，且O为三角形ABC的外心。

如果AB=5，BC=6，AC=7，则这个圆的半径是多少？解答：根据题意，可以知道O为三角形ABC的外心，即三角形的三条边的中垂线交于一点，这个点就是圆心O。

根据中垂线的性质，可以知道中垂线的长度等于对应边的一半。

因此，BO的长度等于AB的一半，即BO=5/2。

类似地，AO和CO的长度分别等于AC和BC的一半，即AO=7/2，CO=6/2=3。

由于O为圆心，所以OA、OB、OC为半径，可以用r表示。

2020届江苏省高考二轮复习专题：隐形圆问题梳理及运用课件(共15张PPT)

Q
小结：核心思想：合理转化
数形合
常见转化途径：三角形外接圆轨迹思想求出圆阿波罗尼斯圆
作业：
1.在三角形ABC 中，角A ，B ，C 所对的边a ，b ，c 满足 2a2+b2+c2=8 ，求三角形ABC面积的最大值． 2.已知A(0，1)，B(1，0)，C(t，0)，点D是直线AC上的动点，若AD ≤ 2BD恒成立，则最小正整数t的值为________________．
5.在平面直角坐标系xOy中，已知圆C经过A(0，2)，O(0，0)，D(t，0) ( t > 0 ) 三点，
M是线段AD上的动点，l1，l2是过点B(1，0)且互相垂直的两条直线，其中l1交y轴于点E，l2 交圆C于P，Q 两点． (1)若t ＝PQ＝6，求直线l2的方程； (2)若t是使 AM ≤ 2BM 恒成立的最小正整数，求三角形EPQ的面积的最小值．
本专题主要来研究发现隐圆并用隐圆解决相关问题.
A
B
C
D
E
轨迹思想
注：ABC 中，若AB为定长，则以下关系表明点C在圆上：
1. AC2 BC2 定值； 2.kAC kBC - 1；
阿波罗尼斯圆
阿波罗尼斯圆：平面上到两个定点的距离之比为定值（不为1）的点的轨迹是一个圆。
.
3.已知点A（2，3），点B（6，-3），点P在直线3x - 4y + 3 = 0上，若满足等式 uuur uuur AP BP 2 0 的点P有两个，则实数的取值范围是_______________．
4.在平面直角坐标系 xOy 中，已知B，C为圆 x2 y2 4 上两点，点A（1，1），且 AB AC ，则线段BC的长的取值范围为_______________．

2020年高考数学压轴填空题闯关：以圆或隐圆为背景的填空题(解析版+原卷版)

1第五关以圆或隐圆为背景的填空题（解析版）【名师综述】直线与圆是高中数学的C 级知识点，是高中数学中数形结合思想的典型体现．近年来，高考对直线与圆的命题，既充分体现自身知识结构体系的命题形式多样化，又保持与函数或不等式或轨迹相结合的命题思路，呈现出“综合应用，融会贯通”的特色，充分彰显直线与圆的交汇价值．类型一以动点轨迹为圆考查直线与圆、圆与圆位置关系典例1．【2020江苏南京初考】已知圆O ：x 2＋y 2＝4和圆O 外一点P (0x ，0y )，过点P 作圆O 的两条切线，切点分别为A ，B ，且∠AOB ＝120°．若点C (8，0)和点P 满足PO ＝λPC ，则λ的范围是_______．【答案】1,13⎡⎤⎢⎥⎣⎦．【解析】【分析】根据4PO =可知220016x y +=，利用PO PC λ=构造方程可求得0215x λ=-；根据044x -≤≤且0λ>可解不等式求得结果．【详解】120AOB ∠=o Q ，2OA OB ==,4cos60AO PO ∴==o，即220016x y +=，又PC =PO PC λ=，()22200816x y λ⎡⎤∴-+=⎣⎦且0λ>，解得：20225115x λλλ-==-， 220016x y +=Q ，044x ∴-≤≤，21454λ∴-≤-≤，解得：1,13λ⎡⎤∈⎢⎥⎣⎦，本题正确结果：1,13⎡⎤⎢⎥⎣⎦。

【名师点睛】本题考查直线与圆的综合应用问题，涉及到两点间距离公式的应用、点的轨迹方程的求解；关键是能够利用λ表示出动点的横坐标，从而根据横坐标范围构造不等式．【举一反三】【2020江苏常州期末考】在平面直角坐标系xOy 中，圆C ：22222210x ax y ay a -+-+-=上存在点P 到点()0,1的距离为2，则实数a 的取值范围是______．【答案】11,01,22⎡⎤⎡+⋃⎢⎥⎢⎣⎦⎣⎦2【解析】【分析】根据题意，求得圆C 的圆心与半径，求出以点()0,1为圆心，半径为2的圆的方程，分析可得，若圆C ：22222210x ax y ay a -+-+-=上存在点P 到点()0,1的距离为2，则圆C 与圆()2214x y +-=有交点，结合圆与圆的位置关系分析可得答案．【详解】∵圆C ：22222210x ax y ay a -+-+-=，∴()()221x a y a -+-=，其圆心(),C a a ，半径1r =．∵点P 到点()0,1的距离为2，∴P 点的轨迹为：22(1)4x y +-=。

江苏省南通市2020届高三数学专题复习课程资源——“隐形圆”(教师版)

隐形圆问题第一讲 “形”现“圆”形问题如图所示，在等腰直角三角形ABC 中，AB ＝BC ＝2，点P 为等腰直角三角形ABC 所在平面内一点，且满足PA ⊥PB ，则PC 的取值范围是__________．1⎤⎦分析本题因为点P 满足PA ⊥PB 即∠APB ＝90°，根据直径所对的圆周角是直角，可知点P 在以AB 为直径的圆上运动，点P 的运动轨迹是一个圆，要求PC 的取值范围，利用PC 与圆心O 三点共线时取得最值，即可解决．可以发现，这里隐藏着一个圆，像这样的问题，我们称为“隐形圆”问题，本题利用初中的平面几何的知识即可解决．变式1 在平面直角坐标系xOy 中，直线l 1的方程为y ＝kx ，直线l 2的方程为x +ky -2k =0，若l 1与l 2的交点为P ，定点(20)C ，，则PC 的取值范围是__________．1⎤⎦分析可以发现直线l 1与l 2是互相垂直的，直线l 1经过原点O （B ），直线l 2经过定点(02)A ，，P 的轨迹是以AB 为直径的圆（不含A 点），于是本题就转换为上述问题，其平面几何背景即为上述问题．变式2（2017年南京二模）在平面直角坐标系xOy 中，直线l 1：kx －y ＋2＝0与直线l 2： x ＋ky －2＝0相交于点P ，则当实数k 变化时，点P 到直线x －y －4＝0的距离AB C P 变式1的最大值为__________．分析直线l 1过定点(02)A ，，直线l 2过定点(20)B ，，AB＝，P 的轨迹是以AB 为直径的圆（不含原点），其圆心为C (1，1)，到直线的距离为P 到直线x －y －4＝0的距离的最大值为+＝圆是高中数学中一种简单但又非常重要的曲线，近几年高考题和高考模拟题中，经常会出现一类有关圆的题目，这类题目在条件中没有直接给出有关圆方面的信息，而是以隐性的形式出现，但我们通过分析和转化，最终都可以利用圆的知识求解．这类题目构思巧妙，综合性强,，充分考查了学生的数形结合、转化和化归等数学思想方法，处理这类题目关键在于能否把"隐形圆"找出来．圆作为几何图形，找“隐形圆”的一个角度可以从“形”的角度来发现．策略一由圆的定义（到定点的距离等于定长的点的轨迹）确定隐形圆例1（1）如果圆(x －2a )2＋(y －a －3)2＝4上总存在两个点到原点的距离为1，则实数a 的取值范围是________．605a -<<【解】到原点的距离为1的点的轨迹是以原点为圆心的单位圆，转化到此单位圆与已知圆相交，从而有13，解得605a -<<．（2）（2016年南京二模）已知圆O ：x 2＋y 2＝1，圆M ：(x －a )2＋(y －a ＋4)2＝1．若圆M 上存在点P ，过点P 作圆O 的两条切线，切点为A ，B ，使得∠APB ＝60°，则a 的取值范围为_________．22a +≤例1（1）【解】由题意得2OP =，所以P 在以O 为圆心2为半径的圆上，即此圆与圆M 有公共点，因此有2221211(4)922OM a a a -+⇒+-⇒≤≤≤≤≤．（3）（2017年苏北四市一模）已知A B 、是圆221:1C x y +=上的动点，AB P 是圆222:(3(4)1C x y -+-=）上的动点，则PA PB +uu r uu r的取值范围是_________．[7,13]【解】取AB 的中点M，由AB C 1M =12，所以M 在以C 1圆心，半径为12的圆上，且2PA PB PM +=uu ruu ruuu r，转化为两圆上动点的距离的最值， PM min ＝ C 1C 2－1－12＝5－1－12＝72 ，PM max ＝C 1C 2＋1＋12＝5＋1＋12＝132，所以PA PB +uu ruu r的取值范围是[7,13]．（4）若对任意α∈R ，直线l ：x cos α＋y sin α＝2sin(α＋6π)＋4与圆C ： (x －m )2＋(y)2＝1均无公共点，则实数m 的取值范围是_________．15(,)22-【解】直线l 的方程为：(x -1)cos α＋(yα＝4，M到l 距离为4，所以l 是以M 为圆心半径为4的定圆的切线系，转化为圆C 内含于圆M ，所以MC ＜3因为M (m)，C3 ，解得1522m -<<．注：直线l ：(x -x 0)cos α＋(y -y 0)sin α＝R 为圆M ：22200()()x x y y R -+-=的切线系．（5）（2016年南通三模）在平面直角坐标系xOy 中，圆()221:12C x y -+=，圆()()2222:C x m y m m -++=，若圆2C 上存在点P 满足：过点P 向圆1C 作两条切线PA 、PB ，切点为A 、B ，ABP ∆的面积为1，则正数m 的取值范围是_________．【解】设P (x ，y )， PA ，PB 的夹角为2θ．△ABP 的面积S=22111sin 212PA PA PA PC θ==．32212PC PA ==+，解得PA 所以12PC =，所以点P 在圆22(1)4x y -+=上．所以22m m -+，解得13m +≤≤策略二由动点P 对两定点A 、B 张角是090（1PA PBk k ⋅=-，或PA PB ⋅=uu r uu r0）确定隐形圆例2 （1）（2014年北京卷）已知圆C ：22(3)(4)1x y -+-=和两点(,0)A m -，(,0)B m (0)m >，若圆上存在点P ，使得∠APB =90°，则m 的取值范围是_________．[]4,6【解】由90APB ∠=o 可知，若点P 存在，则点P 在以AB 为直径的圆O 上，其半径为m ，所以圆O 与圆C 有公共点，从而151m m -≤≤+则m 的取值范围是[]4,6．（2）（海安2016届高三上期末）在平面直角坐标系xOy 中，已知点P (−1，0)， Q (2，1)，直线l ：0ax by c ++=其中实数a ，b ，c 成等差数列，若点 P 在直线 l 上的射影为 H ，则线段 QH 的取值范围是_________．例2（1）【解】直线l 过定点R （1，-2），H 在以PR 为直径的圆上，其圆的半径为12PR，设PR 的中点为M （0，-1），则MQ ＝所以QH min ＝，QH max ＝，则线段 QH的取值范围是．（3）（通州区2017届高三下开学初检测）设m ∈R ，直线1l ：0x my +=与直线 2l ：240mx y m ---=交于点00(,)P x y ，则220002x y x ++的取值范围是_________．[12-+【解】由2222000002(+1)1x y x x y ++=+-，可知其表示00(,)P x y 到定点B (-1，0)的距离的平方减1．因为l 1过定点O (0，0)，l 2过定点A (2，-4)，且l 1 ⊥l 2，则P 在以OA 为直径的圆上，但是由于直线l 1不能表示斜率为0的直线，直线l 2不能表示斜率不存在的直线，所以要除去一点(2，0)．而上述圆的圆心为C (1，-2)，半径为12OA ，由BC＝ PB min ＝BC＝， PB max ＝BC＝222222000002(+1)111x y x x y ,⎡⎤++=+-∈--⎣⎦即[12-+．策略三由圆周角的性质确定隐形圆例3 （1）已知,,a b c 分别为ABC ∆的三个内角,,A B C 的对边，2a =，(a +b )(sin A -sin B )=(c -b )sin C 则ABC ∆面积的最大值为_________【解】原式即为222a b c bc =+-，由余弦定理得cos A ＝12，所以A ＝60°，再由正弦定理，例3(1)例2（3）ABC ∆的外接圆的圆心为O ，则O 到BC，则边BC 上的高h（2）（2017年常州一模）在△ABC 中，∠C ＝45o ，O是△ABC 的外心，若OC mOA nOB=+u u u r u u r u u u r(m ，n ∈R )，则m ＋n 的取值范围是_________．[【解】由圆周角的性质，∠AOB ＝2∠C ＝90°，点C 在以O 为圆心，半径OA 的圆上（在优弧AB 上）．不妨以O 为圆心，OA 所在直线为x 轴，OB 所在直线为y 轴，建立如图所示的直角坐标系，设(1,0)A ，(0,1)B ，(cos ,sin )(2)2C θθθπ<<π，由OC mOA nOB =+u u u r u u r u u u r得到cos sin m n θθ=⎧⎨=⎩，所以m ＋n＝cos sin )4θθθπ++，结合22θπ<<π，得到sin()[4θπ+∈-，故m ＋n的取值范围是[．当圆周角是直角时，即为策略二的情形．策略四由四点共圆的定理来确定隐形圆（如一个四边形的对角互补，则该四边形四点共圆）例4 （2011年全国卷2）设向量a ，b ，c 满足|a |＝|b |＝1，a ·b ＝－12，若a －c 与b －c 的夹角为60°，则|c |的最大值等于． 2【解】设向量a ，b ，c 的起点为O ，终点分别为A ，B ，C ，由已知条件得，∠AOB ＝120°，∠ACB ＝60°，则点C 在△AOB 的外接圆上，当OC 经过圆心时，|c |最大，在△AOB 中，求得AB ＝3，由正弦定理得△AOB 外接圆的直径是3sin120°＝2，||c 的最大值是2．例3（2）例4【同步练习】1．点A ，B 分别在x 轴与y 轴的正半轴上移动，且AB ＝2，若点A 从(3，0)移动到(2，0)，则AB 中点D 经过的路程为．π122．已知O 为坐标原点，向量20(,)OB =uu u r ，22(,)OC =uuu r,)CA αα=uu r，则OA uu r 与OB uu u r 夹角的范围为．[,]1212π5π3．已知直线20:l x y m -+=上存在点M 满足与两点(2,0)A -,(2,0)B 连线的斜率之积为1-，则实数m 的取值范围是．[-4．已知圆C ：x 2＋y 2＝1，点P (x 0，y 0)在直线x －y －2＝0上，O 为坐标原点，若圆C 上存在一点Q ，使得∠OPQ ＝30°，则x 0的取值范围是________．[0,2]5．如图，已知点A (－1,0)与点B (1,0)，C 是圆x 2＋y 2＝1上的动点(与点A ,B 不重合)，连接BC 并延长至D ，使得|CD |＝|BC |，则线段PD 的取值范围．2(,2)3第5题第二讲 “数”现“圆”形解析几何中，找“隐形圆”的另一个角度可以从“数”的角度（求出其方程）来发现．策略五直接由圆（半圆）的方程确定隐形圆例1 （1）(2016年泰州一模)已知实数a ，b ，c 满足222a b c +=，0c ≠，则2ba c-的取值范围为__________．[【解】方法一令a x c =，b y c=，则原题转化为实数x 、y 满足221x y +=，求2yx -的取值范围，归结为以原点为圆心的单位圆上的动点M ()x y ，与定点(20)P ，的斜率的取值范围．方法二令cos a c θ=，sin b c θ=，原题转化为求sin cos 2θθ-的取值范围，而动点(cos sin )θθ，在以原点为圆心的单位圆上，以下同方法一．（2）若方程3x ＋b 有解，则b 的取值范围是． [1－22，3]【解】令y ＝3(x －2)2＋(y －3)2＝4 (1≤y ≤3)，即表示圆心为(2,3)，半径为2的半圆．当直线l ：y ＝x ＋b 与此半圆相切时，满足圆心(2,3)到直线y ＝x ＋b 距离等于2，解得b ＝1＋b ＝1－，因为是下半圆，故可得b ＝1＋当直线过(0,3)时，解得b ＝3，故1－b ≤3．（3）已知实数x 、y满足x y -，则x +y 的最大值是__________．例1(1)例1(3)0s ≥0t =≥，则21x s =-,23y t =-，代入原式并整理，得22119()()222s t -+-=．因此动点()P s t ，的轨迹是圆位于第一象限的一段圆弧（含与x 轴、y 轴的正半轴的交点），此圆的圆心为11()22C ，，半径为r =，而x +y 224s t =+-，所以（x +y ）max 22()444OC r =+-=-=．另法：（基本不等式）原式化为x y +=22()2(13)x y x y +=+++≤即2()2()80x y x y ++--≤，解得x +y ≤4（当且仅当31x y =⎧⎨=⎩时取“＝”）．策略六直接由圆（半圆）的参数方程确定隐形圆例2（1）已知,t R θ∈，则22(cos 2)(sin 2)t t θθ--+-+的取值范围是__________．[9)-+∞【解】点(cos sin )P θθ，在以原点为圆心的单位圆上，(22)Q t t +-，在直线40x y --=上，转化为圆上的动点与直线上的动点的距离的平方的取值范围，圆心到直线的距离为所以，圆上的动点与直线上的动点的距离的最小值为1，其平方为9- （2）（2008年重庆高考）函数f (x02x π≤≤) 的值域是________．[-1,0]【解】f (x )= 当sin x ＝1时，f (x )＝0；例1(1)例2(2)当-1≤sin x ＜1时，f (x) =其中cos 1sin 1x x --的几何意义为以原点为圆心的单位圆上的动点(cos sin )x x ，与定点(11)，构成直线的斜率，则cos 1sin 1x x --≥0，所以得到-1≤f (x ) ≤0．策略七由两定点A 、B ，动点P 满足PA PB λ⋅=uu r uu r（λ是常数）,求出动点P 的轨迹方程确定隐形圆例3 已知圆22341:()()C x y -+-=和两点00(,),(,)A m B m -0()m >．若圆C 上存在点P ，使得1PA PB ⋅=u u r u u r，则m 的取值范围是__________．【解】设点()P x y ，，满足1PA PB ⋅=u u r u u r，得2221x y m +=+，这是一个圆的方程，从而转化为151≤，解得m的取值范围是．注若0PA PB ⋅=uu r uu r，则点P 在以AB 为直径的圆上．变式1 （2017年南通密卷3）已知点(2,3)A ，(6,3)B -，点P 在直线3430x y -+=上，若满足等式20AP BP λ⋅+=u u u r u u u r的点P 有两个，则实数λ的取值范围是__________．【解】设P (x ，y )，则(2,3)AP x y =--u u u r ，(6,3)BP x y =-+u u u r，根据20AP BP λ⋅+=u u u r u u u r ，有()221341322x y λλ⎛⎫-+=-< ⎪⎝⎭.由题意圆：()221341322x y λλ⎛⎫-+=-< ⎪⎝⎭与直线3430x y -+=相交，圆心到直线的距离3d ==<2λ<.变式2 （2017年江苏高考）在平面直角坐标系xOy 中，(120)A -，，(06)B ，，点P 在圆2250O x y +=：上，若20,PA PB ⋅u u u r u u u r≤则点P 的横坐标的取值范围是__________．【解】设点()P x y ，，由20PA PB ⋅u u u r u u u r≤，即22(6)(3)65x y ++-≤，表示点P 在此圆内部（含边界），又在圆O 上，故联立2222(6)(3)6550x y x y ⎧++-=⎪⎨+=⎪⎩，得55x y =-⎧⎨=-⎩或17x y =⎧⎨=⎩，结合圆O的最左边点为(-，所以的横坐标的取值范围是[-．策略八由两定点A 、B ，动点P 满足22PA PB +是定值确定隐形圆例4（1）在平面直角坐标系xOy 中，已知圆C ：(x －a )2＋(y －a ＋2)2＝1，点A (0，2)，若圆C 上存在点M ，满足MA 2＋MO 2＝10，则实数a 的取值范围是__________．[0，3]【解】设M (x ，y )，由MA 2＋MO 2＝10，A (0，2)，得x 2＋(y －1)2＝4，而M 又在圆C ：(x －a )2＋(y －a ＋2)2＝1上，故它们有公共点，则1≤a 2＋(a －3)2≤9，解得实数a 的取值范围是[0，3]．（2）（2017届盐城三模）已知A B C D ，，，四点共面，2BC =，2220AB AC +=，3CD CA =u u u r u u u r，则||BD u u u r的最大值为．10例3变式2【解】以BC 所在直线为x 轴，线段BC 的垂直平分线为y 轴，建立直角坐标系．设()A x y ，，则(10)B -，，(10)C ，，由2220AB AC +=，得229x y +=，所以OA ＝3．取(20)E -，，故3CE CO =u u u r u u u r ，所以ED ＝3OA ＝9，所以点D 在以E 为圆心，半径为9的圆上，故||BD u u u r的最大值为EB ＋9＝10．变式在直角坐标系xOy 中，已知A (－1，0)、B (0，1)，则满足P A 2－PB 2＝4且在圆x 2＋y 2＝4上的点P 的个数为________．2【解】设P (x ，y )，由P A 2－PB 2＝4知[(x ＋1)2＋y 2]－[x 2＋(y －1)2]＝4，整理，得x ＋y －2＝0．又圆心(0，0)到直线x ＋y －2＝0距离d ＝22＝2＜2，因此直线与圆有两个交点，故符合条件的点P 有2个．策略九由两定点A 、B ，动点P 满足01PAPBλλλ=>≠(,)确定隐形圆（阿波罗尼斯圆）例5（1）（2016年南通一模）在平面直角坐标xOy 中，已知点(1,0),(4,0)A B ，若直线0x y m -+=上存在点P 使得12PA PB =,则实数m 的取值范围是________．[-【解】点P 满足圆的方程为224x y +=，转化到直线与圆有交点的问题.例4（2）例5（1）变式1 若12PA PB ≤呢？【解】点P 在圆：224x y +=的内部（含边界），仍然转化到直线与圆有交点的问题. 变式2 （2013年江苏卷第17题改编）在平面直角坐标系xOy 中，已知点00(,)O ，03(,)A ．如果圆22241:()()C x a y a -+-+=上总存在点M 使得2MA MO =，则圆心C 的横坐标a 的取值范围是________．1205[,]【解】设(,)M x y ，由2MA MO =22(1)4x y ++=，其表示以(0,1)D -为圆心，半径为2的圆，则圆D 与圆C 有公共点，得13，解得a 的取值范围是1205[,]．（2）（2016届常州一模）在平面直角坐标系xOy 中，已知圆O ：x 2＋y 2＝1，O 1：(x －4)2＋y 2＝4，动点P在直线0x b -=上，过点P 作圆O ，O 1的两条切线，切点分别为A ，B ，若满足2PB PA =的点P 有且仅有两个，则b 的取值范围_________．20,43⎛⎫⎪⎝⎭－例5（1）变式1例5（1）变式2【解】由2PB PA =平方得224PB PA =，故22144(1)PO PO -=-．设(,)P x y ，代入上式得22464()39x y ++=，其表示以4(,0)3Q -为圆心，半径为83的圆，由题意，则直线0x b -=与圆Q 由两个不同的交点，故48323bd --=<，解出b 的取值范围为20,43⎛⎫⎪⎝⎭－．（3）已知曲线C 的方程221x y +=，()2,0A -，存在一定点()(),02B b b ≠-和常数λ，对曲线C 上的任意一点(),M x y ，都有MA MB λ=成立，则点(),P b λ到直线()220m n x ny n m ++++=的最大距离为_________．【解】方法一：由MA MB λ=得()()222222x y x b y λ⎡⎤++=-+⎣⎦即()()()222222211244x y b x b λλλλ-+--+=- 故2222240411b b λλλ⎧+=⎪⎨-=⎪-⎩，将22b λ=-代入22241b λλ-=-得22520b b ++=，得12b =-，2b =-（舍去），故2λ=．又直线()220m n x ny n m ++++=恒过定点()2,0-，所以由几何性质知点1,22P ⎛⎫- ⎪⎝⎭到直线()220m n x ny n m ++++=的最大距离为点()2,0-与1,22P ⎛⎫-⎪⎝⎭的距离为52．方法二：作为小题，由MA MB λ=知是阿氏圆轨迹，故取圆22:1C x y +=直径上的两个点()()1,0,1,0-，即可得1311b b λ==+-，解得12b =-，2b =-（舍去），故2λ=，以下同方法一．例6（2017年南通二模）一缉私艇巡航至距领海边界线l （一条南北方向的直线）3.8海里的A 处，发现在其北偏东30°方向相距4海里的B 处有一走私船正欲逃跑，缉私艇立即追击．已知缉私艇的最大航速是走私船最大航速的3倍．假设缉私艇和走私船均按直线方向以最大航速航行．（1）略；（2）问：无论走私船沿何方向逃跑，缉私艇是否总能在领海内成功拦截？并说明理由．【解】（1）略（2）如图乙，以A 为原点，正北方向所在的直线为y 轴建立平面直角坐标系xOy ．则(2B ，，设缉私艇在()P x y ，处（缉私艇恰好截住走私船的位置）与走私船相遇，则3PA PB=3=．整理得，()(229944x y -+=，所以点()P xy ，的轨迹是以点(94为圆心，32为半径的圆．因为圆心(94到领海边界线l ： 3.8x =的距离为1.55，大于圆半径32，所以缉私艇能在领海内截住走私船．北(例6)【同步练习】1．已知圆C ：(x －3)2＋(y －4)2＝1，点A (0，－1)，B (0,1)．P 是圆C 上的动点，当|P A |2＋|PB |2取最大值时，点P 的坐标是________．【解】P (x 0，y 0)，则|P A |2＋|PB |2＝x 20＋(y 0＋1)2＋x 20＋(y 0－1)2＝2(x 20＋y 20)＋2，显然x 20＋y 20的最大值为(5＋1)2，∴d max ＝74，此时OP →＝－6PC →，结合点P 在圆上，解得点P 的坐标为⎝⎛⎭⎫185，245.2．（2016年盐城三模）已知线段AB 的长为2，动点C 满足CA CB λ⋅=u u u r u u u r（λ为常数），且点C 总不在以点B 为圆心，12为半径的圆内，则负数λ的最大值是__________．34- 略解：动点C 满足方程221x y λ+=+.3．（2016年苏北四市一模）已知)1,0(A ，)0,1(B ，)0,(t C ，点D 是直线AC 上的动点，若2AD BD ≤恒成立，则最小正整数t 的值为________．44．在平面直角坐标系xOy 中，M 为直线x ＝3上一动点，以M 为圆心的圆记为圆M ，若圆M 截x 轴所得的弦长恒为4．过点O 作圆M 的一条切线，切点为P ，则点P 到直线2x ＋y －10＝0距离的最大值为_____．3 5 【提示】设M (3，t )，P (x 0，y 0)，因为OP ⊥PM ，所以OP →·PM →＝0，可得x 02＋y 02－3x 0－ty 0＝0 ① 又圆M 截x 轴所得的弦长为4，所以4＋t 2＝(x 0－3)2＋(y 0－t )2，整理得x 02＋y 02－6x 0－2ty 0＋5＝0 ② 由①②得x 02＋y 02＝5，即点P 在圆x 2＋y 2＝5上，于是P 到直线2x ＋y －10＝0距离的最大值为105＋5＝35． 5．已知x y ∈R 、且满足22246x xy y ++=，则224z x y =+的取值范围是．[4,12]第三讲 “隐圆”综合隐藏圆问题可以和很多知识点结合，在三角形、向量、圆锥曲线等背景的一些问题中看上去和圆无关，但却隐藏着圆．一、三角形中的隐形圆例1（1）（2017年南京、盐城一模）在ABC ∆中，A ，B ，C 所对的边分别为,,a b c ，若22228a b c ++=，则ABC ∆面积的最大值为__________【解】以AB 的中点为原点，AB 所在直线为x 轴，建系. 设(,0)2c A -，(,0)2cB ，(,)C x y ，则由22228a b c ++=，得22222()()2822c c x y x y c -+++++=，即222544x y c +=-，所以点C 在此圆上，S≤2c r =（2）（2008年高考江苏卷）若=2AB AC ，，则ABC S ∆的最大值是__________．【解】以AB 的中点为原点，AB 所在直线为x 轴，建系. 则(1,0)A -，(1,0)B ，设(,)C x y ，由题意得22(3)=8x y -+，从而C 到AB的距离最大值为ABC S ∆的最大值是变式已知ACD ∆中，B 为CD 的中点，且=2AB CD ，，则ACD S ∆的最大值是_____【解】ACD S ∆是ABC S ∆的两倍，从而转化为上题．例2 （1）在ABC ∆中，BC ＝2，AC ＝1，以AB 为边作等腰直角三角形ABD (B 为直角顶点，C 、D 两点在直线AB 的两侧)．当∠C 变化时，线段CD 长的最大值为． 3【解】过点B 作CB 的垂线，取E 点，使得BE，连接ED ，有BE ＝BC ，BD ＝BA ， ∠DBE ＝∠ABC ，则△BED ≌△BCA ，故ED ＝1，D 在以E 为圆心，1为半径的圆上．故CD max ＝DE ＋CE ＝1＋2＝3．（2）在ABC ∆中，点D 在边BC 上，且DC ＝2BD ，AB ∶AD ∶AC ＝3∶k ∶1，则实数k 的取值范围为．57(,)33【解】不妨设AB ＝3，则AD ＝k ，AC ＝1，由DC ＝2BD ，取AB 上一点E ，使得AE ＝2EB ，则DE 1133AC ==，故D 在以E 为圆心，13为半径的圆上运动，则112233k -<<+，即5733k <<．例2（1）ABCED例2（2）ACEBD二、向量中的隐形圆例3 （1）已知向量a 、b 、c满足=a 3==⋅b a b ，若()()0--=c a c b ，则-b c 的最大值是__________．【解】易知a 、b 的夹角为45°，作OA =u u u r a ，OB =u u u r b ，OC =u u u r c ，则0AC BC ⋅=u u u r u u u r所以C 在以AB 为直径的圆上，AB，CB AB -==u u u r≤b c 变式1 已知向量a 、b 、c满足=a 3==⋅b a b ，若(2)(23)0--=c a b c ，则-b c 的最大值是__________．1【解】由(2)(23)0--=c a b c 得2(2)()03--=c a c b ，易知a 、b 的夹角为45°，作OA =u u u r a ，OB =u u u r b ，OC =u u u r c ，2OA '=u u u r a ，23OB '=u u u u r b ，由余弦定理知2A B ''=，而0CA CB ''⋅=u u u r u u u r ，所以C在以A B ''为直径的圆上，设A B ''的中点为D ，则BD，从而112CB A B BD ''-=+=+u u u r ≤b c变式2 已知向量a ，b ，c 满足|a |=1，|a -b |=|b |，（a -c ）·（b -c ）=0，若对每一个确定的向量b ， |c |的最大值和最小值分别为m ，n ，则对于任意向量b ，m +n 的最小值是__________．32例3（1）BOAC例3（1）变式2AO BDC例3（1）变式1【解】作OA =u u u r a ，OB =u u u r b ，OC =u u u r c ，由|a -b |=|b |得OB ＝AB ，且0AC BC ⋅=u u u r u u u r，所以C 在以AB 为直径的圆上，设AB 的中点为D ，则m ＋n ＝(OD ＋CD )＋(OD －CD ) ＝2OD 因为OD min ＝34，所以m ＋n 的最小值是32．（2）（2016年高考四川理数）在平面内，定点A ，B ，C ，D 满足DA u u u r =DB u u u r =DC u u u r，DA u u u r ⋅DB u u u r =DB u u u r ⋅DC u u u r =DC u u u r ⋅DA u u u r = -2，动点P ，M 满足AP u u u r=1，PM u u u u r =MC u u u u r ，则2BM u u u u r 的最大值是__________．494【解】由已知可得∠ADC ＝∠ADB ＝∠BDC ＝120°，DA ＝DB ＝DC =2，故△ABC 为等边三角形．由M 为PC 的中点，取AC 的中点E ，则ME 为△ACP 的中位线，ME ＝1122AP =，所以M 在以E 为圆心，半径为12的圆E 上BE ＝332BD =，故BM 的最大值为 BE ＋ME ＝3＋12＝72，则2BM u u u u r 的最大值是494．例4 已知OA u u u r ，OB u u u r 为非零的不共线的向量，设111r OC OA OB r r=+++u u u r u u u r u u ur ．定义点集{|}||||KA KC KB KCM K KA KB ⋅⋅==u u u r u u u r u u u r u u u r u u u r u u u r ．当1K 、2K M ∈时，若对任意的2r ≥，不等式12||||K K c AB u u u u u r u u u r ≤恒成立，则实数c 的最小值为__________．43例3（2）CAPDME【解】由111r OC OA OB r r =+++u u u r u u u r u u u r 即AC rCB =u u u r u u u r ，所以1CB CA r=，由||||KA KC KB KCKA KB ⋅⋅=u u u r u u u r u u u r u u u r u u u r u u u r ，有cos cos AKC BKC ∠=∠，所以AKC BKC ∠=∠，即CK 为 ∠AKB 的角平分线，由角平分线定理得1KB CB KA CA r==，所以KA rKB =，故K 的轨迹为阿波罗尼斯圆，其圆心在AB 直线上，若对任意的2r ≥，不等式12||||K K c AB u u u u u r u u u r≤恒成立，则12max 12max ()()K K K K c AB AB=≥，12max ()K K 即为此圆的直径，设此圆和直线AB 的交点为M 、N ，则MN 为圆的直径， 211221111BM BN BM BN r c AB AB AB r r r r r+=+=+==-+--≥当r ≥2时，min 13()2r r -=，故max 24()13r r=-，所以c ≥43，实数c 的最小值为43．例5 （2014年常州高三期末卷）在平面直角坐标系xOy 中，已知圆2216:O x y +=，点P 12(,)，M 、N 为圆O 上两个不同的点，且0PM PN ⋅=uuu r uuu r ，若PQ PM PN =+uu u r uuu r uuu r，则PQ uu u r 的最小值为__________．【解】方法一：显然四边形PMQN 为矩形，设MN 与PQ 的交点为 R (x ，y )，则OM 2＝OR 2+RM 2＝OR 2+PR 2，即222216(1)(2)x y x y =++-+-得22127()(1)24x y -+-=，所以R 的轨迹是以1(1)2S ,的圆，由PSPR min，故2PQ PQ PR ===min min min uu u r例5方法二：显然四边形PMQN 为矩形，由矩形的几何性质（矩形所在平面上的任意一点到其对角线上的两个顶点的距离的平方和相等），有2222OM ON OP OQ +=+，所以OQ＝故Q 在以O为圆心，半径为OP，所以PQ的最小值为．变式1 （2017年南通市一模）在平面直角坐标系xOy 中，已知B ，C 为圆224x y +=上两点，点(11)A ，，且AB ⊥AC ，则线段BC 的长的取值范围为__________．【解】方法一（标解）：设BC 的中点为(),M x y ，因为22222OB OM BM OM AM =+=+，所以()()2222411x y x y =++-+-，化简得22113222x y ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭，所以点M 的轨迹是以1122N ⎛⎫⎪⎝⎭，为圆心，所以AM的取值范围是⎣⎦，所以BC的取值范围是．例5方法二：以AB 、AC 为邻边作矩形BACN ，则BC ＝AN ，由矩形的几何性质（矩形所在平面上的任意一点到其对角线上的两个顶点的距离的平方和相等），有2222OB OC OA ON +=+，所以ON，故N 在以OOA，所以BC 的取值范围是．变式2 已知圆1C ：229x y +=，圆2C ：224x y +=，定点(1,0)P ，动点,A B 分别在圆1C 和圆2C 上，满足90APB ∠=o ，则线段AB 的取值范围__________．1]+【解】以P A 、PB 为邻边构造矩形APBQ ，则AB ＝PQ ，由矩形的几何性质（矩形所在平面上的任意一点到其对角线上的两个顶点的距离的平方和相等），有2222OP OQ OA OB +=+，所以OQ 2＝12，即OQ＝Q 在以O为圆心，半径为的圆上，因为OP ＝1，所以AB的取值范围是11⎡⎤+⎣⎦．变式3 已知向量a 、b 、c 满足3,2,1,()()0===-⋅-=a b p a p b p ，则-a b 范围为__________．1]【解】作向量OA =u u u r a ，OB =u u u r b ，OP =u u u r p ，则0PA PB ⋅=u u u r u u u r，AB -=a b ，不妨以O 为坐标原点，OP 所在直线为x 轴，建立直角坐标系，则本题转化为上题．变式1三、圆锥曲线中的隐形圆例6 在平面直角坐标系xOy 中，已知圆1O ，圆2O 均与x 轴相切且圆心1O ，2O 与原点O 共线，1O ，2O 两点的横坐标之积为6，设圆1O 与圆2O 相交于P ，Q 两点，直线l ：280x y --=，则点P 与直线l 上任意一点M 之间的距离的最小值为__________-【解】设圆心O 1，O 2在直线y ＝tx 上，P (x 0，y 0)，可设O 1(m ，mt )，O 2(n ，nt )，则mn ＝6，所以⊙O 1：(x －m )2+(y －mt )2=(mt )2， ⊙O 2：(x －n )2+(y －nt )2=(nt )2，所以 (x 0－m )2+(y 0－mt )2=(mt )2， (x 0－n )2+(y 0－nt )2=(nt )2，所以m 、n 为(x 0－x )2+(y 0－tx )2=(tx )2即x 2－2(x 0+ y 0t ) x +2200x y +=的两根．由二次方程的根与系数的关系，得mn 22006x y =+= 所以P (x 0，y 0)在圆x 2+ y 2=6上，其圆心为O (0，0)，O 到l，则点P 与直线l 上任意一点M．变式（2015年江苏初赛）如图，在平面直角坐标系xOy 中，圆O 1、圆O 2都与直线l ：y ＝kx 及x 轴正半轴相切．若两圆的半径之积为2，两圆的一个交点为P (2，2)，求直线l 的方程．【解】由题意，圆心O 1，O 2都在x 轴与直线l 的角平分线上．若直线l 的斜率k ＝tanα，设t ＝tan α2，则k ＝2t1－t 2．圆心O 1，O 2在直线y ＝tx 上，可设O 1(m ，mt )，O 2(n ，nt )．交点P (2，2)在第一象限，m ，n ，t ＞0．所以⊙O 1：(x －m )2+(y －mt )2=(mt )2，⊙O 2：(x －n )2+(y －nt )2=(nt )2，所以⎩⎨⎧(2－m )2＋(2－mt )2＝(mt )2，(2－n )2＋(2－nt )2＝(nt )2，即⎩⎨⎧m 2－(4＋4t )m ＋8＝0，n 2－(4＋4t )n ＋8＝0，所以m ，n 是方程X 2－(4+4t )X ＋8=0的两根，mn ＝8．由半径的积(mt )(nt )＝2，得t 2＝14，故t ＝12．所以k ＝2t 1－t 2＝11－14＝43，直线l ：y ＝43x ．例7 设椭圆E ：x 28＋y 24＝1，是否存在圆心在原点的圆，使得该圆的任意一条切线与椭圆E恒有两个交点A ，B ，且OA u u u r ⊥OB u u u r？【解】假设满足题意的圆存在，其方程为x 2＋y 2＝R 2，其中0＜R ＜2．设该圆的任意一条切线AB 和椭圆E 交于A (x 1，y 1)、B (x 2，y 2)两点，o 1当直线AB 的斜率存在时，设直线AB 的方程为y ＝kx ＋m ， ①将其代入椭圆E 的方程并整理得 (2k 2＋1)x 2＋4kmx ＋2m 2－8＝0. 得x 1＋x 2＝－4km2k 2＋1，x 1x 2＝2m 2－82k 2＋1.② 因为OA u u u r ⊥OB u u u r，所以x 1x 2＋y 1y 2＝0.③把①代入③并整理得 (1＋k 2)x 1x 2＋km (x 1＋x 2)＋m 2＝0. 结合② 得m 2＝83(1＋k 2)．④因为直线AB 和圆相切，因此R ＝|m |1＋k 2，由④得R ＝263，所以存在圆x2＋y 2＝83满足题意． o 2当切线AB 的斜率不存在时，易得221283x x ==，由椭圆E 的方程得221283y y ==，容易判断OA u u u r ⊥OB u u u r ．综上所述，存在圆x 2＋y 2＝83满足题意．法二：（引入k 算出A 、B 坐标）o 1当OA 的斜率存在，且不为0时，设直线OA 的方程为y kx =，则直线OB 的方程为1y x k=-，设A (x 1，y 1)、B (x 2，y 2)，将y kx =代入x 28＋y 24＝1，得212812x k =+，则2222128(1)(1)12k OA k x k +=+=+，同理，2228(1)2k OB k +=+，∴22222228(1)8(1)122k k AB OA OB k k ++=+=+++设O 到AB 的距离为d ，则22222222222228(1)8(1)81228(1)8(1)3122k k OA OB k k d k k OA OB k k ++⋅⋅++===++++++． o 2当OA 的斜率不存在或为0时，容易验证283d =∴综上所述，存在圆心在原点的圆x 2＋y 2＝83满足题意．探究：是否可以将此结论推广到一般性的结论呢？对于椭圆：x 2a 2＋y 2b 2＝1(a ＞b ＞0) ，椭圆上的两点A 、B 满足OA OB ⊥，是否存在以AB 为切线且以O 为圆心的定圆？如果存在，其半径是多少?法一：o1当OA 的斜率存在，且不为0时，联列方程222222b x a y a b y kx⎧+=⎨=⎩，得2221222a b x b a k =+ 同理，22222222a b k x b k a=+，则2222221222(1)(1)a b OA k x k b a k=+=++，22222222222221(1)(1)1a b a b OB k k b k a b a k =+=+++ ∴222222222222222(1)(1)a b a b AB OA OB k k b a k b k a =+=+++++ 设O 到AB 的距离为d ，则2222222222222222222222222222222222(1)(1)(1)(1)a b a b k k OA OB a b b a k b k a d R a b a b OA OB a b k k b a k b k a +⋅+⋅++====+++++++． o2当OA 的斜率不存在或为0时，容易验证2d 22222a b R a b==+ ∴存在以AB 为切线且以O 为圆心的定圆，其方程为222222a b x y a b +=+．法二：联列方程222222b x a y a b y kx m⎧+=⎨=+⎩，得222222222()20a k b x a kmx a m a b +++-=∴2122222222122222a km x x a k b a m a b x x a k b ⎧+=-⎪⎪+⎨-⎪=⎪+⎩∵OA u u u r ⊥OB u u u r ，∴x 1x 2＋y 1y 2＝0 ∵11y kx m =+，22y kx m =+ ∴(1＋k 2)x 1x 2＋km (x 1＋x 2)＋m 2＝0 ∴(1＋k 2)2222222a m a b a k b -+＋km 22222()a km a k b -+＋m 2＝0 ∴222222(1)a b m k a b=++则O 到直线y kx m =+的距离为d R ===，∴存在以AB 为切线且以O 为圆心的定圆，其方程为222222a b x y a b +=+．法三：（极坐标思想）以O 点为极点，x 轴正向为极轴方向，设1(,)A ρθ，2(,)2B πρθ+，代人椭圆方程得221122222222(cos )(sin )1(cos())(sin())221a b a b ρθρθππρθρθ⎧+=⎪⎪⎨++⎪+=⎪⎩∴222221222222cos sin 1sin cos 1a b a b θθρθθρ⎧+=⎪⎪⎨⎪+=⎪⎩ ∴ 2222121111a b ρρ+=+ ∴222212222222212111OA OB a b R OA OBρρρρ+++===． ∴ 22222a b R a b =+ 其方程为222222a b x y a b +=+．注：此法也适用于例7．变式（2012年上海高考改编）在平面直角坐标系xOy 中，已知双曲线12:221=-y x C ，椭圆22241C x y +=：，若M 、N 分别是1C 、2C 上的动点，且OM ⊥ON ，求证：O 到直线MN 的距离是定值．【解】方法一：（引入k 算出A 、B 坐标）当直线ON 垂直于x 轴时， ON =1，OM，则O 到直线MN.当直线ON 不垂直于x 轴时，设直线ON 的方程为kx y =（显然||k >），则直线OM 的方程为1y x k=-. 由⎩⎨⎧=+=1422y x kx y ，得22222144x k k y k ⎧=⎪⎪+⎨⎪=⎪+⎩，所以22214k ON k +=+. 同理222121k OM k +=-.设O 到直线MN 的距离为d ，因为22222()OM ON d OM ON +=⋅，所以222221113331k d OM ON k +=+==+，即d.综上，O 到直线MN 的距离是定值.方法二：（极坐标思想）设O 到直线MN 的距离为d ，以O 点为极点，x 轴正向为极轴方向，设1(,)M ρθ，2(,)2N πρθ+，代入1C 、2C 的方程得1222222212cos sin 14cos ()sin ()22θθρππθθρ⎧-=⎪⎪⎨⎪+++=⎪⎩，即1222222212cos sin 14sin cos θθρθθρ⎧-=⎪⎪⎨⎪+=⎪⎩，把两式相加得122222113sin 3cos θθρρ+=+，∴22222222221113OM ON MN OM ON OM ON OM ON d +=+===⋅⋅∴d =．注：本题中直线MN 总是和隐圆2213x y +=相切．【同步练习】1．若a ，b ，c 均为单位向量，且a·b ＝0，(a －c )·(b －c )≤0，则|a ＋b －c |的最大值为_________． 1 2．已知曲线C ：x ＝－4－y 2，直线l ：x ＝6，若对于点A (m ，0)，存在C 上的点P 和l 上的点Q 使得AP u u u r＋AQ u u u r ＝0，则m 的取值范围为．[2，3]解曲线C ：x ＝－4－y 2，是以原点为圆心，2为半径的半圆，并且x P ∈[－2,0]，对于点A (m,0)，存在C 上的点P 和l 上的点Q 使得AP u u u r＋AQ u u u r ＝0，说明A 是PQ 的中点，Q 的横坐标x ＝6，∴m ＝6＋xP2∈[2，3]．3．已知圆()22:11C x y -+=，点(3,0)D ，过动点P 作圆C 的切线PQ ，切点为Q ，若PD =，则△PCD 面积的最大值为__________5．已知是边长为3的等边三角形，点P 是以A 为圆心的单位圆上一动点，点Q 满足2133AQ AP AC =+u u u r u u u r u u u r ，则BQ u u u r 的最小值是__________23。

专题——隐圆问题

隐圆专题（1）一、问题概述江苏省高考考试说明中圆的方程是C 级知识点，每年都考，但有些时候，在条件中没有直接给出圆方面的信息，而是隐藏在题目中的，要通过分析和转化、发现圆（或圆的方程），从而最终可以利用圆的知识来求解，我们称这类问题为“隐形圆”问题．二、求解策略题型一、利用圆的定义（到定点的距离等于定长的点的轨迹）确定隐形圆1．如果圆4)3()2(22=--+-a y a x 上总存在两个点到原点的距离为1，则实数a 的取值范围是．2．已知圆1:22=+y x O ，圆()()14:22=+-+-a y a x M ．若圆M 上存在点P ，过点P 作圆O 的两条切线，切点为B A 、，使得060=∠APB ，则a 的取值范围为．3．已知B A 、是圆1:221=+y x C 上的动点，3=AB ，P 是圆222)4()3(:-+-y x C1=+4．在平面直角坐标系xoy 中，已知C B ,为圆422=+y x 上两点，点)1,1(A ，且AC AB ⊥，则线段BC 的长的取值范围为______________．题型二、动点对两定点B A 、的张角是090（1-=⋅PB PA k k 或0=⋅PB PA ）确定隐形圆 1．已知圆C ：1)4()3(22=-+-y x 和两点)0,(m A -，)0,(m B ，若圆C 上存在点P ，使得090=∠APB ，则m 的取值范围是______________．2．已知直线l ：02=+-m y x 上存在点M 满足与两点)0,2(-A ，)0,2(B 连线的斜率之积为1-，则m 的取值范围是______________．3．在平面直角坐标系xOy 中，直线021=+-y kx l ：与直线02:2=-+ky x l 相交于点P ，则当实数k 变化时，点P 到直线04=--y x 的最大值为____________．4．在平面直角坐标系xOy 中，已知点)0,1(-P ，点)1,2(Q ，直线l ：0=++c by ax ，（其中c b a ,,成等差数列），点P 在直线l 上的射影为H ，则线段QH 的取值范围是________．题型三、两定点B A 、，动点P 满足λ=⋅PB PA 确定隐形圆1．已知圆C ：1)4()3(22=-+-y x 和两点)0,(m A -，)0,(m B （0>m ），若圆C 上存在点P ，使得1=⋅PB PA ，则m 的取值范围是___________．2．在平面直角坐标系xOy 中，已知点)0,(t A -（0>t ），)0,(t B ，点C 满足8=⋅→-→-BC AC ，且点C 到直线l ：02443=+-y x 的最小距离为59，则实数t 的值为___________．3．已知点)3,2(A ，点)3,6(-B ，点P 在直线0343=+-y x 上，若满足等式λ2+⋅BP AP0=的点P 有两个，则实数λ的取值范围是___________．题型四两定点B A 、，动点P 满足22PB PA +是定值确定隐形圆1．在平面直角坐标系xOy 中，已知圆C ：1)2()(22=+-+-a y a x ，点)2,0(A ，若圆C 上存在点P ，满足1022=+PO PA ，则实数a 的取值范围是___________．2．已知B A ,为直线x y l -=:上两动点，且4=AB ，圆026622=+--+y x y x C ：，圆C 上存在点P ，满足1022=+PB PA ，则线段AB 中点M 的横坐标取值范围为 ___________．3．在ABC ∆中，C B A ,,所对的边分别为c b a ,,，若82222=++c b a ，则ABC ∆面积的最大值为___________．三、强化练习1．已知线段AB 的长为2,动点C 满足λ=⋅→-→-CB CA （0<λ），且点C 总不在以点B 为圆心,21为半径的圆内，则负数λ的最大值是___________．2．在平面中，)0,12(-A ，)6,0(B ，点P 在圆O :5022=+y x 上．若20≤⋅→-→-PB PA ，则点P 的横坐标的取值范围是________．3．在平面直角坐标系xOy 中，已知点)2,0(-A ，点)1,1(-B ，P 为圆222=+y x 上一动点，则PAPB的最大值是_________．隐圆专题（2）策略五两定点B A 、动点P 满足λ=PBPA（0>λ且1≠λ）确定隐形圆（阿波罗尼斯圆） 1．已知)0,0(O ，)3,0(A ，如果圆C ：1)42()(22=+-+-a y a x 上总存在点M 使得MO MA 2=，则圆心C 的横坐标a 的取值范围是___________．2．在平面直角坐标系xOy 中，圆122=+y x 交x 轴于B A ,两点，且点A 在点B 左边，若直线03=++m y x 上存在P 使得PB PA 2=，则实数m 的取值范围为_________．3．在平面直角坐标系xOy 中，已知点)01(，A ，)04(，B ，若直线0=+-m y x 上存在点P 使得PB PA 21=,则实数m 的取值范围是___________．4．在平面直角坐标系xOy 中，已知圆1:22=+y x O ，()44221=+-y x O ：，动点P 在直线03=-+b y x 上，过点P 作圆1,O O 的两条切线，切点分别为B A ,，若满足PA PB 2=的点P 有且仅有两个，则实数b 的取值范围为___________．5．在ABC ∆中，若2=AB ，BC AC 2=，则ABC S ∆的最大值为___________．6．在ABC ∆中，2=BC ，1=AC ，以AB 为边作等腰直角三角形ABD （B 为直角顶点， D C ,两点在直线AB 的两侧）．当C ∠变化时，线段CD 长的最大值为________．7．已知点)1,0(A ，)0,1(B ，)0,(t C ，点D 是直线AC 上的动点，若BD AD 2≤恒成立，则最小正整数t 的值为_______．题型六、相关点法确定隐形圆1．在平面直角坐标系xOy 中，若直线)33(-=x k y 上存在一点P ，圆1)1(22=-+y x 上存在一点Q ，满足→-→-=OQ OP 3，则实数k 的最小值为___________．2．已知D C B A ,,,四点共面，2=BC ,2022=+AC AB ,→-→-=CA CD 3，则||→-BD 的最大值为_________．3．已知ABC ∆是边长为3的等边三角形,点P 是以A 为圆心的单位圆上一动点，点Q 满足→-→-→-+=AC AP AQ 3132，则||→-BQ 的最小值是__________．4．在平面直角坐标系xoy 中，已知圆16:22=+y x O ，点)2,1(P ，N M ,为圆O 上两个不同的点，且0=⋅PN PM ,若PN PM PQ +=,则||PQ 的最小值为___________．强化练习1．已知圆9221=+y x C ：，与圆4222=+y x C ：，定点)0,1(P ，动点B A ,分别在圆1C 与圆2C 上，满足090=∠APB ，则线段AB 的取值范围______________．2．已知圆O ：122=+y x ，圆M ：1)2()3(22=-+++a y a x (a 为实数)．若圆O 与圆M 上分别存在点Q P ,，使得030=∠OQP ，则a 的取值范围是__________．3．设R m ∈，直线0:1=+my x l 与直线042:2=---m y mx l 交于),(00y x P ，则020202x y x ++的取值范围_______.4．在平面直角坐标系xOy 中，已知圆C ：2)1(22=++y x ，点)0,2(A ，若圆C 上存在点M 满足1022≤+MO MA ，则点M 的纵坐标的取值范围是______________．5．在平面直角坐标系xOy 中，已知B A ,为圆C ：16)()4(22=-++a y x 上两个动点，且112=AB ．若直线l ：x y 2=上存在唯一的一个点P ，使得→-→-→-=+OC PB PA ，则实数 a 的值为______________．6．在平面四边形ABCD 中，4=AB ，2=AD ，060=∠DAB ，CB CA 3=，则边CD 长的最小值为______________．7．在平面直角坐标系xOy 中，圆()221:12C x y -+=，圆()()2221:C x m y m m -++=，若圆2C 上存在点P 满足：过点P 向圆1C 作两条切线,,PA PB 切点为,A B ，ABP ∆的面积为 1，则正数m 的取值范围是．。

高三数学微专题之隐形圆

策略四方程定圆普通方程、参数方程
策略五定值定圆由两定点 A、B，动点 P 满足P→A·P→B=λ（λ 是常数）,求出动点 P 的轨迹方程确定隐形圆
由两定点A、B,动点P满足PA2+PB2是定值确定隐形圆由两定点 A、B，动点 P 满足PPAB= λ（λ 是常数）确定隐形圆（阿波罗尼斯圆）
“隐形圆”问题
策略一定义定圆
例1.1 如果圆(x－2a)2＋(y－a－3)2＝4上总存在两个点到原点的距离为1，则实数a的取值范围是__(_-_65_,0_)__．
y
O
x
例1.2 已知圆O：x2＋y2＝1，圆M：(x－a)2＋(y－a＋4)2＝
1．若圆M上存在点P，过点P作圆O的两条切线，切点为A，
y
P C2
AM B C1
x
例 1.4 若对任意R，直线 l：xcos＋ysin＝2sin(＋π6)
＋4 与圆 C：(x－m)2＋(y－ 3m)2＝1 均无公共点，则实数 m 15
的取值范围是__(_-2_,_2_)___． y
l
MC
O
x
例 1.5 在平面直角坐标系 xoy 中，圆 C1:(x-1)2+y2=2，圆 C2:(x-m)2+(y+m)2=m2，若圆C2 上存在点 P 满足：过点 P 向圆 C1 作两条切线 PA、PB，切点为 A、B，△ABP 的面积为 1，则正数 m 的取值范围是[_1_,3_+_2___3_] _．
y
B
O C1
Px
A C2
策略二定角定圆
例 2.1 已知 a,b,c 分别为△ABC 的三个内角 A,B,C 的对边，
a=2,(a+b)(sinA-sinB)=(c-b)sinC 则 △ ABC 面积的最大值为

隐形圆”问题 (pdf版)

1 1 ，所以 M 在以 C1 圆心，半径为的圆上，且 2 2
PA PB 2PM ，转化为两圆上动点的距离的最值．
（4）若对任意R，直线 l：xcos＋ysin＝2sin(＋＝1 均无公共点，则实数 m 的取值范围是
)＋4 与圆 C：(x－m)2＋(y－ 3 m)2 6
1 5 ． ( , ) 2 2
2 2 ≤a≤2 ． 2 2
（3）（2017 年苏北四市一模）已知 A、B 是圆 C1 : x2 y 2 1 上的动点， AB= 3 ， P 是圆
2 C2 : ( x 3） ( y 4)2 1 上的动点，则 PA PB 的取值范围是
． [7,13]
略解：取 AB 的中点 M，则 C1M=
l2 ： mx y 2m 4 0 交于点 P( x0 , y0 ) ，则 x02 y02 2 x0 的取值范围
是
． [12 4 10,12 4 10]
略解： l1 过定点 O(0， 0)， l2 过定点 A(2， -4)，则 P 在以 OA 为直径的圆上（除去一点），变式（2017 年南京二模）在平面直角坐标系 xOy 中，直线 l1：kx－y＋2＝0 与直线 l2： x＋ky－2＝0 相交于点 P，则当实数 k 变化时，点 P 到直线 x－y－4＝0 的距离的最大值为．3 2
切点分别为 A，B，若满足 PB 2PA 的点 P 有且仅有两个，则 b 的取值范围
20 _________．－ ,4 3
例 7（2017 年南通二模）一缉私艇巡航至距领海边界线 l（一条南北方向的直线）3.8 海里的 A 处，发现在其北偏东 30° 方向相距 4 海里的 B 处有一走私船正欲逃跑，缉私艇立即追击．已知缉私艇的最大航速是走私船最大航速的 3 倍．假设缉私艇和走私船均按直线方向以最大航速航行．（1）若走私船沿正东方向逃离，试确定缉私艇的追击方向，使得用最短时间在领海内拦截成功；（参考数据： sin17 ° 3 ， 33 5.7446 ） 6 （2）问：无论走私船沿何方向逃跑，缉私艇是否总能在领海内成功拦截？并说明理由．北 l 领海公海 B 30° A 解：（1）略

江苏省2020高考数学一轮复习突破140必备专题07 直线与圆、圆与圆、阿波罗尼斯圆(隐形圆)问题学案

专题07 直线与圆、圆与圆、阿波罗尼斯圆（隐形圆）问题知识点归纳：一、圆的标准方程：222)()(r b y a x =-+-，圆心),(b a ，半径r 圆的一般方程：022=++++F Ey Dx y x当04422>-+F E D 时，才能表示圆，圆心)2,2(ED --，半径4422FE D r -+=当04422=-+F E D ，表示一个点)2,2(ED -- 当04422<-+FE D ，不表示任何图形二、直线与圆的位置关系设圆的标准方程：222)()(r b y a x =-+-，直线方程：0=++C By Ax判别方法1：设圆心到直线的距离为d ，若r d >，直线与圆相离；若r d =，直线与圆相切；若r d <，直线与圆相交；判别方法2：将直线与圆联立方程组消元得到一个关于x 或者y 的一元二次方程，若0>∆，直线与圆相交；若0=∆，直线与圆相切；若0<∆，直线与圆相离；三、圆与圆的位置关系设圆的方程0:111221=++++F y E x D y x C ，0:222222=++++F y E x D y x C 圆21,C C 的圆心距为d ，1C 的半径为1r ，2C 的半径为2r若21r r d +>，两圆相外离；若21r r d +=，两圆相外切；若2121r r d r r +<<-，两圆相交；若21r r d -=，两圆相内切；若21r r d -<，两圆相内含；四、圆系方程①设直线0=++C By Ax 与圆022=++++F Ey Dx y x 相交，则过两交点的圆的方程为0)(22=+++++++C By Ax F Ey Dx y x λ②设圆0:111221=++++F y E x D y x C ，圆0:222222=++++F y E x D y x C 相交，则过两交点的圆的方程为02222211122=+++++++++）（F y E x D y x F y E x D y x λ 注：1-≠λ时，表示过两交点的圆；1-=λ时，表示过两交点的直线方程，即圆与圆的相交弦所在的直线方程以),(b a A ，),(d c B 为直径端点的圆的方程0))(())((=--+--d y b y c x a x 五、阿波罗尼斯圆动点P 到两定点B A ,的距离的比值为一定值，即PB PA λ=，且1≠λ的点的轨迹是圆. 当1=λ时，动点P 的轨迹为线段AB 的垂直平分线，将其称之为阿波罗尼斯圆江苏高考中每年都会有圆的试题，填空题和解答题甚至应用题中都有可能出现，考点也不外乎上述的知识点总结，下面我们通过实例来看看每个知识点的考法。

专题复习-“隐形圆”问题

“隐形圆”问题江苏省通州高级中学一、问题概括江苏省高考考试说明中圆的方程是 C 级知识点，每年都考，但有些时候，在条件中没有直接给出圆方面的信息，而是隐蔽在题目中的，要经过剖析和转变，发现圆（或圆的方程），进而最后能够利用圆的知识来求解，我们称这种问题为“隐形圆”问题．二、求解策略怎样发现隐形圆（或圆的方程）是重点，常有的有以下策略．策略一利用圆的定义（到定点的距离等于定长的点的轨迹）确立隐形圆例 1（ 1）假如圆 (x－ 2a)2＋ (y－ a－ 3)2＝ 4 上总存在两个点到原点的距离为1，则实数 a 的取值范围是． 6 0a5略解：到原点的距离为 1 的点的轨迹是以原点为圆心的单位圆，转变到此单位圆与已知圆订交求解．（2）（2016 年南京二模）已知圆O：x2＋y2＝ 1，圆 M：(x－ a)2＋(y－ a＋4)2＝ 1．若圆 M 上存在点 P，过点 P 作圆 O 的两条切线，切点为A，B，使得∠ APB＝ 60°则， a 的取值范围为．解：由题意得 OP 2，所以P在以O为圆心2 为半径的圆上，即此圆与圆M 有公共点，所以有 2 1 OM 2 1 1≤ a2 (a 4)2≤ 9 2 2≤ a ≤ 2 2 ．2 2（3）（ 2017 年苏北四市一模）已知A、 B 是圆 C : x2 y 2 1 上的动点，AB= 3，P是圆12( y 4) 21 上的动点，则PA PB 的取值范围是． [7,13]C2 : (x 3）略解：取 AB 的中点 M，则 C1M= 1，所以 M 在以 C1圆心，半径为1 的圆上，且2 2PA PB 2 PM ，转变为两圆上动点的距离的最值．（4）若对随意R，直线 l： xcos ＋ ysin ＝ 2sin( ＋)＋ 4 与圆 C： (x－m)2＋ (y－ 3 m) 26＝ 1 均无公共点，则实数m 的取值范围是． ( 1, 5)2 2略解：直线 l 的方程为： (x- 1)cos ＋ (y- 3 )sin ＝ 4，M(1, 3 )到 l 距离为4，所以 l 是以 M 为圆心半径为 4 的定圆的切线系，转变为圆M 与圆 C内含．注：直线 l ： (x- x0 0 ＝R 2 2 2 的切线系．)cos ＋ (y- y )sin 为圆 M： (x x ) (x y ) R0 0例 2（ 2017 年南通市一模）在平面直角坐标系xOy 中，已知 B，C 为圆 x2 y 2 4 上两点，点 A(1，1) ，且 AB⊥ AC，则线段 BC 的长的取值范围为．解：法一（标解）：设 BC 的中点为M x, y ，由于 OB2 OM 2 BM 2 OM 2 AM 2 ，y所以 4 x2 y22 2B M x 1 y 1 ，2 2CA化简得 x 1 y 1 3 ，2 2 2所以点 M 的轨迹是以1 1为圆心，3 2为半径的O 2，2 2圆，所以 AM 的取值范围是 62 ， 62 ，所2 2 例 2以 BC 的取值范围是 6 2 ， 6 2 ．法二：以 AB、 AC 为邻边作矩形 BACN，则 BC＝ AN ，由矩形的几何性质（矩形所在平面上的随意一点到其对角线上的两个极点的距离的平方和相等），有 OB2 OC2 OA2 ON 2，所以 ON＝ 6 ，故 N 在以 O 为圆心，半径为 6 的圆上，所以BC的取值范围是 6 2 ， 6 2 ．变式 1 （ 2014 年常州高三期末卷）在平面直角坐标系xOy 中，已知圆 O : x2 y2 16 ，点P (1, 2) ，M、N 为圆 O 上两个不一样的点，且PM PN 0，若PQ PM PN，则PQ的最小值为． 3 3 5y变式 2 已知圆 C1：x2 y2 9 ，圆C2： x2 y2 4 ，定点 A P(1, 0) ，动点A, B分别在圆 C1 和圆 C2上，知足APB 90 ，则线段 AB 的取值范围． [2 3 1, 2 3 1] BO Px x变式 3已知向量a、b、c知足a3, b 2, c 1,(a c) (b c) 0 ，则 a b 范围为．[2 3 1,2 3 1]策略二动点 P 对两定点 A、B 张角是 900（ k PA k PB 1，或 PA PB 0）确立隐形圆例 3 （1）（2014 年北京卷）已知圆C： (x 3)2 ( y 4)2 1 和两点 A( m, 0) ， B(m, 0) ，若圆上存在点P，使得APB 90 ，则 m 的取值范围是． 4,6略解：由已知以 AB 为直径的圆与圆C有公共点．（2）（海安2016 届高三上期末）在平面直角坐标系xOy 中，已知点P(- 1，0) ，Q(2 ，1) ，直线 l ：ax by c 0 此中实数a，b，c 成等差数列，若点 P 在直线 l 上的射影为H，则线段QH 的取值范围是．[ 2,3 2]解：由题意，圆心 C(1，－2)在直线 ax＋ by＋ c＝ 0 上，可得 a－ 2b＋ c＝ 0，即 c＝ 2b－a．直线 l： (2a－ b)x＋ (2b－ c)y＋ (2c－ a)＝0，即 a(2x＋ y－ 3)＋ b(4－ x)＝ 0，2x y 3 0,，可得 x＝ 4，y＝－ 5，即直线过定点M(4，－ 5)，由4 x由题意，H 在以 PM 为直径的圆上，圆心为A(5， 2)，方程为 (x－ 5)2＋ (y－ 2)2＝ 50，∵ |CA|＝4 2 ，∴ CH 最小为 5 2 － 4 2 ＝ 2 ，CH 最大为 4 2 ＋ 5 2 ＝ 9 2 ，∴线段 CH 长度的取值范围是 [ 2 ， 9 2 ] ．（3）（通州区2017 届高三下开学初检测）设m R ，直线l1：x my 0 与直线l 2： mx y 2m 4 0 交于点 P( x0 , y0 ) ，则 x0 2 y0 2 2x0的取值范围是． [12 4 10,12 4 10 ]略解： l1过定点 O(0，0)，l2过定点 A(2，- 4)，则 P 在以 OA 为直径的圆上（除掉一点），变式（ 2017 年南京二模）在平面直角坐标系xOy 中，直线 l 1： kx－ y＋ 2＝ 0 与直线 l2： x＋ky－ 2＝0 订交于点 P，则当实数k 变化时，点 P 到直线 x－ y－ 4＝ 0 的距离的最大值为． 3 2策略三两定点 A、 B，动点 P 知足 PA PB 确立隐形圆例 4 （ 1）（ 2017 年南通密卷3）已知点 A(2, 3) ，点 B(6, 3) ，点 P 在直线 3x 4 y 3 0上，若知足等式 AP BP 2 0 的点 P 有两个，则实数的取值范围是．解：设 P（x， y），则 AP (x 2, y 3) ， BP ( x 6, y 3) ，依据 AP BP 2 0 ，有 x 4y 2 13 2 13 . 由题意22圆： x 4y 2 13213 圆与直线 3x 4y3 0订交，22圆心到直线的距离 d3 4 4 0 33 132 ，所以2 .223 4（2）（ 2016 年盐城三模）已知线段 AB 的长为 2，动点 C 知足 CA CB（为常数），且点 C 总不在以点 B 为圆心， 1 为半径的圆内，则负数的最大值是.324略解：动点 C 知足方程 x 2 y 21 .策略四两定点 A 、B ，动点 P 知足 PA 2PB 2 是定值确立隐形圆例 5 （ 1）在平面直角坐标系xOy 中，已知圆 C ： (x －a)2＋ (y － a ＋2)2＝ 1，点 A(0， 2)，若圆 C 上存在点 M ，知足 MA 2＋ MO 2＝ 10，则实数 a 的取值范围是．[0，3]略解： M 知足的方程为 x2( y 2 4 ，转变为两圆有公共点1)（2）（ 2017 年南京、盐城一模）在ABC 中， A ，B ， C 所对的边分别为a,b,c ，若a2b22c28 ，则 ABC 面积的最大值为．255解：以 AB 的中点为原点， AB 所在直线为 x 轴，建系 .设 A(c, 0) ， B( c, 0) ， C( x, y) ，则由 a 2 b 2 2c 28 ，2 2得 ( x c )2 y2(x c ) y 22c28 ，即 x2y245c 2 ，224所以点 C 在此圆上， S ≤ crc 4 5 c1(45c ) 5 c≤252222 24 5 4 4 5策略五两定点 A 、 B ，动点 P 知足PA(0,1) 确立隐形圆（阿波罗尼斯圆）PB例 6（1）略解：点 P 知足圆的方程为 x 2y 24 ，转变到直线与圆订交 .（2）（ 2016 届常州一模）在平面直角坐标系xOy 中，已知圆 O ： x 2＋ y 2＝ 1，O 1：(x － 4)2＋y 2＝ 4，动点 P 在直线 x3 y b 0 上，过点 P 作圆 O ，O 1 的两条切线，切点分别为 A ， B ，若知足 PB 2PA 的点 P 有且仅有两个，则b 的取值范围．－20,43例 7（ 2017 年南通二模）一缉私艇巡航至距领海界限限l （一条南北方向的直线） 3.8 海里的A 处，发此刻其北偏东30°方向相距 4 海里的 B 处有一走私船正欲逃跑，缉私艇立刻追击．已知缉私艇的最大航速是走私船最大航速的 3 倍．假定缉私艇和走私船均按直线方向以最大航速航行．（1）若走私船沿正东方向逃离，试确立缉私艇的追击方向，使得用最短时间在领国内拦截成功；（参照数据： sin17 °3 ， 33 5.7446 ）6（2）问：不论走私船沿何方向逃跑，缉私艇能否总能在领国内成功拦截？并说明原因．北 l 领海公海B30°A解：（ 1）略(例 7)（2）如图乙，以 A 为原点，正北方向所在的直线为y 轴成立平面直角坐标系 xOy ．则B2，23 ，设缉私艇在 P(x ，y) 处（缉私艇恰巧截住走私船的地点）与走私22y船相遇，则PA3 ，即xyl( x2 3 3 ．PB2)2y2领海公海x9 29 3 2整理得，y9 ， B444所以点 P(x ，y) 的轨迹是以点9 ，93 为圆心，4 4 603 为半径的圆．Ax2图乙由于圆心9 ，9 3 到领海界限限 l ： x的距离为，大于圆半径 3 ，4 42所以缉私艇能在领国内截住走私船．策略六由圆周角的性质确立隐形圆例 8 （ 1）已知 a,b, c 分别为ABC 的三个内角 A, B, C 的对边， a 2 ，(a+b)(sinA- sinB)=(c- b)sinC 则 ABC 面积的最大值为． 3略解： cos∠ A＝1，∠ A＝ 60°，设ABC 的外接圆的圆心为O，外接圆的半径为 2 3，则2 3O 到 BC 的距离为3，则边 BC 上的高 h 的最大值为3+2 3= 3 ，则面积的最大值3 3 3为 3 ．（2）（ 2017 年常州一模）在△ ABC 中，∠ C＝ 45o，O 是△ ABC 的外心，若 OC mOA nOB (m，n∈ R)，则 m＋ n 的取值范围是． [ 2,1)略解：∠AOB ＝2∠ C＝ 90°，点 C 在以 O 为圆心，半径 OA 的圆上（在优弧 AB 上）．三、同步练习1．已知直线 l : x 2y m 0 上存在点 M 知足与两点 A( 2, 0) , B(2, 0) 连线的斜率之积为 1 ，则实数 m 的取值范围是． [ 2 5 ,2 5 ]2 2 2， c 0 ，则 b 的取值范围2． (2016 年泰州一模 )已知实数 a， b， c 知足 a b ca 2c为． [ 3 , 3 ]3 33．已知 ,t R ，则 (cos t 2) 2 (sin t 2) 2 的取值范围是．[2 2 1,2 2 1] 4．已知圆 C : ( x 3)2 ( y 4)2 1 和两点 A( m, 0), B(m, 0) (m 0) ．若圆 C 上存在点 P，使得PA PB 1 ，则 m 的取值范围是．[ 15, 35]7．（ 2016 年无锡一模）已知圆C : ( x 2)2 y2 4 ，线段 EF 在直线 l : y x 1 上运动，点 P 为线段 EF 上随意一点，若圆 C 上存在两点 A、 B，使得 PA PB ≤ 0 ，则线段 EF 长度的最大值是．148．如图，已知点A(－ 1,0)与点 B(1,0) ， C 是圆 x2＋ y2＝ 1 上的动点 (与点 A,B 不重合 )，连结 BC 并延伸至 D，使得 |CD |＝ |BC|，则线段 PD 的取值范围． ( 2, 2)39．在平面直角坐标系 xOy 中，已知点 A(t ，0)(t 0) ， B(t ，0) ，点 C 知足 AC BC 8 ，且点 C 到直线 l ： 3x4y 24 0 的最小距离为9，则实数 t 的值是．1510．（ 2013 年江苏卷第 17 题改编）在平面直角坐标系 xOy 中，已知点 O(0, 0) ， A(0, 3) 假如圆 C : ( x a)2 ( y 2a 4) 2 1 上总存在点 M 使得 MA 2MO ，则圆心 C 的横坐标 a 的取值范围是． [0,12]511．已知向量 a 、b 、c 知足 a2 ， b a b =3 ，若 (c 2a)(2 b 3c) 0 ，则 b c 的最大值是． 1212．设点 A, B 是圆 x 2y 2 4 上的两点，点 C(1, 0) ，假如 ACB 90 ，则线段 AB 长度的取值范围为． [7 1, 7 1]13．在 ABC 中， BC ＝ 2，AC ＝ 1，以 AB 为边作等腰直角三角形ABD (B 为直角极点， C 、D 两点在直线 AB 的双侧 )．当∠ C 变化时，线段CD 长的最大值为． 314．（ 2016 年南通三模）在平面直角坐标系xOy 中，圆 C 1 : x 122 ，y 2圆 C 1 : xm 22m2，若圆 C 2 上存在点 P 知足：过点 P 向圆 C 1 作两条切线y mPA 、 PB ，切点为 A 、 B ， ABP 的面积为 1，则正数 m 的取值范围是．解：设 P(x ，y) ，设 PA ， PB 的夹角为 2．△ ABP 的面积 S=1PA 2 sin 2PA 22 PA 1 ．2PC 1 PC 13PC 222 ，解得 PA2，由 2PA 1 PA所以 PC 1 2 ，所以点 P 在圆 ( x 1)2 y 2 4 上．所以 m2 ≤ (m 1)2 ( m)2 ≤ m2 ，解得 1≤ m ≤3 2 3 ．。

蓦然回首,那“圆”却在灯火阑珊处——“隐形圆”解题策略研究

•解题技巧与方法JIETI JI Q IAO YU FANGFA••蓦然回首，那“圆”却在灯火阑珊处——“隐衫團”解麵.策◎顾金(江苏省苏州实验中学，江苏苏州215011)江苏数学高考中圆的方程每年都有所涉及,是C级考点，其中一类题目的条件中没有直接给岀圆的方程，但是却隐藏在题目中，需要通过分析和转化去发现圆，将题目中特定的条件化“隐性”为“显性”，进而利用圆的知识解决问题，此类问题便是“隐形圆”问题•其中涉及“隐形圆”的高考题可参考'2017年第13题#2016年第19题、2013年第17题等•本文以最新的高考及模拟题为例，总结了部分“隐形圆”的解题策略.策略一:利用圆的定义确定&隐形圆”利用圆的定义，就是找到某个定点的距离为定值，简单讲就是找定点，找定长.题1已知圆0:%2+-2=1，圆C：(--a)2+(--a+ 4)2=1，若圆C上存在点G,过点G作圆0的两条切线，切点为A，R，使得.AGR二60。

，则a的取值范围为_______•解析提取条件“过点G作圆0的两条切线,切点为A,R,使得.AGR二60。

”，如图1所示，在RtAABC中，.AG0=30。

，贝lj G0长为2,而0点为定点，所以G所在轨迹方程为%2+-2=4,记该圆为圆C,按照题意只要圆0和圆C有交点即可，求岀a的取值范围是[2-//,2+//].点评该题可以再进行一个动态的模拟,特别地，可以将点G先设定在-轴的正半轴上，点G从(1,0)运动到无穷远处，.AGR能取到(0,"),所以在运动的过程中一定存在G，使得.AGR=60。

(0卩1=2"，固定这一状态，将整个图形绕点0旋转一周，那么G形成的轨迹是以0为圆心,2为半径的圆•并且在旋转的任意位置都满足.AG R=60。

，即G的轨迹是圆,从这一动态过程直观感受“隐形圆”的存在.可以推广，过圆外的点作定圆(--a)2+(--6)2=d2的的的是圆,方程为(--a)2+(--6)2二(7D)-策略二：到两定点A,R距离的比值为定值确定&隐形圆”题2(江苏2013高考17题改编)在平面直角坐标系--中，点A(0,3)，直线/：-=2%-4.设圆C的半径为1，圆心在@上•若圆C上存在点C,使CA=2C0,求圆心C的横坐标a的取值范围为_______•解析设C(a,2a-4),C(%,-),带入CA=2C0有//+(-_3)2=2//+-2，化简有%2+(-+1)2=4，这就是题中的，和C：(%-a)2+(--2a+4)2=1交，解岀a#[0,12]•分析已知A,R为定点，点G满足釜=-(-〉0且-+ 1"，则G的轨迹是圆，即阿波罗尼斯圆•若设C,N分别为线段AB按定比入分割的内分点和外分点，则CV为阿波罗尼斯圆的直径,且满足CV=—-AB.-1策略三：到两定点A,B的张角为直角确定&隐形圆”题3(扬州2018期末调研)已知正三角形MBC的边长为2,点P AB中垂线上任意一点,Q为射线AG上—点，且满足AP i AQ=1，则CH的最大值为_______•解析思路一:如图2所示,建立坐标，0AB中，A0=1，AP•AQ=A02，从而-A0P8-AQ0,贝lj.4Q0=90。

2020版高考数学(江苏专用)新增分大一轮课件：第九章平面解析几何微专题四

1－1 －2＋0 ，此圆的圆心 A 的坐标为， 2 2
1 即 A(0，－1)，半径 r＝2PQ＝ 2，
又因为 N(3,3)，所以 AN＝5，所以(MN)max＝5＋ 2.
跟踪训练 2 (2018· 江苏省通州区检测)设 m∈R，直线 l1：x＋my＝0 与直线
2 l2 ：mx－ y－ 2m－4＝0 交于点 P(x0，y0) ，则 x2 ＋ y 0 0 ＋ 2x0 的取值范围是 [12－4 10，12＋4 10] ______________________.
∴tmax＝2 2＋ 5，tmin＝2 2－ 5，
2 2 ∴(x2 ＋ y ＋ 2 x ) ＝ (2 2 ＋ 5) －1＝12＋4 10， 0 0 0 max
2 2 (x2 ＋ y ＋ 2 x ) ＝ (2 2 － 5) －1＝12－4 10， 0 0 0 min
故所求范围是[12－4 10，12＋4 10].
(2)(2019· 江苏省徐州市第一中学月考)若实数a，b，c成等差数列且点P(－1,0) 在动直线ax＋by＋c＝0上的射影为M，点N(3,3)，则线段MN长度的最大值是
5＋ 2 ________.
解析因为a，b，c成等差数列，所以2b＝a＋c，即0＝a－2b＋c，方程ax＋by＋c＝0恒过点Q(1，－2)，又因为点P(－1,0)在动直线ax＋by＋c＝0上的射影为M，所以∠PMQ＝90°，M在以PQ为直径的圆上，
解析设A(－1,0)，B(1,0)，C(x，y)，由已知可得(x＋1)(x－1)＋y2＝λ， ∴x2＋y2＝1＋λ.
λ<0， ∴1＋λ≥0， 1 1＋λ＋ ≤1或 2
1 1＋λ－2≥1，
3 解得－1≤λ≤－4.

2020届江苏高考数学专题复习隐形圆问题

高三数学隐形圆练习题

2020年九年级数学中考专题复习：隐形圆求最值问题(含答案)

2020高考数学热点难点微专题隐圆问题(29张)

2020年九年级数学中考专题复习：隐形圆求最值问题(含答案)

2020届高考数学江苏省二轮课件：微专题6 隐性圆问题

专题58 隐形圆问题-2020年江苏省高考数学考点探究(解析版)

2020高考数学热点难点微专题“隐圆”问题典型试题(3页)

2020江苏高考数学(理)(提高版)大一轮复习课件：微难点10 “隐圆”问题(共31张PPT)

江苏省2020届高三数学二轮复习第10讲 “隐形圆”问题(共50张PPT)

高三数学隐形圆例练习题

2020届江苏省高考二轮复习专题：隐形圆问题梳理及运用课件(共15张PPT)

2020年高考数学压轴填空题闯关：以圆或隐圆为背景的填空题(解析版+原卷版)

江苏省南通市2020届高三数学专题复习课程资源——“隐形圆”(教师版)

专题——隐圆问题

高三数学微专题之隐形圆

隐形圆”问题 (pdf版)

江苏省2020高考数学一轮复习 突破140必备 专题07 直线与圆、圆与圆、阿波罗尼斯圆(隐形圆)问题学案

专题复习-“隐形圆”问题

蓦然回首,那“圆”却在灯火阑珊处——“隐形圆”解题策略研究

2020版高考数学(江苏专用)新增分大一轮课件：第九章 平面解析几何 微专题四

江苏省2020高考数学一轮复习突破140必备专题07 直线与圆、圆与圆、阿波罗尼斯圆(隐形圆)问题学案

2020版高考数学(江苏专用)新增分大一轮课件：第九章平面解析几何微专题四