11.3 多边形及多边形内角和 (练习)(解析版)
11.3 多边形及其内角和(解析版)2021-2022学年八年级数学上册精选新题汇编(人教版)

2021-2022学年人教版数学八年级上册精选新题汇编第十一章《三角形》11.3 多边形及其内角和一、选择题1.(2021八下·瓯海期中)八边形的内角和等于()A.900°B.1080°C.1260°D.1440°【完整解答】B解:八边形的内角和=(8-2)×180°=1080°.故答案为:B.【思路引导】根据n边形的内角和为(n-2)×180°,把n=8代入进行计算,即可得出答案.2.(2020八上·渝北月考)若一个正多边形的每一个外角都等于36°,则它是()A.正九边形B.正十边形C.正十一边形D.正十二边形【完整解答】B解:这个正多边形的边数:360°÷36°=10,故答案为:B.【思路引导】根据多边形的外角和等于360°可求解.3.(2020八上·恩施月考)一个n边形的每一个外角都是72°,则n等于()A.3B.4C.5D.6【完整解答】C解:∵多边形的每一个外角都是72°,360°÷72°=5,所以它的边数是5.故答案为:C.【思路引导】根据多边形的外角和等于360°可求解.4.(2020八上·合江月考)一个多边形的外角和是内角和的一半,这个多边形的边数是( )A.4B.5C.6D.8【完整解答】C解:多边形的内角和是:2×360∘=720∘.设多边形的边数是n,则(n−2)·180=720,解得:n=6.即这个多边形的边数是6.故选:C.【思路引导】根据多边形的外角和是360度,即可求得多边形的内角和的度数,依据多边形的内角和公式即可求解.5.(2021八下·苍南期末)五边形的内角和为( )A.180°B.360°C.540°D.720°【完整解答】C解:五边形的内角和为:(5-2)×180°=540°.故答案为:C.【思路引导】n边形的内角和公式:(n-2)×180°,据此计算.6.(2021八下·贵池期末)一个三角形,剪去一个角后所得的多边形内角和的度数是()A.180°B.360°C.540°D.180°或360°【完整解答】D剪去一个角,若边数不变,则内角和=(3-2)•180°=180°,若边数增加1,则内角和=(4-2)•180°=360°,所以,所得多边形内角和的度数可能是180°,360°.故答案为:D.【思路引导】先求出剪去一个角,若边数不变,则内角和为180°,再求出若边数增加1,则内角和为360°,最后求解即可。
11.3多边形及其内角和练习题

1. 各角都相等的n 边形的一个外角可能取得的值是 ( ) A.(2)180n n-︒ B.360n ︒ C.180n ︒ D.以上都不对 2. 一个多边形的内角和比它的外角的3倍少180°,则这个多边形的边数是( ) A.5 B.6 C.7 D.83. 过n 边形的一个顶点的所有对角线,把多边形分成8个三角形,则这个多边形的边数是( )A.8 B.9 C.10 D.114. 若一个多边形的对角线的条数恰好为边数的3倍,则这个多边形的边数为( ) A.6 B.7 C.8 D.95. 一个多边形的对角线的条数等于它的边数的4倍,求这个多边形的内角和为 度.6. 图中是三种将多边形(3)n ≥分成三角形的不同方法. .7. 乙是 边形.8.9. 已知如图,四边形ABCD 中,B ∠和C ∠的平分线交于点O .求证:1()2BOC A D ∠=∠+∠. 10. 已知,如图,在四边形ABCD 中,12∠=∠,34∠=∠则____E F ∠+∠=.11. 多边形的每一个内角都是150°,则此多边形的一个顶点引出的对角线的条数是 1A2A 3A 4 5A n 1A 2A 3A 4A 5A n A1A 2A 3A 4 5An A ABD O( )A.7 B.8 C.9 D.1012. 在一次数学活动课上,小明将正方形的桌面截去一个角,那么你能帮助小明计算余下多边形的内角和度数吗?13. 一个多边形的内角和等于它的外角和,那么这个多边形是 .14. 如果五边形的五个外角的比是1:3:2:4:5,则五边形中最大的内角与最小的内角的比是 .15. 认真观察下列图形,利用图形中的信息,写出你从中得到的启示而获取的知识点.16.17. 三角形,图4个小三角形.试把这一结论推广至n 边形. 18. (1)n + (A)180 180 360 360⋅19. 若一个多边形的内角和为外角和的3倍,则这个多边形为 ( ) A.八边形 C.十边形D.十二边形20. 如图,一块试验田的形状是三角形(设其为ABC △),管理员从BC 边上的一点D 出发,沿DC CA AB BD →→→的方向走了一圈回到D 处,则管理员从出发到回到原处在途中身体 A.转过90 B.转过180 C.转过270D.转过360 21. 正六边形的一个内角的度数是22、一个多边形截去一个角后,形成另一个多边形的内角和为1800°,你知道原多边形的边数为( )A BC DA B C D E A B C D E F A B CD E F G ① ② ③C(第20题图) DA、11B、12C、13D、11或12或1323、一个多边形除了一个内角外,其余各内角的和为2000°,则这个内角是()A、20°B、160°C、200°D、140°。
11.3 多边形及其内角和 (含答案)

11.3 多边形及其内角和同步练习一、选择题(共10小题)1. 下列几种正多边形中,能单独镶嵌平面的是( )A. 正五边形B. 正六边形C. 正七边形D. 正八边形2. 一个多边形的每个内角均为140∘,则这个多边形是( )A. 七边形B. 八边形C. 九边形D. 十边形3. 若从多边形的某一顶点出发只能画五条对角线,则它是( )A. 六边形B. 七边形C. 八边形D. 九边形4. 商店出售下列四种形状的地砖:①正三角形;②正方形;③正五边形;④正六边形.若只选购其中一种地砖密铺地面,可供选择的地砖共有( )A. 4种B. 3种C. 2种D. 1种5. 过多边形的一个顶点的所有对角线把多边形分成8个三角形,这个多边形的边数是( )A. 8B. 9C. 10D. 116. 已知实数x,y满足∣x−4∣+√y−8=0,则以x,y的值为两边长的等腰三角形的周长是( )A. 20或16B. 20C. 16D. 以上答案均不对7. 为了让居民有更多休闲和娱乐的地方,政府又新建了几处广场.工人师傅在铺设地面时,准备选用同一种正多边形地砖.现有下面几种形状的正多边形地砖,其中不能进行平面镶嵌的是( )A. 正三角形B. 正方形C. 正五边形D. 正六边形8. 一幅美丽的图案,在某个顶点处由四个边长相等的正多边形密铺而成,且其中三个分别为正三角形、正四边形、正六边形,那么另一个为( )A. 正三角形B. 正四边形C. 正五边形D. 正六边形9. 一个多边形,边数每增加1,内角和是( )A. 不变B. 增加1∘C. 增加180∘D. 增加360∘10. 若一个多边形的内角和是其外角和的两倍,则它的边数是( )A. 四B. 五C. 六D. 七二、填空题(共6小题;共48分)11. 一个多边形的内角和为1440∘,则它的边数为.12. 要使七边形木架不变形,至少要钉上根木条.13. 如图所示,若干全等正五边形排成环状.如图所示的是前3个正五边形,要完成这一圆环还需个正五边形.14. 己知正多边形的每个外角都是45∘,则从这个正多边形的一个顶点出发,共可以作条对角线.15. 用正三角形和正十二边形组合铺满地面,每个顶点周围有个正三角形和个正十二边形.16. 如图,∠1,∠2,∠3,∠4是五边形ABCDE的4个外角,若∠A=100∘,则∠1+∠2+∠3+∠4=.三、解答题(共4小题;共52分)17. 试说明正八边形不能铺满平面的理由.18. 当围绕一点拼在一起的几个多边形的内角恰好组成一个周角时,就能拼成一个既不留空隙,又不相互重叠的平面图形,我们称之为镶嵌.一块地板由三种正多边形的小木板镶嵌而成,这三种正多边形的边数分别为a,b,c,求证:1a +1b+1c=12.19. 在一个多边形中,它的内角中最多有几个是锐角?20. 如图①,把边长为4的正三角形各边四等分,连接各分点得到16个小正三角形.(1)如图②,连接小正三角形的顶点得到的正六边形ABCDEF的周长=.(2)请你判断:命题“六个内角相等的六边形是正六边形”是真命题还是假命题?如果是真命题,请你把它改写成 " 如果⋯,那么⋯ " 的形式;如果是假命题,请在图①中画图说明.答案第一部分1. B2. C3. C4. B5. C【解析】设多边形有n条边,则n−2=8,解得n=10.故这个多边形的边数是10.6. B7. C8. B 【解析】正三角形、正四边形、正六边形的内角分别是60∘C,90∘,120∘而360∘−60∘−90∘−120∘=90∘9. C 【解析】设原来的多边形的边数是n,n边形的内角和是(n−2)⋅180∘,边数增加1,则新的多边形的内角和是(n+1−2)⋅180∘,则(n+1−2)⋅180∘−(n−2)⋅180∘=180∘.10. C【解析】设这个多边形的边数为n,根据题意,得(n−2)⋅180=720,解得:n=6.故这个多边形的边数为6.第二部分11. 10【解析】设多边形的边数为n,则有:180∘(n−2)=1440∘,解得:n=10.12. 413. 7【解析】延长正五边形的相邻两边,交于圆心,∵正五边形的外角等于360∘÷5=72∘,∴延长正五边形的相邻两边围成的角的度数为:180∘−72∘−72∘=36∘ .∴360∘÷36∘=10 .∴排成圆环需要10个正五边形.14. 5【解析】正多边形的边数:360÷45=8,从这个正多边形的一个顶点出发,共可以作对角线的条数为:8−3=5 .15. 一,两.16. 280∘【解析】如图,∵∠EAB+∠5=180∘,∠EAB=100∘,∴∠5=80∘.∵∠1+∠2+∠3+∠4+∠5=360∘,∴∠1+∠2+∠3+∠4=360∘−80∘=280∘.第三部分17. 正八边形一个内角的度数是135∘,360∘不能被135∘整除,两个内角的和小于360∘,三个内角的和大于360∘,所以正八边形不能铺满平面.18. 因为1a (a−2)⋅180∘+1b(b−2)⋅180∘+1c(c−2)⋅180∘=360∘,所以a−2a +b−2b+c−2c=2,所以1−2a +1−2b+1−2c=2,即1a +1b+1c=12.19. ∵任意多边形的外角和是360∘,∴在任意多边形的外角中,最多有3个钝角.∴内角中,最多有3个锐角.20. (1)6(2)假命题.反例如下图.。
新人教版八年级上《11.3多边形及其内角和》例题与讲解
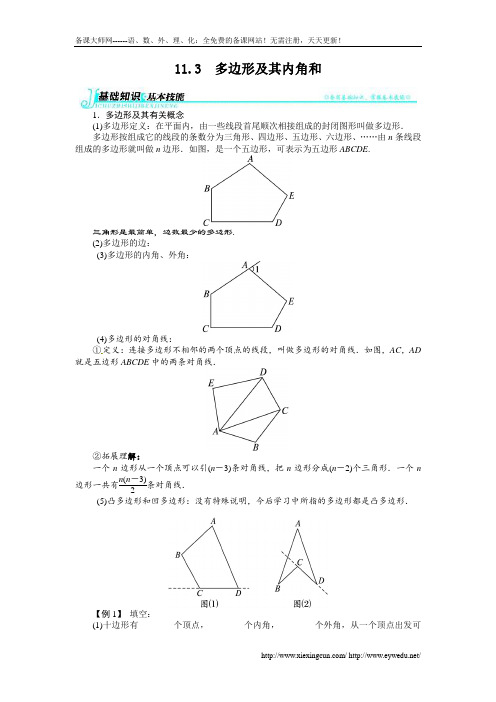
11.3 多边形及其内角和1.多边形及其有关概念(1)多边形定义:在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形. 多边形按组成它的线段的条数分为三角形、四边形、五边形、六边形、……由n 条线段组成的多边形就叫做n 边形.如图,是一个五边形,可表示为五边形ABCDE .三角形是最简单,边数最少的多边形.(2)多边形的边:(3)多边形的内角、外角:(4)多边形的对角线: ①定义:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.如图,AC ,AD 就是五边形ABCDE 中的两条对角线.②拓展理解:一个n 边形从一个顶点可以引(n -3)条对角线,把n 边形分成(n -2)个三角形.一个n边形一共有n (n -3)2条对角线. (5)凸多边形和凹多边形:没有特殊说明,今后学习中所指的多边形都是凸多边形.【例1】 填空:(1)十边形有________个顶点,________个内角,________个外角,从一个顶点出发可画________条对角线,它共有________条对角线.(2)从多边形一个顶点出发画对角线将它分成了四个三角形,这个多边形是________边形.2.正多边形(1)定义:各个角都相等,各条边都相等的多边形叫做正多边形.如等边三角形、正方形等.(2)特点:不仅边都相等,角也都相等,两个条件必须同时具备才是正多边形.如长方形四个角都是直角,都相等,但边不等,所以不是正多边形.【例2】下列说法正确的个数有().(1)由四条线段首尾顺次相接组成的图形是四边形;(2)各边都相等的多边形是正多边形;(3)各角都相等的多边形一定是正多边形;(4)正多边形的各个外角都相等.A.1 B.2 C.3 D.43.多边形的内角和(1)公式:n边形内角和等于(n-2)×180°.(2)探究过程:如图,以五边形、六边形为例.【例3】选择:(1)十边形的内角和为().A.1 260°B.1 440°C.1 620°D.1 800°(2)一个多边形的内角和为720°,那么这个多边形的对角线共有().A.6条B.7条C.8条D.9条4.多边形的外角和(1)公式:多边形的外角和等于360°.(2)探究过程:如图,以六边形为例.【例4】填空:(1)一个多边形每个外角都是60°,这个多边形是__________边形,它的内角和是__________度,外角和是__________度;(2)多边形边数每增加一条,它的内角和会增加__________,外角和增加__________.5.多边形内角和公式的应用【例5-1】若一个四边形的四个内角度数的比为3∶4∶5∶6,则这个四边形的四个内角的度数分别为__________.【例5-2】一个多边形的内角和等于1 440°,则它的边数为__________.【例5-3】一个多边形的内角和不可能是().A.1 800°B.540°C.720°D.810°6.多边形外角、外角和公式的应用【例6-1】 如图所示,已知∠ABE =138°,∠BCF =98°,∠CDG =69°,则∠DAB =__________.【例6-2】 如图,在四边形ABCD 中,∠1,∠2分别是∠BCD 和∠BAD 的邻补角,且∠B +∠ADC =140°,则∠1+∠2等于( ).A .140°B .40°C .260°D .不能确定7.正多边形知识的应用【例7-1】 若八边形的每个内角都相等,则其每个内角的度数是__________.【例7-2】 一个多边形的每一个外角都等于30°,这个多边形的边数是__________,它的内角和是__________.【例7-3】 一个多边形的每一个内角都等于144°,求这个多边形的边数.8.边数、顶点数、内角和、对角线条数之间关系的综合应用在多边形问题中,当多边形的边数n 一定时,不论多边形形状如何,多边形的内角和也是一定的,是(n -2)×180°,多边形对角线的条数也是一定的,是n (n -3)2,并且从一个顶点引出的对角线的条数也是一定的,是(n -3)条,所以在多边形问题中,在这些量中,只要知道其中一个量,就可以求出所有的量.【例8-1】 过n 边形的一个顶点的所有对角线,把多边形分成8个三角形,则这个多边形的边数是( ).A .8B .9C .10D .11【例8-2】 多边形的每一个内角都是150°,则此多边形的一个顶点引出的对角线的条数是( ).A .7B .8C .9D .10【例8-3】 一个多边形的对角线的条数等于它的边数的4倍,求这个多边形的内角和.9.将多边形截去一个角问题的探讨【例9-1】 一个多边形截去一个角后,变为十六边形,则原来的多边形的边数为( ).A .15或17B .16或17C .16或18D .15或16或17【例9-2】 一个多边形截去一个角(截线不过顶点)之后,所形成的一个多边形的内角和是2 520°,那么原多边形的边数是( ).A .13B .15C .17D .19【例9-3】如果一个多边形的边数增加一倍,它的内角和是2 880°,那么原来的多边形的边数是().A.10 B.9 C.8 D.710.多边形内角和少算或多算一个角类型题目探索【例10-1】一个多边形除了一个内角之外,其余内角之和为2 670°,求这个多边形的边数和少加的内角的大小.【例10-2】若多边形所有内角与它的一个外角的和为600°,求这个多边形的边数及内角和.。
专题11.3 多边形及其内角和(讲练)(解析版)(人教版)

专题11.3 多边形及其内角和典例体系一、知识点1、n 边形的内角和=()2180-⨯n; 2、n 边形的外角和=360。
3、一个n 边形的对角线有()23-n n 条,过n 边形一个顶点能作出()3-n 条对角线,把n 边形分成了()2-n 个三角形。
4、各角都相等、各边都相等的多边形叫做正多边形,边数为n 的正多边形,也叫作正n 边形.5、多边形的镶嵌(密铺)问题.二、考点点拨与训练考点1:与多边形内角有关的计算典例:(2020·安徽省初三三模)如图,在五边形ABCDE 中,280A B E EDC BCD ︒∠+∠+∠=∠∠,、的平分线DP CP 、相交于P 点,则P ∠的度数是( )A .40︒B .45︒C .50︒D .55︒【答案】C【解析】 ∵五边形的内角和等于(5-2)×180°=540°,∠A+∠B+∠E=280°,∴∠BCD+∠CDE=540°一280°=260°,∵∠BCD ,∠CDE 的平分线在五边形内相交于点O ,∴∠PDC+∠PCD=12(∠CDE+∠BCD)=130°, ∴∠P=180°-130°=50°,故选:C .方法或规律点拨本题考查了多边形的内角和,角平分线的性质,求出五边形内角和是解题关键.巩固练习1.(2020·福建省初三月考)若一个凸多边形的内角和为720°,则这个多边形的边数为( )A .4B .5C .6D .7【答案】C【解析】设这个多边形的边数为n ,由多边形的内角和是720°,根据多边形的内角和定理得(n -2)180°=720°.解得n=6.故选C.2.(2020·福建省初三二模)已知一个多边形的内角和是540︒,则这个多边形是( )A .四边形B .五边形C .六边形D .七边形【答案】B【解析】 根据多边形内角和定理,n 边形的内角和公式为()n 2180-︒,因此,由()n 2180540︒-=︒得n=5.故选B . 3.(2020·偃师市实验中学初一月考)如果一个多边形的边数增加1倍,它的内角和是2160°,那么原来的多边形的边数是 ( )A .5B .6C .7D .8【答案】C【解析】设多边形原有边数为x ,则(2x−2)×180=2160,2x−2=12,解得x=7,故本题选C.4.(2020·江苏省初一月考)一个多边形的每个内角都等于135°,则这个多边形的边数为( ) A .5B .6C .7D .8 【答案】D【解析】∵一个多边形的每个内角都等于135°,∴这个多边形的每个外角都等于180°-135°=45°,∵多边形的外角和为360度,∴这个多边形的边数为:360÷45=8,故选D.5.(2020·北京初三二模)如图,四边形ABCD 中,过点A 的直线l 将该四边形分割成两个多边形,若这两个多边形的内角和分别为α和β,则αβ+的度数是( )A .360︒B .540︒C .720︒D .900︒【答案】B【解析】 直线l 将四边形ABCD 分成两部分,左边为四边形,其内角和为α=360°,右边为三角形,其内角和为β=180°,因此360180540αβ︒︒︒+=+=故选:B .6.(2019·河南省初一期末)下列选项可能是多边形的内角和的是( )A .580°B .1240°C .1080°D .2010°【答案】C【解析】解:判断哪个度数可能是多边形的内角和,看它是否能被180°整除.580÷180=3...40,1240÷180=6...160,1080÷180=6,2010÷180=11...30,只有1080°能被180°整除.故选:C .7.(2020·江苏省扬州教育学院附中初一期中)一个多边形的每个内角都是120°,这个多边形是( ) A .四边形B .六边形C .八边形D .十边形 【答案】B【解析】解:外角是180°-120°=60°,360÷60=6,则这个多边形是六边形.故选:B.8.(2020·江苏省初一月考)一个正多边形的每个内角度数均为135°,则它的边数为____.【答案】8【解析】设该正多边形的边数为n由题意得:(2)180?nn-⨯=135°解得:n=8故答案为8.考点2:与多边形外角有关的计算典例:(2020·陕西省初二期末)如果一个多边形的内角和与外角和之比是13:2,求这个多边形的边数.【答案】15.【解析】解:设这个多边形的边数为n,依题意得:13(2)1803602n-︒=⨯︒,解得15n=,∴这个多边形的边数为15.方法或规律点拨考查了多边形内角与外角,根据外角和的大小与多边形的边数无关,多边形的外角和等于360度.巩固练习1.(2020·北大附属嘉兴实验学校初二期中)一个多边形的内角和比外角和的3倍多180°,则它的边数是()A.八B.九C.十D.十一【答案】B【解析】根据题意,得:(n-2)•180°=3×360°+180°,解得:n=9,则这个多边形的边数是9.故选B.2.(2020·福建省初一期末)若多边形的边数增加一条,则它的外角和()A.增加180°B.不变C.增加360°D.减少180°【答案】B【解析】根据多边形的外角和定理:多边形的外角和都等于360º,与边数多少无关,故选B.3.(2020·广东省初三一模)已知一个正多边形的每个外角都等于72°,则这个正多边形是( )A.正五边形B.正六边形C.正七边形D.正八边形【答案】A【解析】这个正多边形的边数:360°÷72°=5.故选A.4.(2020·江苏省初一月考)若一个多边形的外角和与它的内角和相等,则这个多边形是()A.三角形B.四边形C.五边形D.六边形【答案】B【解析】解:设多边形的边数为n.根据题意得:(n-2)×180°=360°,解得:n=4.故选:B.5.(2020·山东省济宁学院附属中学初三二模)正十边形的外角和为()A.180°B.360°C.720°D.1440°【答案】B【解析】解:因为任意多边形的外角和都等于360°,所以正十边形的外角和等于360°,.故选:B.6.(2020·重庆西南大学附中初三月考)一个正多边形的外角为45°,则这个正多边形的内角和是()A.540° B.720° C.900° D.1080°【解析】∵正多边形的一个外角是45°,∴360°÷45°=8∴这个正多边形是正八边形∴该正多边形的内角和为:180°×(8-2)=1080°.故答案选:D.7.(2020·陕西省初三一模)已知一个多边形的内角和与外角和之比是3:2,则这个多边形的边数为____.【答案】5【解析】解:设这个多边形的边数为n,依题意得:(n−2)180°=32×360°,解得:n=5.故这个多边形的边数为5.故答案为:5.8.(2020·河南省初二期末)如图的七边形ABCDEFG中,AB,ED的延长线相交于O点,若图中∠1,∠2,∠3,∠4的外角的角度和为220°,则∠BOD的度数为何?( )A.40°B.45°C.50°D.60°【答案】A【解析】解:∵∠1、∠2、∠3、∠4的外角的角度和为220°,∴∠1+∠2+∠3+∠4+220°=4×180°,∴∠1+∠2+∠3+∠4=500°,∵五边形OAGFE内角和=(5﹣2)×180°=540°,∴∠1+∠2+∠3+∠4+∠BOD=540°,∴∠BOD=540°﹣500°=40°,考点3:正多边形的角度计算典例:(2019·吉林省第二实验学校初三二模)如图,以正六边形ABCEDF 的边AB 为直角边作等腰直角三角形ABG ,使点G 在其内部,且90BAG ∠=︒,连接FG ,则EFG 的大小是__________度.【答案】45【解析】解:在正六边形ABCDEF 中, ∵∠AFE=∠BAF=(62)180120,6-⨯︒=︒ ∵∠BAG=90°, ∴∠FAG=120°-90°=30°,又∵AF=AB=AG ,∴∠AFG=1803075,2︒-︒=︒ ∴∠EFG=∠AFE -∠AFG=120°-75°=45°,故答案为:45.方法或规律点拨本题考查了多边形的内角与外角,等腰三角形的性质,熟记多边形的内角和公式是解题方法或规律点拨 巩固练习1.(2019·江苏省初一期中)如图,一块六边形绿化园地,六角都做有半径为1m 的圆形喷水池,则这六个喷水池占去的绿化园地的面积(结果保留π)为( )A .π2mB .2π2mC .4π2mD .n π2m【答案】B∵六边形的内角和为:62180720()-⨯︒=︒,∴六个阴影部分所对的圆心角的和为:720°,∴阴影部分的面积相当于两个圆的面积之和,∴阴影部分的面积为:2π×12=2π(2m )故选B .2.(2018·内蒙古自治区初二期末)有公共顶点A ,B 的正五边形和正六边形按如图所示位置摆放,连接AC 交正六边形于点D ,则∠ADE 的度数为( )A .144°B .84°C .74°D .54°【答案】B 【解析】正五边形的内角是∠ABC =()521805-⨯=108°,∵AB =BC ,∴∠CAB =36°,正六边形的内角是∠ABE =∠E =()621806-⨯=120°,∵∠ADE +∠E +∠ABE +∠CAB =360°,∴∠ADE =360°–120°–120°–36°=84°,故选B . 3.(2020·广东省初三其他)如图,在正六边形ABCDEF 的外侧,作正方形EFGH ,则∠DFH 的度数为____.【答案】75°【解析】观察图形可知,△EFH 是等腰直角三角形,则∠EFH=45°,△DEF 是等腰三角形,∵∠DEF=120°, ∴∠EFD=(180°﹣120°)÷2=30°, ∴∠DFH=45°+30°=75°.4.(2020·陕西省西北工业大学附属中学初三月考)如果一个正多边形的内角和等于1440︒,那么这个正多边形的每一个外角的度数为______.【答案】36【解析】正多边形的内角和等于1440︒∴()21801440n-⨯=解得:10n=多边形的外角和为360,且正多边形的每一个外角均相等∴这个正多边形的每一个外角的度数为3601036÷=故答案是:365.(2020·上海初三二模)我们把正多边形的一个内角与外角的比值叫做正多边形的内外比,内外比为3的正多边形的边数为__________【答案】8【解析】设正多边形的边数为n,∵内角和为(2)180n-⨯,外角和为360°,∴一个内角度数为(2)180nn-⨯,一个外角度数为360n,∴(2)180nn-⨯=3603n⨯,解得n=8,经检验n=8是方程的解且符合题意,故答案为:8.6.(2020·山东省初三一模)如图,该硬币边缘镌刻的正九边形每个内角的度数是_____.【答案】140°.【解析】解:该正九边形内角和()180921260=︒⨯-=︒, 则每个内角的度数12601409︒︒==. 故答案为:140°.7.(2020·江苏省泰兴市实验初级中学初一期中)如图,在五边形ABCDE 中,∠A =∠B =∠C =∠D ,点F 在边AB 上,∠AFE =45°,则∠AEF 与∠AED 的度数的比值是_______.【答案】1:4【解析】解:设∠AEF=x ,∵∠AFE =45°,∴∠A=180°-∠AFE -∠AEF=135°-x∴∠A =∠B =∠C =∠D =135°-x∵∠A +∠B +∠C +∠D +∠AED=180°×(5-2)=540°∴∠AED=540°-4(135°-x )=4x∴∠AEF :∠AED=1:4故答案为:1:4.8.(2020·常州市第二十四中学初一期中)一机器人以0.3m/s 的速度在平地上按下图中的步骤行走,那么该机器人从开始到停止所需时间为__s .【答案】160.【解析】解:360÷45=8,则所走的路程是:6×8=48m ,则所用时间是:48÷0.3=160s.9.(2020·江西省石城二中初三其他)两个完全相同的正五边形都有一边在直线l上,且有一个公共顶点O,其摆放方式如图所示,则∠AOB等于______ 度.【答案】108【解析】∵五边形是正五边形,∴每一个内角都是108°,∴∠OCD=∠ODC=180°-108°=72°,∴∠COD=36°,∴∠AOB=360°-108°-108°-36°=108°.故答案为108考点4:多边形对角线问题典例:(2020·上蔡县思源实验学校初一月考)一个多边形的外角和是它内角和的14,求:(1)这个多边形的边数;(2)这个多边形共有多少条对角线.【答案】(1)边数为10;(2)35条【解析】解:设这个多边形的边数为n,由题意得:180(n-2)×14=360,解得:n=10,答:这个多边形的边数为10;(2)10×(10-3)÷2=35(条).方法或规律点拨本题考查多边形的内角和与外角和、方程的思想.关键是记住内角和的公式与外角和的特征,及多边形对角线的条数公式.巩固练习1.(2020·全国初一)下列多边形中,对角线是5条的多边形是()A.四边形B.五边形C.六边形D.七边形【答案】B【解析】n边形对角线条数为(3)2n n∴A. 四边形有2条对角线,故错误;B. 五边形有5条对角线,正确;C. 六边形有9条对角线,故错误;D. 七边形有14条对角线,故错误;故选B.2.(2020·全国初一)在八边形内任取一点,把这个点与八边形各顶点分别连接可得到几个三角形()A.5个B.6个C.7个D.8个【答案】D【解析】如图,或者根据八边形内一点,和任意一边的两端点均可构成三角形,所以可求得三角形的个数为8.故选:D.3.(2020·全国初一)将一个多边形纸片沿一条直线剪下一个三角形后,变成一个六边形,则原多边形纸片的边数不可能是()A.5B.6C.7D.8【答案】D【解析】如图可知,原来多边形的边数可能是5,6,7.不可能是8.故选:D .4.(2020·温州外国语学校初二月考)从十二边形的一个顶点出发,可引出对角线( )条A .9条B .10条C .11条D .12条【答案】A【解析】解:从十二边形的一个顶点出发,可引出对角线的条数是()1239-=条.故选:A .5.(2019·北京初三其他)若一个多边形从一个顶点出发的对角线共有3条,则这个多边形的内角和为( ) A .360°B .540°C .720°D .1080° 【答案】C【解析】从一个顶点出发的对角线共有3条 ∴这个多边形是一个六边形则这个多边形的内角和为180(62)720︒⨯-=︒故选:C .6.(2019·北京市第四十一中学初二期中)从一个七边形的某个顶点出发,分别连接这个点与其余各顶点,可以把一个七边形分割成( )个三角形.A .6B .5C .8D .7【答案】B【解析】从一个七边形的某个顶点出发,分别连接这个点与其余各顶点,可以把一个七边形分割成7-2=5个三角形.故选B .7.(2019·重庆市凤鸣山中学初一期中)一个多边形除了一个内角外,其余各内角的和为2100°则这个多边形的对角线共有( )A.104条B.90条C.77条D.65条【答案】C【解析】解:22100180113÷=,则正多边形的边数是11+2+1=14.∴这个多边形的对角线共有()()314143==7722n n--条.故选:C.考点5:多边形的镶嵌问题典例:40.(2020·长春市第四十七中学初一期中)如图所示的图形中,能够用一个图形镶嵌整个平面的有()个A.1B.2C.3D.4【答案】C【解析】解:等腰三角形的内角和是180°,能被360°整除,放在同一顶点处能够用一种图形镶嵌整个平面;四边形的内角和是360°,能被360°整除,放在同一顶点处能够用一种图形镶嵌整个平面;正六边形的每个内角是120°,能被360°整除,能够用一种图形镶嵌整个平面;正五边形的每个内角是108°,不能被360°整除,放在同一顶点处不能够用一种图形镶嵌整个平面;圆不能够用一种图形镶嵌整个平面;综上所述,能够用一种图形镶嵌整个平面的有3个.故选:C.方法或规律点拨本题考查了平面镶嵌(密铺),掌握几何图形镶嵌成整个平面的关键是解题的钥匙.巩固练习1.(2020·偃师市实验中学初一月考)用下列边长相同的正多边形组合,能够铺满地面不留缝隙的是()A.正八边形和正三角形B.正五边形和正八边形C.正六边形和正三角形D.正六边形和正五边形【答案】C【解析】A、正八边形的每个内角为:180°-360°÷8=135°,正三角形的每个内角60°.135m+60n=360°,n=6-9m,显然m取任何正整数时,n不能得正整数,故不能铺满;4B、正五边形每个内角是180°-360°÷5=108°,正八边形的每个内角为:180°-360°÷8=135°,108m+135n=360°,m取任何正整数时,n不能得正整数,故不能铺满;C、正六边形的每个内角是120°,正三角形的每个内角是60度.∵2×120°+2×60°=360°,或120°+4×60°=360度,能铺满;D、正六边形的每个内角是120°,正五边形每个内角是180°-360°÷5=108°,120m+108n=360°,m取任何正整数时,n不能得正整数,故不能铺满.故选C.2.(2019·山西省初一月考)用若干个某种正多边形瓷砖可以铺满地面,这种正多边形瓷砖不可能是()A.B.C.D.【答案】D【解析】A.正三角形,其单个内角为60°,360°÷60°=6,A选项满足条件;B.正方形,其单个内角为90°,360°÷90°=4,B选项满足条件;C.正六边形,其单个内角为120°,360°÷120°=3,C选项满足条件;D.正八边形,其单个内角为135°,360°÷135° 2.7≈,D选项不满足条件.故选:D.3.(2020·哈尔滨市中实学校初一期中)能够铺满地面的正多边形组合是()A.正六边形和正方形B.正五边形和正八边形C.正方形和正八边形D.正三角形和正十边形【答案】C【解析】A、正六边形的每个内角是120°,正方形的每个内角是90°,120m+90n=360°,显然n取任何正整数时,m 不能得正整数,故不能铺满;B、正五边形每个内角是180°-360°÷5=108°,正八边形每个内角为135度,135m+108n=360°,显然n取任何正整数时,m 不能得正整数,故不能铺满;C 、正方形的每个内角为90°,正八边形的每个内角为135°,两个正八边形和一个正方形刚好能铺满地面;D 、正三角形每个内角为60度,正十边形每个内角为144度,60m+144n=360°,显然n 取任何正整数时,m 不能得正整数,故不能铺满.故选C .4.(2020·四川省初二期末)只用下列图形不能进行平面镶嵌的是( )A .正六角形B .正五边形C .正四边形D .正三边形【答案】B【解析】解:A 、正六边形的每个内角是120°,能整除360°,能密铺;B 、正五边形每个内角是108°,不能整除360°,不能密铺;C 、正四边形的每个内角是90°,能整除360°,能密铺;D 、正三边形的每个内角是60°,能整除360°,能密铺.故选:B .5.(2019·雷州市第二中学初三一模)在下列四种边长均为a 的正多边形中,能与边长为a 的正三角形作平面镶嵌的正多边形有( )①正方形;②正五边形;③正六边形;④正八边形A .4种B .3种C .2种D .1种 【答案】C【解析】解:正三角形的一个内角度数为180360360-÷=︒,①正方形的一个内角度数为180360490-÷=︒,360290360⨯+⨯=︒,那么3个正三角形和2个正方形可作平面镶嵌;②正五边形的一个内角度数为1803605108-÷=︒,任意若干个都不能和正三角形组成平面镶嵌;③正六边形的一个内角度数为1803606120-÷=︒,2602120360⨯+⨯=︒或460120360⨯+=︒,可作平面镶嵌;④正八边形的一个内角度数为1803608135-÷=︒,任意若干个都不能和正三角形组成平面镶嵌; 能镶嵌的只有2种正多边形.故选C .考点6:多边形的去(多)角问题典例:(2019·江苏省初一期中)小李同学在计算一个n边形的内角和时不小心多加了一个内角,得到的内角之和是1380度,则这个多边形的边数n的值是_______.【答案】9【解析】设多边形的边数为n,多加的内角度数为α,则(n-2)•180°=1380°-α,∵1380°=7×180°+120°,内角和应是180°的倍数,∴n-2=7,n=9;故答案为:9.方法或规律点拨本题考查了多边形的内角和公式,根据多边形的内角和公式判断出多边形的内角和公式是180°的倍数是解题的关键.巩固练习1.(2020·全国初一)将一个四边形截去一个角后,它不可能是()A.六边形B.五边形C.四边形D.三角形【答案】A【解析】当截线为经过四边形对角2个顶点的直线时,剩余图形为三角形;当截线为经过四边形一组对边的直线时,剩余图形是四边形;当截线为只经过四边形一组邻边的一条直线时,剩余图形是五边形;∴剩余图形不可能是六边形,故选A.2.(2019·云南省初三二模)小明在计算一个多边形的内角和时,漏掉了一个内角,结果算得800°,这个多边形应该是()A.六边形B.七边形C.八边形D.九边形【答案】B【解析】解:设多边形的边数是n.依题意有(n﹣2)•180°≥800°,解得:n≥649,则多边形的边数n=7;故选:B.3.(2019·浙江省初二学业考试)一个四边形截去一个角后,形成新的多边形的内角和是()A.180°B.360°或540°C.540°D.180°或360°或540°【答案】D【解析】解:∵一个四边形截去一个角后得到的多边形可能是三角形,可能是四边形,也可能是五边形,∴内角和可能是180°,或(4-2) ×180°=540°,或(5-2) ×180°=540°.故选:D.4.(2018·山西省初一期末)若一个多边形除了一个内角外,其余各内角之和为2570°,则这个内角的度数为()A.90°B.105°C.130°D.120°【答案】C【解析】解:∵2570°÷180°=14…50°,又130°+50°=180°∴这个内角度数为130°故选C5.(2020·偃师市实验中学初一月考)多边形的所有内角与它的一个外角的和为600°,这个多边形的边数是_____【答案】5【解析】解:设边数为n,一个外角为α,则(n-2)×180°+α=600°,∴n=600180α-︒︒+2,∵0°<α<180°,n为正整数,∴当α=60°时,600180α-︒︒为正整数,此时n=5,内角和为(n-2)×180º=540°.故多边形的边数为5.6.(2019·山西省初一月考)如图,有一张正方形桌面,它的4个内角的和为360°,现在锯掉它的一个角,残余桌面所有的内角的和是_____________【答案】540°【解析】解:由题意得,残余桌面为五边形,∴残余桌面所有的内角的和为(5-3)×180°=540°故答案为:540°.。
人教版八年级数学上册金榜名师推荐课时提升作业11.3多边形及其内角和(含答案解析)
课时提高作业 ( 五)多边形及其内角和(30 分钟50分)一、选择题 ( 每题 4 分, 共 12 分)1. 如图 , 以下图形不是凸多边形的是()【分析】选 C.若将侧,有一部分在直线ABAB向双方延伸右边 .,这个图形有一部分在直线AB左【知识概括】多边形的分类多边形有两类 :一类是凸多边形 ,它的每个内角都小于180 °,另一类是凹多边形 ,它的内角中起码有一个大于180°.2.(2014 ·连江理智质检 ) 如下图 , 一个 60°角的三角形纸片 , 剪去这个 60°角后 , 获得一个四边形 , 则∠ 1+∠2 的度数为()A.120 °B.180°C.240°D.300°【分析】选 C.依据三角形的内角和定理得:四边形除掉∠1,∠2 后的两角的度数为180 °-60 °=120 °,则依据四边形的内角和定理得: ∠1+ ∠2=360 °-120 °=240 °.3.多边形的每个内角都等于 150°, 则此后多边形的一个极点出发可作的对角线共有 ()A.8 条B.9条C.10条D.11条【分析】选 B.∵多边形的每个内角都等于 150 °,∴多边形的每个外角都等于180 °-150 °=30 °,∴边数 n=360 °÷30°=12, ∴此后多边形的一个极点出发可作的对角线条数为12-3=9.二、填空题 ( 每题 4 分, 共 12 分)4. 剪掉多边形的一个角 , 则所成的新多边形的内角和.【分析】 n 边形的内角和是 (n-2) ·180 °,因为剪掉一个多边形的一个角,则所得新的多边形的边数可能增添一, 可能不变 ,也可能减少一 , 因此所成的新多边形的内角和增添180°或不变或减少180 °.答案 :增添 180 °或不变或减少180°5.如图 : 小亮从 A 点出发行进 10m,向右转 15°, 再行进 10m,又向右转15° , , 这样向来走下去, 他第一次回到出发点 A 时 , 一共走了m.【分析】此多边形的每个外角均相等,每一条边都相等, 由外角和为360 °,得边数 ==24, 则小亮走的总行程为24 ×10=240(m).答案 :2406. 因为一个多边形的外角最多能有个钝角,所以,一个多边形的内角最多能有个锐角 .【分析】多边形的外角和是360 °,设最多有x 个钝角 ,则 90 °x<360 °,解得 x<4, ∴x 最大取 3,即外角最多有 3 个钝角 .∴内角最多有 3 个锐角 .答案:3 3三、解答题 ( 共 26 分)7.(8分)在一个正多边形中,一个外角的度数等于一个内角度数的,求这个正多边形的边数和它每一个内角的度数.【分析】设这个正多边形的边数为n,由题意得 : (n-2) ×180=360, 解得 :n=9,故每一个内角为180 °-=140 °.答:这个正多边形的边数为 9,每一个内角的度数为 140 °.8.(8 分) 四边形 ABCD中, ∠A=140°, ∠D=80°.(1) 如图 1, 若∠ B=∠C,试求出∠ C的度数 .(2) 如图 2, 若∠ ABC的角均分线 BE交 DC于点 E, 且 BE∥AD,试求出∠ C 的度数 .【分析】 (1)因为∠A+∠B+∠C+ ∠D=360 °,∠B=∠C,所以∠B=∠C===70 °.(2) ∵BE∥AD,∴∠BEC= ∠D=80 °,∠ABE=180 °-∠A=180 °-140 °=40 °.又∵BE 均分∠ABC, ∴∠EBC= ∠ABE=40 °,∴∠C=180 °-∠EBC- ∠BEC=180 °-40 °-80°=60 °.【培优训练】9.(10 分) 小明和小亮分别利用图①、图②的不一样方法求出了五边形的内角和都是 540°. 请你考虑在图③中再用此外一种方法求五边形的内角和 . 并写出求解过程 .【分析】(答案不独一)连结五边形的一对不相邻的极点,获得一个三角形和一个四边形,三角形的内角和是180 °,四边形的内角和是360°,因此五边形的内角和是 180 °+360 °=540 °.。
多边形的内角和(分层作业)(解析版)docx

11.3.2多边形的内角和夯实基础篇一、单选题:1.一个多边形的每一个外角都为72°,这个多边形是()A .五边形B .六边形C .八边形D .十边形【答案】A【解析】【分析】多边形的外角和是360°,依此可以求出多边形的边数.【详解】解:∵一个多边形的每个外角都等于72°,∴多边形的边数为360°÷72°=5.故这个多边形的边数是5.故选:A .【点睛】本题主要考查了多边形的外角和定理:多边形的外角和是360°.2.一个多边形的内角和为1800°,则这个多边形为()A .九边形B .十边形C .十一边形D .十二边形【答案】D【解析】【分析】根据多边形内角和公式“2180()n ”进行计算,即可得.【详解】解:由题意得,(2)1801800n(2)10nn ,12故选D.【点睛】本题考查了多边形的内角和,解题的关键是掌握多边形内角和公式.3.下列哪一个角度可以作为一个多边形的内角和()A.2080 B.1240 C.1980°D.1600【答案】C【解析】【分析】利用多边形的内角和公式逐个选项进行分析即可作出判断.【详解】n ,解:∵多边形内角和公式为 2180∴多边形内角和一定是180的倍数.∵1980°=11×180°,故选:C.【点睛】本题主要考查了多边形内角和公式,在解题时要记住多边形内角和公式,并加以应用即可解决问题.4.如图,从△ABC的纸片中剪去△CED,得到四边形ABDE.若∠1+∠2=230°,则∠C=()A.230°B.130°C.50°D.110°【解析】【分析】根据∠1+∠2的度数,再利用四边形内角和定理得出∠A +∠B 的度数,即可得出∠C 的度数【详解】解:∵四边形ABDE 的内角和为360°,且∠1+∠2=230°.∴∠A +∠B =360°﹣230°=130°.∵△ABC 的内角和为180°,∴∠C =180°﹣(∠A +∠B )=180°﹣130°=50°.故选:C .【点睛】本题主要考查了多边形的内角与外角,掌握“四边形的内角和是360度与三角形内角和是180度”是解题关键.5.如图,1,2,3 是五边形ABCDE 的3个外角,若123210 ,则A B =()A .150B .180C .210D .310【答案】C【解析】根据多边形内角和 2180n ,结合计算即可.【详解】解:(52)180A B AED EDC BCD ∵,540A B ∵(123)540 ,123210A B ,故选:C .【点睛】本题主要考查多边形内角和,熟知多边形内角和公式 2180n 是解题关键.6.如图,A B C D E F G ().A .180°B .270°C .360°D .540°【答案】D【解析】【分析】如图,连接FI ,根据三角形的一个外角等于与它不相邻的两个内角的和可得C E AHI ,BIFD DFI ,再利用三角形的内角和等于180 ,四边形的内角和等于360 求解即可.【详解】解:如图,连接FI ,则C E AHI ,BIF D DFI ,A B C D E F G ,A B AHI BIH GIF IFG G360180 ,540 .故选:D .【点睛】本题考查了多边形的内角和定理与三角形的内角和定理,解题的关键作出辅助线,把六个角的和转化为四边形的内角和与三角形的内角和.7.如图,小明从正八边形(各边相等,各内角也相等)草地的一边AB 上一点S 出发,步行一周回到原处在步行的过程中,小明转过的角度的和是()A .0B .45C .180D .360【答案】D【解析】【分析】根据正八边形的内角和求出每个内角,再求出每次转过的角度45°,一共转8次,利用45°×8计算即可.【详解】解:∵ABCDEFGH 为正八边形,∴每个内角为(8-2)×180°÷8=135°,小明每转一次转过的角为180°-135°=45°,步行一周回到原处,小明一共转八次所有转过的角度之和为45°×8=360°,故选:D .【点睛】本题考查正八边形的内角和、每个内角、外角与外角和,掌握正多边形相关知识是解题关键.二、填空题:8.在四边形ABC D 中,若∠A 与∠C 互补,∠B =55°,则∠D =_____度.【答案】125【解析】【分析】根据四边形内角和可直接进行求解.【详解】解:由四边形内角和可得:360A B C D ,∵∠A 与∠C 互补,∠B =55°,∴36018055125D ;故答案为125.【点睛】本题主要考查多边形内角和,熟练掌握多边形内角和是解题的关键.9.如果过多边形的一个顶点共有3条对角线,那么这个多边形的内角和是______度.【答案】720【解析】【分析】根据过多边形的一个顶点共有3条对角线,则这个多边形的边数是6,n 边形的内角和可以表示成(n-2)•180°,代入公式就可以求出内角和.【详解】解:∵过多边形的一个顶点共有3条对角线,∴该多边形边数为6,∴(6-2)•180°=720°,∴这个多边形的内角和为720°,故答案为:720.【点睛】本题考查了多边形的内角和公式,多边形的对角线,解题的关键是掌握多边形对角线规律.10.若一个正n边形的一个内角与和它相邻的外角的度数之比是3:1,那么n=_________.【答案】8【解析】【分析】设和它相邻的外角的度数为x,则这个内角为3x,根据题意列出方程,即可求解.【详解】解:设和它相邻的外角的度数为x,则这个内角为3x,根据题意得:3180x x,解得:45x ,∴360845n.故答案为:8【点睛】本题主要考查了正多边形的内角和与外角和问题,利用方程思想解答是解题的关键.11.若一个多边形的内角和与外角和之比是的5︰2,则这个多边形的边数是__________.【答案】7【解析】【分析】设这个多边形的边数是n ,则内角和为180(2)n ,然后根据外角和是360度,即可求得边数.【详解】解:设这个多边形的边数是n ,则∴180(2)53602n 解得7n ;故答案为:7.【点睛】本题考查了多边形的计算,理解多边形的外角和是360度,外角和不随边数的变化而变化是关键.12.在五边形ABCDE 中,DC AB ∥,DE AE ,128EAB ,则EDC 的度数是______.【答案】142 ##142度【解析】【分析】根据平行线的性质求得180,B C 根据DE AE ,可得90E ,根据128EAB ,以及五边形的内角和为540 ,即可求解.【详解】∵DC AB ∥,180,B C ∵DE AE ,90E ,∵五边形的内角和为 52180540 ,128EAB ,54090180128142EDC .故答案为:142 .【点睛】本题考查了平行线的性质,垂线的定义,多边形的内角和,掌握以上知识是解题的关键.13.如图,AB ∥CD ,AF 平分∠CAB ,CF 平分∠AC D .(1)∠B +∠E +∠D =________;(2)∠AFC =________.【答案】360 90【解析】【分析】(1)由两直线平行同旁内角互补解得180CAB ACD ,再由五边形内角和540°即可解答;(2)由角平分线的性质,解得11,22FAC BAC FCA ACD ,根据两直线平行同旁内角互补解得180CAB ACD ,最后由三角形内角和180°解答.【详解】解:(1)∵AB ∥CD ,180CAB ACD∵五边形的内角和为 52180540∠B +∠E +∠D =540180360故答案为:360 ;(2)∵AB ∥CD ,180CAB ACD∵AF 平分∠CAB ,CF 平分∠ACD 11,22FAC BAC FCA ACD 11()1809022FAC FCA BAC ACD 1809090AFC故答案为:90 .【点睛】本题考查平行线的性质、五边形内角和、角平分线的性质等知识,是基础考点,掌握相关知识是解题关键.14.如图,将等边三角形、正方形和正五边形按如图所示的位置摆放.1230 ,则3 =___.【答案】42 ##42度【解析】【分析】利用多边形的外角和定理,即360 减去等边三角形的一个内角的度数,减去正五边形的一个内角的度数,减去正方形的一个内角的度数,再减去1 和2 的度数,最后得出答案.【详解】等边三角形的内角的度数是60 ,正方形的内角的度数为90 ,正五边形的内角的度数是(52)1801085,则336060901081242 .故答案为:42【点睛】此题考查了多边形外角和定理,正多边形内角和公式,熟练掌握相关知识及正确运算是解题关键.三、解答题:15.一个多边形的外角和是它的内角和的29,求这个多边形的边数和内角和.【答案】11,1620【解析】【分析】n 边形的内角和是(n −2)⋅180°,外角和是360°,根据一个多边形的内角和与外角和的关系,得到一个关于n 的方程,解得边数n ,即可求得内角和.【详解】解:设这个多边形是n 边形,由题意,得 218023609n ,解得11n .故这个多边形的内角和是 11 21801620 ,∴这个多边形是十一边形,其内角和为1620°.【点睛】本题主要考查了多边形的外角和与内角和,熟练掌握n 边形内角和为(n −2)⋅180°、外角和为360°是解题的关键.16.如图,已知在四边形ABCD 中,70A ,140B .(1)BCD D 的度数为___________;(2)若BCD 的平分线交边AD 于点E ,且CE AB ∥,求D 的度数.【答案】(1)150 (2)70【解析】【分析】(1)根据四边形的内角和求解即可;(2)根据平行线的性质,求出∠BCE 的度数,根据2BCD BCE ,求出∠BCD 的度数,即可得出∠D 的度数.(1)∵在四边形ABC D 中,∠A =70°,∠B =140°,∴∠BCD +∠D =360A B36070140 150 ;故答案为:150°;(2)CE AB ∵ ,180B BCE ,140B ∵,18014040BCE ,CE ∵平分∠BCD ,224080BCD BCE ,1501508070D BCD .【点睛】本题主要考查了四边形的内角和,角平分线的定义和平行线的性质,熟练掌握平行线的性质是解题的关键.17.小红把一副直角三角板按如图所示的方式摆放在一起,其中90B ,90D ,45E ,30A ,求12 的度数.【答案】210【解析】【分析】如图,由三角形的外角的性质可得:14,23,E F 可得1234E F ,再利用三角形的内角和求解1809090E F ,再利用四边形的内角和求解563609030240, 再求解3436056360240120 ,从而可得结论.【详解】解:如图,由三角形的外角的性质可得:14,23,E F 1234E F ,90,45,D E ∵1809090E F ,56360,90,30,A B B A ∵563609030240,3436056360240120 ,1290120210.【点睛】本题考查的是三角形的内角和,四边形的内角和定理,三角形的外角的性质,平角的定义,掌握以上知识是解题的关键.能力提升篇一、单选题:1.一个多边形减去一个角后,所得多边形的内角和是720 ,则这个多边形的边数不可能是()A.4B.5C.6D.7【答案】A【解析】【分析】根据多边形的内角和求出减去一个角后的多边形的边数即可判断.【详解】解:由题意得,n ,解得6(2)180720n ,由于减去一个角后边数为6,则这个多边形不可能为四边形,故选A.【点睛】本题考查了多边形的内角和,熟练掌握多边形的边数与内家和的关系是解题的关键.2.马小虎在计算一个多边形的内角和时,由于粗心少算了2个内角,其和等于830 ,则该多边形的边数是()A.7B.8C.7或8D.无法确定【答案】C【解析】【分析】n边形的内角和是(n-2)•180°,即为180°的(n-2)倍,多边形的内角一定大于0度,小于180度,因而多边形中,除去2个内角外,其余内角和与180度的商加上2,以后所得的数值,比这个数值大1或2的整数就是多边形的边数.【详解】设少加的2个内角和为x度,边数为n.则(n-2)×180=830+x,即(n-2)×180=4×180+110+x,因此x=70,n=7或x=250,n=8.故该多边形的边数是7或8.故选C.【点睛】本题考查了多边形的内角和定理,正确理解多边形内角的大小的特点,以及多边形的内角和定理是解决本题的关键.3.小敏利用最近学习的数学知识,给同伴出了这样一道题:假如你从点A出发,沿直线走10米后向左转 度,接着沿直线前进10米后,再向左转 度……如此下去,当她第一次回到A点时,发现自己走了100米,则 的度数为()A.36°B.40°C.45°D.60°【答案】A【解析】【分析】先求出当小敏第一次回到A点时,她走过的路径是一个正十边形,再根据正多边形的外角和等于360 求解即可得.【详解】解:因为1001010,所以当小敏第一次回到A点时,她走过的路径是如图所示的正十边形,所以3603610,故选:A.【点睛】本题考查了正多边形的外角和,熟练掌握正多边形的外角和等于360 是解题关键.二、填空题:4.已知一个多边形的内角和再加上一个外角共600 ,则这个多边形的边数是________【答案】5【解析】【分析】设多边形的边数是n,加的外角为a,根据多边形的内角和公式(n-2)•180°可知,多边形的内角和是180°的倍数,然后列式求解即可.【详解】解:设多边形的边数是n ,加的外角为a ,∵600÷180=3余60°,且多边形的内角和公式(n -2)•180°,∴n -2=3,a =60°,∴n =5,,即这个多边形的边数是5.故答案为:5【点睛】本题考查了多边形的内角和公式,利用好多边形的内角和是180°的倍数是解题的关键.5.一个凸多边形最小的一个内角为100°,其他的内角依次增加10°,则这个多边形的边数为_____.【答案】8【解析】【详解】设该凸多边形的边数为n (n 为正整数且n >2).将该多边形的内角按角度从小到大排列后,第n 个内角的角度为 1001101090n n .按从小到大以及从大到小的顺序分别写出该多边形的各个内角的角度:100,110,120,,1070,1080,1090n n n ;1090,1080,1070,,120,110,100n n n .可以发现,上下两行对应角度之和均等于10190n ,像这样的和共有n 个.因此,该凸多边形的内角和为 101902n n .根据凸多边形的内角和公式,该凸多边形的内角和为 2180n .根据上述结论,可以列出关于n 的方程:1019021802n n n ,解之,得n 1=9,n 2=8.①当n =9时,该凸多边形最大的内角的角度为91090180 ,不符合题意.②当n =8时,该凸多边形最大的内角的角度为81090170 ,符合题意.故本题应填写:8.点睛:本题考查了凸多边形内角和的相关知识.本题的难点在于如何获得该多边形内角角度的表达式以及由这些表达式得到的内角和的表达式.本题的一个易错点在于忽略对所得最终结果合理性的检验.另外,运用将两列排列顺序相互颠倒的内角角度相加的方式求解内角和的表达式,是数学中的重要方法.6.小明在用计算器计算一个多边形的内角和时,得出的结果为2005°,小芳立即判断他的结构是错误的,小明仔细地复算了一遍,果然发现自己把一个角的度数输入了两遍.你认为正确的内角和应该是________.【答案】1980【解析】【详解】解:设多边形的边数为n ,多加的角度为α,则(n -2)×180°=2005°-α,当n =13时,α=25°,此时(13-2)×180°=1980°,α=25°故答案为1980.三、解答题:7.在一个各内角都相等的多边形中,每一个内角都比相邻外角的3倍还大20 .(1)求这个多边形的边数;(2)若将这个多边形剪去一个角,剩下多边形的内角和是多少?【答案】(1)9;(2)1080º或1260º或1440º.【解析】【分析】(1)设多边形的一个外角为x ,则与其相邻的内角等于320x ,根据内角与其相邻的外角的和是180 列出方程,求出x 的值,再由多边形的外角和为360 ,求出此多边形的边数为360x;(2)剪掉一个角以后,多边形的边数可能增加了1条,也可能减少了1条,或者不变,根据多边形的内角和定理即可求出答案.【详解】解:(1)设每一个外角为x ,则与其相邻的内角等于320x ,180320x x ,40x ,即多边形的每个外角为40 ,∵多边形的外角和为360 ,∴多边形的外角个数为:360940,∴这个多边形的边数为9;(2)因为剪掉一个角以后,多边形的边数可能增加了1条,也可能减少了1条,或者不变,①若剪去一角后边数减少1条,即变成8边形,内角和为 821801080 ,②若剪去一角后边数不变,即变成9边形,内角和为 921801260 ,③若剪去一角后边数增加1,即变成10边形,内角和为 1021801440 ,∴将这个多边形剪去一个角后,剩下多边形的内角和为1080 或1260 或1440 .【点睛】本题考查了多边形的内角和定理,外角和定理,多边形内角与外角的关系,熟练掌握相关知识点是解题的关键.8.阅读并解决下列问题:(1)如图①,ABC 中,60A ,ABC 、ACB 的平分线交于点D ,则BDC ______.(2)如图②,五边形ABCDE 中,AE BC ∥,EF 平分AED ,CF 平分BCD ,若72 EDC ,求EFC 的度数.图①图②【答案】(1)120 ;(2)144【解析】【分析】(1)先根据三角形内角和及角平分线求出60CBD BCD ,然后再根据三角形内角和求出BDC ∠的度数即可.(2)首先根据AE BC ∥得出180A B ,然后根据五边形内角和求出288AED BCD ,由角平分线的性质进而得出144DEF DCF ,再根据四边形内角和即可求出EFC 的度数.【详解】(1)BD Q ,CD 分别平分ABC 、ACB ,ABD CBD ,ACD BCD ,180A ABC ACB ∵,6022180CBD BCD ,60CBD BCD ,180BDC CBD BCD ∵,120BDC .(2)∵EF 平分AED ,CF 平分BCD ,设AEF DEF ,BCF DCF ,∵AE BC ∥,∴180A B ,∵五边形的内角和为540 ,∴540180360AED D BCD ,即2722360 ,∴144 ,∵72 EDC ,∴ 36036072144144EFC D .【点睛】本题考查了多边形的内角和、平行线的性质及角平分线的性质,解题的关键是熟练掌握多边形内角和的求法及灵活运用角平分线的性质.9.如果一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫做正多边形,如图,就是一组正多边形,观察每个正多边形中∠ 的变化情况,解答下列问题.(1)将如表的表格补充完整:正多边形的边数3456……n∠ 的度数……(2)根据规律,是否存在一个正n 边形,使其中的∠ =20°?若存在,求出n 的值;若不存在,请说明理由.【答案】(1)60 ,45 ,36 ,30°,180(n;(2)存在,9n【解析】【分析】(1)根据计算、观察,可发现规律:正n边形中的∠α=180(n;(2)根据正n边形中的∠α=180(n,可得答案.【详解】解:(1)观察上面每个正多边形中的,填写下表:正多边形边数3456 n的度数60 45 36 30° 180()n故答案为:60 ,45 ,36 ,30°,180(n;(2)存在,理由如下:∵设存在正n边形使得20,得18020()n.解得:9n ,存在正n边形使得20.【点睛】本题考查了多边形内角与外角,每题都利用了正多边形的内角:(2)180nn,三角形的内角和定理,等腰三角形的两底角相等.思维拓展篇1.阅读材料:如图1,AB、CD交于点O,我们把△AOD和△BOC叫做对顶三角形.结论:若△AOD和△BOC是对顶三角形,则∠A+∠D=∠B+∠C.结论应用举例:如图2:求五角星的五个内角之和,即∠A+∠B+∠ACE+∠ADB+∠E的度数.解:连接CD,由对顶三角形的性质得:∠B+∠E=∠1+∠2,在△AC D中,∵∠A+∠ACD+∠ADC=180°,即∠A+∠3+∠1+∠2+∠4=180°,∴∠A+∠ACE+∠B+∠E+ADB=180°即五角星的五个内角之和为180°.解决问题:(1)如图①,∠A+∠B+∠C+∠D+∠E+∠F=;(2)如图②,∠A+∠B+∠C+∠D+∠E+∠F+∠G=;(3)如图③,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=;(4)如图④,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=;请你从图③或图④中任选一个,写出你的计算过程.【答案】(1)360°;(2)540°;(3)720°;(4)1080°;过程见解析【解析】【分析】(1)连接CD,由对顶角三角形可得∠A+∠B=∠BDC+∠ACD,再由四边形的内角和定理得出结论;(2)连接ED,由对顶角三角形可得∠A+∠B=∠BED+∠ADE,再由五边形的内角和定理得出结论;(3)连接BH、DE,由对顶角三角形可知∠EBH+∠BHD=∠HDE+∠BED,再根据五边形的内角和定理得出结论;(4)连接ND、NE,由对顶角三角形可知∠1+∠2=∠NGH+∠EHG,再由六边形的内角和定理得出结论.【详解】解:(1)连接CD,由对顶角三角形可得∠A+∠B=∠BDC+∠ACD,则∠A+∠B+∠C+∠D+∠E+∠F=360°;(2)连接ED,由对顶角三角形可得∠A+∠B=∠BED+∠ADE,则∠A+∠B+∠C+∠D +∠E+∠F+∠G=540°;(3)连接BH、DE,∵由对顶角三角形可知∠EBH+∠BHD=∠HDE+∠BED,∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=五边形CDEFG的内角和+△ABH的内角和=540°+180°=720°;(4)连接ND、NE,∵由对顶角三角形可知∠1+∠2=∠NGH+∠EHG,∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=六边形BCFGHM的内角和+△AND的内角和+△NDE的内角和=(6-2)×180°+360°=1080°.故答案为:360°;540°;720°;1080°.【点睛】本题考查的是三角形内角和定理,根据题意作出辅助线,利用△AOD和△BOC叫做对顶三角形的性质及多边形的内角和定理解答是解答此题的关键.。
11.3多边形及其内角和练习题 ?(含答案)八年级数学

11.3多边形及其内角和练习题一.选择题(共16小题)1.(2013•湛江)已知一个多边形的内角和是540°,则这个多边形是()A.四边形B.五边形C.六边形D.七边形2.(2013•梅州)若一个多边形的内角和小于其外角和,则这个多边形的边数是()A.3 B.4 C.5 D.63.(2014•达州)如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠P=()A.90°﹣αB.90°+αC.D.360°﹣α4.(2004•陕西)如图,在锐角△ABC中,CD,BE分别是AB,AC边上的高,且CD,BE相交于一点P,若∠A=50°,则∠BPC=()A.150°B.130°C.120°D.100°5.(2015•丽水)一个多边形的每个内角均为120°,则这个多边形是()A.四边形B.五边形C.六边形D.七边形6.(2015•葫芦岛)如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD,则∠P的度数是()A.60°B.65°C.55°D.50°7.(2015•莱芜)一个多边形除一个内角外其余内角的和为1510°,则这个多边形对角线的条数是()A.27 B.35 C.44 D.548.(2015•南宁)一个正多边形的内角和为540°,则这个正多边形的每一个外角等于()A.60°B.72°C.90°D.108°9.(2014•临沂)将一个n边形变成n+1边形,内角和将()A.减少180°B.增加90°C.增加180°D.增加360°10.(2016•凉山州)一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为()A.7 B.7或8 C.8或9 D.7或8或911.(2015•北仑区一模)一个正多边形的外角与它相邻的内角之比为1:4,那么这个多边形的边数为()A.8 B.9 C.10 D.1212.(2014•大丰市模拟)如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2=()A.90°B.135°C.270°D.315°13.(2015•无锡模拟)如果一个多边形的内角和等于1260°,那么这个多边形的边数为()A.7 B.8 C.9 D.1014.(2015•重庆)已知一个多边形的内角和是900°,则这个多边形是()A.五边形B.六边形C.七边形D.八边形15.(2014•莱芜)若一个正n边形的每个内角为156°,则这个正n边形的边数是()A.13 B.14 C.15 D.1616.(2012秋•渝中区校级期末)从一个七边形的某个顶点出发,分别连接这个点与其余各顶点,可以把一个七边形分割成()个三角形.A.6 B.5 C.8 D.7二.填空题(共8小题)17.(2015•资阳)若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是.18.(2014•巴中)若一个正多边形的一个内角等于135°,那么这个多边形是正边形.19.(2014•遵义)正多边形的一个外角等于20°,则这个正多边形的边数是.20.(2013•巴中)若一个多边形外角和与内角和相等,则这个多边形是边形.21.(2013•乐山)如图,在四边形ABCD中,∠A=45°.直线l与边AB,AD分别相交于点M,N,则∠1+∠2= .22.(2015•盘锦二模)如图所示,一个角60°的三角形纸片,剪去这个60°角后,得到一个四边形,则∠1+∠2= .23.(2016•太原一模)如图,已知正五边形ABCDE,AF∥CD,交DB 的延长线于点F,则∠DFA= 度.24.(2015•崇安区二模)正n边形的一个内角比一个外角大100°,则n 为.三.解答题(共1小题)25.(2015春•沙河市期末)在△ABC中,如果∠A、∠B、∠C的外角的度数之比是4:3:2,求∠A的度数.11.3多边形及其内角和练习题参考答案与试题解析一.选择题(共16小题)1.(2013•湛江)已知一个多边形的内角和是540°,则这个多边形是()A.四边形B.五边形C.六边形D.七边形【解答】解:根据多边形的内角和可得:(n﹣2)180°=540°,解得:n=5,则这个多边形是五边形.故选B.【点评】本题比较容易,主要考查多边形的内角和公式.2.(2013•梅州)若一个多边形的内角和小于其外角和,则这个多边形的边数是()A.3 B.4 C.5 D.6【解答】解:设边数为n,根据题意得(n﹣2)•180°<360°解之得n<4.∵n为正整数,且n≥3,∴n=3.故选A.【点评】本题考查多边形的内角和与外角和、方程的思想.关键是记住内角和的公式与外角和的特征,还需要懂得挖掘此题隐含着边数为正整数这个条件.本题既可用整式方程求解,也可用不等式确定范围后求解.3.(2014•达州)如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠P=()A.90°﹣αB.90°+αC.D.360°﹣α【解答】解:∵四边形ABCD中,∠ABC+∠BCD=360°﹣(∠A+∠D)=360°﹣α,∵PB和PC分别为∠ABC、∠BCD的平分线,∴∠PBC+∠PCB=(∠ABC+∠BCD)=(360°﹣α)=180°﹣α,则∠P=180°﹣(∠PBC+∠PCB)=180°﹣(180°﹣α)=α.故选:C.【点评】本题考查了多边形的内角和外角以及三角形的内角和定理,属于基础题.4.(2004•陕西)如图,在锐角△ABC中,CD,BE分别是AB,AC边上的高,且CD,BE相交于一点P,若∠A=50°,则∠BPC=()A.150°B.130°C.120°D.100°【解答】解:∵BE⊥AC,CD⊥AB,∴∠ADC=∠AEB=90°,∴∠BPC=∠DPE=180°﹣50°=130°.故选B.【点评】主要考查了垂直的定义以及四边形内角和是360度.注意∠BPC与∠DPE互为对顶角.5.(2015•丽水)一个多边形的每个内角均为120°,则这个多边形是()A.四边形B.五边形C.六边形D.七边形【解答】解:外角是180°﹣120°=60°,360÷60=6,则这个多边形是六边形.故选:C.【点评】考查了多边形内角与外角,根据外角和的大小与多边形的边数无关,由外角和求正多边形的边数,是常见的题目,需要熟练掌握.6.(2015•葫芦岛)如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD,则∠P的度数是()A.60° B.65° C.55°D.50°【解答】解:∵五边形的内角和等于540°,∠A+∠B+∠E=300°,∴∠BCD+∠CDE=540°﹣300°=240°,∵∠BCD、∠CDE的平分线在五边形内相交于点O,∴∠PDC+∠PCD=(∠BCD+∠CDE)=120°,∴∠P=180°﹣120°=60°.故选:A.【点评】本题主要考查了多边形的内角和公式,角平分线的定义,熟记公式是解题的关键.注意整体思想的运用.7.(2015•莱芜)一个多边形除一个内角外其余内角的和为1510°,则这个多边形对角线的条数是()A.27 B.35 C.44 D.54【解答】解:设这个内角度数为x,边数为n,∴(n﹣2)×180°﹣x=1510,∵n为正整数,∴n=11,∴=44,故选:C.【点评】此题考查多边形的内角和计算公式以及多边形的对角线条数的计算方法,属于需要识记的知识.8.(2015•南宁)一个正多边形的内角和为540°,则这个正多边形的每一个外角等于()A.60°B.72°C.90°D.108°【解答】解:设此多边形为n边形,根据题意得:180(n﹣2)=540,解得:n=5,∴这个正多边形的每一个外角等于:=72°.故选B.【点评】此题考查了多边形的内角和与外角和的知识.注意掌握多边形内角和定理:(n﹣2)•180°,外角和等于360°.9.(2014•临沂)将一个n边形变成n+1边形,内角和将()A.减少180°B.增加90°C.增加180°D.增加360°【解答】解:n边形的内角和是(n﹣2)•180°,n+1边形的内角和是(n﹣1)•180°,因而(n+1)边形的内角和比n边形的内角和大(n﹣1)•180°﹣(n﹣2)•180=180°.故选:C.【点评】本题主要考查了多边形的内角和公式,是需要识记的内容.10.(2016•凉山州)一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为()A.7 B.7或8 C.8或9 D.7或8或9【解答】解:设内角和为1080°的多边形的边数是n,则(n﹣2)解得:n=8.则原多边形的边数为7或8或9.故选:D.【点评】本题考查了多边形的内角和定理,一个多边形截去一个角后它的边数可能增加1,可能减少1,或不变.11.(2015•北仑区一模)一个正多边形的外角与它相邻的内角之比为1:4,那么这个多边形的边数为()A.8 B.9 C.10 D.12【解答】解:设正多边形的每个外角的度数为x,与它相邻的内角的度数为4x,依题意有x+4x=180°,解得x=36°,这个多边形的边数=360°÷36°=10.故选:C.【点评】本题考查了多边形的外角定理:多边形的外角和为360°.也考查了邻补角的定义.12.(2014•大丰市模拟)如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2=()A.90°B.135°C.270°D.315°【解答】解:∵∠C=90°,∴∠A+∠B=90°.∵∠A+∠B+∠1+∠2=360°,∴∠1+∠2=360°﹣90°=270°.故选:C.【点评】本题考查了直角三角形的性质和四边形的内角和定理.知道剪去直角三角形的这个直角后得到一个四边形,根据四边形的内角和定理求解是解题的关键.13.(2015•无锡模拟)如果一个多边形的内角和等于1260°,那么这个多边形的边数为()A.7 B.8 C.9 D.10【解答】解:根据题意,得(n﹣2)•180=1260,解得n=9,故选C.【点评】本题考查了多边形的内角和,已知多边形的内角和求边数,可以转化为方程的问题来解决.14.(2015•重庆)已知一个多边形的内角和是900°,则这个多边形是()A.五边形B.六边形C.七边形D.八边形【解答】解:设这个多边形是n边形,则(n﹣2)•180°=900°,解得:n=7,即这个多边形为七边形.故本题选C.【点评】根据多边形的内角和定理,求边数的问题就可以转化为解方程的问题来解决.15.(2014•莱芜)若一个正n边形的每个内角为156°,则这个正n边形的边数是()A.13 B.14 C.15 D.16【解答】解:∵一个正多边形的每个内角都为156°,∴这个正多边形的每个外角都为:180°﹣156°=24°,∴这个多边形的边数为:360°÷24°=15,故选:C.【点评】此题考查了多边形的内角和与外角和的知识.此题难度不大,注意掌握多边形的外角和定理是关键.16.(2012秋•渝中区校级期末)从一个七边形的某个顶点出发,分别连接这个点与其余各顶点,可以把一个七边形分割成()个三角形.A.6 B.5 C.8 D.7【解答】解:从一个七边形的某个顶点出发,分别连接这个点与其余各顶点,可以把一个七边形分割成7﹣2=5个三角形.故选:B.【点评】本题考查的知识点为:从n边形的一个顶点出发,可把n边形分成(n﹣2)个三角形.二.填空题(共8小题)17.(2015•资阳)若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是8 .【解答】解:设多边形的边数为n,根据题意,得(n﹣2)•180=3×360,解得n=8.则这个多边形的边数是8.【点评】已知多边形的内角和求边数,可以转化为方程的问题来解决.18.(2014•巴中)若一个正多边形的一个内角等于135°,那么这个多边形是正八边形.【解答】解:∵内角与外角互为邻补角,∴正多边形的一个外角是180°﹣135°=45°,∵多边形外角和为360°,∴360°÷45°=8,则这个多边形是八边形.故答案为:八.【点评】根据外角和的大小与多边形的边数无关,由外角和求正多边形的边数,是常见的题目,需要熟练掌握.19.(2014•遵义)正多边形的一个外角等于20°,则这个正多边形的边数是18 .【解答】解:因为外角是20度,360÷20=18,则这个多边形是18边形.故答案为:18【点评】根据外角和的大小与多边形的边数无关,由外角和求正多边形的边数,是常见的题目,需要熟练掌握.20.(2013•巴中)若一个多边形外角和与内角和相等,则这个多边形是四边形.【解答】解:设这个多边形的边数是n,则(n﹣2)•180°=360°,解得n=4.故答案为:四.【点评】本题考查了多边形的内角和公式与多边形的外角和定理,需要注意,多边形的外角和与边数无关,任何多边形的外角和都是360°.21.(2013•乐山)如图,在四边形ABCD中,∠A=45°.直线l与边AB,AD分别相交于点M,N,则∠1+∠2= 225°.【解答】解:∵∠A=45°,∴∠B+∠C+∠D=360°﹣∠A=360°﹣45°=315°,∴∠1+∠2+∠B+∠C+∠D=(5﹣2)•180°,解得∠1+∠2=225°.故答案为:225°.【点评】本题考查了多边形的内角和公式,熟记多边形的内角和为(n ﹣2)•180°是解题的关键,整体思想的利用也很重要.22.(2015•盘锦二模)如图所示,一个角60°的三角形纸片,剪去这个60°角后,得到一个四边形,则∠1+∠2= 240°.【解答】解:根据三角形的内角和定理得:四边形除去∠1,∠2后的两角的度数为180°﹣60°=120°,则根据四边形的内角和定理得:∠1+∠2=360°﹣120°=240°.故答案为:240°.【点评】主要考查了三角形及四边形的内角和是360度的实际运用与三角形内角和180度之间的关系.23.(2016•太原一模)如图,已知正五边形ABCDE,AF∥CD,交DB 的延长线于点F,则∠DFA= 36 度.【解答】解:∵正五边形的外角为360°÷5=72°,∴∠C=180°﹣72°=108°,∵CD=CB,∴∠CDB=36°,∵AF∥CD,∴∠DFA=∠CDB=36°,故答案为:36.【点评】本题考查了多边形的内角和外角及平行线的性质,解题的关键是求得正五边形的内角.24.(2015•崇安区二模)正n边形的一个内角比一个外角大100°,则n 为9 .【解答】解:设内角为x°,则外角为(x﹣100)°,根据题意得:x+x﹣100=180,解得:x=140,所以外角为40°,∴360°÷40°=9,故答案为:9.【点评】本题考查了多边形的内角与外角,解题的关键是知道多边形的外角和为360°.三.解答题(共1小题)25.(2015春•沙河市期末)在△ABC中,如果∠A、∠B、∠C的外角的度数之比是4:3:2,求∠A的度数.【解答】解:设∠A、∠B、∠C的外角分别为∠1=4x度、∠2=3x度、∠3=2x度.(1分)因为∠1、∠2、∠3是△ABC的三个外角,所以4x+3x+2x=360,解得x=40.(2分)所以∠1=160°、∠2=120°、∠3=80°.(1分)因为∠A+∠1=180°,(1分)所以∠A=20°.(1分)【点评】本题主要考查三角形的外角性质及三角形的内角和定理,解题的关键是熟练掌握三角形的外角性质定理,即三角形的一个外角等于与它不相邻的两个内角之和.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
11.3 多边形及多边形内角和精选练习答案一、单选题(共10小题)1.(2020·湖州市期中)若正多边形的一个外角是60︒,则该正多边形的内角和为()A.360︒B.540︒C.720︒D.900︒【答案】C【分析】根据正多边形的外角度数求出多边形的边数,根据多边形的内角和公式即可求出多边形的内角和. 【详解】由题意,正多边形的边数为360660n︒==︒,其内角和为()2180720n-⋅︒=︒.故选C.2.(2018·虹桥区期中)已知一个多边形的内角和等于900º,则这个多边形是()A.五边形B.六边形C.七边形D.八边形【答案】C【解析】多边形的内角和公式为(n-2)×180°,根据题意可得:(n-2)×180°=900°,解得:n=7.3.(2019·枣庄市期末)如图,小明从A点出发,沿直线前进10米后向左转36°,再沿直线前进10米,再向左转36°……照这样走下去,他第一次回到出发点A点时,一共走的路程是()A.100米B.110米C.120米D.200米【答案】A【分析】根据多边形的外角和即可求出答案.【详解】解:∵360÷36=10,∴他需要走10次才会回到原来的起点,即一共走了10×10=100米.故选A.4.(2019·唐山市期中)将一个四边形截去一个角后,它不可能是()A.六边形B.五边形C.四边形D.三角形【答案】A【解析】试题解析:当截线为经过四边形对角2个顶点的直线时,剩余图形为三角形;当截线为经过四边形一组对边的直线时,剩余图形是四边形;当截线为只经过四边形一组邻边的一条直线时,剩余图形是五边形;∴剩余图形不可能是六边形,故选A.5.(2020·阳泉市期末)已知正多边形的一个外角为36°,则该正多边形的边数为( ).A.12 B.10 C.8 D.6【答案】B【分析】利用多边形的外角和是360°,正多边形的每个外角都是36°,即可求出答案.【详解】解:360°÷36°=10,所以这个正多边形是正十边形.故选:B.6.(2019·哈尔滨市期末)若正多边形的一个内角是150°,则该正多边形的边数是()A.6 B.12 C.16 D.18【答案】B【解析】设多边形的边数为n,则有(n-2)×180°=n×150°,解得:n=12,故选B.7.(2019·长春市期末)马小虎在计算一个多边形的内角和时,由于粗心少算了2个内角,其和等于830,则该多边形的边数是()A.7 B.8 C.7或8 D.无法确定【答案】C【分析】n边形的内角和是(n-2)•180°,即为180°的(n-2)倍,多边形的内角一定大于0度,小于180度,因而多边形中,除去2个内角外,其余内角和与180度的商加上2,以后所得的数值,比这个数值大1或2的整数就是多边形的边数.【详解】设少加的2个内角和为x度,边数为n.则(n-2)×180=830+x,即(n-2)×180=4×180+110+x,因此x=70,n=7或x=250,n=8.故该多边形的边数是7或8.故选C.8.(2020·曲靖市期末)一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为()A.7 B.7或8 C.8或9 D.7或8或9【答案】D【解析】试题分析:设内角和为1080°的多边形的边数是n,则(n﹣2)•180°=1080°,解得:n=8.则原多边形的边数为7或8或9.故选D.9.(2018·焦作市期末)若一个正n边形的每个内角为144°,则这个正n边形的所有对角线的条数是()A.7 B.10 C.35 D.70【答案】C【解析】∵一个正n边形的每个内角为144°,∴144n=180×(n﹣2),解得:n=10,这个正n边形的所有对角线的条数是:(3)2n n-=1072⨯=35,故选C.10.(2019·武清区期中)如果n边形的内角和是它外角和的4倍,则n等于()A.7 B.8 C.10 D.9【答案】C【分析】根据多边形内角和公式180°(n-2)和外角和为360°可得方程180(n-2)=360×4,再解方程即可.【详解】由题意得:180(n-2)=360×4,解得:n=10,故选C.二、填空题(共5小题)11.(2020·临沧市期末)若一个正多边形的内角和是其外角和的3倍,则这个多边形的边数是______.【答案】8【详解】解:设边数为n,由题意得,180(n-2)=360⨯3解得n=8.所以这个多边形的边数是8.12.(2018·平凉市期末)一个正多边形的每个外角为60°,那么这个正多边形的内角和是_____.【答案】720°.【分析】先利用多边形的外角和为360°计算出这个正多边形的边数,然后再根据内角和公式进行求解即可.【详解】这个正多边形的边数为36060︒︒=6,所以这个正多边形的内角和=(6﹣2)×180°=720°,故答案为720°.13.(2019·朝阳区期末)如果一个正方形被截掉一个角后,得到一个多边形,那么这个多边形的内角和是__________.【答案】180°或360°或540°【解析】n边形的内角和是(n-2)•180°,边数增加1,则新的多边形的内角和是(4+1-2)×180°=540°,所得新的多边形的角不变,则新的多边形的内角和是(4-2)×180°=360°,所得新的多边形的边数减少1,则新的多边形的内角和是(4-1-2)×180°=180°,因而所成的新多边形的内角和是540°或360°或180°.故答案为540°或360°或180°.14.(2019鄂州市期中)将两张三角形纸片如图摆放,量得∠1+∠2+∠3+∠4=220°,则∠5=__.【答案】40°【详解】如图所示:∠1+∠2+∠6=180°,∠3+∠4+∠7=180°,∵∠1+∠2+∠3+∠4=220°,∴∠1+∠2+∠6+∠3+∠4+∠7=360°,∴∠6+∠7=140°,∴∠5=180°-(∠6+∠7)=40°.故答案为40°.15.(2019·泰州市期末)图1是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并开始消溶,形状无一定规则,代表一种自然和谐美.图2是从图1冰裂纹窗格图案中提取的由五条线段组成的图形,则∠1+∠2+∠3+∠4+∠5=度.【答案】360.【详解】由多边形的外角和等于360°可知,∠1+∠2+∠3+∠4+∠5=360°,故答案为360.三、解答题(共2小题)16.(2018·遵义市期末)一个多边形的每一个内角都相等,并且每个外角都等于和它相邻的内角的一半.(1)求这个多边形是几边形;(2)求这个多边形的每一个内角的度数.【答案】(1)这个多边形是六边形;(2)这个多边形的每一个内角的度数是120°.【分析】(1)先设内角为x,根据题意可得:外角为12x,根据相邻内角和外角的关系可得:,x+12x=180°,从而解得:x=120°,即外角等于60°,根据外角和等于360°可得这个多边形的边数为:36060=6,(2)先设内角为x,根据题意可得:外角为12x,根据相邻内角和外角的关系可得:,x+12x=180°,从而解得内角:x=120°,内角和=(6﹣2)×180°=720°.【详解】(1)设内角为x,则外角为12 x,由题意得,x+12x=180°,解得:x=120°,12x=60°,这个多边形的边数为:36060=6,答:这个多边形是六边形,(2)设内角为x,则外角为12 x,由题意得: x+12x=180°,解得:x=120°,答:这个多边形的每一个内角的度数是120度.内角和=(6﹣2)×180°=720°.17.(2019·黄冈市期中)如图所示,求A B C D E F∠+∠+∠+∠+∠+∠的度数.【答案】360︒.【详解】解:∵∠1=∠A+∠B,∠2=∠C+∠D,∠3=∠E+∠F,又∵∠1+∠2+∠3=360°,∴∠A+∠B+∠C+∠D+∠E+∠F=360°.。
