第六章证明一练习题
第六章:证明(一)经典试题

第一部分:基础复习八年级数学(下)第六章:证明(一)一、中考要求:l.理解证明的必要性和设置公理的必要性.2.关注现实,并通过具体例子了解定义、命题、定理的含义,会区分命题的条件和结论,知道反倒的意义和作用.3.初步掌握用综合法证明的格式,会证明两直线平行的有关判定定理,两直线平行的有关性质定理,三角形内角和定理及其椎论.4.体会推理的严谨性和结论的确定性,初步树立步步有据的推理意识,发展推理论证能力,同时,要善于表达自己的想法,并能与同伴交流.新课标对本章的要求不高,但比较简单的几何证明题仍是2006年中考的热点.二、中考卷研究(一)中考对知识点的考查:2004、2005年部分省市课标中考涉及的知识点如下表:(二)中考热点:新课标对本章的要求不高,但比较简单的几何证明题仍是2006年中考的热点.三、中考命题趋势及复习对策本章主要考查对命题,定理等概念的理解以及运用定义、定理证明问题的过程,在中考题中以证明题的形式出现,一般占5~7分,因此同学们在复习时应注意认真理解概念,分清题目的条件和结论,正确的写出证明过程.★★★(I)考点突破★★★考点1:一、考点讲解:定义:对名称和术语的含义加以描述,作出明确的规定,就叫做定义·命题:判断一件事情的句子叫命题,每个命题都由条件和结论两部分一组成,条件是已知的事项,结论是由已知事项推断出的事项,一般地,命题都可以写成“如果……,那么……”的形式,其中“如果”引出的部分是条件,“那么”引出的部分是结论.命题分为真命题和假命题.真命题:正确的命题是真命题;假命题:不正确的命题是假命题;要说明一个命题是假命题,通常可以举出一个例子,使之具备命题的条件,而不具有命题的结论,这种例子称为反例.公理:公认的真命题称为公理.证明:除了公理外,其他真命题的正确性都通过推理的方法证实,推理的过程称为证明.定理:经过证明的真命题称为定理.逆命题:把原命题的结论作为命题的条件,原命题的条件作为命题的结论,所组成的命题叫原命题的逆命题.逆定理:如果一个定理的逆命题是真命题,那么这个逆命题就叫原定理的逆定理.二、经典考题剖析:【考题1-1】(2004、宁安,9分)如图l-6-1,四边形ABCD中,点E在边CD上,连结AE、BE。
马克思主义基本原理第六章练习及参考答案

马克思主义基本原理第六章练习及参考答案第六章练习一、单项选择题1、以莫尔的《乌托邦》、康帕内拉的《太阳城》,和闵采尔的“千载太平之国”为主要代表的属哪个阶段的空想社会主义A A.16—17世纪早期空想社会主义B.18世纪空想平均共产主义C.19世纪批判的空想社会主义D.不成熟、不科学的空想社会主义2、空想社会主义的历史功绩是CA.对过去社会作出了天才的反省B.揭示了资本主义灭亡、社会主义胜利的客观规律C.对资本主义的弊病进行了深刻的揭露和猛烈的抨击D.找到了变革社会的革命力量3、科学社会主义创立的理论依据是CA.空想社会主义学说B.德国古典哲学C.唯物史观和剩余价值学说D.英国古典政治经济学4、(B)的发表,标志着科学社会主义的诞生A.《德意志意识形态》B.《共产党宣言》C.《共产主义原理》D.《资本论》5、社会主义从理论到实践的飞跃,具体途径是DA.通过改革和革命实现的B.通过对人民群众的教育和灌输实现的C.实践D.通过无产阶级革命实现的6、马克思说:“暴力是每一个孕育着新社会的旧社会的助产婆”,这说明BA.暴力革命是无产阶级革命的唯一形式B.暴力革命是无产阶级革命的主要的基本形式C.暴力革命与和平发展互相排斥D.暴力革命与和平发展可以相互取代7、列宁对科学社会主义学说的重大贡献是CA.提出了战时共产主义政策B.提出了新经济政策C.提出了社会主义革命将首先在一国或数国取得胜利的理论D.提出了利用国家资本主义过渡社会主义的理论8、在理论上第一次将共产主义社会第一阶段称为社会主义的是CA.马克思B.恩格斯C.列宁D.斯大林9、经济文化相对落后的国家可以先于资本主义国家进入社会主义,其根本原因是由于BA.经济文化相对落后的国家具有较高的精神文明B.革命的客观形势和条件所决定的C.它是以高度社会化的资本主义大生产作为社会主义革命的物质前提的D.社会主义生产关系可以在旧社会的内部孕育生长起来10、美苏冷战全面展开的标志是AA.两大阵营的形成B.杜鲁门主义C.马歇尔计划D.丘吉尔的铁幕演说11、两极终结的标志是BA.两德统一B.苏联解体C.第三世界的崛起D.中国的强大12、列宁得出社会主义可能在一国或数国首先取得胜利的结论依据是BA.资本主义必然灭亡、社会主义和共产主义必然胜利的规律B.帝国主义时代资本主义政治经济发展不平衡的规律C.资本主义国家无产阶级与资产阶级斗争的规律C.资本主义国家无产阶级与资产阶级斗争的规律D.无产阶级是最先进、最革命的阶级的原理13、社会主义必然代替资本主义的主要依据是DA.无产阶级与资产阶级斗争尖锐化B.个别企业有组织的生产与整个社会生产无政府状态之间的矛盾C.现代无产阶级的日益壮大D.生产的社会化与资本主义私人占有制之间的矛盾14、下面哪项不是社会主义建设的主要模式DA.苏联模式B.南斯拉夫模式C.中国特色的社会主义道路D.民主社会主义模式15、社会主义从一国到多国的发展标志是AA.反法西斯战争的胜利B.南斯拉夫联邦人民共和国成立C.中华人民共和国成立D.老挝人民民主共和国成立16、科学社会主义的核心内容是BA.唯物史观B.无产阶级专政和社会主义民主C.无产阶级专政D.国家政权17、无产阶级反对资产阶级的斗争中,最具决定意义的是AA.经济斗争B.政治斗争C.理论斗争D.议会斗争18、无产阶级革命取得胜利的根本保证是AA.无产阶级政党的正确领导B.建立革命的统一战线C.人民群众的革命积极性的极大提高D.国家政权问题19、社会主义的根本任务是DA.进行阶级斗争B.改革生产资料所有制C.进行政治体制改革、经济体制改革D.解放生产力、发展生产力20、(C )是社会主义自我完善的根本途径A.革命B.民主C.改革D.文明二、多项选择题(下列选项中至少有二个选项是符合题目要求的,请选出正有确答案,答对的得2分,少答的或多答的得0分,每小题2分,共40分)1、下列属于社会主义的基本特征的有ABDA.解放和发展生产力,创造高度发达的生产力和比资本主义更高的劳动生产力B.建立和完善生产资料公有制,逐步消灭剥削,消除两极分化,达到共同富裕C.对个人消费实行“各尽所能,按需分配”制度D.建立人民政权,发展社会主义民主政治,建设社会主义政治文明2、社会主义的发展道路必然呈现多样性的特点的原因有ABCA.各个国家的生产力发展状况和社会发展阶段决定了社会注意发展道路具有不同的特点B.历史文化传统的差异性是造成社会主义发展道路多样性的重要条件C.时代和实践的不断发展,是造成社会主义发展道路多样性的现实原因D.社会主义作为新生事物,其成长不会一帆风顺3、下面那些因素决定了社会主义在曲折中发展ABDA.社会主义作为新生事物,其成长不会一帆风顺B.社会主义社会是作为一个过程而发展的,人们对它的认识也有一个逐渐发展的过程C.经济全球化对于社会主义的发展既有机遇又有挑战D.社会发展的过程是曲折的4、下面关于社会主义改革的有BCDA.要坚持革命的正确方向B.要选择正确的改革方式和步骤C.要妥善处理改革、发展与稳定的关系D.有利于促进现阶段生产力的发展5、下面那些表明马克思主义政党是按照民主集中制原则组织起来的团结统一的党ABCDA.马克思主义政党的组织原则是民主集中制B.马克思主义政党是团结统一的党C.马克思主义政党是有坚强纪律和战斗精神的党D.马克思主义政党代表着最广大人民的根本利益6、20世纪的社会主义制度对人类社会历史的发展做出的巨大贡献是BCDA.社会主义开始作为一种新的社会制度发挥出历史作用B.社会主义国家的存在及其在经济、政治、外交、军事上的影响,改变了世界的政治格局C.社会主义力量坚定地支持被压迫民族和被压迫人民,普写世界和平与发展的新篇章D.社会主义在当代引导着世界人民的前进方向7、社会主义首先在经济文化相对落后的国家取得胜利的原因有ABA.经济文化相对落后的国家可以先于发达资本主义国家进入社会主义,是由革命的客观形势和条件所决定B.经济文化相对落后的国家可以先于发达资本主义国家进入社会主义,并不违背生产关系一定要适合生产力状况的规律C.生产力高度发展的原因D.高度社会化的资本主义大生产作为社会主义革命的物质前提8、下列有关无产阶级专政的说法正确的有ABCDA.无产阶级专政思想的诞生,是马克思主义科学思想体系形成的重要标志之一B.无产阶级专政是人类社会国家发展史上的伟大飞跃,它是人类社会先进的新型国家政权C.无产阶级专政是以工农联盟为阶级基础的国家政权D.无产阶级专政的最终目标要消灭剥削、消除阶级,进到无阶级社会9、下列有关社会主义民主正确说法的有ABCDA.社会主义民主首先是社会主义的国家制度B.社会主义民主是目的和手段的统一C.社会主义民主与资本主义民主之间存在着一定的联系D.建设高度的民主需要一个历史过程10、无产阶级革命是迄今历史上最广泛、最彻底、最深刻的革命,是不同于以往一切革命的最新类型的革命,这是因为ABCD A.无产阶级革命是彻底消灭一切私有制、代之以生产资料公有制的革命B.无产阶级革命是要彻底消灭一切阶级和阶级统治的革命C.无产阶级革命是为绝大多数人谋利益的运动D.无产阶级革命是不断前进的历史过程11、无产阶级革命的形式是BCA.发展B.暴力C.和平D.合作12、无产阶级革命和无产阶级专政的第一次伟大的尝试是ADA.巴黎工人起义B.武装起义C.里昂工人起义D.巴黎公社13、列宁领导下的苏维埃俄国对社会主义道路的探索,大体上经历的时期是ABCDA.进一步巩固苏维埃政权时期B.外国武装干涉和国内战争时期即战时共产主义时期C.由战时共产主义转变为新经济政策时期D.由新经济政策时期转变为稳定时期14、社会主义苏联模式的弊端有ABCDA.集中过多B.管得过死C.否定市场的作用D.严重束缚企业和劳动者的积极性15、东欧剧变、苏联解体,最深刻的教训是BCDA.放弃了民主社会主义道路,放弃了无产阶级专政B.放弃了共产党的领导地位,放弃了马克思列宁主义C.结果使得已经相当严重的经济、政治、社会、民族矛盾进一步激化D.最终酿成了制度剧变、国家解体的历史悲剧16、《共产党宣言》发表的理论意义和实践意义是ABCA.标志着科学社会主义的形成B.标志着马克思主义与工人运动的结合C.为国际共产主义运动树立了一面旗帜D.社会主义可以在一国首先胜利17、第二次世界大战后的社会主义阵营的形成ABCDA.打破了资本主义体系在世界上的独霸局面B.有力地支援了亚非拉地区的民族解放斗争,加速了世界殖民主义体系的崩溃C.为战后世界和平提供了强有力的保证D.显示了社会主义的强大生命力,证明社会主义是人类发展的必由之路18、邓小平对社会主义的新认识是ABCA.解放生产力,发展生产力B.消灭剥削,消除两极化C.最终达到共同富裕D.我国的社会主义还处在初级阶段19、十六大以来我们党基于对社会主义的新认识,提出了科学发展观,关于科学发展观的正确认识的有ABCDA.科学发展观的第一要义是发展B.科学发展观的核心是以人为本C.科学发展观的基本要求是全面协调可持续D.科学发展观的根本方法是统筹兼顾20、探索适合本国国情社会主义发展道路应遵循的基本原则ABDA.必须坚持以马克思主义为指导B.必须从本国国情出发,走自己的路C.可以跨越式发展D.必须充分吸收人类一切文明成果三、判断题(只判断对或错,每小题2分,共20分)1、我国目前正处于社会主义初级阶段,经济文化还比较落后,因此在各项工作中都要把效益摆在第一位。
(完整版)第六章线性空间练习题参考答案

第六章 线性空间练习题参考答案一、填空题1.已知0000,,00V a bc a b c R c b ⎧⎫⎛⎫⎪⎪ ⎪=+∈⎨⎬ ⎪⎪⎪ ⎪+⎝⎭⎩⎭是33R ⨯的一个子空间,则维(V ) = 3 , V 的一组基是000000000100,100,010*********⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.2.在P 4中,若1234(1,2,0,1),(1,1,1,1),(1,,1,1),(0,1,,1)k k αααα===-=线性无关,则k 的取值范围是3k ≠(以1234,,,αααα为行或者列构成的行列式不为零). 3.已知a 是数域P 中的一个固定的数,而1{(,,,),1,2,,}n i W a x x x P i n =∈=是P n+1的一个子空间,则a = 0 ,而维(W)=n 4.维数公式为12dim dim V V +=1212dim()dim()V V V V ++.5.设123,,εεε是线性空间V 的一组基,112233x x x αεεε=++,则由基123,,εεε到基231,,εεε的过渡矩阵T =001100010⎛⎫⎪⎪ ⎪⎝⎭,而α在基321,,εεε下的坐标是321(,,)x x x 由基123,,εεε到基233112,,εεεεεε+++的过渡矩阵为T =011101110⎛⎫⎪⎪ ⎪⎝⎭.6.数域P 上n 级对称矩阵全体构成数域P 上(1)2n n +维线性空间,数域P 上n 级反对称矩阵全体构成数域P 上(1)2n n -维线性空间,数域P 上n 级上三角矩阵全体构成数域P 上(1)2n n +维线性空间,数域P 上n 级对交矩阵全体构成数域P 上n 维线性空间,数域P 上n 级数量矩阵全体构成数域P 上 1 维线性空间.二、判断题1.设n n V P ⨯=,则{,0}n n W A A P A ⨯=∈=是V 的子空间.错.行列式为零的两个方阵的和的行列式未必为零,因此W 中矩阵关于矩阵的加法运算不封闭,不能成为子空间.)2.已知{(,),,,}V a bi c di a b c d R =++∈为R 上的线性空间,且维(V )=2. 错.是子空间,但是是4维的,其基为(1,0),(,0),(0,1),(0,)i i .3.设,n n A B P ⨯∈,V 是0A X B ⎛⎫= ⎪⎝⎭的解空间,V 1是AX =0的解空间,V 2是(A +B)X =0的解空间,则12V V V =.正确. 12V V 中的向量既满足AX =0,又满足(A +B)X =0,因此也满足BX =0,即满足0A X B ⎛⎫= ⎪⎝⎭,即为V 中的向量.反之,V 中的向量既在1V 中,又在2V 中,即为12V V 中的向量.因此12V V V =.4.设线性空间V 的子空间W 中每个向量可由W 中的线性无关的向量组12,,,s ααα线性表出,则维(W)=s.正确.根据定理1.5.设W 是线性空间V 的子空间,如果,,V αβ∈但,W W αβ∉∉且则必有.W αβ+∉错误.可能.W αβ+∈如取,αβ为一对互为负向量,则0.W αβ=+∈ 6. }0|),,{(33321=∈=x R x x x W 是3R 的子空间.正确. 基为(1,0,0),(0,1,0),维数为2. 7.}1|),,{(23321=∈=x R x x x W 是3R 的子空间. 错误.不包含零向量.8.}|),,{(3213321x x x R x x x W ==∈= 是3R 的子空间. 正确.基为(1,1,1),维数为1.9.}|),,{(3213321x x x R x x x W -=∈= 是3R 的子空间. 正确. 基为(1,1,0),(1,0,-1),维数为2. 三、计算题1.求所有与A 可交换的矩阵组成的nn P ⨯的子空间()C A 的维数与一组基,其中100020003A ⎛⎫⎪= ⎪ ⎪⎝⎭.解:设矩阵33()ij B b ⨯=与A 可交换,即有AB BA =.即111213111213212223212223313233313233100100020020003003b b b b b b b b b b b b b b b b b b ⎛⎫⎛⎫⎛⎫⎛⎫⎪⎪⎪⎪= ⎪⎪ ⎪⎪ ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭.111213111213212223212223313233313233232222333323b b b b b b b b b b b b b b b b b b ⎛⎫⎛⎫⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭. 所以有,()0,,1,2,3.ij ij ij ib b j i j b i j =-==当i j ≠时,0ij b =,因此11223300()0000b C A b b ⎧⎫⎛⎫⎪⎪⎪=⎨⎬ ⎪⎪⎪ ⎪⎝⎭⎩⎭ 维数为3,基为112233,,E E E .2.在线性空间P 4中,求由基1234,,,αααα到基1234,,,ββββ的过渡矩阵,并求(1,4,2,3)α=在基1234,,,αααα下的坐标,其中1234(1,0,0,0),(4,1,0,0),(3,2,1,0),(2,3,2,1)αααα===-=- 1234(1,1,8,3),(0,3,7,2),(1,1,6,2),(1,4,1,1).ββββ====--- 解:令过渡矩阵为T ,则有10111432131401238761001232210001T --⎛⎫⎛⎫⎪⎪- ⎪ ⎪=⎪ ⎪- ⎪⎪-⎝⎭⎝⎭因此1143210112379801231314633100128761232100132213221T ------⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪--⎪ ⎪ ⎪==⎪ ⎪ ⎪- ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭. 令1234114324012320012301x x x x -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪- ⎪⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭112341432114113611010123401274210012200122400013000133x x x x -----⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪⎪ ⎪-- ⎪ ⎪ ⎪ ⎪⎪ ⎪===⎪ ⎪ ⎪ ⎪⎪ ⎪-- ⎪ ⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭ (1,4,2,3)α=在基1234,,,αααα下的坐标为(-101,21,-4,3) 四、证明题1.V 为定义在实数域上的函数构成的线性空间,令12{()(),()()},{()(),()()}W f x f x V f x f x W f x f x V f x f x =∈=-=∈=--证明:W 1、W 2皆为V 的子空间,且12.V W W =⊕证明:W 1、W 2 分别为偶函数全体及奇函数全体构成的集合,显然W 1、W 2均为非空的.由奇偶函数的性质可得W 1、W 2皆为V 的子空间.()()()()(),()22f x f x f x f x f x V f x +---∀∈=+. 而12()()()(),22f x f x f x f x W W +---∈∈,因此12.V W W =+又12{0}.W W =所以12.V W W =⊕2.设W 是P n 的一个非零子空间,若对于W 的每一个向量12(,,,)n a a a 来说,或者120n a a a ====,或者每一个i α都不等于零,证明:维(W)=1.证明:由W 是P n 的一个非零子空间,可得W 中含有非零向量设1212(,,,),(,,,)n n a a a b b b αβ==是W 中的任二个非零向量,由题意可得每一个,i i a b 都不等于零.考虑向量11112112121211(,,,)(,,,)(0,,,)n n n n b a b a a a a b b b b a a b b a a b W αβ-=-=--∈.由题设条件有1212110n n b a a b b a a b -==-=,即有1212n na a ab b b ===.即W 中的任二个非零向量均成比例,因此维(W)=1.。
2020—2021学年北师大版八年级下册第六章《平行四边形》常考综合题专练(一)

北师大版八年级下册第六章《平行四边形》常考综合题专练(一)1.如图1,在平行四边形ABCD中,过点A作AE⊥BC交BC于点E,连接ED,且ED平分∠AEC.(1)求证:AE=BC;(2)如图2,过点C作CF⊥DE交DE于点F,连接AF,BF,猜想△ABF的形状并证明.2.如图,△ABC中,D是AB边上任意一点,F是AC中点,过点C作CE∥AB交DF的延长线于点E,连接AE,CD.(1)求证:四边形ADCE是平行四边形;(2)若∠B=30°,∠CAB=45°,AC=,CD=BD,求AD的长.3.如图,在▱ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F.(1)求证:CD=BE;(2)若点F为DC的中点,DG⊥AE于G,且DG=1,AB=4,求AE的长.4.【教材呈现】如图是华师版九年级上册数学教材第80页的第3题,请完成这道题的证明.【结论应用】(1)如图②,在上边题目的条件下,延长图①中的线段AD交NM的延长线于点E,延长线段BC交NM的延长线于点F.求证:∠AEN=∠F.(2)若(1)中的∠A+∠ABC=122°,则∠F的大小为.5.如图,▱ABCD的对角线AC、BD交于点O,M,N分别是AB、AD的中点.(1)求证:四边形AMON是平行四边形;(2)若AC=6,BD=4,∠AOB=90°,求四边形AMON的周长.6.已知:如图所示,在平行四边形ABCD中,DE、BF分别是∠ADC和∠ABC的角平分线,交AB、CD于点E、F,连接BD、EF.(1)求证:BD、EF互相平分;(2)若∠A=60°,AE=2EB,AD=4,求线段BD的长.7.如图,在平行四边形ABCD中,M、N分别是AD,BC的中点,连接AN、CM.(1)求证:△ABN≌△CDM;(2)连接MN,过点C作CE⊥MN于点E,连接DN,交OM于点O交CE于点P,若∠AND=90°,PE=1,∠1=∠2,求AN的长.8.已知:在▱ABCD中,点E是边AD上一点,点F是线段AE的中点,连接BF并延长BF至点G,使FG=BF,连接DG、EG.(1)如图1,求证:四边形CDGE是平行四边形;(2)如图2,当DA平分∠CDG时,在不添加任何辅助线的情况下,请直接写出图2中与AB相等的线段(AB除外).9.如图,在▱ABCD中,点E、F分别在BC、AD上,AC与EF相交于点O,且AO=CO.(1)求证:△AOF≌△COE;(2)连接AE、CF,则四边形AECF(填“是”或“不是”)平行四边形.10.如图,已知平行四边形ABCD,过A作AM⊥BC于M,交BD于E,过C作CN⊥AD于N,交BD于F,连接AF、CE.(1)求证:BM=DN;(2)求证:四边形AECF为平行四边形.参考答案1.(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,又∵AE⊥BC,∴∠AEC=90°,又∵ED平分∠AEC,∴∠ADE=∠CED=45°,∴∠AED=∠ADE,∴AE=AD,∴AE=BC;(2)△ABF是等腰直角三角形,证明:∵CF⊥DE,∴∠CFE=90°,又∵∠CEF=45°,∴∠ECF=45°,∴∠FEC=∠FCE=∠AEF,∴EF=CF,在△AEF和△BCF中,,∴△AEF≌△BCF(SAS),∴AF=BF,∠AFE=∠BFC,∴∠AFE﹣∠BFE=∠BFC﹣∠BFE,即∠AFB=∠EFC=90°,∴△ABF是等腰直角三角形.2.(1)证明:∵AB∥CE,∴∠CAD=∠ACE,∠ADE=∠CED.∵F是AC中点,∴AF=CF.在△AFD与△CFE中,.∴△AFD≌△CFE(AAS),∴AD=CE,∴四边形ADCE是平行四边形;(2)解:过点C作CG⊥AB于点G.∵CD=BD,∠B=30°,∴∠DCB=∠B=30°,∴∠CDA=60°.在△ACG中,∠AGC=90°,,∠CAG=45°,∴.在△CGD中,∠DGC=90°,∠CDG=60°,,∴GD=1,∴.3.(1)证明:∵AE为∠BAD的平分线,∴∠DAE=∠BAE.∵四边形ABCD是平行四边形,∴AD∥BC,CD=AB.∴∠DAE=∠E.∴∠BAE=∠E.∴AB=BE.∴CD=BE.(2)解:∵四边形ABCD是平行四边形,∴CD∥AB,∴∠BAF=∠DFA.∴∠DAF=∠DFA.∴DA=DF.∵F为DC的中点,AB=4,∴DF=CF=DA=2.∵DG⊥AE,DG=1,∴AG=GF.∴AG=.∴AF=2AG=2.在△ADF和△ECF中,,∴△ADF≌△ECF(AAS).∴AF=EF,∴AE=2AF=4.4.【教材呈现】证明:∵P是BD的中点,M是DC的中点,∴PM=BC,同理,PN=AD,∵AD=BC,∴PM=PN,∴∠PMN=∠PNM,【结论应用】(1)证明:∵P是BD的中点,M是DC的中点,∴PM∥BC,∴∠PMN=∠F,同理,∠PNM=∠AEN,∵∠PMN=∠PNM,∴∠AEN=∠F;(2)解:∵PN∥AD,∴∠PNB=∠A,∵∠DPN是△PNB的一个外角,∴∠DPN=∠PNB+∠ABD=∠A+∠ABD,∵PM∥BC,∴∠MPD=∠DBC,∴∠MPN=∠DPN+∠MPD=∠A+∠ABD+∠DBC=∠A+∠ABC=122°,∵PM=PN,∴∠PMN=×(180°﹣122°)=29°,∴∠F=∠PMN=29°,故答案为:29°.5.(1)根据平行四边形的性质得到AO=OC,BO=OD,AB∥CD,AD∥BC,由三角形的中位线的性质得到MO∥BC,NO∥CD,∴MO∥AN,NO∥AM,∴四边形AMON是平行四边形;(2)解:∵AC=6,BD=4,∴AO=3,BO=2,∵∠AOB=90°,∴AB===,∴OM=AM=MB=,∴NO=AN=,四边形AMON的周长=AM+OM+AN+NO=2.6.(1)证明:∵四边形ABCD是平行四边形,∴CD∥AB,CD=AB,AD=BC,∵DE、BF分别是∠ADC和∠ABC的角平分线,∴∠ADE=∠CDE,∠CBF=∠ABF,∵CD∥AB,∴∠AED=∠CDE,∠CFB=∠ABF,∴∠AED=∠ADE,∠CFB=∠CBF,∴AE=AD,CF=CB,∴AE=CF,∴AB﹣AE=CD﹣CF即BE=DF,∵DF∥BE,∴四边形DEBF是平行四边形.∴BD、EF互相平分;(2)∵∠A=60°,AE=AD,∴△ADE是等边三角形,∵AD=4,∴DE=AE=4,∵AE=2EB,∴BE=GE=2,∴BG=4,过D点作DG⊥AB于点G,在Rt△ADG中,AD=4,∠A=60°,∴AG=AD=2,∴DG==2,∴BD===2.7.(1)证明:∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,∠B=∠CDM,∵M、N分别是AD,BC的中点,∴BN=DM,在△ABN和△CDM中,,∴△ABN≌△CDM(SAS);(2)解:∵M是AD的中点,∠AND=90°,∴MN=MD=AD,∴∠1=∠MND,∵AD∥BC,∴∠1=∠CND,∵∠1=∠2,∴∠MND=∠CND=∠2,∴PN=PC,∵CE⊥MN,∴∠CEN=90°,∴∠2=∠PNE=30°,∵PE=1,∴PN=2PE=2,∴CE=PC+PE=3,∴CN==,∵N是BC的中点,∴AD=BC=CN=,∴AN=AD×sin∠1=4=.8.解:(1)∵点F是线段AE的中点,∴AF=EF,在△ABF和△EGF中,,∴△ABF≌△EGF(SAS),∴AB=GE,∠ABF=∠FGE,∴AB∥GE,又∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴GE=CD,GE∥DC,∴四边形CDGE是平行四边形;(2)图2中与AB相等的线段为:GE,GD,DC,CE.理由:∵DA平分∠CDG,∴∠CDE=∠GDE,由(1)可得,GE∥CD,∴∠CDE=∠GED,∴∠GDE=∠GED,∴GE=GD,又∵四边形CDGE是平行四边形,∴四边形CDGE是菱形,∴CD=DG=GE=CE,又∵AB=CD,∴图2中与AB相等的线段为:GE,GD,DC,CE.9.(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠OAF=∠OCE,在△AOF和△COE中,,∴△AOF≌△COE(ASA)(2)解:四边形AECF是平行四边形,理由如下:由(1)得:△AOF≌△COE,∴FO=EO,又∵AO=CO,∴四边形AECF是平行四边形;故答案为:是.10.证明:(1)∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∵AM⊥BC,CN⊥AD,∴AM∥CN,∴四边形AMCN为平行四边形,∴CM=AN,∴BC﹣CM=AD﹣AN,即BM=DN;(2)∵AD∥BC,∴∠ADB=∠CBD,∵AM⊥BC,CN⊥AD,∴∠EMB=∠FND=90°,在△BME和△DNF中,,∴△BME≌△DBF(ASA),∴EM=DF,∵四边形AMCN为平行四边形,∴AM=CN,AM∥CN,∴AE=CF,又∵AE∥CF,∴四边形AECF为平行四边形.。
北师大版八年级下册数学第六章平行四边形含辅助线证明题—截长补短类 训练
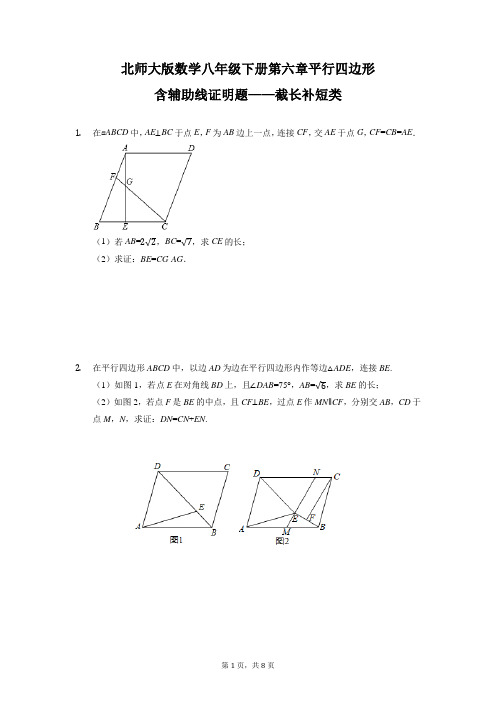
北师大版数学八年级下册第六章平行四边形含辅助线证明题——截长补短类1.在▱ABCD中,AE⊥BC于点E,F为AB边上一点,连接CF,交AE于点G,CF=CB=AE.(1)若AB=2√2,BC=√7,求CE的长;(2)求证:BE=CG-AG.2.在平行四边形ABCD中,以边AD为边在平行四边形内作等边△ADE,连接BE.(1)如图1,若点E在对角线BD上,且∠DAB=75°,AB=√6,求BE的长;(2)如图2,若点F是BE的中点,且CF⊥BE,过点E作MN∥CF,分别交AB,CD于点M,N,求证:DN=CN+EN.3.如图,在▱ABCD中,AE⊥BC,垂足为E,AE=CE.BF⊥AC,垂足为F,分别与AE,AD交于点G,H.(1)若AG=GE=BE=1,求▱ABCD的面积;(2)若CH平分∠BCD,求证:BC=AG+CH.4.已知在▱ABCD中,AE⊥CD,且AB=AE,F为AE上一点,且BF平分∠ABC,(1)若∠ABC=60°,AB=√3,求EF的长;(2)求证:AF+DE=BC.5.在平行四边形ABCD中,E为对角线AC上任意一点,连接BE(1)如图①所示,若AB=BE,AC=BC,∠BAC=75°,AB=2√2,求平行四边形ABCD的面积;(2)如图②所示,延长BE至F,使得EF=EB,连接CF,FD,求证:CE=AE+FD.6.在平行四边形ABCD中,连接BD,过点B作BE⊥BD于点B交DA的延长线于点E,过点B作BG⊥CD于点G.(1)如图1,若∠C=60°,∠BDC=75°,BD=6√2,求AE的长度;(2)如图2,点F为AB边上一点,连接EF,过点F作FH⊥FE于点F交GB的延长线于点H,在△ABE的异侧,以BE为斜边作Rt△BEQ,其中∠Q=90°,若∠QEB=∠BDC,EF=FH,求证:BF+BH=BQ.7.在平行四边形ABCD中,以AB为边作等边△ABE,点E在CD上,以BC为边作等边△BCF,点F在AE上,点G在BA延长线上且FG=FB.(1)若CD=6,AF=3,求△ABF的面积;(2)求证:BE=AG+CE.8.如图,在▱ABCD中,点F是对角线BD上一点,且满足AB=AF,过点F作EG交AD于E,交BC于G,作AH⊥BC于点H,交BD于M.(1)若F为MD中点,AF=2,AM=√3,求BC的长度;(2)若∠ABH=∠AFE,求证:BH+FG=HG.9.如图,平行四边形ABCD中,AB∥CD,AD∥BC,点G是线段BC的中点,点E是线段AD上的一点,点F是线段AB延长线上一点,连接DF,且∠ABE=∠CDG=∠FDG.(1)∠A=45°,∠ADF=75°,CD=3+√3,求线段BC的长;(2)求证:AB=BF+DF.10.如图,△ABC的高AD与中线BE相交于点F,过点C作BE的平行线,过点F作AB的平行线,两平行线相交于点G,连接BG,FG.(1)若AE=2.5,CD=3,BD=2,求AB的长;(2)若∠CBE=30°,求证:CG=AD+EF.11.如图,在□ABCD中,E为BC边的中点,连接AE,F为CD边上一点,且满足∠DFA=2∠BAE.(1)若∠D=100°,∠DAF=30°,求∠FAE的大小;(2)求证:AF=CD+CF.12.已知在平行四边形ABCD中,过点D作DE⊥BC于点E,且AD=DE.连接AC交DE于点F,作DG⊥AC于点G.(1)如图1,若EFDF =12,AF=√13,求DG的长;(2)如图2,作EM⊥AC于点M,连接DM,求证:AM-EM=2DG.13.如图,在平行四边形ABCD中,AE⊥BC于点E,AE=AD,EG⊥AB于点G,延长GE、DC交于点F,连接AF.(1)若BE=2EC,AB=√13,求AD的长;(2)请猜想线段EG、BG、FC之间的等量关系并证明.14.如图,已知平行四边形ABCD中,DE⊥BC于点E,DH⊥AB于点H,AF平分∠BAD,分别交DC、DE、DH于点F、G、M,且DE=AD,CE=3,AB=5.(1)求线段CF的长度;(2)求证:AB=DG+CE.15.如图所示,在平行四边形ABCD中,∠DAC=60°,点E是BC边上一点,连接AE,AE=AB,点F是对角线AC边上一动点,连接EF.(1)如图1,若点F与对角线交点O重合,已知BE=4,OC:EC=5:3,求AC的长度;(2)如图2,若EC=FC,点G是AC边上一点,连接BG、EG,已知∠AEG=60°,∠AGB+∠BCD=180°,求证:BG+EG=DC.16.如图所示,平行四边形ABCD和平行四边形CDEF有公共边CD,边AB和EF在同一条直线上,AC⊥CD且AC=AF,过点A作AH⊥BC交CF于点G,交BC于点H,连接EG.(1)若AE=2,CD=5,求△BCF的周长;(2)求证:BC=AG+EG.。
八年级数学下册第六章证明(一)定义与命题

小结 拓展
1、定义:对名称和术语的含义加以描述, 作出明确的规定,也就是给出它们的定 义.
2、命题的定义:判断一件事情的句子,叫 做命题.
3、命题的结构:每个命题都由条件和结论 两部分组成.条件是已知事项,结论是由 已事项推断出的事项.
1、原名: 某些数学名词称为原名. 2、公理: 公认的真命题称为公理.
3、证明: 除了公理外,其它真命题的正确性都通过
推理的方法证实.推理的过程称为证明.
4、定理: 经过证明的真命题称为定理.
经过证明的真
一些条件
推理的过程 叫证明
命题叫定理
+
推理
证实其它命 题的正确性
原名、公理 温馨提示:证明所需的定义、公理和其它定理都
语句.像这样判断一件事情的句子,叫做命题.
寻找命题的“共同的结构特征”
观察下列命题,试找出命题的共同的结构特征 (1)如果两个三角形的三条边对应相等,那么这两个三角形全等 (2)如果一个四边形的一组对边平行且相等,那么这个四边形是
平行四边形; (3)如果一个三角形是等腰三角形,那么这个三角形的两个底角
第六章 证明(一)
定义与命题
眼见未必为实!
a
线段a与线段b哪个 比较长?
b
a bc
谁与线段d在 一条直线上?
d
a
a bc
b
线段a与线段b哪个 比较长?
d
谁与线段d在 一条直线上?
a
b
a=b
a bc d
假如用一根比地球赤道长1 米的铁丝将 地球赤道围起来,那么铁丝与赤道之间的间 隙能有多大(把地球看成球形)?
数学分析课本(华师大三版)-习题及答案第六章

第六章 微分中值定理及其应用一、填空题1.若0,0>>b a 均为常数,则=⎪⎪⎭⎫ ⎝⎛+→x x x x b a 302lim ________。
2.若21sin cos 1lim 0=-+→x x b x a x ,则=a ______,=b ______。
3.曲线x e y=在0=x 点处的曲率半径=R _________。
4.设2442-+=x x y ,则曲线在拐点处的切线方程为___________。
5.=-+→x e x xx 10)1(lim ___________。
6.设)4)(1()(2--=x x x x f ,则0)(='x f 有_________个根,它们分别位于________ 区间;7.函数x x x f ln )(=在[]2,1上满足拉格朗日定理条件的__________=ξ;8.函数3)(x x f =与21)(x x g +=在区间[]2,0上满足柯西定理条件的_____=ξ;9.函数x y sin =在[]2,0上满足拉格朗日中值定理条件的____=ξ;10.函数2)(xe xf x=的单调减区间是__________; 11.函数x x y 33-=的极大值点是______,极大值是_______。
12.设x xe x f =)(,则函数)()(x f n 在=x _______处取得极小值_________。
13.已知bx ax x x f ++=23)(,在1=x 处取得极小值2-,则=a _______,=b_____。
14.曲线22)3(-=x k y 在拐点处的法线通过原点,则=k________。
15.设)2,1()1()( =-⨯=n x n x f n ,n M 是)(x f 在[]1,0上的最大值,则=∞→n n M lim ___________。
16.设)(x f 在0x 可导,则0)(0='x f 是)(x f 在点0x 处取得极值的______条件;17.函数x bx x a x f ++=2ln )(在1=x 及2=x 取得极值,则______,==b a ;18. 函数3223)(x x x f -=的极小值是_________; 19.函数xx x f ln )(=的单调增区间为__________; 20. 函数x x x f cos 2)(+=在⎥⎦⎤⎢⎣⎡2,0π上的最大值为______,最小值为_____; 21. 设点)2,1(是曲线b a x y +-=3)(的拐点,则___________,==b a ;22. 曲线x e y =的下凹区间为_______,曲线的拐点为________;23. 曲线323x x y -=的上凹区间为________;24. 曲线)1ln(2x y +=的拐点为__________;25.曲线x y ln =在点______处曲率半径最小。
第六章证明(一)测试题

3 在 AA C中 , : 0 , 曰、 C的平分线交 于 0点 , LB C等 于( . B 厶4 5 。 则 O
( 6。 A)5 ( 15 B) 1。 ( )0 C 8。
4 举 反例说明“ . 一个角 的余角大 于这个 角” 假命题 , 是 错误的是 ( () A 设这 个角是 4 。 它的余 角是 4 。但 4 。 4 。 5, 5 , 5 = 5
( ) 0 D 5。
Ⅱ
1下列语 句中 , . 是命 题 的是 ( ( 两点确定一 条直线 吗? A) ( 作 4的平分线 A C) M
2 两条平行线被第三条 直线 所截 , . 那么一组 同旁 内角 的平分线 ( ( 相互重合 A) ( 互 相平 行 B) () C 相互垂直
二、 填空题 ( 每小题 3分 , 2 ) 共 4分
1. n= 3当 时 , n+1n+ , +3 以 , 2 n 为线段长 的三角形是直角三角形. , 结论是 , 它是一个 . . 1. 所有 的质数都是 奇数” 4“ 的题设 是 命题 . 填 “ ” “ ” ( 真 或 假 ) l. 5 把命题 “ 对顶角相等 ” 改成 “ 如果 …… , 那么 ……” 的形式应 为 1. 6 若一个三角形 的三个 内角之 比为 4 3 2 则这个 三角形的最大 内角为 :: ,
=
.
. +LA B< 8 。④ LH C C 10 ; E
2. O 如图 5 下列结论 : , ① A>LA D; LB+LA B=10 一 A; C ② C 8 。 ③
— —
( 填上你认 为正确 的所 有序号 ) .
A
E
B C C
D
圈4
图5
《 新课程导 学》适 八 级 生 读・ 学北 大 下 ) . 合 年 学 阅 数 (师 版・册
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章证明一练习题 姓名
1.△ABC 的三个外角度数比为4∶3∶5,则它的三个内角度数分别为 .
2.如图,△ABC 中,∠ACD=115°,∠B=56°, 则∠A= , ∠ACB= 。
3.已知:直线a ,b 被直线c 所截,∠1+∠2=180°
4.已知:如图,∠3=∠4, 求证:a ∥b 。
求证:∠1+∠2=180°
5.如图,BD 平分∠ABC ,若∠1=∠2,则 ( ) A 、AB ∥CD B 、AD ∥BC C 、AD=BC D 、AB=CD
6.如果点P 是线段AB 的黄金分割点,且AP>PB ,则下列说法正确的是______(仅填序号)。
①AP 2=PB ·AB ;②AB 2=AP ·PB ;③BP 2=AP ·AB ;④AP :AB =PB :AP
7已知,如图,在△ABC 中,AD 平分外角∠EAC ,AD ∥BC , 求证:∠B =∠C
8.已知△ABC 中,∠1是它的一个外角,E 是边AC 上一点,延长BC 到D ,连接DE .求证:∠1>∠5.
9.如图,求证(1)∠BDC >∠A . (2)∠BDC =∠B +∠C +∠A .
10.如图,已知DE∥BC,CD 是∠ACB 的平分线,∠ACB=50°,求∠EDC 的度数.
A
B
C
D
11.已知a ∶b ∶c =2∶3∶4,且a +3b -2c =15.
(1)求a ,b ,c 的值 (2)求4a -3b +c 的值.
12.(1)如图在△ABC 中,P 是AB 上一点,连结 CP ,当满足条件∠ACP= 或∠APC= 时,或 时,△ACP ∽△ABC .
(2)如图,P 为△ABC 的边AB 上一点,且∠ABC =∠ACP ,AP =3 cm, AB =4 cm ,求AC 的长
13.在方格中,△ABC 与△DEF 是否成位似图形?请说明你的理由。
14.把图中的四边形ABCD 以点O 为位似中心沿OA 方向放大2倍(即位似比为2:1)。
15.在△ABC 中,AB=12,AC=9,D 是 AC 上一点,AD=16,在AB 上取一点 E ,使得以 A 、D 、E 为顶点的三角形与△ABC 相似,求AE 的长.
B
A
C D A B
C D
O
.。
