关于牙膏销售量的数学模型课程设计报告书
牙膏营销计划书:目标市场与销售策略

3.2.3 健康保护:含有活性成分和抗菌功效,有效预防龋齿和口腔感染。
4.2.4 清新口气:含有薄荷醇和草本成分,有效清新口气,提升个人形象。
1.3 产品包装与设计
我们的牙膏产品采用简约时尚的设计风格,符合现代人的审美观念。包装盒上印有产品特点和功效,吸引消费者的注意。同时,我们也会提供多种包装选择,以满足不同消费者的需求。
目标市场分析是成功的关键,我们需要了解目标客户的需求和期望
创新功能是推动科技和社会发展的重要动力
提高品牌知名度是扩大市场份额和增强品牌忠诚度的关键
围绕价格策略,让您的产品或服务在市场中更具竞争力
市场份额是公司成功的重要指标,而持续增长则是实现成功的关键
目标市场与销售策略
1
2
3
1 目标消费者群体
我们的目标消费者群体为年龄在20-50岁之间,有一定的消费能力和口腔护理需求的中产阶级人群。他们注重个人形象和口腔健康,对牙膏的清洁效果和舒适度有较高的要求。此外,他们也愿意为高质量的牙膏产品支付一定的价格。
主要竞争者的竞争优势包括品牌知名度、市场份额、产品研发和创新能力。他们使用的营销策略包括广告宣传、社交媒体营销、合作伙伴关系等。
2. 潜在机会和挑战潜在机会包括利用社交媒体平台进行营销,扩大线上销售渠道,加强与牙医诊所的合作。潜在挑战包括竞争对手的持续创新和消费者对牙膏产品的认知。
目标市场分析:市场趋势
牙膏营销计划书:目标市场与销售策略
目标市场分析:竞争者
口腔护理市场正在持续增长,其中牙膏是市场的主要产品之一。随着消费者对口腔健康的关注度提高,牙膏市场预计将继续繁荣。
1. 主要竞争者分析在牙膏市场上,主要竞争者包括高露洁、佳洁士、黑人牙膏、冷酸灵等品牌。这些品牌在市场份额、品牌知名度、产品研发和创新方面都有一定的优势。
牙膏销售量问题的微分方程模型
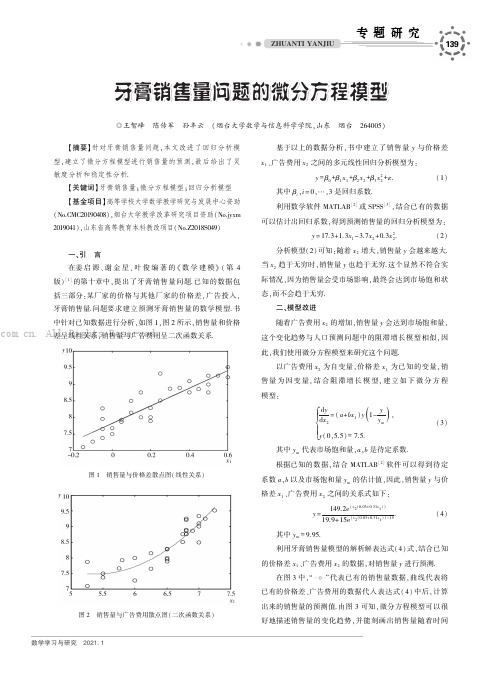
㊀㊀㊀139㊀数学学习与研究㊀2021 1牙膏销售量问题的微分方程模型牙膏销售量问题的微分方程模型Һ王智峰㊀陈传军㊀孙丰云㊀(烟台大学数学与信息科学学院,山东㊀烟台㊀264005)㊀㊀ʌ摘要ɔ针对牙膏销售量问题,本文改进了回归分析模型,建立了微分方程模型进行销售量的预测,最后给出了灵敏度分析和稳定性分析.ʌ关键词ɔ牙膏销售量;微分方程模型;回归分析模型ʌ基金项目ɔ高等学校大学数学教学研究与发展中心资助(No.CMC20190408),烟台大学教学改革研究项目资助(No.jyxm2019041),山东省高等教育本科教改项目(No.Z2018S049)一㊁引㊀言在姜启源㊁谢金星㊁叶俊编著的‘数学建模“(第4版)[1]的第十章中,提出了牙膏销售量问题.已知的数据包括三部分:某厂家的价格与其他厂家的价格差,广告投入,牙膏销售量.问题要求建立预测牙膏销售量的数学模型.书中针对已知数据进行分析,如图1,图2所示,销售量和价格差呈线性关系,销售量与广告费用呈二次函数关系.图1㊀销售量与价格差散点图(线性关系)图2㊀销售量与广告费用散点图(二次函数关系)基于以上的数据分析,书中建立了销售量y与价格差x1㊁广告费用x2之间的多元线性回归分析模型为:y=β0+β1x1+β2x2+β3x22+ε.(1)其中βi,i=0, ,3是回归系数.利用数学软件MATLAB[2]或SPSS[3],结合已有的数据可以估计出回归系数,得到预测销售量的回归分析模型为:y=17.3+1.3x1-3.7x2+0.3x22.(2)分析模型(2)可知:随着x2增大,销售量y会越来越大.当x2趋于无穷时,销售量y也趋于无穷.这个显然不符合实际情况,因为销售量会受市场影响,最终会达到市场饱和状态,而不会趋于无穷.二㊁模型改进随着广告费用x2的增加,销售量y会达到市场饱和量,这个变化趋势与人口预测问题中的阻滞增长模型相似,因此,我们使用微分方程模型来研究这个问题.以广告费用x2为自变量,价格差x1为已知的变量,销售量为因变量,结合阻滞增长模型,建立如下微分方程模型:dydx2=(a+bx1)y1-yym(),y(0,5.5)=7.5.ìîíïïï(3)其中ym代表市场饱和量,a,b是待定系数.根据已知的数据,结合MATLAB[2]软件可以得到待定系数a,b以及市场饱和量ym的估计值,因此,销售量y与价格差x1㊁广告费用x2之间的关系式如下:y=149.2e(x2(0.03+0.31x1))19.9+15e(x2(0.03+0.31x1))-15.(4)其中ym=9.95.利用牙膏销售量模型的解析解表达式(4)式,结合已知的价格差x1㊁广告费用x2的数据,对销售量y进行预测.在图3中,代表已有的销售量数据,曲线代表将已有的价格差㊁广告费用的数据代入表达式(4)中后,计算出来的销售量的预测值.由图3可知,微分方程模型可以很好地描述销售量的变化趋势,并能刻画出销售量随着时间. All Rights Reserved.㊀㊀㊀㊀㊀140数学学习与研究㊀2021 1周期变化的情况.图3㊀改进后模型的预测图三㊁模型检验在使用模型解决问题之前,需要对模型进行检验分析.微分方程模型(3)的检验主要包括稳定性分析和灵敏度分析两个方面.首先我们根据定性分析[4]方法给出稳定性分析.微分方程模型(3)的右端项不显含自变量x2,因此,模型(3)属于一维自治系统,我们使用自治系统的稳定性原理进行分析.我们记右端项为F(y)=(a+bx1)y1-yym().(5)令F(y)=0,可得两个平衡点为:y1=ym或y2=0.现分析右端项的一阶导数在两个平衡点处的符号:(1)当x1<-ck=-0.09,Fᶄ(0)=a+bx1<0.(2)当x1>-ck=-0.09,Fᶄ(ym)=-(a+bx1)<0.结合稳定性原理可知:当价格差大于-0.09时,销售量随着广告费用的增加,最终会稳定在市场饱和值ym.如果价格差小于-0.09,即比别的厂家价格高很多的时候,虽然广告费用不断增加,但是,最终的销售量仍然会趋于0.这个结论是比较符合市场规律的,说明本文建立的微分方程模型可以很好地刻画实际情况,也克服了回归分析模型销售量随着广告费用增加而趋于无穷的弊端.然后,我们结合微分方程的解析解(4)式,进行关于价格差x1的灵敏度分析,如图4所示.图4㊀价格差的灵敏度分析在图4中,我们取不同的价格差x1=[0,0.1,0.2,0.3,0.4,0.5,0.6],画出牙膏销售量y随着广告费用x2的变化曲线.当价格差一定时,随着广告费用x2的增加,销售量会逐渐趋于稳定,到达饱和值ym.当广告费用投入比较少时,价格越实惠,销售量就越大.当广告费用比较大的时候,价格差的作用就比较小了,销售量会更快达到饱和值ym.这个结论也是符合市场规律的.四㊁结㊀论结合牙膏销售量㊁价格差㊁广告费三组数据,本文分析了回归分析模型的不足之处.本文根据牙膏销售量最终会趋于市场饱和量的市场规律,建立了基于阻滞增长模型的微分方程模型,使用已有的三组数据对模型中的未知参数进行了点估计,得到牙膏销售量的预测模型.本文最后对模型进行了稳定性分析和灵敏度分析,得到模型是符合市场客观规律的结论.ʌ参考文献ɔ[1]姜启源,谢金星,叶俊.数学模型:第4版[M].北京:高等教育出版社,2011.[2]司守奎,孙兆亮.数学建模算法与应用:第2版[M].北京:国防工业出版社,2015.[3]周静.SPSS在数学建模中的应用实例[J].天津职业院校联合学报,2012,14(11):93-96.[4]赵静,但琦.数学建模与数学实验:第4版[M].北京:高等教育出版社,2014.. All Rights Reserved.。
数学模型_牙膏的销售量

估计x3 调整x4 控制x1
通过x1, x2预测y
控制价格差x1=0.2元,投入广告费x2=650万元
y ˆˆ0ˆ1 x 1ˆ2x 2ˆ3 x 2 2 8 .29(百3 万支3)
销售量预测区间为 [7.8230,8.7636](置信度95%)
上限用作库存管理的目标值 下限用来把握公司的现金流
两模型销售量预测比较
控制价格差x1=0.2元,投入广告费x2=6.5百万元
y ˆˆ0ˆ1x 1ˆ2x2ˆ3x2 2 yˆ 8.2933(百万支) 区间 [7.8230,8.7636]
yˆ 8.3272(百万支)
y ˆ0 ˆ 1 x 1 ˆ2 x 2 ˆ3 x 2 2 ˆ4 x 1 x 2
yˆ
10 9.5
9 8.5
8 7.5
5
0
0.2
0.4
6
7
0.6 x1
x1=0.2
8 x2
7.5 -0.2
yˆ
10.5 10 9.5 9 8.5 8 5
0
0.2
0.4
6
7
0.6 x1 8 x2
交互作用影响的讨论 y ˆ0 ˆ 1 x 1 ˆ2 x 2 ˆ3 x 2 2 ˆ4 x 1 x 2
y~被解释变量(因变量)
y 10
9.5
x1, x2~解释变量(回归变量, 自变量) 9 8.5
0, 1 , 2 , 3 ~回归系数
8
7.5
~随机误差(均值为零的
正态分布随机变量)
7 5
5.5
6
6.5
x 7
7.5
2
y01x22x2 2
模型求解 MATLAB 统计工具箱
y01 x 12 x 23 x 2 2由数据 y,x1,x2估计
牙膏销售方案范文

牙膏销售方案范文1. 背景牙膏是日常生活中必不可少的洗漱用品之一,对于口腔健康具有重要的作用。
目前,市场上牙膏品牌众多,竞争激烈。
为了提升牙膏销售业绩,制定一份有效的销售方案是至关重要的。
2. 目标本销售方案的主要目标是增加牙膏的销售量,提高品牌知名度和市场份额。
具体目标如下:•将每个季度的牙膏销售量提高10%;•在本地市场中增加品牌知名度,占据30%的市场份额。
3. 市场分析在制定销售方案前,需要对市场进行充分的分析,了解消费者的需求和竞争对手的情况。
3.1 消费者需求分析消费者对于牙膏的需求主要体现在以下几个方面:•口腔清洁效果:消费者希望牙膏能够有效清除牙菌斑和预防口腔疾病;•味道和口感:消费者喜欢口味清新且口感舒适的牙膏;•成分安全性:消费者关注牙膏成分的安全性和对牙齿的影响;•价格:消费者在选择牙膏时会考虑价格因素。
3.2 竞争对手分析牙膏市场竞争激烈,存在许多知名品牌。
竞争对手分析是制定销售方案的重要环节。
主要的竞争对手包括:•奥尔卡:以清洁效果优异、口味独特而闻名;•好维生:注重成分安全性,以天然成分牙膏为卖点;•百威:品牌知名度高,在口腔护理市场占据一定份额。
4. 销售策略基于市场分析结果,制定以下销售策略:4.1 产品优势的宣传我们的牙膏产品具有以下优势:•高效清洁:独特的配方能够有效清洁牙齿表面的牙菌斑;•清新口感:味道清新,口感舒适,使用后口腔清爽宜人;•天然成分:采用天然成分,无任何添加剂,对口腔无刺激;•实惠价格:以实惠的价格销售,满足不同消费者的需求。
通过广告、促销活动等方式宣传产品优势,吸引消费者的关注。
4.2 区域市场推广在本地市场中,通过以下方式推广牙膏产品:•在超市、药店等销售点进行展示和促销活动;•与口腔诊所合作,提供样品和赞助支持;•在社交媒体、电视、广播等渠道进行广告宣传;•参加相关行业展会,扩大品牌影响力。
4.3 建立忠诚度计划通过建立忠诚度计划,提高消费者对我们品牌的忠诚度。
牙膏销售策划书

牙膏销售策划书【牙膏销售策划书】一、背景分析根据市场调查报告显示,牙膏是人们日常生活中必需的卫生用品,随着人们健康意识的提高,对牙膏的需求也逐渐增加。
然而,在如今竞争激烈的市场环境下,牙膏品牌众多,导致销售竞争异常激烈。
为了提高牙膏的市场占有率,本策划书将重点围绕产品特点、定位与目标、市场推广、渠道拓展、销售计划等方面进行全面分析和策划。
二、产品特点1.独特的成分配方:本品牌牙膏采用了独特的成分配方,能够有效清洁牙齿,同时抑制细菌繁殖,有效缓解口腔问题。
2.口感舒适:牙膏采用了柔和的调味剂,能够给用户带来舒适的使用体验,增强产品的可口性。
3.天然无添加:本品牌牙膏没有添加任何对人体健康有害的化学成分,完全符合人体健康的需求。
三、定位与目标1.定位:本品牌牙膏将定位为高性价比的优质口腔护理产品,专注于为消费者提供经济实惠、健康安全的口腔护理产品。
2.目标:以3年为周期,争取将本品牌牙膏在市场上的占有率提高至20%,成为市场的领导品牌。
四、市场推广1.品牌宣传:通过电视、广播、报纸等主流媒体广告,全方位宣传本品牌牙膏的特点和优势。
2.口碑营销:通过微博、微信等社交媒体平台,发起用户分享活动,鼓励用户体验并分享本品牌牙膏的使用感受,增强产品口碑。
3.线下推广:与一线超市、药店等签订合作协议,设置产品陈列区,开展促销活动,并通过送样活动让消费者亲身体验产品的优势。
五、渠道拓展1.与超市合作:与一线超市签署合作协议,争取产品在超市销售区域内享有突出的位置,并与超市进行差异化推广活动。
2.与药店合作:与药店合作开展促销活动,并要求药店员工对产品进行充分了解,提供专业的购买建议。
3.电商渠道:通过与电商平台合作,进行线上销售,提供快捷的购买渠道,同时通过线上推广活动提高品牌知名度。
六、销售计划1.销售目标:第一年销售额达到2000万,第二年销售额达到4000万,第三年销售额达到8000万。
2.市场份额:第一年增加到5%,第二年增加到10%,第三年增加到20%。
牙膏销售问题

b,bint,stats
3)对模型进行改进,确定回归模型系数,求解出教程中模型(5);
Matlab程序:
x1=[-0.05 0.25 0.60 0 0.25 0.20 0.15 0.05 -0.15 0.15 0.20 0.10 0.40 0.45 0.35 0.30 0.50 0.50 0.40 -0.05 -0.05 -0.10 0.20 0.10 0.50 0.60 -0.05 0 0.05 0.55]';
表2模型(3)的计算结果
参数
参数估计值
参数置信区间
17.3244
[5.7282,28.9206]
1.3070
[0.6829,19311]
-3.6956
[-7.4989,0.1077]
0.3486
[0.0379,0.6594]
=0.9054 F=82.9409 p<0.0001 =0.0490
结果分析:表2显示, =0.9054指因变量y(销售量)的90.54%可由模型确定,F值远远超过F检验的临界值,p远小于 ,因而模型(3)从整体来看时可用的。
佛山科学技术学院
上机报告
课程名称数学建模
上机项目牙膏销售问题
专业班级
一、问题提出
根据牙膏销售量与价格、广告费等表格1中的数据,建立三个模型,要求:
1)画出散点图:y对x1的散点图1;y对x2的散点图2;
2)确定回归模型系数,求解出教程中模型(3);
3)对模型进行改进,确定回归模型系数,求解出教程中模型(5);
x1=[-0.05 0.25 0.60 0 0.25 0.20 0.15 0.05 -0.15 0.15 0.20 0.10 0.40 0.45 0.35 0.30 0.50 0.50 0.40 -0.05 -0.05 -0.10 0.20 0.10 0.50 0.60 -0.05 0 0.05 0.55];
牙膏销售策划书

牙膏销售策划书一 :市场分析(一)牙膏中国市场品牌发展历程1998 年,全国牙膏产量达到 28.07 亿支,比 1949 年增长了 133.6 倍, XX 年产量达到了 36 亿支,年人均使用量提高到了 2.8 支,有关专家预计, XX 年中国牙膏产量将达到 45 亿支, 2011 年将达到 54 亿支。
近二十年来,中国牙膏市场大致经历了四个阶段:第一阶段( 1949~1992 年):国内品牌三足鼎立1949 年到 1992 年期间,中华、两面针和黑妹三大国产品牌一直分享了中国庞大的牙膏市场。
但三大品牌几乎没有正面竞争,各居一隅,分别占据着东部、南部和西部市场,相安无事。
第二阶段( 1992~1996 年):洋品牌小试牛刀1992 年,世界最大的牙膏品牌高露洁进入中国市场, 1995 年宝洁公司的佳洁士进入中国。
在这一阶段,由于外国品牌的价格过高(约为国产品牌的 3 倍左右),他们仅仅进入了沿海大中城市的高端市场。
第三阶段( 1996~XX 年):洋品牌洗牌中国市场外资品牌完全改变了中国牙膏市场格局:一方面通过收购国产品牌来取得市场份额和渠道,如联合利华从上海牙膏厂取得了 " 中华 " 和 " 美加净 " 的品牌经营权;另一方面通过出色的营销手段及价格调整,让大众接受自己。
1996 年,国内牙膏 10 强品牌中外资品牌仅占两席,到 1998 年已经增至四席,而 XX 年更是增加到了 6 席。
而 " 蓝天六必治 " 、 " 芳草 " 、 " 两面针 " 等昔日国产名牌整体陷入颓势。
第四阶段( XX 年 ~ )中国牙膏品牌寻求突破" 冷酸灵 " 、 " 田七 " 、 " 蓝天六必治 " 等国内品牌在经历了一轮市场洗礼后,营销手段和品牌管理理念日渐成熟。
牙膏营销策划书

牙膏营销策划书一、项目背景和目标:牙膏是人们日常生活中必备的口腔护理产品,市场竞争激烈。
本次营销策划书旨在推广和销售我们的新型牙膏产品,吸引更多消费者选择我们的产品,并提升市场份额。
目标:1. 提高品牌知名度和在市场中的竞争力。
2. 销售额增加10%。
3. 拓展新的客户群体。
二、目标用户分析:我们的目标用户主要是年轻人和成年人,年龄在18到40岁之间,注重口腔健康和外观。
他们对产品的用处、成分、效果和口感都有一定要求,且对品牌形象有较高的关注度。
三、产品特点和竞争优势:新型牙膏产品具有以下特点和竞争优势:1. 独特的配方和成分,能够有效清洁和保护牙齿。
2. 强调产品的美观和舒适感,提供多种口味和形状选择。
3. 品牌形象鲜明,高品质、高科技的形象体现。
四、市场推广策略:1. 品牌宣传:通过电视广告、网络平台、社交媒体等渠道展示产品特点和优势。
加强与口腔专家和牙科医生的合作,提高信誉度。
2. 产品陈列和推广:与大型超市和药店合作,建立产品陈列特区,提供试用品和优惠活动。
利用店内海报、促销员和产品展示活动吸引消费者。
3. 线上推广:通过建立品牌网站、在线购物平台和社交媒体账号,定期发布相关信息和活动,吸引用户参与和购买。
4. 口碑营销:通过委托口碑营销公司,邀请社交媒体博主和影响者进行产品试用和推荐,提高产品知名度和美誉度。
5. 促销活动:定期举办促销活动,如折扣、赠品等,吸引新用户和回头客。
五、销售预测和市场份额:基于市场调研和分析,预计本次营销活动能够增加销售额10%,提升市场份额。
同时,我们将不断关注市场反馈和用户需求,进行产品优化和创新。
六、预算和时间安排:1. 宣传费用:包括广告制作、媒体购买、产品陈列等费用。
2. 促销费用:包括促销活动、赠品、折扣等费用。
时间安排:根据市场反馈和销售情况不断调整和优化策划,确保活动顺利进行并达到预期目标。
七、营销效果评估:1. 销售额增加情况:通过销售额数据统计,对比前后增长情况。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
统计12-1 李本恩一、 课题名称:牙膏销售量的影响因素 二、 课题条件参考文献::《MATLAB 从入门到精通》 三、 设计任务本文从收集有关牙膏的销售量开始,从牙膏销售量和价格、广告投入之间的关系出发,分别通过对这三个方面的深入研究从而制定出各自的最佳方案,最后再综合这 三个主要因素,进一步深入并细化,从而求得最优解。
四、论文内容摘要内容 :本文从收集有关牙膏的销售量开始,从牙膏销售量和价格、广告投入之间的关系出发,分别通过对这三个方面的深入研究从而制定出各自的最佳方案, 最后再综合这三个主要因素,进一步深入并细化,从而求得最优解。
模块Ⅰ中,我们假设在x 1和x 2对y 的影响独立 ,从而得到了方程εββββ++++=22322110x x x y模块Ⅱ中,我们假设x 1和x 2对y 的影响有交互作用,进一步得到新的方程20112232412y x x x x x βββββε=+++++关键词:线性回归模型 相关系数问题重述:某大型牙膏制造企业为了更好的拓展产品市场,有效地管理 库存,公司董事会要求销售部门根据市场调查,找出公司生产 的牙膏销售量价格,广告投入等之间的关系,从而预测出在不 同价格和广告费用下的销售量。
为此,销售部的研究人员收集 了过去30个销售周期(每个销售周期为4周)公司生产的牙 膏销量,销售价格,投入的广告费用,以及同期其他厂家生产 的同类牙膏的平均销售价格,见表1。
试根据这些数据建立一 个数学模型,分析牙膏销售量与其他因素的关系,为制定价格 策略和广告投入策略提供数据依据。
销售 周期 公司销售价格(元) 其他厂家平均价格(元) 广告费用(百万元) 价格差 (元) 销售量 (百万支) 13.853.805.50-0.057.38(其中价格差指其他厂家平均价格与公司销售价格之差)1.实验设计方案 1) 前期分析:由于牙膏是生活必需品,对大多数顾客来说,在购买同类产品的牙膏时更多的会在意不同品牌之间的价格差异,而不是它们的价格本身。
因此,在研究各个因素对销售量的影响时,用价格差代替公司销售价格和其他厂家平均价格更为合适。
记牙膏销售量为y ,其他厂家平均价格与公司销售价格之差(价格差)为x 1公司投入的广告费用为x 2 ,其他厂家平均价格与公司销售价格分别为x 3和x 4 ,x 1=x 3-x 4。
基于上面的分析,我们尽利用x 1和x 2来建立y 的预测模型。
2) 模型假设:1 在一定时期内假设市场总需求量没有太大的变化。
2 同类产品在一定时期内价格无明显变化。
3 通过调节本公司的价格调整都能够达到理想的价格差 3) 建立模型:εββββ++++=22322110x x x y4) 编写程序:[b,bint,r,rint,stats]=regress(y,x,alpha)5) 对结果进行分析,讨论诸如:结果的合理性、正确性,算法的收敛性,模型的适用性和通用性,算法效率与误差等。
2.基本模型为了大致分析y 与1x 和2x 的关系,首先利用散点图观察销售量y 与价格差1x 及y 与广告投入量2x 之间的关系。
y 与1x 的关系: y 与2x 的关系:图1 y 对1x 散点图(1) 图2 y 对2x 的散点图从图(1)发现,随着1x 增加,y 的值有明显的线性增加趋势,图中直线用线性模型011y x ββε=++ (1)拟合的(其中ε是随机误差)在图2 中,当2x 增大时,y 有向上弯曲增加的趋势,图中的曲线用二次函数模型:εβββ+++=223220x x y (2) 拟合。
综上分析,结合模型(1)和(2)建立如下回归模型20112232y x x x ββββε=++++ (3) 其中,y 是建立的模型,我们用=∧y 22322110x x x ββββ+++对y 进行估计,其中3210,,,ββββ是我们待估计的参数。
3.模型求解利用MATLAB 统计工具箱中的命令regress 求解,使用格式为: [b,bint,r,rint,stats]=regress(y,x,alpha)得到模型(3)的回归系数的估计值及其置信区间(置信水平05.0=α)、检验统计量P F R ,,2,S 2的结果见下表2表 2 4.结果分析由表中的数据显示,2R =0.9054指因变量的y 的90.54%可由模型确定,F值远远超过F 检验的临界值,p 远远小于α,因而模型(3)可用。
表2的回归系数给出了模型(3)中0β,1β,2β,3β的估计值0β∧=17.3244,1β∧=1.3070,2β∧=-3.6956,3β∧=0.3486。
检查它们的置信区间发现,只有2β的置信区间包含零点(但区间右端点距零点很近),表明回归变量2x (对因变量y 的影响)不是太显著的,但由于22x 是显著的,我们仍将变量2x 保留在模型中。
5.销售量预测经回归系数的估计值代入模型(3),即可预测公司未来某个销售周期牙膏的销售量y ,将预测值记为y ∧,得到模型(3)的预测方程:y ∧=20123122x x x ββββ∧∧∧∧+++ (4) 只需知道该销售周期的价格差1x 和投入的广告费用2x ,就可以计算预测值y ∧。
公司无法直接确定价格差1x ,只能制定公司的牙膏销售价格4x ,但是其它厂家的平均价格一般可以通过根据市场情况及原材料的价格变化等估计。
模型中用价格差做为回归变量的好处在于公司可以更灵活地来预测产品的销售量或市场需求量,因为其它厂家的平均价格不是公司所能控制的。
预测时只要调整公司的牙膏销售价格达到设定的回归变量价格差1x 的值。
回归模型的一个重要应用是,对于给定的回归变量的取值,可以以一定的置信度预测因变量的取值范围,即预测区间。
6.模型改进模型(3)中回归变量1x ,2x 对因变量y 的影响是相互独立的,即牙膏销售量y 的均值和广告费用2x 的二次关系由回归系数2β,3β确定,而不依赖与价格差1x ,同样,y 的均值与1x 的线性关系由回归系数1β确定,不依赖于2x 。
根据经验可参想,1x 和2x 之间的交互作用会对y 有影响,简单的用1x ,2x 的乘积代表他们的交互作用,将模型(3)增加一项,得到:20112232412y x x x x x βββββε=+++++ (5)在这个模型中,y 的均值与2x 的二次关系为22232412x x x x βββ++,由系数2β,3β,4β确定,并依赖与价格差1x 。
下面让我们用表1的数据估计模型(5)的系数。
利用MATLAB 的统计工具箱得到的结果见表3.验统计量P F R ,,2,S 2的结果见下表1表 3表3与表2的结果相比,R 2有所提高,说明模型(5)比模型(3)有所改进,相信模型(5)更符合实际。
用模型(5)对公司的牙膏销售量做预测,仍设在某个销售周期中,维持产品的价格差X1=0.2元,并投入X2=6.5百万元的广告费用,则该周期牙膏销售量y 的估计值为=∧y ∧β0 + ∧β1x 1 +∧β2x 2+∧β3x 22+∧β4x 1x 2 =29.1133 + 11.134 ×0.2– 7.608×6.5 + 0.6712 ×6.52 -1.4777 ×0.2 ×6.5 =8.3253百万支,置信度为95%的预测空间为[7.8953,8.7592],与模型(3)的结果相比,∧y 略有增加,而预测区间长度短些。
在保持广告费用x 2=6.5百万元不变的条件下,分别对模型(3)和(5)中牙膏销售量的均值∧y 与价格差x 1的关系作图,见图3和图4图3 模型(3)∧y 与x 1 的关系 图4 模型(5)∧y 与x 1 的关系 在保持价格差x 1=0.2元不变的条件下,分别对模型(3)和(5)中牙膏销售量的均值∧y 与广告费用x 2的关系作图,见图5和图6图5 模型(3)∧y 与2x 的关系 图6 模型(5)∧y 与2x 的关系 可以看出,交互作用项1x 2x 加入模型,对∧y 与1x 的关系稍有影响,而∧y 与2x 的关系有较大变化,当2x < 6时∧y 出现下降,2x > 6以后∧y 上升则快得多。
进一步讨论: 为了解1x 和2x 之间的相互作用,考察模型(5)的预测方程 ∧y =29.1133+11.13421x -7.60802x +0.67122x 2 -1.47771x 2x (6)如果取价格差1x =0.1元,代入(6)可得∧y1x =0.1 =30.2267 -7.75582x +0.67122x 2 (7)再取1x =0.3元,代入(6)可得∧y1x =0.3 =32.4536 -8.05132x +0.67122x 2 (8)它们均为2x 的二次函数,其图形见图7,且∧y1x =0.3 -∧y1x =0.1 = 2.2269-0.29552x (9)由(9)式可得,当 2x < 7.5360时,总有∧y1x =0.3 >∧y1x =0.1,即若广告费用不超过大约7.5百万元,价格差定在0.3元时的销售量,比价格差定在0.1元的大 ,也就是说,这时的价格优势会使销售量增加。
图7 y与x的关系((7)与(8)的图形)2附录:源程序x1=[-0.05;0.25;0.60;0;0.25;0.20;0.15;0.05;-0.15;0.15;0.20;0.10;0.40;0.45;0.35;0 .30;0.50;0.50;0.40;-0.05;-0.05;-0.10;0.20;0.10;0.50;0.60;-0.05;0;0.05;0.55];y=[7.38;8.51;9.52;7.50;9.33;8.28;8.75;7.87;7.10;8.00;7.89;8.15;9.10;8.86;8.90;8.87;9.26;9.00;8.75;7.95;7.65;7.27;8.00;8.50;8.75;9.21;8.27;7.67;7.93;9.26]; aa=polyfit(x1,y,1);y1=polyval(aa,x1);plot(x1,y1,x1,y,'ro')%图1:Y对X1的散点图x1=[-0.05;0.25;0.60;0;0.25;0.20;0.15;0.05;-0.15;0.15;0.20;0.10;0.40;0.45;0.35;0 .30;0.50;0.50;0.40;-0.05;-0.05;-0.10;0.20;0.10;0.50;0.60;-0.05;0;0.05;0.55];x2=[5.50;6.75;7.25;5.50;7.00;6.50;6.75;5.25;5.25;6.00;6.50;6.25;7.00;6.90;6.80 ;6.80;7.10;7.00;6.80;6.50;6.25;6.00;6.50;7.00;6.80;6.80;6.50;5.75;5.80;6.80]; y=[7.38;8.51;9.52;7.50;9.33;8.28;8.75;7.87;7.10;8.00;7.89;8.15;9.10;8.86;8.90;8.87;9.26;9.00;8.75;7.95;7.65;7.27;8.00;8.50;8.75;9.21;8.27;7.67;7.93;9.26]; aa=polyfit(x2,y,2);x3=5.25:0.05:7.25;y2=polyval(aa,x3);plot(x2,y,'ro',x3,y2)%图2:Y对X2的散点图dx4=[ones(30,1),x1,x2,x2.^2]; [b,bint,r,rint,stats]=regress(y,x4) %表2x5=[ones(30,1),x1,x2,x2.^2,x1.*x2]; [b,bint,r,rint,stats]=regress(y,x5) %表3x1=[-0.05;0.25;0.60;0;0.25;0.20;0.15;0.05;-0.15;0.15;0.20;0.10;0.40;0.45;0.35;0 .30;0.50;0.50;0.40;-0.05;-0.05;-0.10;0.20;0.10;0.50;0.60;-0.05;0;0.05;0.55]; ytu3=17.3244+1.307*x1+(-3.6956)*6.5+0.3486*6.5*6.5;plot(x1,ytu3)grid on %图3x1=[-0.05;0.25;0.60;0;0.25;0.20;0.15;0.05;-0.15;0.15;0.20;0.10;0.40;0.45;0.35;0 .30;0.50;0.50;0.40;-0.05;-0.05;-0.10;0.20;0.10;0.50;0.60;-0.05;0;0.05;0.55]; ytu4=29.1133+11.1342*x1+(-7.608*6.5)+0.6712*6.5*6.5+(-1.4777)*6.5*x1;plot(x1,ytu4)grid on %图4x2=[5.50;6.75;7.25;5.50;7.00;6.50;6.75;5.25;5.25;6.00;6.50;6.25;7.00;6.90;6.80 ;6.80;7.10;7.00;6.80;6.50;6.25;6.00;6.50;7.00;6.80;6.80;6.50;5.75;5.80;6.80]; ytu5=17.3244+1.307*0.2+(-3.6956)*x2+0.3486*x2.*x2;bb=polyfit(x2,ytu5,2);xtu5=5.25:0.05:7.25;ytu51=polyval(bb,xtu5);plot(xtu5,ytu51)grid on %图5x2=[5.50;6.75;7.25;5.50;7.00;6.50;6.75;5.25;5.25;6.00;6.50;6.25;7.00;6.90;6.80 ;6.80;7.10;7.00;6.80;6.50;6.25;6.00;6.50;7.00;6.80;6.80;6.50;5.75;5.80;6.80]; ytu6=29.1133+11.1342*0.2+(-7.608*x2)+0.6712*x2.*x2+(-1.4777)*x2*0.2;bb=polyfit(x2,ytu6,2);xtu6=5.25:0.05:7.25;ytu61=polyval(bb,xtu6);plot(xtu6,ytu61)grid on %图6x2=[5.50;6.75;7.25;5.50;7.65;6.50;6.75;5.25;5.25;6.00;6.50;6.25;7.00;6.90;6.80;6.80;7.10;7.00;6.80;6.50;6.25;6.00;6.50;7.00;6.80;6.80;6.5 0;5.75;5.80;6.80];xtu7=sort(x2);ytu7=30.2267-7.7558*xtu7+0.6712*xtu7.^2;plot(xtu7,ytu7)grid onhold onytu8=32.4536-8.0513*xtu7+0.6712*xtu7.^2;plot(xtu7,ytu8)hold off%图7经过讨论和模型的改进,可以预测出在不同价格和广告费用下的牙膏销售量。
