第十届全国周培源大学生力学竞赛(个人赛)试题参考答案
第 届全国周培源大学生力学竞赛个人赛试题答案

第 9 题(6 分)
(1)、①; (2)、 2 EI 。 2l 2
第 10 题(8 分) (1)、 2 2 m ;
9
(2)、 5 2 m或 5 2 m 。
18
18
-2-
第二部分 提高题部分(计算题,共60分)
第11题(共15分)
解答
组合刚体的运动存在两个阶段,一是绕 O 的定轴转动;
二是质心水平速度保持不变的平面运动。
(1分) (1分)
M A sin( )dA
(1分)
计算出积分,可得
M Er4 sin 4R
于是转角为
(1分)
sin1
E r4 4RM
sin1
E r4 4mR2
(1分)
(3) 内力的最大值Mmax
当=π/2 时,M=Mmax。
M max
Er4 4R
(1分) (1分)
-7-
第14题(共15分)
由质心运动定理
FN 2 2m aCn sin aC cos
(3)
aCn = r2, aC = r 。方程(3)也可由动静法得到。式(3)中代入加速度
FN 2
2mgr 2 JO
sin
3cos
2
(2 分)
球与凸台分离的角度由FN2 0 确定。
0
cos1
2 3
( 4 ) (1 分)
对应角速度0 2
解:(1)
记 D D t
①钢丝的伸长量 由力的平衡可得
g D F 2
qD F
2
q g
F 2n P
解此方程,得
F ( ) Pe ( 2n )
F F d
g d
q F()
周培源力学竞赛题目

一力学竞赛简介在各门科学中,力学和数学是最为基础和影响范围最广的两门学科,也是关系最为密切的两门学科。
简练的说数理化天地生可统一归纳为物理科学,形象的说,物理科学是一根梁,力学和数学就是两根支柱。
1988年第一届全国青年力学竞赛,每四年举行一次,后来受到周培源基金会的支持,改名周培源大学生力学竞赛,1996年第三届全国周培源大学生力学竞赛,2007年开始每两年举行一次。
力学竞赛宗旨:推动作为基础课的力学教学,增加学生对力学学科的兴趣,活跃教学与学习氛围,发现人才,吸引全社会对力学学科的关注与投入。
竞赛题目特点,总体新颖有趣,难度适中,简明又富于启发性,特别从实践中提炼出来的赛题是亮点。
竞赛题目围绕理论力学和材料力学两门课程进行。
材料力学以理论力学知识为基础,两门课程密切相关。
理论力学主要研究刚体,材料力学研究变形体,两门课程在力学模型和分析方法方面都有所不同。
应仔细研究和了解两门课程在理论模型和方法方面的联系与区别。
力学建模是不可或缺的基本能力之一,也是材料力学教学中相对薄弱的环节。
力学建模要求对实际问题的力学机制有深刻理解,要求有把握全局的定性分析能力。
从不同的角度切入,同一工程问题的力学模型可能具有多样性,对关键因素的提炼有不同见解,造成结果有所差别,只是精度之差,而非正确与错误之别。
二近几届力学竞赛题目分析从2007年开始每两年举行一届全国周培源大学生力学竞赛,出题学校是清华大学,个人卷满分120分,时间三小时,试题总共四题,每道题设置三个问题,内容包括理论力学和材料力学,两个科目的内容和分数基本上各占一半。
不乏理论力学和材料力学的混合问题。
本次试题的风格是趣味性,灵活性和发散性,特点是,把学生所熟悉的力学问题改写成未经加工提炼的状态,这样学生看到的是“问题”或“现象”,而不再是熟悉的“习题”了。
所以特别考察学生的基础知识是否扎实,解题技巧是否灵活,观察能力是否敏锐,建模能力,以及面对复杂问题时能否抓住问题的核心,直接洞察问题实质的能力。
周培源力学竞赛分

周培源力学竞赛分摘要:1.周培源力学竞赛概述2.周培源力学竞赛的参赛对象和要求3.周培源力学竞赛的竞赛内容4.周培源力学竞赛的历届获奖情况5.周培源力学竞赛对于参赛者的意义正文:【周培源力学竞赛概述】周培源力学竞赛,全名为“周培源大学生力学竞赛”,是我国一项面向全国大学生的力学学科竞赛。
该竞赛旨在激发大学生学习力学的兴趣,提高力学教学质量,培养学生的创新能力和实践能力,选拔和培养优秀的力学人才。
【周培源力学竞赛的参赛对象和要求】周培源力学竞赛的参赛对象主要为全国范围内的大学生,包括本科生和研究生。
参赛者需具备一定的力学基础知识,同时具有较强的力学分析和解决问题的能力。
参赛团队需由三名选手组成,每名选手需分别完成个人赛和团体赛两个阶段的竞赛。
【周培源力学竞赛的竞赛内容】周培源力学竞赛的内容主要包括两个方面:个人赛和团体赛。
个人赛主要测试参赛选手的力学基础知识和分析解决问题的能力;团体赛则侧重于考察参赛团队的协作能力和创新能力。
竞赛题目一般涵盖了力学的基本理论、实验方法和应用技术等多个方面。
【周培源力学竞赛的历届获奖情况】自周培源力学竞赛创立以来,吸引了众多优秀大学生参赛,历届获奖情况也备受瞩目。
众多获奖者中,有的后来成为力学领域的专家学者,有的则在其他领域取得了卓越成就。
这些获奖者都在竞赛中锻炼了自己的能力,积累了宝贵的经验。
【周培源力学竞赛对于参赛者的意义】参加周培源力学竞赛对于参赛者具有重要意义。
首先,竞赛有助于提高参赛者的力学素养,培养其分析和解决问题的能力;其次,竞赛为参赛者提供了一个展示自己才能的平台,有助于提高参赛者的自信心和综合素质;最后,竞赛还有助于拓展参赛者的人际交往,结识志同道合的伙伴,为今后的学术和职业发展奠定基础。
全国周培源大学生力学竞赛辅导力学竞赛-静力学平衡方程
0.5 m C P
FAx FAy
FBy
解:研究系统,受力如图,由方程:∑Fx=0,∑Fy=0,∑MA=0,可 解得FAx=0、FAy=20 kN、MA=20 kN· m。
研究杆BEC,受力如图,由方程:∑Fx=0,∑Fy=0,∑MB=0,可 解得FBx=0、FBy=-20 kN、FDE=40 kN· m。
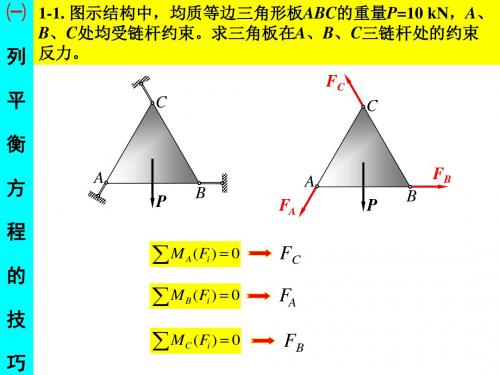
㈠ 1-1. 图示结构中,均质等边三角形板ABC的重量P=10 kN,A、
B、C处均受链杆约束。求三角板在A、B、C三链杆处的约束 列 反力。 FC 平 C C
衡 方 程 的 技 巧
A P
B
( Fi ) 0 ( Fi ) 0 (Fi ) 0
A FA P
FB B
M M M
A
FC FA
A A C B
D
FA
E
F P FC C FB
B
A FA D FD
C
B
E
F P
㈢ 3-1. 图示结构,已知P=20 kN,求支座A处反力及杆 物 DE的受力。 体 系 平 衡 问 题 基 本 解 法
B FBx 0.5 m A 0.5 m D B E C P D MA A B E C P
0.5 m
E FDE
0.6 m 0.6 m
A C
B
0.8 m
0.6 m
0.6 m
D
F
0.6 m 0.6 m
E
A M C
B
0.8 m
P 4-2′图示结构,已知 P=10 kN,求支座A、E处反力及 杆CF、BF的受力。 0.6 m 0.6 m
A M C
B
0.8 m
D P
F
0.6 m 0.6 m
周培源力学竞赛试题(第六届—第十届)

A Pi
O
θ
B H E C D
S
二、骄傲自满的大力士(35 分)
有位大力士总是自命不凡,他夫人决定找机会教训他一下。正好附近足球场的 球门坏了一半,剩下的半边球门如图:立柱 OA 垂直固定于水平地面上,沿 x 轴方 向,高为 H = 2.4m ,横梁 AB 平行于地面,沿 z 轴负方向,长为 L = H 。立柱和 横梁均为实心圆柱,直径均为 D = 0.06m 。夫人经过计算后想出了主意:和丈夫 比赛,看谁能把球门拉倒。比赛规则是:通过系在横梁 B 端中点的绳索,只能用 静力拉球门;绳索上有且只有 B 点系在与地面固定的物体上。绳索的重量不计, 长度不限。球门不计自重,采用第三强度理论,材料的屈服应力 σ s = 57MPa 。 大力士认为自己肯定不会输,因为他知道两人鞋底与地面摩擦系数都是
r )的无弹性台阶后, 能不 2
3.演员又用细铁棍推动题 2 中匀质圆环在水平地面上匀速纯滚动,假设圆环
保持在铅垂平面内滚动,如图所示。又知铁棍与圆环之间的静摩擦因数为 ft , 圆环与地面间的滚动摩阻系数为 δ 。试求为使铁棍的推力(铁棍对圆环的作用 力)最小,圆环上与铁棍的接触点的位置。
三、趣味单杠 (30 分 )
一半球形高脚玻璃杯, 半径 r =5cm, 其质量 m1=0.3 kg, 杯底座半径 R =5 cm, 厚度不计,杯脚高度 h =10 cm。如果有一个质量 m2 = 0.1 kg 的光滑小球自杯子的 边缘由静止释放后沿杯的内侧滑下,小球的半径忽略不计。已知杯子底座与水平 (1)高脚玻璃杯会不会 面之间的静摩擦因数 fs = 0.5。试分析小球在运动过程中: 滑动; (2)高脚玻璃杯会不会侧倾(即一侧翘起) 。
EI 。两均质水晶圆球的半径均为 r ,重量均为 P = ql 。
周培源力学竞赛 参考书

周培源力学竞赛参考书周培源力学竞赛参考书近年来,力学竞赛在学生中越来越受欢迎。
而要在这个竞赛中取得好成绩,选择一本优质的参考书是至关重要的。
本文将为大家推荐几本适合作为周培源力学竞赛的参考书。
首先,推荐《周培源力学竞赛指南》。
这本书由周培源教授亲自编写,以力学竞赛的考点和难点为导向,详细介绍了力学竞赛的各个知识点和解题技巧。
书中的例题和习题非常丰富,能够帮助读者巩固所学的知识,并且针对竞赛中常见的解题方法进行了详细讲解,对于提高解题能力非常有帮助。
第二本推荐的参考书是《力学竞赛全能宝典》。
这本书总结了历年来的力学竞赛试题,通过对试题的分类整理,帮助读者更好地理解各个知识点的考察方式。
书中还提供了详细的解题思路和方法,使读者能够更加深入地理解解题过程。
此外,书中还附有大量的习题和模拟试题,供读者进行自我测试和练习。
第三本推荐的参考书是《力学竞赛经典题解精选》。
这本书选取了一些经典的力学竞赛试题,并给出了详细的解题过程和思路。
通过阅读这些题解,读者可以了解到不同题目的解题思路和方法,并且能够学习到一些解题的技巧和窍门。
这本书对于提高解题能力和应对竞赛中的难题非常有帮助。
需要注意的是,以上推荐的参考书都是为了帮助读者提高力学竞赛的成绩而编写的,并无任何广告信息或侵权争议。
这些书籍都是经过严格筛选和审查的,确保内容准确无误,没有敏感词汇或其他不良信息。
总而言之,要在周培源力学竞赛中取得好成绩,选择一本优质的参考书是必不可少的。
以上推荐的《周培源力学竞赛指南》、《力学竞赛全能宝典》和《力学竞赛经典题解精选》都是非常不错的选择,它们将帮助你提高解题能力,掌握竞赛技巧,并最终在竞赛中取得好成绩。
希望本文的推荐能够对你有所帮助。
第十届全国周培源大学生力学竞赛(团体赛)获奖名单
第十届全国周培源大学生力学竞赛(团体赛)获奖名单
佚名
【期刊名称】《力学与实践》
【年(卷),期】2015(0)5
【摘要】"理论设计与操作"团体赛特等奖:湖南大学一等奖:中国人民解放军军械工程学院中国科学技术大学二等奖:上海交通大学武汉大学哈尔滨工业大学(威海)【总页数】1页(P661-661)
【关键词】南京工程学院;交通大学;河北工业大学;航空航天;国防科技大学;南京理工大学;华北电力大学;中国矿业大
【正文语种】中文
【中图分类】O3
【相关文献】
1.第七届全国周培源大学生力学况赛团体赛获奖名单 [J],
2.第十三届全国周培源大学生力学竞赛个人赛全国特、一、二等奖获奖名单 [J],
3.第十届全国周培源大学生力学竞赛个人赛获奖名单 [J],
4.第十届全国周培源大学生力学竞赛“理论设计与操作”团体赛即将拉开序幕 [J],
5.第九届全国周培源大学生力学竞赛(团体赛)获奖名单 [J],
因版权原因,仅展示原文概要,查看原文内容请购买。
周培源力学竞赛试题与解答
解上述六个方程�由于桌腿不能提供拉力�令 Ni>0(i=1,„„,6)�得到不等式 |3x±4y|<2a
得到解的区域为菱形 BCHI�不含边界��其中 B 点坐标为 下面设模特儿位于桌面第一象�限讨论其他几种情形。
�b�五腿受力�设腿 1 不受力�令 N1=0 �舍去方程(5)�求得均自然满足�根据
�2�如果 a �求空隙的函数表达式 0 > Γ a �并画出示意图。 Γ 0 与 Γ a 有何关系� 设 AB 与 yz 平面的交点是 P � BP 的长度为 ξ 。则根据几何关系� P 点的坐标为
消去参变量 ξ �有
所以 点的轨迹是抛物线�的一部分��这也就是空隙的方程。而曲线 Γ 0 是 Γ a 的渐进线。
第 6 届周培源全国大学生力学竞赛初赛�样题�
时间 3 小时�满分 120 分
一、奇怪的独木桥�25 分� 一位游客在某处发现有座独木桥�上面写着�禁止独自一人过桥。他发现当地居民的确都
是成双结队并且好像以某种相互配合的方式过桥。他觉得很奇怪�为什么 2 个人可以过桥 而 1 个人却不能。等周围没有其它人时他想独自试试�结果没走到半程�就把独木桥压断了 而掉入水中。
�3�当 时�设 P 点是 AB 杆与 yz 平面的交点�当 P 点位于 AB 杆中点且时�如果要求 P 点 的速度和加速度�你如何考虑�如果取
速度和加速度是多少� 思路�采用点的复合运动关系�以 p 为动点� AB 杆为动系。相对运动沿 AB 杆�牵连运动作定 轴转动�绝对运动是在 yz 平面内的抛物线上运动。 当 P 为 AB 杆中点时�设 P 点的坐标为 (xp,yp , zp) � B 点的坐标为(xB,yB ,zB ) ∠BOC= θ 。 其中
全国周培源大学生力学竞赛模拟试题-徐州工程学院
周培源全国大学生力学竞赛模拟题(徐州工程学院)一 某杂技团作飞车走壁表演,设车由A 点开始沿路径AEDBCE 运动,路径的DBC 段为一圆的缺口,而α==<<BOD BOC ,不计摩擦。
(25分)(1)小车在DBC 段运动时与力学中的哪些知识相关? (2)问高度h 应为多少才能使小车越过缺口循上述路径运动? (3)又如欲使h 值为最小,则α角应为若干?题一图二 长为l 的钢尺,用两手食指在两端水平托起,当两手食指慢慢平行靠近时,钢尺首先只在一只手上滑动,当滑动一定长度后,又换为只在另一只手上滑动。
(35分)(1)用力学知识简要解释这一现象。
(2)钢尺沿长度方向自重的荷载集度为q ,钢尺与手之间的静摩擦因数为s f ,动摩擦因数为f ,求钢尺在首先滑动的手上能滑动的最大距离d 。
(3)钢尺的材料弹性模量为E ,横截面对中性轴的惯性矩为z I ,求当钢尺在首先滑动的手上滑动最大距离d 时,钢尺两端的转角。
三 人们常可见到这样的杂技表演:一人躺在地上,身上压着一块石板,另一人挥铁锤击石板,石板破了而其底下的人却安然无恙。
(25分)(1)请指出这一表演中所包含的力学概念(或力学问题)。
(2)如果铁锤的质量为1m ,击石头时的速度为1v ,石头的质量为2m ,两者间的恢复因数为k ,碰撞的能量损失为多少?(3)如果铁锤与石板的恢复系数.k=0.5,铁锤1m =5kg , 2m =75kg ,被表演者吸收转变为身体的变形能的能量为多少?四 一条长为2m 的黄铜管,外径D =150mm ,壁厚δ=5mm ,两端封闭,用直径d =2.5mm 的钢丝绕在上面,如图1所示(已知钢的弹性模量s E =200GPa ,泊松比s μ=0.25,黄铜的弹性模量c E =200GPa ,泊松比c μ=0.34)。
(35分)题四 图1(1)计算该钢丝中产生的最大应力如下:MPa 7.32785.21505.210200223maxmax max max =+⨯⨯=+=+====d D Ed d D dEEy I y EI I My z z z ρρσ如果钢丝的屈服极限为235Mpa ,上述算式是否正确,为什么?(2)如果在力F =400N 作用下用钢丝将管紧密地缠绕一层,计算该钢丝中产生的最大应力,求铜管的应力。
周培源力学竞赛试题
3.(17分)一质量为m,半径为r的均质圆轮,自半径为R的半圆弧面顶点无初速度的只滚动不滑动下落。求:
3.(3分)有一空间平衡力系,若其所有力的作用线均与空间直角坐标系的z轴平行,则该力系的平衡方程为。
4.(3分)如图示,物块重P=8 N,靠在铅垂的墙壁上,作用力F= 10 N,θ=30º,若物块与墙壁之间的摩擦系数f=0.4,则物块所受到的摩擦力大小为,方向。
5.(2分)设一动点M沿螺旋线自外向内作匀速运动,如图所示,则其加速度的大小将如何变化?。
3.如图所示,物块重W =10N,水平力P=50N,已知摩擦系数f=0.3,则物块受到的摩擦力为()。
4一质点只受到重力作用时,它一定作直线运动()。
5.如图所示,一绳缠绕在鼓轮上,绳端系一重物,重物M以速度v和加速度a向下运动,问绳上的A和与轮接触的点D之速度是否相同(),加速度是否相同()。
6已知图示二杆O1A与O2B长度相等,互相平行,则正确的答案应是()。
题1图题2图
2.平面机构如图所示,曲柄OA=r,以匀角速度ω绕水平轴O转动,通过滑块A带动BC作水平往复运动。求θ=60º的瞬时BC的速度和加速度。(2分)
3.平面机构由杆O1A、O2B与矩形板ABCD铰接而成,OlA=AD=r,O2B=AB=2r,设O1A以匀角速度ω绕O1轴转动,图示瞬时O1A、O2B均与A B垂直。试求此时C点的速度和加速度的大小。
题7图
南京理工大学2001年理论力学试题
一、杆AB、CD由铰链C联结,并由铰链A、D固定如图示。在AB杆上作用一力偶从不计杆重,试求支座D处的重直方向反力。(1分)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
度 v0 作匀速运动,此时若 v0 > v1 min,则
√
smin = 4
2b [1 − sin(45◦ + θ)] 3(sin θ + f cos θ)
若 v0 < v1 min,s 不管取何值,均无法满足要求.
当 θ > arctan fs,货箱与传送带同速后还将继
续向下作加速运动,此时若 v0 v1 min,smin 的表达
堆放多少块金属板?
第十届全国周培源大学生力学竞赛(个人赛) 试题参考答案
出题学校:山东科技大学
第 1 题 (30 分)
(1) 不会翻倒.
(2) 货箱与刚支承碰撞前至少具有如下速度
v1 min
=
2 3
√ 6 2gb [1 − sin(45◦ + θ)]
当 θ arctan fs,货箱与传送带同速后,将以速
林清华 天津大学
陈 桥 南京航空航天大学 郭宏达 哈尔滨工业大学 杨唯超 北京航空航天大学 冯 瑞 北京航空航天大学
二等奖获得者
王祥宇 天津大学
武 迪 清华大学
汤学璁 北京航空航天大学 崔 达 国防科大
王再兴 浙江大学
谢金哲 武汉大学
张旭波 武汉大学
欧吉辉 天津大学
厉晓侠 南京理工大学
胡云皓 南京航空航天大学 陈思诺 南京航空航天大学 孙伟召 华中科技大学
张佳鑫 西南交大峨眉校区 柳超然 中南大学
赵志晔 中国科学技术大学 卓荣枢 武汉理工大学
吴 稳 同济大学
黄 彪 同济大学
王 聪 同济大学
张昱哲 南京理工大学
邢 占 南京航空航天大学 张 宇 华中科技大学
吴 迪 华中科技大学
祝志磊 华北电力大学
何建宏 武汉大学
万广超 北京大学
马 充 清华大学
金 涛 浙江大学
胡艳杰 河海大学
丁祥文 同济大学
杨嘉靖 浙江大学
张元龙 清华大学
章凯翔 南京理工大学
王开淼 南京航空航天大学 黄金钊 哈尔滨工业大学 邓 昊 北京航空航天大学 袁凯华 武汉大学
何泽远 清华大学
赵超凡 南京航空航天大学 王 强 南京航空航天大学 季 攀 哈尔滨工业大学 (威海)
王仕青 湖南大学
熊永丰 中国科学技术大学 杨 涛 武汉大学
盛云锋 武汉大学
马宇沫 清华大学
陆 畅 北京航空航天大学 李 意 北京航空航天大学 林逢雨 哈尔滨工业大学 (威海)
曾智敏 中南大学
黄道兴 西南交通大学
贠国霖 中国科学技术大学 李 晟 中国科学技术大学
姚 熠 武汉大学
陈百鸣 清华大学
王 瑞 南京理工大学
1
−
cos
√
3g R
t
第 3 题 (30 分)
(1) P 点应力状态单元体如图 1(a) 所示,各应
力分量表达式为
σx
=
4htL + 3qL2 bh2
,
σy
=
−
q b
,
τxy
=
−
t b
Q 点应力状态单元体如图 1(b) 所示,应力表达式为
σx
=
−
2htL + 3qL2 bh2
图1
(2) C 截面切应力表达式为
式同上式;若 v0 < v1 min,则
smin
=
√ 4 2b
[1
−
sin(45◦
+
3(sin θ − f cos θ)
θ)] −
f cos θv02 g(sin2 θ − f 2 cos2 θ)
第 2 题 (25 分) √
(1)
tan θ
=
2d
− 3R
3R
(2) 猴乙的行走规律为
√
s=
2
3R 3
范珏雯 南京航空航天大学
王 浩 南京航空航天大学 朱 征 河海大学
郑 滔 哈尔滨工业大学 李 唐 北京航空航天大学
徐 翔 华北电力大学
王盈聪 南京工程学院
李 越 河北工业大学
王珂瑶 北京航空航天大学
汪剑辉 扬州大学
李桂光 重庆大学
肖羚玮 武汉大学
张 宁 同济大学
邵枝淳 清华大学
刘 莹 华中科技大学
李 峥 东南大学
(2) 截取圆杆长度 H∗ = 1 010.6 mm,使之处于
铅垂位置,在离右端 a = 417.9 mm 处与横梁强行 安装. 这样设计的结构具有最大的许用荷载 [q] = 34.35 kN/m.
(3) 最多可以放置 17 块金属板.
第十届全国周培源大学生力学竞赛 个人赛获奖名单
特等奖获得者
张川 陆星阳
τ =−
3qL 2bh
1
−
4y2 h2
+
t 4b
1
−
4y h
−
12y2 h2
.
(3) C 截面上,σx 和 σy 的一般表达式为
σx(y)
==
tL bh
+
6(qL2 + htL)y bh3
σy (y)
=
−
q 2b
1
+
3y h
−
4y3 h3
在该截面中线处应力分量
σx
=
tL bh
,σy
=
−
q 2b
.
在 C 截面侧面中线处沿轴向贴一个应变片
第 4期
第十届全国周培源大学生力学竞赛 (个人赛) 试题参考答案
553
(1) 定性分析:如何使用这根圆杆,使之与横梁 形成合理的结构,才能尽可能多地放置金属板?
(2) 不计横梁和圆杆的重量,根据问题 (1) 的要 求,设横梁和圆杆的安全因数均为 [n] = 2,设计和
定量地计算这一结构. 结果中长度精确到 0.1 mm. (3) 根据你的设计,加上支撑后的横梁最多可以
徐 康 三峡大学
李家其 清华大学
余 航 北京航空航天大学 顾丁炜 北京大学
曹世辉 中国科学技术大学 杨伟东 清华大学
吴瀚枭 北京航空航天大学 金 瑞 重庆大学
焦亚基 东南大学
陈路华 武汉大学
薛彤辉 南京理工大学
邹慧辉 解放军理工大学
郑再峰 哈尔滨工业大学 池宇希 北京航空航天大学 许思为 上海交通大学
哈尔滨工业大学 中国科学技术大学
陈金 余明
南京航空航天大学 哈尔滨工程大学
李逸良
清华大学
一等奖获得者
张智飞 哈尔滨工业大学 刘和鑫 武汉大学
王风范 东南大学
夏冬冬 南京理工大学
彭 辉 武汉理工大学
郑 阳 清华大学
张 航 南京航空航天大学 曹 越 北京航空航天大学
谢江岳 中国矿业大学
徐兴春 天津大学
宋清华 华中科技大学
王旭祥 东南大学
史迪威 北京大学
苑斌杰 清华大学
颜 晔 南京航空航天大学 董丹丹 河海大学
胡毓涵 浙江大学
俞嘉晨 清华大学
高 叶 清华大学
陆 欢 南京航空航天大学
马超智 兰州交通大学
王苑佐 哈尔滨工业大学 沈强强 哈尔滨工业大学 陈怡林 东南大学
张 竞 东南大学
鲍存余 北京航空航天大学 饶智祥 北京航空航天大学 孙 嘉 武汉理工大学
ε(1),沿横向贴一个应变片 ε(2),则
t
=
Ebh L(1 − ν
2)
(ε(1)
+
ν ε(2) )
q
=
−
2Eb 1 − ν2
(ε(2)
+
ν ε(1) )
554
力学与实践
2015 年 第 37 卷
Байду номын сангаас
第 4 题 (35 分) (1) 圆杆应铅垂放置,并且左右位置调整,长度
取得比 1 000 mm 略长,利用装配应力 (即预应力) 来 提高横梁的强度.
