相对运动图解法共32页
合集下载
理论力学—相对运动动力学PPT

(1)当动系相对于定系仅作平动时 (1)当动系相对于定系仅作平动时
m r = F +F a Ie
(2)当动系相对于定系作匀速直线平动时 (2)当动系相对于定系作匀速直线平动时 (3)当质点相对于动参考系静止时 (3)当质点相对于动参考系静止时
m r =F a
F +F =0 Ie
质点相对静止的平衡方程:即质点在非惯性参考系中保持相对 质点相对静止的平衡方程: 静止时,作用在质点上的力与质点的牵连惯性力相互平衡。 静止时,作用在质点上的力与质点的牵连惯性力相互平衡。 (4)当质点相对于动参考系匀速直线运动时 (4)当质点相对于动参考系匀速直线运动时 质点相对平衡方程
m r = F + F +F a Ie IC
9
m r = F +F +F a Ie IC
非惯性系中质点的运动微分方程
d2r′ m 2 = F +F +F Ie IC dt
质点的质量与质点的相对加速度的乘积等于作 用在质点上的外力的合力与牵连惯性力以及科氏 力的矢量和。 力的矢量和。
10
m r = F +F + F a Ie IC
ω地
解:取地球为非惯性参考系,考察任一点M 取地球为非惯性参考系,考察任一点M FIC 应提供其圆周运动的向心力。 应提供其圆周运动的向心力。
F = m C = m⋅ 2 evr = 2m 地vr sinϕ a ω ω IC
该处应在南半球
2 vr m =FIC= 2m 地vr sinϕ ω R
aC vr
15
慢速转动的大盘使快速运动的皮带变形
16
由于地球的 自转引起的水 流科氏惯性力。 流科氏惯性力。
m r = F +F a Ie
(2)当动系相对于定系作匀速直线平动时 (2)当动系相对于定系作匀速直线平动时 (3)当质点相对于动参考系静止时 (3)当质点相对于动参考系静止时
m r =F a
F +F =0 Ie
质点相对静止的平衡方程:即质点在非惯性参考系中保持相对 质点相对静止的平衡方程: 静止时,作用在质点上的力与质点的牵连惯性力相互平衡。 静止时,作用在质点上的力与质点的牵连惯性力相互平衡。 (4)当质点相对于动参考系匀速直线运动时 (4)当质点相对于动参考系匀速直线运动时 质点相对平衡方程
m r = F + F +F a Ie IC
9
m r = F +F +F a Ie IC
非惯性系中质点的运动微分方程
d2r′ m 2 = F +F +F Ie IC dt
质点的质量与质点的相对加速度的乘积等于作 用在质点上的外力的合力与牵连惯性力以及科氏 力的矢量和。 力的矢量和。
10
m r = F +F + F a Ie IC
ω地
解:取地球为非惯性参考系,考察任一点M 取地球为非惯性参考系,考察任一点M FIC 应提供其圆周运动的向心力。 应提供其圆周运动的向心力。
F = m C = m⋅ 2 evr = 2m 地vr sinϕ a ω ω IC
该处应在南半球
2 vr m =FIC= 2m 地vr sinϕ ω R
aC vr
15
慢速转动的大盘使快速运动的皮带变形
16
由于地球的 自转引起的水 流科氏惯性力。 流科氏惯性力。
04-02_相对运动图解法及其应用解析

根据同一构件上相对速度原理写出相对加速度矢量方程式
4.2.1 在同一构件上的点间的速度和加速度的求法
式中: aCBn 表示点 C相对点 B的法 向加速度,其方向从C指向B;
aCBt表示点C相对点B的切向
加速度,其方向垂直CB。
4.2.1 在同一构件上的点间的速度和加速度的求法
因速度多边形已作出,所 以上式法向加速度都可求出,
b"
n a EB
b'
c"
4.2.1 在同一构件上的点间的速度和加速度的求法
各加速度矢量构成的多边形称为加速度多边形。△ bce 与 机构位置图中△BCE相似,且两三角形顶角字母顺序方向一致, 图形
ce BCE的加速度影像。当已知一构件上两点的 b称为图形
加速度时利用加速度影像便能很容易地求出该构件上其他任一 点的加速度。
b3 '
t aB 3
b3 "
4.2.2 组成移动副的两构件重合点间的速度与加速度的求法
用图解法求解构件上点的速度和加速度是算、画、量交替 进行的过程。其精度取决于作图的精度,包括矢量的大小和方 向的准确性。用计算机作图(如使用绘图软件AutoCAD)可以 得到很高的精度。
3 vB3B2
b1 (b2 )
而 vB3B2 位 于 平 面 运 动 平 面 之 内 , 故 θ
=90°
k 从而 a B 3 B 2 2 2 v B 3 B 2
k 哥氏加速度 a B 3 B 2 的方向是将vB3B2
vB3B2
P
b3
沿ω2的转动方向转90°
4.2.2 组成移动副的两构件重合点间的速度与加速度的求法
t aC
aC uac
§1-4 相对运动

3. 加速度变换
将伽利略速度变换对时间求一次导数
考虑到 t t 伽利略加速度变换
aPK aPK aKK
ax ay
ax ay
az
az
若 aKK 0
则 aPK aPK
例:某人骑摩托车向东前进,其速率为10ms-1时 觉得有南风,当其速率为15ms-1时,又觉得 有东南风,试求风速度。
O 风速的方向:
X (东)
v 102 52
11.2(m / s)
arctg 5 2634
10 为东偏北2634'
例 一升降机以加速度 1.22 m/s2 上升,当一上升
速度为2.44m/s时,有一螺母自升降机的天花 板松落,天花板与升降机的底板相距 2.74m。 计算螺母自天花板落到底板所需的时间及螺 母相对于升降机外固定柱的下降距离。
r xi y j zk
P(x, y, z)
r r
r xi y j zk
o R o' x' x
z z'
r r R 成立的条件:
且 t t
绝对时空观!
绝对时空观
r r R r vt
t t
P(或P)在 K在 系
和 K系的空间坐 标、时间坐标的 对应关系为:
t 2h 0.71 s ga
s
v0t
1 2
a螺地t 2
0.74(m)
§1-4 相对运动
太阳、地球、月球系统
相对运动
运动是绝对的,运动的描述具有相对性。在不 同参考系中研究同一物体的运动状态会完全不同。
机械原理 第二章-2相对运动图解、解析
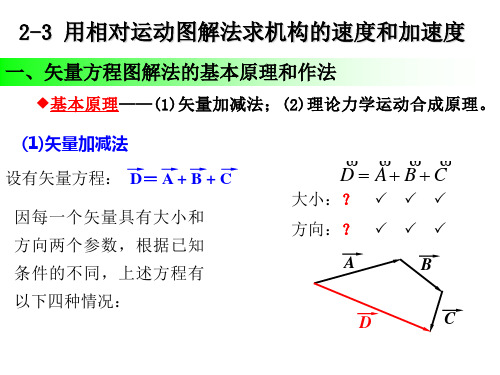
速度影像原理: 同一构件上若干点形成的几 何图形与其速度矢量多边形 中对应点构成的多边形相似.
c p
极点
e b
速度多边形的特性:
1) 在速度多边形中,由极点 p
向外放射的矢量代表构件上相应 点的绝对速度,方向由极点 p 指 极点 向该点。
速度多边形
c
p
b
2)在速度多边形中,联接绝对速度矢端两点的矢量,代 表构件上相应两点的相对速度,例如 : bc 代表
1. 速度分析:
1) 依据原理列矢量方程式 将构件1扩大至与C2点重合。
B
vC2 2 C
VC 2 VC1 VC 2C1
ω1
1
大小: ? √ ? 方向: ⊥CD ⊥AC ∥AB
1
vC1 c2 (c3)
3
D 4
A
4
2) 取速度比例尺 v , 作速 度多边形,由速度多边 形得:
vC 3 vC 2 pc2 v vC 2C1 c1c2 v vC 3 pc2 v 3 lCD lCD
P
c1
( 顺时针 )
2. 加速度分析:
1) 依据原理列矢量方程式 分析:
aC2 = aC1 + aC2C1
B
2 C akC2C1
当牵连点系(动参照系)为 转动时,存在科氏加速度。 3
D 4
ω1
1
1
c2 (c3)
r k aC2C1 aC2C1 aC2C1
科氏加速度
A
4 P c1
k r a 2 v
(4) 求aE6和6
2
A
ω3 a3 5
akE6E5 =
n3
b
机械原理 第二章-2相对运动图解、解析

1
3
aC1n c2 (c3) aC1t 4 D
A
4 P c1
一步减少未知数的个数。
n t k r aC2 aC3D aC3D aC1 aC2C1 aC2C1
2 3 l3
大小: 方向:
? 3l3
√ √
21vC 2C 1 ?
√ ∥AB
C→D ⊥CD
2) 取速度比例尺a , 作 加速度多边形。
P
c1
( 顺时针 )
2. 加速度分析:
1) 依据原理列矢量方程式 分析:
aC2 = aC1 + aC2C1
B
2 C akC2C1
当牵连点系(动参照系)为 转动时,存在科氏加速度。 3
D 4
ω1
1
1
c2 (c3)
r k aC2C1 aC2C1 aC2C1
科氏加速度
A
4 P c1
k r a 2 v
√
√
22lBC
C→B
?
⊥BC
b) 根据矢量方程式,取加速度比例尺
a
实际加速度
c´ 图示尺寸
m/
s2
p
mm
, 作矢量多边形。
c e b
p
极点
n
b
由加速度多边形得:
aC a pc m / s2
t 2 aCB l BC a nc l BC
同样,如果还需求出该构件上E 点的加速度 aE,则
pe 则代表 aE
由加速度多边形得:
p c´ n
aE pea
△b’c’e’ ~ △BCE , 叫 做
△BCE 的加速度影像,字 母的顺序方向一致。
04-02 相对运动图解法及其应用

而不能应用于机构的不同构件上的 各点。
b
e c
4.2.1 在同一构件上的点间的速度和加速度的求法
在速度多边形中,点p称为极点, 代表该构件上速度为零的点; 连接点p与任一点的矢量便代表该 点在机构图中的同名点的绝对速度,
其指向是从p点指向该点;
连接其他任意两点的矢量便代表 该两点在机构图中的同名点间的相对 速度,其指向适与速度的角标相反, 例如矢量bc代表vCB而不是vBC。
b
则向量pe便代表vE,其大小为
e c
P
4.2.1 在同一构件上的点间的速度和加速度的求法
各速度矢量构成的多边形 pbec 称为速度多边形,代表各相对速度 的矢量bc、ce和be分别垂直于机构图 中 的 BC 、 CE 和 BE , 因 此 △ bce 和 △ BCE 相似,且两三角形顶角字母 bce 和 BCE 的顺序相同均为顺时针方 向,图形 bce 称为图形 BCE 的速度影 像。
m/s ,它表示图上每1mm代表的 mm
b
速度值。
矢量pc代表vC: vC=uvpc 矢量bc 代表vCB:vCB=uvbc
c
P
4.2.1 在同一构件上的点间的速度和加速度的求法
为求点E的速度vE,根据同一构件上点E相对点C及点E相对 点B的相对速度原理写出相对速度矢量方程式
由于点E的速度vE的大小与方向均未知,故必须借助于点 E
相对 C和点 E相对 B 的两个相对速度矢量方程式联立求解,这时 式中仅包含vEC和vEB的大小为未知而可以求解。
4.2.1 在同一构件上的点间的速度和加速度的求法
s mm
m
过点 b 作直线垂直于 EB 代
表vEB 的方向线,再过点C作直
b
e c
4.2.1 在同一构件上的点间的速度和加速度的求法
在速度多边形中,点p称为极点, 代表该构件上速度为零的点; 连接点p与任一点的矢量便代表该 点在机构图中的同名点的绝对速度,
其指向是从p点指向该点;
连接其他任意两点的矢量便代表 该两点在机构图中的同名点间的相对 速度,其指向适与速度的角标相反, 例如矢量bc代表vCB而不是vBC。
b
则向量pe便代表vE,其大小为
e c
P
4.2.1 在同一构件上的点间的速度和加速度的求法
各速度矢量构成的多边形 pbec 称为速度多边形,代表各相对速度 的矢量bc、ce和be分别垂直于机构图 中 的 BC 、 CE 和 BE , 因 此 △ bce 和 △ BCE 相似,且两三角形顶角字母 bce 和 BCE 的顺序相同均为顺时针方 向,图形 bce 称为图形 BCE 的速度影 像。
m/s ,它表示图上每1mm代表的 mm
b
速度值。
矢量pc代表vC: vC=uvpc 矢量bc 代表vCB:vCB=uvbc
c
P
4.2.1 在同一构件上的点间的速度和加速度的求法
为求点E的速度vE,根据同一构件上点E相对点C及点E相对 点B的相对速度原理写出相对速度矢量方程式
由于点E的速度vE的大小与方向均未知,故必须借助于点 E
相对 C和点 E相对 B 的两个相对速度矢量方程式联立求解,这时 式中仅包含vEC和vEB的大小为未知而可以求解。
4.2.1 在同一构件上的点间的速度和加速度的求法
s mm
m
过点 b 作直线垂直于 EB 代
表vEB 的方向线,再过点C作直
04相对运动 (相对运动与惯性参照系)

车速u
V 雨 速
300
雨 迹 V’
u tg30 v 10 v 3 10 km / h 0 tg30
0
u sin 30 v'
0
u v' 2 10 20 km/ h 0 sin 30
7
例3、某人骑自行车以速率 1 m/s 向北行驶,感觉风 从正西吹来,将速率增加到 2.73m/s 时,则感觉风从 北偏西 300 的方向吹来。求风速和风向。
1 2 带入: r gt j R uti 2 1 2 得: r ' R r uti gt j 2
x ut 再由 1 2 y 2 gt
r R r'
得
gx y 2 2u
2
6
例2、一列火车以10Km/h的速率向东行驶时,相对于地 面竖直下落的雨滴在列车的窗子上形成的雨迹偏离窗上 竖直方向30o,求雨滴相对于地面的速率和雨滴相对于火 车的速率。 解: v u v '
O’相对于s的原点O 位矢 R
(1)
2
或文字表述:绝对位矢=牵连位矢+相对位矢
位置矢量间的关系
经过△t后,位移为 对1式两端求导 对3式两端求导
r R r' r R r ' v u v' du a a' dt
(1) (2) (3) (4)
解: V’ u
人 速 风 速
v u v'
由条件 1 知风速向北的分量为 1m/s 由条件 2 知风速向东的分量为 1m/s, 风速为:
v 1 1 1.414 m / s
V 雨 速
300
雨 迹 V’
u tg30 v 10 v 3 10 km / h 0 tg30
0
u sin 30 v'
0
u v' 2 10 20 km/ h 0 sin 30
7
例3、某人骑自行车以速率 1 m/s 向北行驶,感觉风 从正西吹来,将速率增加到 2.73m/s 时,则感觉风从 北偏西 300 的方向吹来。求风速和风向。
1 2 带入: r gt j R uti 2 1 2 得: r ' R r uti gt j 2
x ut 再由 1 2 y 2 gt
r R r'
得
gx y 2 2u
2
6
例2、一列火车以10Km/h的速率向东行驶时,相对于地 面竖直下落的雨滴在列车的窗子上形成的雨迹偏离窗上 竖直方向30o,求雨滴相对于地面的速率和雨滴相对于火 车的速率。 解: v u v '
O’相对于s的原点O 位矢 R
(1)
2
或文字表述:绝对位矢=牵连位矢+相对位矢
位置矢量间的关系
经过△t后,位移为 对1式两端求导 对3式两端求导
r R r' r R r ' v u v' du a a' dt
(1) (2) (3) (4)
解: V’ u
人 速 风 速
v u v'
由条件 1 知风速向北的分量为 1m/s 由条件 2 知风速向东的分量为 1m/s, 风速为:
v 1 1 1.414 m / s
大学物理精品课件1.3 相对运动

第一章 运动的描述 1.4 相对运动 例1、某人骑自行车以5m.s-1的速度向北行 驶,觉得有西北风(西偏北45。)吹来, 其大小为10m.s-1,求实际风速 y
V人对地
x V风对地 V风对人
1.4 相对运动
第一章 运动的描述
例 一人能在静水中以1.1m•s-1的速率划船前进,今欲 横渡一宽度为4000m、水流速度为0.55m•s-1的大河。 (1) 若要达到河正对岸的一点,应如何确定划行方向? 需要多少时间? (2) 如希望用最短的时间过河,应如何确定划行方 向?船到达对岸的位置在何处? B
1.4 相对运动
第一章 运动的描述
一、经典力学平动坐标系变换
考虑两个参考系中的坐标 系S和S‘ (Oxyz和O'x'y'z')
矢量关系:
r r R
若两个参考系只有相对平动,有速度关系:
dr dr dR v v u v dt dt dt
d r dt
2 2
加速度关系
d r dt
2
2
d R
2
dt 2
a a A
1.4 相对运动
第一章 运动的描述
速度、加速度关系的角标表示法
rPA rPB rBA
a PA a PB a BA
v PA v PB v BA
4199( s )
70(min)
A
0.55m•s-1
1.4 相对运动
(2)
第一章 运动的描述
分析(1)的速度合成图
需要的时间最短,vAK在垂直于河岸的方向 v A K 投影量最大,= 90°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
方向 ? 图中已 E ® B ^ EB 图中已 E ® C ^ EB 大小 ? 作出 LECw22 LEBa2 作出 LECw22 LEBa2
p '─ 加速度极点。 ma = aC / p'b' (m / s2 ) / mm
p 'c
B
e'
BE ' n 'BE
A 1
aE = p'e' × ma
E C
C = B + CB
4)根据矢量方程式按适当比例尺作矢量多边形 5)从封闭的矢量多边形中求出运动参数的大小或 方向
谢谢!
2
F
Ñb'c'e' 称为构件BCE加速度影像
(6)加速度多边形的特点:
●从点p′出发的向量代表绝对加速度, 例如p'c' ® aC
●不经过点p′的向量代表相对加速度,
例如b'c' ® aCB
●已知同一构件上两点的加速度,用影像原理可
求出该构件其它各点的加速度。
p 'c
E
n 'c
B
C
1
2
3
c' e' b'
A
D
F
3. 应用点的运动合成定理求解
D
2B
1 1
A
3
C
E
【解】 1.速度分析
(1)求已知速度 B2 1lAB
D
2B
1 1
A
3
C
E
D (2)列方程
B3 B2 B3B2
2B
方向 BC AB //DE 1 1
大小 ?
√
?
A
3
C
E
(3)画速度图
(4)结果
b3 p
b1、b2
2.加速度分析 (1)求已知加速度
F =pf·
2.2 加速度求解
已知:各杆杆长
1
求:aC aE α2 α3
2E
B 1
1
A
C
2 3 3
D
F
(1)加速度分析
已知加速度
aB = aBn = w12lAB
aCn = w32 lCD
aCnB = w22lBC
A
B
1
E
2
C
3
D F
(2)列方程
aCn + aCt = +atB + aBn + aCnB + aCt B
1 1
C 3 A E
小结
1)从原动件开始,根据机构的组成顺序,按杆组 由近及远地进行运动分析 2)先分析各个杆组本身所包含的基本运动副的点 或其他点的运动,再分析该杆组中非基本运动副的 点或其他点的运动 根据杆组中作平面复杂运动的构件(连杆)参与 组成的两个基本运动副的类型,决定采用基点法 或重合点法
D F
(5)加速度影像原理:
●原理:同一构件在机构简图上的图形,与加速度 图上相应图形相似;且字母的排列顺序一致。
●应用:已知同一构件上两点的加速度,用影像原 理可求出该构件其它各点的加速度。
●加速度极点p′:是各构件加速度为零的点的影像。
p 'c
E
n 'c
B
C
c' e'
Ñb'c'e' ~ ÑBCE1
该平面运动刚体的绝对运动可视为随基点B的牵连
平移及绕基点作相对转动的合成。 CB
C
C = B + CB CB = 1lBC
C
B
aB
aC = aB + aCB D
= 1
a = α1
B
α1 1 B
aB
1.2 两平面运动刚体上重合点之间的运动关系
B2 点 的 绝 对 运 动 可 视 为
随 B1 点 作 牵 连 运 动 与 B2
方向 CD AB ^ CB
大小 ? 1lBC ?
C
3
D
F
选择适当的速度比例尺
c
2
E
B
B
A 1
C
3
D
F
p
C =pc· b 3= C /lCD = pc · /lCD
CB =bc· 2= CB /lBC = bc · /lBC
b) E
E = B + EB
2
E
B
方向 大小
? AB
? 1lBC 2lBE A
b3 p
b1、b2
D
方向:B3B2沿3方向转90°
2B
1 1
A
3
C
E
(2)列方程
方向 B→C ⊥BC B→A // DE
大小 √
?
√
?
√
(3)画加速度图
a aB2 / p'b2'
p’
b3’
D
2
1 1
B
A k’
3C E
(4)结果 p’
b3’
D
2
1 1
B
A k’
3C E
如果是如下图的机构呢?
D
2B
1.基本原理
平面运动刚体上一个点的绝对运动,是牵连 运动和相对运动的和。
a = e + r
aa = ae + ar
牵连运动为平动
aa = ae + ar + ac 牵连运动为转动
、α —— 在任一瞬时,图形绕其平面内任何
点转动的角速度及角加速度都相同,称为平面图
形的角速度及角加速度。
1.1 同一平面运动构件上两点之间运动关系
a)同一平面运动构件上两点之间运动关系
刚体的平面运动 = 随基点的平动 + 绕基点的转动 基点法,同一构件的两点
b)两平面运动刚体上重合点之间的运动关系
点的复合运动 = 动系(重合点)的牵连运动 + 相对(该重合点的)运动
重合点法,两构件重合点
3)列出机构中运动参数待求点与运动参数已知点 之间的运动分析矢量方程式
点 相 对 于 B1 点 的 相 对 移
2
动的合成。
a21
21
1
1
α1
B1 B2
2.应用刚体运动合成定理求解
2.1 速度求解
【例1】已知:各
B
杆杆长,1
求:C E
A 1
2 3
E
2
C
3
D F
【解】
2
E
(1)选择长度比例尺1
做机构运动简图
B
(2)速度分析:
B
a) C 3 2
A
1
B=1lBC
C = B + CB
方向 E ® B ^ CD B ® A ^ EB B ® C LCD
大小 LCDw32 ?
LABw22
0
LCBw22
?
(3)画加速度图
p '─ 加速度极点。
ma = aC / p'b'
(m / s2) / mm
p 'c
c'
nC' B
n 'c
b'
B
A 1
E C
D F
aCn + aCt = aB + aCnB + aCt B
(4)结果
aC = p'c' × ma
aCt = nC' c' × ma
aCt B = nC' Bc' × ma
aCB = b'c' × ma a3 = aCt / lCD
a2 = aCt B / lBC
p 'c
E
c'
n 'c
b'
B
1
2
A
C 3
D
F
同理E点的加速度可联立方程求解,即
aE = aB + atEB + aEnB = aC + aEnC + aEtC
B
1
E = C + EC
方向 大小
? CD
? 3lCD 2lCE
C
3
D F
c
2
E
p e
B
C
3
B
A
1
D
b
F
E =pe·
c
2
E
p e
B
C
3
B
A
1
D
b
F
影像法
已知一个构件上两点的速度,求该构件上第三点 的速度。
速度多边形中速度极点p点是所有速度为零点的
影像
p f
c
2
E
B
C
3
e
B
bA
1
D
F
CD:DF = cp:pf
p '─ 加速度极点。 ma = aC / p'b' (m / s2 ) / mm
p 'c
B
e'
BE ' n 'BE
A 1
aE = p'e' × ma
E C
C = B + CB
4)根据矢量方程式按适当比例尺作矢量多边形 5)从封闭的矢量多边形中求出运动参数的大小或 方向
谢谢!
2
F
Ñb'c'e' 称为构件BCE加速度影像
(6)加速度多边形的特点:
●从点p′出发的向量代表绝对加速度, 例如p'c' ® aC
●不经过点p′的向量代表相对加速度,
例如b'c' ® aCB
●已知同一构件上两点的加速度,用影像原理可
求出该构件其它各点的加速度。
p 'c
E
n 'c
B
C
1
2
3
c' e' b'
A
D
F
3. 应用点的运动合成定理求解
D
2B
1 1
A
3
C
E
【解】 1.速度分析
(1)求已知速度 B2 1lAB
D
2B
1 1
A
3
C
E
D (2)列方程
B3 B2 B3B2
2B
方向 BC AB //DE 1 1
大小 ?
√
?
A
3
C
E
(3)画速度图
(4)结果
b3 p
b1、b2
2.加速度分析 (1)求已知加速度
F =pf·
2.2 加速度求解
已知:各杆杆长
1
求:aC aE α2 α3
2E
B 1
1
A
C
2 3 3
D
F
(1)加速度分析
已知加速度
aB = aBn = w12lAB
aCn = w32 lCD
aCnB = w22lBC
A
B
1
E
2
C
3
D F
(2)列方程
aCn + aCt = +atB + aBn + aCnB + aCt B
1 1
C 3 A E
小结
1)从原动件开始,根据机构的组成顺序,按杆组 由近及远地进行运动分析 2)先分析各个杆组本身所包含的基本运动副的点 或其他点的运动,再分析该杆组中非基本运动副的 点或其他点的运动 根据杆组中作平面复杂运动的构件(连杆)参与 组成的两个基本运动副的类型,决定采用基点法 或重合点法
D F
(5)加速度影像原理:
●原理:同一构件在机构简图上的图形,与加速度 图上相应图形相似;且字母的排列顺序一致。
●应用:已知同一构件上两点的加速度,用影像原 理可求出该构件其它各点的加速度。
●加速度极点p′:是各构件加速度为零的点的影像。
p 'c
E
n 'c
B
C
c' e'
Ñb'c'e' ~ ÑBCE1
该平面运动刚体的绝对运动可视为随基点B的牵连
平移及绕基点作相对转动的合成。 CB
C
C = B + CB CB = 1lBC
C
B
aB
aC = aB + aCB D
= 1
a = α1
B
α1 1 B
aB
1.2 两平面运动刚体上重合点之间的运动关系
B2 点 的 绝 对 运 动 可 视 为
随 B1 点 作 牵 连 运 动 与 B2
方向 CD AB ^ CB
大小 ? 1lBC ?
C
3
D
F
选择适当的速度比例尺
c
2
E
B
B
A 1
C
3
D
F
p
C =pc· b 3= C /lCD = pc · /lCD
CB =bc· 2= CB /lBC = bc · /lBC
b) E
E = B + EB
2
E
B
方向 大小
? AB
? 1lBC 2lBE A
b3 p
b1、b2
D
方向:B3B2沿3方向转90°
2B
1 1
A
3
C
E
(2)列方程
方向 B→C ⊥BC B→A // DE
大小 √
?
√
?
√
(3)画加速度图
a aB2 / p'b2'
p’
b3’
D
2
1 1
B
A k’
3C E
(4)结果 p’
b3’
D
2
1 1
B
A k’
3C E
如果是如下图的机构呢?
D
2B
1.基本原理
平面运动刚体上一个点的绝对运动,是牵连 运动和相对运动的和。
a = e + r
aa = ae + ar
牵连运动为平动
aa = ae + ar + ac 牵连运动为转动
、α —— 在任一瞬时,图形绕其平面内任何
点转动的角速度及角加速度都相同,称为平面图
形的角速度及角加速度。
1.1 同一平面运动构件上两点之间运动关系
a)同一平面运动构件上两点之间运动关系
刚体的平面运动 = 随基点的平动 + 绕基点的转动 基点法,同一构件的两点
b)两平面运动刚体上重合点之间的运动关系
点的复合运动 = 动系(重合点)的牵连运动 + 相对(该重合点的)运动
重合点法,两构件重合点
3)列出机构中运动参数待求点与运动参数已知点 之间的运动分析矢量方程式
点 相 对 于 B1 点 的 相 对 移
2
动的合成。
a21
21
1
1
α1
B1 B2
2.应用刚体运动合成定理求解
2.1 速度求解
【例1】已知:各
B
杆杆长,1
求:C E
A 1
2 3
E
2
C
3
D F
【解】
2
E
(1)选择长度比例尺1
做机构运动简图
B
(2)速度分析:
B
a) C 3 2
A
1
B=1lBC
C = B + CB
方向 E ® B ^ CD B ® A ^ EB B ® C LCD
大小 LCDw32 ?
LABw22
0
LCBw22
?
(3)画加速度图
p '─ 加速度极点。
ma = aC / p'b'
(m / s2) / mm
p 'c
c'
nC' B
n 'c
b'
B
A 1
E C
D F
aCn + aCt = aB + aCnB + aCt B
(4)结果
aC = p'c' × ma
aCt = nC' c' × ma
aCt B = nC' Bc' × ma
aCB = b'c' × ma a3 = aCt / lCD
a2 = aCt B / lBC
p 'c
E
c'
n 'c
b'
B
1
2
A
C 3
D
F
同理E点的加速度可联立方程求解,即
aE = aB + atEB + aEnB = aC + aEnC + aEtC
B
1
E = C + EC
方向 大小
? CD
? 3lCD 2lCE
C
3
D F
c
2
E
p e
B
C
3
B
A
1
D
b
F
E =pe·
c
2
E
p e
B
C
3
B
A
1
D
b
F
影像法
已知一个构件上两点的速度,求该构件上第三点 的速度。
速度多边形中速度极点p点是所有速度为零点的
影像
p f
c
2
E
B
C
3
e
B
bA
1
D
F
CD:DF = cp:pf
