数学建模台阶问题
台阶和平台计算讲解

台阶和平台计算讲解首先,我们来介绍一下台阶的计算方法。
在一般情况下,台阶是由一级级的梯形或矩形构成的,每一级的高度和宽度可能是不一样的。
如果台阶的高度和宽度相同,那么计算起来会非常简单。
我们可以用以下的公式来计算台阶的总数:总台阶数=总高度/单级台阶高度例如,如果我们有一个高度为100米的台阶,每级台阶高度为1米,那么总台阶数就是100。
这意味着我们需要上100级台阶才能到达100米的高度。
然而,在实际情况中,台阶的高度和宽度可能是不一致的。
在这种情况下,我们需要对每一级台阶的高度和宽度进行单独的计算,并且将每一级的高度累加起来,直到总高度。
接下来是平台的计算方法。
在一般情况下,平台是一个较大的平坦区域,可以供人们休息、活动或进行其他活动。
平台的计算方法与台阶有所不同。
如果我们要计算平台的面积,我们只需要知道平台的长度和宽度即可。
平台面积=平台长度x平台宽度例如,如果平台的长度为10米,宽度为5米,那么平台的面积就是50平方米。
这意味着平台的整个表面积是50平方米。
另外,如果我们要计算平台上物体的体积,我们需要知道平台的长度、宽度和高度。
平台体积=平台长度x平台宽度x平台高度例如,如果平台的长度为10米,宽度为5米,高度为2米,那么平台的体积就是100立方米。
这意味着平台的整个体积是100立方米。
在实际情况中,台阶和平台的计算可能更为复杂。
例如,如果台阶是曲线形状的,我们可能需要使用积分等数学方法来计算。
如果平台是不规则形状的,我们可能需要将其划分为多个较小的形状,然后计算每个形状的面积或体积,并将它们相加。
计算台阶的公式

计算台阶的公式
【实用版】
目录
1.计算台阶的公式简介
2.台阶公式的推导过程
3.台阶公式的应用实例
4.结论
正文
1.计算台阶的公式简介
计算台阶的公式,也被称为楼梯的爬升高度公式,是一个在几何学和物理学中经常用到的公式。
它可以用来计算一个多级台阶的总高度,或者计算每一级台阶的高度。
这个公式的推导过程相对简单,应用广泛,可以帮助人们在设计楼梯或者计算行走过程中的能量消耗时提供便利。
2.台阶公式的推导过程
假设我们要计算一个 n 级台阶的总高度,每一级台阶的高度为 h,我们可以通过以下步骤推导出计算公式:
首先,我们可以想象将这 n 级台阶平铺开来,形成一个直角三角形,其中直角边的长度为 h,斜边的长度为 nh(n 为台阶数)。
根据勾股定理,我们有:
h = h + (n-1)h
化简后,我们得到:
h = nh - h + h
2h = h
h = 2h
h = √2 * h
因此,每一级台阶的高度 h 等于总高度除以根号 2,即:
h = 总高度 / √2
3.台阶公式的应用实例
例如,如果我们要设计一个高度为 10 米的楼梯,我们需要计算出每一级台阶的高度。
假设我们希望每一级台阶的高度相等,我们可以通过台阶公式计算出每一级台阶的高度:
h = 10 / √2 ≈ 7.07 米
因此,我们需要设计大约 14 级台阶(10 / 0.707 ≈ 14)才能达到10 米的总高度。
4.结论
计算台阶的公式是一个简单而实用的公式,可以帮助我们在设计楼梯或者计算行走过程中的能量消耗时提供便利。
递归台阶问题的数学原理

递归台阶问题的数学原理Initially, let's explore the mathematical principles behind the recursive staircase problem. This classic problem involves finding the number of ways a person can climb a staircase with N steps, given that they can take either 1 or 2 steps at a time. This scenario lends itself to a recursive solution, where we break down the problem into smaller subproblems and gradually build up the solution. The key insight here is to recognize that the number of ways to climb N steps is equal to the sum of the number of ways to climb N-1 steps and N-2 steps. This forms the basis for the recursive formula f(N) = f(N-1) + f(N-2), with base cases f(1) = 1 and f(2) = 2.首先,让我们探究递归台阶问题背后的数学原理。
这个经典问题涉及一个人在N个台阶上的爬行方式数目,假设他们每次可以走1步或2步。
这种情况适合用递归方法解决,我们将问题分解为更小的子问题,并逐渐构建解决方案。
关键的见解在于认识到爬N个台阶的方式数目等于爬N-1个和N-2个台阶的方式数目之和。
数学阶梯问题

数学阶梯问题阶梯问题是一种基础的数学难题,需要我们掌握基本的数学知识,比如等差数列,算术平均数,几何平均数等等。
在此非常荣幸能够为大家讲解阶梯问题的解决方法及其实际应用。
首先,什么是阶梯问题呢?在数学上,阶梯问题是指一组数排列成阶梯形式,其中每个数与它的相邻数的差都相同。
例如,一个简单的阶梯数列可能是1,5,9,13,17……,其中每一对相邻数的差都是4。
而解决这种问题的关键在于找到每个数之间的规律性。
接下来我们来探讨如何解决阶梯问题。
首先,我们需要确定差值,即相邻两项之间的差值。
这个差值被称为公差,通常用字母d表示。
对于任意的阶梯数列,公差的数值都是相等的。
例如,对于上述的例子,公差是4。
我们可以通过相邻两项的差值来计算公差,即:d = a(n) - a(n-1)其中a(n)表示数列中的第n项,a(n-1)表示数列中的第n-1项,d 表示公差。
有了公差,我们就可以利用以下公式推导出阶梯数列中任意一项的数值:a(n) = a(1) + (n-1)*d其中a(n)表示数列中的第n项,a(1)表示数列中的第一项,n表示数列中第n项的位置,d表示公差。
通过这个公式,我们可以计算出阶梯数列中任意一项的值。
这对于解决阶梯问题非常有用。
比如说,如果我们知道数列的首项和公差,那么我们就可以轻松地计算任意项的数值。
举例来说,假设我们有一个阶梯数列:3,7,11,15,19……,公差是4。
我们想计算第8项的数值。
根据上面的公式,我们可以得出:a(8) = a(1) + (8-1)*da(8) = 3 + 7*4a(8) = 31因此,第8项的数值是31。
这个解法非常简单,只需要将两个已知的量带入公式进行计算即可。
除了计算每个数值之外,阶梯问题还可以用于解决其他类型的问题。
比如,我们可以根据阶梯数列求出该数列的平均值。
这个平均值通常指的是算术平均数或者几何平均数。
算术平均数是数列中所有数值的总和再除以整个数列的项数。
数学建模基础问题梯子长度问题(含程序和数据)

梯子最短长度问题的优化模型摘要本文建立了一个关于当存在紧靠墙壁的长方体障碍物时,如何确定靠墙梯子最短长度问题的优化模型。
本文首先将梯子问题抽象成一个几何问题:在xy平面上,过定点(2,3)的直线l被x轴、y轴所截的线段最小长度。
即:直线l以点()3,2为轴,从与x轴平行顺时针旋转到与x轴垂直的过程中,被x轴、y轴所截的线段最小长度。
模型I,模型II分别应用直角三角形边角关系原理和相似三角形相关边成比例原理,以直线l与x轴夹角和直线l与x轴交点与点()0,2的距离为变量建立了求单变量最小化的数学模型。
应用牛顿迭代法中的三等分点搜索法对模型I,模型II进行求解,并同时对模型I,模型II的函数是单峰函数给出了证明。
模型I和模型II的求解结果是:7的梯子会碰坏温室顶棚;当梯子与地面的夹角为0.8528rad,梯子在地面的长度为m落脚点与温室水平直线距离为2.6207m时,所需梯子长度最短,最短长度7.0235m。
模型III应用同线向量斜率原理,以直线l与x轴、y轴交点距原点距离为变量,建立了一个二元变量有约束非线性最优化模型。
应用序列二次规划法()SQT对模型III进行求解:当梯子在地面的落脚点距离楼房的水平直线距离为4.6207m,梯子靠墙处与温室地面的直线距离为6.5162m时,所需梯子长度最短,最短长度为7.0235m。
三个模型的求解结果是一致的且当梯子取最短长度时,各变量的取值互不矛盾。
关键字:单变量最小化二元变量有约束非线性最优化牛顿迭代法一、问题的重述与分析在一栋楼的后面有一个很大的花园,在花园的边上有一个紧靠着楼房的温室,温室伸入花园2米,高3米,在温室的正上方是楼房的窗台,现有一架7米的梯子,我们能否将这架梯子的一端放在花园中,另一端靠在楼房的墙上,使得梯子不碰坏温室棚?若否,问题梯子至少应为多长?我们所关心的是:如何使梯子长度最小,以何种函数形式表示出梯子长度L。
从左视图观察我们可以把问题抽象为一个几何问题(如图1):在xy平面上,过定点(2,3)的直线l被x轴、y轴所截的线段最小长度。
数学建模阶梯问题

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): A 我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):参赛队员 (打印并签名) :1.2.3.指导教师或指导教师组负责人 (打印并签名):日期: 2010 年 9 月 13 日赛区评阅编号(由.赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):阶梯电价问题摘要阶梯问题共分为三问:问题一:保证80%的居民家庭电价平稳。
对北京市进行研究,通过查找相关信息现在居民用电即为2760度,而当阶梯电价改革后,草案一即以80%的居民用电量为第一档的标准电价,草案二的用电标准高于草案一第一档的用电量。
所以,能够保证80%的居民用电平衡。
问题二:评判一个好电价。
我们用五个因素进行论证:一.与现在相比,阶梯电价对居民的用电支出影响大小。
以北京市的阶梯电价进行研究,我们通过对现在的电价标准与阶梯电价进行比较得出表格。
利用excel画出饼图。
同时我们利用一家庭进行举例说明,得出结论。
二.阶梯电价与地区经济发展的关系。
通过利用GDP,恩格尔系数作为经济水平的指标。
利用EXCEL画出电量与两指标和年份的曲线图,同时利用SPSS的Bivariate过程用电量和两个指标进行相关性检验,得出阶梯电价与地区经济发展水平成正相关。
数学阶梯问题

数学阶梯问题标题:数学阶梯问题摘要:数学阶梯问题是一种常见的数学谜题,通常描述为一条阶梯,其高度逐渐减小,每一级的高度相等。
问题的目标是找出一条路径,使得从第一级到第十级的所有级都可以通过这条路径到达。
本文将介绍一些常见的解法和数学原理。
正文:数学阶梯问题是一种常见的数学谜题,通常描述为一条阶梯,其高度逐渐减小,每一级的高度相等。
问题的目标是找出一条路径,使得从第一级到第十级的所有级都可以通过这条路径到达。
本文将介绍一些常见的解法和数学原理。
一种常见的解法是使用代数方法。
我们可以将问题转化为一个方程,即 $10x=h$,其中 $x$ 表示到达第十级所需的步数,$h$ 表示阶梯的总高度。
我们的目标是找到一个 $x$ 的值,使得等式成立。
我们可以通过解这个方程来求得 $x$ 的值,然后根据这个值来计算到达每一级的步数。
另一种常见的解法是使用图形方法。
我们可以将阶梯问题看作是一个二维图形的问题,即一个带有高度信息的二维平面。
我们可以绘制这个平面上的所有的点,然后找到一条路径,使得这条路径穿过所有的点,并且路径的长度最小。
这种方法通常可以使用 Dijkstra 算法来实现。
数学阶梯问题还可以使用一些数学原理来解决。
例如,我们可以使用斐波那契数列来计算到达每一级的步数。
另外,我们可以通过分析阶梯的问题,来介绍一些基本的图论知识和算法,例如最小生成树和最短路径算法等。
拓展:除了以上介绍的解法和数学原理外,还有许多其他的解法和数学原理可以用来解决数学阶梯问题。
例如,我们可以通过构建一个二次函数,来求解到达每一级的步数。
另外,我们还可以使用分治算法来解决这个问题,即将问题分成若干个子问题,然后分别解决这些子问题,最终得到整个问题的解。
数学阶梯问题还可以应用在许多其他的领域,例如程序设计、网络优化和物理模拟等。
因此,数学阶梯问题不仅是一种有趣的数学谜题,也是一种有用的数学工具。
台阶建模操作手册
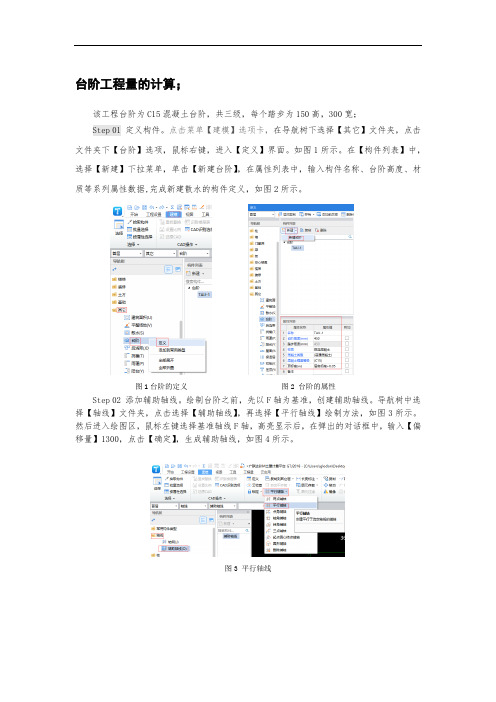
台阶工程量的计算;
该工程台阶为C15混凝土台阶,共三级,每个踏步为150高,300宽;
Step 01 定义构件。
点击菜单【建模】选项卡,在导航树下选择【其它】文件夹,点击文件夹下【台阶】选项,鼠标右键,进入【定义】界面。
如图1所示。
在【构件列表】中,选择【新建】下拉菜单,单击【新建台阶】,在属性列表中,输入构件名称、台阶高度、材质等系列属性数据,完成新建散水的构件定义,如图2所示。
图1台阶的定义 图2 台阶的属性 Step 02 添加辅助轴线。
绘制台阶之前,先以F 轴为基准,创建辅助轴线。
导航树中选择【轴线】文件夹,点击选择【辅助轴线】,再选择【平行轴线】绘制方法,如图3所示。
然后进入绘图区,鼠标左键选择基准轴线F 轴,高亮显示后,在弹出的对话框中,输入【偏移量】1300,点击【确定】,生成辅助轴线,如图4所示。
图3 平行轴线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
台阶设计中的建模分析一.问题的提出台阶,楼梯是我们日常生活中常见的,天天行走的建筑结构,良好的台阶设计不仅可以节省上楼时间,也可最大限度的减少体力消耗。
然而,不合理的设计会使人们上楼时既费时又费力,甚至还会发生危险。
所以我们不禁要问,怎样设计台阶长度宽度比才能达到最优呢?二.问题的分析符号表示:M 人体质量g 重力加速度l 人的小腿长度v 人的正常行走速度F 上楼过程中腿部力量H 楼梯总体高度h 台阶高度r 台阶长度P 人体登上高度H的楼梯时最舒适的输出功率C 人的脚长模型的假设:1,人每走一步脚的前端接触到B点。
2,人的所有重量可以看成质点并集中在O(与集中在N是等价的),其他部位没有重量3,每一步迈出同样的距离(台阶宽),并且连续前进。
4,人体上升的力量全部来自支撑腿的力F,F与h有关且在h取定的情况下F 大小不变且始终保持ON方向。
5,上台阶过程做功只在DN段,并且人总是以所谓最舒适的感觉(P恒定)上楼。
6,台阶宽度大于等于脚长运动的分解:可以将登上台阶看为两个运动过程1.(由M到N)人若想登上台阶,向前倾斜重心将是第一步,毕竟人是前进的。
要在D点发力,将M点移动到N点将是合理的。
而且此过程与人在平地行走时的状态非常接近(这里将它们等同看待,速度也为v,v的方向近似水平)。
为了简化计算,可以令此段做功充分小从而可以忽略(因为我们的主要矛盾是上楼,此段做功的变化也是相当于平地上走5米与10米的区别,而这种差别在正常人看来是微乎其微的)2.(N点竖直向上达到直立并回到初始状态)在此过程中所做的功为F的贡献(这里腿部的屈申很类似课堂上铅球投掷模型中球的出手过程,因为当时的主要矛盾为球的初速度,所以可以将其近似看做线性关系,然而此时的重点是这个屈申过程,因此假设与模型机理自然不同)。
随后根据生物课所学知识,可以知道,人腿的运动都是靠肌肉细胞的伸缩变化产生伸缩力的(伸缩方向只能沿腿的方向),因此这里可以将所有肌肉的发力等效看为一个力,方向总是沿着腿的方向,大小恒定(实际上F要随着角度的变化而变化,为了简化问题可以将其设为恒定)。
由于考虑到人在2过程上升时做的功实际为非保守力所做功(并不是w=mgh),一个很简单的直观,就是同样登上两米的高度我们分10步与分2步腿部做功一定不同。
造成这种差异的根源在于腿的承重能力与发力方向角度的大小(也就是说台阶越高,我们所做的额外功越多)。
所以要去用数学的观点度量所谓“腿部做功”这个概念,假设4将是必要的。
其次我们要去度量所谓“舒适”与“疲劳”的概念。
通常,在短距离内造成我们疲劳的主要原因实际为腿的运动强度过高,即功率P过大。
这就使我们度量“舒适”成为可能。
三.模型的建立由假设台阶总数即为(有分数出现时如则可近似看为取每一小段时间的倍。
这种误差是可以被忽略的)设那么过程一的时间为且满足关系代入可得过程一的总时间为过程二的总时间为其中为h,l,F,p的函数由于我们假设了M,N点有近似相同的高度。
那么是与x 无关的函数。
若令总时间最小,一定要求x最小。
所以可得。
我们得到结论台阶宽度应设计为近似脚长的宽度。
并据此讨论h的变化由于我们先假设F大小恒定。
若F能带动人体上移,必要求Fy至少等于mg,那么在最省力的情况下,我们取 .此时我们已将F分解。
因此N点运动到S点过程中要求F所做的功只需对Fx Fy分别求功即可。
当台阶高为h时Fy方向上的做功:设NNm的长度为变量m,当Nm由N运动到S时。
M由0→h变化。
计算得用微元分析,当m变化△m时。
其中S(△m)为Om竖制直方向上运动距离。
对m积分2,当台阶高为h时Fx方向上的做功:微元分析,增加△m,我们得到两边同除△m,并令△m→0。
因此其中S(m)为PmOm的长度。
对m积分由于我们假定的F为h的函数(h取定时大小恒定)。
所以取综上我们得到上楼总时间下面我们来由此式确定T的最小值,将参数P待定。
以上计算都可交给maple完成。
计算过程如下⌝ t:=m->sqrt(0.47^2-((2*0.47-h+m)/2)^2);⌝ diff(t(m),m);⌝e:=m->-sqrt(0.47^2-((2*0.47-h+m)/2)^2)*1/2/(.2209-(.4700000000-1/2*h+1/2* m)^2)^(1/2)*(-.4700000000+1/2*h-1/2*m)/0.47;⌝ int(e(m),m=0..h);⌝ wy:=h->(2*0.47*h-h^2/2)/(4*0.47);⌝ F:=h->(2*0.47*53*9.8)/(2*0.47-h);⌝ wx:=h->> .4999999999*h-.2659574468*h^2由此,我们发现,Wx,Wy做功基本是一样的。
所以最终,总时间表示为>f:=h->H*(1.2*(2*0.47*53*9.8)/(2*0.47-h)*(.4999999999*h-.2659574468*h^2+. 5*h-.2659574468*h^2)+0.26*P)/(h*P*1.2);而且根据如上结果我们可以观察出人腿做功(Wx(h)+Wy(h))与实际有效功Mgh 之间的关系随h变化的过程图。
其中红线为人腿做的总功,黄线为有效功Mgh。
这种变化也是符合我们感觉的,例如,随h的增大,我们迈上台阶会感到越发的费力,h越大这种变化越明显。
随后进行几组实验来确定P的近似取值。
分别选取不同的楼梯,从下走到上按一般速率(不感到劳累),并记录下经过的时间。
并根据假设与上式分别求得P,得到下表次数台阶数n 台阶高度h 总高度H 时间t 功率P1 20 0.17 3.4 18.11 142.342 18 0.15 2.7 14.83 140.493 25 0.14 3.5 18.92 133.094 16 0.18 2.88 15.06 144.315 20 0.16 3.2 16.87 146.186 22 0.17 3.74 18.87 152.947 20 0.15 3 15.79 148.928 18 0.16 2.88 14.91 149.799 16 0.17 2.72 15.10 134.85经实践证明,P并没有随总高度H以及h的变化而发生太大变化,说明我们之前的假设是基本合乎情理的。
这里取9次测量的平均值作为P,所以我们得到P=143.66.我们在第一种情况下对T进行分析。
取H=3.4>f:=h->3.4*(1.2*(2*0.47*53*9.8)/(2*0.47-h)*(.4999999999*h-.2659574468*h^2 +.5*h-.2659574468*h^2)+0.26*143.65)/(h*143.65*1.2);⌝ plot(f(h),h=0.1..0.5);由图象,我们观察到,确实存在这样一个h使得总时间最少,也就是说任意给出某h下上楼的时间,就可以算得在此情况此功率P下,时间最小时h的理想高度。
上图中,从0.19到0.24米间减少的时间在0.2秒左右,而这种时间的优化由于太小(0.2秒)以致于我们可以不去考虑(可以近似看为不变)。
而时间迅速减少的阶段在0.1到0.19段。
那么为了使腿部用力尽量的小,我们不妨将h定在0.19米。
随后我们要问,这种模型的可靠性如何,由于v P是粗略度量的,所以下面我们要对这两个参数进行灵敏度分析。
⌝ plot3d(f(h,v),h=0.1..0.5,v=1.1..1.3,axes=boxed);⌝ plot3d(f(h,p),h=0.1..0.5,p=140..154,axes=boxed);从三维图形可以观察出,模型还是比较可靠的。
这里没有用老师上课应用的灵敏分析方法是因为我只想直观的表现出解对参数的连续依赖程度。
仅仅用离散数据似乎是不直观的。
到这里为止,已经算得对于我来说,最佳的台阶高度应该为0.19米左右,也就是说,这个高度可以最充分而有效的利用我的正常功率,使上楼总时间最短,而不致超过限度而感到疲劳。
这里顺便说明一下下楼过程,人的下楼过程在短距离内完全可以近似看为腿部做0功并完全由重力做功的过程。
由于重力是保守力,那么下楼时间应该于h近似无关。
但是长时间下楼为何又使我们感到疲劳呢?原因也许是下楼时的缓冲用力。
毕竟人不同于木块和小球,过快的下降对腿部以及身体的冲击造成人的不适感,因此腿部总要做一些功使其缓慢下降,平稳着陆。
我在这里引入缓冲时间这一变量并且其中T为下楼实际总时间,L为台阶宽度,v为水平行走速度。
显然便为缓冲(延迟)时间总和。
对于大部分正常人,在短的距离下楼过程中,在h正常范围内(上文算得的范围内),都可近似看为0。
则我们只许讨论上楼的过程即可。
然而,是不是可以永远被忽略呢?答案显然是否定的。
例如当H很大时就是H与h的函数了(H的影响不可忽略),又如一些特殊人群老年人,残疾人等等便会相当大,这时下楼这一过程就要单独考虑了。
五.模型的检验由于这个以上数据的特殊性,便使模型过分特殊化了,毕竟台阶不是我一人走。
然而自己是个正常人,即使考虑到众多人参数的不确定性因素,变化也不会太大。
经调查发现,校园内各台阶都是在0.16到0.2米之间变动,最低为科技楼前台阶,最高为四食堂前台阶。
宽度都为近似脚的长度,说明模型的结论还是勉强可以的(虽不那么准确)。
这就相当于对模型做了一定程度的检验(因为台阶的高度可以根据实践进行适当调整,不适当的高度一定无法存在的,或是被改造,或是在下一次建设中改进)进一步,我们可以参考1999年6月1日起实施的《建筑设计规范GB50096-1999》的相关规定:“楼梯踏步宽度不应小于0.26m,踏步高度不应大于0.175m,坡度为33.94°,接近舒适性标准。
”而其中的0.26一定是脚长,0.175便是最佳高度。
(此结果也许是相关力学家与统计学家做出的结果,应该是比较权威的数据)误差分析:从上面的检验可以看出,计算的结果与实际确实有着差异,计算的h 偏大,造成这种偏差的原因我归结为如下几点(1) 人的体重差异(2) 身高以及腿长的差异(3) 人的脚长差异(4) 身体前倾的速度(这里取为行走速度,然而过程一,只是前倾过程,其速度一定要比行走速度大,可不易测量,因此误差一定不可避免)(5) F随腿的运动而变化的函数未精确知道(将涉及复杂的人体动力学,由于所学知识有限,为化繁为简,只好假设其大小恒定。
计算结果又无太大偏差,说明假设基本合理,但误差同样不可避免)(6) 人的正常功率的差异,例如:老年人与青壮年,专业运动员与普通人所能承受的运动量一定不同因此如果能够精确知道如上数据,有理由相信计算结果的误差会非常之小。
