初中数学竞赛专题选讲-三点共线
三点共线、线共点
MC 第三讲点共线、线共点在本小节中包括点共线、线共点的一般证明方法及梅涅劳斯定理、塞瓦定理 的应用。
1.点共线的证明点共线的通常证明方法是:通过邻补角关系证明三点共线:证明两点的连线 必过第三点;证明三点组成的三角形面积为零等。
力(心4)点共线可转化为三点 共线。
例1如图,设线段初的中点为G BFCG 。
乂作平行四边形67彻, 以M 和 伪为对角线作平行四边形力应D CGKE.求证:H. G &三点共线。
证连必;DG. HB 。
山题意,AD£EC£KG,知 平行四边形,于是恥%。
同 四边形肋弘是平行四边形, 互相平分。
而。
是曲中点, 故久G 〃三点共线。
例2如图所示,菱形個⑦中,ZJ=120° , ©0为△/!庞外接圆,〃为其上一 点,连接必交曲于£ 劝交3延长线于斤 求证:A E,尸三点共线。
CF _ CFMA ~CA~~CD乂因为AAMOBAC.所以△ AMC^^EAC.得MC AC AD证如图,连月G DF 、DE 。
因为弭在©0上, 则 Z&炉60° 二ZABUZACB, 有△如ezum 得四边形AKGD 是 样可证AK 邑HB 。
其对角线月S KH 线段胡过C 点,BF, P ,肋与 虑的延长线交于点III Q 作该圆的两条切线他和0;切点分 别为£ F 。
求证:P, E, F 三点共线。
证 如图。
连接尸@并在〃上取一点必使得B, C, 尸四点共圆,连QA 欣设厅与圆的另一交点为F ,并作%丄 PF,垂足为G 。
易如QE 二 QM ・ QKQC ・ QB ①APMOAABOAPDQ.从而G D, 0, %四点共圆,于是PM ・PgPC ・PD ②由①,②得PM ・ P3Q\I ・ PgPC ・ PD^QC ・ QB 、 艮卩PgQC • Q 陕PC ・PD.易知 PD ・ PUPE' ・ PF, 乂 QF 二QC ・ QB 、有PE'・ PHQF 二PD ・ PC+QC ・ AB=P©,即欣'・P &P Q-Q F 。
证明三点共线方法举要
222F E B O A DC证明三点共线方法举要四川省广元市宝轮中学 唐明友有些数学问题要求你证三点共线,或者过程中需要你证三点共线,不少同学觉得无从下手,茫然失措,有些同学甚至想当然地把这三点看成在一条直线上,显然有失严密性,造成解题不完整或失误。
本文介绍证明三点共线的若干种方法,希望对你有所帮助。
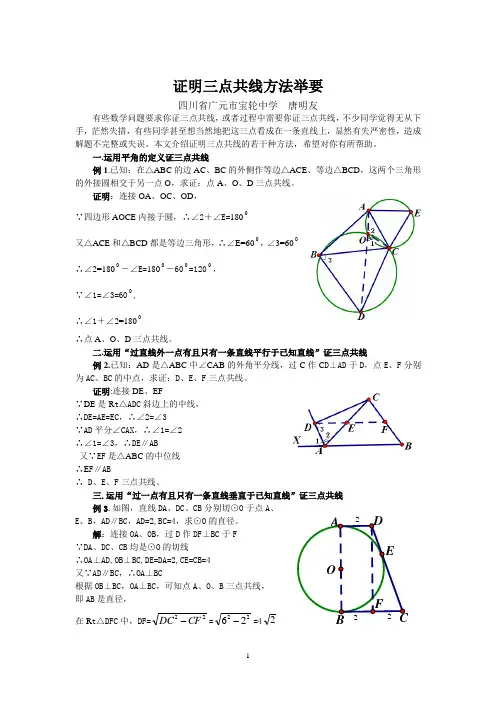
一.运用平角的定义证三点共线例1.已知:在△ABC 的边AC 、BC 的外侧作等边△ACE 、等边△BCD ,这两个三角形的外接圆相交于另一点O ,求证:点A 、O 、D 三点共线。
证明:连接OA 、OC 、OD ,∵四边形AOCE 内接于圆,∴∠2+∠E=1800又△ACE 和△BCD 都是等边三角形,∴∠E=600,∠3=600∴∠2=1800-∠E=1800-600=1200,∵∠1=∠3=600,∴∠1+∠2=1800∴点A 、O 、D 三点共线。
二.运用“过直线外一点有且只有一条直线平行于已知直线”证三点共线例2.已知:AD 是△ABC 中∠CAB 的外角平分线,过C 作C D ⊥AD 于D ,点E 、F 分别为AC 、BC 的中点,求证:D 、E 、F 三点共线。
证明:连接DE 、EF∵DE 是R t △ADC 斜边上的中线,∴DE=AE=EC ,∴∠2=∠3∵AD 平分∠CAX ,∴∠1=∠2∴∠1=∠3,∴DE ∥AB又∵EF 是△ABC 的中位线∴E F ∥AB∴ D 、E 、F 三点共线。
三.运用“过一点有且只有一条直线垂直于已知直线”证三点共线例3.如图,直线DA 、DC 、CB 分别切⊙O 于点A 、E 、B ,AD ∥BC ,AD=2,BC=4,求⊙O 的直径。
解:连接OA 、OB ,过D 作DF ⊥BC 于F∵DA 、DC 、CB 均是⊙O 的切线 ∴OA ⊥AD,OB ⊥BC,DE=DA=2,CE=CB=4 又∵AD ∥BC ,∴OA ⊥BC根据OB ⊥BC ,OA ⊥BC ,可知点A 、O 、B 三点共线,即AB 是直径, 在R t △DFC 中,DF=22CF DC -=2226-=42因此,⊙O 的直径AB 为42四.运用“连接其中的两点构成的两条线段重合”证三点共线例1.如图,在梯形ABCD 中,AD ∥BC ,AD 、BC 的中点分别是M 、N ,∠B +∠C=900,且BC>AD,求证:MN=21(BC -AD ) 证明:延长BA 、CD 相交与G ,分别连接GM 、GN ,由已知得△GBC 、△GAD 都是R t △,先在Rt △GAD 中,GM 是斜边上的中线,∴GM=GA=MD ,∴∠MGA =∠1同理可证∠NGB=∠B∵AD ∥BC ,∴∠1=∠B∴∠MGA=∠NGB ,即∠MGA 与∠NGB 是同一个角,GM 和GN 重合∴点G 、M 、N 三点共线由直角三角形斜边上中线的性质有:GM=21AD,GN=21BC 因此,MN=GN -GM=21(BC -AD )。
中考数学复习课件:三点共线与距离最值(共27张PPT)

如图假定任选位置造桥MN, A 连接AM和BN,从A到B的路径是 AM+MN+BN,那么折线AMNB在 什么情况下最短呢?
M
a
b
N
B
由于河宽是固定的,因此当 AM+NB最小时,AM+MN+NB最小.
分析: A
A’
N
M
a b
B
如图,如果将点A沿与河岸垂直的方向平移到点A′, 使AA′等于河宽,则AA′=MN,AM=A′N,问题转化为:当 点N在直线b的什么位置时,A′N+NB最小?
E A P d
Hale Waihona Puke B Fc2、如图,矩形ABCD中,AB=6,MN在 边AB上运动,MN=3,AP=2,BQ=5, PM+MN+NQ最小值是___________。 P’ +3
2 、如图1,抱物线y= ー x2+bx+c与x轴相于点A, C.与y轴相交于点B,连接AB,BC,点A的坐标为(2,0), tan∠BAO=2,以段BC为直径作⊙M的交AB于点D,过点B作直线 l∥AC,与抛物线和⊙M的另一个交点分别是E,F。 (1)求该抛物线的函数表达式 (2)求点C的坐标和线段EF的长 (3)如图2,连接CD并延长,交直线l于点N,点P,O为射线 NB上的两个动点(点P在点Q的右侧,且不与N重合)段PQ与 EF的长度相等,连接DP,CQ,四边形CDPO的周长是否有最小 值?若有,求出此时点P的坐标并直接写出四边形CDPQ周长 的最小值;若没有,请说明理由
A
C
B
l
B′
在连接AB′两点的线中,线段AB′最短. 因此, 线段AB′与直线 l 的交点C的位置,使A 、B′ 、C 三点共线,点C即为所求.
证明:如图. 在直线 l 上任取另一点C′ , 连接AC′ 、BC′ 、B′ C′ . A ∵直线 l 是点B、B′的对称轴, C′ 点C、C′在对称轴上, ∴BC=B′C,BC′=B′C′. ∴AC+BC=AC+B′C=AB′. 在△AB′C′中,AB′< AC′+B′C′, ∴AC+BC < AC′+B′C′, 即AC+BC最小.
初中数学动点典型题分析-利用“三点共线”解决最值问题(2)

初中数学动点典型题分析-利用“三点共线”解决最值问题
(2)
公众号典型题分析均摘自《初中数学典型题思路分析》,本书题型多样典型,分析透彻,送给同学们一支猎枪,而不只是一堆猎物!购书赠送数套电子版精选资料。
qq群453495932分享样本及其他精选资料。
所谓“动点问题”是指图形中有一个或多个动点,在线段、射线或者弧线上运动的一类开放性题目,而解决这类题的关键是动中取静,让动点定下来,灵活地运用相关数学知识解决问题.在变化中找到不变的性质是解决数“动点”问题的基本思路.数学压轴题正逐步转向数形结合、动态几何、动手操作、实验探究等方向,加强了对几何图形运动变化的考核,从变化的角度来研究三角形、四边形、函数图象等,通过“对称”“翻折”“平移”“旋转”等研究手段和方法来探究图形性质及变化.让学生经历探索的过程,培养学生分析问题、解决问题的能力,把运动观点、方程思想、数形结合思想、分类思想、转化思想有机地结合起来.
一、利用“垂线段最短”解决最值问题
二、利用“三点共线”解决最值问题
【典型例题2】难度★★★
【思路分析】点A 、C 分别在x 轴、y 轴上,当点A 在z 轴运动时,点C 随之在y 轴上运动,线段OB的长度随之发生变化,因此需要寻找与点O、点B 有关的不变的量.仔细观察,我们可以发现在运
动过程中,点O在到AC的中点的距离不变,点B 到AC 的中点的距离也不变,然后求解即可.
【答案解析】解:。
初中数学_中考专题——动点问题之三点共线求线段最值教学设计学情分析教材分析课后反思

中考专题复习——动点问题之三点共线求线段最值考点分析:出题背景将动点放在三角形、菱形、矩形、正方形、圆、抛物线中,进行综合考察。
题目灵活多变,新题层出不穷。
所用知识点“两点之间线段最短”、“三角形两边之和大于第三边,两边之差小于第三边”、“垂线段最短”……判断动点轨迹时会用到“平行线之间的距离处处相等”、“90°的圆周角所对的弦是直径”、“到定点的距离等于定长的点都在圆周上”……。
考的较多的还是“将军饮马问题”和“圆周上的旋转”。
教学目标:1、理解并掌握实际生活中最短问题的实质就是垂线段最短;两点之间,线段最短;三角形两边之和大于第三边,两边之差小于第三边2、培养学生动手操作进行模拟实验的意识,发展、提高学生的空间想象能力,渗透模型解题法。
重点、难点分析:教学重点:借助两大变换转实现三点共线,进而达到化“折”为“直”。
教学难点:①在旋转变换中,通过空间想象发现动点的运动轨迹;②通过探索解决问题的过程,进行方法的归纳和建模,形成解决问题的通法。
②正确合理的添加辅助线,寻找解决问题的方法;教学过程一、三点共线之轴对称——诗词中数学通过《诗词大会》之——“看图说诗”引入“将军饮马”问题,进而分析模型特点——两定一动一直线,归纳解题方法原理——“两点之间线段最短”、“三角形任意两边之和大于第三边”,进而归纳解题模型:1、确定对称轴——动点所在直线2、作对称点;3、连线。
【设计意图】:通过《诗词大会》之“看图说诗”这个小活动,打破初四复习课的单调,提高学生的学习兴趣,丰富数学的文化内涵,引出第一个数学模型——轴对称型的三点共线。
1、(2017安顺)正方形ABCD的边长为1,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为___【设计意图】:直接套用解题模型,体现了模型解题法的优越性。
2、如图,正方形ABCD的边长为4,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE 上的动点,则DQ+PQ的最小值是________.【设计意图】:是模型解题的变式和升级——以正方形为背景、两个动点的两条线段和最小问题,找出问题本质利用对称化“折”为“直”,再用“两点之间线段最短”,实现共线,总结出数学模。
证明三点共线问题的方法

又 PE = PF ,则
AB ·FC·DE
CD B F EA
=
PA ·PC·PE
PC PF PA
= 1.
故 AB ·FC·DE = B F·CD·EA .
因此 , AC 、BD 、EF 三线共点 ,即 E、K、F
三点共线.
练习题
1. 在 △ABC 中 , AB > BC > CA , 它 的 内 切 圆 切 BC、CA 、AB 于 D 、E、F. 设 FE 与 BC 交于 A′, FD 与 AC 交于 B′, DE 与 BA 交于 C′. 求证 : A′、B′、C′三点 共线.
数学竞赛的教练和优秀选手经常用塞瓦定理的逆定理来证明三线共点问题并不是因为人们对此定理有所偏爱而是因为它好用且适用比同一法更加行之有效
2
●数学活动课程讲座 ●
证明三点共线问题的方法
中等数学
黄全福
(安徽省怀宁县江镇中学 ,246142)
(本讲适合初中) 证明三点共线问题的方法很多 ,从初中
所涉及的数学知识的范围考虑 ,大体有以下 几种.
7 利用塞瓦定理的逆定理
变三点共线为三线共点 ,利用塞瓦定理
的逆定理. 在圆内接凸六边形 ABCDEF 中 ,
若 AB ·CD·EF = BC·DE·FA ,则 AD 、B E、CF
三线共点 ;反之亦然. 利用这个结果来证明某
些三点共线问题 ,可立竿见影.
例 7 如图 7 ,凸
四边形 ABCD 内接于
同理 , S △FMN
=
1 4
. S 四边形ABCD
因此 , S △EMN = S △FMN . 此时 ,直线 MN 平
21-22版:微专题3 利用共线向量巧解三点共线(步步高)
微专题3 利用共线向量巧解三点共线先利用共线向量的思想,佐证出关于三点共线问题的解决方法,启迪了思维,拓展了解题思路,同时,通过具体例题,强化新结论的应用.一、共线向量定理的性质例1 试证明如下问题.如图,A ,B ,C 是平面内三个点,P 是平面内直线AB 外任意一点,若点C 在直线AB 上,则存在实数λ,使得PC →=λP A →+(1-λ)PB →.证明 ∵向量BC →与向量BA →共线,∴BC →=λBA →,即PC →-PB →=λ(P A →-PB →),PC →=λP A →+PB →-λPB →,∴PC →=λP A →+(1-λ)PB →.反思感悟 由上述过程的证明可以得出两条性质性质1:已知A ,B ,C 是平面内三个点, P 是平面内直线AB 外任意一点,若A ,B ,C 三点共线,则存在实数λ,μ,使得PC →=λP A →+μPB →,则有λ+μ=1.性质2:已知A ,B ,C 是平面内三个点,P 是平面内直线AB 外任意一点,若存在实数λ,μ,有PC →=λP A →+μPB →,且λ+μ=1,则A ,B ,C 三点共线.二、共线向量定理的应用例2 如图所示,在平行四边形ABCD 中,AE →=13AB →,AF →=14AD →,CE 与BF 相交于G 点,记AB →=a ,AD →=b ,以a ,b 为基底表示AG →.解 ∵E ,G ,C 三点共线,∴由平面内三点共线可得:存在唯一的实数x 使得AG →=xAE →+(1-x )AC →,∵ AE →=13AB →=13a ,AC →=a +b , ∴AG →=x ×13a +(1-x )(a +b )=⎝⎛⎭⎫1-2x 3a +(1-x )b .① 又∵F ,G ,B 三点共线,∴由平面内三点共线可得:存在唯一的实数λ使得AG →=λAB →+(1-λ)AF →,∵AF →=14AD →=14b , ∴AG →=λa +(1-λ)14b .② 由①②两式可得⎩⎨⎧λ=1-2x 3,1-λ4=1-x ,∴⎩⎨⎧ x =67,λ=37,∴AG →=37a +17b . 反思感悟 本题的解法中由两组三点共线(F ,G ,B 以及E ,G ,C 三点在一条直线上),利用平面内三点共线构造方程组求解,避免了用向量的加法和平面向理基本定理解答本题的复杂运算,达到了简化解题过程的效果.例3 如图,在△OAB 中,OC →=14OA →,OD →=12OB →,AD 与BC 交于M 点,设OA →=a ,OB →=b .(1)用a ,b 表示OM →;(2)在已知线段AC 上取一点E ,在线段BD 上取一点F ,使EF 过点M .设OE →=pOA →,OF →=qOB →.求证:17p +37q=1. (1)解 因为B ,M ,C 三点共线,所以存在实数m 使得OM →=mOC →+(1-m )OB →=m ·14OA →+(1-m )OB →=14m a +(1-m )b ; 又因为A ,M ,D 三点共线,所以存在实数n 使得OM →=nOA →+(1-n )OD →=n a +12(1-n )b . 由于a ,b 不共线,所以有⎩⎨⎧ 14m =n ,1-m =12(1-n ), 解得⎩⎨⎧ m =47,n =17.故OM →=17a +37b . (2)证明 因为E ,M ,F 三点共线,所以存在实数λ使得OM →=λOE →+(1-λ)OF →=λp a +(1-λ)q b .结合(1),易得出⎩⎨⎧ λp =17,(1-λ)q =37,消去λ得,17p +37q=1. 反思感悟 本题是以a ,b 作为一组基底,其他向量都由它们线性表示.(1)中的实数m ,n的几何意义为m =|BM →||BC →|=47,n =|DM →||DA →|=17, m ,n ∈(0,1);(2)中的实数λ=|FM →||FE →|=17p . 例4 如图,平行四边形ABCD 中,点P 在线段AB 上,且AP PB =m ,Q 在线段AD 上,且AQ QD =n ,BQ 与CP 相交于点R ,求PR RC的值.解 设PR RC =λ,则PR PC =λλ+1,BR →=λλ+1BC →+⎝⎛⎭⎫1-λλ+1BP →. ∵AP PB =m ,∴BP →=1m +1BA →, 且BR →=λλ+1BC →+1λ+1·1m +1BA →. 又AQ QD =n ,∴AQ →=n n +1AD →=n n +1BC →, ∵BQ →=BA →+AQ →,即BQ →=n n +1BC →+BA →. 又∵BR →与BQ →共线,∴λλ+1-n n +1·1(λ+1)(m +1)=0, 解得λ=n (m +1)(n +1). ∴PR RC =n (m +1)(n +1). 反思感悟 我们先要确定好一组基底BA →,BC →,看准BR →,BQ →如何由它们线性表示;而欲求目标数值,因P ,R ,C 三点共线,中途要以BP →,BC →作基底,BR →由它们线性表示出时,分析清楚该两基底系数所表示的几何意义,由性质1,得BR →=λλ+1BC →+⎝⎛⎭⎫1-λλ+1BP →;最终BR →与BQ →都得转化到由BA →,BC →两基底线性表示,此时容易由共线向量性质列出等式,从而求出结果.。
三点共线、线共点
第三讲 点共线、线共点在本小节中包括点共线、线共点的一般证明方法及梅涅劳斯定理、塞瓦定理的应用。
1. 点共线的证明点共线的通常证明方法是:通过邻补角关系证明三点共线;证明两点的连线必过第三点;证明三点组成的三角形面积为零等。
n (n ≥4)点共线可转化为三点共线。
例1 如图,设线段AB 的中点为C ,以AC 和CB 为对角线作平行四边形AECD ,BFCG 。
又作平行四边形CFHD ,CGKE 。
求证:H ,C ,K 三点共线。
证 连AK ,DG ,HB 。
由题意,AD EC KG ,知四边形AKGD 是平行四边形,于是AK DG 。
同样可证AK HB 。
四边形AHBK 是平行四边形,其对角线AB ,KH 互相平分。
而C 是AB 中点,线段KH 过C 点,故K ,C ,H 三点共线。
例2 如图所示,菱形ABCD 中,∠A =120O 为△ABC 外接圆,M 为其上一点,连接MC 交AB 于E ,AM 交CB 延长线于F 。
求证:D ,E ,F 三点共线。
ABCDEFHKG证 如图,连AC ,DF ,DE 。
因为M在O 上,则∠AMC =60°=∠ABC =∠ACB , 有△AMC ∽△ACF ,得CDCFCA CF MA MC ==。
又因为∠AMC =BAC ,所以△AMC ∽△EAC ,得AEADAE AC MA MC ==。
所以AEADCD CF =,又∠BAD =∠BCD =120°,知△CFD ∽ △ADE 。
所以∠ADE =∠DFB 。
因为AD ∥BC ,所以∠ADF =∠DFB =∠ADE ,于是F ,E ,D 三点共线。
例3 四边形ABCD 接于圆,其边AB 与DC 的延长线交于点P ,AD 与BC 的延长线交于点Q 。
由Q 作该圆的两条切线QE和QF ,切点分别为E ,F 。
求证:P ,E ,F 三点共线。
证 如图。
连接PQ ,并在PQ 上取一点M ,使得 B ,C ,M ,P 四点共圆,连CM ,PF 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学竞赛专题选讲
三点共线
一、内容提要
1. 要证明A ,B ,C 三点在同一直线上, A 。
B 。
C 。
常用方法有:①连结AB ,BC 证明∠ABC 是平角
②连结AB ,AC 证明AB ,AC 重合
③连结AB ,BC ,AC 证明 AB +BC =AC
④连结并延长AB 证明延长线经过点C
2. 证明三点共线常用的定理有:
① 过直线外一点有且只有一条直线和已知直线平行
② 经过一点有且只有一条直线和已知直线垂直
③ 三角形中位线平行于第三边并且等于第三边的一半
④ 梯形中位线平行于两底并且等于两底和的一半
⑤ 两圆相切,切点在连心线上
⑥ 轴对称图形中,若对应线段(或延长线)相交,则交点在对称轴上
二、例题
例1.已知:梯形ABCD 中,AB ∥CD ,点P 是形内的任一点,PM ⊥AB ,
PN ⊥CD
求证:M ,N ,P 三点在同一直线上 证明:过点P 作EF ∥AB , ∵AB ∥CD ,∴EF ∥CD ∠1+∠2=180 ,∠3+∠4=180
∵PM ⊥AB ,PN ⊥CD
∴∠1=90 ,∠3=90 ∴∠1+∠3=180
∴ M ,N ,P 三点在同一直线上
例2.求证:平行四边形一组对边的中点和两条对角线的交点,三点在同一直
线上
已知:平行四边形ABCD 中,M ,N 分别是AD 和BC 的中点,O 是AC 和
BD 的交点
求证:M ,O ,N 三点在同一直线上
证明一:连结MO ,NO ∵MO ,NO 分别是△DAB 和△CAB 的中位线
∴MO ∥AB ,NO ∥AB
根据过直线外一点有且只有一条直线和已知直线平行
∴ M ,O ,N 三点在同一直线上
证明二:连结MO 并延长交BC 于N
, ∵MO 是△DAB 的中位线 ∴MO ∥AB
在△CAB 中
∵AO =OC ,ON ,∥AB ∴BN ,=N ,C ,即N ,是BC 的中点 ∵N 也是BC 的中点,
∴点N ,和点N 重合
∴ M ,O ,N 三点在同一直线上
例3.已知:梯形ABCD 中,AB ∥CD ,∠A +∠B =90 ,M ,N 分别是AB
和CD 的中点,BC ,AD 的延长线相交于P
求证:M ,N ,P 三点在同一直线上 证明:∵∠A +∠B =90 ,
∠APB =Rt ∠
连结PM ,PN 根据直角三角形斜边中线性质 PM =MA =MB ,PN =DN =DC ∴∠MPB =∠B ,∠NPC =∠B
∴PM 和PN 重合 ∴M ,N ,P 三点在同一直线上 例4.在平面直角坐标系中,点A 关于横轴的对称点为B ,关于纵轴的对称
点是C ,求证B 和C 是关于原点O 解:连结OA ,OB ,OC ∵A ,B 关于X 轴对称, ∴OA =OB ,∠AOX =∠BOX 同理OC =OA ,∠AOY =∠COY ∴∠COY +∠BOX =90
X ∴B ,O ,C 三点在同一直线上 ∵OB =OC
∴ B 和C 是关于原点O 的对称点 例5.已知:⊙O 1和⊙O 2相交于A ,B 两点,过点B 的直线EF 分别交⊙O 1
和⊙O 2于E ,F 。
求证:AE ,AF 和⊙O 1和⊙O 2的直径成比例
,
证明:作⊙O 1和⊙O 2的直径AM ,AN ,连结AB ,BM ,BN
∵AM ,AN 分别是⊙O 1和⊙O 2的直径 ∴∠ABM =Rt ∠,∠ABN =Rt ∠ ∴M ,B ,N 在同一直线上
∴∠M =∠E ,∠N =∠F ∴△AMN ∽△AEF ∴AF AN AE AM
三、练习
1. 已知:梯形ABCD 中,AB ∥CD ,M ,N ,P 分别是AD ,BC ,AC 的中
点 求证:M ,N ,P 三点在同一直线上
2. 已知:△ABC 中,BE ,CF 是中线,延长BE 到G ,使EG =BE ,延长
CF 到H ,使FH =CF ,
求证:G ,A ,H 三点共线
3. 已知:正方形ABCD 中,M ,N 分别是BC ,CD 的中点,DE ⊥AN 于E ,
求证:点M 在DE 的延长线上(同33第5)
4. 求证:梯形两腰中点和两条对角线的中点,四点在同一直线上
5. 已知:梯形ABCD 中,AB ∥CD ,∠A 和∠D 的平分线相交于O ,
求证:点O 在梯形的中位线上
6. 已知:△ABC 中,∠ABM ,∠ACN 分别是∠B ,∠C 的邻补角,从点
A 作∠
B ,∠
C ,∠ABM ,∠CAN 四个角平分线的垂线段A
D ,A
E ,A
F ,
AG ,垂足是D ,E ,F ,G
求证:D ,E ,F ,G 四点在同一直线上
7. 已知:点P 在等边△ABC 外,PA=PB+PC ,以PA 为一边作等边△APQ
使点Q 和点C 在PA 的同一侧
求证:PQ 必过点C
8. 已知:△ABC 中,AB=AC ,直线AP ∥BC ,点D 和点C 是关于直线
AP 的对称点
求证:点D 和点B 是关于点A 的对称点
练习题参考答案
1. 连结MP ,NP 证明都与AB 平行
2. 连结AG ,AH 证明都与BC 平行
3. 连结DM 证明DM ⊥AN
5.证明MP平行于底边
6.根据中位线性质,垂足连线平行于底边
7.连结CQ,证明∠AQC=60
8.证明∠DAP+∠PAC+∠CAB=180
[文章来源:教师之家/转载请保留出处] [相关优质课视频请访问:教学视频网/]。
