Mander约束混凝土模型
横向约束对混凝土性能的影响分析

_re>1 时 :
f、9 、
CD段 为 二次抛 物 线 。
直线 段公 式 为 :
= t3" 一
,
一 s,)
曲线 段公 式 为 :
-(嚣 1+0.6sin(丌嚣 ]]
(4)
张 秀琴模 型表 明 了配箍 率 的提 高 ,可 明 显改 善}昆
= (嚣 丁
其中:r/=1+√ / 。
者 一
㈩
其中, “ sec2 : 意0“ 0 一z 蠹0 0l一o“ ;
置为卸载线 的初始切线模 量 ,f l"u、e 为卸载点 的 应力 、应变 ,s 为卸载时的残余 塑性应变 。
③再加载曲线由两部分构成 ,其 中sc段为直线 ,
③再加载曲线BD的公式为 : ore 1 时 :
析 对 比试验 结果 ,提 出如 图2所 示模 型 。
①骨架 曲线ONAD段 的公式为 :
厶
:
一 1+x
(2)
M 一 :
作者简 介 :苏仁 智(1990-),男 ,福建泉州人 ,毕业 于华南理工 大学建 筑 与 土木 工程专业 ,工程硕 士。主要从事结构检测 、大型结构的施工监控 和健康监 测等 工作和研 究。
钢筋混凝土构件受到轴 向压力作用使其混凝土 产生侧 向变形 ,由于箍 筋的横 向约束作用 ,限制 了混 凝土的侧 向变形 ,由于箍筋与混凝土相互作用 ,使得 混 凝土 处 于三 向受 压 的空 间应 力 状态 ,该 部 位混 凝 土 称为横 向约束混凝土。一般情况下箍筋对横向混凝土 的侧 向压力远小于其受到的轴 向压力 ,在箍筋的横 向 约束 下 ,混 凝土 强 度得 到提 高 。
(完整版)Xtract参数说明

Ucfyber 参数说明在Ucfyber 中,混凝土所用模型是Mander 模型,各参数说明如下:1.Mander confine concrete--约束混凝土(1).28days compressive strength 'c f指所应用的混凝土28天抗压强度,为标准值,可以由规范中查询。
这里用的是混凝土圆柱体。
我国的规范应用的是立方体强度(指混凝土标号)。
二者的换算关系为'0.85c S f R =(2).Tension strength指所应用的混凝土的抗拉强度,在进行弯矩曲率分析计算时,一般不考虑混凝土的抗拉,所以为0。
(3).Confine concrete strength: 'cc f指约束混凝土的峰值纵向压应力,在谢旭的书中,图为p155图7.3。
其计算情况分为两种情况① .圆形截面''''2 1.254l cc cc f f f f ⎛⎫=- ⎪ ⎪⎝⎭ 在上面的公式中:'c f —无约束混凝土的圆柱体的抗压强度,常用的单位是Mpa,混凝土立方体标准试件的强度与其他各种试件强度之间的换算关系:'0.85c S f R =,其中s 是混凝土的标号。
'l f —有效横向约束应力,''2yh sp l e f A f K D S =,其中:e K 是截面的有效约束系数。
圆形截面取0.95;yh f 是圆形或螺旋钢筋的屈服强度(钢筋的设计强度),可以查规范;sh A 是圆形或螺旋钢筋截面总面积(单位为mm 的平方.上下单位统一即可.可以约掉),即纵向钢筋的总面积—g nA ;'D 是圆形或螺旋钢筋的环的直径。
如下图所示:S 是纵向箍筋的间距。
②矩形截面矩形截面在两个主轴方向的有效约束应力分别为:'lx e x yh f K f r =贩, 'ly e y yh f K f r =贩其中: e K —截面的约束混凝土的系数。
钢筋混凝土柱动力滞回性能两尺度数值模拟

钢筋混凝土柱动力滞回性能两尺度数值模拟许斌;王治原;陈洪兵【摘要】为提高钢筋混凝土柱在快速循环加载下的动力滞回性能数值模拟计算效率并反映局部破坏特征,对通用有限元分析程序ABAQUS进行二次开发,编写了适用于三维纤维梁单元的混凝土和钢筋本构模型程序,在实现纤维梁单元和实体单元界面连接变形协调的基础上,建立了由三维实体单元和纤维梁单元组成的两尺度有限元模型.为了比较计算精度和效率,分别建立了试件的三维纤维梁单元模型和三维实体单元模型.分别对3种模型进行往复荷载作用下考虑混凝土材料应变率效应的钢筋混凝土柱动力滞回性能数值模拟,将两尺度模型的计算结果与试验结果进行比较.结果表明:所开发的材料本构模型程序以及两尺度模型能较好地反映钢筋混凝土柱在快速循环加载下的承载能力及滞回性能;所建立的两尺度模型既可节约计算成本,又能实现钢筋混凝土柱试件关键部位的精细化分析.%In order to improve the simulation efficiency and investigate the local failure pattern of reinforced concrete (RC) column specimens under dynamic cyclic loadings, the subroutines describing the dynamic constitutive laws of concrete materials and reinforcement which were suitable for three dimensional (3D) fiber beam elements were developed in ABAQUS.Then, a two-scale finite element method (FEM) model composed of 3D fiber beam elements and 3D solid elements was established to simulate the dynamic cyclic behavior of the RC column specimens under cyclic loading.In the model, the deformation of the 3D fiber beam elements and the 3D solid elements at the interface was compatible.For comparison, two FEM models for the RC columns specimens composed of the fiber elements and solid elementssolely were developed.The simulation results from the two-scale FEM model were compared with the test results firstly.The results show that the two-scale model using the developed subroutines describing the constitutive laws can simulate the load-carrying capacity and the dynamic hysteretic performance of the RC columns under rapid cyclic loading.The two-scale model can limit computation cost and achieve fine analysis of the RC column.【期刊名称】《建筑科学与工程学报》【年(卷),期】2017(034)003【总页数】8页(P16-23)【关键词】钢筋混凝土柱;动力滞回性能;ABAQUS二次开发;多尺度模型;数值模拟;应变率【作者】许斌;王治原;陈洪兵【作者单位】湖南大学土木工程学院,湖南长沙 410082;湖南大学土木工程学院,湖南长沙 410082;湖南大学土木工程学院,湖南长沙 410082【正文语种】中文【中图分类】TU323.1进入21世纪以来,中国正经历有史以来最大规模的基础设施建设。
mander本构模型

Mander 本构模型在杆系混凝土有限元分析中,应该如何考虑箍筋对受压构件截面核心区混凝土的约束作用呢?直接在模型中建立箍筋的方法显然是不经济的,可以通过混凝土的应力-应变全曲线方程来反应箍筋的作用,即采用约束混凝土本构模型。
下面主要介绍Mander 等提出的约束混凝土模型,它既适用圆形箍筋,也适用矩形箍筋。
如下图所示,它基于Popovics (1973)提出的方程,适合于低应变率(准静态)和循环加载。
著名的截面分析软件XTRACT 即采用此模型。
受压区f c =xrf cc′r −1+x r其中,f cc ′为约束混凝土强度(将在后面定义)x =εc εcc其中,εc 为混凝土的纵向压应变:εcc =εco [1+5(f cc′f co′−1)]其中,f co ′和εco 为对应未约束混凝土的抗压强度和峰值应变,可取,εco =0.002. r =E c E c −E sec,其中E c =5000√f c ′(Mpa)为混凝土的切线模量(ACI )规范 E sec =f cc′εcc为混凝土的割线模量。
对于保护层混凝土,假定其应力-应变曲线在ε>2εcc 后为直线,应力在剥落应变εsp 处减小为零。
混凝土的压缩应变εcu 可按下式计算,εcu =0.004+1.4εsu ρ′f y f cc′其中,εsu 为箍筋拉断时的应变; ρ′为箍筋的体积配筋率; f y 为箍筋的屈服强度;约束混凝土强度的确定分两个步骤: (1) 有效约束压力与有效约束系数 在相邻箍筋间的各个截面上,约束压力的大小是不同的,中间截面最小,箍筋所在截面最大。
为简化计算,假设核心区混凝土表面的约束压力均匀分布,于是通过对钢筋和核心区混凝土的隔离体建立静力平衡方程,可以求得此均布压力, 圆形截面:f l′=12k e ρs f yℎ矩形截面:f lx ′=k e ρx f yℎ f ly ′=k e ρy f yℎ其中,f yℎ为箍筋的屈服强度;ρs ,ρx ,ρy 分别为圆形截面,矩形截面x 方向、矩形截面y 方向体积配箍率。
UCfber在钢筋混凝土截面弯矩_曲率计算中的应用

4 混凝土二次衬砌
为保证二次衬砌进度,并做到内实、外美,采用
2 台 9m 长整体钢模衬砌台车,台车总重量达 60t,主 骨架部分在厂家生产,现场安装后,焊接顶面钢板, 为保证模板周转使用不变形,采用 8mm 厚钢板,现 场安装需要一个月时间。二次衬砌要做到仰拱先行 创造环境,适时衬砌保安全。7 月初开始衬砌,在雨 季前完成进出口二次衬砌,施工安全得到保证。
Moment/kN*m Moment/kN*m
244800。如果该桥梁在罕遇地震顺桥向作用下,固定 墩墩底截面弯矩小于 92710,则说明固定墩墩底截 面处于弹性工作状态;如果固定墩墩底截面弯矩大 于 92710 但小于 476000,说明固定墩墩底截面已经 达到屈服状态但是尚未破坏,上述两种状态证明该
ρx,ρy—分别为箍筋在 x, y 的体积含筋率。由公
式(5)计算。
ρx
=
Asx s×dc
(5a)
ρy
=
Asy s×bc
(5b)
其中:
dc —矩形截面沿 Y 轴方向算到箍筋外缘的宽;
bc —矩形截面沿 X 轴方向算到箍筋外缘的宽;
S—纵向箍筋的间距。
算出 f′lx 和 f′ly 之后,就可以利用约束应力与约
开裂弯矩 /kN·m 28460 77040 67690 144900 92710 186300
表 1 各墩墩底截面弯矩 - 曲率计算结果
开裂曲率 /rad·m-1 1.237e-4 4.837e-5 1.124e-4 4.747e-5 9.684e-5 4.539e-5
屈服弯矩 /kN·m 90100 237500 171300 375000 223200 476000
Mander及规范本构
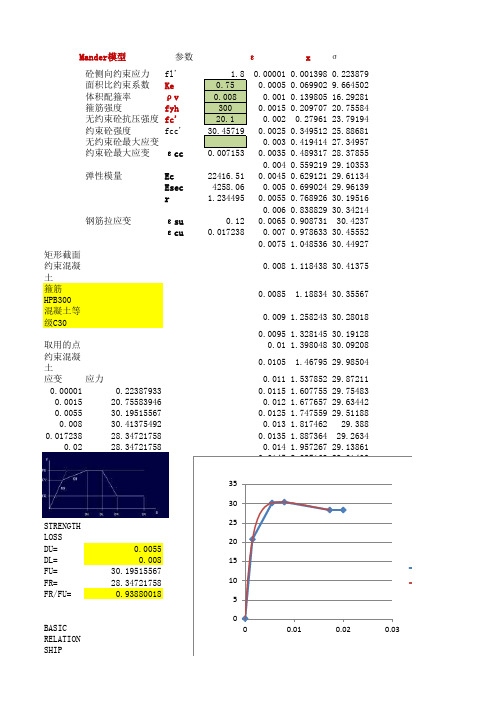
0.93880018
ε
xσ
1.8 0.75 0.008 300 20.1 30.45719
0.007153
22416.51 4258.06
1.234495
0.12 0.017238
0.00001 0.001398 0.223879 0.0005 0.069902 9.664502
0.001 0.139805 16.29281 0.0015 0.209707 20.75584
0.002 0.27961 23.79194 0.0025 0.349512 25.88681
0.003 0.419414 27.34957 0.0035 0.489317 28.37855
0.004 0.559219 29.10353 0.0045 0.629121 29.61134
2.21519 -5.0841 11.30096 227.1492 11.30096
2.531646 -18.8881 9.652686 194.019 9.652686
2.848101 -35.1772 8.372628 168.2898 8.372628
3.164557 -53.69 7.364551 148.0275 7.364551
构
6.012658 -277.239 3.417762 68.69701 3.417762
62.0329114 -303.611 3.220664 64.73535 3.220664
6.64557 -329.331 3.044633 61.19712 3.044633
61.5962025 -354.137 2.886516 58.01896 2.886516
OpenSees中Mander模型用于模拟钢筋混凝土柱滞回性能的适用性

OpenSees中Mander模型用于模拟钢筋混凝土柱滞回性能的适用性赵金钢;杜斌;占玉林【摘要】对OpenSeS软件提供的Concrete04和Concrete07两种基于Mander模型开发的混凝土本构模型的计算原理和参数取值进行详细的归纳;并建立有限元模型,对钢筋混凝土柱进行滞回性能分析.同时选取不同的塑性铰长度和等效刚度计算公式,分析其对钢筋混凝土柱滞回性能计算结果的影响.研究表明:采用Concrete07模型和中国规范给出的塑性铰长度计算公式,对钢筋混凝土柱滞回性能模拟的稳定性较好;不同的等效刚度取值对钢筋混凝土柱滞回性能计算结果的影响较小.%The calculation principle and parameter valuation for two concrete constitutive models Concrete04 and Concrete07 provided by software OpenSees and developed on the basis of Mander model were summed up in detail,and finite element models were established to analyze the hysteretic behavior of reinforced concrete columns.Meantime,the influence of several computational formulas selected for calculation of plastic hinge length and effective stiffness on the computation result of hysteretic behavior of reinforced concrete columns was analyzed,also.The research shows that the stability of simulation for hysteretic behavior of reinforced concrete columns by using the Concrete07 model and the computation formula of plastic hinge length stipulated by Chinese norm will be better and the valuation of different effective stiffness will have little effect on the computation result of hysteretic behavior of reinforced concrete columns.【期刊名称】《兰州理工大学学报》【年(卷),期】2017(043)005【总页数】7页(P127-133)【关键词】钢筋混凝土柱;塑性铰长度;等效刚度;滞回性能;OpenSees【作者】赵金钢;杜斌;占玉林【作者单位】贵州大学土木工程学院,贵州贵阳550025;贵州大学土木工程学院,贵州贵阳550025;西南交通大学土木学院,四川成都610031;陆地交通地质灾害防治技术国家工程实验室,四川成都610031【正文语种】中文【中图分类】TU311;TU375.3混凝土是由多种材料组成的多相复合材料,力学性能复杂,难以建立精确的本构模型.1984年Mander等[1]在对31个不同配筋、不同形状,接近足尺的墙、柱试件进行轴向破坏试验研究的基础上提出了Mander模型.该模型可以充分反映箍筋对混凝土的约束作用和处于三向应力作用下的混凝土延性[2],广泛适用于各种截面. OpenSees是一款由PEER开发的开源软件平台,具有非常突出的动力非线性处理能力.OpenSees提供了Concrete04和Concrete07两种基于Mander模型的混凝土本构模型.本次研究首先对Concrete04和Concrete07本构模型的计算原理和参数取值进行汇总归纳,然后分别采用这两种本构模型对选取的钢筋混凝土柱拟静力构件建立有限元模型.通过数值模拟结果与试验结果的对比分析,研究两种混凝土本构模型在模拟钢筋混凝土结构动力非线性分析中的适用性,同时分析塑性铰长度和等效刚度的不同计算公式对钢筋混凝土柱滞回性能计算结果的影响.根据文献[1],Mander模型混凝土轴向压应力fc计算公式如下:式中:为约束混凝土抗压强度;混凝土轴向压应变,为非约束混凝土抗压强度;r=,Esec为混凝土割线模量,Esec=.1) 圆形截面对于圆形截面(如图1a所示),箍筋约束区混凝土的有效侧压力为=keρsfyh/2式中:fyh为箍筋的屈服强度,MPa;ρs为箍筋体积配筋率,ρs=·;ke为有效约束系数,ke=,Ae为侧面有效约束面积,Ae=k,Acc为约束区混凝土面积,Acc=(1-ρcc);ds为圆形箍筋或螺旋箍筋的中心直径;s′为箍筋纵向净距;s为箍筋纵向间距;k对于圆形箍筋取2,对于螺旋箍筋取1;ρcc为纵筋与核心混凝土的面积比率,ρcc=;Ash为箍筋截面面积;Ast为纵筋截面面积.因此,箍筋约束区混凝土有效侧压力可表示为2) 矩形截面对于矩形截面(如图1b所示),侧面有效约束面积Ae为式中:为相邻纵筋的横向间距;bc和dc分别为矩形截面两个方向的箍筋长度. 约束区混凝土面积Acc为矩形截面不同方向的有效侧压力数值不同(见图1b),x和y方向的有效侧压力可以表示为式中:ρx=,Asx为x方向的横向钢筋面积;ρy=,Asy为y方向的横向钢筋面积.3) 约束混凝土的抗压强度对于采用螺旋或圆形箍筋等有效侧压力相等的约束混凝土抗压强度的计算公式,由文献[1]可知为矩形截面约束混凝土的抗压强度的值,需要通过查找文献[1]中提供的约束强度计算图来确定,但是该方法非常复杂并需要多次迭代.Mander等在文献[3]中提出的Chang-Mander模型中给出了约束混凝土抗压强度的近似计算公式,采用该公式可以方便地计算矩形截面约束混凝土的抗压强度.计算公式为式中和B是考虑由箍筋约束效应引起混凝土强度提高的参数.A=6.888 6-(0.606 9+17.275r)e-4.989r,B=-5,和是混凝土两个方向的有效约束应力.OpenSees提供的Concrete04模型,当混凝土弹性模量E0=5 000时,Concrete04模型受压骨架曲线就变为Mander模型;Concrete07模型是基于Waugh[4]修改后的Chang-Mander模型的混凝土模型,并可考虑箍筋约束效应.1) Concrete04模型Concrete04模型是以Popovice提出的可以考虑约束效应的混凝土模型为基础开发的,并且卸载和重加载规则按Filippou修正后的Karsan-Jirsa模式确定,同时该模型考虑了混凝土受拉力学性能.Concrete04模型受压骨架曲线如图2所示.Concrete04模型受压骨架曲线应力-应变为式(1~7).Concrete04模型中,约束混凝土的极限压应变εu为第一根箍筋断裂时混凝土的压应变(如图2所示).根据文献[2],εu按下式计算取值:式中:εsu为箍筋的极限拉应变,其余符号意义同前.通常典型εu值约为非约束混凝土的4~16倍.Concrete04模型受拉区上升段的拉伸弹性模量与原点切线刚度E0一致;过了峰值点后,混凝土开裂进入下降段,下降段采用指数形式,如下式所示:OpenSees中,Concrete04模型参数格式如下:uniaxialMaterial Concrete04 $matTag $fpc $epsc0 $epsU $E0 $ft $epst0 $beta其中:$fpc $epsc0 $epsU的意义如图2所示,$epst0=2$ft/$E0.根据文献[5],$beta取0.1.2) Concrete07模型Concrete07模型考虑因素全面,对于普通和高强混凝土均适用,并可考虑箍筋约束效应.Concrete07模型应力-应变关系如图3所示.Concrete07模型不考虑箍筋约束效应作用时:ε0=1/4/1 152.7,E0=8 2003/8,ft=0.62,εt=2ft/E0,r=/5.2-1.9,xp=2,xn=2.3.Concrete07模型考虑箍筋约束效应作用的约束混凝土抗压强度采用式(8)计算.约束抗压强度对应的应变为对于普通箍筋(fy≤413.7 MPa),k2=5k1;对于高强箍筋(fy>413.7 MPa),k2=3k1.对于约束混凝土非线性下降段的参数r,Waugh建议按下式计算:OpenSees中,Concrete07模型参数格式如下:uniaxialMaterial Concrete07 $matTag $fpc $epsc0 $E0 $ft $epst $xp $xn $r 其中:$xp为受拉中直线段下降段开始的应变点的无量纲值;$xn为受压中直线段下降段开始的应变点的无量纲值;$r为控制非线性下降段的参数.钢筋混凝土柱有限元模型应能正确反映纵向钢筋的屈曲现象,否则难以准确模拟出钢筋混凝土柱在反复荷载作用下强度和刚度的退化行为[6].OpenSees平台提供的ReinforcingSteel钢筋材料模型可以较为准确地反映钢筋的实际应力-应变关系,并且可以考虑钢筋的等向强化、初始屈服流幅、Bauschinger效应、钢筋屈曲或循环加载导致的强度和刚度退化以及钢筋断裂等现象.OpenSees提供的基于柔度法的塑性铰单元是一种精度较高且计算成本较低的梁柱单元.因此,采用塑性铰单元和ReinforcingSteel钢筋材料模型分别与Concrete04模型、Concrete07模型结合建立有限元模型,进行钢筋混凝土柱滞回性能分析.国内外学者开展了大量钢筋混凝土柱的拟静力试验,研究钢筋混凝土结构的动力非线性性能.本次分别选用清华大学开展的钢筋混凝土框架柱拟静力试验[7]、Tanaka 等[8]开展的矩形截面钢筋混凝土柱、Lehman等[9]和Kunnath等[10]分别开展的圆形截面钢筋混凝土柱拟静力试验中的部分试件进行数值模拟.选用钢筋混凝土柱的主要设计参数见表1.根据保护层混凝土和核心区混凝土的特性,采用Concrete04模型和Concrete07模型对每个钢筋混凝土柱试验模型分别建立有限元模型,进行滞回性能分析,对比研究基于Mander模型的Concrete04模型和Concrete07模型对钢筋混凝土柱滞回性能模拟的差异,为钢筋混凝土结构动力非线性分析提供参考.Concrete04模型和Concrete07模型对矩形截面钢筋混凝土柱的核心区约束混凝土的抗压强度均采用式(8)计算.试验测试结果与数值模拟结果对比如图4所示.由图4可见,Concrete04模型和Concrete07模型均可以较好地体现钢筋混凝土柱的捏缩效应和滞回特性;Concrete07模型对边柱的计算结果更接近试验结果,而Concrete04模型的模拟峰值承载力和加/卸载刚度均大于Concrete07模型计算结果;Concrete04模型和Concrete07模型对5号柱、430号柱和A2号柱的计算结果基本一致,均能很好地模拟试件的滞回性能.塑性铰长度和等效刚度是进行钢筋混凝土柱延性和塑性性能计算分析的重要参数.下面分析这些影响因素的不同取值对钢筋混凝土柱滞回性能的影响.1) 塑性铰长度取值的影响在侧向力作用下,钢筋混凝土柱底部区域易进入塑性状态,形成塑性铰,并产生较大的非弹性变形.准确地计算钢筋混凝土柱的塑性铰长度对于计算分析其滞回性能是非常重要的.国内外学者提出了多种塑性铰长度计算公式,由于每种公式都有一定的使用范围,因此有必要对这些公式进行对比分析.限于篇幅,选取4种有代表性的塑性铰长度计算公式对钢筋混凝土柱滞回性能进行对比分析.计算公式见表2.滞回性能对比如图5所示.注:L为柱高;db为纵筋直径;fy为纵筋屈服强度;k1对于软钢为0.7,对于冷加工钢为0.9;k3=0.9-;z为临界截面到反弯点的距离;h0为柱截面有效高度;c为极限弯矩作用下截面中和轴的深度;为混凝土圆柱体抗压强度.由图5可见,采用中国规范给出的塑性铰长度计算公式,4个钢筋混凝土柱滞回性能的计算结果与试验结果均拟合较好;采用Baker模型430号柱的模拟结果在加载后期峰值响应和卸载刚度均大于试验结果;采用Sawyer模型边柱的模拟结果在加载后期峰值响应小于试验结果,而卸载刚度大于试验结果;采用Berry模型430号柱的模拟结果在加载后期峰值响应小于试验结果,而A2号柱的模拟结果在加载后期峰值响应大于试验结果.因此,采用中国规范给出的塑性铰长度计算公式对于钢筋混凝土柱滞回性能的模拟来说较为稳定.2) 等效刚度取值的影响文献[11]中指出,E2地震作用下,对于延性构件取毛截面计算出的结构变形偏小,偏不安全,取开裂的后截面等效刚度进行计算分析是合理的.选取有代表性的3种等效刚度计算公式(见表3),对钢筋混凝土柱试件的滞回性能进行对比分析,判断不同等效刚度取值对钢筋混凝土柱滞回性能的影响.滞回性能对比如图6所示.注:μ为轴压比;P为轴压力;Ag为柱毛截面面积;为混凝土圆柱体抗压强度;db为纵筋直径;D为截面高度;L为柱高度;ρl为纵筋配筋率;EIeff为截面等效刚度;EcIg为毛截面刚度.由图6可见,分别采用3种等效刚度计算公式得到的钢筋混凝土柱滞回曲线基本一致,并且均可以较好地体现钢筋混凝土柱的捏缩效应和滞回特性.因此,计算时可以根据所知条件,选择方便计算的等效刚度计算公式.对OpenSees提供的2种基于Mander模型的Concrete04和Concrete07混凝土本构模型的计算原理和具体参数取值进行详细归纳,并对4个钢筋混凝土柱拟静力试验试件进行数值模拟对比,同时分析采用塑性铰长度和等效刚度的不同计算公式对钢筋混凝土柱滞回性能计算结果的影响,得出以下结论.1) Concrete04和Concrete07模型均可以体现钢筋混凝土柱的捏缩效应和滞回特性,但是Concrete07对混凝土影响因素考虑较全面,对4个试件滞回性能的计算结果与试验结果更接近,稳定性更好.2) 采用中国规范给出的塑性铰长度计算公式,4个钢筋混凝土柱滞回性能的计算结果与试验结果均拟合较好,对钢筋混凝土柱滞回性能的模拟更为稳定.3) 采用3种等效刚度计算公式得到的钢筋混凝土柱滞回曲线基本一致.可以根据已知条件,选择方便计算的等效刚度计算公式进行钢筋混凝土柱的滞回性能分析.致谢:本文得到贵州大学引进人才项目(201517)和四川省高等学校绿色建筑与节能重点实验室开放课题(szjj2016-096)的资助,在此表示感谢.【相关文献】[1] MANDER J B,PRIESTLEY M J N,PARK R.Theoretical stress-strain model for confined concrete [J]. Journal of Structural Engineering,1988,114(8):1804-1826.[2] 扶长生.地震工程学:理论与实践 [M].北京:中国建筑工业出版社,2013.[3] CHANG G A,MANDER J B.Seismic energy based fatigue damage analysis of bridge columns:part 1 evaluation of seismic capacity [R].New York:State University of New York,1994.[4] WAUGH D.Nonlinear analysis of T-shaped concrete walls subjected to multi-directional displacements [D].Ames,Iwoa:Iowa State University,2009.[5] MCKENNA F,FENVES G L,MAZZONI S.Open system for earthquake engineering simulation [M].Berkeley,CA:Pacific Earthquake Engineering Research Center,2011.[6] 司炳君,孙治国,任晓丹,等.钢筋混凝土桥墩滞回性能的有限元模拟分析 [J].哈尔滨工业大学学报,2009,41(12):105-109.[7] 陆新征,叶列平,潘鹏,等.钢筋混凝土框架结构拟静力倒塌试验研究及数值模拟竞赛Ⅱ:关键构件试验 [J].建筑结构,2012,42(11):23-26.[8] TANAKA H,PARK R.Effect of lateral confining reinforcement on the ductile behavior of reinforced concrete columns [D].Christchurch,New Zealand:University of Canterbury,1990.[9] LEHMAN D E,MOEHLE J P.Seismic performance of well-confined concrete bridge column [R].California:Pacific Earthquake Engineering Research Center,1998.[10] KUNNATH S K,EL-BAHY A,TAYLOR A T,et al.Cumulative seismic damage of reinforced concrete bridge piers:NISTIR6075 [R].Gaithersburg:National Institute of Standards and Technologh,1997.[11] 中华人民共和国交通运输部.公路桥梁抗震设计细则:JTG/T B02-01-2008[S].北京:人民交通出版社,2008.[12] BAKER A L L,AMARAKONE A M N.Inelastic hyperstatic frame analysis [C]∥Proceedings of the International Symposium on the Flexural Mechanics of ReinforcedConcrete.Miami:ASCE-ACI,1964.[13] SAWYER H A.Design of concrete frames for two failure states [C]∥Proceedings of the International Symposium on the Flexural Mechanics of Reinforced Concrete.Miami:ASCE-ACI,1964.[14] BERRY M P,LEHMAN D E,LOWES L N.Lumped-plasticity models for performance simulation of bridge columns [J].ACI Structural Journal,2008,105(3):270-279.[15] FEMA.Prestandard and commentary for the seismic rehabilitation of buildings:FEMA 356 [R].Washington, DC:Federal Emergency Management Agency,2000.[16] ELWOOD K J,EBERHARD M O.Effective stiffness of reinforced concrete columns [J].ACI Structural Journal,2010,106(4):476-484.。
Mander及规范本构

εc* αa αd fc*
x
y(x<1)
y(x>1)
应力 (σ)
绘图应力
0.00158 0.006329 0.262217 0.109707 2.205109 0.262217
2.0684 0.316456 10.9119 7.3775 148.2877 10.9119
1.168 0.632911 17.5087 16.09699 323.5495 17.5087
应变 应力
0.00001
0.22387933
0.0015
20.75583946
0.0055
30.19515567
0.008
30.41375492
0.017238
28.34721758
0.02
28.34721758
STRENGTH LOSS DU= DL= FU= FR= FR/FU=
0.0055 0.008
5.379747 0.961863 0.984738 9.725039 3.891838 3.891838
4.746835 -170.46 4.51243 90.69985 4.51243
0.008 30.41375
0.0085 30.35567
0.009 30.28018
0.0095 30.19128 0.01 30.09208
0.0105 29.98504
0.011 29.87211 0.0115 29.75483 0.012 29.63442 0.0125 29.51188 0.013 29.388 0.0135 29.2634 0.014 29.13861 0.0145 29.01403 0.015 28.88999 0.0155 28.76675 0.016 28.64453 0.0165 28.5235 0.017 28.40377
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Mander 约束混凝土模型(1988)
(J.B. Mander, M.J.N. Priestly, R. Park. Theoretical Stress-Strain Model for Confined Concrete[J]. Journal of Structural Division, ASCE, Vol.114, No.8, pp.1804~1826,August,1988)
基本参数:
应力——应变曲线:
单一曲线描述,
当cu c εε≤≤0时,r cc
c x r xr f +-=1σ 约束混凝土相对应变:cc
c x εε= 约束混凝土应力——应变曲线系数:sec E E E r c c -=
素混凝土弹性模量(MPa ):c c f E 5000= 约束混凝土峰值割线模量:cc cc f E ε=
sec
约束混凝土抗压强度:
⎥⎥⎦⎤⎢⎢⎣⎡-++-=c l c l c cc f f f f f f 294.71254.2254.1(圆形截面) 约束混凝土极限应变:
cc hu
yh s cu f f ερε4.1004.0+= 约束混凝土峰值应变:⎥⎦⎤⎢⎣
⎡⎪⎪⎭⎫ ⎝⎛-+=151c cc pc cc f f εε 有效约束应力:
圆形截面径向约束应力l f (Mpa ):yh s e l f k f ρ2
1=
矩形截面x 方向约束混凝土有效约束应力(Mpa ):yh x e lx f k f ρ= 矩形截面y 方向约束混凝土有效约束应力(Mpa ):yh y e lx f k f ρ=(矩形截面) 圆形截面体积配箍率:s
d dA sh s 42
ππρ= 矩形截面x 方向体积配箍率:s B A sx x '=ρ 矩形截面y 方向体积配箍率:s
D A sy y '=ρ 有效约束系数:cc e e A A k = 圆形截面有效混凝土核心面积:2
24⎪⎭⎫ ⎝⎛'-=s d A e π 矩形截面有效混凝土核心面积:()⎪⎭⎫ ⎝⎛''-⎪⎭⎫ ⎝
⎛''-⎥⎦⎤⎢⎣⎡'-''=∑=D s B s W D B A n i i e 2121612 ()c cc cc A A ⨯-=ρ1
符号说明:
cc f :约束混凝土抗压强度
cc ε:约束混凝土峰值应变
cu ε:约束混凝土极限应变
s ρ:横向钢筋体积配箍率
yh f :横向钢筋屈服强度
hu ε:横向钢筋极限应变
cc
c x εε=:约束混凝土相对应变 c f :混凝土单轴抗压强度
pc ε:素混凝土峰值受压应变,一般002.0=pc ε
f:约束混凝土侧向压应力Mpa
l
f:x方向约束混凝土有效约束应力Mpa
lx
f:y方向约束混凝土有效约束应力Mpa
ly
k:有效约束系数
e
A:有效混凝土核心面积
e
A:矩形截面平行x方向横向钢筋总面积
sx
A:矩形截面平行y方向横向钢筋总面积
sy
B':矩形截面约束混凝土核心宽度,至约束钢筋中心D':矩形截面约束混凝土核心长度,至约束钢筋中心
W':约束钢筋净间距
i
s':约束钢筋垂直净间距(中心距离s)。
