第二章__声子
材料物理基础习题
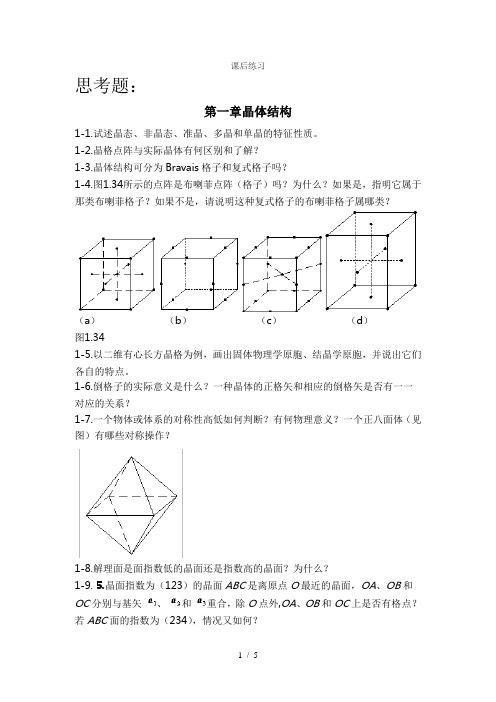
课后练习思考题:第一章晶体结构1-1.试述晶态、非晶态、准晶、多晶和单晶的特征性质。
1-2.晶格点阵与实际晶体有何区别和了解?1-3.晶体结构可分为Bravais格子和复式格子吗?1-4.图1.34所示的点阵是布喇菲点阵(格子)吗?为什么?如果是,指明它属于那类布喇菲格子?如果不是,请说明这种复式格子的布喇菲格子属哪类?(a)(b)(c)(d)图1.341-5.以二维有心长方晶格为例,画出固体物理学原胞、结晶学原胞,并说出它们各自的特点。
1-6.倒格子的实际意义是什么?一种晶体的正格矢和相应的倒格矢是否有一一对应的关系?1-7.一个物体或体系的对称性高低如何判断?有何物理意义?一个正八面体(见图)有哪些对称操作?1-8.解理面是面指数低的晶面还是指数高的晶面?为什么?1-9. 5.晶面指数为(123)的晶面ABC是离原点O最近的晶面,OA、OB和OC分别与基矢、和重合,除O点外,OA、OB和OC上是否有格点?若ABC面的指数为(234),情况又如何?1-10.带轴为[001]的晶带各晶面,其面指数有何特点?1-11. 与晶列[l1l2l3]垂直的倒格面的面指数是什么?1-12. 在结晶学中,晶胞是按晶体的什么特性选取的?1-13. 六角密积属何种晶系?一个晶胞包含几个原子?1-14.体心立方元素晶体, [111]方向上的结晶学周期为多大?实际周期为多大?1-15. 面心立方元素晶体中最小的晶列周期为多大?该晶列在哪些晶面内?1-16. 在晶体衍射中,为什么不能用可见光?第二章固体的结合2-1.试述离子键、共价键、金属键、范德瓦尔斯键和氢键的基本特征.2-2.有人说“晶体的内能就是晶体的结合能”,对吗?2-3.当2个原子由相距很远而逐渐接近时,二原子间的力与势能是如何逐渐变化的?2-4.为什么金属比离子晶体、共价晶体易于进行机械加工并且导电、导热性良好?2-5.是否有与库仑力无关的晶体结合类型?2-6.如何理解库仑力是原子结合的动力?2-7.晶体的结合能,晶体的内能,原子间的相互作用势能有何区别?2-8.原子间的排斥作用取决于什么原因?2-9.原子间的排斥作用和吸引作用有何关系?起主导的范围是什么?2-10.共价结合为什么有“饱和性”和“方向性”?2-11.共价结合,两原子电子云交迭产生吸引,而原子靠近时,电子云交迭会产生巨大的排斥力,如何解释?2-12.试解释一个中性原子吸收一个电子一定要放出能量的现象.2-13.如何理解电负性可用电离能加亲和能来表征?2-14.何为杂化轨道?2-15.你认为固体的弹性强弱主要由排斥作用决定呢,还是吸引作用决定?第三章晶格振动与晶体的热学性质3-1.什么是简谐近似?3-2.试定性给出一维单原子链中振动格波的相速度和群速度对波矢的关系曲线,并简要说明其意义。
东南大学固体物理基础课后习题解答

《电子工程物理基础》课后习题参考答案第一章 微观粒子的状态1-1一维运动的粒子处在下面状态(0,0)()0(0)xAxe x x x λλψ-⎧≥>=⎨<⎩①将此项函数归一化;②求粒子坐标的概率分布函数;③在何处找到粒子的概率最大? 解:(1)由归一化条件,可知22201xAx edx λ∞-=⎰,解得归一化常数322A λ=。
所以归一化波函数为:322(0,0)()0(0)xxex x x λλλψ-⎧⎪≥>=⎨⎪<⎩(2)粒子坐标的概率分布函数为:32224(0,0)()()0(0)xx e x w x x x λλλψ-⎧≥>==⎨<⎩(3)令()0dw x dx =得10x x λ==或,根据题意,在x=0处,()w x =0,所以在1x λ=处找到粒子的概率最大。
1-2若在一维无限深势阱中运动的粒子的量子数为n 。
①距势阱的左壁1/4宽度内发现粒子概率是多少? ②n 取何值时,在此范围内找到粒子的概率最大?③当n→∞时,这个概率的极限是多少?这个结果说明了什么问题?解:(1)假设一维无限深势阱的势函数为U (x ),0x a ≤≤,那么在距势阱的左壁1/4宽度内发现粒子概率为:22440211()()(sin )sin422a a n n P x x dx x dx a a n ππψπ===-⎰⎰。
(2)当n=3时,在此范围内找到粒子的概率最大,且max 11()+46P x π=。
(3)当n→∞时,1()4P x =。
此时,概率分布均匀,接近于宏观情况。
1-3一个势能为221()2V x m x ω=的线性谐振子处在下面状态2212()()x m x Aeαωψα-=求:①归一化常数A ;②在何处发现振子的概率最大;③势能平均值2212U m x ω=。
解:(1)由归一化条件,可知2221x A e dx α+∞--∞=⎰,得到归一化常数4A απ=。
声子名词解释

声子名词解释声子(sound particle),顾名思义,就是产生声音的粒子。
比如我们熟悉的电磁波、 X射线等都属于声波。
声子的基本特征是不带电荷,其物理学量是频率。
“声子”这个词在高中物理课本上出现的次数非常之多。
比如在讲到光的传播时,第二章第三节课的“波动光学”就用“光是以频率为波长的声波”来代替。
我觉得这样处理更加简洁明了。
4-(liquid crystals)高分子——相对分子质量为4的有机物。
相对分子质量为6的塑料具有很好的耐热性能,所以称之为高分子。
其中可燃性纤维素类塑料俗称为尼龙,可作为汽车的高速挡泥板和翼子板等。
5-液晶(liquid crystal)液晶是一种结构复杂的化合物,其分子的排列像液体。
它主要用于制造液晶显示器,用于计算机,收录机,电视机等。
最著名的液晶品种是醋酸纤维素及其衍生物,透明度和光亮度极高。
由于不存在色散现象,可以制成超高分辨率显示屏,被广泛应用于大屏幕彩电,计算机和便携式电子设备中。
8-芳香族卤化物(aromatic ethers)芳香族卤化物,通式(R)XH2 CH2(CH23)n+1。
通常指含有一个卤素原子的烷基卤化物。
如氯代甲烷、氯代乙烯、氯代苯、氯代萘、三氯甲烷等。
在卤代烃中卤素是通过电子对互斥作用和离子键与碳原子相联系的,其化学性质取决于价电子的轨道。
芳香族卤化物不溶于水、稀酸、稀碱和各种有机溶剂。
芳香族卤化物可由相应的醇或卤代烃经亲核取代反应制得。
这些卤代烃可以发生消除反应生成卤仿和烃基自由基。
自由基也可被还原成卤原子。
11-(pyridyl ethers)炔烃。
又称“顺式”炔烃,是链状的烃。
其通式为(R)R12x(R′-CH3)n+1。
它是饱和烃,分子中只含一个碳碳双键,因此没有同分异构体。
烷基是一个稳定的三级醇,结构中的双键不会发生加成反应。
根据卤素与氢的活泼性的差异,炔烃的化学性质也不同。
13-(bromo ethers)卤代芳烃。
一般含有三个氯原子和一个氧原子,呈浅黄色。
固态电子论-第二章习题参考解答

3、晶体中的空位数高低。空位越多,替代的概率越高。
第16题 硅晶体中的层错发生在[111]晶向,发生抽出型堆垛层错和插入型堆垛层错。
在该晶向上,硅原子密排面层的正常堆垛是„ABCABCABC„„。
晶体,正负离子的相对振动,在晶体中形成交替变化的电偶极子,等效为高频率电
磁波。
晶体振动声学波的特点: 是弹性波,振动频率较低,振动频率随波矢变化较大。
第10题 根据教材中给出的一维双原子晶格色散关系,
光学波
o max
2( 1 2 ) m o min
禁带
声学波
2 2 m
A max
3、4称为杂质点缺陷,是由于杂质存在形成的。
线缺陷的定义: 原子排斥偏离理想晶体周期性结构形成的一维缺陷称为线缺陷。 晶体中的线缺陷包括: 1、刃位错;2、螺位错;
第15题 影响晶体中杂质替位概率的主要因素: 1、替位杂质原子的大小与被替代的晶格原子的大小的接近程度。原子大 小越接近,替代的概率越高; 2、替位杂质原子的价电子壳层与被替代的晶格原子的价电子壳层结构相 似程度。电子壳层结构越相似,替代的概率越高。
第4题 提出杂化轨道概念的原因: 金刚石结构的基本结构单元是同种原子构成的正四面体,正四面体中心的原子 贡献1个电子与四个顶角原子各贡献一个电子形成等同的4个共价键。尽管原子具有4 个价电子,但其中的S态价电子和P态价电子是不同的,不能解释金刚石结构的4个共 价键等同这一现象。而泡林提出的杂化轨道概念可以很好解释金刚石结构成键。 杂化轨道概念对硅晶体结构特点的解释: 硅原子的价电子3s电子和3p电子能量相近。形成晶体时,一个3s电子被激发到 3p态,S态、P态波函数杂化,形成4个未配对电子,使得一个硅原子可与周围四个
材料物理性能复习资料整理

材料在外力作用下发生形状和尺寸的变化,称为形变。
材料承受外力作用、抵抗变形的能力及其破坏规律,称为材料的力学性能或机械性能。
材料在单位面积上所受的附加内力称为应力。
法向应力导致材料伸长或缩短,而剪切应力引起材料的切向畸变。
应变是用来表征材料在受力时内部各质点之间的相对位移。
对于各向同性材料,有三种基本类型的应变:拉伸应变ε,剪切应变γ和压缩应变Δ。
若材料受力前的面积为A0,则σ0=F/A0称为名义应力。
若材料受力后面积为A,则σT=F/A称为真实应力。
对于理想的弹性材料,在应力作用下会发生弹性形变,其应力与应变关系服从胡克(Hook)定律(σ=Eε)。
E是弹性模量,又称为弹性刚度。
弹性模量是材料发生单位应变时的应力,它表征材料抵抗形变能力(即刚度)的大小。
E越大,越不容易变形,表示材料刚度越大。
弹性模量是原子间结合强度的标志之一。
泊松比:在拉伸试验时,材料横向单位面积的减少与纵向单位长度的增加之比值。
粘性形变是指粘性物体在剪切应力作用下发生不可逆的流动形变,该形变随时间增加而增大。
材料在外应力去除后仍保持部分应变的特性称为塑性。
材料发生塑性形变而不发生断裂的能力称为延展性。
在足够大的剪切应力τ作用下或温度T较高时,材料中的晶体部分会沿着最易滑移的系统在晶粒内部发生位错滑移,宏观上表现为材料的塑性形变。
滑移和孪晶:晶体塑性形变两种基本形式。
蠕变是在恒定的应力σ作用下材料的应变ε随时间增加而逐渐增大的现象。
位错蠕变理论:在低温下受到阻碍而难以发生运动的位错,在高温下由于热运动增大了原子的能量,使得位错能克服阻碍发生运动而导致材料的蠕变。
扩散蠕变理论:材料在高温下的蠕变现象与晶体中的扩散现象类似,蠕变过程是在应力作用下空位沿应力作用方向(或晶粒沿相反方向)扩散的一种形式。
晶界蠕变理论:多晶陶瓷材料由于存在大量晶界,当晶界位相差大时,可把晶界看成是非晶体,在温度较高时,晶界粘度迅速下降,应力使得晶界发生粘性流动而导致蠕变。
声子的概念和特点

声子的概念和特点声子(Phonon)是固体物理学中描述晶体中晶格振动的量子发生器的概念。
声子是晶体中的一个虚拟粒子,它表示的是晶格振动的量子。
声子的概念是为了描述固体中的宏观振动现象及其与固体中其他粒子相互作用的研究提供一个有用的理论框架。
声子的特点有以下几个方面:1. 粒子性质:声子是晶格振动的量子化现象,其具有粒子性质。
晶体中的振动能量按量子化的方式传递,其中每个声子对应一个能量和动量,其传播速度与晶体中的声速有关。
2. 统计性质:声子是一种玻色子,遵循玻色-爱因斯坦分布。
根据玻色子性质,声子之间是可以相互叠加的。
这使得声子能够形成声子气体,从而影响固体的热导率、声学性质等。
3. 激发行为:声子在晶体中的产生可以通过热激发或外加能量的方式。
当系统受到外界扰动时,原子或分子之间的相互作用使得晶格发生振动,这些振动以声子的形式传播。
4. 能量谱:声子能量与动量之间存在一个关系,称为能谱。
能谱基本上是晶体中离子力学矩阵的函数,它描述了声子的能量与其频率和波矢之间的关系。
在一维晶格中,能谱是连续的,而在二维和三维晶格中,能谱是分散的。
5. 声子晶体学:声子是晶体中晶格振动的变分量子,声子晶体学是一种将振动波矢(声子)引入到晶体学中的方法。
在声子晶体学中,声子的离散能谱导致了晶体中声学和光学模式的出现。
6. 热传导:声子在固体中的传播是晶体的热传导的基础。
因为声子具有一定的动量,当声子在晶格中传播时,会导致晶格的振动,进而导致晶格的温度升高。
声子的能量传递机制是固体中热传导的重要机制之一。
总之,声子作为固体物理学中的基本概念,在研究固体中的振动性质、热传导机制、声学行为等方面起着重要作用。
通过对声子的理解和研究,可以更好地解释晶体的宏观性质和固体的热力学行为。
同时,声子也是新材料、热电材料等领域的重要研究方向,这些研究有望为材料设计和能源利用提供新的思路。
声子的相互作用和倒逆过程
→
问题与讨论
a)声子的速度是由什么决定的?与温度关 系如何?与格波关系又如何? b)声子有几种可能的散射机制?它们与温 度的关系又如何? c)声子参与各种物理过程,与其他元激发 等产生相互作用,导致或影响多种物理现 象,设想发现了一种新的现象,请设计一 个实验判断声子是否参与影响该现象。
→
推荐网站
固体物理讲义: /course/course/ 10/build/content.htm
→
谢谢! 谢谢
→
式子
其中C为晶格热容, 和 分别是声子的自由 程和速度,v一般是固体中的速度。
在高温下, ;而在低温下 所以T→0K,κ→∞。
。
→
电声子的相互作用
电声子相互作用是常规超导体中形成库帕对的机制. 先介绍BCS理论: BCS理论是以近自由电子模型为基础, 是在电子-声子作用很弱的前提下建立起来的理论。BCS 理论 (BCS theory)是解释常规超导体的超导电性的微 观理论(所以也常意译为超导的微观理论)。 而B C S B S理论的基本出发点-“电声子相互作用”是今后 各种微观电磁理论必须考虑的重要因素,其正确的核心是 只要吸引力存在、粒子就可以形成束缚态,能量就能够降 低成为列稳定的超导态,在电子能谱中就会一个能隙。但 是它对金属的相互作用作了太多的简化和近似,理论处理 局限於动量空间,因此难以解释目前高Te超导研究中的 一些新的成果。但是我们不能否认它的成果。
→
在简谐近似中,声子间无相互作用,(声 子之间是相互“透明”的,就象两束光相 遇后互不干涉地离开对方一样)故晶格振 动的每个状态能被任何数目的不可区分的 声子占据,声子仅与晶格振动的能量值有 关,即与温度有关,在T=0K时,没有任何 声子被激发。
第二章晶格振动与声子
m2 eiaq eiaq 2 2 cosaq 1
解得
2 sin 1 aq
m2
—— 色散关系
原子链的分立性与布里渊区
un
(q
2
a
)
un
(q)
(q)
q
- - 2 a
0
a
2 aa
q —— 布里渊区
a
a
(q 2 ) (q)
a
➢晶格振动的所有可能状态都 包含在该布里渊区中,这个 区域之外的波矢q不提供任何 新的振动状态。
简约区中波数q的取值总数 q 2 Na 2
a 2 a
=N=晶体链的原胞数
晶格振动格波的总数=N·1 =晶体链的自由度数
*波矢的分立性,与系统限度的有限性有关,L无限长 时,波矢是连续的。
一维双原子链的振动
考虑由P、Q两种原子等距相间排列的一维双原子链
一、运动方程及其解
2a
Mm
{
n 2n+2 2n-1 2n+1
当q0时, 0, 原胞内两种原子的振动位相完全相同。
q0时
2
M
Mm
m
1
1
4Mm
M m2
sin
2
aq
M
m
1
Mm
1
4Mm
M m2
aq
2
2
M
Mm
m
2Mm
M m2
aq 2
2
M m
aq 2
a
2 q q
M m
这与连续介质的弹性波 =vq 一致。
当q0时
u2n u2n1
q0
1
在长波极限下,原胞内两种原子的运动完全一致,振 幅和位相均相同,这时的格波非常类似于声波,所以我们 将这种晶格振动称为声学波或声学支。
5.2.2 声子
( q 由此可知: h ) 就是入射的波或粒子流与晶体中振动着的原子
发生相互作用时所交换的能量, 这正是声子的能量; q h 就是入射 的波或粒子流与晶体中振动着的原子 发生相互作用时所交换的
动量,可称之为声子的动量。 这表明,入射的波或粒子流与晶体中 振动着的原子发生相互作用时所产生的能量交换和动量交换是按吸 收或发射声子的方式进行的。
e
i ( k(' 0 ) k )d
e
i(' 0 ) t
i[( k ('1 ) k ) qh ]( Rl Rl ' )
2 NM ' ' ( k ' k ) e ( ) ( q ) i[( k( 1 ) k ) qh ] Rl ' i[( k( 1 ) k ) qh ] Rl i ( k ('1 ) k )d i(' 1 ) ]t (1) h e e [ ] e e 2 NM l
(qh ) 的格波。
振动的所有原子的原子集体运动呈现出一个波矢为 q h 、频率为
在量子力学理论中,晶体中所有原子共同参与的一个频率为 (qh )
的简正振动其能量本征值是量子化的
1 (qh ) [n (qh ) ] (qh ) , n (qh ) 0、 1、 2、 2 ( q ) 即能量的改变量 h 只能是 能量量子 ( qh ) 的整数倍。
运用声子的概念, 这表明: 量子态 (Q) 相当于晶体中有 q n (q h ) 个波矢为 h 的γ类声子: 1、 2、 3s ,
h h h qh 1 b1 2 b2 3 b3 N1 N2 N3 ,
八年级物理第2章声知识点
八年级物理第2章声知识点第一部分声的基本知识声是一种能够使人听到的纵波机械波,是物体振动产生的,需要通过介质(如空气)传播。
声波的特征包括:振动、周期、频率、波长、速度、强度、声波的形状和波束。
声音由一系列连续的波形组成,它们组合在一起的效果形成了声音的质感和基调。
第二部分声波的性质声波具有波动的性质和传播的性质,主要包括:频率、振动、声音、衰减和共振。
声波的传播速度主要取决于介质的特性,而不是声波的频率或强度。
在退化的情况下,空气中的声速大约是340米/秒。
声波经过物体时会发生反射、折射和干涉现象。
声波还会产生共振效应,这是指声波与固体或空气中的振动系统发生共振的现象,这些振动系统称为共振腔。
第三部分声音产生的机制声音是由物体的振动引起的机械波,可分为直接声和反射声两类。
直接声是指来自演讲者的声音,而反射声是指声音被其他表面反射并到达听者的声音。
声音的频率和音高取决于发声体的特性和振动速度。
例如,大声说话会导致喉咙和声带的振动,产生音调更高的音高。
第四部分声音的应用声音在许多地方都有应用,包括音乐、通讯、声学研究、医学和计量学。
音乐是最常见和广泛的应用程序之一,人们可以通过创建和演奏音乐来表达情感和感情。
通信和声学研究也是声音应用的关键领域。
人们使用声音进行电话和广播通信,并使用声音研究空气和其它介质中声波的传播和反射。
在医学领域,人们使用声波来进行医学影像学和诊断,并通过超声波治疗各种疾病。
最后,声音也在计量学和物理学中发挥重要作用。
声音可以用来测量物体的密度和压力,或者作为声波仪器来探测地震等自然灾害。
结论本文介绍了声波的产生和传播,包括声波的特征、性质和应用,深入了解这些领域将有助于深入了解声波及其在我们日常生活中的作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 () 0, 声学模
由此可知,复式晶格的声学模为元胞内各原子的同向运动,即元胞的质心运动 每个k值有3个独立的解属于声学模。
() 0 , 即其它(3r-3)个解属于格波的光学模 在一般情况下,
如果(s=1,2),当
' 时点的实极化矢量满足正交关系:
e ' (1) e (1) e (2) e (2) e (1)e ' (1) e (2)e ' (2) 0 '
可得系统的运动方程
M ul (l l ' )ul'
l ',
利用平移对称性及布洛赫定理
ul eikRl u0
对于确定的k,运动方程的解表现出下列特征: 1.各元胞中原子振动的方向相同,振幅相等。 2.有特定的相位关系,按
e
ikRl 变化
因此,每一确定的k 的解代表波长为
因子)在固体物理学中称为简正坐标;
ek 代表格波的偏振方向,称为极化矢量,它是单位矢。
对于具有r 个原子的复式晶格,本征频率
(k )
ul ( s ) 1
( 1,2,..,3r )
NM s
k,
ek (s)Qk eik Rl
2.格波的特性
1. (k ) 的共性 i)格波的本征频率是倒点阵的周期函数
l l' 2 s, s ' u ( s )u ( s ' ) l l' 0
同样,复式晶格的刚性位移不产生应力
l l' s, s' 0 l ',s '
将 k 0时的D 代入本征方程可得
(k ) (k K n )
ii) (k ) 具有点阵所属点群的全部对称性
(k ) (k )
iii)存在一个普遍的关系式
(k ) (k )
它是时间反演对称性的结果。 2. 声学模与光学模 声学模: 色散曲线具有k=0时,=0特征的格波称为声学模。 光学模: 反之,当k=0时,
(i)线(包含、M点) 横向声学模:极化矢量e与传播方向垂直; 纵向声学模:极化矢量e与传播方向平行;
(ii)线(包含、X点) 存在横向声学模和纵向声学模
(iii)Z线(包含X、M点) 既非横波,也非纵波。
一维复式晶格 既存在声学模,也存在光学模
3. 简正坐标
在简谐近似下晶格振动已由简正模的线性叠加表示
it Uk ~ ek e
结合以上方程可知:
1 i[ k Rl t ] ul ~ ek e N 代表波矢为k、偏振为、频率 (k ) 为的格波解。
在BZ中,一定时刻t的格波解
N e eikRl
1 2 k
称为简振膜。
根据正格矢与倒格矢之间的关系可得
D (k Kn ) D (k )
2 的集体振动,称为格波 |k|
令 u0 U k 对应于用波矢k标记的特解 可将3N自由度的耦合方程组简化为N个独立的3自由度耦合方程。 而每个波矢满足方程
Uk D (k )U k
, x, y, z
D (k )
1 M
ik Rl ( l ) e l
其中s,s’=1,…,r,代表元胞中不同的原子。 格波频率由下式决定:
k 2 det || D ss ' || 0 s, s '
k D s, s '
1 s M s'
l ikRl s, s ' e l
Qk k2 Qk 0
与简谐振子的运动方程在形式上相同。
利用傅里叶变换
Qk 1 NM
M N
l ,
( e u )e
k l l
ik Rl
ik Rl ( e u ) e k l
Pk 1 NM
1 NM
l ,
ik Rl ( e p ) e k l l
(l l ' ) 0
l'
因为当整体作刚性运动(即每个原子均作 子受到其它原子作用力之总和为零;即
ul v )时,晶格中任一原
F (l )
( l l ' ) u l ' u l '
(l l ' )v 0 l'
e 1 ( s) () Ms Ms
2
l l ' e ( s' ) s, s ' M ,l ', s ' s'
( 1,2,...,3r )
如果某确定的的解在长波限满足条件
x, y, z
总势能为
1 0 (l )ul (l , l ' )ul ul' ... 2 l , l ' l ,
0为常数,是平衡位置时 的势能。 (l ) u l 0 0 (l ' , l ) 0
ul
1 NM
k,
Qk ek e ik Rl
其 Qk 是复简正坐标,由于 u l 中为实量,则
* ek Qk ek Qk
ul* ul 那么;
若约定极化矢量满足关系式
ek ek
则复简正坐标
* Qk Qk
1 T M ul ul 2 l 1 Qk ' ' Qk (ek ' ' ek ) k ', k 2 k ,k ' , ' 1 * Qk ' Qk (ek ' ek ) 2 k , ' 1 * Qk Qk 2 k ,
因此,光学模代表元胞的质心不动,元胞内原子的相对运动。 3. 格波频率的计算 二维的正方晶格 D (k )
1 M
(l )e
l
ik Rl
l fl l l
l 0
1 1 i , 5 (i j ) 2
设为声学模,由于对声学模有
e (1) e ( 2) M1 M2
代入上式可得
e (1) M1
M 1 e ' (1) M 2 e ' (2) 0
由于3个声学模解的极化向量 e (s) 因此,光学模满足条件
( 1,2,3) 彼此正交。
M 1 e ' (1) M 2 e ' (2) M 1ul (1) M 2ul (2) 0
(一次量子化)
ll ' i ( , x, y, z )
那么容易求得简正坐标的对易律:
[ Pk , Qk ' ' ]
1 N
i ( k Rl k ' Rl ') ( e e )[ p , u ] e k k ' ' l l ' l ,l ' ,
0的格波解称为光学模。
可以证明:简单晶格中的全部格波解都属于声学模 因为:
D (k )
1 M
(l )e
l
ik Rl
1 D (k 0) M
(l ) 0
l
在复式晶格中,同时存在声学模和光学模 对于元胞中有r个原子的复式晶格有本征方程
k 2 D e ( s ' ) ek ( s) k s, s ' ,s '
对于动能
晶格振动的势能
其中
1 u ( l l ' ) u l l' 2 l ,l ' ,
1 1 * Q Q k k ' ' N 2 k ,k ' , '
e
l
i ( k ' k ) Rl
A
1 ik ' ( Rl Rl ' ) A ek ( l l ' ) e ek ' ' M l ek D ( k ' )ek ' '
2 ( ek ek ' ' ) ' ( k ' )
那么
1 2 * (k )Qk Qk 2 k ,
1 * 2 * H Qk Qk (k )Qk Q k 2 k ,
晶格振动的哈密顿可简化为
H在简正坐标中表示为3N个独立项之和; 利用拉氏函数
L T
Pk L Qk
可求出Qk的共轭动量
Q
* k
1 * 2 * H Pk Pk (k )Qk Qk 2 k ,
根据正则方程
Pk
H Qk
可求出简正坐标满足方程
第二章
声子
1.晶格动力学
本节用经典力学的方法讨论完整晶格中原子(离子)绕平衡位置的振动
晶格振动
首先我们考虑一个元胞中只有一个原子(离子)的简单晶格 晶体的元胞数为N,原子质量为M,原子l 的位置:
X l (t ) Rl ul (t )
ul (t ) 则代表此原子的位移。
晶格振动的总动能
1 T M ul ul 2 l ,
