测量物体的高度(一)演示文稿
合集下载
《测量物体的高度》教学课件

测 得 数 据
MN=Ltanα+ a
α
L
E
N
C a A
测量项目 测倾器高a
第一次
a =1.23m
第二次 α=19°49 ′
a =1.21 m
平均值
倾斜角α α=30°15′
AN的长L
L=20.15m
α=30°2 ′
a =1.22m
L=19.97m
L=20.06m
计 算 过 程 活 动 感 受
≈ 在Rt MCE中,ME = ECtanα= ANtanα=20.6× tan30° 2′ 20.6× 0.578=11.60m, MN=ME+EN=ME+AC=11.60+1.22=12.82m
根据测量数据,你 能求出物体MN的 M 高度吗?说说你的 理由.
E N
(p21)
β
D B
α
b
C
a
A
根据测量数据,物体MN的高度计算过程:
在Rt△MDE中, ED=
ME tan
ME a
ME
ME tan
M
在Rt△MCE中,
E
β
D
α
b
C a A
EC = tan
EC-ED= tan a
-
=b
N
B
ME tan ME tan a tan a tan
90° 90°
60° 30° 30°
60°
0°
活动一:测量倾斜角.
M
根据刚才测量
数据,你能求出
水平线 1 2 3
目标M的仰角或
俯角吗?说说你
4
的理由.
活动二: 测量底部可以到达的物体的高度.
MN=Ltanα+ a
α
L
E
N
C a A
测量项目 测倾器高a
第一次
a =1.23m
第二次 α=19°49 ′
a =1.21 m
平均值
倾斜角α α=30°15′
AN的长L
L=20.15m
α=30°2 ′
a =1.22m
L=19.97m
L=20.06m
计 算 过 程 活 动 感 受
≈ 在Rt MCE中,ME = ECtanα= ANtanα=20.6× tan30° 2′ 20.6× 0.578=11.60m, MN=ME+EN=ME+AC=11.60+1.22=12.82m
根据测量数据,你 能求出物体MN的 M 高度吗?说说你的 理由.
E N
(p21)
β
D B
α
b
C
a
A
根据测量数据,物体MN的高度计算过程:
在Rt△MDE中, ED=
ME tan
ME a
ME
ME tan
M
在Rt△MCE中,
E
β
D
α
b
C a A
EC = tan
EC-ED= tan a
-
=b
N
B
ME tan ME tan a tan a tan
90° 90°
60° 30° 30°
60°
0°
活动一:测量倾斜角.
M
根据刚才测量
数据,你能求出
水平线 1 2 3
目标M的仰角或
俯角吗?说说你
4
的理由.
活动二: 测量底部可以到达的物体的高度.
测量物体的高度(1)PPT课件

2.在测点A与物体之间的B处安置测倾(A,B与N在
一条直线上),测得M的仰角∠MCE=β.
3.量出测倾器的高度AC=BD=a,以及测点
A,B之间的距离AB=b.
根据测量数据,你能求出物体MN的
高度202吗0年1?0月说2日说你的理由.
6
知识在于积累
(1)到目前为止,你有哪些测量物体高度的方法?
(2)如果一个物体的高度已知或容易测量,那 么如何测量某测点到该物体的水平距离.
根据测量数据,你能求出物体MN的
高度吗?说说你的理由.
2020年10月2日
5
测量物体的高度
活动三:测量底部不可以到达 的物体的高度.
所谓“底部不可以到达”,就 是在地面上不能直接测得测点 与被测物体底部之间的距离.
如图,要测量物体MN的高度,可以按下列步骤进行:
1.在测点A处安置测倾器,测得M的仰角∠MCE=α.
测量倾斜角可以用测倾器,简单的测 倾器由度盘,铅垂和支杆组成(如图).
使用测倾器测量倾斜角的步骤如下 : 1.把支杆竖直插入地面,使支杆的 中心线,铅垂线和度盘的00刻线重合, 这时度盘的顶线PQ在水平位置. 2、转动转盘,使度盘的直径对准目 标M,记下此时铅垂线所指的度数.
2020年10月2日
4
测量物体的高度
九年级数学(下)第一章 直角三角形的边角关系
5.测量物体的高度(1)
2020年10月2日
1
回顾与思考1
直角三角的边角关系
直角三角形三边的关系: 勾股定理 a2+b2=c2.
直角三角形两锐角的关系:两锐角互余 ∠A+∠B=900.
直角三角形边与角之间的关系:锐角三角函数
sinAcoBsa, c
测量物体的高度(第一课时)
2、在测点A与物体之间的B处安置测倾器,测得此时M的仰角 ∠MDE=β; 3、量出测倾器的高度AC=BD=a,以及测点A,B之间的距离 AB=b.根据测量数据,可求出物体MN的高度.
某校数学兴趣小组要测量摩天轮 A
的高度。如图,他们在C处测得摩
天轮的最高点A的仰角为30°,再
往摩天轮方向前进50m至D处,测
回顾复习
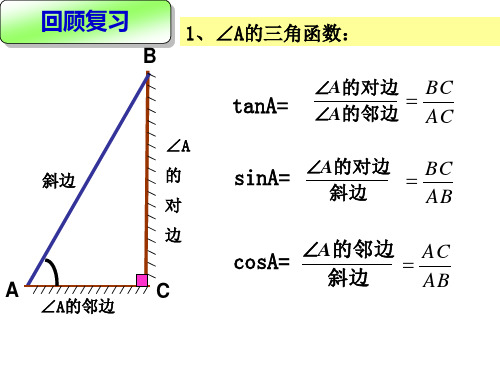
1、∠A的三角函数:
B
tanA=
A的对边 A的邻边
BC AC
∠A
斜边
的 对
sinA=
A的对边 斜边
BC AB
边
A
C
∠A的邻边
cosA=
A的邻边 斜边
AC AB
三角函数值 三角函数 sinα
角α
30°
1
2
45°
2
2
60°
3
2
cosα tanα
3
3
2
3
2
1
2
1
2
3
1、仰角、俯角:
铅 垂
仰角
M
C
l
E
a
A
N
1、在测点A安置测倾器,测得M的仰角∠MCE=α;
l 2、量出测点A到物体底部N的水平距离AN= ;
3、量出测倾器的高度 AC=a,可求出MN的高度。
如图,小明去测量学校主楼的高度,经测量,大门 距主楼的距离是30m,在大门处测得主楼顶部的仰角 是30°,而当时侧倾器离地面1.4m,求学校主楼的高度.
M
解:如图,作EM垂直CD于M点, CM=BE=1.4m,∠DEM=30°,BC=EM=30 m, 在Rt△DEM中,DM=EMtan30°≈30×0.577 =17.32(m) CD=DM+CM=17.32+1.4=18.72(m)
数学九年级下测量物体的高度课件

90 90
M
30°
0
2、转动转盘,使度盘的直径对准目标M,记下此时铅垂线 所指的度数。
大家要认真 思考吆
活动二: .测量底部可以到达的物体的高度.
所谓“底部可以到达”,就是在地
面
上可以无障碍地直接测得测点M 注 意 要 领 啊!
与如被图测,物要体测底量部物之体间MN的距高离度.,
需测量哪些数据?步骤如下: 1.在测点A处安置测倾器, 测得M的仰角∠MCE=α.
测得数据
测量项目 第一次 第二次
平均值
计算过程 活动感受 负责人及参加人员
计算者和复核者 指导教师审核意见
备注
想一想
(p21)
A,B之间的距离AB=b. M
根据测量数据,你能
求出物体MN的高度吗?
说说你的理由.
E
N
β Dα
C
ba
B
A
总结
(1)侧倾器的使用 (2)误差的解决办法---用平均值
(3)到目前为止,你有那些测量物体高度的方法?
测量底部可以到达的 物体的高度,如左图
测量底部不可以直接到达 的物体的高度,如右图
思考:
大家要认真 思考吆!
如何测量底部不可以到达的物体的高度.
所谓“底部不可以到达”,就是在地面 上不能直接测得测点与被测物体底部之 间的距离.
M
要测量物体MN的 高度,使用侧倾器 测一次仰角够吗? E
α
C
a
N
A
活动三: 测量底部不可以到达的物体的高度.
要测量物体MN的高度,测一次仰角是不够的. 还需哪些条件,测量哪 些数据?
E
tanα+ a N
α
C
人教版数学活动测量物体的高度

测量底部可以直接到 M
达的物体的高度:
Cα
E
A
N
1、在测点A安置测角仪,测得M的仰角∠MCE=α ; 2、量出测点A到物体底部N的水平距离AN=d; 3、量出测角仪的高度AC=h,可求出MN的高度。
MN=ME+EN=d·tanα +h
测量底部不可以直接到
M
达的物体的高度:
C αD β
E
N
A
B
1、在测点A处安置测角仪,测得此时M的仰角∠MCE=α ;
如右图
测量物体的高度
出谋划策
小明很想知道学校旗杆的高度,你有什 么办法吗?
解决问题
小鸣将测角仪安放在与旗杆AB底部相距6m的C处,量出测角
仪的高度CD=1m,测得旗杆顶端B的仰角 =60°,则旗
杆AB的高度为
(计算结果保留根号)
实践活动中,要求测教学楼的高度
备注
第一次
第二次
平均值
探索总结一
我们直接测量出这根木棒的长度为2.32米。你们小组 的测量结果与此相接近吗?有差距的原因是什么?
结论: 一是误差引起的。这种误差主要来源于我们自制的测角 仪; 二是读数错误。
探索总结二:测量物体高度有哪些方 法?
当测量底部可以到达的物体的高度时,如左图 当测量底部不可以直接到达的物体的高度时,
1、把支架竖直插入地面,使支架的中心线、铅垂线和度盘 的0°刻度线重合,这时度盘的顶线PQ在水平位置。
90 90
M
30°
0
2、转动转盘,使度盘的直径对准目标M,记下此时铅垂线 所指的度数。
活动内容
以6~8人为一小组,合作测量旗杆的高度,并填写记录。
鲁教版九年级数学上册测量物体的高度课件

使用测倾器测量倾斜角的步骤如下
• 1、把支杆竖直插入地面,使支杆的中心 线、铅垂线和度盘的0°刻度线重合,这 时度盘的顶端的顶线PQ在水平位置。 • 2、转动度盘,使度盘的直径对准目标M, 记下此时铅垂线所指的读数。 • 根据测量数据,你能求出目标M的仰角 吗?说说你的理由。
测量物体的高度
活动二:测量底部可以到达的物体的高度
测量物体的高度
测量物体的高度
巩固与拓展
1、甲、已两楼相距30米,甲楼高40米,自甲楼楼 顶看已楼楼顶,仰角为30°,甲已两楼相距30米, 已楼有多高?(精确到1米)
2、为了测量山坡的护坡石坝与地面的倾角α,把 一根长为4.5的竹杆AC斜靠在石坝旁,量出竿长1米 时它离地面的高度为0.6米,有量得竿顶与坝角的 距离BC=2.8米,这样∠α就可以量出来了。请你 算算。
“所谓“底部可以到达”,就是 在地面上可以无障碍的直接测 得测点与被测物体的底部之间 的距离,如图,要测量物体 MN的高度,可按下列步骤进 行:
测量物体的高度
活动三:测量底部不可以到达的物体 的高度
• 所谓“底部不可以到达”,就是在地面上不可 以直接测得测点与被测物体之间的距离。如图, 要测量物体MN的高度,可按下列步骤进行:
M
C A
测量物体的高度
D B
E
N
步骤:
• 1、在测点A处安置测倾器,测得此时M的仰角 ∠MCE=α。 • 2、在测点A与物体之间的B处安置测倾器(A, B与N在一条直线上),测得此时M的仰角 ∠MDE=β。 • 3、量出测倾器的高度AC=BD=a,以及测点 A,B之间的距离AB=b。 • 根据测量数据,你能求出物体MN的高度吗? 说说你的理由。
测量物体的高度
议一议
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
M
解:如图,作EM垂直CD于M点,根据题意,可知 EB=1.4m,∠DEM=30°,BC=EM=30 m, CM=BE=1.4m 在Rt△DEM中,DM=EMtan30°≈30×0.577 =17.32(m) CD=DM+CM=17.32+1.4=18.72(m)
三、测量底部不可以直接到达的物体的高度
1、在测点A安置测倾器,测得M 的仰角∠MCE=α ;
2、量出测点A到物体底部N的水 平距离AN=l; 3、量出测倾器的高度AC=a,可 求出MN的高度。
C α
A
E
N
MN=ME+EN=l· tanα +a
如图,某中学在主楼的顶部和大门的上方之间挂一些彩 旗.经测量,得到大门的高度是5m,大门距主楼的距离是 30m,在大门处测得主楼顶部的仰角是30°,而当时侧倾器离 地面1.4m,求学校主楼的高度 (精确到0.01m)
M
P Q 9下:
2、转动度盘,使度盘的直径对准目标M,记下此时铅垂线所指的读数。
M
P
30°
Q
二、测量底部可以直接到达的物体的高度
• 所谓“底部可以到达”---就是在地面上可以无障碍地 直接测得测点与被测物体的底部之间的距离. • 如图,要测量物体MN的高度,可按下列步骤进行: M
C
A
α
D
B
β
E N
ME ME b, MN ME a tan tan
下表是小亮所填实习报告的部分内容: 课题 在平面上测量地王大厦的高AB A
测量示意图 E C 测量项目 测得数据 第一次 第二次 平均值
α
F D
β
∠α
30° 16’ 29° 44’
G B ∠β
44° 35’ 45° 25’
CD的长 60.11m 59.89m
1.请根据小亮测得的数据,填写表中的空格; 2.通过计算得,地王大厦的高为(已知测倾器的高 CE=DF=1m)______m (精确到1m). 1. 30°, 45°, 60m 2. 在Rt△AEG中,EG=AG/tan30°=1.732AG 在Rt△AFG中,FG=AG/tan45°=AG EG-FG=CD 1.732AG-AG=60 AG=60÷0.732≈81.96 AB=AG+1≈83(m)
• 所谓“底部不可以到达”---就是在地面上不可以直接 测得测点与被测物体之间的距离。 • 如图,要测量物体MN的高度,可按下列步骤进行:
1、在测点A处安置测倾器,测得 此时M的仰角∠MCE=α ;
M
2、在测点A与物体之间B处安置 测倾器,测得此时M的仰角 ∠MDE=β ; 3、量出测倾器的高度AC=BD=a, 以及测点A,B之间的距离AB=b.根 据测量数据,可求出物体MN的高 度。
课题
测量示意图 测量项目 测得数据 第一次 第二次 平均值
计算过程
活动感受 负责人及参加人员
计算者和复核者 指导教师审核意见
备注
E
D
总
结
(1)侧倾器的使用 (2)误差的解决办法---用平均值
(3)到目前为止,你有那些测量物体高度的方法?
测量底部可以到达的 物体的高度,如左图
测量底部不可以直接到达 的物体的高度,如右图
作
业
1. 分组制作简单的测倾器. 2.选择一个底部可以到达的物体,测量它的高度并撰写 一份活动报告,阐明活动课题、测量示意图、测得数据 和计算过程等. 3.选择一个底部不可以到达的物体,测量它的高度 并撰写一份活动报告,阐明活动课题、测量示意图、 测得数据和计算过程等. (下表作参考)
第一章 直角三角形的边角关系
第五节 测量物体的高度(一)
一、如何测量倾斜角
•测量倾斜角可以用测倾器。 ----简单的侧倾器由度盘、铅锤和支杆组成
P
Q
度盘
9 0 0
90
铅锤
支杆
使用测倾器测量倾斜角的步骤如下:
1、把支架竖直插入地面,使支架的中心线、铅锤线和度盘的0°刻度线重 合,这时度盘的顶线PQ在水平位置。
拓展应用
• 1.(2005深圳)大楼AD的高为100米,远处有一塔BC, 某人在楼底A处测得塔顶B处的仰角为60°,爬到楼 顶D测得塔顶B点仰角为30°,求塔BC的高度.
B
D
A
C
• 2.如图,在离铁塔150米的A处,用测角仪测得塔顶的仰角为 30°,已知测角仪高AD=1.5米,求铁塔高BE.
B
A
解:如图,作EM垂直CD于M点,根据题意,可知 EB=1.4m,∠DEM=30°,BC=EM=30 m, CM=BE=1.4m 在Rt△DEM中,DM=EMtan30°≈30×0.577 =17.32(m) CD=DM+CM=17.32+1.4=18.72(m)
三、测量底部不可以直接到达的物体的高度
1、在测点A安置测倾器,测得M 的仰角∠MCE=α ;
2、量出测点A到物体底部N的水 平距离AN=l; 3、量出测倾器的高度AC=a,可 求出MN的高度。
C α
A
E
N
MN=ME+EN=l· tanα +a
如图,某中学在主楼的顶部和大门的上方之间挂一些彩 旗.经测量,得到大门的高度是5m,大门距主楼的距离是 30m,在大门处测得主楼顶部的仰角是30°,而当时侧倾器离 地面1.4m,求学校主楼的高度 (精确到0.01m)
M
P Q 9下:
2、转动度盘,使度盘的直径对准目标M,记下此时铅垂线所指的读数。
M
P
30°
Q
二、测量底部可以直接到达的物体的高度
• 所谓“底部可以到达”---就是在地面上可以无障碍地 直接测得测点与被测物体的底部之间的距离. • 如图,要测量物体MN的高度,可按下列步骤进行: M
C
A
α
D
B
β
E N
ME ME b, MN ME a tan tan
下表是小亮所填实习报告的部分内容: 课题 在平面上测量地王大厦的高AB A
测量示意图 E C 测量项目 测得数据 第一次 第二次 平均值
α
F D
β
∠α
30° 16’ 29° 44’
G B ∠β
44° 35’ 45° 25’
CD的长 60.11m 59.89m
1.请根据小亮测得的数据,填写表中的空格; 2.通过计算得,地王大厦的高为(已知测倾器的高 CE=DF=1m)______m (精确到1m). 1. 30°, 45°, 60m 2. 在Rt△AEG中,EG=AG/tan30°=1.732AG 在Rt△AFG中,FG=AG/tan45°=AG EG-FG=CD 1.732AG-AG=60 AG=60÷0.732≈81.96 AB=AG+1≈83(m)
• 所谓“底部不可以到达”---就是在地面上不可以直接 测得测点与被测物体之间的距离。 • 如图,要测量物体MN的高度,可按下列步骤进行:
1、在测点A处安置测倾器,测得 此时M的仰角∠MCE=α ;
M
2、在测点A与物体之间B处安置 测倾器,测得此时M的仰角 ∠MDE=β ; 3、量出测倾器的高度AC=BD=a, 以及测点A,B之间的距离AB=b.根 据测量数据,可求出物体MN的高 度。
课题
测量示意图 测量项目 测得数据 第一次 第二次 平均值
计算过程
活动感受 负责人及参加人员
计算者和复核者 指导教师审核意见
备注
E
D
总
结
(1)侧倾器的使用 (2)误差的解决办法---用平均值
(3)到目前为止,你有那些测量物体高度的方法?
测量底部可以到达的 物体的高度,如左图
测量底部不可以直接到达 的物体的高度,如右图
作
业
1. 分组制作简单的测倾器. 2.选择一个底部可以到达的物体,测量它的高度并撰写 一份活动报告,阐明活动课题、测量示意图、测得数据 和计算过程等. 3.选择一个底部不可以到达的物体,测量它的高度 并撰写一份活动报告,阐明活动课题、测量示意图、 测得数据和计算过程等. (下表作参考)
第一章 直角三角形的边角关系
第五节 测量物体的高度(一)
一、如何测量倾斜角
•测量倾斜角可以用测倾器。 ----简单的侧倾器由度盘、铅锤和支杆组成
P
Q
度盘
9 0 0
90
铅锤
支杆
使用测倾器测量倾斜角的步骤如下:
1、把支架竖直插入地面,使支架的中心线、铅锤线和度盘的0°刻度线重 合,这时度盘的顶线PQ在水平位置。
拓展应用
• 1.(2005深圳)大楼AD的高为100米,远处有一塔BC, 某人在楼底A处测得塔顶B处的仰角为60°,爬到楼 顶D测得塔顶B点仰角为30°,求塔BC的高度.
B
D
A
C
• 2.如图,在离铁塔150米的A处,用测角仪测得塔顶的仰角为 30°,已知测角仪高AD=1.5米,求铁塔高BE.
B
A
