22-3
COST DOWN专案评比奖励办法3-22

一、目的:对COST DOWN专案改善提出明确要求,制定具体可行的评比奖励制度,发挥专案小组之创造力、团队协助能力,以达成公司COST DOWN下降30%的整体目标。
二、适用范围:适用于本公司COST DOWN专案成效的评审,为奖励标准提供依据。
三、定义:COST DOWN:围绕公司的经营战略、方针目标推动的改善活动,以材料费用节约、效率提升、人员减少、不良下降等方面降低综合成本,运用自动化技术、工业(IE)手法等展开。
四、权责区分:1.主导方主导惟达内部之改善方向,配合圜达改善事项的推动,整合惟达各专案小组改善对策之进度、成效回报圜达主导者。
改善成果之确认、评比,奖励之申请2.专案负责人改善方案确认、对策拟定及对策执行跟进确认3.小组成员<冲压> 改善方案之提出, 冲压模具之改善及变更, 提供改善之零件,试作单的快速配合,现场数据的提供<塑胶> 改善方案之提出, 塑料模具之改善及变更,提供改善之零件, 试作单的快速配合,现场数据的提供<设备、研发> 改善方案之提出,设备及制程改善, 新设备开发<生产、生技> 试作单的快速配合,设备及制程改善,现场数据的提供<品保> 改善方案之提出,试作品质量确认及快速信赖性验证<采购> 改善方案之提出,协寻新物料及厂商审查五 . 内容:1. COST DOWN改善活动范围1.1材料费用节约:材质变更、新旧次料比等;1.2效率提升:机台稼动率提升,作业员工、设备产能提升等;1.3人员减少:人机比下降、设备取代人员作业、工序优化等;1.4不良率下降:制程不良率下降等;2、改善活动评比时间12/E3、改善活动评比标准,见附件一评分标准.doc4、奖项设置4.1 奖项产生4.1.1得奖要求:达成成本下降30%目标4.1.2依评分标准得分排名产出一、二名4.1.3无法排名前两名时,获得鼓励奖4.2六 . 附件:1.评分标准.........................................附件一。
八年级生物下册第22章第3节植物的主要类群精练新版北师大版含答案

第3节植物的主要类群知识点一苔藓植物1.生活环境: 阴湿的地面、背阴的墙壁和树皮上。
2.结构(1)没有真正的根,假根只起固定植物体的作用,不能吸收水分和无机盐。
(2)有茎和叶的分化。
①茎:弱小,没有输导组织。
②叶:进行光合作用,吸收水分和无机盐。
3.举例: 葫芦藓、地钱、小墙藓等。
4.作用(1)对二氧化硫等有毒气体非常敏感,可作为监测空气污染的指示植物。
(2)涵蓄水分,保持水土。
(3)植物界的拓荒者,与土壤的形成有关。
(4) 北极冻原的主要绿色植物,是某些植食动物的食物之一。
知识点二蕨类植物5.生活环境:森林、溪沟、田野的阴湿环境里。
6.特征(1)一般都具有根、茎、叶等器官,并有输导组织和机械组织。
(2)靠孢子繁殖后代。
7.作用(1)大量的古代蕨类植物形成了煤炭。
(2)现存的蕨类植物。
①作为野菜,如蕨的嫩叶。
②入药,如贯众、卷柏。
③观赏,如芒萁、巢蕨。
④作为绿肥和饲料,如满江红。
知识点三种子植物8.特征(1)体内有维管组织——韧皮部和木质部。
(2)能产生种子并用种子繁殖。
9.分类(1)依据:种子外面是否有果皮包被。
(2)类型:①裸子植物:种子裸露,其外层没有果皮包被。
②被子植物:种子外层有果皮包被。
10.裸子植物(1)生活环境:主要分布在温带地区和热带、亚热带海拔较高的山区。
(2)我国被誉为“裸子植物的故乡”。
(3)我国的银杉、水杉和秃杉等是世界上的珍稀树种。
11.被子植物:植物界中等级最高、种类最多、分布最广、与人类关系最密切的植物类群。
(1)单子叶植物。
①特点:叶多是平行脉,花瓣为3或3的倍数。
②举例: 玉米、小麦、大麦等。
(2)双子叶植物。
①特点:叶多是网状脉,花瓣为4、5或4、5的倍数。
②举例: 白菜、萝卜、花生等。
知识点一苔藓植物1.葫芦藓的叶不能完成的生理过程是(D)A.光合作用B.水的吸收C.吸收无机盐D.运输水分2.苔藓植物植株一般都很矮小,在形态结构上的明显特征是(C)A.没有茎和叶B.不能进行生殖C.没有真正的根D.受精作用离不开水3.成片的苔藓植物对水土保持有一定的作用,这是因为苔藓植物(A)A.密植的植株间的缝隙能够蓄积大量的水分B.输导组织中能蓄积大量的水分C.根系发达,能吸收大量的水分D.环境湿润,叶的蒸腾作用非常小4.联系生活实际,回答问题。
22--3激光原理及在军事上的应用(三)

C)激光致盲器 ) 发射一较强激光, 发射一较强激光, 烧坏敌人眼睛, 烧坏敌人眼睛, 使之致盲的武器
呀!我的眼看 不见了! 不见了!
激光致盲器是目前 真正进入实用阶段 的激光武器. 的激光武器.
"魟鱼"激光致盲武器 魟鱼" 魟鱼 激光弦目描准具(英国) 激光弦目描准具(英国) 是一种激光致盲描准具, 是一种激光致盲描准具,1982年马鸟战争期间 年马鸟战争期间 安装在"竞技神"号战舰上, 安装在"竞技神"号战舰上,不料实战中效果良 造成3架阿根廷飞机失事 架阿根廷飞机失事. 好,造成 架阿根廷飞机失事.所有这一切均是保 密的.直致1989年英军舰"考文垂"号上因帆布 年英军舰" 密的.直致 年英军舰 考文垂" 未盖好才被记者拍下照片, 年公布于世. 未盖好才被记者拍下照片,1990年公布于世. 年公布于世
据称可破坏10公 据称可破坏 公 激光排 激光燃料箱 里外的低空直升 气/热 热 飞机的蒙皮和20 飞机的蒙皮和 公里远的红外制 导导弹和光学传 前西德高能激光防空坦克 前西德高能激光防空坦克 感器 可以预期: 世纪的战场将是 世纪的战场将是" 可以预期:21世纪的战场将是"光"与"箭"的战场
激光器
一)激光告警与侦察设备 类型: 类型: 1)光电探测阵列型激光告警器; )光电探测阵列型激光告警器; 英国产: 如:英国产:RL1 RL2 ,SAVIOUR型 型 法国产: 法国产:THOMSON--CSF型 型 以色列: 以色列:LWS--2型 型 有激光! 有激光! 快转移! 快转移! 中国:LWR--1型 中国: 型 (单兵钢盔激光告警器和 防护镜.) 防护镜.)
数3--22真题答案

2022年考研数学(三)试卷答案速查一、选择题(1)C. (2)A. (3)C. (4)A. (5)B. (6)D. (7)C. (8)D. (9)B. (10)B.二、填空题(11)12e . (12)ln 3−. (13)0. (14)2e 2e 1−+. (15)1−. (16)58. 三、解答题(17)斜渐近线2y x =. (18)384. (19)2(π1)−. (20)收敛域[]1,1,−[)(]arctan 12ln ,1,00,1,()22,0.x xx S x x x xx +⎧+∈−⎪=−⎨⎪=⎩(21)(I)01000⎛⎫ ⎪⎪= ⎪ ⎪ ⎝Q,12321323,,,x y y x y x y y ⎧=+⎪⎪⎪=⎨⎪⎪=−⎪⎩222123()442f y y y =++x ; (II )见解析.(22)1111ˆ2n m i j i j X Y n m θ==⎛⎫=+ ⎪+⎝⎭∑∑;21n mθ+.2022年全国硕士研究生入学统一考试数学(三)参考答案一、选择题:1~10小题,每小题5分,共50分.下列每题给出的四个选项中,只有一个选项是符合题目要求的. (1)【答案】(C ). 【解析】①若()()x x αβ,则0()lim 1()x x x →=αβ.因此2200()()()lim lim 111()()()x x x x x x x x →→=⋅=⋅=αααβββ,①正确;②错,反例:(),()x x x x ==−αβ; ③若()()x x αβ,则0()lim1()x x x →=αβ,则00()()()()limlim 110()()()x x x x x x x x x αβαβααα→→⎡⎤−=−=−=⎢⎥⎣⎦, 因此()()(())x x o x −=αβα,③正确;④若()()(())x x o x −=αβα,则0()()lim0()x x x x →−=αβα,则0()()lim ()()x x x x x αβαα→⎡⎤−=⎢⎥⎣⎦0()1lim0()x x x →−=βα,则0()lim1()x x x →=βα,即()()x x αβ,④正确. 因此真命题有①③④,选(C ).(2)【答案】(A ). 【解析】1212lim 1,2n n a a a →∞=>=>=故根据极限的保号性,存在*N N ∈,当n N >时,恒有12,n a a a >>故{}n a 的最大和最小值一定在其前N 项中取得,选(A ).(3)【答案】(C ).【解析】(,)()()d ()d ()d ()d ,x yx yx yx yF x y x y t f t t x f t t y f t t tf t t −−−−=−−=−−⎰⎰⎰⎰0()d ()()()()()d x y x y F f t t xf x y yf x y x y f x y f t t x −−∂=+−−−−−−=∂⎰⎰,00()()d ()()()()d x y x y Fxf x y f t t yf x y x y f x y f t t y−−∂=−−−+−+−−=−∂⎰⎰,.F Fx y∂∂∴=−∂∂又2222(),(),F F f x y f x y x y∂∂=−=−∂∂ 2222.F F x y ∂∂∴=∂∂综上,正确选项为(C ). (4)【答案】(A ).【解析】先比较12,I I ,令()ln(1),(0,1)2xf x x x =−+∈,则111()0,(0,1)212(1)x f x x x x −'=−=<∈++,又(0)0,f =所以()(0)0f x f <=,ln(1)2(1cos )1cos x x x x+<++,12I I <; 再比较23,I I ,ln(1)2,111cos 1cos 11sin sin 22x x xx xx x x x +<=++++23I I <,故选(A ).(5)【答案】(B ).【解析】A 有3个不同的特征值,则A 一定可以对角化,故存在可逆矩阵P ,使得1−=A P P Λ,反之也成立,选(B );(A )选项中=A P Q Λ意味着A 和Λ等价,不对; (C )选项A 未必是对称阵,必要性不一定成立; (D )选项中T =A P P Λ意味着A 和Λ合同,不对. (6)【答案】(D ).【解析】()222211111111,120111140113a a a a b b b b ⎛⎫⎛⎫ ⎪ ⎪=→−−⎪ ⎪ ⎪ ⎪−−⎝⎭⎝⎭A b ,当1a =或1b =时,此时方程组无解;当1a ≠且1b ≠时, ()11111,0111310011a a b a b a ⎛⎫⎪ ⎪⎪→+ ⎪− ⎪ ⎪−−−−⎝⎭A b , 当a b =时,31011b a −≠−−,()(),r r <A A b ,此时方程组无解; 当a b ≠时,()(),3r r ==A A b ,此时方程组唯一解.故答案选(D ). (7)【答案】(C ).【解析】()22123422311111,,,11011110111⎛⎫⎛⎫⎪ ⎪=→−−− ⎪ ⎪⎪ ⎪−−−⎝⎭⎝⎭λλλααααλλλλλλλλλλλ 2221101100(2)(1)(1)(1)⎛⎫ ⎪→−−− ⎪ ⎪+−−+⎝⎭λλλλλλλλλλ,已知3ααα12,,与124,,ααα等价,则须有()()()1231241234,,,,,,,αααααααααα==r r r . 若1λ=−,()()123124,,3,,,2r r αααααα==,矛盾,故1λ≠−; 若2λ=−,()()123124,,2,,,3r r αααααα==,矛盾,故2λ≠−; 若1λ=,()()123124,,,,1r r ==αααααα,满足题意;若1,2,1λλλ≠−≠−≠,()()123124,,,,3r r ==αααααα,满足题意,故选(C ). (8)【答案】(D ).【解析】(31)()9()D X Y D X D Y −+=+, 由1~(0,4),~(3,)3X N Y B 知,2()4,()3D X D Y ==,故(31)10D X Y −+=,选(D ). (9)【答案】(B ).【解析】由大数定律知, 211n i i X n =∑依概率收敛于2()E X .由于122211()()d (1)d 6E X x f x x x x x +∞−∞−==−=⎰⎰,故选(B ). (10)【答案】(B ). 【解析】令事件(){}max ,2A X Y ==,(){}min ,1B X Y ==,则(){}{}1,21,20.1P A P X Y P X Y b ==−=+===+, (){}{}1,11,20.2P B P X Y P X Y ===+===, (){}1,20.1P AB P X Y ====,因为事件,A B 独立,所以()()()P AB P A P B =,即()0.10.20.1b +⨯=,又由规范性知0.6a b +=,则可得0.2,0.4a b ==,所以X 的边缘分布律为Y则()10.610.40.2,E X =−⨯+⨯=−()00.310.220.5 1.2,E Y =⨯+⨯+⨯=()()10.120.410.120.10.6,E XY =−⨯+−⨯+⨯+⨯=−所以()()()()Cov ,0.36X Y E XY E X E Y =−=−. 二、填空题:11~16小题,每小题5分,共30分. (11)【答案】 12e . 【解析】cot 1e lim cot ln201e lim e 2xx xx x x →+⋅→⎛⎫+= ⎪⎝⎭,其中00001e 1e ln 11e e1122lim cot ln lim lim lim 2tan 22x x x x x x x x x x x x →→→→++−+−⋅====,所以原式12e =. (12)【答案】ln 3. 【解析】22222200024226d d d 242424x x xx x x x x x x x−+=−++++++⎰⎰⎰ ()()22221ln 246d 13x x x x =++−++⎰ln12ln 4=−ln 3=. (13)【答案】0.【解析】()f x 是周期为2π的偶函数,()f x '''为周期为2π的奇函数,(2π)(0)0f f ''''''==.(14)【答案】2e 2e 1−+. 【解析】()()11d d de e d x x y x xx f x f y x y x y+∞+∞+−−∞−∞−=⎰⎰⎰⎰()111120d e d e e d e 2e 1x yx x xx y x ++==−=−+⎰⎰⎰.(15)【答案】1−.【解析】100100211001110110010001100−−⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪−=− ⎪ ⎪ ⎪ ⎪ ⎪ ⎪−⎝⎭⎝⎭⎝⎭A , 则11100211100010110110001001001100010111−−−−−⎛⎫⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪ ⎪=−−=− ⎪⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪−−−⎝⎭⎝⎭⎝⎭⎝⎭A ,故1()1tr −=−A . (16)【答案】58. 【解析】()()()P B C P BC A B C P A B C =,由B 与C 相互独立知,5()()()()()9P B C P B P C P B P C =+−=, 又A 与B 互不相容,A 与C 互不相容,()()()()()()()()P A B C P A P B P C P AB P AC P BC P ABC =++−−−+8()()()()9P A P B P C P BC =++−=, 得5()8P BC A B C =. 三、解答题:17~22小题,共70分.解答应写出文字说明、证明过程或演算步骤. (17)【答案】斜渐近线2y x =.【解析】(e2ed xxy x C −⎡⎤=+⎢⎥⎢⎥⎣⎦⎰2e x C =+. 将()13y =代入可得e C =,即()12e0y x x =+>.由函数解析式可知,曲线没有垂直渐近线; 又由于()()12elim lim x x y x x →+∞→+∞+==+∞,曲线没有水平渐近线;又()1limlim 2e 2x x y x k xx x →+∞→+∞=+==,()()1lim lim 20e 2x x b y x kx x x →+∞→+∞=−==⎡⎤⎣⎦+−,故曲线有斜渐近线2y x =. (18)【答案】384.【解析】由题意得利润函数()111632681160 1.5681392021668L pQ x y Q Q x y x y xy x y =−−=−−−=−−−,111632521632696021660,23207280,L x y y xL x y xy y−−−⎧∂=−−=⎪∂⎪⎨∂⎪=−−=⎪∂⎩解得唯一驻点256,64,x y =⎧⎨=⎩ 由实际意义可知此时利润最大,对应的产量384Q =.(19)【答案】2(π1)−.【解析】将积分区域D 分为两部分12D D D =+,其中:1{(,)2,20,02}D x y yx x y=+−,222{(,)4,0,0}D x y x y x y =+,故1222122222()()d d d d =+D D x y x y I x y x y I I x y x y −−=+++⎰⎰⎰⎰记. 其中:()()()2ππ22sin cos ππ12222=d cos sin d cos sin d πsin cos I r r θθθθθθθθθθ−−=−⋅=−⎰⎰⎰,()()()πππ22222220=d cos sin d 2cos sin d 21sin 2d π2I r r θθθθθθθθ−=−=−=−⎰⎰⎰⎰,故:()π2π2π1I =−+=−. (20)【答案】收敛域[]1,1,−[)(]arctan 12ln ,1,00,1,()22,0.x xx S x x x xx +⎧+∈−⎪=−⎨⎪=⎩【解析】设()()241()421nn n n u x x n −+=+,由1()lim 1()n n nu x u x +→∞<得(1,1)x ∈−,收敛区间为(1,1),−当()()()()00041111,42121421n nn nn n n x n n n ∞∞∞===−+−=±=++++∑∑∑收敛,则收敛域为[]1,1−. ()()()()222000411142121421n nn n nn nn n n x x x n n n ∞∞∞===−+−=++++∑∑∑, 记()()22120011(),().21421nnn nn n S x x S x x n n ∞∞==−==++∑∑ 对于1()S x ,当0x =时,1(0)1,S =当0x ≠时,()211011()21nn n S x xx n ∞+=−=+∑,记()21301()21nn n S x x n ∞+=−=+∑, 则()23201()11n nn S x x x ∞='=−=+∑,33201()d (0)arctan ,1x S x t S x t=+=+⎰ [)(]1arctan ,1,00,1,()1,0.xx S x xx ⎧∈−⎪=⎨⎪=⎩对于2()S x ,当0x =时,2()1,S x =当0x ≠时,212021()212n n x S x x n +∞=⎛⎫= ⎪+⎝⎭∑,记21401()212n n x S x n +∞=⎛⎫= ⎪+⎝⎭∑,则242012()224n n x S x x∞=⎛⎫'== ⎪−⎝⎭∑,4420212()d (0)ln ,422x x S x t S t x +=+=−−⎰ [)(]212ln,1,00,1,()21,0.x x S x x xx +⎧∈−⎪=−⎨⎪=⎩则[)(]arctan 12ln ,1,00,1,()22,0.x xx S x x x xx +⎧+∈−⎪=−⎨⎪=⎩(21)【答案】(I)01000⎛⎫ ⎪⎪= ⎪ ⎪ ⎝Q,12321323,,,x y y x y x y y ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩222123()442f y y y =++x ;(II )见解析. 【解析】(I )()22212312313,,3432f x x x x x x x x =+++,二次型矩阵为301040103⎛⎫⎪= ⎪ ⎪⎝⎭A ,则特征方程为2301040(4)(2)103λλλλλλ−−−=−=−−−−E A ,得特征值1234,2λλλ===. 当124λλ==时,解(4)−=0E A x ,得T T 12(0,1,0),(1,0,1)==ξξ, 当32λ=时,解(2)−=0E A x ,得T 3(1,0,1)=−ξ.将T T T 123(0,1,0),(1,0,1),(1,0,1)===−ξξξ正交化、单位化得T T T123(0,1,0),,1)===−ηηη ,可得01000⎛⎫ ⎪ ⎪= ⎪⎪ ⎝Q ,即12321323,,,x y y x y x y y ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩222123()442f y y y =++x . (II )由(I )知222123()442f y y y =++x ,=x Qy ,故T T T T==x x y Q Qy y y , 故222123T T 222123442()()y y y f g y y y ++==++x y x x y y 22122221232222y y y y y +=+++, 当1230,0y y y ==≠时,可取到最小值2. 所以存在非零向量y ,即存在非零向量x ,使得T()f x x x取到最小值2,得证. (22)【答案】1111ˆ2n m i j i j X Y n m θ==⎛⎫=+ ⎪+⎝⎭∑∑;21n mθ+. 【解析】由题意得,1X λθ=,12Y λθ=,则11e 0,()0x X x f x θθ−⎧>⎪=⎨⎪⎩, , 其它,,121e 0,()20y Y y f y θθ−⎧>⎪=⎨⎪⎩ , ,其它,设12,,n x x x ,12,,m y y y 为12,,n X X X ,12,,m Y Y Y 的样本观察值,则11()()()nmX i Y j i j L f x f y θ===∏∏,当0,0i j x y >>时,1111111122()11()e e2ee2mmnnjjiij j i i nmy y x x m n m L θθθθθθθθ====−−−−−−+∑∑∑∑⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭,1111ln ()ln 2()ln ,2nmi j i j L m n m x y θθθθ===−−+−−∑∑令2211d ln ()110,d 2nmiji j L n m x yθθθθθ==+=−++=∑∑,得θ的最大似然估计量为1111ˆ2n m i j i j X Y n m θ==⎛⎫=+ ⎪+⎝⎭∑∑. 1111ˆ()2n m i j i j D D X Y n m θ==⎡⎤⎛⎫=+⎢⎥ ⎪+⎢⎥⎝⎭⎣⎦∑∑()211[()()]4i j nD X mD Y n m =++ ()222211144n m n m n m θθθ⎛⎫=+⋅= ⎪+⎝⎭+ .。
专利法第22条第3款

专利法第22条第3款《专利法第22条第3款》:第三款:不符合公开条件或者没有实质完成发明创造的专利申请,以及不符合本法规定的专利申请,专利局可以依法做出不予授权的决定。
专利是一种重要的知识产权,是维护人们知识积累获取的加工处理成果,强化投资者和知识产权权利者的利益所产生的法律和技术事宜。
专利法第22条第3款明确规定,不符合公开条件或者没有完成实质性发明创造的专利申请,以及不符合本法规定的专利申请,都将被专利局依法不予授权。
此前,有关专利权的审查,是由相关部门分配的各级专利局进行的,但是各级专利局的审查质量不一,因此,为了加强专利的审查和管理,我国制定了《专利法》,其中明确规定,不符合公开条件或者没有完成实质性发明创造的专利申请,以及不符合本法规定的专利申请,都将被专利局依法不予授权。
具体来说,在申请专利时,首先要确定申请的专利具有实质发明创造的性质,是否符合法定的公开的条件,即实用新型专利是否具有新颖性,外观设计是否符合相关法律规定,以及其他发明创造的实质性性质等。
如果不符合法定条件,专利局就不会授予专利权,让申请人拿不到专利权。
另外,法律还规定如果某位申请人未能提供有效的专利权书,或不能履行法定义务,比如不能预先向专利局支付专利权费,以及不能提交相关的证据和文件,就会因为专利法第22条不符合本法规定的专利申请,而被专利局依法不予授权,失去了申请专利的权利和机会。
申请专利权时,要遵守《专利法》第22条第3款,及时、认真了解法律法规,了解申请专利所需条件,规范准备申请时所需要的证据和文件,确保申请过程规范,以防拉低专利申请的审核质量和评估效率。
对于不符合本法规定的专利申请,专利局可以依法做出不予授权的决定,以保护我国专利权的审查质量,有效地支持知识产权的保护,从而有效的推动我国发展创新产业,推动经济结构和技术水平的优化升级。
综上所述,《专利法》第22条第3款规定,不符合公开条件或者没有完成实质性发明创造的专利申请,以及不符合本法规定的专利申请,都将被专利局依法不予授权。
22-二甲基-3-乙烯结构简式

22-二甲基-3-乙烯结构简式
这种化合物可由乙烯和甲醇通过催化剂反应制备而成。
在实验室中,
还可以通过氢化二甲基二乙烯(C6H10)来合成它。
氢化反应在乙二烯的
双键上引入了两个甲基基团,将乙烯的氢原子取代掉。
2,2-二甲基-3-乙烯是一种无色液体,具有特殊的气味。
它的密度较小,熔点为-49℃,沸点为68-71℃。
由于它在常温下是液体形式,因此
可以很容易地与其他化合物发生反应。
例如,它可以与氯化氢发生加成反
应生成氯基化合物。
在有机合成中,2,2-二甲基-3-乙烯广泛应用于合成其他有机化合物。
它可以作为含有甲基基团的试剂,用于引入甲基化基团,增加化合物的碳
链长度。
此外,它还可以作为溶剂,用于溶解其他有机化合物。
总之,2,2-二甲基-3-乙烯是一种重要的有机化合物,由两个甲基和
一个乙烷基连接而成。
它具有特殊的气味,易于与其他化合物发生反应。
在有机合成中,它可以用于合成其他化合物,同时还有广泛的应用领域,
如溶剂、清洁剂和个人护理产品等。
新课标人教版数学Ⅱ课本练习选修2-12-22-34-44-5答案 (3)

高三理科党整合,仅供高三复习全部书参考,以及高一二订正,不建议直接抄袭。
只要努力一切来得及在高考吧里零基础学生逆袭高考仅一年时间考上一本重点的例子不少。
课本是一切知识的基础,万变不离其宗! 望广大学子加油考上自己理想的大学!感谢各位提供资料的老师与同学。
答案包括选修2-1 2-2 2-3 4-4极坐标与参数方程4-5 不等式- 7 左整合人教版数学选修2—1第一章常用逻辑用语1.1.命题及其关系1.1.1命题1.1.2 四种命题1.C 2.C 3.D 4.若A不是B的子集,则A∪B≠B 5.① 6.逆7.(1)若一个数为一个实数的平方,则这个数为非负数.真命题(2)若两个三角形等底等高,则这两个三角形全等.假命题8.原命题:在平面中,若两条直线平行,则这两条直线不相交.逆命题:在平面中,若两条直线不相交,则这两条直线平行.否命题:在平面中,若两条直线不平行,则这两条直线相交.逆否命题:在平面中?若两条直线相交,则这两条直线不平行。
以上均为真命题9.若ab≠0,则a,b都不为零.真命题10.逆否命题:已知函数f(x)在R上为增函数,a,b∈R,若f(a)+f(b)<f(-a)+f(-b),则a+b<0,真命题.证明略11.甲1.1.3 四种命题间的相互关系1.C 2.D 3.B 4.0个、2个或4个 5.原命题和逆否命题6.若a+b是奇数,则a,b至少有一个是偶数;真7.逆命题:若a^2=b^2,则a=b.假命题.否命题:若a≠b,则a^2≠b^2.假命题.逆否命题:若a^2≠b^2,则a≠b.真命题8.用原命题与逆否命题的等价性来证.假设a,b,c都是奇数,则a^2,b^2,c2也都是奇数,又a^2+b^2=c^2,则两个奇数之和为奇数,这显然不可能,所以假设不成立,即a,b,c不可能都是奇数9.否命题:若a^2+b^2≠0,则a≠0或b≠0.真命题.逆否命题:若a≠0,或b≠0,则a2+b2≠0.真命题10.真┌(4a)2一4(一4a+3)<0,11.三个方程都没有实数根的情况为┤(a-1)2一4a2<0, =>-3/2<a<-l└4a2+8a<0 所以实数a的取值范围a≥一l,或a≤-3/21.2 充分条件与必要条件1.2.1 充分条件与必要条件1.A 2.B 3.A 4.(1) ≠> (2) ≠> (3) ≠> (4)≠> 5.充分不必要6.必要不充分 7.“c≤d”是“e≤f”的充分条件 8.充分条件,理由略9.一元二次方程ax^2+2x+l=0 (a≠0)有一个正根和一个负根的充要条件为a<010.m≥9 11.是1.2.2 充要条件1.C 2.B 3.D 4.假;真 5.C和D 6.λ+μ=1 7.略 8.a=-39.a≤l 10.略 11.q=-1,证明略1.3 简单的逻辑联结词1.3.1 且(and)1.3.2 或(or)1.3.3 非(not)1.A 2.C 3.C 4.真 5.①③ 6.必要不充分7.(1)p:2<3或q:2=3;真 (2)p:1是质数或q:1是合数;假 (3)非p,p:0∈φ;真(4)p:菱形对角线互相垂直且q:菱形对角线互相平分;真8,(1)p∧q:5既是奇数又是偶数,假;p∨q:5是奇数或偶数,真;┑p:5不是偶数,真(2)p∧q:4>6且4+6≠10,假;p∨q:4>6或4+6≠10,假;┑p:4≤6,真9.甲的否定形式:x∈A,且x∈B;乙的否命题:若(x-1)(x-2)=0,则x=1,或x=2 10.m<-l 11.(5/2,+∞)1.4 全称量词与存在量词1.4.1 全称量词1.4.2 存在量词1.D 2.C 3.(1)真 (2)真 4,③5.所有的直角三角形的三边都满足斜边的平方等于两直角边的平方和6.若一个四边形为正方形,则这个四边形是矩形;全称;真7.(1)x,x^2≤0 (2)对x,若6|x则3|x (3)正方形都是平行四边形8.(1)全称;假 (2)特称;假 (3)全称;真 (4)全称;假9.p∧q:有些实数的绝对值是正数且所有的质数都是奇数,假;p∨q:有些实数的绝对值是正数或所有的质数都是奇数,真;┑p:所有实数的绝对值都不是正数,假10.(1)存在,只需m>一4即可 (2)(4,+∞) 11.a≥一21.4.3 含有一个量词的命题的否定1.C 2.A 3.C 4.存在一个正方形不是菱形 5.假6.所有的三角形内角和都不大于180°7.(1)全称;┑p假 (2)全称;┑p假 (3)全称;┑p真8.(1)┑p:存在平方和为0的两个实数,它们不都为0(至少一个不为0);假⑵┑p: 所有的质数都是偶数;假 (3)┑p:存在乘积为0的三个实数都不为0;假9.(1)假 (2)真 (3)假 (4)真 10.a≥3 11.(一√2,2)单元练习1.B 2.B 3.B 4.B 5.B 6.D 7.B 8.D 9.C 10.D11.5既是17的约数,又是15的约数:假 12.[1,2)13.在△ABC中,若∠C≠90°,则∠A,∠B不都是锐角 14.充要;充要;必要 15.b≥016.既不充分也不必要 17.①③④ 18.a≥319.逆命题:两个三角形相似,则这两个三角形全等;假;否命题:两个三角形不全等,则这两个三角形不相似;假;逆否命题:两个三角形不相似,则这两个三角形不全等;真;命题的否定:存在两个全等三角形不相似;假20.充分不必要条件21.令f(x) = x^2+(2k一1)x+k^2,方程有两个大于1的实数根┌ △=(2k2-1)-4k2≥0,<=>┤->1,即是k<-2,所以其充要条件为k<-2.└ f (1)>0,22.(-3,2]10.a√3/3第一章导数及其应用第二章推理与证明第三章数系的扩充与复数的引入。
注会笔记-税法-22年-第3章 消费税
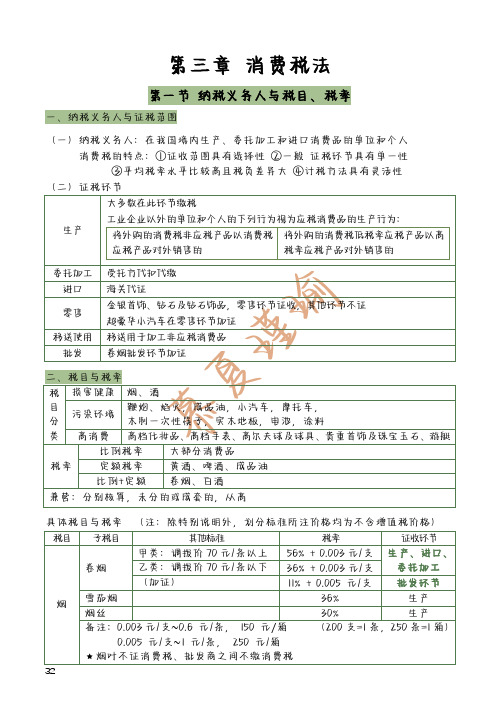
第三章 消费税法第一节 纳税义务人与税目、税率一、纳税义务人与征税范围(一)纳税义务人:在我国境内生产、委托加工和进口消费品的单位和个人 消费税的特点:①征收范围具有选择性 ②一般 征税环节具有单一性③平均税率水平比较高且税负差异大 ④计税方法具有灵活性 (二)征税环节生产 大多数在此环节缴税工业企业以外的单位和个人的下列行为视为应税消费品的生产行为:将外购的消费税非应税产品以消费税应税产品对外销售的将外购的消费税低税率应税产品以高税率应税产品对外销售的委托加工 受托方代扣代缴 进口 海关代征零售 金银首饰、钻石及钻石饰品,零售环节征收,其他环节不征 超豪华小汽车在零售环节加征移送使用 移送用于加工非应税消费品 批发 卷烟批发环节加征二、税目与税率税目分类 损害健康 烟、酒污染环境鞭炮、焰火,成品油,小汽车,摩托车,木制一次性筷子,实木地板,电池,涂料高消费 高档化妆品、高档手表、高尔夫球及球具、贵重首饰及珠宝玉石、游艇税率比例税率 大部分消费品定额税率 黄酒、啤酒、成品油 比例+定额 卷烟、白酒兼营:分别核算,未分的或成套的,从高具体税目与税率 (注:除特别说明外,划分标准所注价格均为不含增值税价格) 税目子税目其他标准税率征收环节烟 卷烟甲类:调拨价70元/条以上 56% + 0.003元/支 生产、进口、委托加工乙类:调拨价70元/条以下 36% + 0.003元/支(加征) 11% + 0.005 元/支 批发环节雪茄烟 36% 生产烟丝 30% 生产备注:0.003元/支~0.6 元/条, 150 元/箱(200支=1条,250条=1箱)0.005 元/支~1 元/条, 250 元/箱★烟叶不征消费税、批发商之间不缴消费税32税目子税目其他标准税率征收环节酒 白酒 包括其他配制酒20% + 0.5元/500克(1元/千克,1000元/吨0.1万元/吨)生产 啤酒甲类:每吨出厂价≥3000元 250元/吨 生产乙类:每吨出厂价<3000元 220元/吨 生产★包括果啤,★饮食业、商业、娱乐业举办的啤酒屋(啤酒坊)利用啤酒生产设备生产的啤酒(默认按甲类)★每吨出厂价:含包装物及包装物押金。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
z
∫∫
S
x 2 dydz + y 2 dzdx + z 2 dxdy
2 2 2 y + z )dxdy = ∫∫∫ ( x + x y z V = 2 ∫∫∫ ( x + y + z )dxdydz (在柱坐标变换下) 在柱坐标变换下)
V
y
x
= 2 ∫ dθ ∫ dr ∫ ( r cos θ + r sin θ + z )rdz
∫∫ Pdydz + Qdzdx + Rdxdy, z
S
其中S取外侧, 其中S取外侧, 即
S2
P ∫∫∫ x dxdydz = ∫∫ Pdydz , V S Q ∫∫∫ y dxdydz = ∫∫ Qdzdx, V S R ∫∫∫ z dxdydz = ∫∫ Rdxdy. V S
S3
o
Dxy
x
S1
y
S
= ∫∫∫ (
V
3 3 3 x + y + z )dxdydz x y z
在球坐标变换下) = 3∫∫∫ ( x 2 + y 2 + z 2 )dxdydz (在球坐标变换下)
= 3∫ dθ ∫ dr ∫
0 0
V 2π
1
π
0
12 r r sin d = π . 5
2 2
例6 计算
∫∫ ( xdydz + ydzdx + zdxdy ),
R I = ∫∫∫ ( xy + yz + zx )dxdydz = ∫∫∫ dxdydz = z V V
∫∫ Rdxdy.
S
=Байду номын сангаас1 外,均与
I=
∫∫ Rdxdy = ∫∫ R( x, y, z )dxdy + ∫∫ R( x, y, z )dxdy
S
S1
S2
= ∫∫ R( x , y , 0)dxdy + ∫∫ R( x , y ,1)dxdy =
D xy
o
Dxy
S1
y
x
又由第二型曲面积分的计算公式, 又由第二型曲面积分的计算公式,得 ∫∫ Rdxdy = ∫∫ Rdxdy + ∫∫ Rdxdy + ∫∫ Rdxdy,
S
= ∫∫ R( x , y , z2 ( x , y ))dxdy ∫∫ R( x , y , z1 ( x , y ))dxdy +0,
z
a a
边长为a的正立方体表面并取外侧. 边长为a的正立方体表面并取外侧. 由高斯公式, 解: 由高斯公式,得
∫∫
S
y( x z )dydz + x 2 dzdx + ( y 2 + xz )dxdy
x ( y( x z )) + ( x 2 ) + ( y 2 + xz )]dxdydz x y z
如图所示, 如图所示,设V为xy型区域,其边界由曲面 xy型区域, 型区域
S3
z 2 ( x , y ) R R ∫∫ ∫∫∫ z dxdydz = D dxdy ∫z1 ( x , y ) z dz V xy = ∫∫ ( R( x , y , z2 ( x , y )) R( x , y , z1 ( x , y ))dxdy .
例4 计算
∫∫
S
2 2 2 其中S x 2 dydz + y 2 dzdx + z 2 dxdy , 其中S是锥面 x + y = z
与平面z=h(>0)所围的空间区域的表面,方向取外侧. 所围的空间区域的表面,方向取外侧. 与平面 所围的空间区域的表面 围成的区域为V,由高斯公式, V,由高斯公式 解: 设S围成的区域为V,由高斯公式,得
(空间闭区域V上的三重积分与其边界S上的第二型曲面积分的关系) 空间闭区域V上的三重积分与其边界S上的第二型曲面积分的关系)
R dxdydz = 证: 只证 ∫∫∫ z V
∫∫
S
Rdxdy .
z
S2
S1 : z = z1 ( x , y ),( x , y ) ∈ Dxy , S2 : z = z2 ( x , y ),( x , y ) ∈ Dxy , 组成, 以及垂直于 Dxy边界的柱面 S3 组成,则
S
其中S 其中S是上半球面
z
的外侧. z = a 2 x 2 y 2 的外侧. 一起构成 解: 添加平面 S1 : z = 0, 与S一起构成 封闭曲面 S2 , 取外侧为正 并设围成的区域 取外侧为正,并设围成的区域 由高斯公式,得 为V,由高斯公式 得 由高斯公式
o
y
x
∫∫ ( xdydz + ydzdx + zdxdy )
∫∫
S V
2 2 2 x dydz + y dzdx + z dxdyx = ∫∫∫ ( x + y + z )dxdyz x y z V
2 2 2
a a a
= ∫∫∫ 2( x + y + z )dxdyz = 2 ∫ dx ∫ dy ∫ ( x + y + z )dz = 3a 4 . 0 0 0
例3 计算 表面的外侧; 表面的外侧;
∫∫
S
zx + xy )dxdyz =0. = ∫∫∫ ( yz + x y z V x 2 dydz + y 2 dzdx + z 2 dxdy , 其中S是立方体0 ≤ x , y , z ≤ a 其中S
S
围成的区域为V,由高斯公式, V,由高斯公式 解: 设S围成的区域为V,由高斯公式,得
Dxy D xy
∫∫ ( xy +
D xy
1 1 11 y + x )dxdy = . 2 2 24
�
S2
= ∫∫ ( xdydz + ydzdx + zdxdy ) + ∫∫ ( xdydz + ydzdx + zdxdy )
3 y + z )dxdydz = 3∫∫∫ dxdydz = 2π a , = ∫∫∫ ( x + x y z V V
注意到
S S1
∫∫ ( xdydz + ydzdx + zdxdy ) = 0, 所以
D xy
S2
S1
S3
Dxy
R dxdydz = 所以 ∫∫∫ z V
∫∫ Rdxdy.
S
若V不是xy区域的情形,可将其分割成若干个xy区域来讨论. 不是xy区域的情形,可将其分割成若干个xy区域来讨论. xy区域的情形 xy区域来讨论
例1 计算
∫∫
S
y( x z )dydz + x 2 dzdx + ( y 2 + xz )dxdy ,其中S是如图所示 其中S
P ∫∫∫ x dxdydz = ∫∫ Pdydz , V S x Q ∫∫∫ y dxdydz = ∫∫ Qdzdx, V S R ∫∫∫ z dxdydz = ∫∫ Rdxdy, V S 故可将三重积分化为关于 xy , yz , xz 的第二型曲面积分 的第二型曲面积分.
2 2 都与xy平面垂直 平面垂直, 由于曲面 x = 0, y = 0, 与x + y = 1都与 平面垂直 故化为
a a a 0 0 0
o a
y
= ∫∫∫ [
V
= ∫∫∫ ( y + x )dxdydz = ∫ dx ∫ dy ∫ ( y + x )dz = a 4 .
V
例2 计算
2 2 2
其中S ∫∫ yzdydz + zxdzdx + xydxdy, 其中S是单位球面
S
x + y + z = 1 的外侧; 的外侧; 2 2 2 的区域为V,由高斯公式, V,由高斯公式 解: 设 x + y + z = 1 的区域为V,由高斯公式,得 ∫∫ yzdydz + zxdzdx + xydxdy
S1
3 ( xdydz + ydzdx + zdxdy )= 2π a . ∫∫
S
例7
利用高斯公式计算
2
其中V ∫∫∫ ( xy + yz + zx )dxdydz 其中V是由
V
所确定的区域. x ≥ 0, y ≥ 0, 0 ≤ z ≤ 1与x + y ≤ 1 所确定的区域.
2
z
分析: 由高斯公式,有 分析: 由高斯公式 有
§3 一 高斯公式
高斯公式与斯托克斯公式
定理22.3 设空间区域V由分片光滑的双侧封闭曲面S围成. 定理22.3 设空间区域V由分片光滑的双侧封闭曲面S围成.若函 数P(x,y,z),Q(x,y,z),R(x,y,z)在V连续,且有一阶连续偏导数,则 在 连续,且有一阶连续偏导数,
P Q R ∫∫∫ ( x + y + z )dxdydz = V
0 0 r
2π
h
h
1 4 = h π. 2
例5 计算
∫∫
S
x 3dydz + y 3dzdx + z 3dxdy , 其中S是单位球面 其中S
x 2 + y 2 + z 2 = 1 的外侧. 的外侧.
围成的区域为V,由高斯公式, V,由高斯公式 解: 设S围成的区域为V,由高斯公式,得 x 3dydz + y 3dzdx + z 3dxdy ∫∫
y
关于xy的第二型曲面积分比较简单 关于 的第二型曲面积分比较简单. 的第二型曲面积分比较简单 使得 转化的关键: 转化的关键: 求R,使得
