应急中心的选址问题数学建模
数学建模之应急设施的位置

数学建模之应急设施的位置应急设施的位置选择是一个重要的决策问题,它直接关系到应急管理的有效性和应对突发事件的能力。
在数学建模中,我们可以运用空间分析、最优化等方法来研究应急设施的位置选择问题。
本文主要探讨数学建模在应急设施位置选择中的应用,包括数学模型的建立、求解方法的选择以及结果的分析。
首先,建立一个数学模型是研究应急设施位置选择问题的基础。
在建模过程中,我们需要考虑以下几个方面的因素:需求点的分布、设施的容量限制、应急响应时间等。
以城市的应急设施的位置选择为例,我们可以将该城市划分为若干个网格,每个网格代表一个潜在的设施位置。
假设有n个需求点需要被覆盖,我们可以使用二进制变量xi表示第i个网格是否选择建立应急设施,其中i=1,2,…,m,m表示网格的总数。
另外,我们需要引入距离变量dij表示第i个网格与第j个需求点之间的距离,以及容量限制变量ci表示第i个网格的容量限制。
最后,对结果进行分析是问题求解的最后一步。
通过对结果进行分析,我们可以评估不同位置方案的优劣,并对进一步决策提供依据。
例如,我们可以计算每个需求点到最近的应急设施的距离,从而评估覆盖范围的有效性。
另外,我们还可以根据建设和维护成本、应急响应时间等指标来评估不同网格的选择。
通过综合考虑各种因素,我们可以得出一个最优的设施位置方案。
总之,数学建模在应急设施位置选择中起到了重要的作用。
通过建立数学模型、选择合适的求解方法以及对结果进行分析,我们可以为应急管理提供科学、高效的决策支持,提高城市的应急响应能力。
教师培训课件:数学建模中的选址

总结词
求解选址问题的方法可以分为两大类:解析法和启发式算法。解析法包括线性规划、整数规划等,适用于小规模问题;启发式算法包括模拟退火、遗传算法等,适用于大规模问题。选择合适的求解方法需要根据问题的规模和特点进行选择。
详细描述
解析法是一种精确求解方法,通过建立数学模型和求解方程或不等式来找到最优解。这种方法适用于小规模问题,但对于大规模问题可能会因为计算量大而变得不适用。启发式算法是一种基于经验或直观的近似求解方法,通过模拟或启发式的搜索过程来寻找近似最优解。这种方法适用于大规模问题,但可能无法找到最优解或最优解的精度不够高。在实际应用中,可以根据问题的规模和特点选择合适的求解方法,或者结合多种方法进行求解。
选址问题的数学建模
总结词
数学模型是用来描述选址问题的数学工具,通过数学模型可以将实际问题转化为数学问题,以便进行定量分析和求解。建立数学模型的过程包括问题分析、变量定义、建立方程和不等式等步骤。
详细描述
建立选址问题的数学模型需要先对问题进行深入分析,明确问题的目标、约束条件和相关因素。然后定义变量,包括决策变量和参数变量,并根据问题的实际情况建立数学方程或不等式。最后通过数学模型将实际问题转化为数学问题,为后续的求解提供基础。
明确问题、建立模型、求解模型、验证结果和改进模型。
总结词
明确问题是数学建模的第一步,需要清晰地理解问题的背景、目标和约束条件。建立模型是将问题抽象化,用数学语言进行描述。求解模型是运用数学方法和技巧进行计算的过程。验证结果是对比实际数据和模型结果的符合程度。改进模型是根据验证结果对模型进行修正和优化的过程。
课程总结与展望
案例分析
通过实际案例展示了数学建模在选址问题中的应用和效果。
模型求解与优化
应急物资储备点选址多目标优化模型及算法研究

应急物资储备点选址多目标优化模型及算法研究冯舰锐;盖文妹【摘要】为应急物资储备点的选址问题提供一个合理的解决方法,提高应急救援工作的响应能力,基于运筹学中求解多目标优化问题的理论和方法,根据紧急情况下物资运输调度的时效性与经济性特征,构造相应目标函数,引入权重综合考虑时效性和经济性,并利用可变权重因子构造辅助函数,进而建立应急选址问题的优化模型;在此基础上,借用智能算法中系统动态演化方法,提出求解权重的算法,并拓展到多目标决策,将多目标问题逐步转化为单目标问题进而解决;实例计算结果验证了所提算法的正确性及优势,以及求解效率、辅助函数性质的正确性,可以为决策者提供多种在灾变条件下的选择方案;此外,提出的算法也可用于应急管理领域中其他相关优化与选址问题.%To provide a reasonable solution for the problem of site selection for the reserve sites of emergency materials,and improve the response ability of emergency rescue work,based on the threory and method to solve the multi-objective optimiza-tion problem in the operational research,the corresponding objective functions were constructed accoring to the characteristics of timeliness and economy in the transportation and scheduling of emergency materials under the emergency situation.The timeliness and economy were comprehensively considered by introducing into the weights,and the auxiliary functions were constructed by using the variable weight factor,thus the optimization model of emergency site selection was established.On this basis,the algorithm for solving the weights was put forward by using the system dynamic evolution method of the intelli-gent algorithm,and it was extended to the multi-objectivedecision-making to convert the multi-objective problem into the sin-gle objective problem step by step for solving.The correctness and advantages of the proposed new algorithm were verified by the calculation results of case,as well as the solving efficiency and the correctness of the properties of auxiliary functions.It can provide various selection schemes under the catastrophic conditions to the decision makers,and can also be applied in other relevant optimization and site selection problems in the field of emergency management.【期刊名称】《中国安全生产科学技术》【年(卷),期】2018(014)006【总页数】6页(P64-69)【关键词】应急管理;多目标优化;应急物资;选址【作者】冯舰锐;盖文妹【作者单位】中国地质大学(北京)工程技术学院,北京100083;中国地质大学(北京)工程技术学院,北京100083【正文语种】中文【中图分类】X913.40 引言随着城市的不断发展,建筑物、各类网络系统工程密集程度增加。
突发事件应急设施选址问题的模型及优化算法

突发事件应急设施选址问题的模型及优化算法下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!突发事件应急设施选址问题的模型及优化算法1. 引言在现代社会中,突发事件(如自然灾害、事故等)频繁发生,给人们的生命财产安全带来了严重威胁。
选址问题数学模型

选址问题数学模型选址问题数学模型摘要本题是用图论与算法结合的数学模型,来解决居民各社区生活中存在三个的问题:合理的建立3个煤气缴费站的问题;如何建立合理的派出所;市领导人巡视路线最佳安排方案的问题。
通过对原型进行初步分析,分清各个要素及求解目标,理出它们之间的联系.在用图论模型描述研究对象时,为了突出与求解目标息息相关的要素,降低思考的复杂度。
对客观事物进行抽象、化简,并用图来描述事物特征及内在联系的过程.建立图论模型是为了简化问题,突出要点,以便更深入地研究问题针对问题1:0-1规划的穷举法模型。
该模型首先采用改善的Floyd-Warshall算法计算出城市间最短路径矩阵见附录表一;然后,用0-1规划的穷举法获得模型目标函数的最优解,其煤气缴费站设置点分别在Q、W、M社区,各社区居民缴费区域见表7-1,居民与最近的缴费点之间平均距离的最小值11.7118百米。
针对问题2:为避免资源的浪费,且满足条件,建立了以最少分组数为目标函数的单目标最优化模型,用问题一中最短路径的Floyd算法,运用LINGO软件编程计算,得到个社区之间的最短距离,再经过计算可得到本问的派出所管辖范围是2.5千米。
最后采用就近归组的搜索方法,逐步优化,最终得到最少需要设置3个派出所,其所在位置有三种方案,分别是:(1)K区,W区,D区;(2)K区,W区,R区;(3)K区,W区,Q区。
最后根据效率和公平性和工作负荷考虑考虑,其第三种方案为最佳方案,故选择K区,W区,Q区,其各自管辖区域路线图如图8-1。
针对问题3:建立了双目标最优化模型。
首先将问题三转化为三个售货员的最佳旅行售货员问题,得到以总路程最短和路程均衡度最小的目标函数,采用最短路径Floyd算法,并用MATLAB和LINGO软件编程计算,得到最优树图,然后按每块近似有相等总路程的标准将最优树分成三块,最后根据最小环路定理,得到三组巡视路程分别为11.8 、11 和12.5 ,三组巡视的总路程达到35.3 ,路程均衡度为12%,具体巡视路线安排见表9-1和图9.2 。
超大型城市应急物资储备库选址研究——以北京为例

29刘晨君,首都经济贸易大学博士研究生。
研究方向:决策优化与管理、 人工智能、安全与应急管理。
近期主要从事应急物资储备库选址与物资调度研究,探究国家级、省市级储备库的选址问题与各级别储备库协同选址问题。
主持参与科研项目5项,含“中国高校产学研创新基金”项目、校级科技创新项目等,发表论文6篇。
读博期间获2次一等奖学金和1次二等奖学金,求学期间曾获校级优秀共青团员、优秀共产党员、优秀毕业生等荣誉称号。
引言随着城市化进程的加快,城市人口日益集中、密度增大,突发事件多重叠加给城市安全运行带来的风险和影响越发明显。
2012年7月北京遭遇近百年来最强暴雨及洪涝灾害,造成160.2万人受灾,经济损失高达116.4亿元;2023年7月北京暴雨导致死亡33人,18人失踪,近129万人受灾。
超大型城市在遭受突发自然灾害的情况时,因救援不力导致的人员伤害、财产损失和经济损失都是非常巨大的。
2022年2月应急管理部印发《“十四五”国家应急体系规划》,明确提出要加强物资实物储备,完善储备仓库布局。
2022年10月,应急管理部发文提出应急物资保障存在短板和不足,应急物资储备结构布局还需优化。
现有文献结合具体地区特点、综合考虑影响因素、选址目标定量化、科学确定选址数量、合理设定约束条件和响应合理分区等进行实证研究的则很少。
本文针对超大型城市救援储备库选址问题,分析了超大型城市自身的特殊性、选址目标定量化、约束条件体系化等,构建了多层次指标评价体系,合理确定城市选址数量并运用Voronoi 图进行了响应分区。
既统筹考虑了救援储备基地的建设成本和运行维护成本,又考虑了应急物资储备系统的整体布局,进而实现了在规定救援时限内综合应急救灾成本的最小化。
超大型城市应急物资储备库选址研究——以北京为例刘晨君 武装* 杜佳琪 付琬舒CITY AND DISASTER REDUCTION问题提出(一)基于应急物资储备库选址的超大型城市的特殊性分析由于受全球气候变化影响,北京防灾减灾救灾形势严峻复杂。
数学建模:城市消防站选址
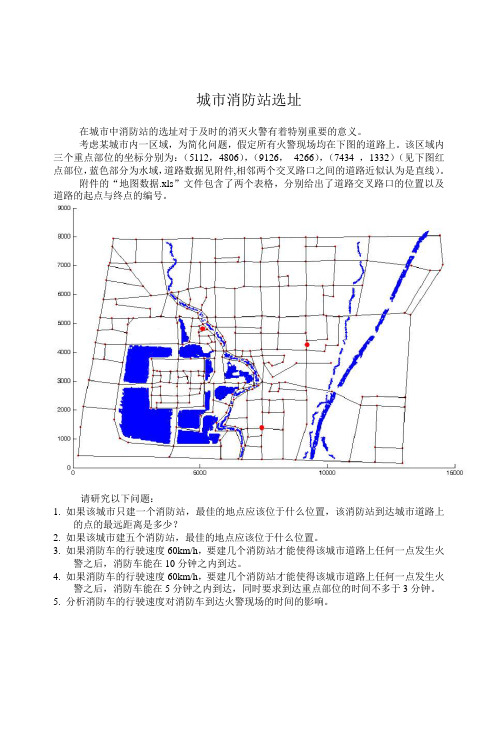
城市消防站选址
在城市中消防站的选址对于及时的消灭火警有着特别重要的意义。
考虑某城市内一区域,为简化问题,假定所有火警现场均在下图的道路上。
该区域内三个重点部位的坐标分别为:(5112,4806),(9126,4266),(7434 ,1332)(见下图红点部位,蓝色部分为水域,道路数据见附件,相邻两个交叉路口之间的道路近似认为是直线)。
附件的“地图数据.xls”文件包含了两个表格,分别给出了道路交叉路口的位置以及道路的起点与终点的编号。
请研究以下问题:
1. 如果该城市只建一个消防站,最佳的地点应该位于什么位置,该消防站到达城市道路上
的点的最远距离是多少?
2. 如果该城市建五个消防站,最佳的地点应该位于什么位置。
3. 如果消防车的行驶速度60km/h,要建几个消防站才能使得该城市道路上任何一点发生火
警之后,消防车能在10分钟之内到达。
4. 如果消防车的行驶速度60km/h,要建几个消防站才能使得该城市道路上任何一点发生火
警之后,消防车能在5分钟之内到达,同时要求到达重点部位的时间不多于3分钟。
5. 分析消防车的行驶速度对消防车到达火警现场的时间的影响。
应急物资储备库选址优化模型

应急物资储备库选址优化模型汇报人:日期:•引言•应急物资储备库选址问题概述•建立优化模型•模型应用与案例分析•模型优化与改进建议目•结论与展望录引言01 CATALOGUE随着全球自然灾害和突发事件的频繁发生,应急物资储备库的选址问题越来越受到关注。
优化选址能够提高应急物资的供应效率和响应速度,对于减轻灾害损失和保障社会稳定具有重要意义。
研究背景与意义建立一个应急物资储备库选址优化模型,以实现选址问题的科学决策。
研究目的综合运用数学建模、GIS分析和优化算法等方法,构建一个适用于实际情况的选址优化模型。
研究方法研究目的和方法应急物资储备库选址问题概述02CATALOGUE定义应急物资储备库选址问题是指在应对突发事件时,对应急物资储备库的选址和布局进行优化,以最大限度地满足救援需求,提高救援效率,并降低成本。
特点应急物资储备库选址问题具有紧迫性、不确定性、复杂性、多目标性等特点。
在选址过程中需要充分考虑各种因素,如地理位置、交通状况、资源供应、气候条件等。
选址问题的定义和特点选址问题的重要性和现实意义重要性应急物资储备库的选址问题直接关系到应急救援的效率和效果,对于保障人民生命财产安全具有重要意义。
一个合理的选址方案可以提高救援速度,减少灾害损失,并为灾后重建提供有力支持。
现实意义在现实生活中,突发事件具有不可预测性和随机性,但通过建立科学合理的选址模型,可以对应急物资储备库的选址问题进行优化,从而在应对突发事件时能够更好地保障人民生命财产安全。
选址问题的研究现状和发展趋势研究现状目前,国内外学者对应急物资储备库选址问题的研究主要集中在建立数学模型、应用优化算法、引入GIS技术等方面。
这些研究为解决实际问题提供了有力的理论支持和实践指导。
发展趋势未来,应急物资储备库选址问题的研究将更加注重多学科交叉、智能化、精细化等方面的发展。
随着大数据、人工智能等技术的不断应用,对应急物资储备库选址问题的研究将更加深入,从而为提高应急救援效率和效果提供更加科学和有效的支持。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
救护中心建立问题的研究摘要本文对某小镇建立两个救护中心,使应对突发事件总的响应时间最少的问题进行了分析,并建立了数学模型进行了求解。
在假设(I)的前提下,即需要救护的事件集中在每个街区的中心。
考虑到街区数目不是很多,本文采用穷举法进行了最优解的搜索。
即先任意选取两点作为救护中心的位置,然后计算其他街区到这两个救护中心的总响应时间,总响应时间最少的旧最优的方案。
同时为了考虑障碍区域和水塘,本文首先对那些设置救护中心需要穿越障碍区域和水塘的点进行了剔除,然后在利用计算机一一穷举。
在假设(Ⅱ)的前提下,需要救护的事件均匀分布在街道上,在计算总响应时间时,本文把整个街道的事件发生频率集中在街道的中心位置处进行计算。
同时本文证明了当救护中心仍设立在街角处时所需的总响应时间是最少的,这样仍可以按照假设(I)中的穷举方法求出救护中心设立的最优位置。
关键词:穷举法;剔除;街道中心;街角一.问题的重述某小镇开始计划建立两个救护中心,把救护站、消防队和派出所结合在一起。
图1指出每个长方形街区所发生的需要救护事件的次数,北边的L形区域是障碍,而南边的长方形区域是浅水池,救护车辆驶过一条南北向的街道平均花15秒,而救护车辆驶过一条东西向的街道平均花20秒,请确定这两个救护中心的位置,使得总响应时间最少。
(1)假定需要救护的事件集中在每个街区的中心,救护中心位于街角处。
(2)假定需要救护的事件沿包围每个街区的街道上均匀分布,救护中心可位于街道的任何地方。
图1 小镇的街区分布图二.问题分析对于假设(I)的情况,要建立救助站的位置,使总的响应时间最短。
在考虑障碍区域的情况下,可以首先把那些建立救护站需要穿过障碍区域的点剔除掉,然后可以考虑穷举法利用计算机求出最佳的建立救护中心的位置。
对于假设(Ⅱ)的情况,由于突发事件是均匀分布在每条街道上的,可以利用每条街道的中心点位置来作为这整条街道突发事件的频率集中点。
同时可以证明:在街角处设置救护中心是所需总响应时间最短的。
这样建立救护中心的位置使有限的,仍可以考虑穷举法利用计算机进行求解。
三.符号说明1122T(X ,Y ,X ,Y ) 建立两个救护中心所需最少时间的函数t(X ,Y ,,)m n i j 第(i,j)个小区到(X ,Y m n )个救护站的时间函数P 街区的事故发生频率矩阵(,)P i j 坐标中第(i,j)个区域的应急事件次数i 每个街区街角的横坐标j 每个街区街角的纵坐标四.模型假设1.在同一时刻各街区及街区内不会同时发生两件应急事件;2.应急事件集中在街区中心,而应急设施在街角处;3.障碍区及浅水塘区应急事件次数为零;4.应急车辆的响应时间只考虑在街道上行驶的时间,不考虑转弯的时间;5.假设应急需求沿包围每个街区的街道是均与分布的,而应急措施可以位于街道的任何地方。
五.模型的建立与求解5.1 问题一的模型建立与求解在假定(I)的前提下,应急需求集中在每个街区的中心,本文进一步假定应急车辆只要到达该街区四个街角中最近的一个,就认为到达率该街区。
则有假定(I)每个应急设施选在街角处,可能的位置只有6×11=66个,两个应急设施的位置的可能组合至多只有66×65/2=2145个。
考虑到这个数目不是很大,可以利用计算机进行穷举,对每种组合一一算出所对应的总响应时间,依次比较得出最小的响应时间及其对应的选址方案,具体的算法是:建立直角坐标系,一该镇的东北角为原点,以从东到西为X 轴的正方向,以从北向南为Y 轴的正方向,在南北和东西方向分别以一个街区的长作为单位长,则街角的坐标(X,Y)是满足条件05,010X Y ≤≤≤≤的整数。
而每个街区的中心的坐标具有形式(0.5,0.5)i j ++,其中i ,j 满足的条件:04,09i j ≤≤≤≤的整数。
如果不考虑障碍和水塘的影响则应急车辆从设在(X,Y)点的应急到一(0.5,0.5)i j ++为中心的街区的行驶时间等于:记(,)P i j 为以(0.5,0.5)i j ++为中心的街区的事故发生频率(即在图上该街区所标的数字)。
用矩阵P 表示,则P 为则如果应急设施设在11(,)X Y ,22(,)X Y 这两点,则该设置方案的总响应时间为让1X 取遍0—4,2X 取遍1X —4,12,Y Y 分别独立地取遍0—10,依次对1122(,,,)X Y X Y 的每一个值计算出对应的总响应时间1122(,,,)T X Y X Y 。
通过比较可得出所有这些总响应时间的最小值。
以上计算的过程没考虑障碍区域和水塘的情况,对于考虑障碍区域和水塘的情况,见图2.图2.障碍区域只要不把救护站设在图2所标记的A 、B 、C 、D 、E 等点,则救护的路线就不会穿越障碍区域。
所以在计算中可以事先把这些点剔除。
同理对于水塘障碍区域见图3.只要剔除F 、G 点即可保证救护车的路线不会穿越水塘。
图3. 水塘区域按照以上计算过程利用计算机求解可得在M 和N 处建立救护中心,所需的最少时间为5065秒。
见图4.图4.救护中心的位置按照以上计算过程利用计算机求解可得在M 和N 处建立救护中心,所需的最少时间为5065秒。
即两个救护中心分别建立在(2,2)和(2,6)两点。
见图4.(求解代码见附件)5.2 模型二的建立与求解在假定(Ⅱ)的情况下,由于允许应急设施在街道上任何位置,这就有无穷多种可能,不能直接用计算机穷举,不过,本文可以证明:应急设施仍应设在街角处,才能使总的响应时间最短。
对已选定的两个应急设施的位置A 和B 。
首先,本文将街道上所有的点的集合划分成两个责任区V A 和V B ,分别由A ,B 进行救助:街道上的点P 如果由A 点去救助比由B 点去救助的时间更短,就将P 划进A 的责任区V A ,反之就划进V B 。
为了叙述方便,本文将每个长方形街区的死条边中的每一条称为一条“街道”,街道的一段称为“街段”。
没挑街道中属于V A 的点与属于V B 的点各组成一个街段。
分别成为A 的或B 的责任段。
一条街道最多被分成两个责任段,责任段只有有限多条。
对于每个应急设施,分别计算出它的每个责任段的总响应时间,将总响应时间求和就得到这个设施的责任区的总响应时间,将两个责任区各自的总响应使劲相加就得到这一选址方案的总响应时间。
下面需要知道:任一设施A 到它的一个责任区段EF 的总响应时间怎样计算。
按假定(Ⅱ),街区出现事故的频率平均分布在它周围的四条街道上,每条街段的事故发生频率与它的长度成正比。
将应急车辆每秒钟行驶的路程作为长度单位,则当街区事故频率为p ,街段的长度为t 是,这一街段的事故频率为p ×t/70,70是街区的周长,即车辆绕街区行驶一周需70秒,在大多数情况下,一条街段同时与两个街区相邻,两个街区的事故它都有份,它的事故频率应为(p+q)×t/70,p,q 分别是这两个街区的事故的总频率。
事实上,由于EF 的每一小段的事故发生频率只与这一小段的长度有关,换句话说:频率密度是常数,只要求出EF 到A 的平均行驶时间T ,再乘以EF 的总的事故频率就行了。
当A 设在街角处时,平均行驶时间也就是A 到EF 的中点M 的行驶时间122015MA T X m Y m =-+-秒,这里(X,Y),(1m ,2m )分别是A ,M 的坐标,将MA T 乘以EF 的事故频率,就得到EF 的总响应时间。
若应急设施A 不是设在街角处,而是设在某条街道CD 的两个端点C 、D 之间,则可能出现这样的情况:从A 出发到EF 中的某些点的最短救助路线应该向C 方向行驶,而到另一些点去则应向D 方向行驶。
这时,平均时间就不等于A 到EF 中点M 的时间MA T ,而是比MA T 小。
在这样的情况下EF 可以分成两段EG 、GF ,从A 到其中一段上的所有的点的最短救助路线应向C 方向行驶,而到另一段上的所有的点则应向D 方向行驶。
分别计算EG 、GF 的事故发生频率EG P ,GF P ,将这两个频率分别集中在EG 、GF 各自的中点1M ,2M ,就可分别算出EG 、GF 的总响应时间,再将他们相加就得到EF 的总响应时间。
下面证明:最短的总响应时间必可又这在街角处的应急设施A 、B 来实现,假定已选择两个应急设施A 、B 的位置使总响应时间最短,且至少有一个设施(比如A)不是设在街角处,而是设在某一条街道CD 的两个端点C 、D 之间。
本文证明:可以吧这个设施从A 移到C 或D ,使总响应时间不增加。
证明的主要想法是:将设施迁移到街角后,它到某些街段缩短了一段路程,同时到另外某些街段增加同样长的一段路程。
如果路程缩短的那些街段的事故总频率大于路程增加的那些街段的事故总频率,则总的响应时间缩短了,设施位置得到优化,说明原来的位置不是最优。
设P 是A 的责任区A V 内需要救助的一点。
从A 出发到P ,有两种可能的最短救助路线AP :一种是沿AC 、经由C 点到P ;另一种是沿AD 、经由D 点到P 。
凡是AP 属于前一种情况的,这样的点P 组成的集合记作C U ;凡是AP 属于后一种情况的,这样的点P 组成的集合记作D U 。
这样就将A 的责任区按最短救助路线出发时的两个不同方向分成了两个区域。
比较C U ,D U 这两个区域各自的事故总频率C P ,D P 的大小。
如果C P 比D P 大,就将设施从A 移到C ,向C U 靠拢;反之,当D P 比C P 大时,将设施由A 迁到D 去靠近D U ;当C P =D P 时将设施任意迁到C 或D 都可以。
本文将证明:将设施经过这样的迁移后,总响应时间只可能减少,不可能增加。
因此假如迁移前的方案最优,迁移后一定还是最优(事实上,当C D P P ≠时,迁移后的方案一定比原来最优,说明原来的不可能最优)。
不妨先假定C D P P ≥,设施从A 迁到C 点为了便于比较迁移前后的总响应时间的变化情况,本文先作下面两个假设:(1) 应急设施从A 搬迁到C 后,两个旧的责任区A V ,B V 先仍分别由C 和B 负责救助,暂时不变。
如果在这样不改变责任区的情形下都能证明总响应时间不增加,则再进一步合理调整C 、B 的责任区还可能进一步缩短(至少不会增加)总响应时间。
(2) 搬迁后从新设施C 到旧区域C U 中的任何一点P 的救助路线为:从C 出发离开CD ,沿原先A 的旧的救助路线到P 。
从C 到旧区域D U 的任何一点P 的救助路线为:从C 出发沿CD (经过A )到D ,再沿原先A 的旧的救助路线到P 。
设应急车辆从A 到C 的行驶时间为T 。
则按(2)的行驶路线,C U 的点到设施的路程减少了AC ,行驶时间减少T ,总响应时间减少C P T ;D U 的点则相反,路程都增加了AC ,行驶时间都增加T ,总响应时间增加D P T 。
