(完整word版)数据结构-树练习题
数据结构课后练习题(树)

数据结构习题书面作业练习题习 题 六 树 和 二 叉 树6.1 单项选择题1. 下图所示的4棵二叉树,____不是完全二叉树。
2. 下列编码中属前缀码的是( ) (A ){1,01,000,001} (B ){1,01,011,010}(C ){0,10,110,11} (D ){0,1,00,113. 已知某二叉树的后序遍历序列是dabec ,中序遍历序列是debac ,它的前序遍历序列是____。
A. acbedB. decabC. deabcD. cedba4.设a,b 为一棵二叉树上的两个结点,在中序遍历时,a 在b 前的条件是 。
A .a 在b 的右方B .a 在b 的左方C .a 是b 的祖先D .a 是b 的子孙5. 假定在一棵二叉树中,双分支结点数为15,单分支结点数为30个,则叶子结点数为 个。
A .15B .16C .17D .476. 按照二叉树的定义,具有3个结点的二叉树有____种。
A. 3B. 4C. 5D. 6(A)(B)(C)(D)图8.7 4棵二叉树7. 树的基本遍历策略可分为先根遍历和后根遍历;二叉树的基本遍历策略可分为先序遍历、中序遍历和后序遍历。
这里,我们把由树转化得到的二叉树叫做这棵数对应的二叉树。
结论____是正确的。
A. 树的先根遍历序列与其对应的二叉树的先序遍历序列相同B. 树的后根遍历序列与其对应的二叉树的后序遍历序列相同C. 树的先根遍历序列与其对应的二叉树的中序遍历序列相同D. 以上都不对8. 深度为5的二叉树至多有____个结点。
A. 16B. 32C. 31D. 109. 树最适合用来表示____。
A. 有序数据元素B. 无序数据元素C. 元素之间具有分支层次关系的数据D. 元素之间无联系的数据10. 设有13个值,用它们组成一棵赫夫曼树,则该赫夫曼树共有( )个结点。
A .13 B. 12 C. 26 D. 256.2 应用题1. 有一棵树如图8.12所示,回答下面的问题:⑴ 这棵树的根结点是____;⑵ 这棵树的叶子结点是____;⑶ 结点k3的度是____; ⑷ 这棵树的度是____;⑸ 这棵树的深度是____;⑹ 结点k3的子女是____; ⑺ 结点k3的父结点是____;2. 深度为k 的完全二叉树至少有____个结点。
数据结构-习题-第六章-树

数据结构-习题-第六章-树和二叉树E F D G A B / + + * - C * 第六章 树和二叉树一、选择题1.已知一算术表达式的中缀形式为 A+B*C-D/E ,后缀形式为ABC*+DE/-,其前缀形式为( )A .-A+B*C/DE B. -A+B*CD/EC .-+*ABC/DE D. -+A*BC/DE【北京航空航天大学 1999 一、3 (2分)】2.算术表达式a+b*(c+d/e )转为后缀表达式后为( )【中山大学 1999 一、5】A .ab+cde/*B .abcde/+*+C .abcde/*++D .abcde*/++ 3. 设有一表示算术表达式的二叉树(见下图), 它所表示的算术表达式是( )【南京理工大学1999 一、20(2分)】A. A*B+C/(D*E)+(F-G)B.(A*B+C)/(D*E)+(F-G)C. (A*B+C)/(D*E+(F-G ))D.A*B+C/D*E+F-G4. 设树T 的度为4,其中度为1,2,3和4的结点个数分别为4,2,1,1 则T 中的叶子数为( )A .5B .6C .7D.8【南京理工大学 2000 一、8 (1.5分)】5. 在下述结论中,正确的是()【南京理工大学 1999 一、4 (1分)】①只有一个结点的二叉树的度为0; ②二叉树的度为2;③二叉树的左右子树可任意交换;④深度为K的完全二叉树的结点个数小于或等于深度相同的满二叉树。
A.①②③ B.②③④ C.②④ D.①④6. 设森林F对应的二叉树为B,它有m个结点,B的根为p,p的右子树结点个数为n,森林F中第一棵树的结点个数是()A.m-n B.m-n-1 C.n+1 D.条件不足,无法确定【南京理工大学2000 一、17(1.5分)】7. 树是结点的有限集合,它( (1))根结点,记为T。
其余结点分成为m(m>0)个((2))的集合T1,T2,…,Tm,每个集合又都是树,此时结点T称为Ti的父结点,Ti称为T的子结点(1≤i≤m)。
数据结构(树)习题与答案

一、单选题1、树最适合用来表示()。
A.元素之间具有分支层次关系的数据B.有序数据元素C.元素之间无联系的数据D.无序数据元素正确答案:A2、在树结构中,若结点A有三个兄弟,且B是A的双亲,则B的度是()。
A.5B.4C.3D.2正确答案:B3、下列陈述中正确的是()。
A.二叉树是度为2的有序树B.二叉树中结点只有一个孩子时无左右之分C.二叉树中每个结点最多只有两棵子树,并且有左右之分D.二叉树中必有度为2的结点正确答案:C4、设深度为h的二叉树中只有度为0和度为2的结点,则此类二叉树中所包含结点数至少为()。
A.2h-1B.2h+1C.h+1D.2h正确答案:A解析: A、除根之外,每层只有两个结点,且互为兄弟。
5、设深度为h的二叉树中只有度为0和度为2的结点,则此类二叉树中所包含结点数至多为()。
A.2h-1B. 2h+1-1C. 2h-1-1D. 2h+1正确答案:A解析: A、构成完全二叉树。
6、具有n(n>0)个结点的完全二叉树的深度为()。
A.⌊ log2(n)⌋ +1B.⌈log2(n)⌉C.⌊ log2(n)⌋D.⌈log2(n)+1⌉正确答案:A7、具有32个结点的完全二叉树有()个叶子结点。
A.16B.14C.15D.17正确答案:A解析: A、对结点按层序编号,32号结点的双亲结点编号为16,则17至32号结点都为叶子,共16个。
8、一棵完全二叉树的第6层上有23个叶子结点,则此二叉树最多有()结点。
A.81B.78C.80D.79正确答案:A解析: A、完全二叉树的叶子结点只能在最下两层,要使结点最多,这棵二叉树深度为7,前6层结点数共为63,第6层有32个结点,其中叶子为23个,非叶子为9个,它们的度都为2,第7层只有18个结点,故整棵二叉树结点数为81.9、具有3个结点的二叉树有()种。
A.6B.3C.5D.4正确答案:C10、若一棵二叉树有9个度为2的结点,5个度为1的结点,则叶子结点的个数为()。
树练习题(答案)

《树》练习题一、单项选择题1、在一棵度为3的树中,度为3的结点数为2个,度为2的结点数为1个,度为1的结点数为2个,则度为0的结点数为()个。
A. 4B. 5C. 6D. 72、假设在一棵二叉树中,双分支结点数为15,单分支结点数为30个,则叶子结点数为()个。
A. 15B. 16C. 17D. 473、假定一棵三叉树的结点数为50,则它的最小高度为()。
(根为第0层)A. 3B. 4C. 5D. 64、在一棵二叉树上第3层的结点数最多为()(根为第0层)。
A. 2B. 4C. 6D. 85、用顺序存储的方法将完全二叉树中的所有结点逐层存放在数组中R[1..n],结点R[i]若有左孩子,其左孩子的编号为结点()。
(若存放在R[0..n-1]则左孩子R[2i+1])A. R[2i+1]B. R[2i]C. R[i/2]D. R[2i-1]6、将含100个结点的完全二叉树,按照从上层到下层、同层从左到右的次序依次给它们编以从0开始的连续自然数,则编号为40的结点X的双亲的编号为( )。
A.19B.20C. 21D.397、由权值分别为3,8,6,2,5的叶子结点生成一棵哈夫曼树,它的带权路径长度为()。
A. 24B. 48C. 72D. 538、设n , m 为一棵二叉树上的两个结点,在中序遍历序列中n在m前的条件是()。
A. n在m右方B. n在m 左方C. n是m的祖先D. n是m的子孙9、如果F是由有序树T转换而来的二叉树,那么T中结点的前序就是F中结点的()。
A. 中序B. 前序C. 后序D. 层次序10、下面叙述正确的是()。
A. 二叉树不是树B. 二叉树等价于度为2的树C. 完全二叉树必为满二叉树D. 二叉树的左右子树有次序之分11、任何一棵二叉树的叶子结点在先序、中序和后序遍历序列中的相对次序()。
A. 不发生改变B. 发生改变C. 不能确定D. 以上都不对12、已知一棵完全二叉树的结点总数为9个,则最后一层的结点数为()。
数据结构练习第六章树

数据结构练习第六章树一、选择题1.树最适合用来表示( )。
A.有序数据元素B.无序数据元素C.元素之间具有分支层次关系的数据D.元素之间无联系的数据2.二叉树的第k层的结点数最多为( ).A.2k-1 B.2K+1 C.2K-1 D. 2k-13.设哈夫曼树中的叶子结点总数为m,若用二叉链表作为存储结构,则该哈夫曼树中总共有()个空指针域。
A. 2m-1B. 2mC. 2m+1D. 4m4.设某棵二叉树的中序遍历序列为ABCD,前序遍历序列为CABD,则后序遍历该二叉树得到序列为()。
A. BADCB. BCDAC. CDABD. CBDA5.设某棵二叉树中有2000个结点,则该二叉树的最小高度为()。
A. 9B. 10C. 11D. 126.设一棵二叉树的深度为k,则该二叉树中最多有()个结点。
A. 2k-1 B .2k C. 2k-1 D. 2k-17.设某二叉树中度数为0的结点数为N0,度数为1的结点数为Nl,度数为2的结点数为N2,则下列等式成立的是()。
A. N0=N1+1 B. N=Nl+N2C. N=N2+1 D. N=2N1+l8.设一棵m叉树中度数为0的结点数为N0,度数为1的结点数为Nl,……,度数为m的结点数为Nm,则N=()。
A. Nl +N2+……+Nm B. l+N2+2N3+3N4+……+(m-1)NmC. N2+2N3+3N4+……+(m-1)Nm D. 2Nl+3N2+……+(m+1)Nm9.设一组权值集合W={2,3,4,5,6},则由该权值集合构造的哈夫曼树中带权路径长度之和为()。
A. 20B. 30C. 40D. 4510.设二叉树的先序遍历序列和后序遍历序列正好相反,则该二叉树满足的条件是()。
A. 空或只有一个结点B. 高度等于其结点数C. 任一结点无左孩子D. 任一结点无右孩子11.设某棵三叉树中有40个结点,则该三叉树的最小高度为()。
A. 3B. 4C. 5D. 612.深度为k的完全二叉树中最少有()个结点。
《数据结构》应用题参考习题

一.《树》应用题1. 已知一棵树边的集合为{<i,m>,<i,n>,<e,i>,<b,e>,<b,d>,<a,b>,<g,j>,<g,k>,<c,g>,<c,f>,<h,l>,<c,h>,<a,c>},请画出这棵树,并回答下列问题:(1)哪个是根结点?(2)哪些是叶子结点?(3)哪个是结点g的双亲?(4)哪些是结点g的祖先?(5)哪些是结点g的孩子?(6)哪些是结点e的孩子?(7)哪些是结点e的兄弟?哪些是结点f的兄弟?(8)结点b和n的层次号分别是什么?(9)树的深度是多少?(10)以结点c为根的子树深度是多少?2. 一棵度为2的树与一棵二叉树有何区别。
3. 试分别画出具有3个结点的树和二叉树的所有不同形态?4. 已知用一维数组存放的一棵完全二叉树:ABCDEFGHIJKL,写出该二叉树的先序、中序和后序遍历序列。
5. 一棵深度为H的满m叉树有如下性质:第H层上的结点都是叶子结点,其余各层上每个结点都有m棵非空子树,如果按层次自上至下,从左到右顺序从1开始对全部结点编号,回答下列问题:(1)各层的结点数目是多少?(2)编号为n的结点的父结点如果存在,编号是多少?(3)编号为n的结点的第i个孩子结点如果存在,编号是多少?(4)编号为n的结点有右兄弟的条件是什么?其右兄弟的编号是多少?6. 找出所有满足下列条件的二叉树:(1)它们在先序遍历和中序遍历时,得到的遍历序列相同;(2)它们在后序遍历和中序遍历时,得到的遍历序列相同;(3)它们在先序遍历和后序遍历时,得到的遍历序列相同;7. 假设一棵二叉树的先序序列为EBADCFHGIKJ,中序序列为ABCDEFGHIJK,请写出该二叉树的后序遍历序列。
8. 假设一棵二叉树的后序序列为DCEGBFHKJIA,中序序列为DCBGEAHFIJK,请写出该二叉树的后序遍历序列。
完整word版,6、树

6 树一、单项选择题(15题)1、按照二叉树的定义,具有3个结点的二叉树有()种。
A.3B.4C.5D.62、深度为5的二叉树至多有()个结点。
A.16B.32C.31D.103、在一非空二叉树的中序遍历序列中,根结点的右边()。
A 只有右子树上的所有结点B 只有右子树上的部分结点C 只有左子树上的部分结点D 只有左子树上的所有结点4、深度为4的完全二叉树至少有()个结点。
A 16B 15C 8D 75、具有n个结点的二叉树若采用链式存储,则空闲的指针域有()个。
A nB n-1C n+1D 2n6、针对右图的这棵二叉树,下列哪个说法是正确的?()A 该树的度为3B 该树的深度为4C 结点D的度为0D 结点A是结点D和F的双亲7、某二叉树高度为h,所有结点的度为0或为2,则这棵二叉树最少有()个结点。
A 2hB 2h-1C 2h+1D h+18、针对右图的这棵二叉树,下列哪个说法是不正确的?()A 该树的度为3B 该树的深度为4C 结点D的度为0D 结点A是结点B和C的双亲9、二叉树是非线性数据结构,所以()。
A) 它不能用顺序存储结构存储 B)它不能用链式存储结构存储C)顺序存储结构和链式存储结构都能存储 D)顺序存储结构和链式存储结构都不能使用10、设n,m为一棵二叉树上的两个结点,在中序遍历时,n在m前的条件是()。
A.n在m右方 B.n是m祖先 C.n在m左方 D.n是m子孙11、由权值分别为3,8,6,2,5的叶子结点生成一棵哈夫曼树,它的带权路径长度为( )。
A. 24B. 48C. 72D. 5312、高度k的二叉树的最大结点数为( )。
A. 2k-1 B 2k+1 C.2k-1 D. 2 k-113、有n(n>0)个结点的完全二叉树的深度为( )。
A)⎡log2(n)⎤ B) ⎣ log2(n)⎦ C)⎣ log2(n) ⎦+1 D)⎡log2(n)+1⎤14、设二叉树根结点的层次为1,所有含有63个结点的二叉树中,最小高度是()。
(完整word版)数据结构应用题练习
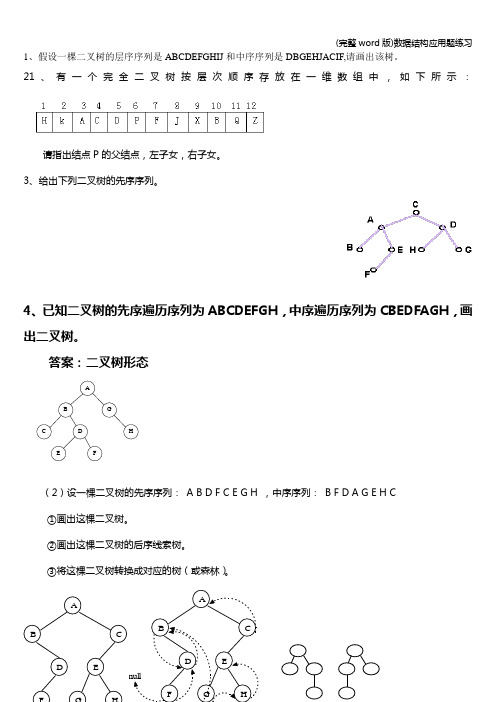
1、假设一棵二叉树的层序序列是ABCDEFGHIJ 和中序序列是DBGEHJACIF,请画出该树。
21、有一个完全二叉树按层次顺序存放在一维数组中,如下所示:请指出结点P 的父结点,左子女,右子女。
3、给出下列二叉树的先序序列。
4、已知二叉树的先序遍历序列为ABCDEFGH ,中序遍历序列为CBEDFAGH ,画出二叉树。
答案:二叉树形态AFHGDECB(2)设一棵二叉树的先序序列: A B D F C E G H ,中序序列: B F D A G E H C ①画出这棵二叉树。
②画出这棵二叉树的后序线索树。
③将这棵二叉树转换成对应的树(或森林)。
ABFD CE HG(1) (2)1、已知一棵二叉树的前序序列为:A,B,D,G,J,E,H,C,F,I,K,L中序序列:D,J,G,B,E,H, A,C,K,I,L,F。
i.写出该二叉树的后序序列;ii.画出该二叉树;iii.求该二叉树的高度(假定空树的高度为-1)和度为2、度为1、及度为0的结点个数。
该二叉树的后序序列为:J,G,D,H,E,B,K,L,I,F,C,A。
该二叉树的形式如图所示:该二叉树高度为:5。
度为2的结点的个数为:3。
度为1的结点的个数为:5。
度为0的结点个数为:4。
5、试用权集合{12,4,5,6,1,2}构造哈夫曼树,并计算哈夫曼树的带权路径长度。
答案:215611187341230WPL=12*1+(4+5+6)*3+(1+2)*4=12+45+12=696、已知权值集合为{5,7,2,3,6,9},要求给出哈夫曼树,并计算带权路径长度WPL 。
答案:(1)树形态:325510199761332(2)带权路径长度:WPL=(6+7+9)*2+5*3+(2+3)*4=44+15+20=79(3) 假设用于通信的电文仅由8个字母组成,字母在电文中出现的频率分别为0.07,0.19,0.02,0.06,0.32,0.03,0.21,0.10。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数据结构-树练习题
一、选择题
1、二叉树的深度为k,则二叉树最多有( C )个结点。
A. 2k
B. 2k-1
C. 2k-1
D. 2k-1
2、用顺序存储的方法,将完全二叉树中所有结点按层逐个从左到右的顺序存放在一维数组R[1..N]中,若结点R[i]有右孩子,则其右孩子是( B )。
A. R[2i-1]
B. R[2i+1]
C. R[2i]
D. R[2/i]
3、设a,b为一棵二叉树上的两个结点,在中序遍历时,a在b前面的条件是( B )。
A. a在b的右方
B. a在b的左方
C. a是b的祖先
D. a是b的子孙
4、设一棵二叉树的中序遍历序列:badce,后序遍历序列:bdeca,则二叉树先序遍历序列为()。
A. adbce
B. decab
C. debac
D. abcde
5、在一棵具有5层的满二叉树中结点总数为( A )。
A. 31
B. 32
C. 33
D. 16
6、由二叉树的前序和后序遍历序列( B )惟一确定这棵二叉树。
A. 能
B. 不能
7、某二叉树的中序序列为ABCDEFG,后序序列为BDCAFGE,则其左子树中结点数目为(C )。
A. 3
B. 2
C. 4
D. 5
8、若以{4,5,6,7,8}作为权值构造哈夫曼树,则该树的带权路径长度为(C )。
A. 67
B. 68
C. 69
D. 70
9、将一棵有100个结点的完全二叉树从根这一层开始,每一层上从左到右依次对结点进行编号,根结点的编号为1,则编号为49的结点的左孩子编号为(A )。
A. 98
B. 99
C. 50
D. 48
10、表达式a*(b+c)-d的后缀表达式是( B )。
A. abcd+-
B. abc+*d-
C. abc*+d-
D. -+*abcd
11、对某二叉树进行先序遍历的结果为ABDEFC,中序遍历的结果为DBFEAC,则后序遍历的结果是( B )。
A. DBFEAC
B. DFEBCA
C. BDFECA
D. BDEFAC
12、树最适合用来表示( C )。
A. 有序数据元素
B. 无序数据元素
C. 元素之间具有分支层次关系的数据
D. 元素之间无联系的数据
13、表达式A*(B+C)/(D-E+F)的后缀表达式是( C )
A. A*B+C/D-E+F
B. AB*C+D/E-F+
C. ABC+*DE-F+/
D. ABCDED*+/-+
14、任何一棵二叉树的叶结点在先序、中序和后序遍历序列中的相对次序()。
A. 不发生改变
B. 发生改变
C. 不能确定
D. 以上都不对
15、假定在一棵二叉树中,度为2的结点数为15,度为1的结点数为30,则叶子结点数为()个。
A. 15
B. 16
C. 17
D. 47
16、由权值为3,6,7,2,5的叶子结点生成一棵哈夫曼树,它的带权路径长度为()。
A. 51
B. 23
C. 53
D. 74
二、判断题
()1、存在这样的二叉树,对它采用任何次序的遍历,结果相同。
()2、中序遍历一棵二叉排序树的结点,可得到排好序的结点序列。
()3、对于任意非空二叉树,要设计其后序遍历的非递归算法而不使用堆栈结构,最适合的方法是对该二叉树采用三叉链表。
()4、在哈夫曼编码中,当两个字符出现的频率相同时,其编码也相同,对于这种情况应做特殊处理。
(T )5、一个含有n个结点的完全二叉树,它的高度是log2n+1。
(T )6、完全二叉树的某结点若无左孩子,则它必是叶结点。
三、填空题
1、具有n 个结点的完全二叉树的深度是 log 2n +1 。
2、哈夫曼树是其树的带权路径长度 最小 的二叉树。
3、在一棵二叉树中,度为0的结点的个数是n0,度为2的结点的个数为n2,则有 n0= N2+1 。
4、树内各结点度的 最大值 称为树的度。
四、综合题
1、假设用于通讯的电文仅由8个字母A 、B 、C 、D 、E 、F 、G 、H 组成,字母在电文中出现的频率分别为:0.07,0.19,0.02,0.06,0.32,0.03,0.21,0.10。
请为这8个字母设计哈夫曼编码。
6511193262
3032
38
100
17
10721A H C F
D B
E G 000
111
00001111 A 000
B 101
C 10000
D 1001
E 11
F 10001
G 01
H 001
2、已知权值集合为{5,7,2,3,6,9},要求给出哈夫曼树,并计算带权路径长度WPL 。
21561118
7
3
4
1230
WPL=12*1+(4+5+6)*3+(1+2)*4=12+45+12=69
3、已知一棵二叉树的先序序列:ABDGJEHCFIKL ;中序序列:DJGBEHACKILF 。
画出二叉树的形态。
A
L K I H F C E J G
D
B。
