2007全国数学建模中国人口增长预测
中国人口增长的中短期和长期趋势预测数学模型
中国人口增长的中短期和长期趋势预测数学模型【摘要】中国是人口大国，人口的预测问题始终是关系到社会和谐发展的关键因素之一。
首先，本文就近几年中国人口结构的变化情况进行“生存——生育”双因素分析，按照人口性别分类，考虑老龄化进程、出生人口性别比以及乡村人口城镇化等因素，根据近几年城、镇、乡的统计数据，建立基于概率方法的Leslie矩阵，利用Matlab软件进行编程求解，对中国人口进行了中短期预测。
其次，在对人口进行长期预测时，引入净再生产率（NRR）和总和生育率（TFR）。
根据已知数据计算出1994—2005每年的NRR和TFR，通过曲线拟合预测出未来的TFR趋势。
而各年TFR的变化是由相应年各年龄女性生育率的变化引起的，各年龄女性生育率的变化比例即是TFR的变化比例，得到新的生育率，即得到了新的Leslie矩阵，计算出该Leslie矩阵的唯一的正的特征根λ，当λ接近于1时，则人口趋于稳定。
此时求得各年人口预测的新的Leslie矩阵，利用新的每年Leslie矩阵连乘，并乘于2005年各年龄人口数向量，则可预测中长期人口数量。
主要问题结论：1、对中国人口增长的中短期进行预测。
首先以2001年人口数据为基数，对2002年—2005年进行预测，并与真实年份（年）2002 2003 2004 2005 预测总人口数（万人）实际总人口数（万人）128453 129227 129988 130756 相对误差（%）虑各年份生育率的影响。
其次，由上表可知模型较为准确，可以2005年人口数据为基数，利用模型年份2006 2007 2008 2009 2010 预测总人口数（万人）年份2011 2012 2013 2014 2015 预测总人口数（万人）的变化得到每年各年龄女性生育率的变化，运用新的生育率得到该年的Leslie矩阵，计算出该Leslie矩阵的唯一的正的特征根λ，当2033年λ较为接近1时，则2033年后人口达到峰值趋向稳定，且此时NRR2033年=，亦接近于目前发达国家的NRR指标。
数学建模全国赛07年A题一等奖论文
关于中国人口增长趋势的研究【摘要】本文从中国的实际情况和人口增长的特点出发，针对中国未来人口的老龄化、出生人口性别比以及乡村人口城镇化等，提出了Logistic、灰色预测、动态模拟等方法进行建模预测。
首先，本文建立了Logistic阻滞增长模型，在最简单的假设下，依照中国人口的历史数据，运用线形最小二乘法对其进行拟合，对2007至2020年的人口数目进行了预测，得出在2015年时，中国人口有13.59亿。
在此模型中，由于并没有考虑人口的年龄、出生人数男女比例等因素，只是粗略的进行了预测，所以只对中短期人口做了预测，理论上很好，实用性不强，有一定的局限性。
然后，为了减少人口的出生和死亡这些随机事件对预测的影响，本文建立了GM(1,1) 灰色预测模型，对2007至2050年的人口数目进行了预测，同时还用1990至2005年的人口数据对模型进行了误差检验，结果表明，此模型的精度较高，适合中长期的预测，得出2030年时，中国人口有14.135亿。
与阻滞增长模型相同，本模型也没有考虑年龄一类的因素，只是做出了人口总数的预测，没有进一步深入。
为了对人口结构、男女比例、人口老龄化等作深入研究，本文利用动态模拟的方法建立模型三，并对数据作了如下处理：取平均消除异常值、对死亡率拟合、求出2001年市镇乡男女各年龄人口数目、城镇化水平拟合。
在此基础上，预测出人口的峰值，适婚年龄的男女数量的差值，人口老龄化程度，城镇化水平，人口抚养比以及我国“人口红利”时期。
在模型求解的过程中，还对政府部门提出了一些有针对性的建议。
此模型可以对未来人口做出细致的预测，但是需要处理的数据量较大，并且对初始数据的准确性要求较高。
接着，我们对对模型三进行了改进，考虑人为因素的作用，加入控制因子，使得所预测的结果更具有实际意义。
在灵敏度分析中，首先针对死亡率发展因子θ进行了灵敏度分析，发现人口数量对于θ的灵敏度并不高，然后对男女出生比例进行灵敏度分析得出其灵敏度系数为0.8850，最后对妇女生育率进行了灵敏度分析，发现在生育率在由低到高的变化过程中，其灵敏度在不断增大。
数学建模插值与拟合实验题
数学建模插值与拟合实验题
1.处理2007年大学生数学建模竞赛A题：“中国人口增长预测”附件中的数据，得到以下几个问题的拟合结果，并绘制图形
（1）对1994-2005年出生婴儿的性别比进行拟合，并以此预测2006-2022年间的性别比。
（2）生育率随年龄的变化而变化，试以生育年龄为自变量，生育率为因变量，对各年的育龄妇女生育率进行拟合；
（3）按时间分布对城、镇、乡生育率进行分析，以时间为自变量，生育率为因变量，对城、镇、乡的生育率进行拟合，并预测2006-2022年间的生育率。
（4）将某年的城镇化水平PU(t)定义为当年的城镇人口数与总人口数之
比,Karmehu(1992年)研究发现20世纪50年代以来发达国家随着经济发展水平的提高，城镇人口的增长相对农村要快一些，但是随着城镇化水平的提高，并趋向100%时，速度会减缓，城镇化水平的增长曲线大致表现为一条拉伸的“S”型Logitic曲线[4]，对附录2中所给出2001年—2005年中国人口1%调查数据进行曲线拟合，求得该曲线，并绘制2001-2050年的城镇化水平的曲线图。
2.处理2022年大学生数学建模竞赛A题：“城市表层土壤重金属污染分析”附件中的数据，完成下列问题
（1）以城区取样点位置为节点进行插值，绘制城区的地形图和等高线图；（2）绘制城区的8种重金属浓度的空间分布图。
并指出浓度最高和最低的点所在的位置。
插值的方法可用三次插值、kriging插值、Shepard插值等。
工具可用Matlab，也可用urfer软件实现。
2007A竞赛论文【中国人口增长预测】娄贞贞、白荣华、殷文芳
中国人口增长预测摘要本文从中国人口的实际情况和人口增长的特点出发，根据题目和中国统计年鉴中的相关数据，建立了两个关于中国人口增长的数学模型，并对中国人口做出了分析和预测。
模型一：利用中国统计年鉴中2000—2005 年人口的数据，运用灰色理论的基本原理建立GM(1,1) 模型。
该模型利用离散数据列进行生态处理，建立动态的微分方程，对我国近5年、10年、20年的总人口分别进行了预测。
又根据中国人口城乡分布不同且总趋势也不同的特点，把全国人口分为城市人口、城镇人口、乡村人口三部分分别进行灰色预测。
结果表明，该模型较好的反映并预测中国人口短中期和长期的变化情况。
模型二：按人口年龄结构特征，将人口分为幼年（0—14岁）男女、中年（15—49岁）男女、老年（50岁以上）男女。
各年龄段的人口变化是由出生率、死亡率和转化为其他年龄段的转化人数决定的。
根据各年龄段人口数量变化特点，对各年龄段转化人数引入转化因子，改进马尔萨斯模型，附带出生率、死亡率、生育率、出生性别比率等约束条件，建立了新的具有年龄结构的人口增长模型。
结合我国人口的特点，运用已知数据和利用微分方程的数值解，预测出男性和女性幼年、中年、老年的人口数量。
可反映中国不同年龄结构的人口分布情况。
关键词：灰色预测；小误差频率；微分方程组；人口模型；转移因子一．问题重述中国是一个人口大国，人口问题始终是制约我国发展的关键因素之一。
因此人口预测的科学性、准确性是至关重要的。
英国人口学家马尔萨斯的人口指数增长模型和荷兰生物学家的Logistic模型都是经典的人口预测模型。
但是，影响中国人口的因素较多，人口结构较复杂，这些模型对人口预测很粗略，甚至是不准确的。
因此，我们要根据我国具体的人口结构现状（如老龄化进程加速）、人口的分布现状（如乡村人口城镇化）、人口比率现状（如出生人口性别比持续升高）等特点，来较准确、较具体地对中国人口进行预测，建立人口增长的数学模型，由此对中国人口中短期和长期增长趋势做出预测。
数学建模国赛2007A
国家人口发展战略研究报告（全文）中国人口网2007-02-01 15:59:21/fzzlbg/bgyw/t20070111_172058513.html基本判断：一、如果人口总量（不含香港、澳门特别行政区和台湾省，下同）峰值控制在15亿人左右，全国总和生育率在未来30年应保持在1.8左右，过高或过低都不利于人口与经济社会的协调发展。
二、人口和计划生育工作成就巨大，来之不易。
目前的低生育水平反弹势能大，维持低生育水平的代价高，必须创新工作思路、机制和方法。
三、确定人口发展战略，必须既着眼于人口本身的问题，又处理好人口与经济社会资源环境之间的相互关系。
四、构建社会主义和谐社会，统筹解决人口数量、素质、结构、分布问题，必须调整发展思路，优先投资于人的全面发展。
战略思路：以邓小平理论和“三个代表”重要思想为指导，全面落实科学发展观，按照构建社会主义和谐社会的要求，坚持以人为本，推进体制创新，优先投资于人的全面发展：稳定低生育水平，提高人口素质，改善人口结构，引导人口合理分布，保障人口安全；实现人口大国向人力资本强国的转变，实现人口与经济社会资源环境的协调和可持续发展。
为落实2004年中央人口资源环境工作座谈会关于加强人口发展战略研究的重要指示精神，组成了由蒋正华、徐匡迪和宋健同志任组长的国家人口发展战略研究课题组，集中了包括十多位两院院士在内的300多位专家学者，自2004年2月至2006年4月，对科学发展观、人口发展态势、人口与经济社会资源环境重大关系等3个分课题及其42个子课题，进行了广泛、深入地调研和专题研究论证，取得了阶段性成果。
一、全面建设小康社会面临的人口形势与严峻挑战（一）人口发展的成就与经验近半个世纪以来，世界人口发展的基本态势：一是生育水平逐步下降，人口总量经历高速增长后进入增速趋缓时期。
发展中国家总和生育率从6.2下降到2.9,发达国家从2.8下降到1.6。
据联合国预测，到本世纪中叶，全球人口再生产类型转变将基本完成。
数学建模之中国人口增长的预测和人口结构的简析
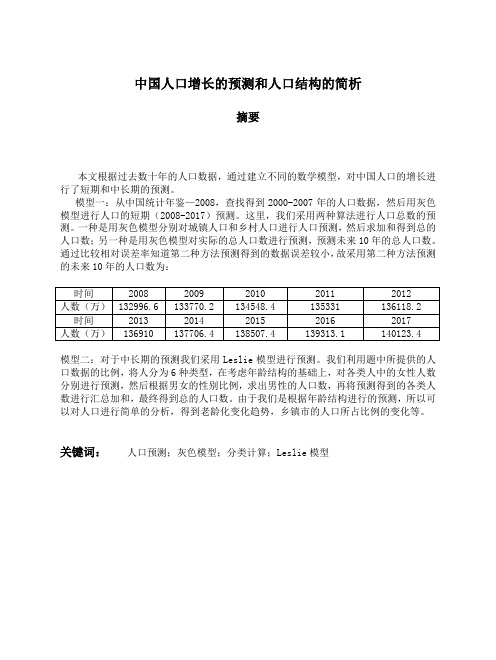
中国人口增长的预测和人口结构的简析摘要本文根据过去数十年的人口数据，通过建立不同的数学模型，对中国人口的增长进行了短期和中长期的预测。
模型一：从中国统计年鉴—2008，查找得到2000-2007年的人口数据，然后用灰色模型进行人口的短期（2008-2017）预测。
这里，我们采用两种算法进行人口总数的预测。
一种是用灰色模型分别对城镇人口和乡村人口进行人口预测，然后求加和得到总的人口数；另一种是用灰色模型对实际的总人口数进行预测，预测未来10年的总人口数。
通过比较相对误差率知道第二种方法预测得到的数据误差较小，故采用第二种方法预测的未来10年的人口数为：模型二：对于中长期的预测我们采用Leslie模型进行预测。
我们利用题中所提供的人口数据的比例，将人分为6种类型，在考虑年龄结构的基础上，对各类人中的女性人数分别进行预测，然后根据男女的性别比例，求出男性的人口数，再将预测得到的各类人数进行汇总加和，最终得到总的人口数。
由于我们是根据年龄结构进行的预测，所以可以对人口进行简单的分析，得到老龄化变化趋势，乡镇市的人口所占比例的变化等。
关键词：人口预测；灰色模型；分类计算；Leslie模型一、模型假设模型一的假设：1、不考虑国际迁移，认为国家内部迁移不改变人口总量；2、不考虑自然灾害、疾病等因素对人口数量的影响；3、文中短期预测到2017年4、大面积自然灾害、疾病的发生以及人们的生育观念等因素会对当年的生育率和人口数量产生影响，认为这些因素在预测误差允许的范围内．模型二的假设：1、每一年龄组的女性在每一个时间段内有相同的生育率和死亡率；2、在预测的时间段内男女的性别比例保持现状不变；3、不考虑人口的迁入和迁出；4、不考虑空间等自然因素的影响，不考虑自然灾害对人口数量的影响。
二、问题分析中国是一个人口大国，随着经济的不断发展，生产力达到较高的水平，现在的问题已不是仅仅满足个人的需要，而是要考虑社会的需要。
中国未富先老，对经济的发展产生很大的影响。
07A人口预测
中国人口增长预测摘要本文利用所给数据，结合中国人口的增长特点，针对中国未来人口的老龄化、出生人口性别比例以及城镇化的变化趋势等，提出了Logistic模型、灰色预测模型、基于Leslie的模型等，用于预测中国未来人口数的中短期和长期趋势，并对人口老龄化、人口抚养比例等一系列评价指标进行了预测。
首先，本文建立了Logistic阻滞增长模型。
在最简单的假设下，通过上网搜集的中国人口的历史数据，运用线性最小二乘法对其数据进行拟合。
在此模型中，由于并没有考虑人口的年龄、出生人数男女比例等因素，只是粗略的进行了预测，所以只对中短期人口做了预测。
运用1980年到2005年的全国总人口的数据预测得到2010年、2015年、2020年全国总人口数分别为13.5274亿、13.8674亿、14.1470亿。
然后，为了减少人口的出生和死亡等这些随机事件对预测的影响，本文建立了GM(1,1) 灰色预测模型，采用最小二乘法，对2006年到2020年的人口数进行了预测。
理论上，GM(1,1)模型相比于Logistic模型精度较高。
根据从1990年到2005年的总人口数据建立模型，进行人口预测。
预测结果得到2010年、2015年、2020年的总人口数分别为13.4976亿、13.8554亿、14.1651亿。
与Logistic模型预测数据基本一致。
最后，考虑到年龄结构对人口预测的影响，本文建立了基于Leslie的人口预测模型。
该模型中考虑到了新出生的男女比例、人口老龄化、农村人口城镇化等符合中国特殊国情的影响人口数量的因素。
根据所给的材料确定新生男女比例为100:115，城镇化水平为每年1%，人口的总和生育率为1.8，构造Leslie矩阵，建立相应的Leslie模型。
预测结果是：我国总人口数在2020年达到15.0713亿、2030年为14.9817亿、2040年为14.4382亿、2050年为13.5200亿，在2024年达到我国人口最高峰约有15.1282亿。
中国人口增长预测模型
0
h r
r r1,r r2
1 1 e r r
r r1
a
r2 r r1
其中：r1 15 r2 49, 并取 2 n 2
拟合得到：
由于中国人口迁移主要是在于内部城市之间， 因此g(r,t)可近似为0 通过模型：
中国是一个人口大国，人口问题始终是制 约我国发展的关键因素之一。根据已有数据， 运用数学建模的方法，建立中国人口增长的 数学模型，并由此对中国人口增长的中短期 和长期趋势做出预测；特别要指出模型中的 优点与不足之处。
中国是一个人口大国，人口问题始终是制约我国 发展的关键因素之一。 进来，中国人口发展出现了一些新的特点，例如： 人口老龄化、出生人口性别比例持续升高、以及乡 村人口城镇化等因素，都影响着当今中国的人口增 长。 通过已经积累得到的大量数据资料，就中国实际 人口情况和人口增长的上述特点，建立中国人口的 增长模型，对中国人口短期、长期状况下进行预测， 并指出模型的优缺点。
通过已经计算拟合的数据，便可以计算得 到未来几年中，中国人口的预测数量。
计算未来几年男性人数得到：
通过已有的2001～2005年间的人口数据，和拟合得到的 数据进行比较计算，对P r,t 进行误差分析得到：
年份 误差 2001 …… 2002 0.085 2003 -0.091 2004 -0.012 2005 0.079
首先，可以看到该模型中男婴出生比例 (m)，是静止不 变的，这不能体现当今中国人口所呈现的性别出生比的上 升和老龄化进程的特点。所以在提出的中国人口发展模型 中对 (m)，s1(n -1)引进时间参数t，将其动态化为 (m,t)，s(r,t)。 然后用灰色预测模型对这两个参数进行预测。 . 其次，进一步分析p1(0,t) b1(t 1) g1(0)项，其意思是该年出 生的人在下一年作为0岁的人数计算，而附录所给统计数据0岁 所对应的是当年所出生的人数，所以宋健的人口发展模型是 滞后一年的。将其修正为p1(0,t) s(0,t 1)b1(t 1) g1(0,t 1)
中国人口增长预测_灰色模型——全国数学建模大赛
根据所给的附表，计算出2001年到2005年的出生率和死亡率，见下表：
年份
死亡率
(2)计算 序列的均方差：
= =0.0001262
(3)计算残差的均值： = [ ]=0.0000281
(4)计算残差的均方差：
= =0.00003725
(5)计算C： =0.00003725/0.0001262=0.2952
(6)计算小残差概率： =0.6745 0.0001261=0.00008505
实际值（万）
预测值
相对误差
2006
131448
1311616568
0.218%
2007
132129
1318021656
0.247%
2008
132802
1324335575
0.277%
2009
133861
1330587368
0.599%
结果分析
从上述预测结果来看，前三年的预测值与实际值的误差的相对误差稳定在0.3%以内，而第四年的预测值与实际值的相对误差达到0.599%，较之前的翻了一倍，说明第四年的预测已经不是很准。所以，我们认为GM(1,1)模型只适用于比较准确的预测三年之内的总人数。
0.010147
4.283%
2005
0.009367
0.0096969
3.522%
因为 ，那就可得各年份死亡率的预测值，与现实值进行比较得出该模型精度较高，可进行预测和预报。
中国人口增长预测
中国人口增长预测1问题重述中国是一个人口大国，人口问题始终是制约我国发展的关键因素之一。
根据已有数据，运用数学建模的方法，对中国人口做出分析和预测是一个重要问题。
近年来中国的人口发展出现了一些新的特点，例如，老龄化进程加速、出生人口性别比持续升高，以及乡村人口城镇化等因素，这些都影响着中国人口的增长。
2007年初发布的《国家人口发展战略研究报告》(附录1) 还做出了进一步的分析。
关于中国人口问题已有多方面的研究，并积累了大量数据资料。
附录2就是从《中国人口统计年鉴》上收集到的部分数据。
试从中国的实际情况和人口增长的上述特点出发，参考附录2中的相关数据（也可以搜索相关文献和补充新的数据），建立中国人口增长的数学模型，并由此对中国人口增长的中短期和长期趋势做出预测；特别要指出你们模型中的优点与不足之处。
2 模型假设1、假设在中国在未来会长期保持安定的局面2、不考虑突发事件（如传染病暴发，战争等）和因不可抗力（地震，海啸等）对人口数量造成的影响。
3、将全中国作为一个独立的人口系统，不考虑迁入迁出，即忽略中国人向海外移民和外国人定居中国对中国人口分布状况和总数的影响.4、假设在中短期内死亡率和生育率保持相对稳定，5、假设相同年龄段的人口性别比基本稳定6、假设计划生育等国家基本政策保持不变，7、假设人口生育率不受传统观念和个人主观因素的影响，如属相问题等3 符号说明T∆： 年龄区间Tm ∆：妇女能够生存的最大年龄)(j x i ：第i 个年龄组在时刻Tj ∆的人数)(j x ： 年龄密度分布 i b ： 各年龄组生育率 i s ： 存活率，G ： 莱斯利矩阵i d ： 死亡率城女A ：抽样调查到的城市女性总数镇女A ：抽样调查到的城镇女性总数， 乡女A ：抽样调查到的乡村女性总数城女a ：城市女性占总女性人数的比例镇女a ：城镇女性占总女性人数的比例 乡女a ：乡村女性占总女性人数的比例i d 女： 女性第i 年龄组死亡率i d 城女城市女性第i 年龄组死亡率i d 镇女：城镇女性第i 年龄组死亡率 i 乡女d ：乡村女性第i 年龄组死亡率女，b ：女婴出生率 城女，b ：城市女婴出生率 镇，女，b ：城镇女婴出生率 乡，女b ：乡村女婴出生率)0(i x 女：在起始时刻女性第ｉ年龄组的人口密度i,j x 乡女：第j 数据组年龄为i 的乡村女性人数 i,j x 城女：第j 数据组年龄为i 的城市女性人数 i,j x镇女：第j 数据组年龄为i 的城镇女性人数ij d,：第j 数据组年龄为i 的人口死亡率i j b ,：第j 数据组年龄为i 的人口生育率c ：指数平滑常数i 女s ：第i 年龄组女性存活率)0(i x 女：全国第ｉ年龄组女性分布率)t (x 女：第ｔ年女性人数密度分布 )t (女F ：第ｔ年女性人数总数)t (x i 女：第ｉ年龄组第ｔ年全国女性人口率)(t p ：男女比例矩阵)t (p i ：第i 年龄组的男女比例函数，是)(t p 的对角线元素ij p , ：第j 数据组第i 年龄组的男女性别比)1(,i j p ：指数平滑处理过的ij p ,)(t f ：初生男女婴儿比例函数)(t F ：第t 年全国总人口数)(t H ：第t 年全国年龄大于65岁的人口数)(t Q ：全国老龄化程度)(t x 城：第t 年城市人口年龄分布)t (城男x ：第t 年城市男性人口年龄分布 )t (城女x ：第t 年城市女性人口年龄分布：城市男女性别比例矩阵p)t(城：第t年城镇人口年龄分布x)(t镇G：城市女性人口的莱斯利矩阵城女)t(x：第t年城镇男性人口年龄分布镇男x：第t年城镇女性人口年龄分布)t(镇女：乡村男女性别比例矩阵p)t(乡x：第t年乡村男性人口年龄分布)t(乡男x：第t年乡村女性人口年龄分布)t(乡女：乡村男女性别比例矩阵)t(p乡G：乡村女性人口的莱斯利矩阵乡女w：乡村向城市迁移的人数占城市总人数的比例（城市迁移率）城w乡村向城镇迁移的人数占城镇总人数的比例（城镇迁移率）：镇w：乡村人口外迁人数占总人数的比例（乡村迁移率）乡V：转移到城市的人口占转移到城镇和城市总人口的比例)t(z：城市人口占总人口数的比例城z：城镇人口占总人口数的比例)t(城z：乡村人口占总人口数的比例)t(城：第ｔ年城市总人口数F)t(城：第ｔ年城镇总人口数F)t(镇：第ｔ年乡村总人口数F)t(乡F：第t年中国总人口数)(t4 问题分析我们针对中国人口增长的问题，建立了中国人口增长的模型，由此对中国人口增长的中短期和长期趋势做出了预测。
2007建模-中国人口预测模型的实证分析(常微分方程)
3
组为 0 岁（即出生婴儿），第 1 组为 1 岁，依次类推……直到第 89 组为 89 岁，第 90 组（最后一个年龄组）为 90 岁及以上。 (2) 以 1 年为一个时段，2001 年为第 1 个间隔时段，2002 年为第 2 个间隔时段，2005 年为第 5 个间隔时段。(注：为什么不分成 5 年一个间隔？) (3) 在相当一段时期内，生育政策保持不变。并设女性的生育年龄为 g1~g2，即 b1，…， bg1-1，b g2+1，…，bn＝0。现根据数据资料[3]，取 g1=15，g2=49。 (4) 对于市镇乡，分别取其 2001~2005 年育龄女性各年龄组男婴生育率平均值，作为每 年女性各育龄年龄组固定男婴生育率，同理可得各育龄各年龄组固定女婴生育率。
一． 问题分析
人口预测是人口研究中重要课题,准确的人口预测为制定合理的社会经济发展规划 提供了合理的科学依据。近年来中国的人口发展出现了一些新的特点，例如，老龄化进 程加速、出生人口性别比持续升高，以及乡村人口城镇化等因素，这些都影响着中国人 口的增长。
人们通常只做粗线条的总人口趋势的定性分析，而没有分析年龄结构具体形态。理 论上，任何时点上人口结构都是历史上人口结构生育、死亡、迁徙的结果，也是未来研 究人口过程的基础。事实上，要制定生育计划就要知道未来女性生育率，要改善社会保 障体系就要知道未来老年人口数，要确定人才引进策略和户籍管理制度就要知道城镇化 迁徙人口年龄分布。政府可以根据未来人口年龄分布信息状况制定宏观经济政策，进行 社会产业调整，使劳动力资源得到充分利用。
中国人口预测模型的实证分析
摘要 （注：要好好写， 优点突出） 为了针对中国人口近年来的发展特点，对于中国人口的发展趋势进行定量预测和分 析，我们选用了两个常用模型——Logistic 阻滞增长模型和 Leslie 差分方程模型，并对 它们进行了改进和实证分析。 由于原始数据中存在部分异常数据和较大随机性波动，为了减小这些因素对结果的 影响，我们经过多次尝试，选用移动平均法对数据进行了预处理。针对中国人口市、镇、 乡以及性别的 6 个组别，以及他们之间的关联，建立了 Leslie 差分方程组模型， 并引 进了人口迁移项。考虑到最高年龄组的实际情况，我们对 Leslie 模型作了必要的修正， 将最高年龄组的演变考虑为最高年龄组和次高年龄组存活人口总和。 本文利用 Leslie 差分方程组模型对预处理后的数据进行预测，着重考虑了人口年 龄结构的变化、老龄化现象、乡村人口城镇化、以及人口性别比例变化等问题。与一些 权威的统计数据或中短期预测数据进行比较，基本吻合，从而验证了模型的有效性。 在总人口的长期数据的预测上，Logistic 模型有较好的拟合度。在这一点上，虽然 Leslie 模型的结果的相对误差在可接受范围内，但考虑到中国总人口基数很大，绝对数 值仍有较大误差。为了改进 Leslie 模型的中长期预测效果，我们引进了模型中死亡率下 降因子，使得死亡率参数随着时间的变化，得到较好中长期预测结果。 关键词： Leslie 模型，老龄化，城镇化，性别比，Logistic 模型
2007年全国大学生数学建模竞赛A题优秀论文—人口预测模型
中国人口预测模型摘要本文对人口预测的数学模型进行了研究。
首先，建立一次线性回归模型，灰色序列预测模型和逻辑斯蒂模型。
考虑到三种模型均具有各自的局限性，又用加权法建立了熵权组合模型，并给出了使预测误差最小的三个预测模型的加权系数，用该模型对人口数量进行预测，得到的结果如下：其次，建立Leslie人口模型，充分反映了生育率、死亡率、年龄结构、男女比例等影响人口增长的因素，并利用以1年为分组长度方式和以5年为负指数函数，并给出了反映城乡人口迁移的人口转移向量。
最后我们BP神经网络模型检验以上模型的正确性关键字：一次线性回归灰色序列预测逻辑斯蒂模型Leslie人口模型BP神经网络一、问题重述1. 背景人口增长预测是随着社会经济发展而提出来的。
在过去的几千年里，由于人类社会生产力水平低，生产发展缓慢，人口变动和增长也不明显，生产自给自足或进行简单的以货易货，因而对未来人口发展变化的研究并不重要，根本不用进行人口增长预测。
而当今社会，经济发展迅速，生产力达到空前水平，这时的生产不仅为了满足个人需求，还要面向社会的需求，所以必须了解供求关系的未来趋势。
而人口增长预测是对未来进行预测的各环节中的一个重要方面。
准确地预测未来人口的发展趋势，制定合理的人口规划和人口布局方案具有重大的理论意义和实用意义。
2. 问题人口增长预测有短期、中期、长期预测之分，而各个国家和地区要根据实际情况进行短期、中期、长期的人口预测。
例如，中国人口预期寿命约为70岁左右，因此，长期人口预测最好预测到70年以后，中期40—50年，短期可以是5年、10年或20年。
根据2007年初发布的《国家人口发展战略研究报告》（附录一）及《中国人口年鉴》收集的数据（附录二），再结合中国的国情特点，如老龄化进程加速，人口性别比升高，乡村人口城镇化等因素，建立合理的关于中国人口增长的数学模型，并利用此模型对中国人口增长的中短期和长期趋势做出预测，同时指出此模型的合理性和局限性。
07年全国数学建模大赛--中国人口增长预测模型1
承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网上咨询等）与队外的任何人（包括指导教师）研究、讨论与赛题有关的问题。
我们知道，抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺，严格遵守竞赛规则，以保证竞赛的公正、公平性。
如有违反竞赛规则的行为，我们将受到严肃处理。
我们参赛选择的题号是（从A/B/C/D中选择一项填写）：我们的参赛报名号为（如果赛区设置报名号的话）：所属学校（请填写完整的全名）：参赛队员(打印并签名) ：1.2.3.指导教师或指导教师组负责人(打印并签名)：日期：年月日赛区评阅编号（由赛区组委会评阅前进行编号）：编号专用页赛区评阅编号（由赛区组委会评阅前进行编号）：全国统一编号（由赛区组委会送交全国前编号）：全国评阅编号（由全国组委会评阅前进行编号）：中国人口增长预测模型摘要：在中国的人口增长预测问题中，老龄化进程加速，出生人口性别比的变化，乡村人口城镇化，是影响人口预测的主要因素。
在中短期预测的过程中，由于影响人口的各项主要因素变化范围较小，可以直接根据我们建立的模型进行预测。
老年人的死亡率变化较大，出生的男女百分比得到遏制并逐渐趋于正常的水平。
我们将根据年龄将人口分成两部分，0到60岁的人口的预测，和60岁以后人口的预测。
通过原来的模型对0岁到60岁的中国妇女的人口数预测，进而通过中国男女比例变化与年份的关系来预测出相应的0岁到60岁中国男性数目的总和，得到了中国0到60岁人口总和的预测，根据附件一中的资料预测出相应年份的60岁以上的人口数目总和，这样我们就合理的得到了长期人口数目的预测。
通过预测我们得到：在 2010年人口达到13.8亿人，城镇化率达到46.7% 在2020年人口总数变为：14.7亿人，城镇化率达到53.26% ，2035年人数达到高峰，城镇化率达到56.53％，以后各年直到2050年保持基本稳定的状态。
中国人口增长预测(2007a 国家二等奖
6 模型的建立与求解
6.1 人口总数预测模型的建立与求解 6.1.1 相关名词解释 ①出生率=某地某年活产数/同期该地区年平均人口数×1000‰ ②生育率=一年内出生人数/同期育龄妇女人数×1000‰ ③年龄别生育率=一年内某年龄组妇女生育的活产数/同年该年龄组妇女数×1000‰ ④总和生育率=年龄别生育率之和 ⑤死亡率=该地该年死亡人数/该地该年年均人口数×1000‰ 6.1.2 短中期预测模型的建立与求解 6.1.2.1 短中期预测模型的建立 人口增长为非线性趋势的时间序列，且人口的增长现象的倒数逐期增长量的环比发 展速度大致相等时，所以我们考虑使用 Logistic 曲线函数： 1 K + ab t K > 0, a > 0,0 < b ≠ 1
中国人口增长预测
摘要
庞大的人口数量一直是中国国情的最显著特点之一，人口问题也是始终是制约我国 发展的关键因素。要实现可持续发展战略，必须首先解决人口问题。本文结合国内实际 情况从中国的人口数量、人口结构和人口控制考虑，分三个步骤对中国的人口问题进行 探讨。为解决中国的人口问题提供了一个切实可行的参考方案。 第一步，对中国人口数量分短中期和长期进行预测。 人口数短期预测， 我们考虑应用 Logistic 曲线来预测， 对 1979～2005 年全国总人口 数进行拟合并将其与实际值作比较，发现最大误差不超过 0.6%，拟合效果比较好，然 后我们再采用该曲线对以后的 15 年全国人口进行了中短期预测，结果显示到 2010 年我 国总人口将达到 13.502 亿，2020 年将达到 13.919 亿。 人口数长期预测，我们首先仍考虑能否也用 Logistic 曲线来预测长期的人口增长， 经过计算验证发现用 Logistic 曲线来预测长期变化，误差很大，故考虑用 Leslie 模型来 预测长期的人口增长。在进行简单的预测后，发现误差比较大，最小误差达到 6.345%。 在进一步考虑我国的迁移人口对于我国人口的影响，以及我国的男性因素（即考虑总人 口中男女比例不是定值）的基础上，我们对 Leslie 模型做出了很大的改进，使误差降低 到不超过 2%。最后我们用改进的 Leslie 模型对中国的人口进行了长期的预测，根据预 测结果，中国总人口数在 2030 年达到峰值，届时人口总数达到 15.37838 亿；之后人口 总数将有所下降，到 2050 年，人口总数为 14.55 亿。 第二步，对中国人口结构进行预测。我们仍然运用上面得到的数据，我们从人口老 龄化、城市(镇)化、男女性别比三方面分别进行预测分析。 在分析老龄化问题时，把人口中 65 岁及以上老年人认为是老年人，当老年人百分 比超过 7%时，即认为我国进入老龄化阶段。我们预测了 2002 年～2100 年的老年人比 例，预测结果显示我国已经进入老年型，并且老龄化趋势不断加剧，到 2088 年达到峰 值，此时老年人占全国总人口的 28.39%。 在分析城市(镇)化进程时，我们通过城市和城镇的人口之和占全国总人口的比例变 化，来研究我国的城市( 镇)化问题。预测结果显示城市(镇 )化进程随着时间成近似直线 的速度增长，我国居民的整体平均素质也随着提高，到 2050 年城市和城镇的人口将占 全国总人口的 61.15%。 在分析性别比时，我们通过男性总人数与女性总人数的比值来分析，预测结果显示 性别比在 2050 年之前也随着时间呈近似直线增长， 在 2050 年男女性别比达到 1.086951； 到 2073 年达到峰值，为 1.104778972。 第三步， 对中国的人口控制进行研究。 由于本文的预测结果略高于国家的战略目标， 所以需要通过对人口加以控制。本文基于 Leslie 模型建立控制模型，以出生率、人口迁 移、男女出生比例为参数，通过控制这三个参数来控制总的人口数量。 接着我们根据上面的结果，结合中国的实际情况和提出的战略目标，提出了一些较 有参考价值的政策性建议，希望能够在实际中得到应用。 最后，本文还特别对所建的模型的优缺点进行了评价，发现用 Logistic 曲线来预测 中国的中短期人口总数相当准确，但是预测长期变化误差就会变得很大。而我们改进后 的 Leslie 模型预测长期变化就比较准确。之后，本文将模型进行了推广。 关键词： 人口预测 Logistic 曲线 Leslie 模型 人口结构 人口控制
07年全国数学建模优秀论文
l23
N2 (t)) N2m
其中 p, q = 1, 2,3. 分别表示市、镇、乡这三个地区， lqp 是迁移系数，正数时表示迁
入，负数时表示迁出。lqp / Nm 体现了居民从地区 q 迁到地区 p 时对地区 p 人口增长的影
响。 为求解此方程，不失一般性的取 Dt = 1 ，则原微分方程组化为差分方程组：
现在考虑市、镇、乡三个地区的总人口变化规律，假定在一段时期内，这三个地区 各自均处于稳定状态，出生率和死亡率都没有太大变化。然而居民在三个地区间的迁移 会对总人口产生一定的影响。对原 Logistic 模型进行修改，得到多地区条件下的改进模 型：
ì ï ï
dN1 (t dt
)
=
r1 N1 (t )(1 -
题中所给 5 年我国人口 1%调查数据是对人口的抽样调查数据，由于数据的不完备 性，并不能由它来估计当时的全国总人口数。但基于抽样调查的等概率性，可以认为它 所反应的市、镇、乡三个地区的人口比例及男女比例是与实际较为接近的。从《中国人 口统计年鉴 2006》[1]可以得到 2001~2005 年具体的全国总人口数。进而可以得到各部分 人口数。所得数据见表 1。
建立模型对人口发展过程进行定量预测，就是根据现有的人口统计资料和原始数 据，从当前实际的人口状况出发，并对未来的人口发展过程，提出合理的控制要求和假 定，应用科学的方法，预测出未来几年、几十年甚至上百年的人口发展趋势，包括人口 总数、人口的性别、年龄和城乡结构，人口出生、死亡和自然增长率的变化以及在未来 的人口构成中劳力和抚养水平及老化水平等。
模型一需要的原始数据少，操作简单，适合于中短期预测，但长期预测效果不佳； 模型二综合考虑了各因素，对中短期和长期均有较好的预测效果，但所需数据量大，操 作较为复杂。
中国人口发展趋势的预测模型-07年全国大学生数学建模竞赛全国二等奖论文
中国人口发展趋势的预测模型摘要本文从宏观和微观两方面讨论了中国人口发展问题：建立时间序列分析法中的ARMA 模型, 对中国人口总数进行宏观预测；建立了微分方程的模型, 对中国人口的年龄结构以及男女性别比等几个方面进行微观预测。
对人口总数进行宏观预测时，根据处理后的数据的自相关函数和偏相关函数的拖尾性，估计出ARMA的参数p、q，并对估计的参数进行验证和调节，最终确定参数，建立出ARMA(p ,q)模型。
用此模型预测出2020年和2050年的人口分别为138135.3万人和143352.6万人，而且到2050年人口呈现缓慢下降趋势。
对人口组成结构进行微观预测时，引用Shape-Lotka-Mckendrick模型。
根据中国人口发展的特点，并加入影响因素改进原始模型，分别建立了带移民因素和两性具有不同出生率、死亡率的微分方程模型，并讨论得出带移民因素的模型对我国人口结构预测比Shape-Lotka-Mckendrick模型更合理。
在求解的过程中，本文将连续的微分方程离散化，用多项式拟合得到预测数据，求出方程的数值解，得到2006-2010年人口按年龄的结构分布(男女比例分布、生育率、死亡率、迁移率)，并进一步预测出未来人口老龄化指数，其中2020年和2050年的老龄化指数分别为0.511和0.566。
关键字：时间序列微分方程模型连续函数的离散化多项式拟合摘要 (1)一问题的重述与分析 (3)1.1 问题重述 (3)1.2 问题的分析 (3)二模型的基本假设和符号说明 (3)2.1 模型假设 (3)2.2 符号说明 (3)三模型的建立及求解 (4)3.1 模型一 (4)3.2 模型二 (7)3.2.1 只考虑出生率和死亡率的Shape-Lotka-Mckendrick模型]4[ (7)3.2.2 考虑竞争死亡率的模型 (7)3.2.3 考虑两性具有不同出生率和死亡率的人口模型 (8)3.3模型的求解 (8)3.4 对结果的分析 (11)四模型的评价 (11)五参考文献 (12)六附录................................................. 错误！未定义书签。
中国人口增长的预测模型-王子兰、赵军、史彦峰(07年国家一等奖)综述
中国人口增长的预测模型摘要本文根据中国人口增长的特点，首先将其总人口按照区域、性别和年龄进行划分，然后根据2001～2005年人口的历史统计数据和Leslie矩阵原理建立了差分方程组预测模型，解决了中国人口的中短期预测的问题；并利用差分方程的稳定性原理对中国人口长期发展趋势进行了分析。
我们结合中国出生人口性别比持续升高和乡村人口城镇化的人口发展特征，运用Leslie矩阵方法分别从男性和女性人口预测入手，利用影响人口增长的主要因素，包括人口数，人口比率、死亡率（存活率）、生育率、迁移率，建立了差分方程组模型。
该模型首先将人口按区域、性别和年龄进行分组；其次将各区域看作一个系统，各区域内的男性和女性人口再作为一个子系统，以子系统为描述单位；然后结合女性人口总和生育率和生育模式分布函数以及出生婴儿性别比例，对各子系统人口增长的发展变化趋势进行了模型描述，最后运用MATLAB对该模型进行求解。
对 2006～2050年中国总人数进行了预测，模型结果表明：1、全国总人口呈现先增加后减少的变化趋势，并在2032年到达峰值，此时人口数为15.4亿，城镇人口呈逐渐递增的变化趋势，乡村人口则逐渐递减，这与乡村人口城镇化速度不断提高是相关联的；2、全国老龄化系数呈现出不规则的变动，但其总体变化趋势是增加的，这将进一步增加社会负担；3、依赖性指数呈现不断上升的趋势，这与人口老龄化程度不断加强是分不开的。
其中2032年全国总人口的预测值为15.4亿人；性别比为114；市镇乡人口所占比例分别为0.35，0.25和0.4；依赖性指数为0.43。
结合差分方程的特殊性，我们利用特征根法对该差分方程组的稳定性进行了探讨，并利用MATLAB软件求得了相关稳定分布值：稳定年限为2044年，市、镇、乡自然增长率为1.0254、1.0112、0.9685；男性比例为0.54，女性的为0.46；老龄化指数为0.9235。
本文最大的特色在于结合人口发展变化的实际规律，按不同区域、不同性别、不同年龄将总人口预测划分为多个子预测，充分反映了不同区域和不同性别人口增长的发展变化规律，所建立的模型简单可行，而且都是矩阵形式，方便计算的同时也充分利用了2001～2005年人口历年的统计数据，在人口实际预测工作中具有一定的应用价值。
2007高教社杯全国大学生数学建模竞赛(中国人口增长预测模型)II
中国人口增长预测模型的建立与分析摘要针对我国人口发展过程中出现的老龄化进程加快，出生人口性别比持续升高，乡村人口城镇化的新特点，我们基于LESLIE 矩阵，着重考虑城镇与乡村间的人口迁移及女性人口比例变化对我国人口增长的影响，经过两次改进建立了便于计算机求解的差分方程模型，对我国2005年以后45年的人口增长进行了预测。
随后利用时间段参数设置法，对差分方程模型又进行了一次改进。
然后运用等维灰色系统预测法对该差分方程模型的中短期预测进行了检验，同时根据2001年人口基本数据运用此模型对2001年～2005年进行了预测，并用实际数据对预测结果进行了检验。
我们将预测区间分为2006～2020年、2021～2035年、2036～2050年三个区间，以量化短期、中期与长期。
通过调整模型中相关参数及输入条件，定量地分析了男女性别比例、老龄化和乡村人口城镇化对我国人口增长的影响。
预测结果表明，从短期来看，我国的出生性别比变化不明显，将在短期内维持基本不变，老龄化进程在15年内在上升了8个百分点，人口扶养比持续升高，这将加重我国的人口压力，乡村人口城镇化水平进展缓慢；从中期来看，总人口性别比将保持在1与1.1之间，老龄化进程将呈线性增加趋势，乡村人口城镇化水平将持续发展；从长期来看，老龄化进程将在2035到2045年经历老龄人口高峰平台，老龄人口比重在0.3以上，育龄妇女人数持续下降，总人口数将在2023年达到峰值14.05亿。
关键词：LESLIE矩阵，人口预测，性别比例，城镇化，老龄化，灰色系统预测一、问题的重述人口问题是中国社会发展的重要问题，对中国人口的中长期预测有助于政府制定相应的政策保持中国的长治久安。
现需要解决的问题如下：1.主要根据2001～2005年的人口统计数据，对中国人口增长的中短期和长期趋势作出预测，特别要关注老龄化，出生人口性别比及乡村人口城镇化等因素。
2.指出所建模型的优点和不足之处。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2007全国数学建模中国人口增长预测摘要：针对题目所提要求，我们建立了两个中国人口预测模型，分别用于对中国人口的发展趋势做短期和中长期的预测。
为了对中国人口发展做短期的预测，考虑到题目所给的数据资料的不全面，我们由马尔萨斯的人口指数增长模型得到启发，针对中国人口发展的特点，把出生率和死亡率函数这两大对人口增长起主要作用的因素作为建模的关键参数，在附件中没有给出中国近年总人口数的情况下，建立了短期内预测中国人口增长的微分方程模型。
在该模型中，为了得到出生率和死亡率函数这两个重要参数，我们通过分析题目所给数据，提取出有效信息，计算归纳出2001年到2005年的出生率和死亡率，并在此基础上引入灰色模型，用于对出生率和死亡率进行预测，得出了出生率和死亡率关于时间的函数。
较准确的估计出了人口增长的关键参数，使得建立的人口增长短期预测模型不仅符合中国人口的发展特点，而且简单易用，能在未知总人口数的情况下预测人口的相对发展变化，这一优点使得可以方便且准确的用于预测中国人口短期内的发展趋势。
为了对中国人口发展做中长期的预测，考虑到短期模型在预测人口中长期发展中的局限性以及影响人口发展的众多因素的不确定性和它们之间关系的复杂性，我们利用灰色动态模型的特点，从《中国统计年鉴》中查到了中国近年的人口总数（见附表一），把人口数做为灰色量，对原始各年人口序列进行分段建模，对各分段模型进行定性分析比较，根据各阶段宏观指标的相关确定一组适当的权数，进行预测模型的最优组合，以确定最优预测模型，从而建立了中长期预测中国人口增长的灰色动态系统人口模型，对中国人口进行了中长期的预测。
在对中国总人口进行短期和中长期的总体预测后，我们从附件中提取出城、镇、乡三地人口、男女出生性别比、妇女生育率、老龄人口比率等相关数据，对中国未来城、镇、乡三地人口比例、男女出生性别比、妇女生育率、老龄人口比率等影响人口发展的主要因素做趋势预测，从而达到了对中国人口全方位的预测。
关键词：出生率、死亡率、指数增长模型、灰色动态模型、性别比、老龄化、生育率。
一、问题重述中国是一个人口大国，人口问题始终是制约我国发展的关键因素之一。
根据已有数据，运用数学建模的方法，对中国人口做出分析和预测是一个重要问题。
近年来中国的人口发展出现了一些新的特点，例如，老龄化进程加速、出生人口性别比持续升高，以及乡村人口城镇化等因素，这些都影响着中国人口的增长。
2007年初发布的《国家人口发展战略研究报告》(附录1) 还做出了进一步的分析。
关于中国人口问题已有多方面的研究，并积累了大量数据资料。
附录2就是从《中国人口统计年鉴》上收集到的部分数据。
试从中国的实际情况和人口增长的上述特点出发，参考附录2中的相关数据（也可以搜索相关文献和补充新的数据），建立中国人口增长的数学模型，并由此对中国人口增长的中短期和长期趋势做出预测；特别要指出你们模型中的优点与不足之处。
二、基本假设1、把市镇乡看成独立封闭的系统，即不考虑迁入迁出的因素对人口的影响。
2、妇女的总和生育率设为1.8。
3、忽略经济，社会环境，资源等因素对人口的影响。
三、符号说明City(T):附件所给数据中的第T年城市人数Town(T):附件所给数据中的第T年城镇人数Village(T):附件所给数据中的第T年的乡村人数M：i=1,2,3分别表示城市，城镇，乡村男性比率iW：i=1,2,3分别表示城市，城镇，乡村女性比率iMd：i=1,2,3分别表示城市，城镇，乡村男性死亡比率iWd：i=1,2,3分别表示城市，城镇，乡村女性死亡比率iDeads：死亡人数Borns:出生人数i B ：育龄妇女比率(15岁～49岁) i=1,2,3分别表示城市，城镇，乡村育龄妇女比率i Bc ：i=1,2,3分别表示城市，城镇，乡村女性生育率 T ：年份t:年份表达变量b(t):出生率随时间变化的函数 d(t):死亡率随时间变化的函数 N(t):总人口数随时间变化的函数0N ：2001年人口数量（见附录一）四、问题分析与建模及人口预测中国人口增长的数学模型： 4.1 用于短期预测的模型：根据附件所给材料中的数据，计算第T 年的死亡人数及出生人数： 公式为：Deads=City(T)*(M1*Md1+W1*Wd1)+Town(T)*(M2*Md2+W2*Wd2)+Village(T)*(M3*Md3+W3*Wd3)Borns=City(T)*B1*Bc1+Town(T)*B2*Bc2+Village(T)*B3*Bc3计算第T 年的出生率b(t)=Borns/(City(T)+Village(T)+Town(T))死亡率d(t)=Deads/(City(T)+Village(T)+Town(T)) 得如下表格：对于序列X(t)={X(0),X(1),X(2)…X(n)}根据灰色模型中较常用的GM(1,1)模型：()()dX t aX t u dt+= （1） 来预测b(t),d(t)的趋势。
（1）参数a,u 的估计及X(t)预测方程的求解将（1）写成()[()]dX t a X t u dt-+=，将t 换为t+1并与原式做算术平均得： 11{[()(1)]}['()'(1)]22a X t X t u X t X t -+++=++ （2）我们可以用差分DX(t)=X(t+1)-X(t)近似代替（2）式右端得：1{[()(1)]}()2a X t X t u DX t -+++=记A=a u ⎛⎫⎪⎝⎭，用最小二乘法估计出系数矩阵A 。
A=()()1T T B B B C -。
其中，1((0)(1))121((1)(2))12........1((1)())12X X X X B X n X n ⎡⎤-+⎢⎥⎢⎥⎢⎥-+⎢⎥=⎢⎥⎢⎥⎢⎥--+⎢⎥⎣⎦((0),(1)...(1))T C DX DX DX n =-,(DX(t)=X(t+1)-X(t))有了a,u 的估计值之后，我们就可以求解（1）的微分方程。
（1） 式两端同乘以at e 得()()at at at dX t e ae X t e u dt+=，可化为{()}at at de X t e u dx= （3）两边取不定积分得()at e X t =at e udt c +⎰（c 为待定常数）解得X(t)= at u ce a -+，将t=0代入得c=X(0)- ua 。
所以有X(t)预测方程： X(t)=[X(0)- u a ]at e -+ua。
（2）短期预测模型将b(t),d(t) (t=0~4)的值代入上述GM(1,1)模型的X(t)中求解。
<1>对于b(t)={ 0.01740845, 0.016390372, 0.015774741, 0.016341515, 0.014339363}得0.020*******.019297710.0192697510.01840841b B -⎛⎫⎪-⎪= ⎪-⎪-⎝⎭(0.001018078,0.000615631,0.000566774,0.002002152)T b C =--- 1()()(0.21878,0.00515288)T T Tb b b b b A B B B C -==--,即a=-0.21878,u=-0.00515288 得预测方程：0.21878()0.002662660.0235528t b t e =-+ (4)<2>对于d(t)={ 0.00963373, 0.00936573, 0.00911349, 0.00896989, 0.00789073}0.0094997310.0092396110.0090416910.008430311d B -⎛⎫⎪-⎪= ⎪-⎪-⎝⎭(0.000268,0.00025224,0.0001436,0.00107916)T d C =---- 1()()(0.209686,0.0023334)T T T d d d d d A B B B C -==--得预测方程0.209686()0.001494370.0111281t d t e =-+ (5)所以增长率函数为0.2096860.21878()0.001494370.002662660.0124247t t g t e e =-+ 则对总人口数N(t)，有： 0.2096860.21878()()(0.001494370.002662660.0124247)t t dN t g t N e e N dt ==-+（6）且有初值条件N(0)= 0N =12.7627亿人(0N 为2001年的总人口数，由参考文献[]得)解该微分方程（6）得：0.2096860.218780.00712670.012170.01242470.00504330()t t e e t N t N e-++= 此式可用来预测短期内（附件所给数据截至2005年，预测期为2006~2011年）的人口趋势4.2 用于中长期预测的模型：鉴于影响人口发展的众多不确定因素，我们应用灰色动态模型GM(1,1). 为了得到最准确的预测结果，在选取数据年份和年数上，我们进行了认真的分析验证。
数据筛选过程如下：1、我们选取了1970—1980 和1980—1990这两段时间的人口数，带入灰色动态模型中，计算出1995-1999这个时间段的人口数，和查得的资料数据进行比较，得到表格如下：年实际总人口(万人)1970-1980预测值预测误差1980-1990预测值预测误差1965-1980预测值预测误差1995 121121 120866 0.21 122651 1.26 129429 6.86 1996 122389 122345 0.04 124330 1.59 131458 7.41 1997 123626 123825 0.16 126004 1.92 133622 8.09 1998 124810 125309 0.4 127694 2.31 135870 8.86 1999 125909 126901 0.71 129404 2.78 138151 9.72结论1：年份越近，预测越准。
2、我们选取1989-1994 6年和 1988-1995 8年的时间段的人口数，带入灰色动态模型中，计算出1996-1999这个时间段的人口数，和查得的资料数据进行比较，得到表格如下：年实际总人口(万人)1989-1994预测值预测误差1988-1995预测值预测误差1996 122389 122216 0.141 122543 0.126 1997 123626 123337 0.234 123796 0.138 1998 124810 124400 0.329 125052 0.194 1999 125909 126066 0.325 126309 0.318结论2：年份越少，预测越准。